Appendix A. Analysing the Statistical Significance
Due to the small size of the test sets it is hard to draw statistically significant conclusions using a standard approach of reporting the accuracy and an error margin. Therefore we take a Bayesian approach. As we have not seen such analysis often in other papers, it seems that it warrants an additional discussion. Let us illustrate this with an example.
Consider two different cases where two systems,
A and
B, are compared on a test set containing 1000 examples (see
Table A1). In each of the cases, the system
A achieves accuracy
and the system
B achieves accuracy
on the test set. In Case (a) there are 698 examples where both systems are correct and 288 examples where both systems are wrong. In Case (b) there are 500 examples where both systems are correct and 90 examples where both systems are wrong. Although in both cases the accuracies of the compared systems are the same, in Case (a) we can be quite confident that
A performs better than
B, but not so much in Case (b).
Table A1.
The number of examples with the given results. X corresponds to an example where system X gave the correct answer, and —to an example where it gave an incorrect answer.
| Case (a) | Case (b) |
|---|
| | A | | | A | |
| B | 698 | 2 | B | 500 | 200 |
| 12 | 288 | | 210 | 90 |
In Case (a), we have observed 6 times as many examples in the test data where A outperformed B, when compared with the number of examples where B outperformed A (12:2). This is very unlikely to have happened only by chance. We could reasonably expect that on a new example, that is similar to the test examples, the both systems will perform alike (either both will be correct, or both will be wrong). However, if there will be a discrepancy, it is much more likely that the system A will be correct and B—wrong.
In Case (b), the respective numbers (210:200) are relatively much closer to each other, while having the same absolute difference. It is not unreasonable to expect that on another test set that contains different 1000 examples we could obtain results that are the other way around (200:210).
Therefore, any method that analyzes the confidence that A outperforms B based only on their accuracies on the test set will either be underconfident in Case (a), or overconfident in Case (b). Hence, to more precisely compare two systems on a small dataset, it is important to remember that they are tested on the same test set and take into account the correlation of their errors.
Let T be a distribution of examples and let us assume that the test set comprises of examples x∼T drawn from this distribution. Let be the intent given by a system A on an example x and be the real intent of x.
Let
denote the event that
A gives the correct answer on
x:
Then we define the accuracy as the probability that A gives a correct answer on a random example. We estimate the accuracy of a system by evaluating it on a test set. We want to estimate the likelihood that one system is better than another, based on the observed results on the test set.
We say that system
A is better than system
B if
, i.e., if
. Observe that:
Notice that the difference in accuracy only depends on the cases where one system gives a correct answer and the other one – an incorrect, but not on the cases where both systems are correct or both are wrong.
Let and be the probability that A outperforms B, and the probability that B outperforms A, respectively, on a random example. Therefore, is equivalent to .
is an unknown quantity that we want to estimate. Before observing any results, we assume that is uniformly distributed in the interval (i.e., we assume a non-informative prior). That corresponds to ∼, where is the beta distribution. Then, after observing S successes (examples x, where ) and F failures (all other examples x) on the test set, is distributed according to the posterior distribution ∼. We can apply a similar reasoning for .
Let us return to the above-mentioned cases.
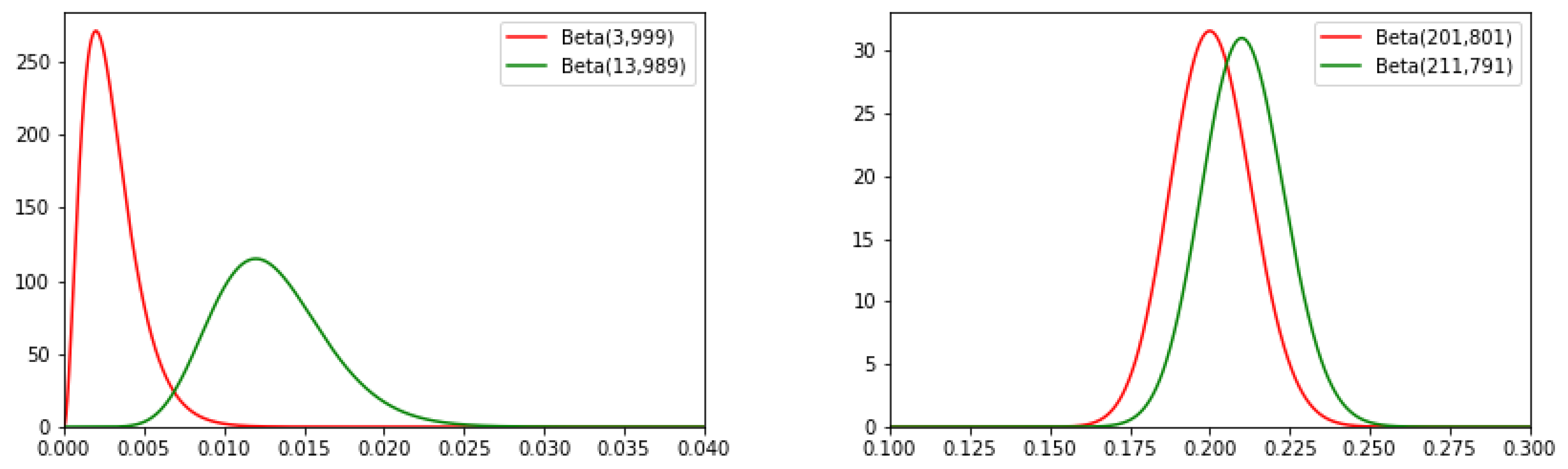
In Case (a), after the observations on the test set: ∼, ∼.
In Case (b): ∼, ∼.
As shown in
Figure A1, the probability density functions overlap more significantly in Case (b) than in Case (a). The probability that
is much larger in Case (a).
Figure A1.
The overlap of probability density functions of the Beta functions corresponding to and in Case (a) (left) and Case (b) (right).
Conveniently, if
∼
,
∼
, and all parameters are integers, then the probability of
can be evaluated in a closed form (
http://www.evanmiller.org/bayesian-ab-testing.html)
where
B is the beta function:
However, this approach is slightly inaccurate, as is not entirely independent of (for example, ). More precisely, on each test example there are three possible outcomes we are interested in: A is correct and B is wrong; B is correct and A ir wrong; and both are correct or both are wrong. Therefore, and (and the probability that both systems perform the same on a test example) are distributed according to the trivariate Dirichlet distribution .
Assuming a non-informative prior , after observing a total of N examples of which and is the number of examples where A outperformed B, and B outperformed A, respectively, the posterior distribution is .
If we consider only in the cases where one system outperforms another, they are distributed according to . The likelihood that corresponds to the probability that a variable p drawn from has .
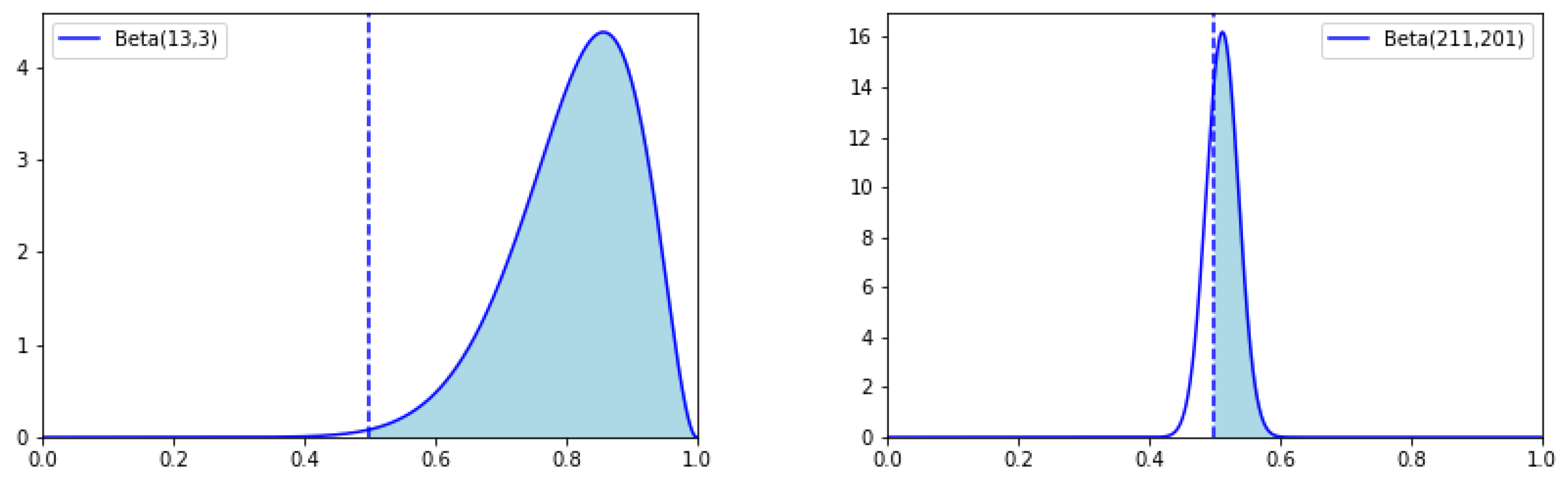
We can calculate that
and
, therefore, confirming our previous intuitive reasoning that in Case (a) we can be much more confident that the system
A is better than
B (see
Figure A2 for illustration).
Figure A2.
The probability distributions corresponding to the Cases (a) (left) and Case (b) (right).
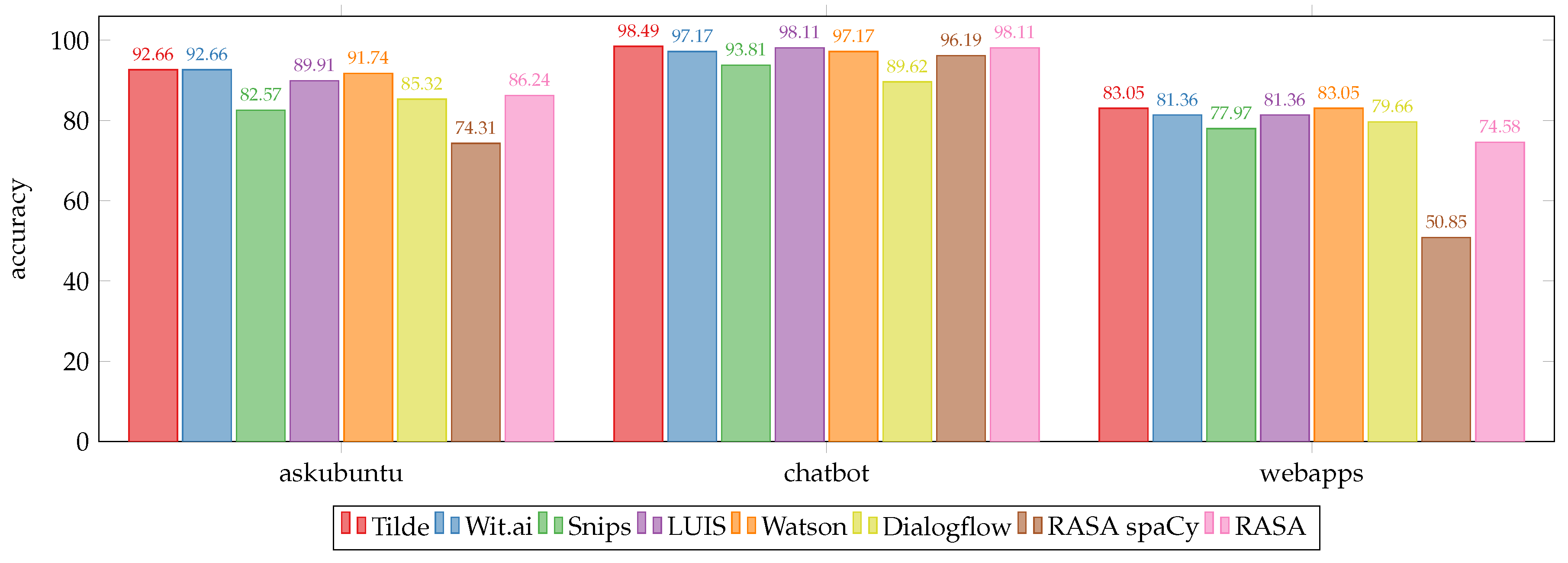
In our paper, the datasets used are quite small. Therefore, we consider the combined results on all 3 datasets and all 5 languages for each of the systems. This results in a total of test examples to compare the systems on.
We report the numbers
and
for all the compared models in
Table A2. They correspond to the probabilities that
given in
Table A3.
Table A2.
and
for pairs of models, where
A is the model corresponding to the row and
B is the model corresponding to the column. Models are listed in the same order as in
Table 6.
| | NN[n] W | NN[n] T | NN W | NN T | CNN W | CNN T | Wit | LUIS |
|---|
| NN[n] W | 0-0 | 28-28 | 26-21 | 28-44 | 37-34 | 16-52 | 29-48 | 76-55 |
| NN[n] T | 28-28 | 0-0 | 39-34 | 8-24 | 44-41 | 13-49 | 33-52 | 73-52 |
| NN W | 21-26 | 34-39 | 0-0 | 27-48 | 28-30 | 17-58 | 28-52 | 78-62 |
| NN T | 44-28 | 24-8 | 48-27 | 0-0 | 52-33 | 17-37 | 39-42 | 77-40 |
| CNN W | 34-37 | 41-44 | 30-28 | 33-52 | 0-0 | 12-51 | 33-55 | 76-58 |
| CNN T | 52-16 | 49-13 | 58-17 | 37-17 | 51-12 | 0-0 | 43-26 | 84-27 |
| Wit | 48-29 | 52-33 | 52-28 | 42-39 | 55-33 | 26-43 | 0-0 | 81-41 |
| LUIS | 55-76 | 52-73 | 62-78 | 40-77 | 58-76 | 27-84 | 41-81 | 0-0 |
Table A3.
Comparison of the models. In row A and column B—the probability (in percent) that model A is better than model B. Probabilities greater than (or smaller than ) are shown in bold.
| | NN[n] W | NN[n] T | NN W | NN T | CNN W | CNN T | Wit | LUIS |
|---|
| NN[n] W | 50.00 | 50.00 | 76.46 | 3.02 | 63.80 | 0.00 | 1.54 | 96.64 |
| NN[n] T | 50.00 | 50.00 | 71.93 | 0.23 | 62.67 | 0.00 | 1.99 | 96.95 |
| NN W | 23.54 | 28.07 | 50.00 | 0.77 | 39.74 | 0.00 | 0.36 | 91.12 |
| NN T | 96.98 | 99.77 | 99.23 | 50.00 | 98.01 | 0.32 | 37.03 | 99.97 |
| CNN W | 36.20 | 37.33 | 60.26 | 1.99 | 50.00 | 0.00 | 0.96 | 93.95 |
| CNN T | 100.00 | 100.00 | 100.00 | 99.68 | 100.00 | 50.00 | 97.93 | 100.00 |
| Wit | 98.46 | 98.01 | 99.64 | 62.97 | 99.04 | 2.07 | 50.00 | 99.99 |
| LUIS | 3.36 | 3.05 | 8.88 | 0.03 | 6.05 | 0.00 | 0.01 | 50.00 |
There are some limitations of applying this approach to our data. The limitations include the following:
When combining the results on all datasets, all test examples are treated equally. However, the test set for webapps is considerably smaller than the test sets for askubuntu and chatbot. Therefore this dataset is underrepresented in the test set, while the other two are overrepresented.
This approach assumes that the test examples are independent of each other. However, this is not true, because, for different languages, the examples are translations of each other.
This approach works for comparing two systems. Increasing the number of different systems, increases the probability that some system will get better results simply by chance.
However, we still believe that this approach gives a reasonable estimate of the confidence that one system outperforms another.