Efficient Ensemble Classification for Multi-Label Data Streams with Concept Drift
Abstract
1. Introduction
- (1)
- To address the issue of concept drift, a change detection mechanism is employed to offer fast reactions to sudden concept changes. Moreover, a periodic weighting mechanism is adopted to cope with the gradual concept drift.
- (2)
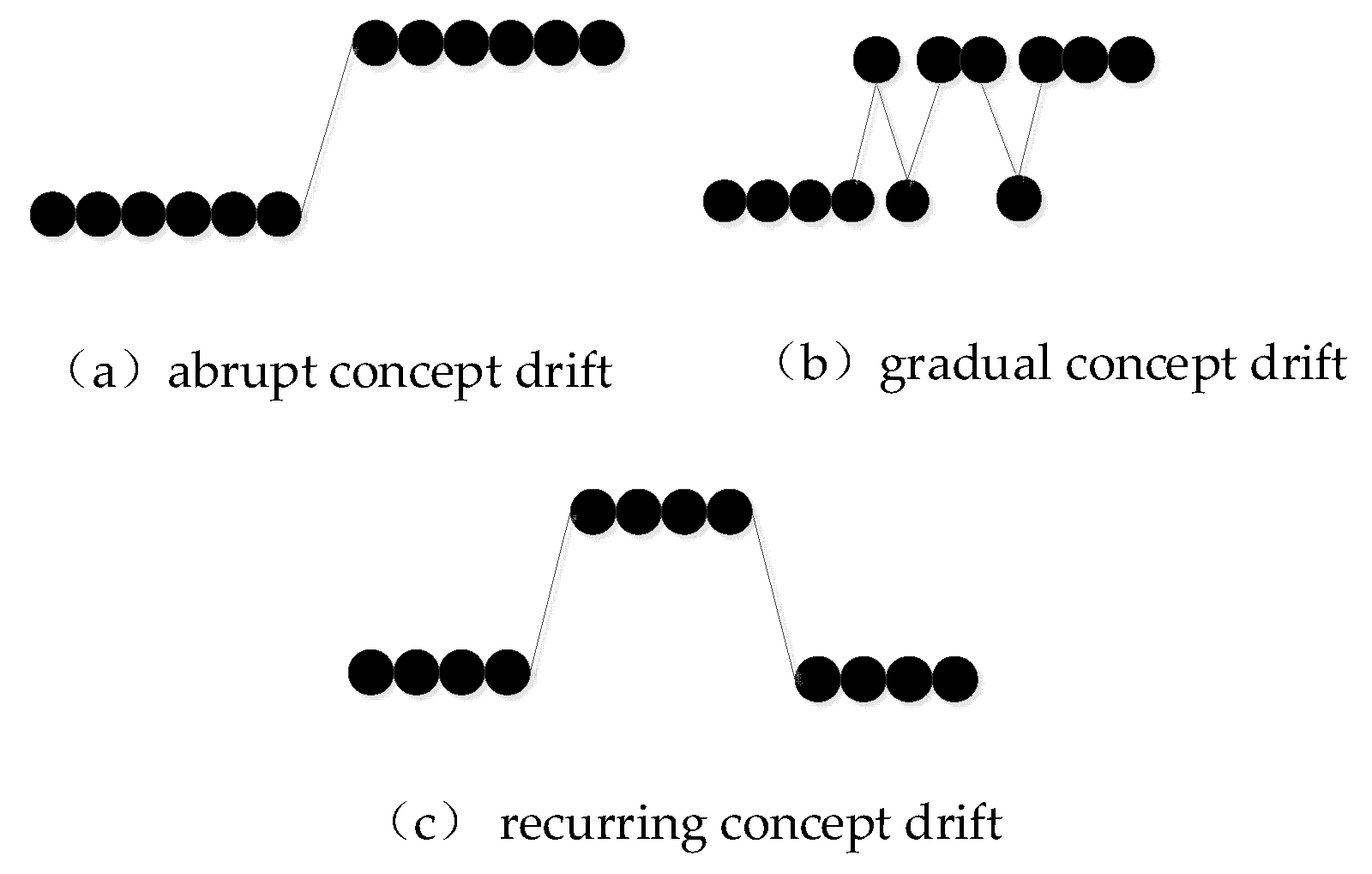
- To deal with the problem of recurrent concept drift, the Jensen–Shannon divergence is selected as a metric to measure the distribution between two consecutive windows, which represent the older and the more recent instances, respectively. Moreover, a novel ensemble classification framework is presented, which maintains a pool of classifiers (each classifier represents one of the existing concepts) and predicts the class of incoming instances using a weighted majority voting rule. Once a change occurs, a new classifier is learned and then a new concept is identified and added to the pool.
- (3)
- A label dependency is taken into account by pruning away some infrequent label combinations to enhance classification performance.
2. Related Work
2.1. Basic Concepts and Notations
2.2. Multi-Label Learning Algorithms
2.3. Classifiers for Multi-Label Data Streams
3. Proposed Method
3.1. Change Detection Based on Jensen–Shannon Divergence
| Algorithm 1 Two-windows-based change detection. |
| input: data streams S, window size n; output: ChangeAlarm; 01: Initialization t = 0; 02: Set reference window W1 = {xt+1, …, xt+n}; 03: Set current window W2 = { xt+n+1, …, xt+2n}; 04: for each instance in S do 05: calculate d(W1, W2) according to Equation (2); 06: calculate ε according to Theorem 2; 07: if d(W1, W2) > ε then 08: t←current time; 09: Report a change alarm at time t; 10: Clear all the windows and goto 02; 11: else if d(W1, W2) = = 0 then 12: alarm a recurring concept; 13: end if 14: else slide W2 by 1 point; 15: end if 16: end for 17: end |
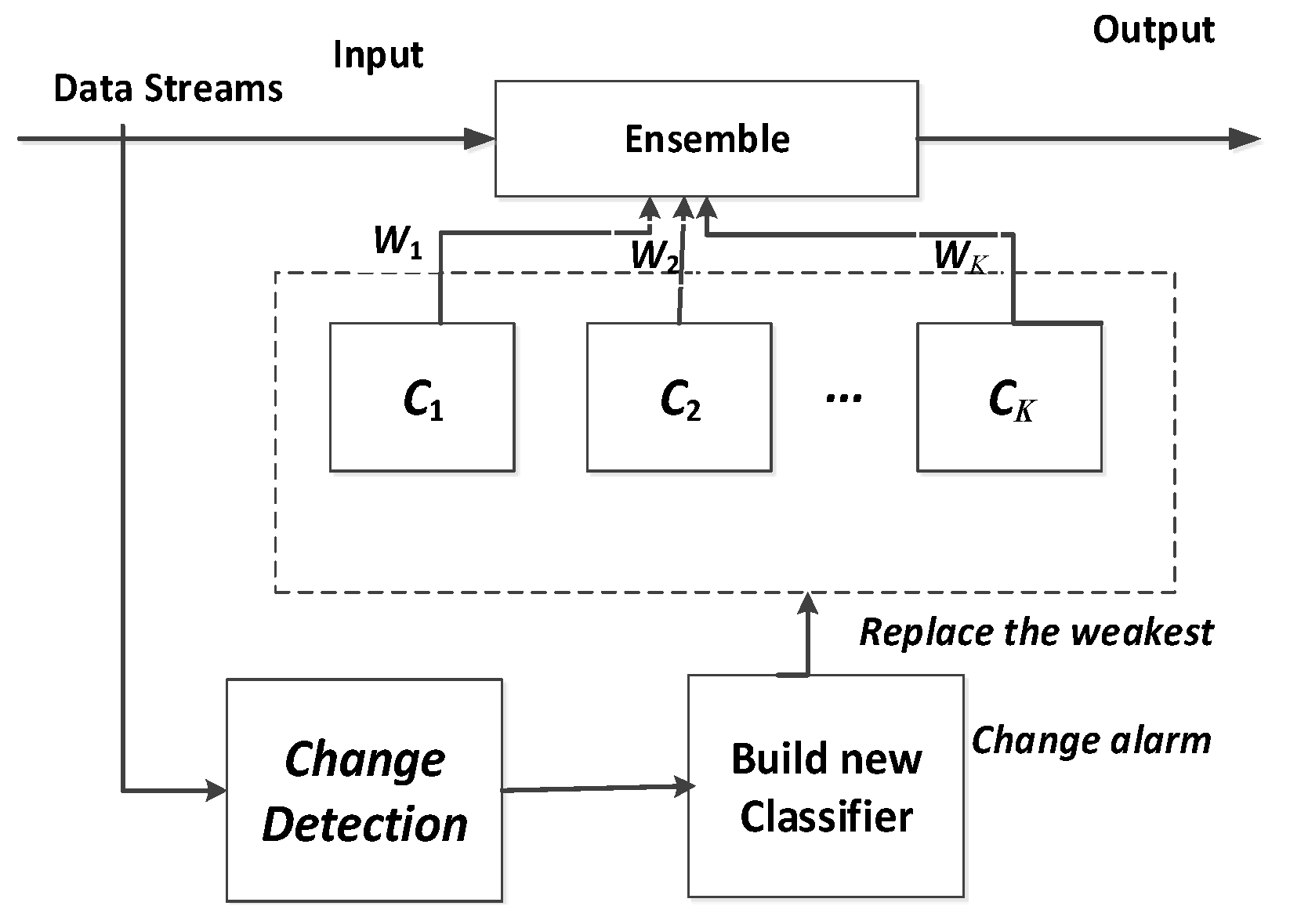
3.2. Ensemble Classifier for Multi-Label Data Streams Using Change Detection
3.2.1. The Framework of Our Method
3.2.2. Exploiting Label Dependency
3.2.3. Weighting Mechanism
| Algorithm 2 MLAW Algorithm. |
| input:S: multi-label data streams, k: number of ensemble members |
| output:E: ensemble of k weighted classifiers |
| 01: begin |
| 02: E←Ø; |
| 03: for all instances xt ∈ S do |
| 04: W ← W ∪ {xt}; |
| 05: if change detected == true then |
| 06: create a new classifier C’; |
| 07: update the weight of all classifiers in ensemble; |
| 08: if |E| < k then E ← E ∪ C’; |
| 09: else prune the worst classifier; |
| 10: else if concept is recurring |
| 11: reuse the classifier in E; |
| 12: end if |
| 13: end if |
| 14: end if |
| 15: end for |
| 16: end |
4. Experiments
4.1. Datasets
4.2. Evaluation Metrics
- (1)
- Hamming loss: The Hamming loss averages the standard 0/1 classification error over the m labels and hence corresponds to the proportion of labels whose relevance is incorrectly predicted. Hamming loss is defined as Equation (6):where ⊕ represents the symmetric difference between two sets. When considering the Hamming loss as the performance measure, the smaller the value, the better the algorithm performance is. For the next measures, greater values indicate better performance.
- (2)
- (3)
- F1 measure can be described as a weighted average of the recall and precision measures. The calculation equation is as follows:
- (4)
- Log-Loss distincts from other measures because it punishes worse errors more harshly, and thus provides a good contrast to other measures [20].where
4.3. Methods and Results
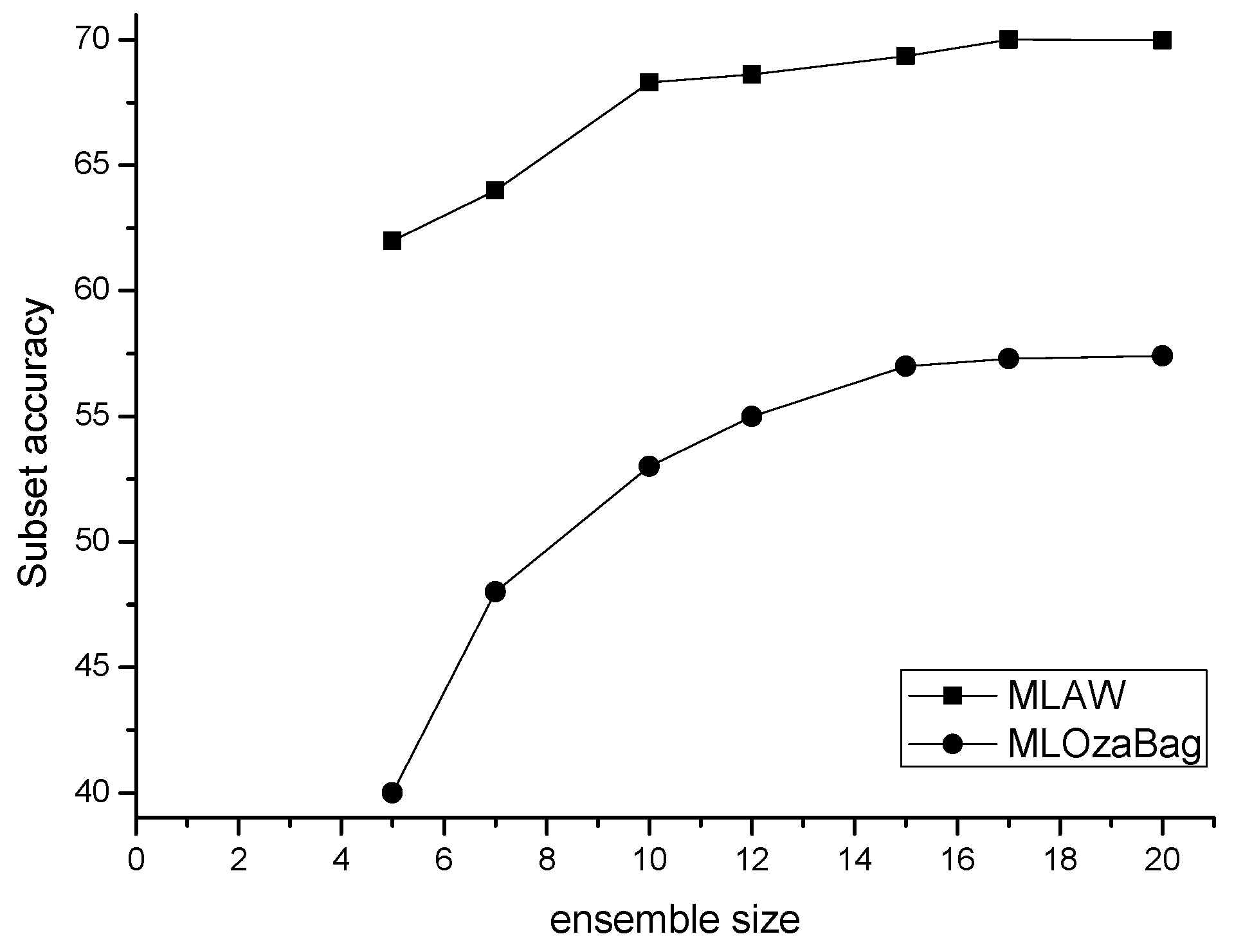
4.3.1. Parameter Sensitiveness
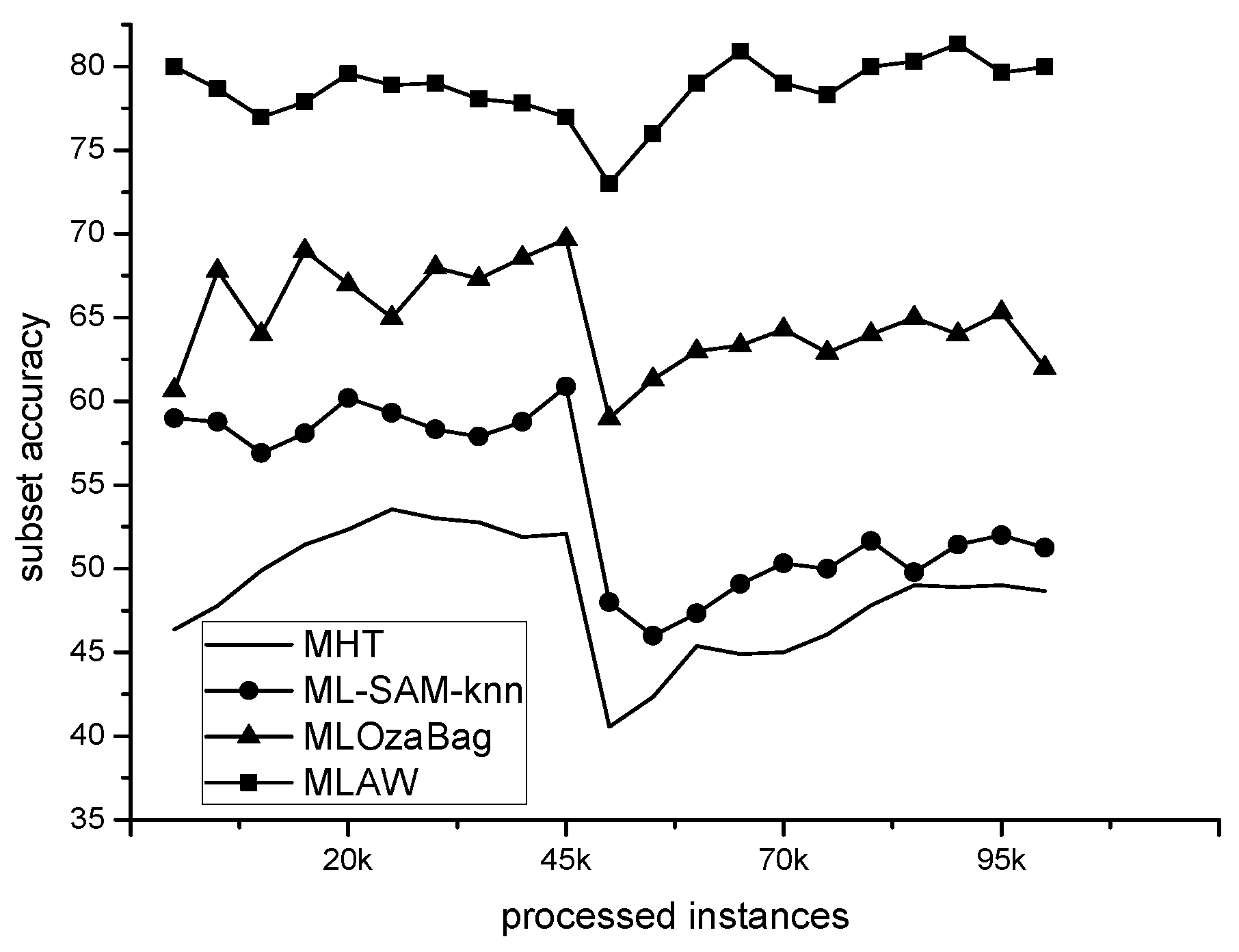
4.3.2. Comparative Performance Study
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cohen, L.; Avrahami-Bakish, G.; Last, M.; Kandel, A.; Kipersztok, O. Real-time data mining of non-stationary data streams from sensor networks. Inf. Fusion 2008, 9, 344–353. [Google Scholar] [CrossRef]
- Bhuiyan, H.; Ashiquzzaman, A.; Juthi, T.I. A Survey of existing E-mail spam filtering methods considering machine learning techniques. Glob. J. Comput. Sci. Technol. 2018, 18, 21–29. [Google Scholar]
- Costa, K.A.; Papa, J.P.; Lisboa, C.O.; Munoz, R.; Albuquerque, V.H.C. Internet of Things: A survey on machine learning-based intrusion detection approaches. Comput. Netw. 2019, 151, 147–157. [Google Scholar] [CrossRef]
- Livieris, I.E.; Kiriakidou, N.; Kanavos, A.; Tampakas, V.; Pintelas, P. On Ensemble SSL Algorithms for Credit Scoring Problem. Informatics 2018, 5, 40. [Google Scholar] [CrossRef]
- Gama, J. Knowledge Discovery from Data Streams; Chapman & Hall/CRC: London, UK, 2010. [Google Scholar]
- Domingos, P.; Hulten, G. Mining high-speed data streams. In Proceedings of the Sixth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD 2000), Boston, MA, USA, 20–23 August 2000; pp. 71–80. [Google Scholar]
- Read, J.; Bifet, A.; Holmes, G.; Pfahringer, B. Scalable and efficient multi-label classification for evolving data streams. Mach. Learn. 2012, 88, 243–272. [Google Scholar] [CrossRef]
- Tsymbal, A. The Problem of Concept Drift: Definitions and Related Work; Technical Report; Department of Computer Science, Trinity College: Dublin, Ireland, 2004. [Google Scholar]
- Gama, J.; Žliobaitė, I.; Bifet, A.; Pechenizkiy, M.; Bouchachia, A. A survey on concept drift adaptation. ACM Comput. Surv. 2014, 46, 231–238. [Google Scholar] [CrossRef]
- Livieris, I.E.; Kanavos, A.; Tampakas, V.; Pintelas, P. A Weighted Voting Ensemble Self-Labeled Algorithm for the Detection of Lung Abnormalities from X-Rays. Algorithms 2019, 12, 64. [Google Scholar] [CrossRef]
- Webb, G.I.; Hyde, R.; Cao, H.; Nguyen, H.L.; Petitjean, F. Characterizing concept drift. Data Mining Knowl. Discov. 2016, 30, 964–994. [Google Scholar] [CrossRef]
- Zhang, M.L.; Zhou, Z.H. A review on multi-label learning algorithms. IEEE Trans. Knowl. Data Eng. 2014, 26, 1819–1837. [Google Scholar] [CrossRef]
- Zhou, Z.H. Ensemble Methods: Foundations and Algorithms; Chapman and Hall/CRC: London, UK, 2012. [Google Scholar]
- Tsoumakas, G.; Katakis, I.; Vlahavas, I. Mining Multi-Label Data. Data Mining and Knowledge Discovery Handbook; Springer: Boston, MA, USA, 2010; pp. 667–685. [Google Scholar]
- Clare, A.; King, R.D. Knowledge discovery in multi-label phenotype data. In Proceedings of the Fifth European Conference on Principles of Data Mining and Knowledge Discovery (PKDD 2001), Freiburg, Germany, 3–5 September 2001; pp. 42–53. [Google Scholar]
- Zhang, M.; Zhou, Z.H. Ml-knn: A lazy learning approach to multi-label learning. Patt. Recogn. 2007, 40, 2038–2048. [Google Scholar] [CrossRef]
- Zhang, M.L.; Zhou, Z.H. Multi-label neural networks with applications to functional genomics and text categorization. IEEE Trans. Knowl. Data Eng. 2006, 18, 1338–1351. [Google Scholar] [CrossRef]
- Schapire, R.E.; Singer, Y. Boostexter: A boosting-based system for text categorization. Mach. Learn. 2000, 39, 135–168. [Google Scholar] [CrossRef]
- Read, J.; Pfahringer, B.; Holmes, G.; Frank, E. Classifier chains for multi-label classification. Mach. Learn. 2011, 85, 333–359. [Google Scholar] [CrossRef]
- Cheng, W.; Hullermeier, E. Combining instance-based learning and logistic regression for multilabel classification. Mach. Learn. 2009, 76, 211–225. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, K. Multi-label learning by exploiting label dependency. In Proceedings of the Sixteenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD 2010), Washington, DC, USA, 25–28 July 2010; pp. 999–1008. [Google Scholar]
- Dembczynski, K.; Waegeman, W.; Cheng, W.; Hüllermeier, E. On label dependence and loss minimization in multi-label classification. Mach. Learn. 2012, 88, 5–45. [Google Scholar] [CrossRef]
- Qu, W.; Zhang, Y.; Zhu, Y.J. Mining multi-label concept-drifting data streams using dynamic classifier ensemble. In Proceedings of the First Asian Conference on Machine Learning (ACML 2009, LNCS 5828), Nanjing, China, 2–4 November 2009; pp. 308–321. [Google Scholar]
- Kong, X.; Yu, P.S. An ensemble-based approach to fast classification of multi-label data streams. In Proceedings of the Seventh International Conference on Collaborative Computing: Networking, Applications and Worksharing (CollaborateCom 2011), Orlando, FL, USA, 15–18 October 2011; pp. 95–104. [Google Scholar]
- Read, J.; Bifet, A.; Pfahringer, B. Efficient Multi-Label Classification for Evolving Data Streams; Technical Report; University of Waikato: Hamilton, New Zealand, 2011. [Google Scholar]
- Xioufis, E.S.; Spiliopoulou, M.; Tsoumakas, G. Dealing with concept drift and class imbalance in multi-label stream classification. In Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence (IJCAI 2011), Barcelona, Spain, 16–22 July 2011; pp. 1583–1588. [Google Scholar]
- Shi, Z.; Wen, Y.; Feng, C. Drift detection for multi-label data streams based on label grouping and entropy. In Proceedings of the Fourteenth International Conference on Data Mining Workshop (ICDM 2014), Shenzhen, China, 14 December 2014; pp. 724–731. [Google Scholar]
- Aljaž, O.; Panov, P.; Džeroski, S. Multi-label classification via multi-target regression on data streams. Mach. Learn. 2017, 106, 745–770. [Google Scholar]
- Roseberry, M.; Cano, A. Multi-label kNN Classifier with Self Adjusting Memory for Drifting Data Streams. In Proceedings of the Second International Workshop on Learning with Imbalanced Domains: Theory and Applications, Dublin, Ireland, 10–14 September 2018; pp. 23–37. [Google Scholar]
- Büyükçakir, A.; Bonab, H.; Can, F. A novel online stacked ensemble for multi-label stream classification. In Proceedings of the 27th ACM International Conference on Information and Knowledge Management, Torino, Italy, 22–26 October 2018; pp. 1063–1072. [Google Scholar]
- Gama, J.; Medas, P.; Castillo, G.; Rodrigues, P.P. Learning with drift detection. In Proceedings of the Seventeenth Brazilian Symposium on Artificial Intelligence (SBIA 2004, LNCS 3171), São Luis, Maranhão, Brazil, 29 September–1 October 2004; pp. 286–295. [Google Scholar]
- Bifet, A.; Gavalda, R. Learning from time-changing data with adaptive windowing. In Proceedings of the Seventh SIAM International Conference on Data Mining (SDM 2007), Bethesda, MD, USA, 20–22 April 2006; pp. 443–448. [Google Scholar]
- Ross, G.J.; Adams, N.M.; Tasoulis, D.K. Exponentially weighted moving average charts for detecting concept drift. Patt. Recogn. Lett. 2012, 33, 191–198. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Statist. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, Z.; Liu, H. Online Ensemble Using Adaptive Windowing for Data Streams with Concept Drift. Int. J. Distrib. Sens. Netw. 2016, 1–9. [Google Scholar] [CrossRef]
- Bifet, A.; Holmes, G.; Kirkby, R.; Pfahringer, B. MOA: Massive online analysis. J. Mach. Learn. Res. 2010, 11, 1601–1604. [Google Scholar] [CrossRef]
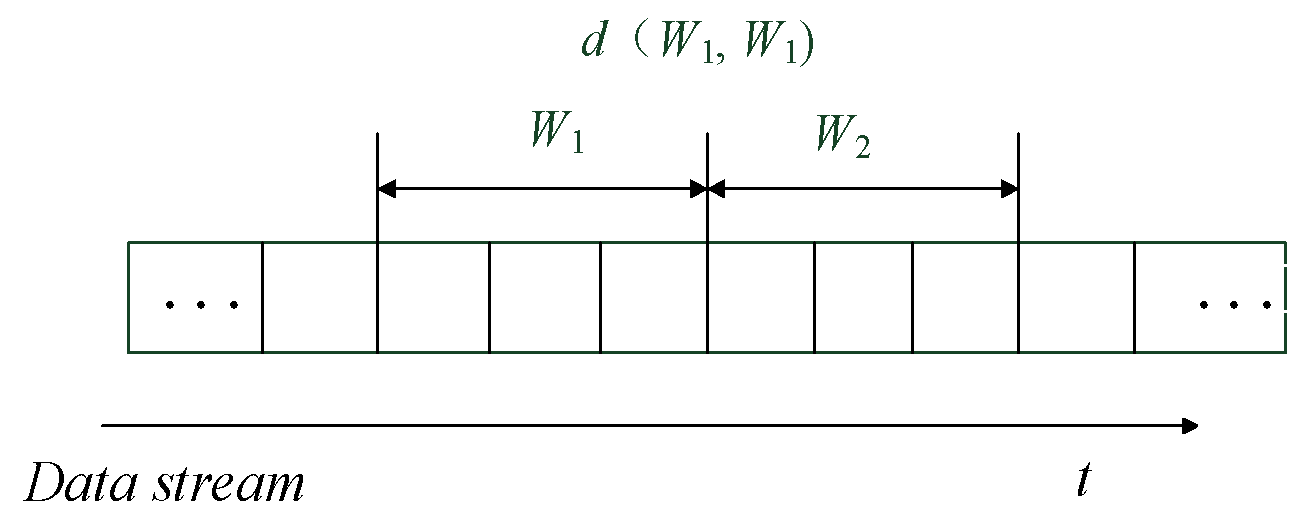
| Dataset | Domain | |D| | |X| | |L| | LC |
|---|---|---|---|---|---|
| TMC2007-500 | Text | 28,596 | 500b | 22 | 2.219 |
| Medical Mill | Video | 43,907 | 120n | 101 | 4.376 |
| IMDB | Image | 95,424 | 1001b | 28 | 1.999 |
| Random Tree | Tree-based | 100,000 | 30b | 6 | 1.8 → 3.0 |
| RBF | RBF-based | 100,000 | 80n | 25 | 1.5 → 3.5 |
| Sizes of Windows | |||||||
|---|---|---|---|---|---|---|---|
| 500 | 750 | 1000 | 1250 | 1500 | 1750 | 2000 | |
| TMC2007-500 | 0.0524 | 0.0498 | 0.0579 | 0.0603 | 0.0599 | 0.0625 | 0.694 |
| Medical Mill | 0.0132 | 0.0126 | 0.0109 | 0.0218 | 0.0179 | 0.0230 | 0.0289 |
| IMDB | 0.0993 | 0.0963 | 0.0986 | 0.0850 | 0.0911 | 0.0979 | 0.0985 |
| Random Tree | 0.2030 | 0.1183 | 0.1035 | 0.1891 | 0.2100 | 0.2301 | 0.2354 |
| RBF | 0.0753 | 0.0698 | 0.0650 | 0.0642 | 0.0653 | 0.0668 | 0.0697 |
| Sizes of Windows | |||||||
|---|---|---|---|---|---|---|---|
| 500 | 750 | 1000 | 1250 | 1500 | 1750 | 2000 | |
| TMC2007-500 | 71.69 | 72.31 | 72.23 | 72.01 | 71.61 | 72.01 | 71.25 |
| Medical Mill | 76.68 | 77.59 | 78.69 | 78.12 | 78.02 | 77.12 | 77.01 |
| IMDB | 81.16 | 81.25 | 81.36 | 81.54 | 80.95 | 81.53 | 82.01 |
| Random Tree | 93.16 | 93.30 | 93.26 | 93.10 | 93.01 | 93.05 | 90.00 |
| RBF | 88.58 | 87.90 | 89.89 | 89.05 | 89.49 | 89.71 | 89.69 |
| ML-SAM-knn | MHT | MLOzaBag | MLAW | |
|---|---|---|---|---|
| TMC2007-500 | 0.0475 (2) | 0.1706 (4) | 0.0521 (3) | 0.0509 (1) |
| Medical Mill | 0.1013 (3) | 0.0665 (2) | 0.0392 (1) | 0.1039 (4) |
| IMDB | 0.0456 (1) | 0.1095 (3) | 0.1304 (4) | 0.0986 (2) |
| Random Tree | 0.0541 (2) | 0.0614 (4) | 0.0589 (3) | 0.0135 (1) |
| RBF | 0.0811 (2) | 0.1400 (4) | 0.0934 (3) | 0.0650 (1) |
| Average Rank | 2.00 | 3.40 | 2.80 | 1.80 |
| ML-SAM-knn | MHT | MLOzBag | MLAW | |
|---|---|---|---|---|
| TMC2007-500 | 0.213 (3) | 0.170 (4) | 0.521 (2) | 0.673 (1) |
| Medical Mill | 0.197 (4) | 0.265 (3) | 0.392 (1) | 0.301 (2) |
| IMDB | 0.154 (2) | 0.195 (1) | 0.134 (3) | 0.129 (4) |
| Random Tree | 0.550 (4) | 0.574 (3) | 0.689 (2) | 0.792 (1) |
| RBF | 0.678 (3) | 0.590 (4) | 0.746 (1) | 0.703 (2) |
| Average Rank | 3.20 | 3.00 | 1.80 | 2.00 |
| ML-SAM-knn | MHT | MLOzBag | MLAW | |
|---|---|---|---|---|
| TMC2007-500 | 7.9 (3) | 7.5 (2) | 8.2 (4) | 6.2 (1) |
| Medical Mill | 15.2 (3) | 9.8 (1) | 19.8 (4) | 13.0 (2) |
| IMDB | 5.3 (1) | 19.0 (4) | 7.1 (3) | 9.3 (2) |
| Random Tree | 6.4 (2) | 17.5 (4) | 7.6 (3) | 3.8 (1) |
| RBF | 3.7 (2) | 5.8 (4) | 4.6 (3) | 2.7 (1) |
| Average Rank | 2.20 | 3.00 | 3.40 | 1.40 |
| ML-SAM-knn | MHT | MLOzBag | MLAW | |
|---|---|---|---|---|
| TMC2007-500 | 0.214 (3) | 0.026 (4) | 0.285 (2) | 0.457 (1) |
| Medical Mill | 0.028 (4) | 0.034 (3) | 0.042 (2) | 0.103 (1) |
| IMDB | 0.105 (1) | 0.021 (4) | 0.087 (2) | 0.016 (4) |
| Random Tree | 0.173 (3) | 0.103 (4) | 0.261 (1) | 0.254 (2) |
| RBF | 0.389 (2) | 0.274 (4) | 0.378 (3) | 0.436 (1) |
| Average Rank | 2.60 | 3.80 | 2.00 | 1.80 |
| ML-SAM-knn | MHT | MLOzBag | MLAW | |
|---|---|---|---|---|
| TMC2007-500 | 8 (1) | 14 (2) | 45 (4) | 36 (3) |
| Medical Mill | 34 (1) | 71 (2) | 457 (4) | 89 (3) |
| IMDB | 285 (1) | 680 (4) | 359 (2) | 543 (3) |
| Random Tree | 38 (3) | 19 (4) | 87 (2) | 9 (1) |
| RBF | 113 (1) | 133 (2) | 201 (4) | 152 (3) |
| Average Rank | 1.40 | 2.40 | 3.20 | 2.60 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Shao, H.; Wang, S. Efficient Ensemble Classification for Multi-Label Data Streams with Concept Drift. Information 2019, 10, 158. https://doi.org/10.3390/info10050158
Sun Y, Shao H, Wang S. Efficient Ensemble Classification for Multi-Label Data Streams with Concept Drift. Information. 2019; 10(5):158. https://doi.org/10.3390/info10050158
Chicago/Turabian StyleSun, Yange, Han Shao, and Shasha Wang. 2019. "Efficient Ensemble Classification for Multi-Label Data Streams with Concept Drift" Information 10, no. 5: 158. https://doi.org/10.3390/info10050158
APA StyleSun, Y., Shao, H., & Wang, S. (2019). Efficient Ensemble Classification for Multi-Label Data Streams with Concept Drift. Information, 10(5), 158. https://doi.org/10.3390/info10050158




