Dynamic Evolution Model of a Collaborative Innovation Network from the Resource Perspective and an Application Considering Different Government Behaviors
Abstract
:1. Introduction
2. Literature Review
- (1)
- Research into the collaborative innovation network. A collaborative innovation network is comprised of enterprises and other subjects (universities, research institutes, governments, intermediaries, etc.) [12]. To increase the chance of success in innovation, subjects are increasingly dependent on complementary knowledge from other subjects. The tendency towards cooperation is becoming increasingly apparent. The network innovation model of multi-subject interaction exhibits a nonlinear effect on system superposition through in-depth cooperation and resource integration [13]. Innovation is no longer a separate activity. Instead, it is a holistic activity that is performed by a complex network. However, when compared with a general innovation network, the collaborative innovation network emphasizes knowledge interaction and technology transfer. It focuses more on the role that is played by the government and institutional environments and it emphasizes the synergistic effect and periodic cooperation [14]. Jianyu’s study showed that knowledge transfer and innovation capacity are the dominant factors in the evolution of the Chinese industry–university-research collaborative innovation [15]. Fernandez-Esquinas et al. explored the knowledge transfer mechanism of a collaborative innovation system and then categorized it into five potential dimensions [16]. Rehm et al. analyzed how those small-and-medium-sized enterprises (SMEs) use knowledge management to address the three challenges in establishing partnerships, integrating partner value, and positioning innovation in the formation and operation of a collaborative innovation network [17]. The competitive drive of a collaborative innovation network is reflected in the information that is received and the feedback speed of the subject’s innovation ability [18]. The complementary advantages and resource integration reflect functional collaboration [19]. Both are the major forms of the collaborative network transfer mechanism.
- (2)
- Research into network evolution. The core of innovation network evolution lies with the complementary resources (funding, technology, and market), member changes, preferential link mechanisms, and periodic cooperation [20]. Changes in the relationships within the main elements of a collaborative innovation network, including enterprises, universities, research institutions, government, and social service systems, inevitably lead to the evolution of network structure. Ivan reported that the cognitive distance, cognitive ability, and communication mechanism of the R&D innovation subject are the main factors in a collaborative network structure. The dynamic cooperation is formed through the selection mechanism of knowledge space [21]. Gay and Dousset also stated that the frequency of the entry and exit for enterprises leads to changes to the network, and that the time and spatial boundaries of network construction change as a result [22]. Correspondingly, changes to network structure can show the evolution process and characteristics. Xia’s research regarding information and communication technology industry showed that, as scale increases, the innovation network has obvious small-world effects and scale-free characteristics [23]. Tatarynowicz determined the different network structure characteristics of industries that are driven or stabilized by technology [24]. With changes in the network, specific characteristics are formed and enterprises show adaptive collaborative behavior. Van’s study found that, as knowledge transfer is a dynamic process, the decisions of an enterprise change according to the new circumstances and knowledge base [25]. This state continues over time, which leads to a continuous interactive iteration between the collaborative innovation behavior and the network structure.
- (3)
- Research into innovation resources. Current findings suggest that the amount of resources that is required for the innovation process is increasing. As a result of certain constraints, the gap between the resources that are owned by a single entity and those needed to conduct innovative activities increases [26]. Therefore, to ensure success in innovation, the key is to have a basis for innovation profitability, including professional manufacturing capabilities, heterogeneous knowledge, channels, and other innovation resources. The “innovation resource” is a new type of resource that consists of a series of shareable material resources and non-material resources, including human resources, knowledge, and technology [27]. The view on the network and resource is that, while providing information and knowledge resources through enterprise network partners, it can address the problem of resource constraints. The integration of resources can lead to benign resources in the business process and reduce the risk of participation identification and information acquisition. Due to the scarcity of resources, enterprises must cooperate with the external resource controllers to access the required resources [28]. The network contains key resources, and a common language or value system in the network that enables enterprises to improve their ability to exchange, integrate, and acquire innovative resources, such as information and knowledge [29,30]. Ritala and Hurmelinna-Laukkanen’s study showed that, if enterprises collaborate with their competitors, their ability to access external resources improves and their resource boundaries expand. This facilitates the spreading, innovation, and application of knowledge [31]. Enterprises can consider integrating similar and complementary resources through cooperation, thereby jointly achieving value creation [32].
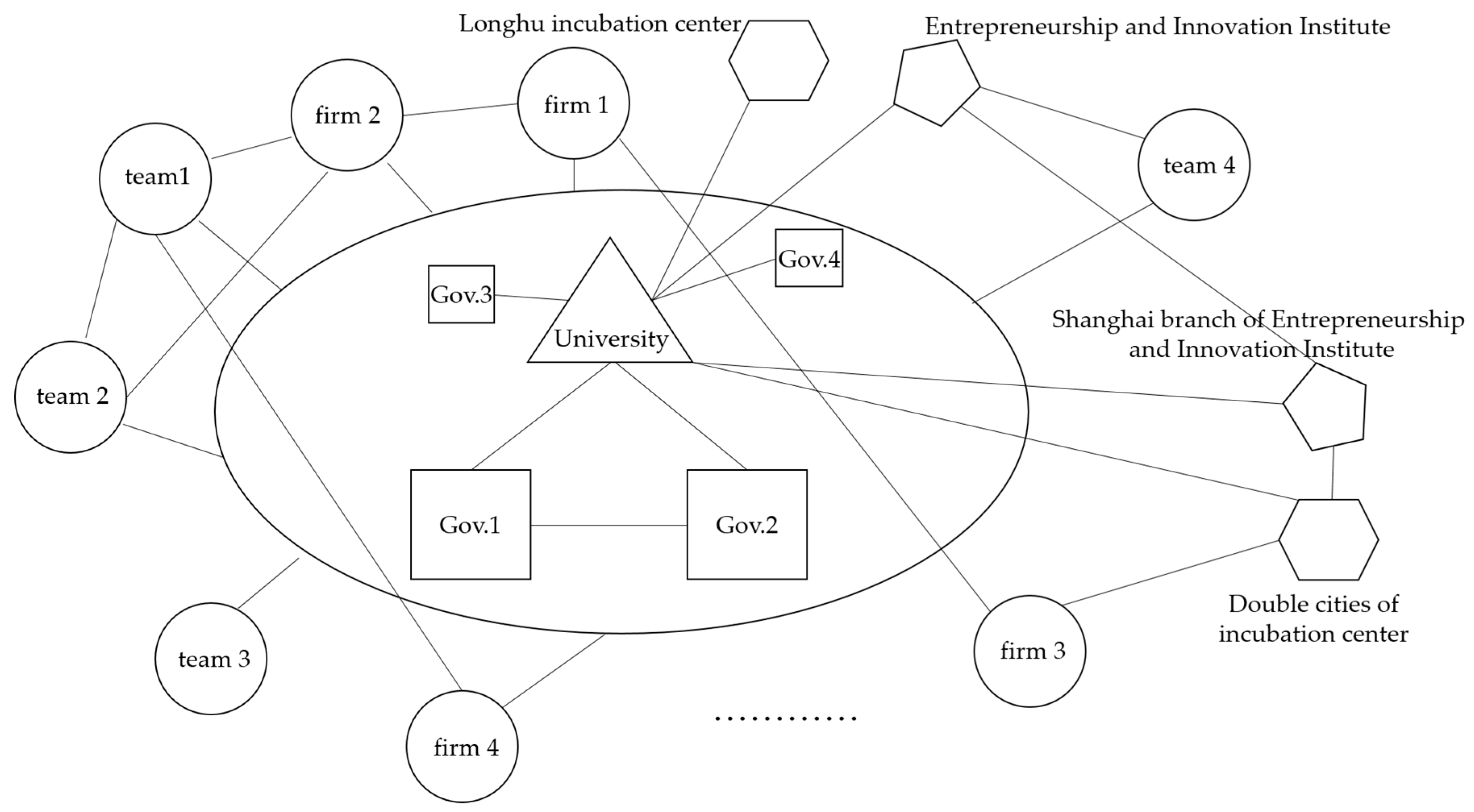
3. Exploratory Case Study
4. Model
4.1. Model Establishment
4.1.1. Resource-Priority Rule
4.1.2. Resource Growth Rule
4.2. Basic Assumptions
4.3. Simulation Steps
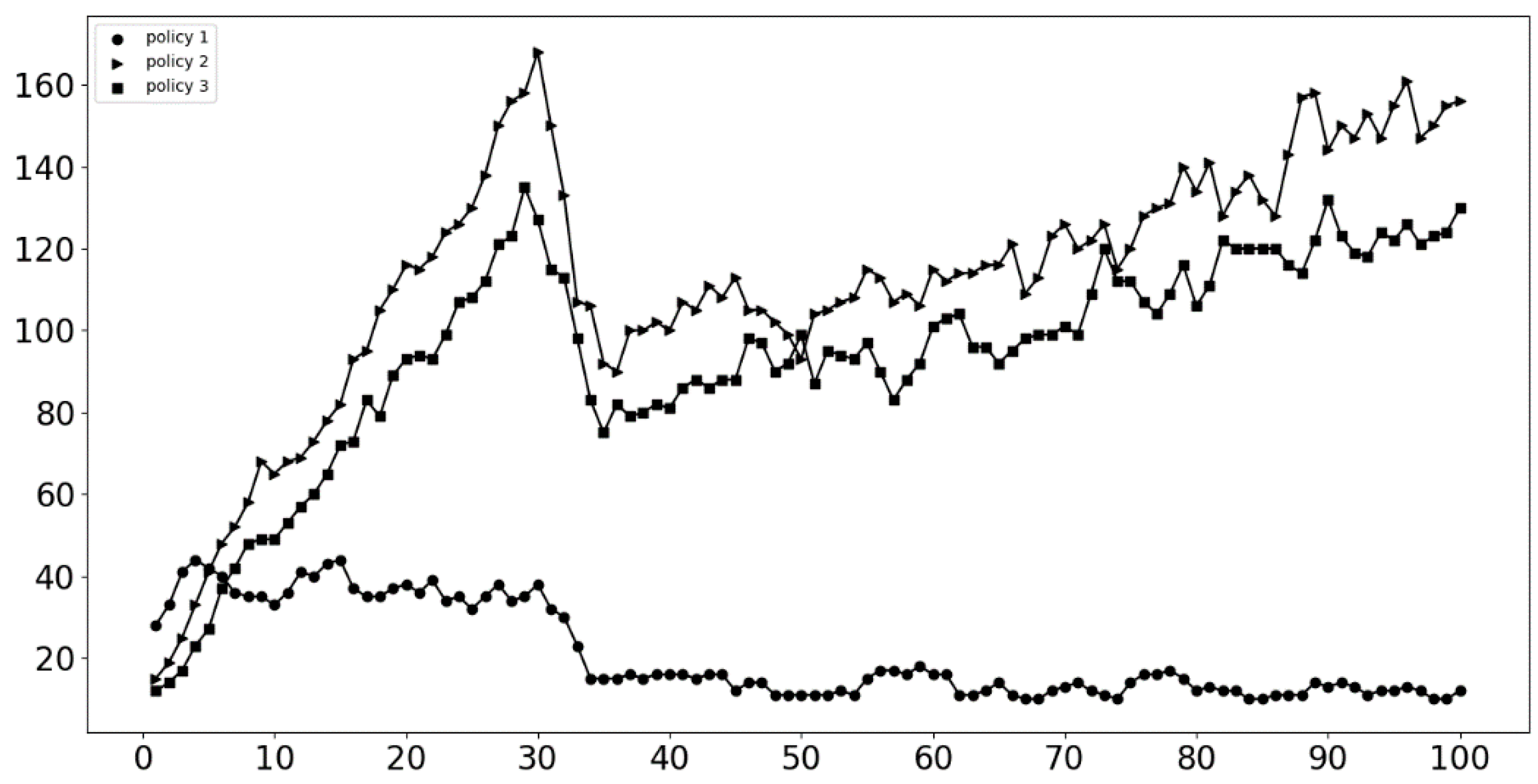
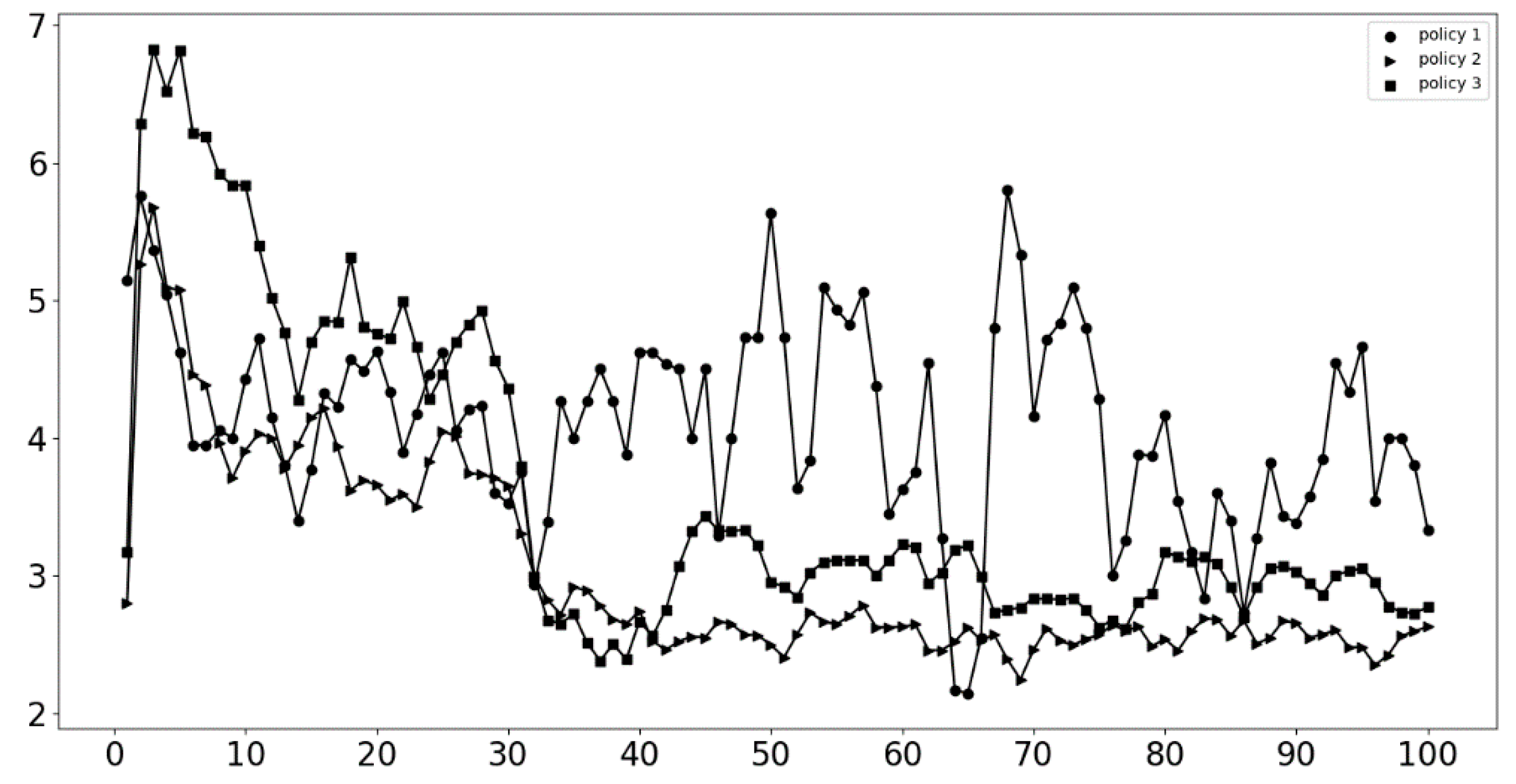
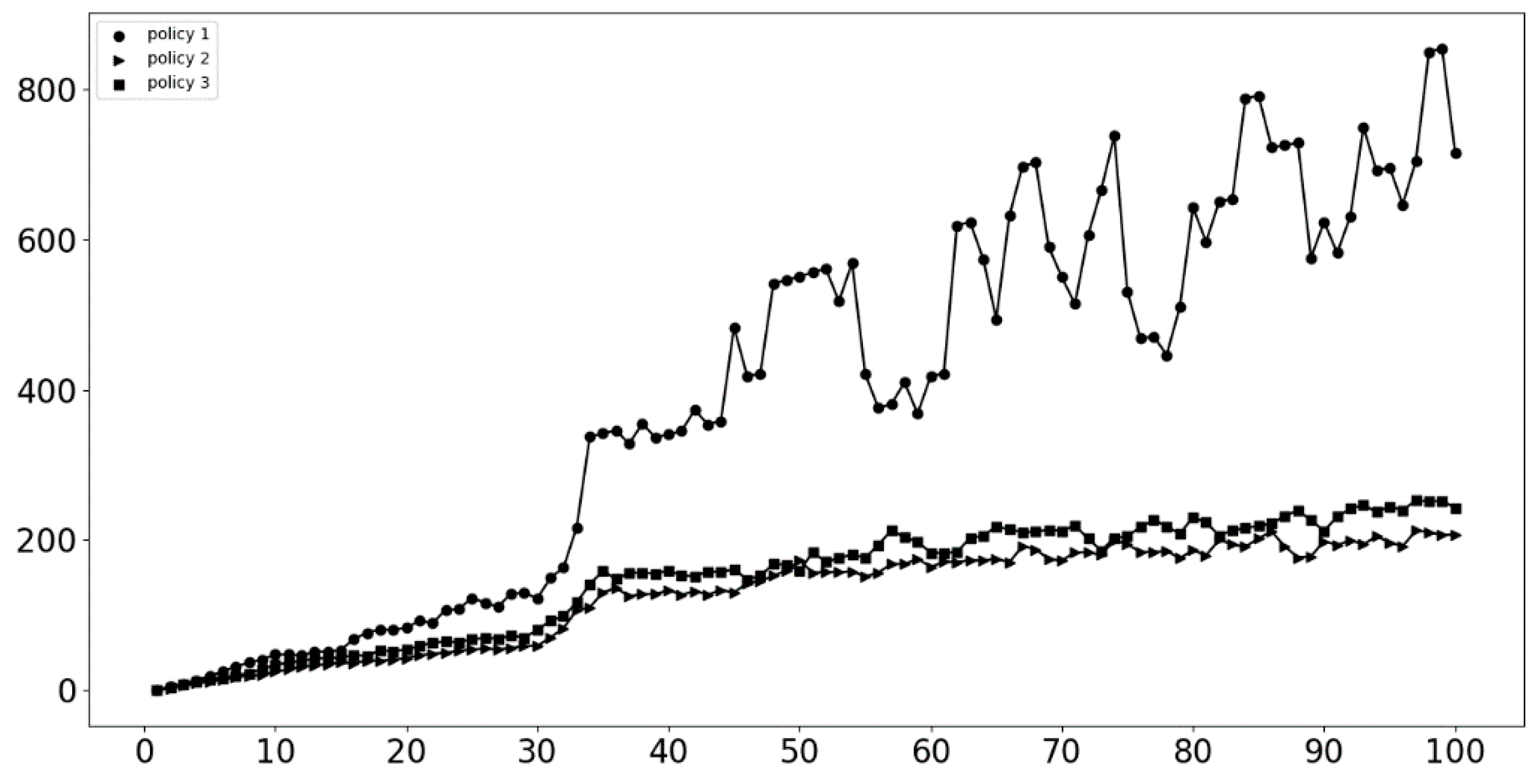
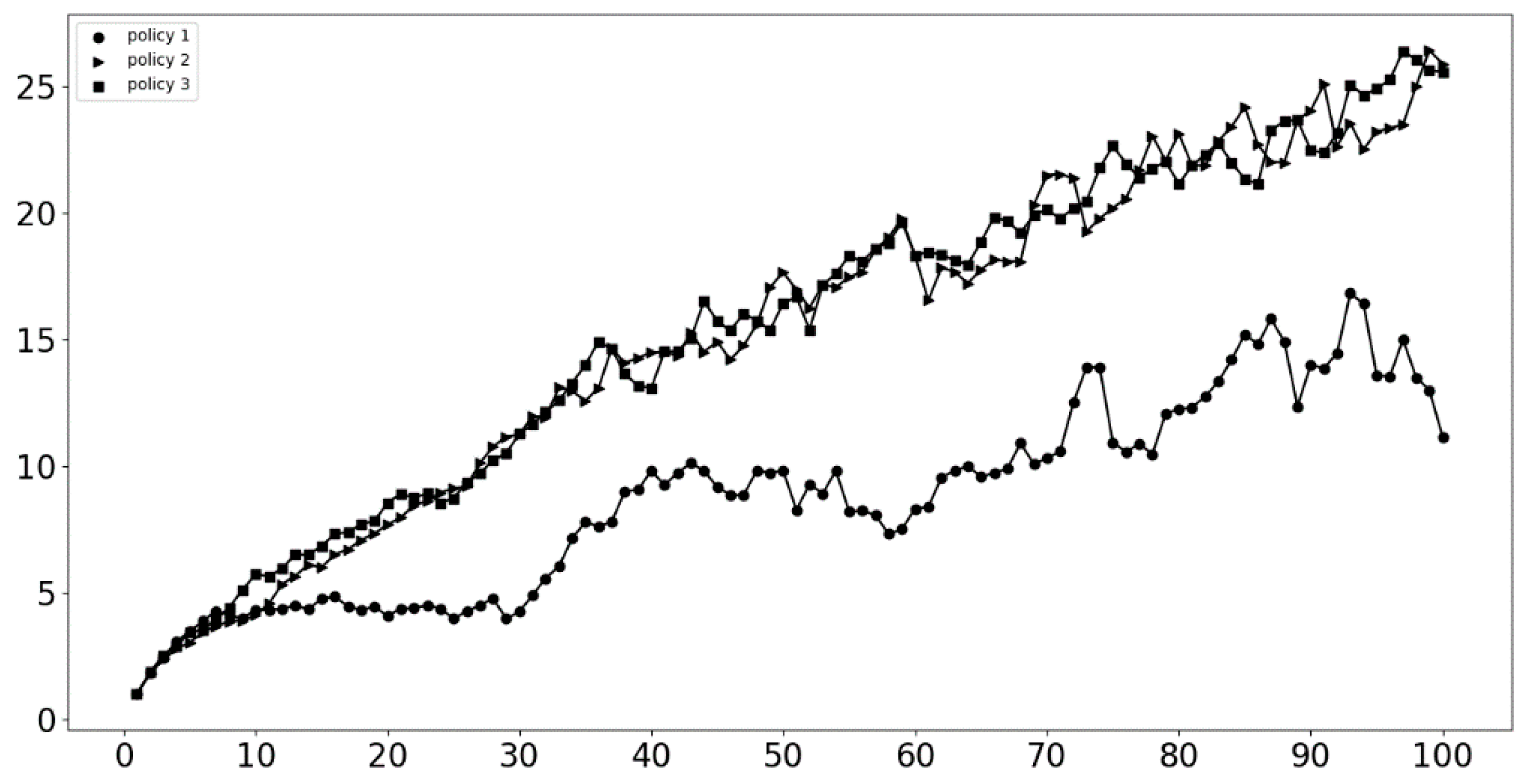
5. Simulation Results and Discussion
5.1. Changes in the Number of Innovative Network Enterprises
5.2. Innovation Network Average Transformation
5.3. Innovation Network Historical Average Transformation
5.4. Innovation Network Average Age Change
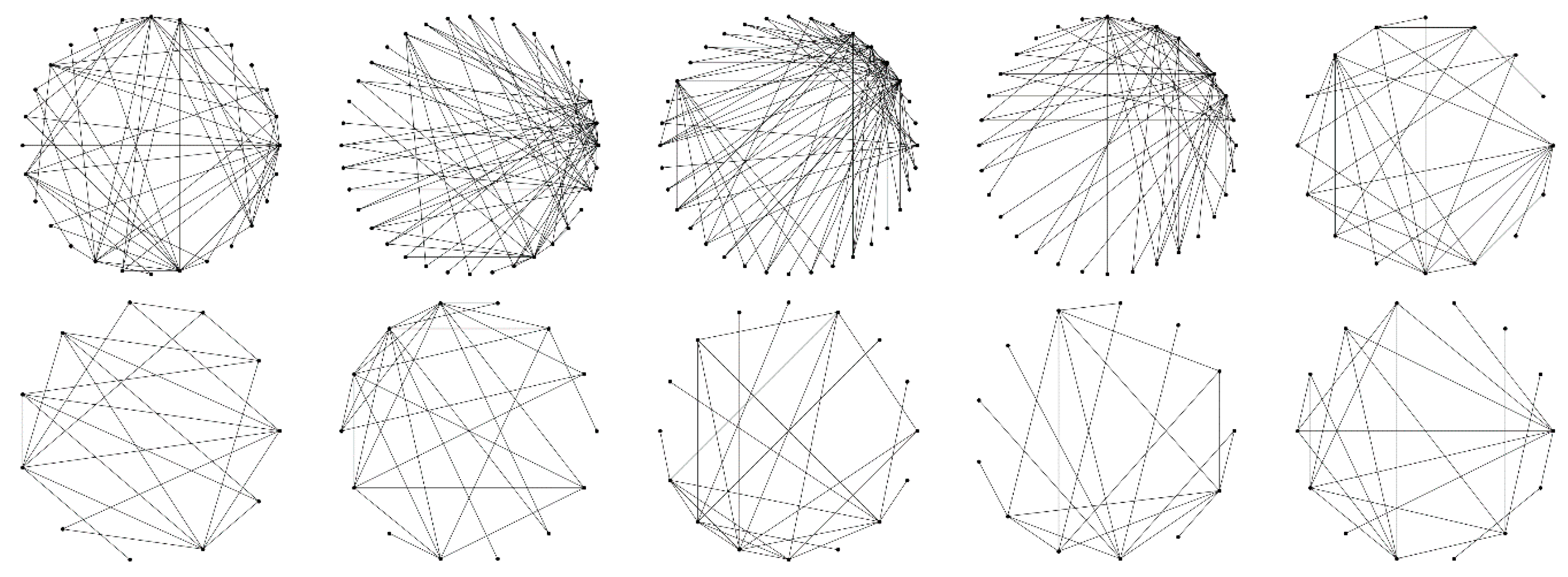
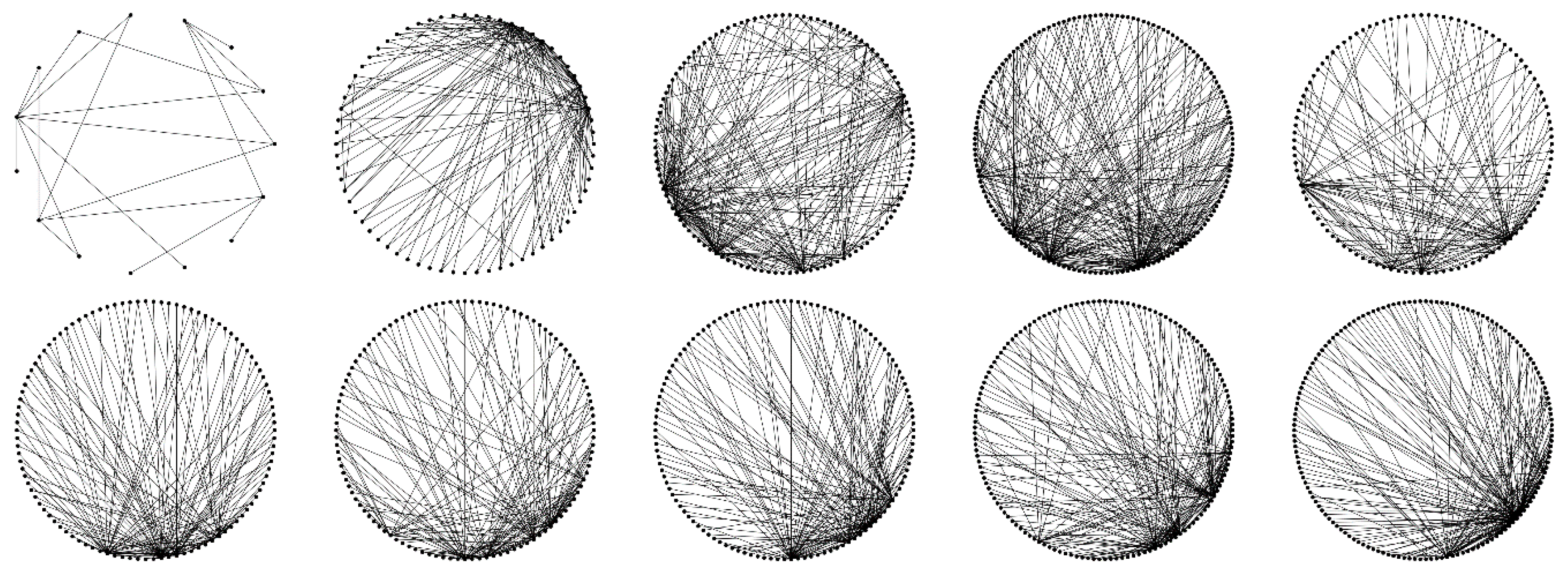
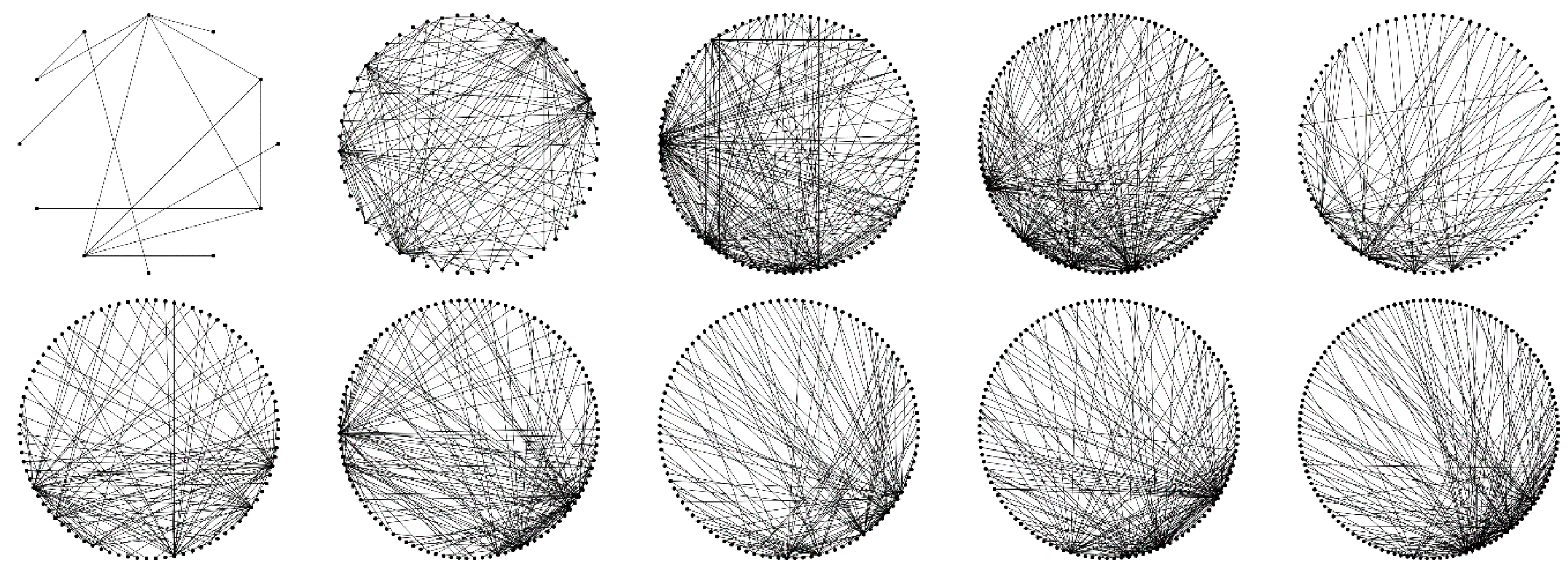
5.5. Evolution of the Innovation Network
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shao, Y.; Zhan, K.; Wu, Y. Breakthrough Technology Innovation:Literature Review and Prospect. Technol. Econ. 2017, 36, 30–37. [Google Scholar]
- Xie, X. Empirical study on synergic innovative networks and innovation performance of SMEs. J. Manag. Sci. China 2010, 13, 51–64. [Google Scholar]
- Peng, J.; Wu, L. On the model and construction of technology collaborative innovation. R&D Manag. 2000, 5, 12–16. [Google Scholar]
- Zobel, A. Benefiting from Open Innovation: A Multidimensional Model of Absorptive Capacity. J. Prod. Innov. Manag. 2017, 34, 269–288. [Google Scholar] [CrossRef]
- Rijnsoever, F.J.V.; Berg, J.V.D.; Koch, J. Smart innovation policy: How network position and project composition affect the diversity of an emerging technology. Res. Policy 2015, 44, 1094–1107. [Google Scholar] [CrossRef]
- Gulati, R.; Nohria, N.; Zaheer, A. Strategic networks. Strateg. Manag. J. 2000, 21, 203–215. [Google Scholar] [CrossRef]
- Gnyawali, D.R.; Madhavan, R. Cooperative networks and competitive dynamics: A structural embeddedness perspective. Acad. Manag. Rev. 2001, 26, 431–445. [Google Scholar] [CrossRef]
- Ye, C.; Yu, X.; Li, W. Empirical analysis on evolution and small world effect of Chinese enterprise-enterprise patent cooperation network: From the perspective of open innovation. Information 2013, 4, 398–410. [Google Scholar] [CrossRef]
- Cao, L. A Comparison Research on Networks Structure of Industrial Cluster. China Ind. Econ. 2008, 8, 143–152. [Google Scholar]
- Powell, W.W.; White, D.R.; Koput, K.W.; Owen-Smith, J. Network dynamics and field evolution: The growth of interorganizational collaboration in the life sciences. Am. J. Sociol. 2005, 110, 1132–1205. [Google Scholar] [CrossRef]
- Cantner, U.; Graf, H. The network of innovators in Jena: An application of social network analysis. Res. Policy 2006, 35, 463–480. [Google Scholar] [CrossRef]
- Hadjimanolis, A.; Dickson, K. Development of national innovation policy in small developing countries: The case of Cyprus. Res. Policy 2001, 30, 805–817. [Google Scholar] [CrossRef]
- Chen, J. Collaborative Innovation and National Research Capacity Building. Stud. Sci. Sci. 2011, 29, 1762–1763. [Google Scholar]
- Xie, X.; Zuo, L. Characteristics of Collaborative Innovation Networks and Innovation Performance of Firms: The Mediating Effect of Knowledge Absorptive Capacity. Nankai Bus. Rev. 2013, 16, 47–56. [Google Scholar]
- Zhao, J.; Wu, G. Evolution of the Chinese Industry-University-Research Collaborative Innovation System. Complexity 2017, 2017, 4215805. [Google Scholar] [CrossRef]
- Fernández-Esquinas, M.; Pinto, H.; Yruela, M.P.; Pereira, T.S. Tracing the flows of knowledge transfer: Latent dimensions and determinants of university–industry interactions in peripheral innovation systems. Technol. Forecast. Soc. Chang. 2016, 113, 266–279. [Google Scholar] [CrossRef]
- Rehm, S.V.; Goel, L.; Junglas, I. Information management for innovation networks—An empirical study on the “who, what and how” in networked innovation. Int. J. Inf. Manag. 2016, 36, 348–359. [Google Scholar] [CrossRef]
- Ozkaya, H.E.; Droge, C.; Hult, G.T.M.; Calantone, R.; Ozkaya, E. Market orientation, knowledge competence, and innovation. Int. J. Res. Mark. 2015, 32, 309–318. [Google Scholar] [CrossRef]
- Chung, H.F.L. Market orientation, guanxi, and business performance. Ind. Mark. Manag. 2011, 40, 522–533. [Google Scholar] [CrossRef]
- Dyer, J.H.; Nobeoka, K. Creating and managing a high-performance knowledge-sharing network: The Toyota case. Strateg. Manag. J. 2000, 21, 345–367. [Google Scholar] [CrossRef]
- Savin, I.; Egbetokun, A. Emergence of innovation networks from R&D cooperation with endogenous absorptive capacity. J. Econ. Dyn. Control 2016, 64, 82–103. [Google Scholar]
- Gay, B.; Dousset, B. Innovation and network structural dynamics: Study of the alliance network of a major sector of the biotechnology industry. Res. Policy 2005, 34, 1457–1475. [Google Scholar] [CrossRef]
- Gao, X.; Chen, K. The complex network analysis of the structure evolution of collaborative innovation networks. Sci. Res. Manag. 2015, 36, 28–36. [Google Scholar]
- Tatarynowicz, A.; Sytch, M.; Gulati, R. Environmental demands and the emergence of social structure: Technological dynamism and interorganizational network forms. Adm. Sci. Q. 2016, 61, 52–86. [Google Scholar] [CrossRef]
- Van Burg, E.; Berends, H.; Van Raaij, E.M. Framing and interorganizational knowledge transfer: A process study of collaborative innovation in the aircraft industry. J. Manag. Stud. 2014, 51, 349–378. [Google Scholar] [CrossRef]
- Li, W. Relationship between innovation and market structure in industrial evolution—A Chinese interpretation of Schumpeterrian hypothesis. Sci. Res. Manag. 2009, 30, 39–47. [Google Scholar]
- Zhang, Y.; Li, C. Research on the Innovation Network Structural Impact on Innovation Resource Utilization. Sci. Manag. 2010, 1, 17. [Google Scholar]
- Miotti, L.; Sachwald, F. Co-operative R&D: Why and with whom? An integrated framework of analysis. Res. Policy 2003, 32, 1481–1499. [Google Scholar]
- Pfeffer, J.; Gerald, R.S. The External Control of Organizations: A Resource Dependence Perspective; Stanford University Press: Stanford, CA, USA, 2003. [Google Scholar]
- Chen, J.; Wu, B. The impact of open-ness on the acquisition of external key resources by enterprises with open innovation. Sci. Res. Manag. 2012, 33, 10–22. [Google Scholar]
- Ritala, P.; Hurmelinna-Laukkanen, P. Incremental and radical innovation in coopetition—The role of absorptive capacity and appropriability. J. Prod. Innov. Manag. 2013, 30, 154–169. [Google Scholar] [CrossRef]
- Cai, L.; Liu, Q. The Empirical Research on the Relationship between Shared Resources and Innovation Performance of Technology-Based Firm in Entrepreneurial Cluster. J. Ind. Eng. Eng. Manag. 2008, 22, 19–23. [Google Scholar]
- Brondoni, S.M. Innovation and Imitation: Corporate Strategies for Global Competition. Symph. Emerg. Issues Manag. 2012, 10–24. [Google Scholar] [CrossRef]
- Cheng, C.C.J.; Chen, J.S. Breakthrough innovation: The roles of dynamic innovation capabilities and open innovation activities. J. Bus. Ind. Mark. 2013, 28, 444–454. [Google Scholar] [CrossRef]
- Li Keqiang: Speech at the 8th Summer Davos Forum. Available online: http://www.gov.cn/guowuyuan/2014-09/11/content_2748703.htm (accessed on 11 April 2019).
- Government Working Report. Available online: http://www.gov.cn/premier/2019-03/16/content_5374314.htm (accessed on 11 April 2019).
- Promote “Internet + Innovation and Entrepreneurship” with the “One School, One Belt” Strategy. Available online: https://news.uestc.edu.cn/?n=UestcNews.Front.Document.ArticlePage&Id=50603 (accessed on 11 April 2019).
- Electronic Science and Technology University and Chengdu High-tech Zone Signed a Contract to Jointly Build a National Independent Innovation Demonstration Zone and a “One School, One Belt” Plan. Available online: https://news.uestc.edu.cn/?n=UestcNews.Front.Document.ArticlePage&Id=51408 (accessed on 11 April 2019).
- Fang, W.; Wang, L. Collaborative innovation network:Current situation and future trend. Sci. Res. Manag. 2018, 39, 30–41. [Google Scholar]
- Barabási, A.L.; Albert, R.; Jeong, H. Mean-field theory for scale-free random networks. Phys. A Stat. Mech. Its Appl. 1999, 272, 173–187. [Google Scholar] [CrossRef]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47. [Google Scholar] [CrossRef]
- Li, X.; Chen, G. A local-world evolving network model. Phys. A Stat. Mech. Its Appl. 2003, 328, 274–286. [Google Scholar] [CrossRef]
- Fu, R. Anaiysis of the Stability of Resource-Based Business Networking. J. Manag. China 2005, 2, 173–187. [Google Scholar]
- Wei, L.H. Analysis of Local Government Behavior in the Process of Industrial Cluster Upgrade—Based on the Perspective of Local Governance. Theory Mon. 2010, 7, 74–77. [Google Scholar]
- Brenner, T.; Schlump, C. Policy measures and their effects in the different phases of the cluster life cycle. Reg. Stud. 2011, 45, 1363–1386. [Google Scholar] [CrossRef]
- Depret, M.H.; Hamdouch, A. Multiscalar Clusters and Networks as the Foundations of Innovation Dynamics in the Biopharmaceutical Industry. Soc. Sci. Electron. Publ. 2010, 33, 227–268. [Google Scholar] [CrossRef]
- Sotarauta, M. Policy learning and the ‘cluster-flavoured innovation policy’ in Finland. Environ. Plan. C Gov. Policy 2012, 30, 780–795. [Google Scholar] [CrossRef]
- Stevenson, L.; Anders, L. Patterns and trends in entrepreneurship/SME. In Policy and Practice in Ten Economies; Elanders Gotab: Vällingby, Sweden, 2001; Volume 3. [Google Scholar]
- Hite, J.M.; Hesterly, W.S. The evolution of firm networks: From emergence to early growth of the firm. Strateg. Manag. J. 2001, 22, 275–286. [Google Scholar] [CrossRef]
- Yi, J.; Meng, W.-D. The phasic study on the evolvement of the region innovation network. Sci. Res. Manag. 2005, 5, 3. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Shao, Y.; Feng, L. Dynamic Evolution Model of a Collaborative Innovation Network from the Resource Perspective and an Application Considering Different Government Behaviors. Information 2019, 10, 138. https://doi.org/10.3390/info10040138
Wu Z, Shao Y, Feng L. Dynamic Evolution Model of a Collaborative Innovation Network from the Resource Perspective and an Application Considering Different Government Behaviors. Information. 2019; 10(4):138. https://doi.org/10.3390/info10040138
Chicago/Turabian StyleWu, Zhaoyang, Yunfei Shao, and Lu Feng. 2019. "Dynamic Evolution Model of a Collaborative Innovation Network from the Resource Perspective and an Application Considering Different Government Behaviors" Information 10, no. 4: 138. https://doi.org/10.3390/info10040138
APA StyleWu, Z., Shao, Y., & Feng, L. (2019). Dynamic Evolution Model of a Collaborative Innovation Network from the Resource Perspective and an Application Considering Different Government Behaviors. Information, 10(4), 138. https://doi.org/10.3390/info10040138



