1. Introduction
Recently, due to the rapid development of wireless communication technology, the demand for data rate, service quality and number of users has multiplied and research on large-scale MIMO technology, a key technology in wireless communication technology, has been deepened, both domestically and overseas [
1]. In a massive MIMO system, the RZF precoding algorithm can obtain approximately optimal linear precoding performance by increasing the number of antennas of the base station (BS). However, the complexity of hardware platform implementation and signal processing will also increase accordingly. When the ratio of the number of BS antennas to the number of user antennas is greater than 10, although the number of BS transmit antennas is very large, the complexity of RZF precoding mainly focuses on the inverse budget of the matrix which is related to the number of users [
2]. The dimension of inverse matrix in the massive MIMO system is also large relative to the conventional MIMO system. The direct matrix inversion incurs a very high computational complexity in massive MIMO systems when the large-dimensional matrix inversion needs to be performed for RZF precoding.
The idea of estimating computation has been applied in many ways. For example, the articles in [
3,
4,
5,
6] use the coprime array interpolation to estimate the related source parameters, direction-of-arrival and so on. Recently, related research work in large-scale MIMO systems is also very plentiful. The authors of [
7] present a wide choice of low-complexity sub-optimal rules about channel-aware decision fusion over MIMO channels which efficiently exploit large-array benefits. In [
8], a diagonal band Newton iteration (DBNI) method is proposed. The contribution of [
9] is that solve the decentralized multi-sensor estimation problem over uniform power allocation in massive MIMO mobile communications. Channel-aware (through pilot-based channel estimation) decision fusion over massive MIMO has been analyzed in [
10].
The exact inverse of the matrix methods in common include the QR decomposition based on the Gram–Schmidt method [
11,
12] and the Gauss–Jordan elimination method [
13], but they need lots of calculations. In order to reduce the complexity of the high dimensional inverse matrix, many scholars have started research. The underlying idea of [
14] is to carry out an approximate matrix inversion using a small number of Neumann-series terms and on this basis proposes a novel VLSI architecture. A low-complexity precoding scheme based on matrix polynomial for downlink large-scale MIMO systems is presented in [
15]. The RZF precoding algorithms based on the truncated Neumann series expansion [
16] and the truncated Taylor series expansion [
17] are the most common method of truncation. However, these algorithms do not consider the influence of the corresponding order factor in the expansion series, and the convergence is not good.
In this paper, the Kapteyn series polynomial is used to represent the inverse matrix of high dimensional matrix in RZF precoding algorithm. That is, we use the Kapteyn series to precode the signal. The inverse matrix is expanded and truncated by the Kapteyn series, taking the N terms before the polynomial. The constraint conditions for the series convergence are established and the value of N and corresponding order factor are studied. When the total transmitted power is constant and the channel state information is known, the correspondence between the signal-to-interference-noise ratio (SINR) and the polynomial coefficients is established. In the case of the fixed N value, the optimal solution of polynomial coefficient is sought to optimize SINR, so as to obtain the low-complexity pre-coding matrix.
The rest of this paper is organized as follows.
Section 2 describes the system model.
Section 3 proposes an improved RZF precoding based on the truncated Kapteyn series expansion to approximate the inverse matrix in RZF precoding and optimizes the expansion coefficients. Then the computational complexity of the proposed algorithm is calculated and compared with the one of the traditional RZF precoding. Simulation results of the proposed algorithm are presented to compare the channel performance to the ones of the RZF precoding with other truncated series expansions in
Section 4.
Section 5 concludes this paper.
We summarize the following notations used throughout the paper to facilitate the reader. Specifically, the boldface uppercase letters denote the matrices and the boldface lowercase letters represent the column vectors. In addition, , and are the Hermitian transpose, transpose and trace of the matrix, respectively. Moreover, is the conjugate operator, represents the norm of the matrix, respectively. Finally, denotes the circular symmetric complex Gaussian distribution with mean vector and covariance matrix .
4. Simulation Results and Analysis
Numerical simulations were conducted to evaluate the channel performance of listed precoding algorithms in
Table 1. In the simulations, if they were not specially defined, the default noise power variance was 1, the actual transmission signal power satisfied
, and the simulation model was a large-scale single-cell MIMO system. Further, the default number of BS transmitting antennas
and the number of users
if they were not specially defined. The channel correlation matrix was modelled as [
26]
where
.
The channel performance was evaluated by the average achievable data rate at the UTs, which is given by
This rate is further averaged by the values obtained under different channel implementations in the simulations.
Figure 2,
Figure 3,
Figure 4 and
Figure 5 illustrate the average achievable rate versus the SINR of the transmitted signal to the users. The performance of the traditional RZF precoding algorithm was considered as the “perfect” value for comparison.
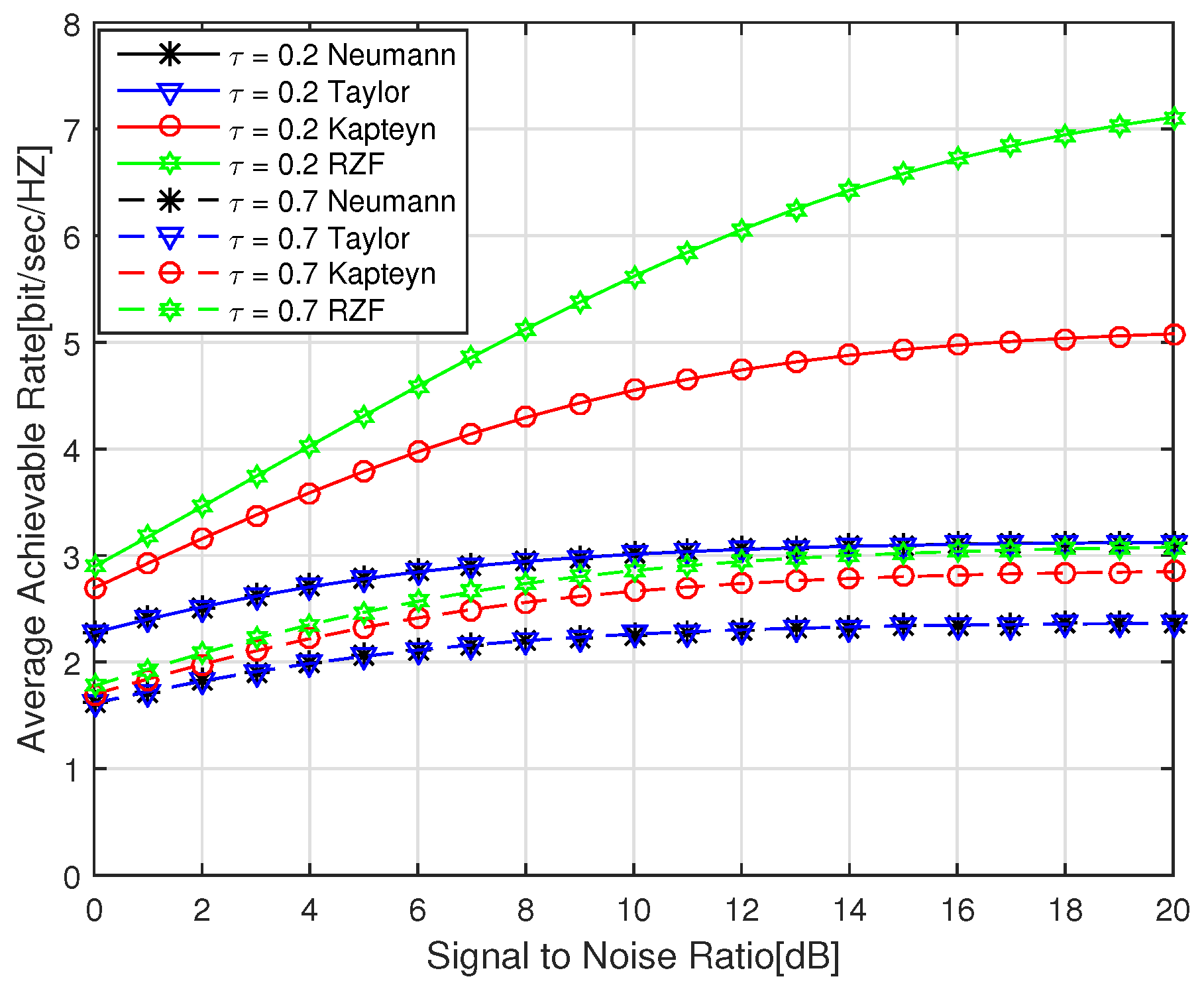
From
Figure 2, it can be observed that under the well estimated channel condition (lower value), all the compared RZF precoding algorithms perform better than the corresponding ones under poor estimated channel condition (higher value). Under certain channel estimation quality, the RZF precoding algorithm based on truncated Kapteyn series expansion performed much better than the ones with Taylor series expansion and Neumann series expansion, while the performance of the latter two ones was nearly identical. Especially when the channel estimation was very imperfect, the performance of the proposed RZF precoding based on the truncated Kapteyn series expansion is very close to the traditional RZF precoding algorithm.
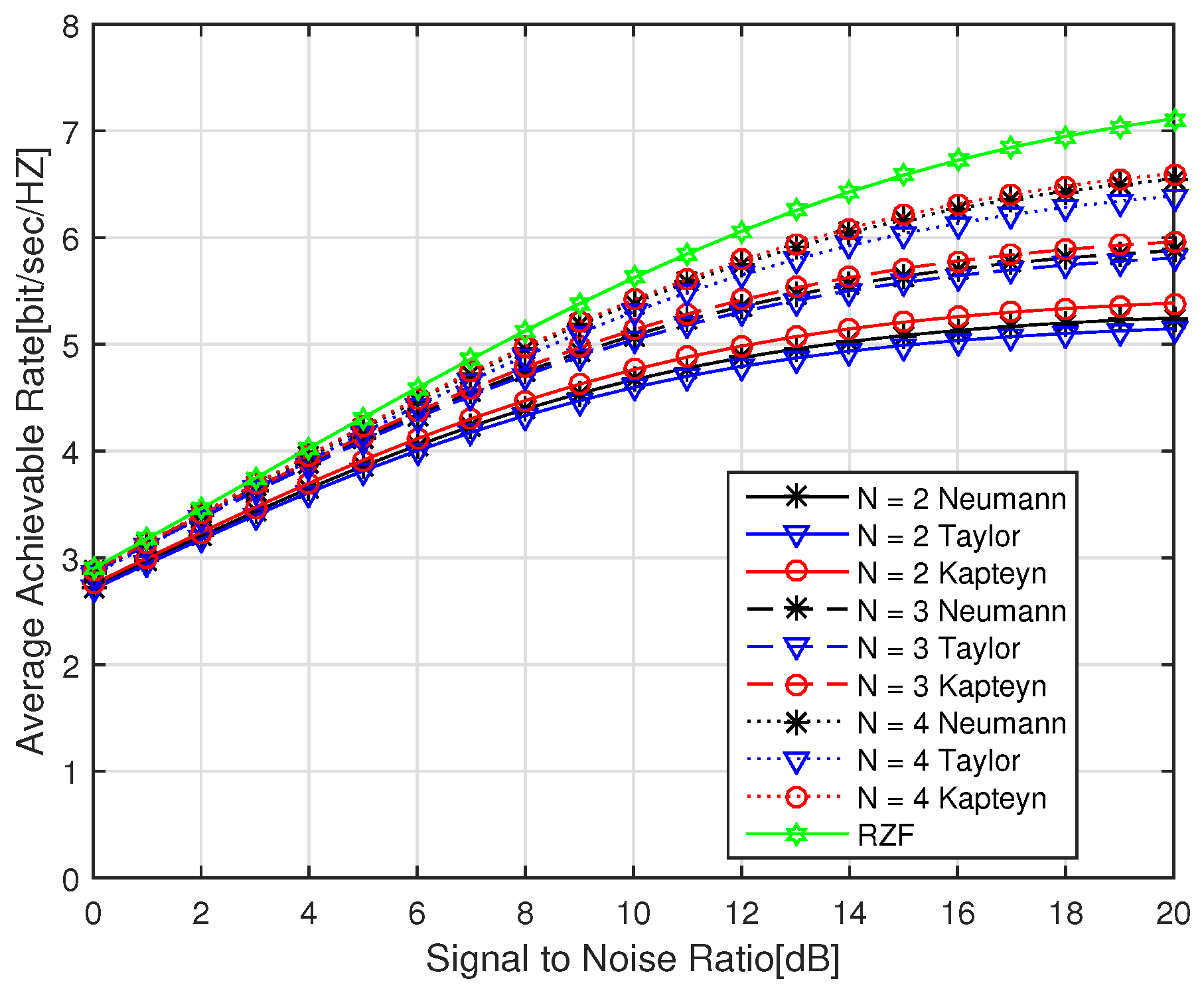
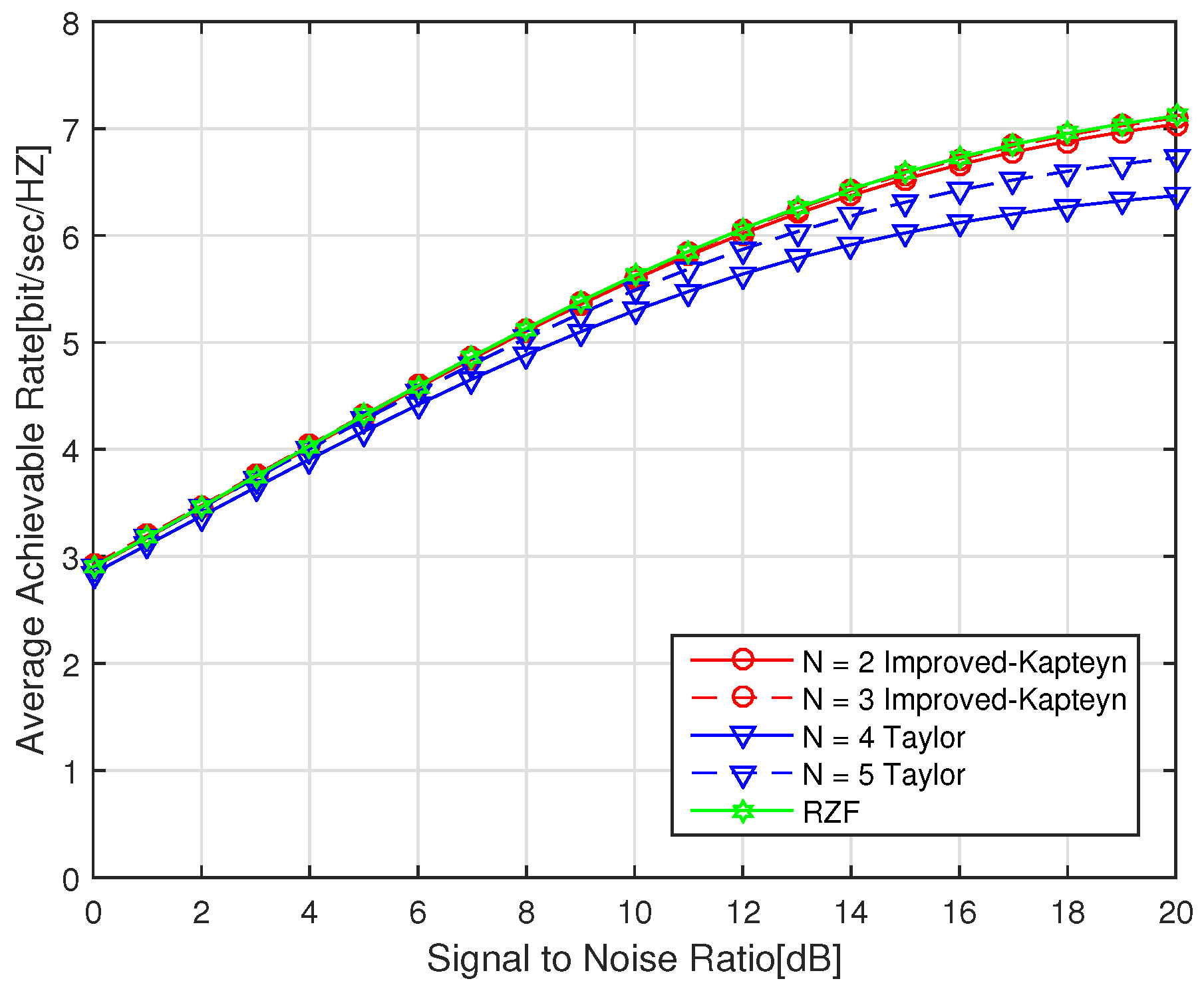
Figure 3 shows that the channel performance of the precoding algorithms with all compared truncated series expansions is getting close to the “perfect” traditional RZF precoding when the truncation order
N is increased (e.g., from 2 to 4 in the simulations). Again, it shows the better channel performance of the proposed RZF precoding algorithm than other truncation algorithms under the various
N values.
Furthermore, the coefficient optimization efforts were evaluated with the RZF precoding algorithm based on truncated Kapteyn series expansion.
Figure 4 illustrates the channel performance at the user when the coefficients optimization process was performed in RZF precoding.
From
Figure 4, it can be easily seen that the channel performance of the proposed algorithm with coefficients optimization was always better than the one without the optimization effects. When SINR increased, the performance gap between two cases got higher. In the cases when the truncation order was 2, the performance of proposed RZF precoding algorithm with coefficients optimization was almost the same as the performance of the traditional RZF algorithm.
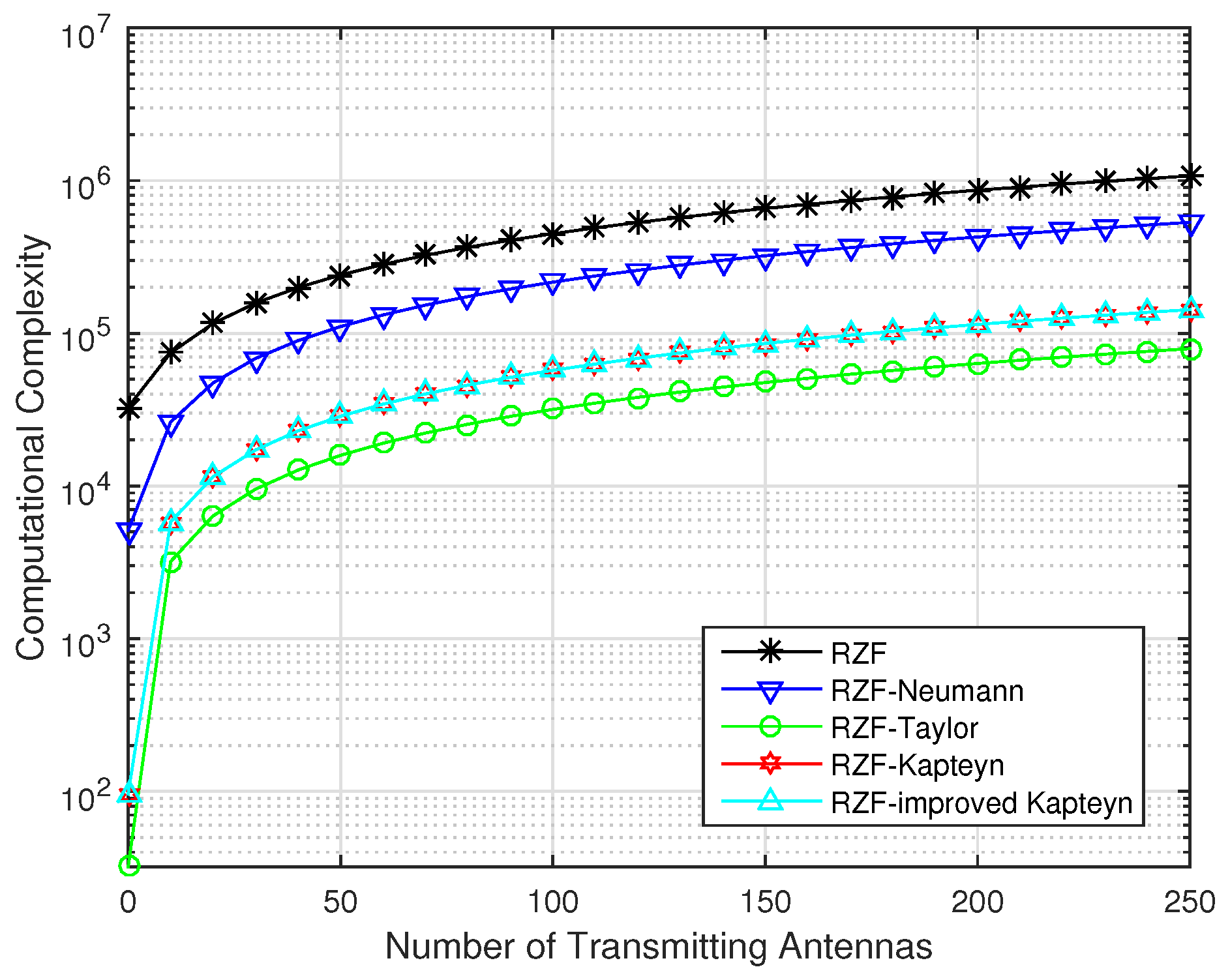
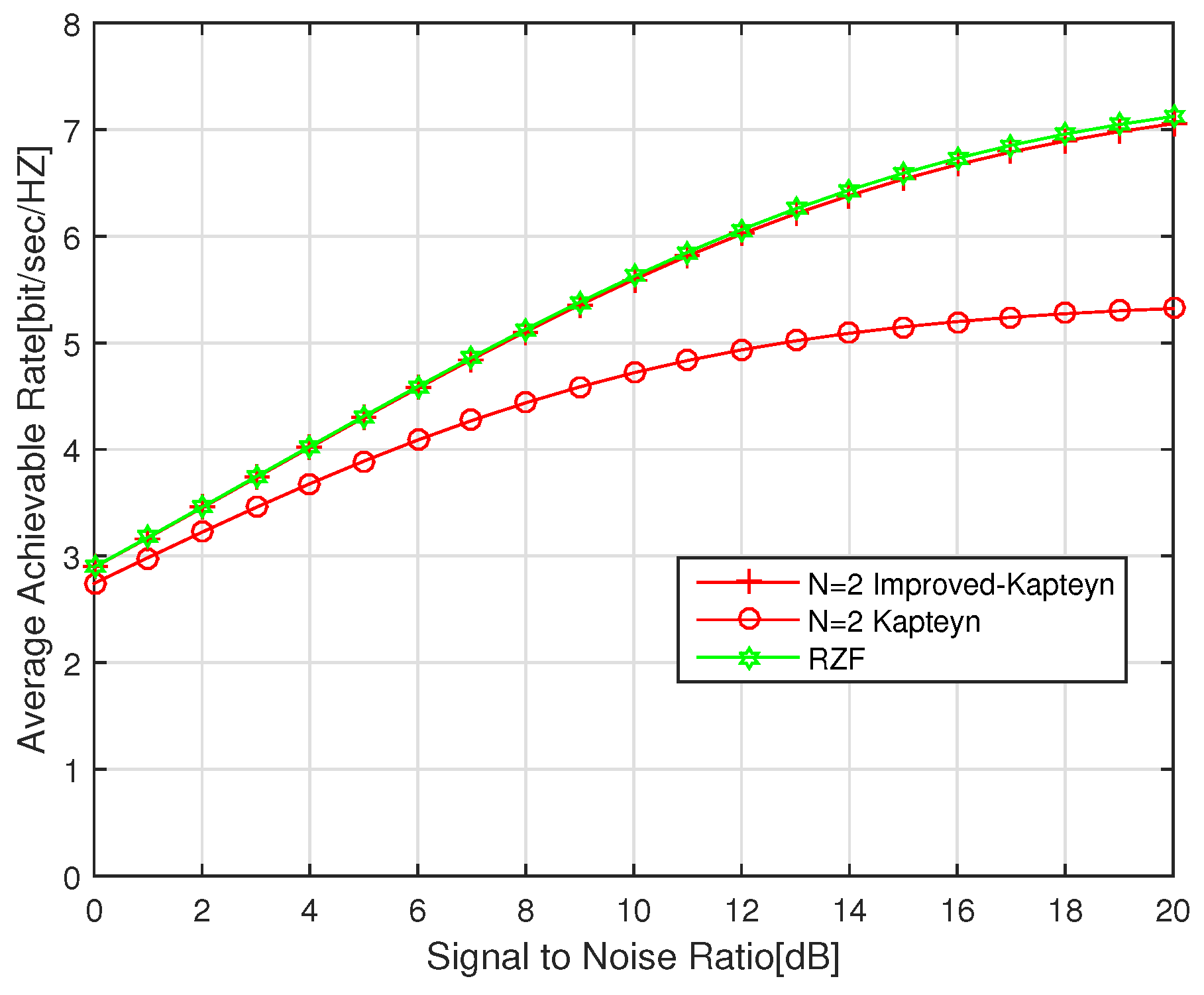
Finally, we end this section by comparing the channel performance of Kapteyn algorithm and Taylor algorithm with certain computational complexity considered. Specifically, the RZF precoding matrix based on truncated Taylor series expansion is given by
According to
Table 1, it can be found that the computational complexity of the improved Kapteyn algorithm with the truncated order of
N is the same as the one of the Taylor algorithm with the truncated order of
. It is interesting that
Figure 5 shows that the average achievable rate obtained by the proposed improved Kapteyn algorithm when
or
compared the one obtained by the Taylor algorithm with
or
. This observation implies that in the case of the same computational complexity, the improved Kapteyn algorithm performs much better than the Taylor algorithm.
Author Contributions
X.X. and Y.M. conceived of the proposed algorithms, designed the simulation scheme, and finished the draft manuscript. Z.L. validated the proposed algorithms, provided considerable technique review. S.X., Y.L., B.L. and Q.W. analyzed the data and improved the quality of the final manuscript. All authors have read and approved the final manuscript.
Funding
This work is supported in part by the National Natural Science Foundation of China (No. 61571108 & No. 61701197 & No. 61801193), the open research fund of National Mobile Communications Research Laboratory of millimeter wave, Southeast University (No. 2018D15), the open research fund of the National Key Laboratory of millimeter wave, Southeast University (No. K201918), and the Open Foundation of Key Laboratory of Wireless Communication, Nanjing University of Posts and Telecommunication (No. 2017WICOM01), and Project funded by China Postdoctoral Science Foundation (No. 2018M641354).Part of the article was published in 2016 IEEE International Conference on Communication Systems (ICCS).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ashikhmin, A.; Li, L.; Marzetta, T.L. Interference Reduction in Multi-Cell Massive MIMO Systems with Large-Scale Fading Precoding. IEEE Trans. Inf. Theory 2018, 64, 6340–6361. [Google Scholar] [CrossRef]
- Prabhu, H.; Rodrigues, J.N.; Edfors, O.; Rusek, F. Approximative matrix inverse computations for very-large MIMO and applications to linear pre-coding systems. In Proceedings of the 2013 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 7–10 April 2013; pp. 2710–2715. [Google Scholar]
- Zhou, C.; Gu, Y.; Fan, X.; Shi, Z.; Mao, G.; Zhang, Y. Direction-of-Arrival Estimation for Coprime Array via Virtual Array Interpolation. IEEE Trans. Signal Process. 2018, 66, 5956–5971. [Google Scholar] [CrossRef]
- Zhou, C.; Gu, Y.; He, S.; Shi, Z. A Robust and Efficient Algorithm for Coprime Array Adaptive Beamforming. IEEE Trans. Veh. Technol. 2018, 67, 1099–1112. [Google Scholar] [CrossRef]
- Shi, Z.; Zhou, C.; Gu, Y.; Goodman, N.A.; Qu, F. Source Estimation using Coprime Array: A Sparse Reconstruction Perspective. IEEE Sens. J. 2017, 3, 755–765. [Google Scholar] [CrossRef]
- Zhou, C.; Gu, Y.; Shi, Z.; Zhang, Y. Off-Grid Direction-of-Arrival Estimation Using Coprime Array Interpolation. IEEE Signal Process. Lett. 2018, 25, 1710–1714. [Google Scholar] [CrossRef]
- Ciuonzo, D.; Rossi, P.; Dey, S. Massive MIMO Channel-Aware Decision Fusion. IEEE Trans. Signal Process. 2015, 63, 604–619. [Google Scholar] [CrossRef]
- Tang, C.; Liu, C.; Yuan, L.; Xing, Z. High Precision Low Complexity Matrix Inversion Based on Newton Iteration for Data Detection in the Massive MIMO. IEEE Commun. Lett. 2016, 20, 490–493. [Google Scholar] [CrossRef]
- Shirazinia, A.; Dey, S.; Ciuonzo, D.; Salvo Rossi, P. Massive MIMO for Decentralized Estimation of a Correlated Source. IEEE Trans. Signal Process. 2016, 64, 2499–2512. [Google Scholar] [CrossRef]
- Ciuonzo, D.; Salvo Rossi, P.; Dey, S. Massive MIMO meets decision fusion: Decode-and-fuse vs. decode-then-fuse. In Proceedings of the 2014 IEEE 8th Sensor Array and Multichannel Signal Processing Workshop (SAM), A Coruna, Spain, 22–25 June 2014; pp. 265–268. [Google Scholar]
- Hoffmann, W. Iterative algorithms for Gram-Schmidt orthogonalization. Computing 1989, 41, 335–348. [Google Scholar] [CrossRef]
- Rice, J.R. Matrix Computations and Mathematical Software; McGraw-Hill Inc.: New York, NY, USA, 1981. [Google Scholar]
- Arias-García, J.; Jacobi, R.P.; Llanos, C.H.; Ayala-Rincón, M. A suitable FPGA implementation of floating-point matrix inversion based on Gauss-Jordan elimination. In Proceedings of the Programmable Logic (SPL), Cordoba, Argentina, 13–15 April 2011; pp. 263–268. [Google Scholar]
- Wu, M.; Yin, B.; Vosoughi, A.; Studer, C.; Cavallaro, J.; Dick, C. Approximate matrix inversion for high-throughput data detection in the large-scale MIMO uplink. In Proceedings of the 2013 IEEE International Symposium on Circuits and Systems (ISCAS2013), Beijing, China, 19–23 May 2013; pp. 2155–2158. [Google Scholar]
- Zarei, S.; Gerstacker, W.; Müller, R.; Schober, R. Low-complexity linear precoding for downlink large-scale MIMO systems. In Proceedings of the 2013 IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), London, UK, 8–11 September 2013; pp. 1119–1124. [Google Scholar]
- Prabhu, H.; Edfors, O.; Rodrigues, J.; Liu, L.; Rusek, F. Hardware efficient approximative matrix inversion for linear pre-coding in massive MIMO. In Proceedings of the 2014 IEEE International Symposium on Circuits and Systems (ISCAS), Melbourne, Australia, 1–5 June 2014. [Google Scholar]
- Zhang, W.; Lamare, R.; Pan, C.; Chen, M.; Wu, B.; Bao, X. Correlation-driven optimized Taylor expansion precoding for massive MIMO systems with correlated channels. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Zhang, C.; Li, Z.; Shen, L.; Yan, F.; Wu, M.; Wang, X. A Low-Complexity Massive MIMO Precoding Algorithm Based on Chebyshev Iteration. IEEE Access 2017, 5, 22545–22551. [Google Scholar] [CrossRef]
- Chen, G.; Zheng, J.; Shen, F. A Preset Threshold Based Cross-Tier Handover Algorithm for Uplink Co-Channel Interference Mitigation in Two-Tier Femtocell Networks. Wirel. Netw. 2016, 22, 1819–1835. [Google Scholar] [CrossRef]
- Wagner, S.; Couillet, R.; Debbah, M.; Slock, D.T. Large system analysis of linear precoding in correlated MISO broadcast channels under limited feedback. IEEE Trans. Inf. Theory 2012, 58, 4509–4537. [Google Scholar] [CrossRef]
- Jankov, D.; Pogány, T. On coefficients of Kapteyn-type series. Math. Slovaca 2014, 64, 403–410. [Google Scholar] [CrossRef]
- Stuber, G.L.; Barry, J.R.; Mclaughlin, S.W.; Li, Y.; Ingram, M.A.; Pratt, T.G. Broadband MIMO-OFDM wireless communications. Proc. IEEE 2004, 92, 271–294. [Google Scholar] [CrossRef]
- Dominici, D. A new Kapteyn series. Integr. Transforms Spec. Funct. 2007, 18, 409–418. [Google Scholar] [CrossRef]
- Man, Y.; Li, Z.; Yan, F.; Xing, S.; Shen, L. Massive MIMO pre-coding algorithm based on truncated Kapteyn series expansion. In Proceedings of the 2016 IEEE International Conference on Communication Systems (ICCS), Shenzhen, China, 14–16 December 2016; pp. 1–5. [Google Scholar]
- Muller, A.; Kammoun, A.; Björnson, E.; Debbah, M. Linear precoding based on polynomial expansion: Reducing complexity in massive MIMO. EURASIP J. Wirel. Commun. Netw. 2016, 2016, 63. [Google Scholar] [CrossRef] [PubMed]
- Shariati, N.; Björnson, E.; Bengtsson, M.; Debbah, M. Low-complexity channel estimation in large-scale MIMO using polynomial expansion. In Proceedings of the 2013 IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), London, UK, 8–11 December 2013; pp. 1157–1162. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).