Improved Massive MIMO RZF Precoding Algorithm Based on Truncated Kapteyn Series Expansion

Abstract

In order to reduce the computational complexity of the inverse matrix in the regularized zero-forcing (RZF) precoding algorithm, this paper expands and approximates the inverse matrix based on the truncated Kapteyn series expansion and the corresponding low-complexity RZF precoding algorithm is obtained. In addition, the expansion coefficients of the truncated Kapteyn series in our proposed algorithm are optimized, leading to further improvement of the convergence speed of the precoding algorithm under the premise of the same computational complexity as the traditional RZF precoding. Moreover, the computational complexity and the downlink channel performance in terms of the average achievable rate of the proposed RZF precoding algorithm and other RZF precoding algorithms with typical truncated series expansion approaches are analyzed, and further evaluated by numerical simulations in a large-scale single-cell multiple-input-multiple-output (MIMO) system. Simulation results show that the proposed improved RZF precoding algorithm based on the truncated Kapteyn series expansion performs better than other compared algorithms while keeping low computational complexity.

1. Introduction

Recently, due to the rapid development of wireless communication technology, the demand for data rate, service quality and number of users has multiplied and research on large-scale MIMO technology, a key technology in wireless communication technology, has been deepened, both domestically and overseas [1]. In a massive MIMO system, the RZF precoding algorithm can obtain approximately optimal linear precoding performance by increasing the number of antennas of the base station (BS). However, the complexity of hardware platform implementation and signal processing will also increase accordingly. When the ratio of the number of BS antennas to the number of user antennas is greater than 10, although the number of BS transmit antennas is very large, the complexity of RZF precoding mainly focuses on the inverse budget of the matrix which is related to the number of users [2]. The dimension of inverse matrix in the massive MIMO system is also large relative to the conventional MIMO system. The direct matrix inversion incurs a very high computational complexity in massive MIMO systems when the large-dimensional matrix inversion needs to be performed for RZF precoding.

The idea of estimating computation has been applied in many ways. For example, the articles in [3,4,5,6] use the coprime array interpolation to estimate the related source parameters, direction-of-arrival and so on. Recently, related research work in large-scale MIMO systems is also very plentiful. The authors of [7] present a wide choice of low-complexity sub-optimal rules about channel-aware decision fusion over MIMO channels which efficiently exploit large-array benefits. In [8], a diagonal band Newton iteration (DBNI) method is proposed. The contribution of [9] is that solve the decentralized multi-sensor estimation problem over uniform power allocation in massive MIMO mobile communications. Channel-aware (through pilot-based channel estimation) decision fusion over massive MIMO has been analyzed in [10].

The exact inverse of the matrix methods in common include the QR decomposition based on the Gram–Schmidt method [11,12] and the Gauss–Jordan elimination method [13], but they need lots of calculations. In order to reduce the complexity of the high dimensional inverse matrix, many scholars have started research. The underlying idea of [14] is to carry out an approximate matrix inversion using a small number of Neumann-series terms and on this basis proposes a novel VLSI architecture. A low-complexity precoding scheme based on matrix polynomial for downlink large-scale MIMO systems is presented in [15]. The RZF precoding algorithms based on the truncated Neumann series expansion [16] and the truncated Taylor series expansion [17] are the most common method of truncation. However, these algorithms do not consider the influence of the corresponding order factor in the expansion series, and the convergence is not good.

In this paper, the Kapteyn series polynomial is used to represent the inverse matrix of high dimensional matrix in RZF precoding algorithm. That is, we use the Kapteyn series to precode the signal. The inverse matrix is expanded and truncated by the Kapteyn series, taking the N terms before the polynomial. The constraint conditions for the series convergence are established and the value of N and corresponding order factor are studied. When the total transmitted power is constant and the channel state information is known, the correspondence between the signal-to-interference-noise ratio (SINR) and the polynomial coefficients is established. In the case of the fixed N value, the optimal solution of polynomial coefficient is sought to optimize SINR, so as to obtain the low-complexity pre-coding matrix.

The rest of this paper is organized as follows. Section 2 describes the system model. Section 3 proposes an improved RZF precoding based on the truncated Kapteyn series expansion to approximate the inverse matrix in RZF precoding and optimizes the expansion coefficients. Then the computational complexity of the proposed algorithm is calculated and compared with the one of the traditional RZF precoding. Simulation results of the proposed algorithm are presented to compare the channel performance to the ones of the RZF precoding with other truncated series expansions in Section 4. Section 5 concludes this paper.

We summarize the following notations used throughout the paper to facilitate the reader. Specifically, the boldface uppercase letters denote the matrices and the boldface lowercase letters represent the column vectors. In addition, ${\left(·\right)}^{\mathrm{H}}$, ${\left(·\right)}^{\mathrm{T}}$ and $tr\left(·\right)$ are the Hermitian transpose, transpose and trace of the matrix, respectively. Moreover, ${\left(·\right)}^{*}$ is the conjugate operator, ${∥·∥}_2$ represents the ${\mathbf{I}}_2$ norm of the matrix, respectively. Finally, $CN\left(\mathbf{m},\mathsf{\Phi }\right)$ denotes the circular symmetric complex Gaussian distribution with mean vector $\mathbf{m}$ and covariance matrix $\mathsf{\Phi }$.

2. System Model

A fading downlink channel is considered in a massive MIMO system consisting of a BS with M transmitting antennas and K single-antenna users. The channel matrix $\mathbf{H}\in {\mathbb{C}}^{M\times K}$ is given by

$$\mathbf{H}=\left[{\mathbf{h}}_1,\dots ,{\mathbf{h}}_K\right],{\mathbf{h}}_K\in {\mathbb{C}}^{M\times 1}$$

(1)

where ${\mathbf{h}}_k$ is the channel fading coefficient vector between the k-th user and the BS, which elements obey the Gaussian distribution with zero mean.

The estimated channel matrix obtained by the BS after acquiring the channel state information (CSI) is defined as $\widehat{\mathbf{H}}={\mathbb{C}}^{M\times K}$, which can also be expressed as

$$\widehat{\mathbf{H}}=\left[{\widehat{\mathbf{h}}}_1,\dots {\widehat{\mathbf{h}}}_K\right]\in {\mathbb{C}}^{M\times K},$$

(2)

where ${\widehat{\mathbf{h}}}_k\in {\mathbb{C}}^{M\times 1}$ is the estimated channel matrix between the BS and the k-th user with the elements to be assumed to follow Gaussian distribution, i.e., ${\widehat{\mathbf{h}}}_k\sim CN\left({\mathbf{0}}_{M\times 1},\mathsf{\Phi }\right)$ where $\mathsf{\Phi }\in {\mathbb{C}}^{M\times M}$ is the channel covariance matrix. However, the BS may not be able to accurately obtain the estimated CSI matrix in the real channel environment. Hence we model the distribution of the channel estimate [18] as follows:

$${\widehat{\mathbf{h}}}_k=\sqrt{1-{\tau }^2}{\mathbf{h}}_k+\tau {\mathbf{n}}_k,$$

(3)

where ${\mathbf{h}}_k$ is the real channel matrix, and ${\mathbf{n}}_k$ is the channel noise which follows the Gaussian distribution ${\mathbf{n}}_k\sim CN\left(0,{\sigma }^2\right)$ and is distributed with the matrix ${\mathbf{h}}_k$ independently and identically. In (3), $\tau \in \left[0,1\right]$ is the channel estimation parameter and when $\tau =0$, the estimated channel matrix equals to the real one.

The received signal by the k-th user terminal (UT) can be expressed as

$${\mathbf{y}}_k={\mathbf{h}}_k^{\mathrm{H}}\mathbf{x}+{\mathbf{z}}_k,$$

(4)

where ${\mathbf{z}}_k$ denotes the additive white Gaussian noise at the k-th user and $\mathbf{x}$ is the transmitted signal from the BS.

Let the signal sent by the BS to K users be $\mathbf{s}={\left[s_{\mathbf{1}},\dots ,s_K\right]}^{\mathrm{T}}\sim CN\left({\mathbf{0}}_{K\times 1},{\mathbf{I}}_{K\times 1}\right)$, which is pre-coded to reduce the multi-user interference [19], yielding

$$\mathbf{x}=\mathbf{Gs},$$

(5)

where $\mathbf{G}=\left[{\mathbf{g}}_{\mathbf{1}},\dots ,{\mathbf{g}}_K\right]\in {\mathbb{C}}^{M\times K}$ is the precoding matrix.

3. Using Kapteyn Series to Estimate the Inverse Matrix in RZF Precoding

This section formulates the RZF precoding matrix based on the truncated Kapteyn series expansion and optimizes the polynomial coefficients. Then the computational complexity of some RZF precoding algorithms are analyzed and compared.

3.1. Truncated Kapteyn Series Expansion Algorithm

To start, let us define the RZF precoding matrix as [20]

$${\mathbf{G}}_{\mathrm{RZF}}=\beta \widehat{\mathbf{H}}{\left({\widehat{\mathbf{H}}}^{\mathrm{H}}\mathbf{H}+\xi {\mathbf{I}}_K\right)}^{-1},$$

(6)

where $\beta$ is set to ensure ${\mathbf{G}}_{\mathrm{RZF}}$ satisfies the power constraint $tr\left(G{G}^H\right)=K$. In Equation (6), the scalar regulation coefficient $\xi$ can be selected as shown in [20].

Denote $\mathbf{X}=\left({\widehat{\mathbf{H}}}^{\mathrm{H}}\widehat{\mathbf{H}}+\xi {\mathbf{I}}_K\right)$. Let the eigenvalue of the matrix $\mathbf{I}-\alpha \mathbf{X}$ be $\lambda$ which satisfies the following inequality.

$$\left|\frac{\lambda \exp \sqrt{1-{\lambda }^2}}{1+\sqrt{1-{\lambda }^2}}\right|\le 1.$$

(7)

Then, according to the definition of the Kapteyn series [21], if the eigenvalues of the positive definite matrix $\mathbf{X}$ satisfy $\left|{\lambda }_m\left(\mathbf{X}\right)\right|<1$, we have

$${\left(\mathbf{I}-\mathbf{X}\right)}^{-1}=\mathbf{I}+2\sum _{n=1}^{\infty }{\mathbf{Y}}_n\left(\mathbf{I}\right)·{\mathbf{J}}_n\left(n\mathbf{X}\right),$$

(8)

where ${\mathbf{Y}}_n\left(I\right)={\displaystyle \sum _{m=0}^{\left(n-1\right)/\phantom{\left(n-1\right)2}2}}\frac{2^{n-2m-1}·{\left(n-2m\right)}^2\left(n-m-1\right)!}{m!n^{n-2m+1}}$ and ${\mathbf{J}}_n\left(n\mathbf{X}\right)$ is the Bessel function of the first kind. Rewriting (8) to the summation form yields

$$\begin{array}{c}{\left(\mathbf{I}-\mathbf{X}\right)}^{-1}={\displaystyle \sum _{n=0}^{+\infty }}{w}_n{\mathbf{J}}_n\left(n\mathbf{X}\right)\hfill \\ ={\displaystyle \sum _{n=0}^{+\infty }}{w}_n{\mathbf{X}}^n·{\displaystyle \sum _{n=0}^{+\infty }}{\mathbf{J}}_n\left(k\right){\mathbf{X}}^{2k}\hfill \end{array},$$

(9)

where $w_n\stackrel{\mathsf{\Delta }}{=}\left\{\begin{array}{c}{Y}_0\left(I\right),n=0\hfill \\ 2Y_n\left(I\right),n=1,2,\dots \hfill \end{array}\right.$, $J_n\left(\lambda \right)=\frac{{\left(-1\right)}^{\lambda }}{\lambda !}·\frac{1}{\left(n+\lambda \right)!}·{\left(\frac{n}{2}\right)}^{2\lambda +n}$. Similarly, since all eigenvalues of any positive definite matrix $\mathbf{X}$ and $0<\alpha <2/\phantom{2\max \left({\lambda }_n\left(\mathbf{X}\right)\right)}\max \left({\lambda }_n\left(\mathbf{X}\right)\right)$ are less than 1, the matrix polynomial based on Kapteyn series expansion can be obtained via Equation (9).

The inverse of matrix $\mathbf{X}$ can be expressed as [22,23].

$${\mathbf{X}}^{-1}=\alpha \frac{1}{\mathbf{I}-\left(\mathbf{I}-\alpha \mathbf{X}\right)}=\alpha \left(\mathbf{I}+2\sum _{n=1}^{\infty }{J}_n\left(n\left(\mathbf{I}-\alpha \mathbf{X}\right)\right)\right),$$

(10)

where $J_n\left(n\left(\mathbf{I}-\alpha \mathbf{X}\right)\right)={\displaystyle \sum _{k=0}^{\infty }}\frac{{\left(-1\right)}^k}{k!}\frac{1}{\left(n+k\right)!}{\left(\frac{n\left(\mathbf{I}-\alpha \mathbf{X}\right)}{2}\right)}^{2k+n}$.

Denote ${\mathbf{f}\mathbf{l}}_n\left(\mathbf{X}\right)={\displaystyle \sum _{k=0}^{\infty }}\frac{{\left(-1\right)}^k}{k!}\frac{1}{\left(n+k\right)!}{\left(\frac{n}{2}\right)}^{2k+n}{\left(\mathbf{I}-\alpha \mathbf{X}\right)}^{2k}$, Equation (10) can be rewritten as

$${\mathbf{X}}^{-1}=\alpha \frac{1}{\mathbf{I}-\left(\mathbf{I}-\alpha \mathbf{X}\right)}=\alpha \left(\mathbf{I}+2{\sum _{n=1}^{\infty }{\mathbf{fl}}_n\left(\mathbf{X}\right)\left(\mathbf{I}-\alpha \mathbf{X}\right)}^n\right).$$

(11)

Substituting Equation (11) into Equation (6), we have

$${\mathbf{G}}_{\mathrm{RZF}}=\alpha \beta \widehat{\mathbf{H}}\left(\mathbf{I}+2{\sum _{n=1}^{\infty }{\mathbf{fl}}_n\left({\widehat{\mathbf{H}}}^{\mathrm{H}}\widehat{\mathbf{H}}+\xi {\mathbf{I}}_K\right)\left(\mathbf{I}-\alpha \left({\widehat{\mathbf{H}}}^{\mathrm{H}}\widehat{\mathbf{H}}+\xi {\mathbf{I}}_K\right)\right)}^n\right).$$

(12)

Thus, by truncating Equation (12) and taking the first N terms, we obtain the RZF precoding matrix with the truncated Kapteyn polynomial expansion as [24]

$${\mathbf{G}}_{\mathrm{Kapteyn}}=\alpha \beta \widehat{\mathbf{H}}\left(\mathbf{I}+2\sum _{n=1}^{N-1}{\mathbf{fl}}_n\left({\widehat{\mathbf{H}}}^{\mathrm{H}}\widehat{\mathbf{H}}+\xi {\mathbf{I}}_K\right){\left(\mathbf{I}-\alpha \left({\widehat{\mathbf{H}}}^{\mathrm{H}}\widehat{\mathbf{H}}+\xi {\mathbf{I}}_K\right)\right)}^n\right).$$

(13)

Note that ${\mathbf{fl}}_n\left(\mathbf{X}\right)$ is the sum of infinite terms. Hence it is also necessary to perform the truncation of ${\mathbf{fl}}_n\left(\mathbf{X}\right)$ to further reduce the computational complexity. When only taking the first term of ${\mathbf{fl}}_n\left(\mathbf{X}\right)$, we have

$${\mathbf{fl}}_n\left(\mathbf{X}\right)=\frac{1}{\left(n\right)!}{\left(\frac{n}{2}\right)}^n\mathbf{I}$$

(14)

which results in the corresponding RZF precoding matrix with the truncated Kapteyn polynomial expansion, shown as

$${\mathbf{G}}_{\mathrm{Kapteyn}\_1}=\alpha \beta \widehat{\mathbf{H}}\left(\mathbf{I}+2\sum _{n=1}^{N-1}\frac{1}{\left(n\right)!}{\left(\frac{n}{2}\right)}^n{\left(\mathbf{I}-\alpha \left({\widehat{\mathbf{H}}}^{\mathrm{H}}\widehat{\mathrm{H}}+\xi {\mathbf{I}}_K\right)\right)}^n\right).$$

(15)

Using the equation ${\left(a+b\right)}^n={\displaystyle \sum _{m=0}^n}{C}_m^n{a}^{n-m}{b}^m$ to expand Equation (15), we have

$${\mathbf{G}}_{\mathrm{Kapteyn}\_1}=\alpha \beta \widehat{\mathbf{H}}\left(\mathbf{I}+2\sum _{n=1}^{N-1}\sum _{m=0}^n\frac{1}{n!}{\left(\frac{n}{2}\right)}^n\left(C_m^n{\left(1-\alpha \xi \right)}^{n-m}{\left(-\alpha {\widehat{\mathbf{H}}}^{\mathrm{H}}\widehat{\mathbf{H}}\right)}^m\right)\right).$$

(16)

Denote ${\mathsf{\Psi }}_n=\frac{1}{n!}{\left(\frac{n}{2}\right)}^n$, $n\ge 1$, (16) is finally expressed as

$$G_{\mathrm{Kapteyn}\_2}=\alpha \beta \widehat{\mathbf{H}}\left(\mathbf{I}+2\sum _{n=1}^{N-1}\left(\frac{1}{\left(n!\right)}{\left(\frac{n}{2}\right)}^n\mathbf{I}-\frac{1}{\left(n+1\right)!}{\left(\frac{n}{2}\right)}^{2+n}{\left(\mathbf{I}-\alpha \mathbf{X}\right)}^2\right){\left(\mathbf{I}-\alpha \mathbf{X}\right)}^n\right).$$

(17)

Similarly, when taking the first two terms of ${\mathbf{fl}}_n\left(\mathbf{X}\right)$, i.e.,

$$\mathbf{fl}{}_n\left(\mathbf{X}\right)=\frac{1}{\left(n\right)!}{\left(\frac{n}{2}\right)}^n\mathbf{I}-\frac{1}{\left(n+1\right)!}{\left(\frac{n}{2}\right)}^{2+n}{\left(\mathbf{I}-\alpha \mathbf{X}\right)}^2,$$

(18)

the corresponding RZF precoding matrix with the truncated Kapteyn polynomial expansion is given by

$$G_{\mathrm{Kapteyn}\_2}=\alpha \beta \widehat{\mathbf{H}}\left(\mathbf{I}+2\sum _{n=1}^{N-1}\left(\frac{1}{\left(n!\right)}{\left(\frac{n}{2}\right)}^n\mathbf{I}-\frac{1}{\left(n+1\right)!}{\left(\frac{n}{2}\right)}^{2+n}{\left(\mathbf{I}-\alpha \mathbf{X}\right)}^2\right){\left(\mathbf{I}-\alpha \mathbf{X}\right)}^n\right).$$

(19)

Equation (19) is further simplified as

$${\mathbf{G}}_{\mathrm{Kapteyn}\_2}=\beta \alpha \widehat{\mathbf{H}}\sum _{n=0}^{N+1}{\omega }_n{\left(\mathbf{I}-\alpha \left({\widehat{\mathbf{H}}}^{\mathrm{H}}\widehat{\mathbf{H}}+\xi \mathbf{I}\right)\right)}^n.$$

(20)

Using the equation ${\left(a+b\right)}^n={\displaystyle \sum _{m=0}^n}{C}_m^n{a}^{n-m}{b}^m$ to expand Equation (20), we have

$${\mathbf{G}}_{\mathrm{Kapteyn}\_2}=\beta \alpha \widehat{\mathbf{H}}\sum _{n=0}^{N+1}{\omega }_n\sum _{m=0}^n\left(C_m^n\left(1-\alpha \xi \right){}^{n-m}{\left(-\alpha {\widehat{\mathbf{H}}}^{\mathrm{H}}\widehat{\mathbf{H}}\right)}^m\right).$$

(21)

For ${\displaystyle \sum _{n=0}^{N+1}}{\omega }_n{\displaystyle \sum _{m=0}^n}\left(C_m^n\left(1-\alpha \xi \right){}^{n-m}{\left(-\alpha {\widehat{\mathbf{H}}}^{\mathrm{H}}\widehat{\mathbf{H}}\right)}^m\right)$, expanding it and adding the k-th column of each item, it can be further manipulated to obtain the Equation (22).

$$G_{\mathrm{Kapteyn}\_2}=\alpha \beta \widehat{\mathbf{H}}\sum _{n=0}^{N+1}\left(\sum _{x=n}^{N+1}{\omega }_x{C}_n^x{\left(1-\alpha \xi \right)}^{x-n}\right){\left(-\alpha {\widehat{\mathbf{H}}}^{\mathrm{H}}\widehat{\mathbf{H}}\right)}^n.$$

(22)

3.2. Polynomial Coefficients Optimization

Let us consider Equation (22) and examine its polynomial coefficients by denoting ${\phi }_n=\alpha \beta {\displaystyle \sum _{x=n}^{N+1}}{\omega }_x{C}_n^x{\left(1-\alpha \xi \right)}^{x-n}{\left(-\alpha \right)}^n$. Then Equation (22) is expressed as

$${\mathbf{G}}_{\mathrm{Kapteyn}\_2}=\widehat{\mathbf{H}}\sum _{n=0}^{N+1}{\phi }_n{\left({\widehat{\mathbf{H}}}^{\mathrm{H}}\widehat{\mathbf{H}}\right)}^n.$$

(23)

It is observed that the existing $N+2$ degrees of freedom in Equation (23) can be optimized. Specifically, the $N+2$ coefficients $\mathsf{\Psi }={\left[{\phi }_0\dots {\phi }_{N+1}\right]}^{\mathrm{H}}$ are optimized to improve the signal acceptance performance at the users, which are described as below.

In the RZF precoding, the SINR at the k-th user is defined as

$$\mathrm{SIN}{\mathrm{R}}_k=\frac{{\mathbf{h}}_k^{\mathrm{H}}\mathbf{G}{\mathbf{e}}_k{\mathbf{e}}_k^{\mathrm{H}}{\mathbf{G}}^{\mathrm{H}}{\mathbf{h}}_k}{{\mathbf{h}}_k^{\mathbf{H}}\mathbf{G}{\mathbf{G}}^{\mathrm{H}}{\mathbf{h}}_k-{\mathbf{h}}_k^{\mathrm{H}}\mathbf{G}{\mathbf{e}}_k{\mathbf{e}}_k^{\mathrm{H}}{\mathbf{G}}^{\mathrm{H}}{\mathbf{h}}_k+{\sigma }^2}.$$

(24)

Our objective is to maximize the SINR at the users. Firstly, according to Equations (23) and (24), we obtain

$${\mathbf{h}}_k^{\mathrm{H}}\mathbf{G}{\mathbf{e}}_k{\mathbf{e}}_k^{\mathrm{H}}{\mathbf{G}}^{\mathrm{H}}{\mathbf{h}}_k={\mathsf{\Psi }}^{\mathrm{H}}{\mathbf{P}}^{\mathrm{H}}{\mathbf{e}}_k{\mathbf{e}}_k^{\mathrm{H}}\mathbf{P}\mathsf{\Psi }$$

(25)

$${\mathbf{h}}_k^{\mathrm{H}}\mathbf{G}{\mathbf{G}}^{\mathrm{H}}{\mathbf{h}}_k={\mathsf{\Psi }}^{\mathrm{H}}{\mathbf{B}}_k\mathsf{\Psi }$$

(26)

$$\mathrm{tr}\left(\mathbf{G}{\mathbf{G}}^{\mathrm{H}}\right)={\mathsf{\Psi }}^{\mathrm{H}}\mathbf{C}\mathsf{\Psi }=K,$$

(27)

where $\mathsf{\Psi }={\left[{\phi }_0\dots {\phi }_{N+1}\right]}^{\mathrm{H}}$, $\mathbf{P}=\left[{\left({\widehat{\mathbf{H}}}^{\mathrm{H}}\widehat{\mathbf{H}}\right)}^0{\widehat{\mathbf{H}}}^{\mathrm{H}}{\mathbf{h}}_k\dots {\left({\widehat{\mathbf{H}}}^{\mathrm{H}}\widehat{\mathbf{H}}\right)}^{N+1}{\widehat{\mathbf{H}}}^{\mathrm{H}}{\mathbf{h}}_k\right]$, ${\mathbf{A}}_k={\mathbf{P}}^{\mathrm{H}}{\mathbf{e}}_k{\mathbf{e}}_k^{\mathrm{H}}\mathbf{P}$, ${\mathbf{B}}_k={\mathbf{P}}^{\mathrm{H}}\mathbf{P}$, respectively.

Proof. 

See the Appendix A. □

Hence, according to Equations (25)–(27), we formulate the optimization problem as

$$\left\{\begin{array}{c}\underset{\mathsf{\Psi }}{\max }\frac{{\mathsf{\Psi }}^{\mathrm{H}}{\mathbf{A}}_k\mathsf{\Psi }}{{\mathsf{\Psi }}^{\mathrm{H}}{\mathbf{B}}_k\mathsf{\Psi }-{\mathsf{\Psi }}^{\mathrm{H}}{\mathbf{A}}_k\mathsf{\Psi }+{\sigma }^2}\\ \mathrm{s}.t\mathrm{tr}\left(\mathbf{G}{\mathbf{G}}^{\mathrm{H}}\right)={\mathsf{\Psi }}^{\mathrm{H}}\mathbf{C}\mathsf{\Psi }=K.\end{array}\right.$$

(28)

The optimal value ${\mathsf{\Psi }}_{opt}$ of the coefficients $\mathsf{\Psi }$ can be obtained by solving (28). However, the matrices ${\mathbf{A}}_k$, ${\mathbf{B}}_k$ and $\mathbf{C}$ in Equation (28) are varying with the change of the channel matrix $\mathbf{H}$. Consider that the channel matrix behaves as deterministic in the large-scale MIMO system. Hence when both the number of transmitting antennas at BS and the number of single-antenna users tend towards infinity, the limits of the matrices ${\mathbf{A}}_k$, ${\mathbf{B}}_k$ and $\mathbf{C}$ can be obtained by the random matrix theory, and the optimal value ${\mathsf{\Psi }}_{opt}$ is then obtained [25]. Specifically, assume that the limit values of ${\mathbf{A}}_k$, ${\mathbf{B}}_k$ and $\mathbf{C}$ are ${\overline{\mathbf{A}}}_k$, ${\overline{\mathbf{B}}}_k$ and $\overline{\mathbf{C}}$ respectively. We can rewrite Equation (28) as

$$\left\{\begin{array}{c}\underset{\mathsf{\Psi }}{\max }\frac{{\mathsf{\Psi }}^{\mathrm{H}}{\overline{\mathbf{A}}}_k\mathsf{\Psi }}{{\mathsf{\Psi }}^H\left({\overline{\mathbf{B}}}_k-{\overline{\mathbf{A}}}_k\right)\mathsf{\Psi }+{\sigma }^2}\\ \mathrm{s}.t\mathrm{tr}\left(\mathbf{G}{\mathbf{G}}^{\mathrm{H}}\right)={\mathsf{\Psi }}^{\mathrm{H}}\overline{\mathbf{C}}\mathsf{\Psi }=K.\end{array}\right.$$

(29)

Further, since the matrices ${\mathbf{A}}_k$, ${\mathbf{B}}_k$ and $\mathbf{C}$ are all real symmetric matrices, simplifying Equation (29) leads the objective function becoming

$$\frac{{\mathsf{\Psi }}^{\mathrm{H}}{\overline{\mathbf{A}}}_k\mathsf{\Psi }}{{\mathsf{\Psi }}^{\mathrm{H}}\left({\overline{\mathbf{B}}}_k-{\overline{\mathbf{A}}}_k+\frac{{\sigma }^2}{K}\overline{C}\right)\mathsf{\Psi }}.$$

(30)

Note that for any real symmetric matrices $\mathbf{R}$, we have $\mathbf{R}={\left({\mathbf{R}}^{1/2}\right)}^{\mathrm{H}}{\mathbf{R}}^{1/2}$. Hence Equation (30) can be further manipulated into

$$\frac{{\mathsf{\Psi }}^{\mathrm{H}}{\overline{\mathbf{A}}}_k\mathsf{\Psi }}{{\left[{\left({\overline{\mathbf{B}}}_k-{\overline{\mathbf{A}}}_k+\frac{{\sigma }^2}{K}\overline{\mathbf{C}}\right)}^{\frac{1}{2}}\mathsf{\Psi }\right]}^{\mathrm{H}}\left({\left({\overline{\mathbf{B}}}_k-{\overline{\mathbf{A}}}_k+\frac{{\sigma }^2}{K}\overline{\mathbf{C}}\right)}^{\frac{1}{2}}\mathsf{\Psi }\right)}.$$

(31)

Let $\mathsf{Ø}={\left({\overline{\mathbf{B}}}_k-{\overline{\mathbf{A}}}_k+\frac{{\sigma }^2}{K}\overline{\mathbf{C}}\right)}^{\frac{1}{2}}\mathsf{\Psi }$, then $\mathsf{\Psi }={\left({\overline{\mathbf{B}}}_k-{\overline{\mathbf{A}}}_k+\frac{{\sigma }^2}{K}\overline{\mathbf{C}}\right)}^{-\frac{1}{2}}\mathsf{Ø}$, which is substituted into Equation (31) to achieve

$$\frac{{\mathsf{Ø}}^{\mathrm{H}}{\left[{\left({\overline{\mathbf{B}}}_k-{\overline{\mathbf{A}}}_k+\frac{{\sigma }^2}{K}\overline{\mathbf{C}}\right)}^{-\frac{1}{2}}\right]}^{\mathrm{H}}{\overline{\mathbf{A}}}_k{\left({\overline{\mathbf{B}}}_k-{\overline{\mathbf{A}}}_k+\frac{{\sigma }^2}{K}\overline{\mathbf{C}}\right)}^{-\frac{1}{2}}\mathsf{Ø}}{{\mathsf{Ø}}^{\mathrm{H}}\mathsf{Ø}}.$$

(32)

The maximum value of the objective function in Equation (32) is the maximum eigenvalue of the matrix ${\left[{\left({\overline{\mathbf{B}}}_k-{\overline{\mathbf{A}}}_k+\frac{{\sigma }^2}{K}\overline{\mathbf{C}}\right)}^{-\frac{1}{2}}\right]}^{\mathrm{H}}{\overline{\mathbf{A}}}_k{\left({\overline{\mathbf{B}}}_k-{\overline{\mathbf{A}}}_k+\frac{{\sigma }^2}{K}\overline{\mathbf{C}}\right)}^{-\frac{1}{2}}$. Thus let the maximum eigenvalue of the matrix be ${\lambda }_{\max }$ and the corresponding eigenvector be $\mathbf{b}$, then $\mathsf{Ø}=k\mathbf{b}$, where k is a specific normal number.

According to $\mathsf{\Psi }={\left({\overline{\mathbf{B}}}_k-{\overline{\mathbf{A}}}_k+\frac{{\sigma }^2}{K}\overline{\mathbf{C}}\right)}^{-\frac{1}{2}}\mathsf{Ø}$, we have

$$\mathsf{\Psi }={\left({\overline{\mathbf{B}}}_k-{\overline{\mathbf{A}}}_k+\frac{{\sigma }^2}{K}\overline{\mathbf{C}}\right)}^{-\frac{1}{2}}\mathsf{Ø}.$$

(33)

Substituting Equation (33) into ${\mathsf{\Psi }}^{\mathrm{H}}\mathbf{C}\mathsf{\Psi }=K$, we have

$$k^2{\left[{\overline{\mathbf{C}}}^{\frac{1}{2}}{\left({\overline{\mathbf{B}}}_k-{\overline{\mathbf{A}}}_k+\frac{{\sigma }^2}{K}\overline{\mathbf{C}}\right)}^{-\frac{1}{2}}\mathbf{b}\right]}^{\mathrm{H}}\left[{\overline{\mathbf{C}}}^{\frac{1}{2}}{\left({\overline{\mathbf{B}}}_k-{\overline{\mathbf{A}}}_k+\frac{{\sigma }^2}{K}\overline{\mathbf{C}}\right)}^{-\frac{1}{2}}\mathbf{b}\right]=K.$$

(34)

Solving Equation (34) results in

$$k=\sqrt{\frac{K}{{∥{\overline{\mathbf{C}}}^{\frac{1}{2}}{\left({\overline{\mathbf{B}}}_k-{\overline{\mathbf{A}}}_k+\frac{{\sigma }^2}{K}\overline{\mathbf{C}}\right)}^{-\frac{1}{2}}\mathbf{b}∥}_2}}.$$

(35)

Therefore the final solution of ${\mathsf{\Psi }}_{opt}$ is

$${\mathsf{\Psi }}_{opt}=\sqrt{\frac{K}{{∥{\overline{\mathbf{C}}}^{\frac{1}{2}}{\left({\overline{\mathbf{B}}}_k-{\overline{\mathbf{A}}}_k+\frac{{\sigma }^2}{K}\overline{\mathbf{C}}\right)}^{-\frac{1}{2}}\mathbf{b}∥}_2}}{\left({\overline{\mathbf{B}}}_k-{\overline{\mathbf{A}}}_k+\frac{{\sigma }^2}{K}\overline{\mathbf{C}}\right)}^{-\frac{1}{2}}\mathbf{b}.$$

(36)

3.3. Analysis of Computational Complexity

A thorough analysis of the computational complexity of RZF precoding based on the truncated Kapteyn series expansion is presented in this section, where the computational complexity was measured in terms of the total number of multiplication and addition operations that are needed for determining the polynomial. The complexity of the traditional RZF precoding algorithm was also evaluated for comparison.

Let us examine the computational complexity of the traditional RZF precoding algorithm first. Assume that $T_{\mathrm{data}}$ is the number of time slots during which the base station downlink transmits information to the user in each coherence period.

The traditional RZF precoding matrix is ${\mathbf{G}}_{\mathrm{RZF}}=\beta \widehat{\mathbf{H}}{\left({\widehat{\mathbf{H}}}^{\mathrm{H}}\widehat{\mathbf{H}}+\xi {\mathbf{I}}_K\right)}^{-1}$. Assuming that $\widehat{\mathbf{H}}$ and $\xi {\mathbf{I}}_K$ are constant, which can be obtained without any calculations. Then, the precoding matrix needs to be computed by the steps of (1) one matrix and matrix multiplication for ${\widehat{\mathbf{H}}}^{\mathrm{H}}\widehat{\mathbf{H}}$; (2) one matrix and matrix addition for ${\widehat{\mathbf{H}}}^{\mathrm{H}}\widehat{\mathbf{H}}+\xi {\mathbf{I}}_K$; (3) one K-order matrix inversion for ${\left({\widehat{\mathbf{H}}}^{\mathrm{H}}\widehat{\mathbf{H}}+\xi {\mathbf{I}}_K\right)}^{-1}$; (4) one matrix and matrix multiplication for $\widehat{\mathbf{H}}{\left({\widehat{\mathbf{H}}}^{\mathrm{H}}\widehat{\mathbf{H}}+\xi {\mathbf{I}}_K\right)}^{-1}$; and (5) one constant and matrix multiplication for $\beta \widehat{\mathbf{H}}{\left({\widehat{\mathbf{H}}}^{\mathrm{H}}\widehat{\mathbf{H}}+\xi {\mathbf{I}}_K\right)}^{-1}$. The corresponding step calculations are $2K^{2}M-K^2$, K, $K^3+K^2+K$, $2M{K}^2-MK$, $MK$, respectively. Hence the total number of calculations of a traditional RZF precoding matrix is $K^3+4K^{2}M$. In addition, when the RZF precoding matrix is obtained, the precoding signal needs to be calculated by $\mathbf{x}=\mathbf{Gs}$, which requires the calculations of $2KM-M$. Therefore, the computational complexity of the traditional RZF precoding algorithm in a coherence period is summarized as

$$C_{\mathrm{RZF}}=K^3+4M{K}^2+2K+T_{\mathrm{data}}\left(2KM-M\right).$$

(37)

From above discussion, it can be observed that the required calculation of the K-order matrix inversion in the traditional RZF precoding algorithm is very large, which increases dramatically with the number of users.

We are now in a position to examine the computational complexity of RZF precoding based on the truncated Kapteyn series expansion. Let us denote ${\mathsf{\Omega }}_n={\displaystyle \sum _{x=n}^{N+1}}{\omega }_x{C}_n^x{\left(1-\alpha \xi \right)}^{x-n}{\left(-\alpha \right)}^n$. According to Equation (22), ${\mathbf{G}}_{\mathrm{Kapteyn}\_2}$ can be rewritten as

$${\mathbf{G}}_{\mathrm{Kapteyn}\_2}=\alpha \beta \widehat{\mathbf{H}}\sum _{n=0}^{N+1}{\mathsf{\Omega }}_n{\left({\widehat{\mathbf{H}}}^{\mathrm{H}}\widehat{\mathbf{H}}\right)}^n.$$

(38)

Because ${\mathsf{\Omega }}_n$ is independent of the channel matrix $\mathbf{H}$, it can be calculated and stored in advance, which will not consume additional calculations when computing the RZF precoding in the coherence period. The pre-coded signal from BS to the user is $\mathbf{x}=\alpha \beta \widehat{\mathbf{H}}{\displaystyle \sum _{n=0}^{N+1}}{\mathsf{\Omega }}_n{\left({\widehat{\mathbf{H}}}^{\mathrm{H}}\widehat{\mathbf{H}}\right)}^n\mathbf{s}$. Let ${\widehat{\mathbf{s}}}_0={\left({\mathbf{H}}^{\mathrm{H}}\mathbf{H}\right)}^0\widehat{\mathbf{s}}$ and ${\widehat{\mathbf{s}}}_n={\left({\mathbf{H}}^{\mathrm{H}}\mathbf{H}\right)}^n\widehat{\mathbf{s}}=\left({\mathbf{H}}^{\mathrm{H}}\mathbf{H}\right){\widehat{\mathbf{s}}}_{n-1}$, where $n>0$. Hence the calculations of ${\widehat{\mathbf{s}}}_n$ are counted as $4MK-M-K$, and the calculations of $\mathbf{x}=\alpha \beta \widehat{\mathbf{H}}{\displaystyle \sum _{n=0}^{N+1}}{\mathsf{\Omega }}_n{\widehat{\mathbf{s}}}_n$ are thus $2MK-M+\left(N+2\right)K+\left(N+1\right)K$.

Therefore, the computational complexity of ${\mathbf{G}}_{\mathrm{Kapteyn}\_2}$ is given by

$$C_{\mathrm{Kapteyn}\_2}=T_{\mathrm{data}}\left(\left(10+4N\right)MK-\left(N+3\right)M+\left(N+1\right)K\right).$$

(39)

Obviously, the computational complexity in Equation (39) increases with the truncation order of ${\mathbf{fl}}_n\left(\mathbf{X}\right)$. The larger the truncation order of ${\mathbf{fl}}_n\left(\mathbf{X}\right)$, the closer the convergence of the RZF precoding with truncated Kapteyn polynomial expansion to the one without truncation. Numerical simulation results in Section 4 show that the good convergence effects can be achieved when ${\mathbf{fl}}_n\left(\mathbf{X}\right)$ truncation order is two or above. When this truncation order is greater than two, the impact of truncated expression on the convergence of the Kapteyn series is reduced. Therefore, this paper only analyzes the case where the ${\mathbf{fl}}_n\left(\mathbf{X}\right)$ truncation order is 2 for the greatest reduction of the computational complexity.

Moreover, it can be observed from Equation (36) that the optimal coefficients are independent of the actual channel matrix element values. Hence the optimal coefficients can be calculated in advance when the truncation order is determined and the information of the number of BS transmitting antennas and the number of users are received; no extra computation cost will be added during the precoding of the transmitting signal, which makes the RZF precoding with Kapteyn optimization the same computational complexity as the proposed Kapteyn algorithm without coefficients optimization.

Finally, the computational complexities of RZF precoding algorithms based on truncated Neumann series expansion and truncated Taylor series expansion are obtained in the similar way as the one with truncated Kapteyn series expansion. The computational complexity of these listed and aforementioned precoding algorithms are shown in

Table 1. Computational complexity comparison of five algorithms.

Algorithm	Computational Complexity
Traditional RZF	$K^3+4M{K}^2+2K+T_{\mathrm{data}}\left(2KM-M\right)$
RZF precoding with truncated	$2K^{2}M+K^2+K+T_{data}\left(2MK-M+2N{K}^2\right)$
Neumann series expansion
RZF precoding with truncated	$T_{data}\left(\left(2+4N\right)MK-\left(N+1\right)M+\left(N-1\right)K\right)$
Taylor series expansion
RZF precoding with truncated	$T_{\mathrm{data}}\left(\left(10+4N\right)MK-\left(N+3\right)M+\left(N+1\right)K\right)$
Kapteyn series expansion
RZF precoding with truncated	$T_{\mathrm{data}}\left(\left(10+4N\right)MK-\left(N+3\right)M+\left(N+1\right)K\right)$
and coefficients optimization
Kapteyn series expansion

for comparison.

Table 1 shows the significant reduction of the computational complexity of the proposed RZF precoding with truncated Kapteyn series expansion compared to the traditional RZF precoding algorithm. For convenience, we also provide a corresponding figure showing the comparison of the computational complexity of the five algorithms for varying number of transmitting antennas. From Figure 1, we can see that the computational complexity of the proposed algorithm is much less than the one of the truncated Neumann series expansion algorithm, although it is slightly higher than the one of the truncated Taylor series expansion algorithm. In Section 4, we compare the performances of five algorithms including our proposed one and show that the improved RZF precoding algorithm based on the truncated Kapteyn series performs the best in terms of the average achievable rate among the compared algorithms given the same computational complexity.

4. Simulation Results and Analysis

Numerical simulations were conducted to evaluate the channel performance of listed precoding algorithms in Table 1. In the simulations, if they were not specially defined, the default noise power variance was 1, the actual transmission signal power satisfied $\mathrm{tr}\left(\mathbf{G}{\mathbf{G}}^{\mathrm{H}}\right)=K$, and the simulation model was a large-scale single-cell MIMO system. Further, the default number of BS transmitting antennas $M=256$ and the number of users $K=32$ if they were not specially defined. The channel correlation matrix was modelled as [26]

$${\mathsf{\Phi }}_{i,j}=\left\{\begin{array}{c}{a}^{j-i}i\le j\hfill \\ {\left(a^{i-j}\right)}^{*}i>j\hfill \end{array}\right.$$

(40)

where $a=0.1$.

The channel performance was evaluated by the average achievable data rate at the UTs, which is given by

$$\mathrm{r}=\frac{1}{K}\sum _{k=1}^K{\log }_2(1+\mathrm{SIN}{\mathrm{R}}_k).$$

(41)

This rate is further averaged by the values obtained under different channel implementations in the simulations.

Figure 2, Figure 3, Figure 4 and Figure 5 illustrate the average achievable rate versus the SINR of the transmitted signal to the users. The performance of the traditional RZF precoding algorithm was considered as the “perfect” value for comparison.

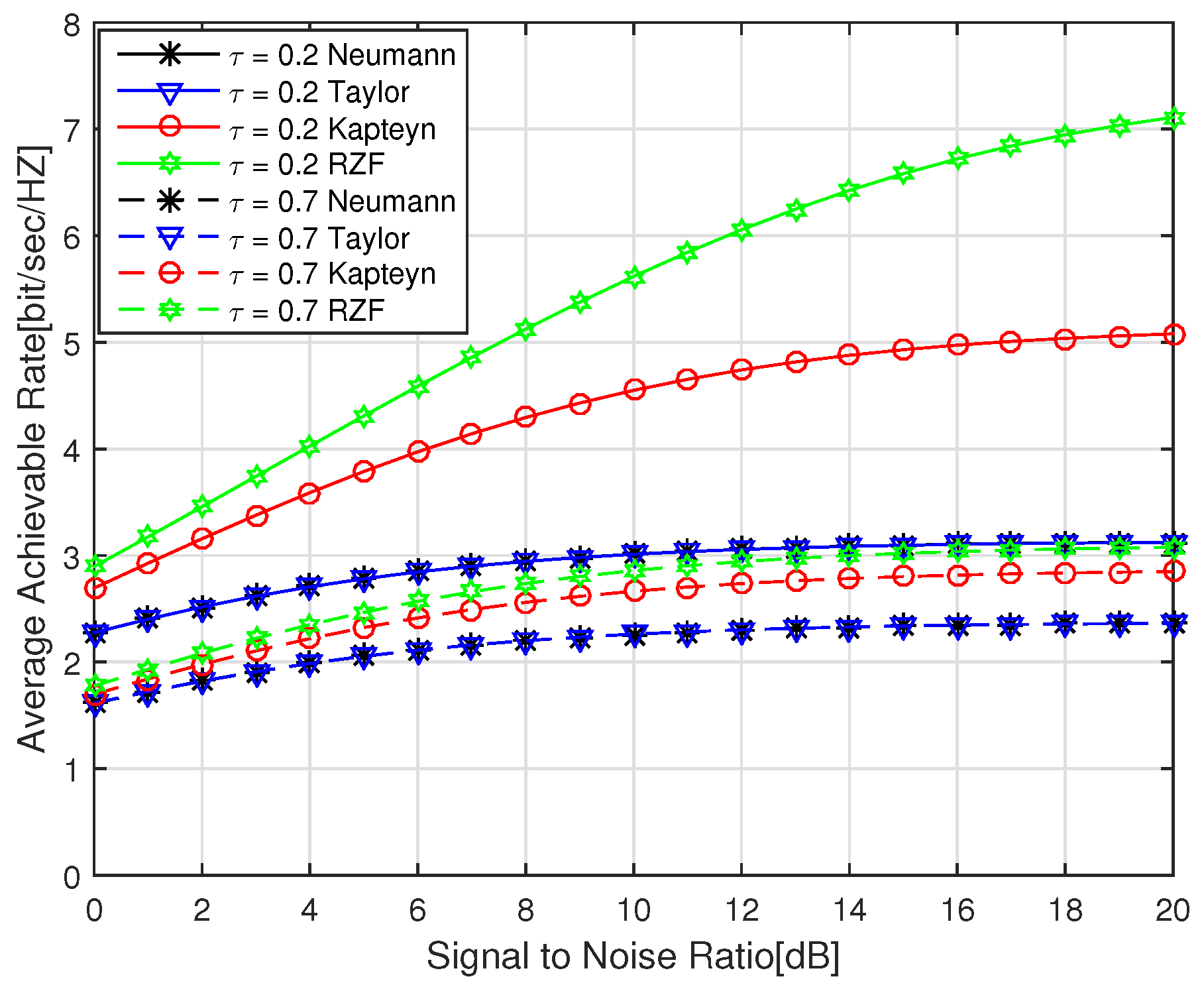
From Figure 2, it can be observed that under the well estimated channel condition (lower value), all the compared RZF precoding algorithms perform better than the corresponding ones under poor estimated channel condition (higher value). Under certain channel estimation quality, the RZF precoding algorithm based on truncated Kapteyn series expansion performed much better than the ones with Taylor series expansion and Neumann series expansion, while the performance of the latter two ones was nearly identical. Especially when the channel estimation was very imperfect, the performance of the proposed RZF precoding based on the truncated Kapteyn series expansion is very close to the traditional RZF precoding algorithm.

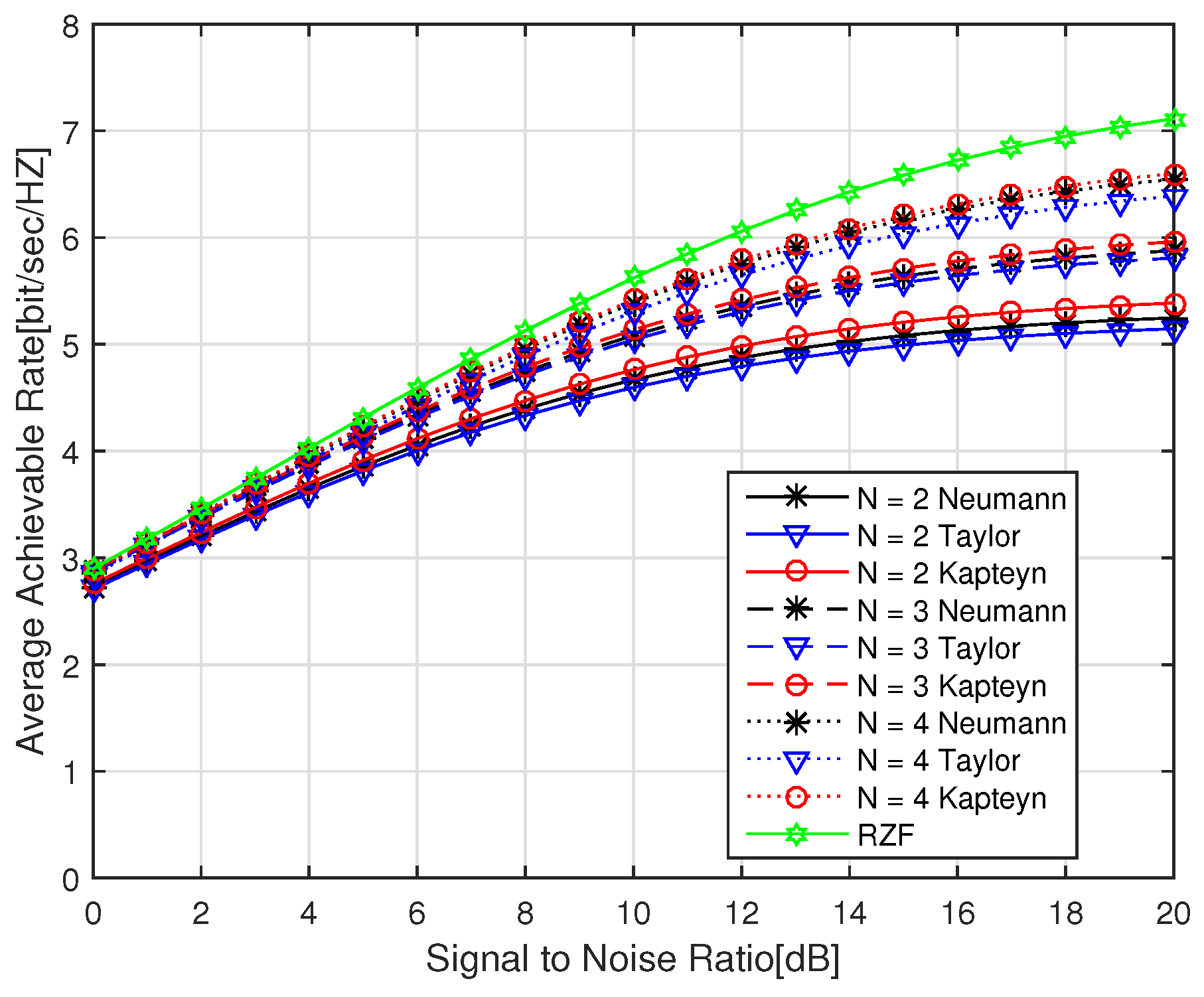
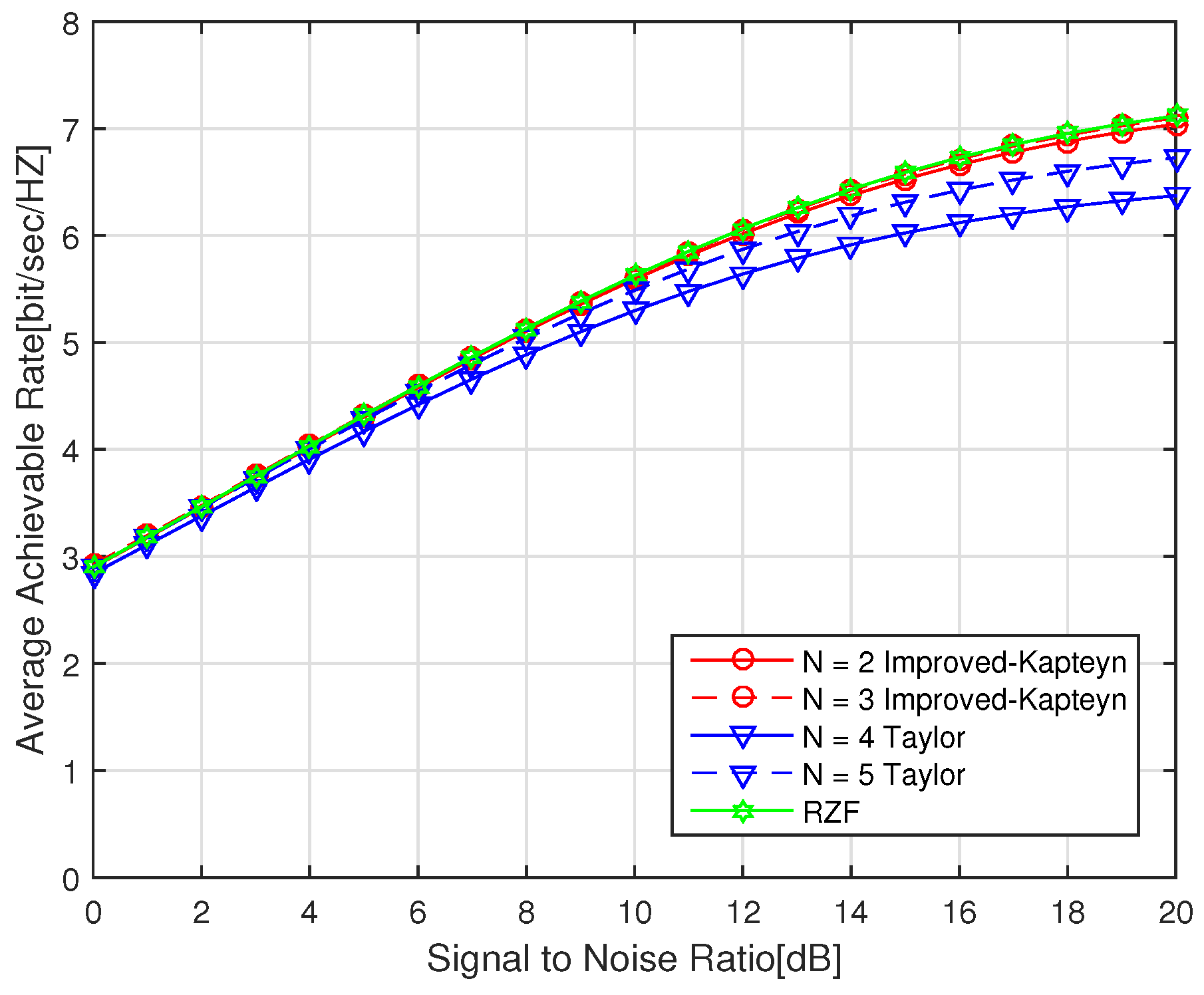
Figure 3 shows that the channel performance of the precoding algorithms with all compared truncated series expansions is getting close to the “perfect” traditional RZF precoding when the truncation order N is increased (e.g., from 2 to 4 in the simulations). Again, it shows the better channel performance of the proposed RZF precoding algorithm than other truncation algorithms under the various N values.

Furthermore, the coefficient optimization efforts were evaluated with the RZF precoding algorithm based on truncated Kapteyn series expansion. Figure 4 illustrates the channel performance at the user when the coefficients optimization process was performed in RZF precoding.

From Figure 4, it can be easily seen that the channel performance of the proposed algorithm with coefficients optimization was always better than the one without the optimization effects. When SINR increased, the performance gap between two cases got higher. In the cases when the truncation order was 2, the performance of proposed RZF precoding algorithm with coefficients optimization was almost the same as the performance of the traditional RZF algorithm.

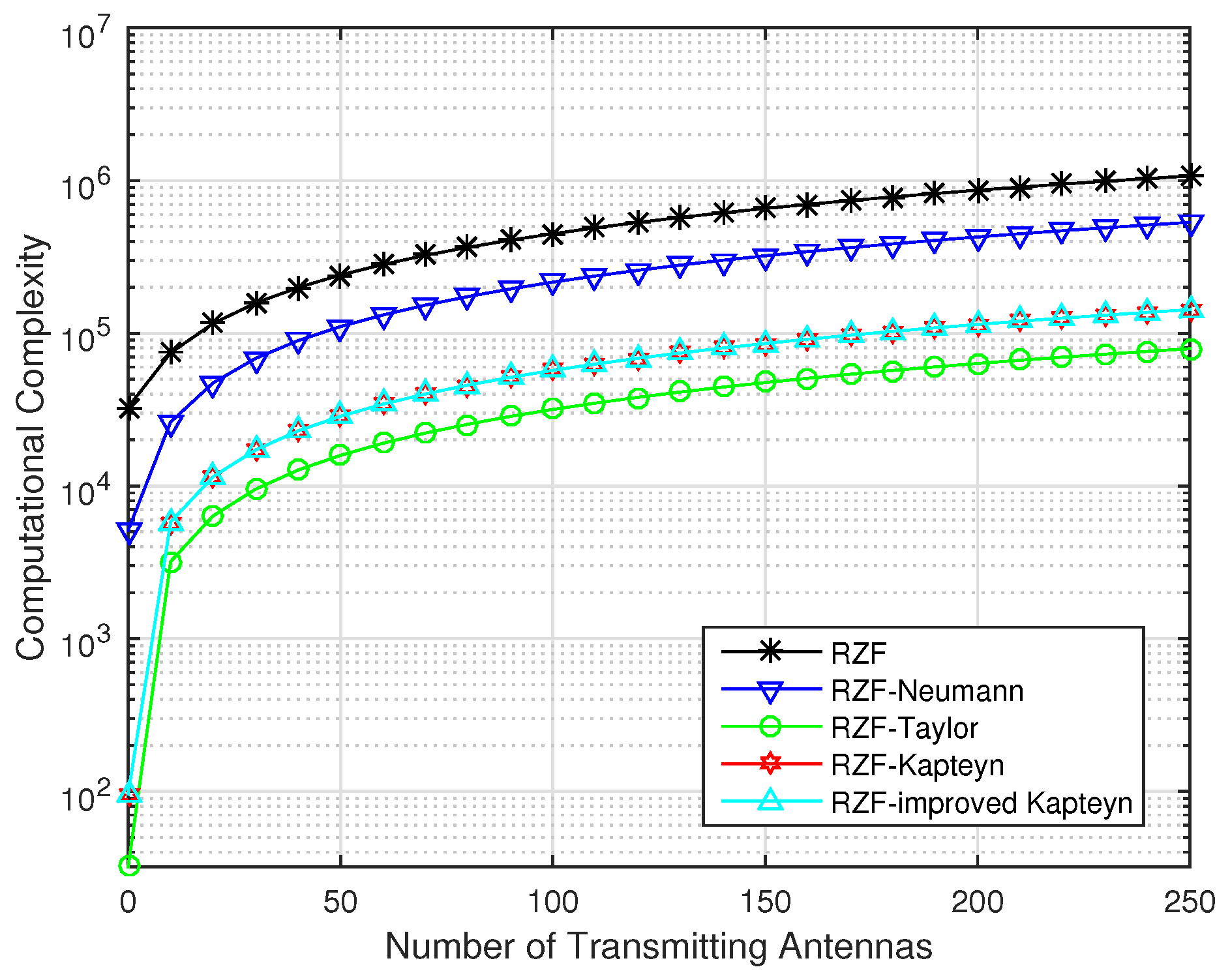
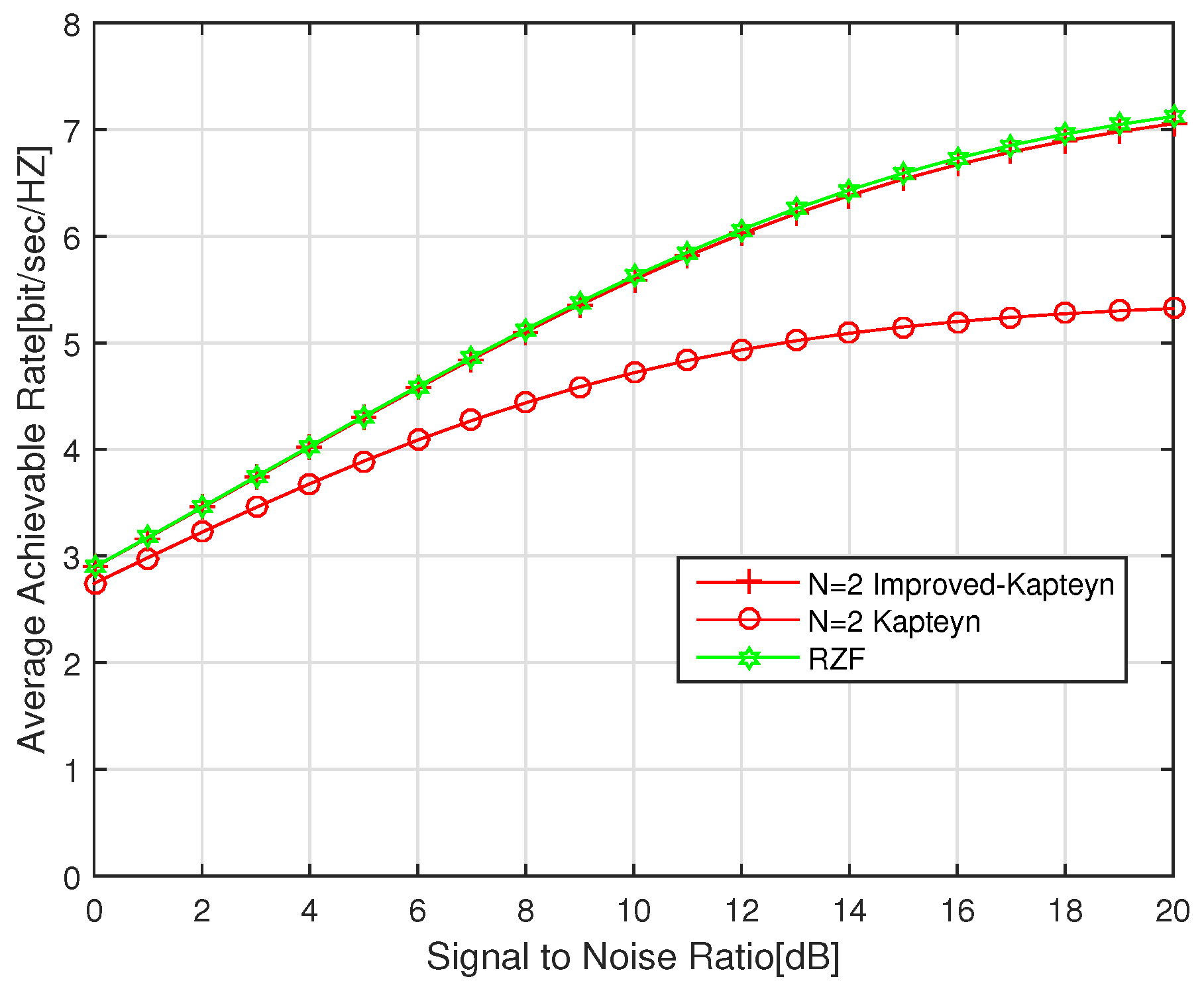
Finally, we end this section by comparing the channel performance of Kapteyn algorithm and Taylor algorithm with certain computational complexity considered. Specifically, the RZF precoding matrix based on truncated Taylor series expansion is given by

$$G_{\mathrm{Taylor}}=\beta \alpha \widehat{\mathbf{H}}\sum _{l=0}^{N-1}\left(\sum _{n=l}^{N-1}{C}_l^n{\left(1-\alpha \xi \right)}^{n-l}{\left(\alpha {\widehat{\mathbf{H}}}^{\mathrm{H}}\widehat{\mathbf{H}}\right)}^l\right).$$

(42)

According to Table 1, it can be found that the computational complexity of the improved Kapteyn algorithm with the truncated order of N is the same as the one of the Taylor algorithm with the truncated order of $N+2$. It is interesting that Figure 5 shows that the average achievable rate obtained by the proposed improved Kapteyn algorithm when $N=2$ or $N=3$ compared the one obtained by the Taylor algorithm with $N=4$ or $N=5$. This observation implies that in the case of the same computational complexity, the improved Kapteyn algorithm performs much better than the Taylor algorithm.

5. Conclusions

In this paper, we propose an improved RZF precoding algorithm based on the truncated Kapteyn series expansion and optimize its expansion coefficients for fast precoding convergence. As the SINR increases for the users, the average achievable data amount obtained by utilizing the proposed coefficients optimization algorithm of the truncated Kapteyn series expansion is much higher than that of the truncated Kapteyn series expansion without coefficients optimization. Compared with the direct matrix inversion required in RZF precoding, the computational complexity of the proposed algorithm is significantly reduced and the computational complexity of the proposed algorithm does not increase with coefficients optimization. Numerical results show that the downlink channel performance in terms of the average achievable rate at the users of the proposed algorithm is better than the ones of the truncated Neumann series and Taylor series expansions in a large-scale single-cell MIMO system. Furthermore, under the condition of same complexity, the performance of the improved RZF precoding algorithm is the best among these compared algorithms. Further work will focus on the research and could target extending the proposed optimization to signal detector in massive MIMO systems in order to reduce the computational complexity.