Predict Electric Power Demand with Extended Goal Graph and Heterogeneous Mixture Modeling
Abstract
1. Introduction
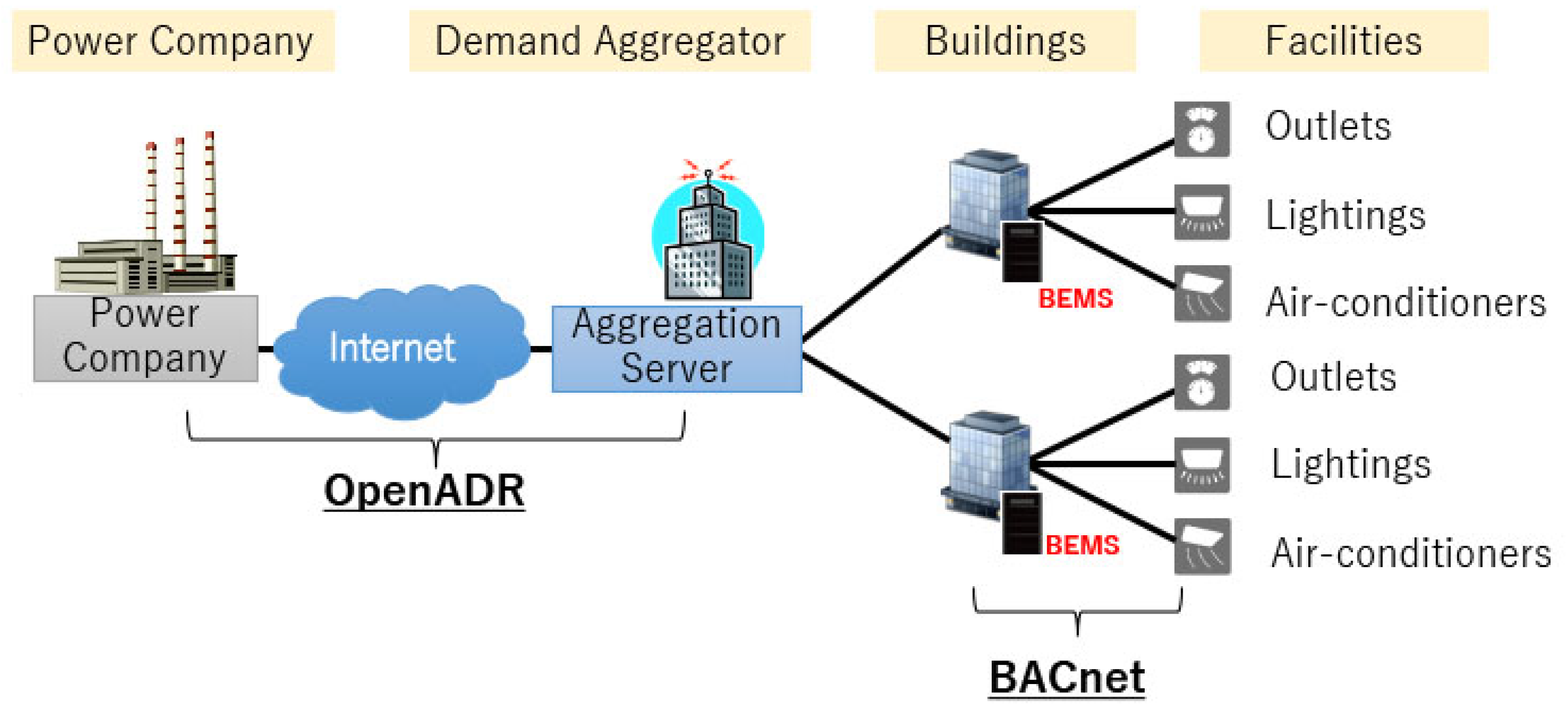
2. Overviews of Building Energy Management System and Energy Demand Prediction Methods
3. Issues and Solutions for Energy Prediction Technique
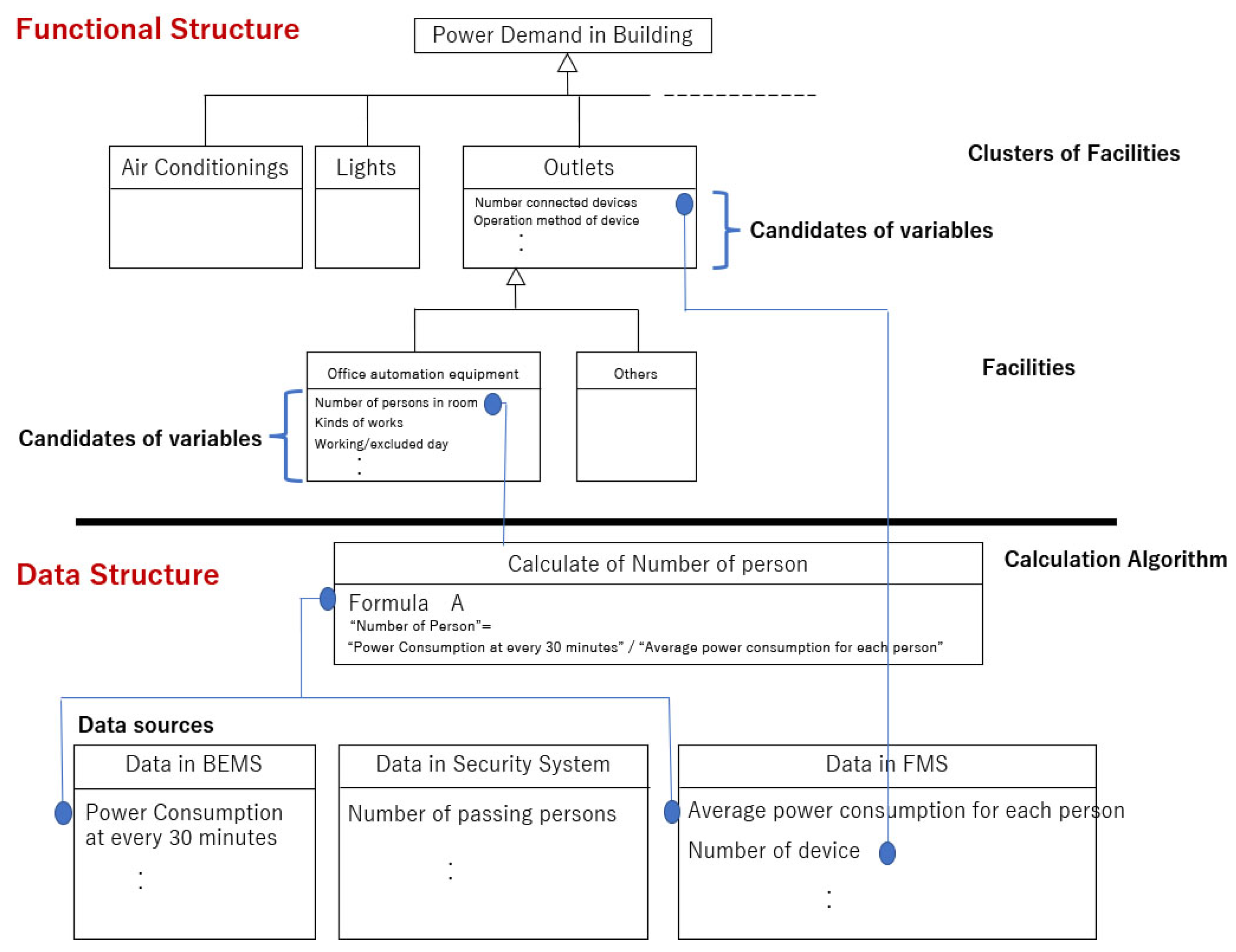
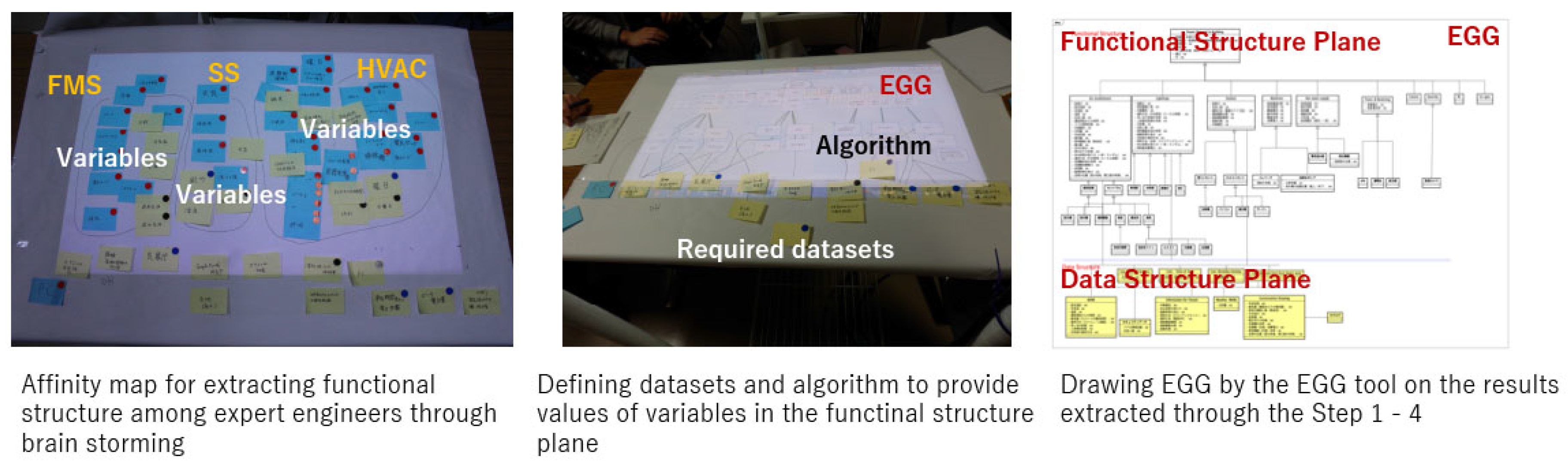
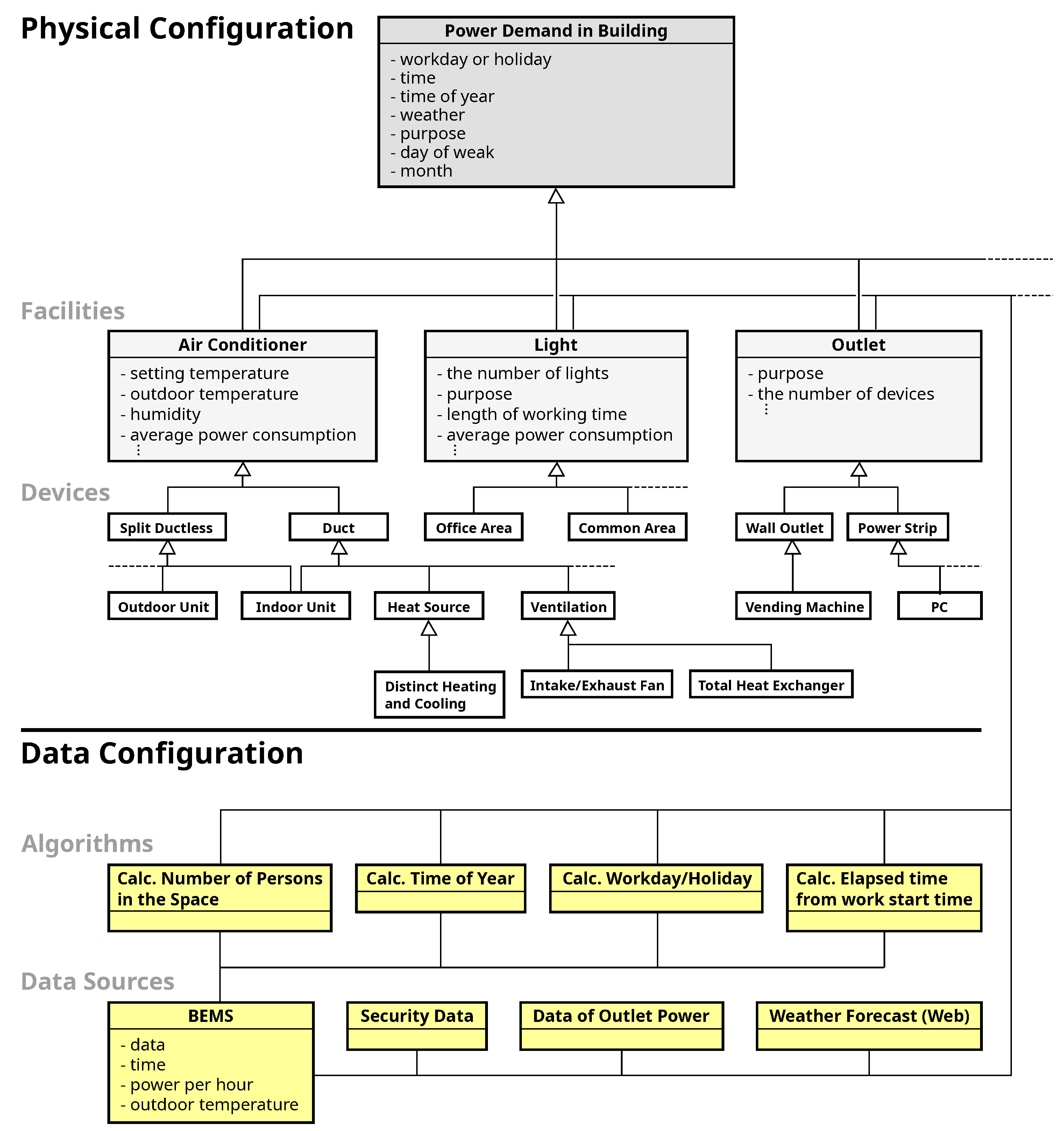
4. Extended Goal Graph (EGG) Tool
- Step1:
- Step2:
- Extract variables to each element in the functional structure plane with brainstorming among domain engineers
- Step3:
- Collect required datasets including the variables (Figure 4 middle)
- Step4:
- Design algorithm for calculating variables indirectly from raw data included in the above datasets
- Step5:
- Draw EGG by using the EGG tool based on the results extracted through Step1–Step4 (Figure 4 right).
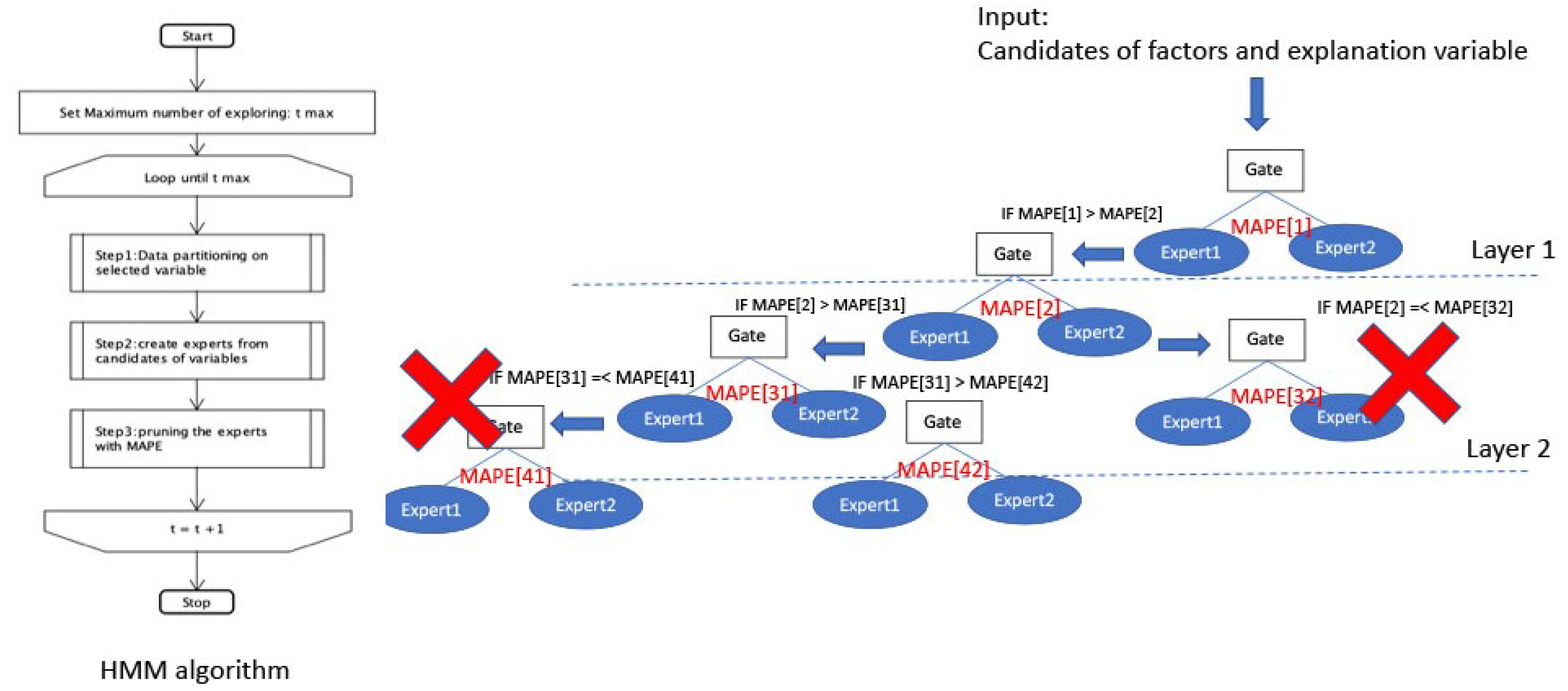
5. Energy Prediction (EP) Tool on the Heterogeneous Mixture Modeling
- Step1:
- Select optional factor from the candidates of factors and separate datasets into more than one datasets with the selected factor. The factors, which are used to separate the datasets per each day (e.g., Workday/Holiday) are given priority to the factors used to separate the datasets per every time (e.g., outdoor temperature and the number of people). The interdependency of the divided datasets is validated with the Kruskal-Wallis H-test [20].
- Step2:
- Create local experts with candidates of explanatory variables for linear regression and calculate the Mean Absolute Percentage Error (MAPE). The correlation among candidates of variables is checked within the divided datasets. The local experts are created with the independent variables through all search, and the expert which achieves most accurate in the MAPE is selected.
- Step3:
- Pruning the local experts with the MAPE. Select another factor from the candidates and execute Step1 and Step2. If the MAPE for the current expert is less than the MAPE for the previous expert, the algorithm prunes the gate and the local experts.
6. Estimation on the Field Data
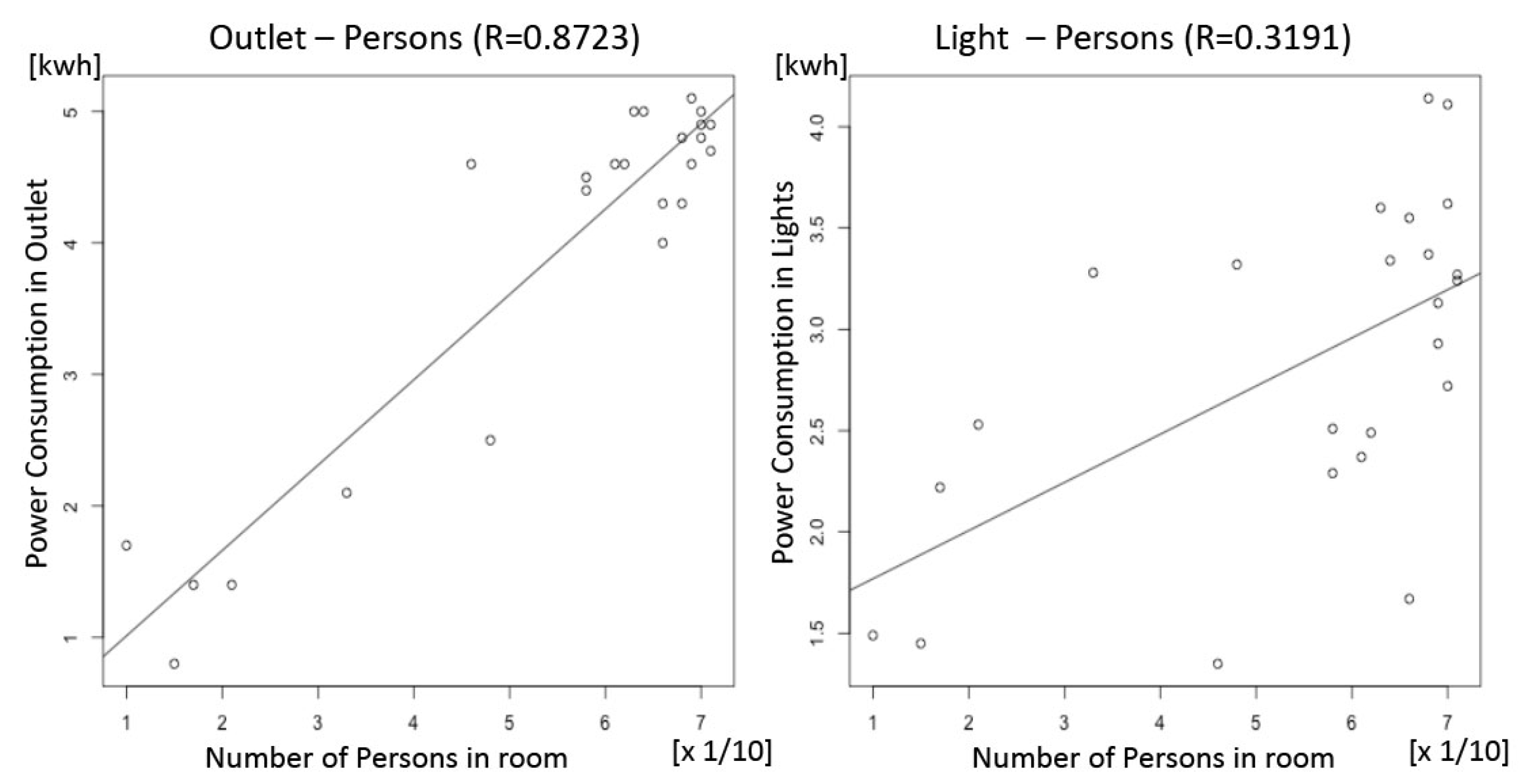
6.1. Extract Candidates for Variables by the EGG Tool
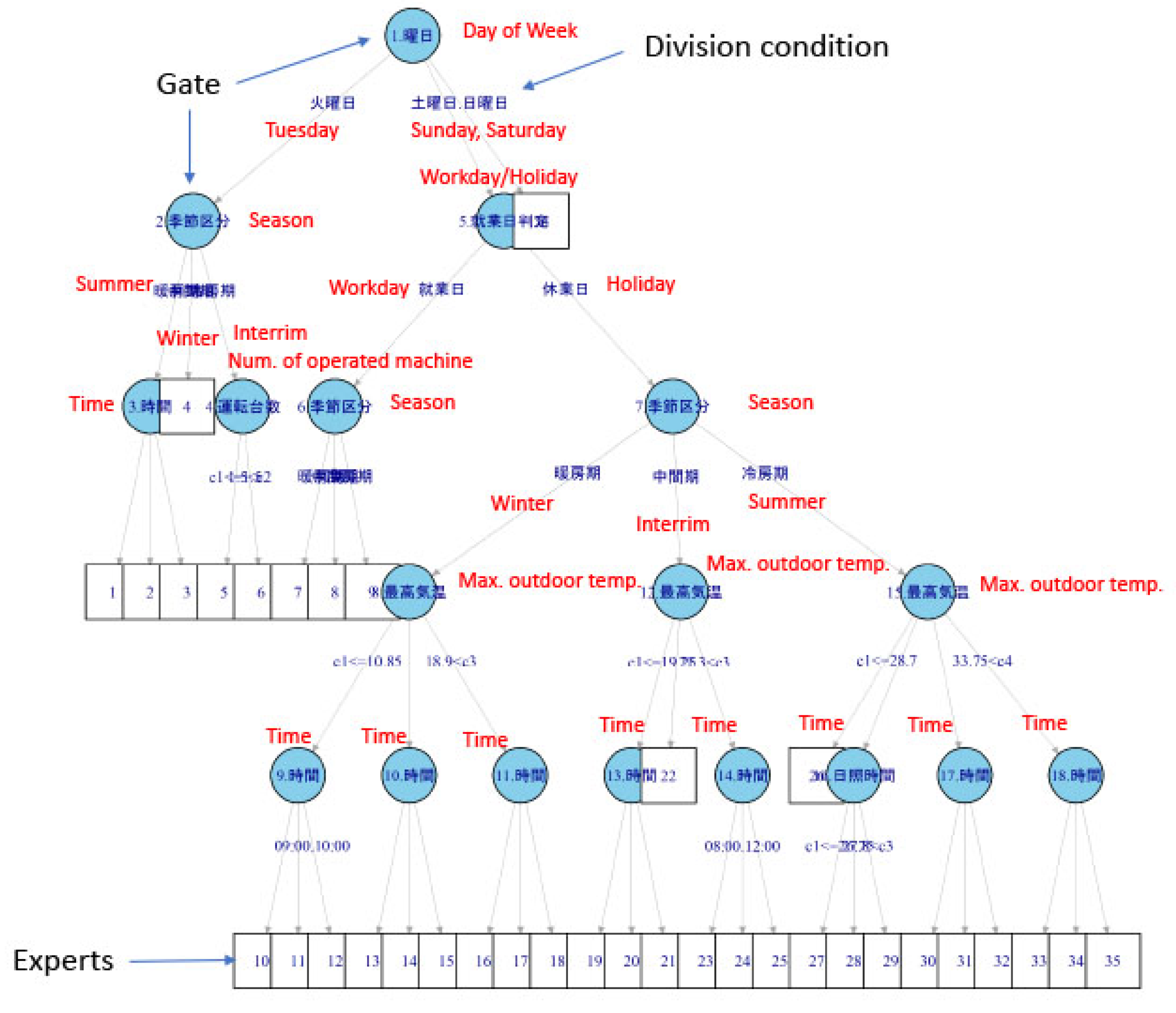
6.2. Create Prediction Model by the EP Tool
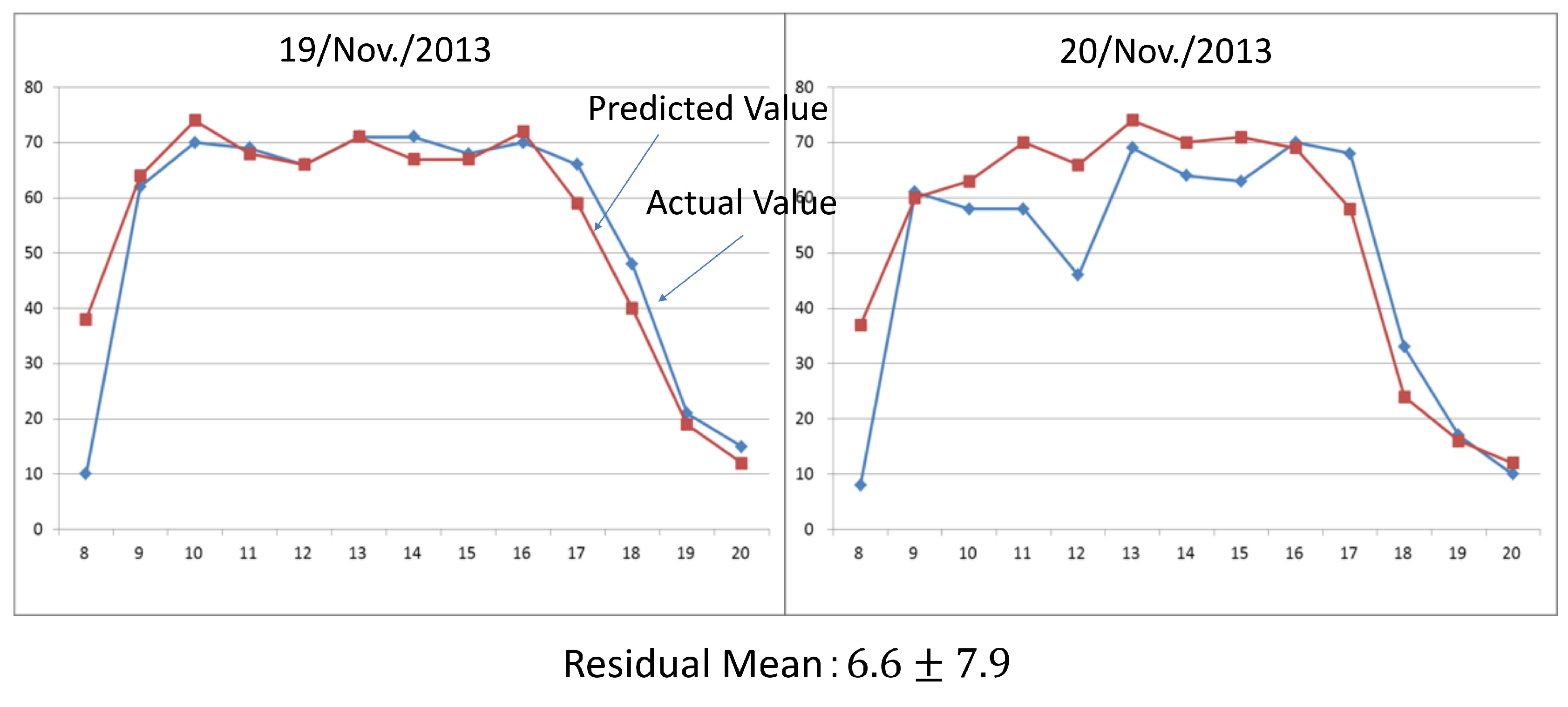
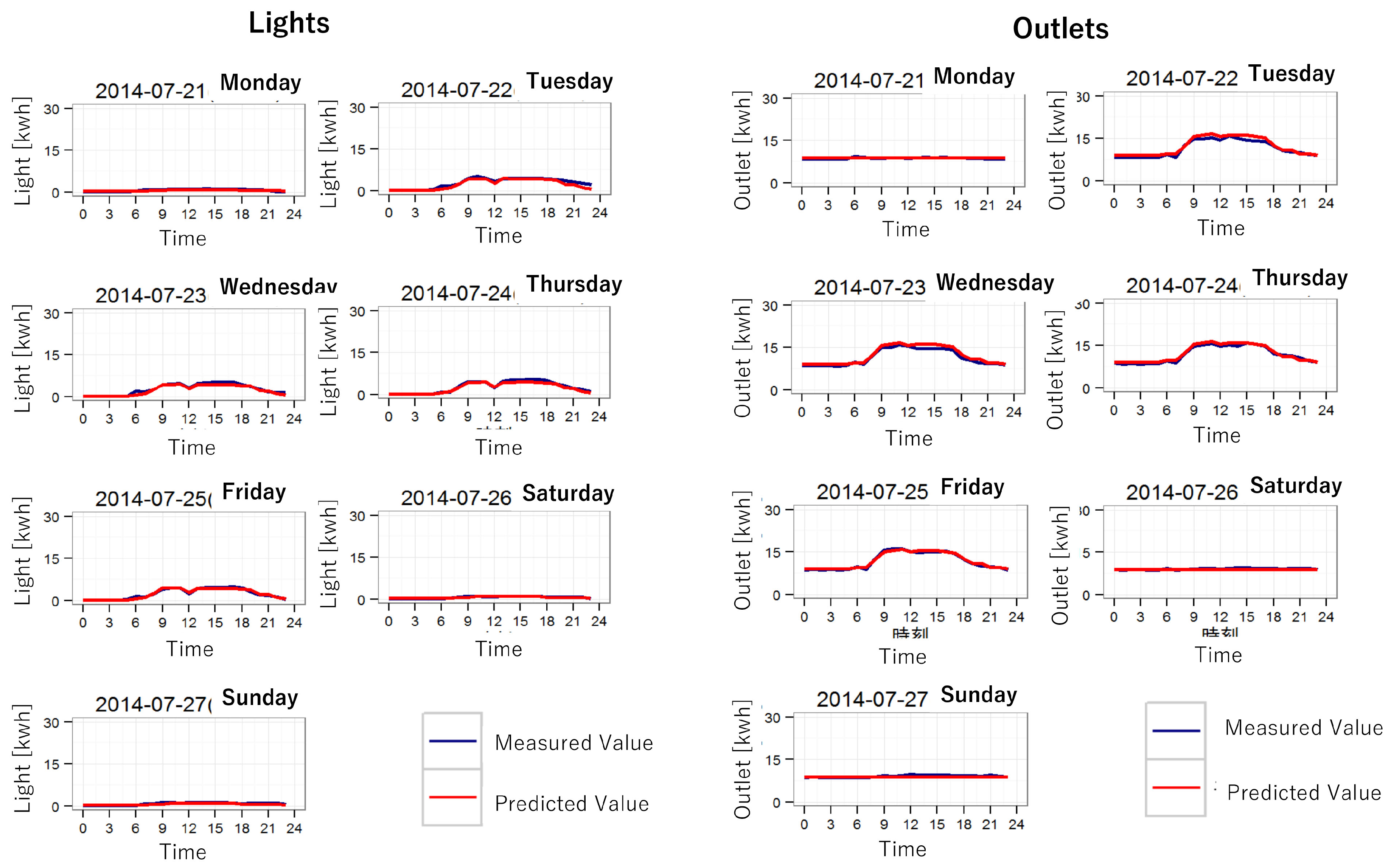
6.3. Results of the Power Demand Forecasting
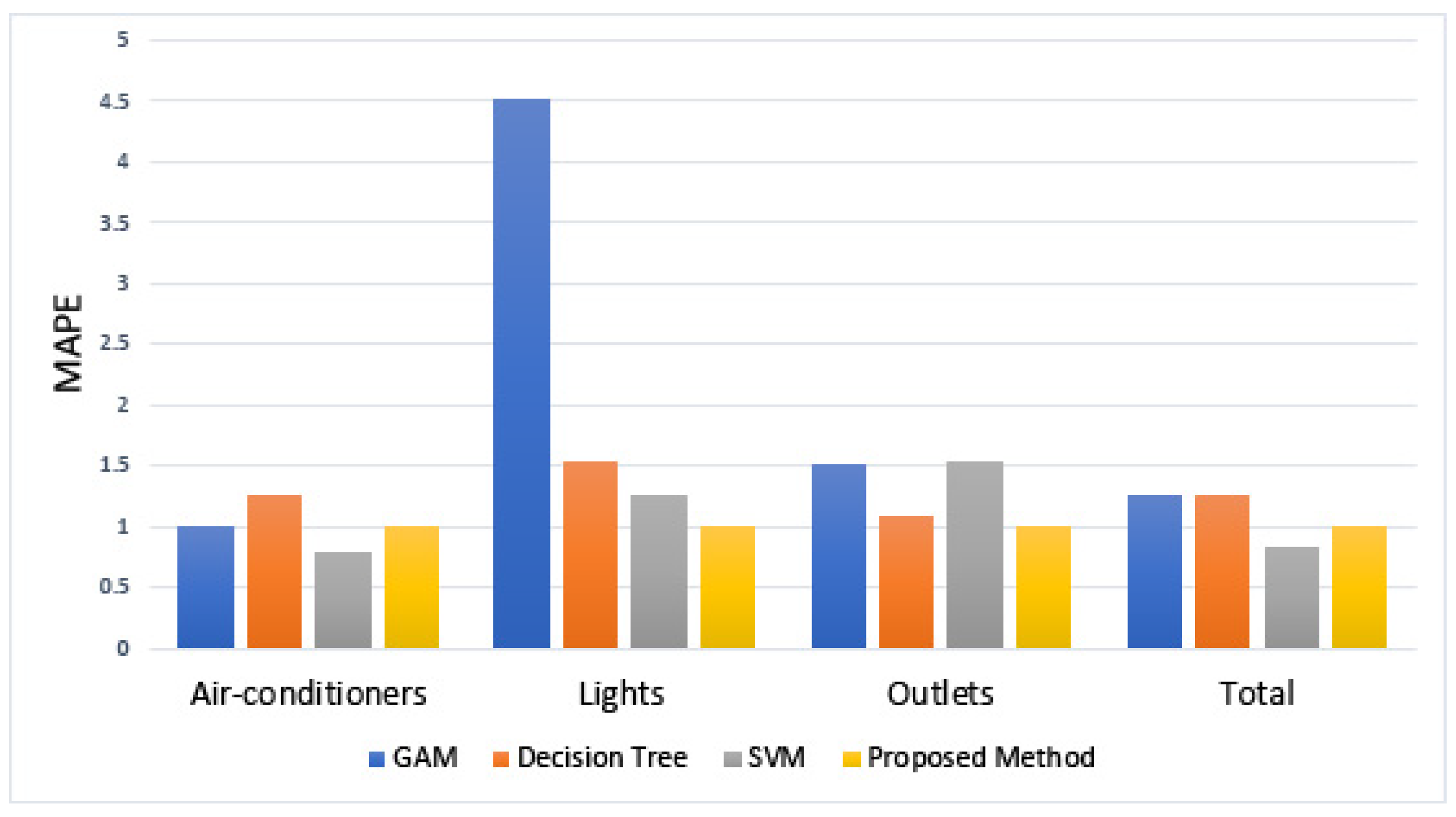
6.4. Comparing Accuracies with the Other Prediction Method
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Agency for Natural Resources and Energy in Japan. The 5th Strategic Energy Plan. Available online: https://www.enecho.meti.go.jp/en/ (accessed on 8 April 2019).
- Edwardsa, R.E.; Newb, J.; Parker, L.E. Predicting future hourly residential electrical consumption: A machine learning case study. Energy Build. 2012, 49, 591–603. [Google Scholar] [CrossRef]
- Mancasi, M.; Vatu, R.; Ceaki, O.; Porumb, R.; Seritan, G. Evolution of smart buildings. A Romanian case. In Proceedings of the 50th International Universities Power Engineering Conference (UPEC), Staffordshire, UK, 1–4 September 2015. [Google Scholar]
- Rudin, C. Algorithm for interpretable machine learning. In Proceedings of the 20th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD), New York, NY, USA, 24–27 August 2014. [Google Scholar]
- MacKay, D.J. Bayesian nonlinear modeling for the prediction competition. ASHRAE Trans. 1994, 100, 1053–1062. [Google Scholar]
- Dong, B.; Cao, C.; Lee, S. Applying support vector machines to predict building energy consumption in tropical region. Energy Build. 2005, 37, 545–553. [Google Scholar] [CrossRef]
- Iijima, M.; Takeuchi, R.; Takagi, K.; Matsumoto, T. Piecewise-linear regression on the ASHRAE time-series data. ASHRAE Trans. 1994, 100, 1088–1095. [Google Scholar]
- Fujimaki, R.; Sogawa, Y.; Morinaga, S. Online heterogeneous mixture modeling with marginal and copula selection. In Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 21–24 August 2011. [Google Scholar]
- Oiwa, H.; Fujimaki, R. Partition-wise linear models. Adv. Neural Inf. Process. Syst. 2014, 27, 3527–3535. [Google Scholar]
- Eto, R.; Fujimaki, R.; Morinaga, S.; Tamano, H. Fully-automatic bayesian piecewise sparse linear models. In Proceedings of the 17th International Conference on Artificial Intelligence and Statistics, Reykjavik, Iceland, 22–24 April 2014. [Google Scholar]
- Kushiro, N.; Shimizu, T.; Ehira, T. Requirements elicitation with extended goal graph. In Proceedings of the 20th International Conference on Knowledge Based and Intelligent Information and Engineering System, KES2016, York, UK, 5–7 September 2016; pp. 1691–1700. [Google Scholar]
- Ifuku, M.; Kushiro, N.; Aoyama, Y. Requirements definition with extended goal graph. In Proceedings of the IEEE International Conference on Data Mining, Singapore, 17–20 November 2018. [Google Scholar]
- OpenARD Alliance. OpenADR2.0 Specifications. Available online: https://www.openadr.org (accessed on 8 April 2019).
- ASHRAE. A Data Communication Protocol for Building Automation and Control Networks. Available online: http://www.bacnet.org/Overview/index.html (accessed on 8 April 2019).
- Mega, T.; Kitagami, S.; Kawawaki, S.; Kushiro, N. Experimental evaluation of a fast demand response system for small and medium sized office buildings. In Proceedings of the 31st IEEE International Conference on Advanced Information Networking and Application (WAINA2017), Taipei, Taiwan, 27–29 March 2017. [Google Scholar]
- Ryan, S.E.; Porth, L.S. A Tutorial on the Piecewise Regression Approach Applied to Bed Load Transport Data; General Technical Report RMRS-GTR-189; US Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2007. Available online: https://www.fs.usda.gov/treesearch/pubs/all/27004 (accessed on 8 April 2019).
- Hofmann, T.; Schlkopf, B.; Smola, A.J. Kernel methods in machine learning. Ann. Stat. 2008, 36, 11711220. [Google Scholar] [CrossRef]
- Friedentahl, S.; Moore, A.; Steiner, R. A Practical Guide to SysML; Morgan Kaufmann OMG Press: Needham, MA, USA, 2012. [Google Scholar]
- Gray, D.; Brown, S.; Macnufo, J. Game Storming a Playbook for Innovators, Rule Breakers, and Change Makers; O’REILLY: Springfield, MO, USA, 2010. [Google Scholar]
- Corder, G.W.; Foreman, D.I. Nonparametric Statistics for Non-Statisticians a Step-by-Step Approach; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Porumb, R.; Postolache, P.; Seritan, G.; Vatu, R.; Ceaki, O. Load profiles analysis for electricity market. Comput. Methods Soc. Sci. 2013, 1, 30–38. [Google Scholar]
- Hastie, T.J.; Tibshirani, R.J. Generalized Additive Models; Chapman & Hall: Boca Raton, FL, USA, 1990. [Google Scholar]
- Kaminski, B.; Jakubczyk, M.; Szufel, P. A framework for sensitivity analysis of decision trees. Cent. Eur. J. Oper. Res. 2017, 26, 135–159. [Google Scholar] [CrossRef] [PubMed]
- Lander, J.P. R for Everyone: Advanced Analytics and Graphics; Addison-Wesley: Boston, MA, USA, 2017. [Google Scholar]
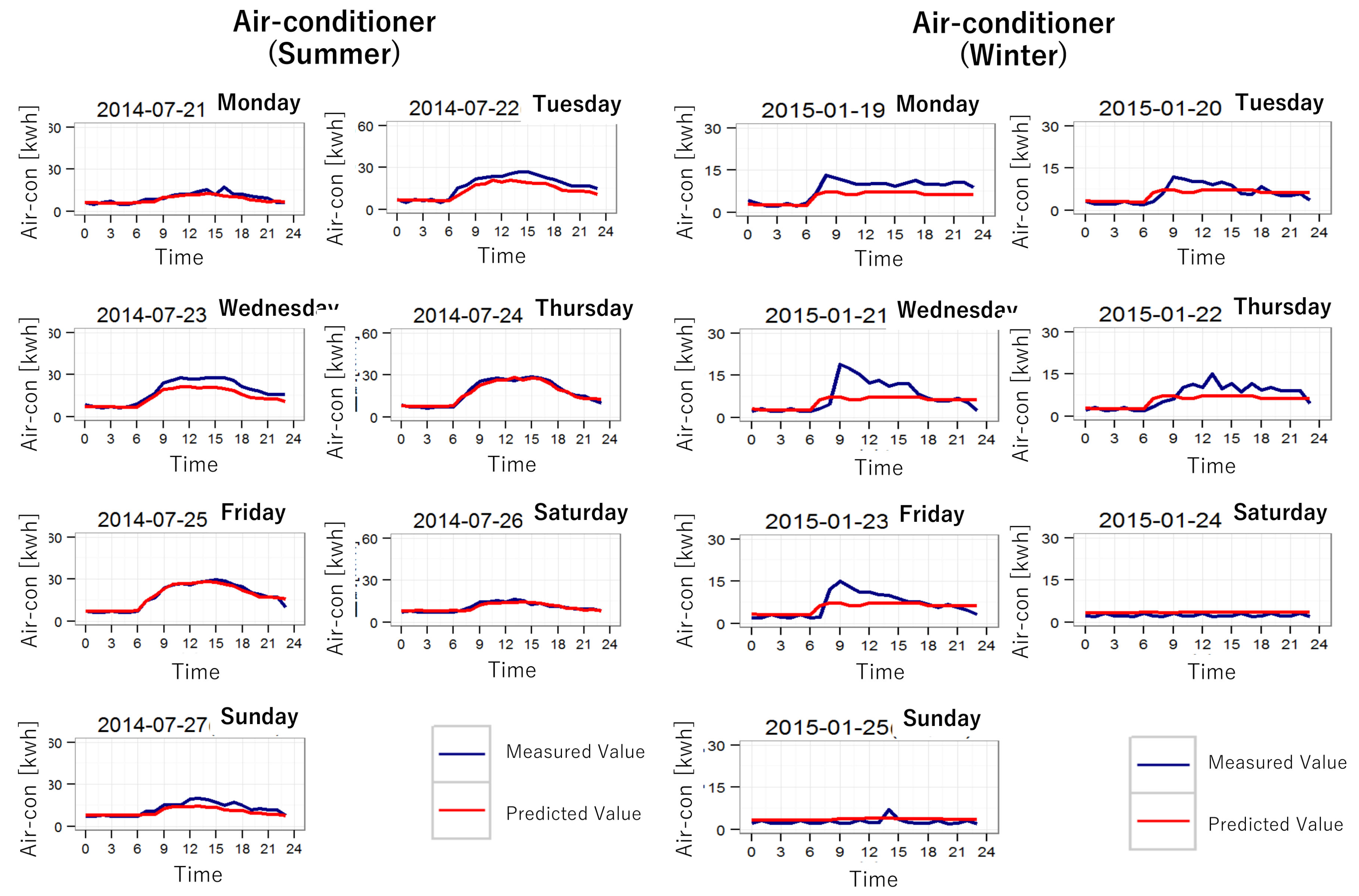
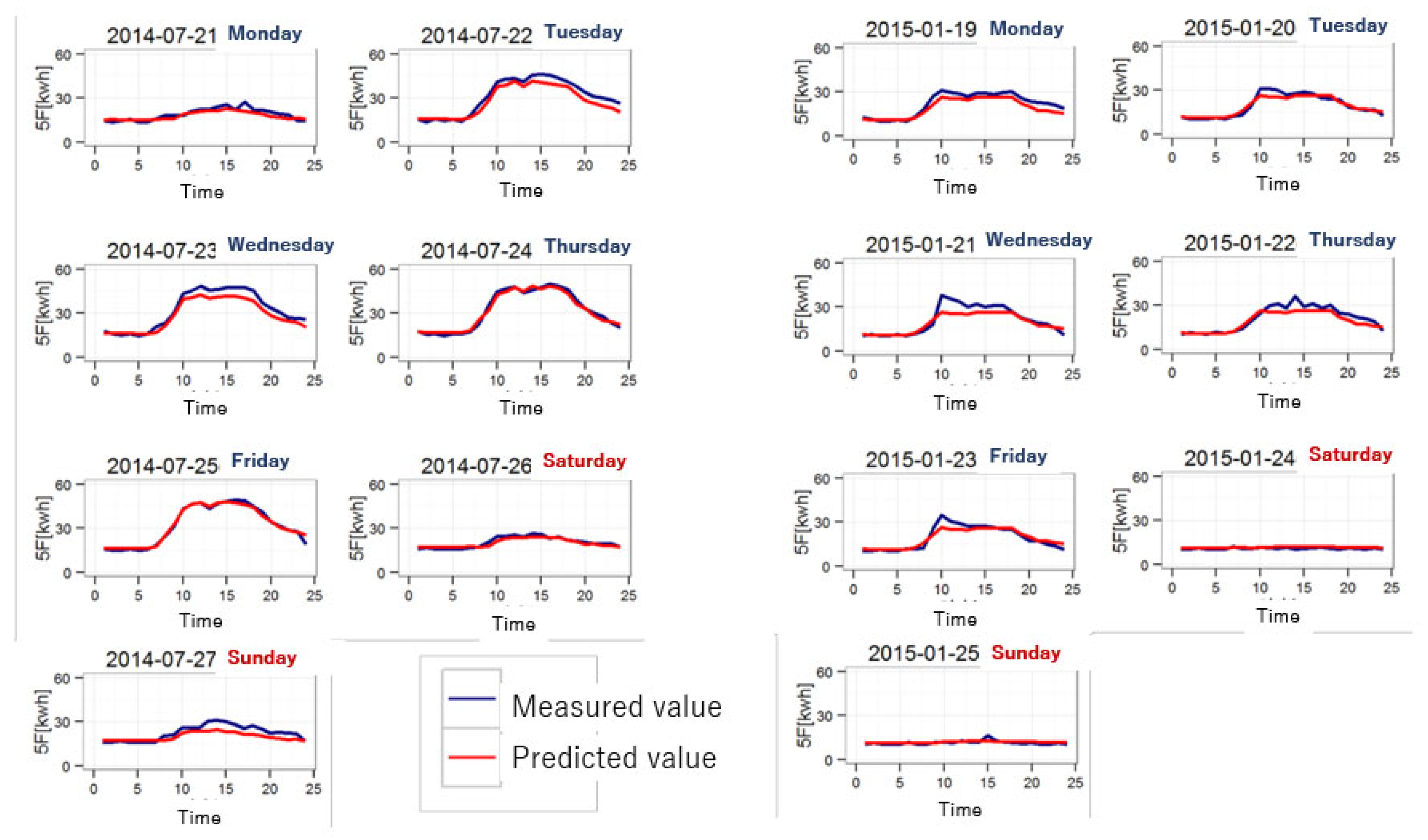
| Num. | Functions |
|---|---|
| 1 | Define appropriate prediction model on the learning data with the candidates of factors and explanation variables obtained in the EGG |
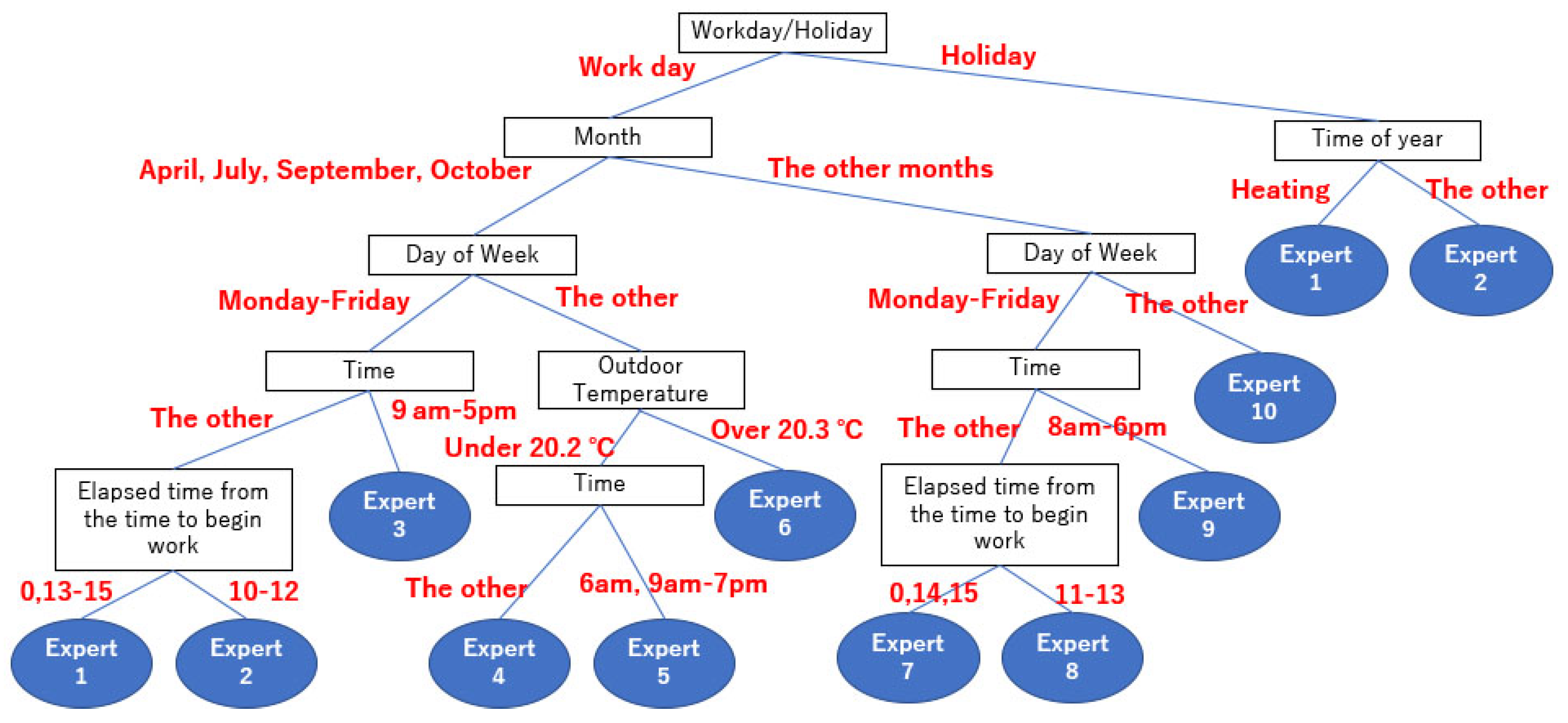
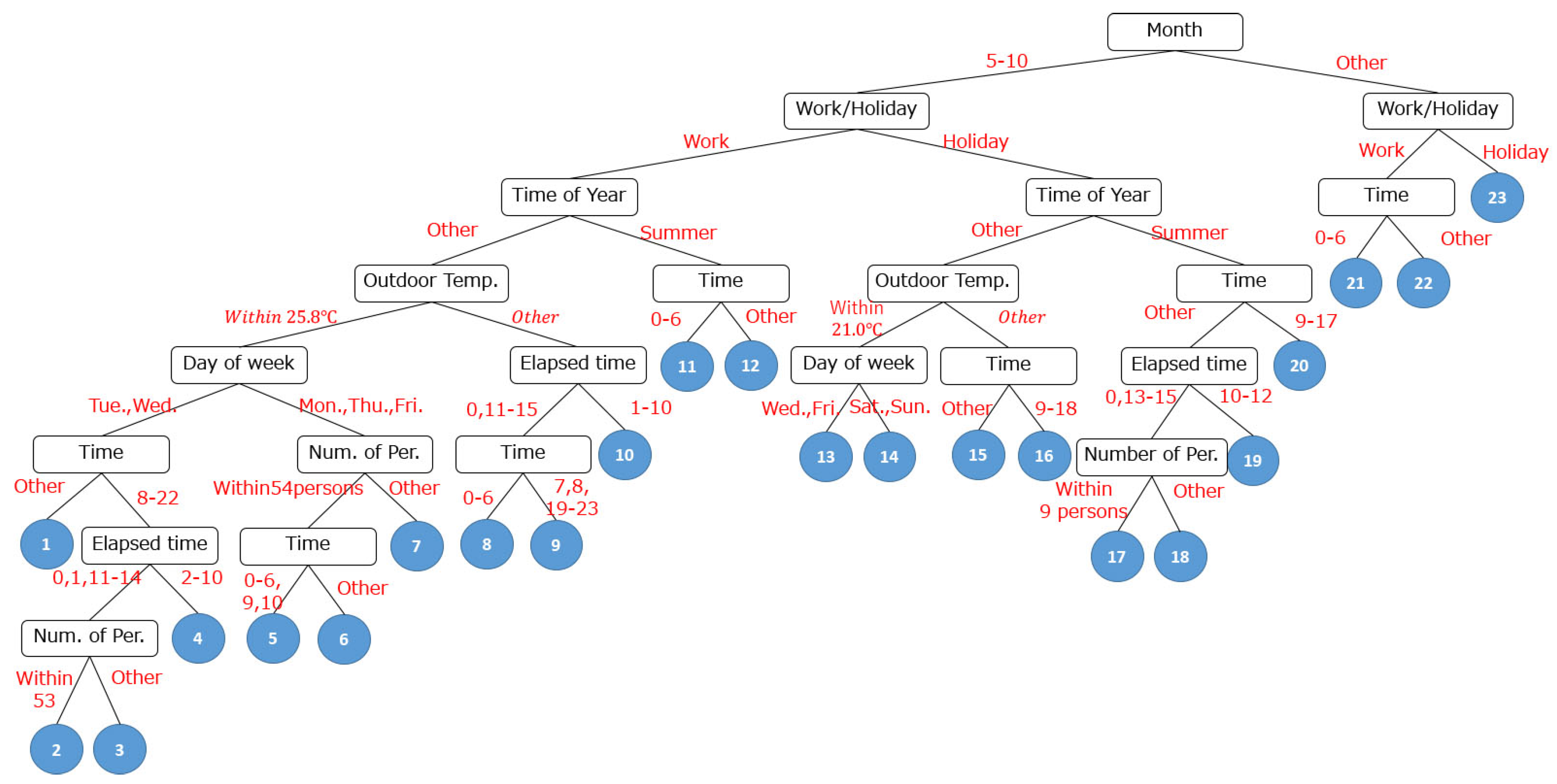
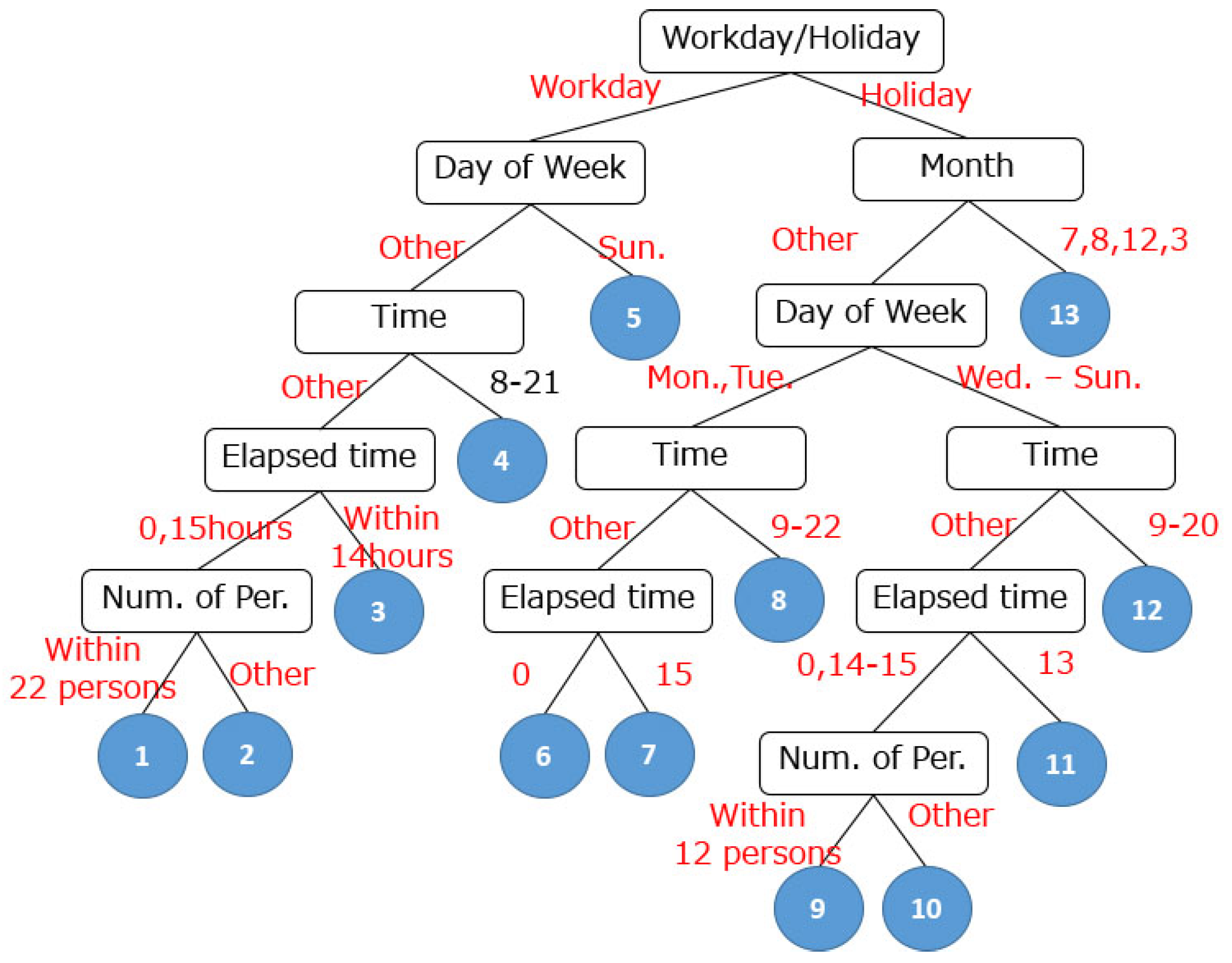
| 2 | Visualize hierarchical structure of factors and local experts (Figure 6) |
| 3 | Predict the energy demand on the testing data |
| 4 | Calculate MAPE in comparison with the predicted value and the measured value |
| Item | Detail |
|---|---|
| Targeted data | BEMS data for eight stories office building |
| Data period | 1 March 2013–31 March 2015 (730 days) |
| Data for learning | 1 April 2013–31 March 2014 (365 days) |
| Data for estimation | 31 March 2015 (365 days) |
| Variables included in datasets | date + time + power per hour + outdoor temperature |
| File format and Size | CSV (about 8 MB) |
| Candidate of Variable | Source of Datasets |
|---|---|
| Workday/Holiday | Calculated indirectly with the algorithm on BEMS data |
| Day of week | BEMS data |
| Time | BEMS data |
| Elapsed time the from work start time | BEMS data |
| Month | BEMS data |
| Time of year (cooling/heating/the other) | Calculated indirectly with the algorithm on BEMS data |
| Outdoor temperature | BEMS data |
| Number of people in the space | Calculated indirectly with the algorithm on BEMS data |
| Methods | Air-Conditioners | Lightings | Outlets | Total |
|---|---|---|---|---|
| Generalized Additive Model (GAM) | 1.00 | 4.54 | 1.52 | 1.29 |
| Decision Tree | 1.27 | 1.55 | 1.09 | 1.25 |
| Support Vector Machine (SVM) | 0.81 | 1.26 | 1.54 | 0.85 |
| Proposed Methods | 1.00 | 1.00 | 1.00 | 1.00 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kushiro, N.; Fukuda, A.; Kawatsu, M.; Mega, T. Predict Electric Power Demand with Extended Goal Graph and Heterogeneous Mixture Modeling. Information 2019, 10, 134. https://doi.org/10.3390/info10040134
Kushiro N, Fukuda A, Kawatsu M, Mega T. Predict Electric Power Demand with Extended Goal Graph and Heterogeneous Mixture Modeling. Information. 2019; 10(4):134. https://doi.org/10.3390/info10040134
Chicago/Turabian StyleKushiro, Noriyuki, Ami Fukuda, Masatada Kawatsu, and Toshihiro Mega. 2019. "Predict Electric Power Demand with Extended Goal Graph and Heterogeneous Mixture Modeling" Information 10, no. 4: 134. https://doi.org/10.3390/info10040134
APA StyleKushiro, N., Fukuda, A., Kawatsu, M., & Mega, T. (2019). Predict Electric Power Demand with Extended Goal Graph and Heterogeneous Mixture Modeling. Information, 10(4), 134. https://doi.org/10.3390/info10040134




