A New Rapid Incremental Algorithm for Constructing Concept Lattices
Abstract
1. Introduction
2. The Basis of Formal Concept Lattice
- (1)
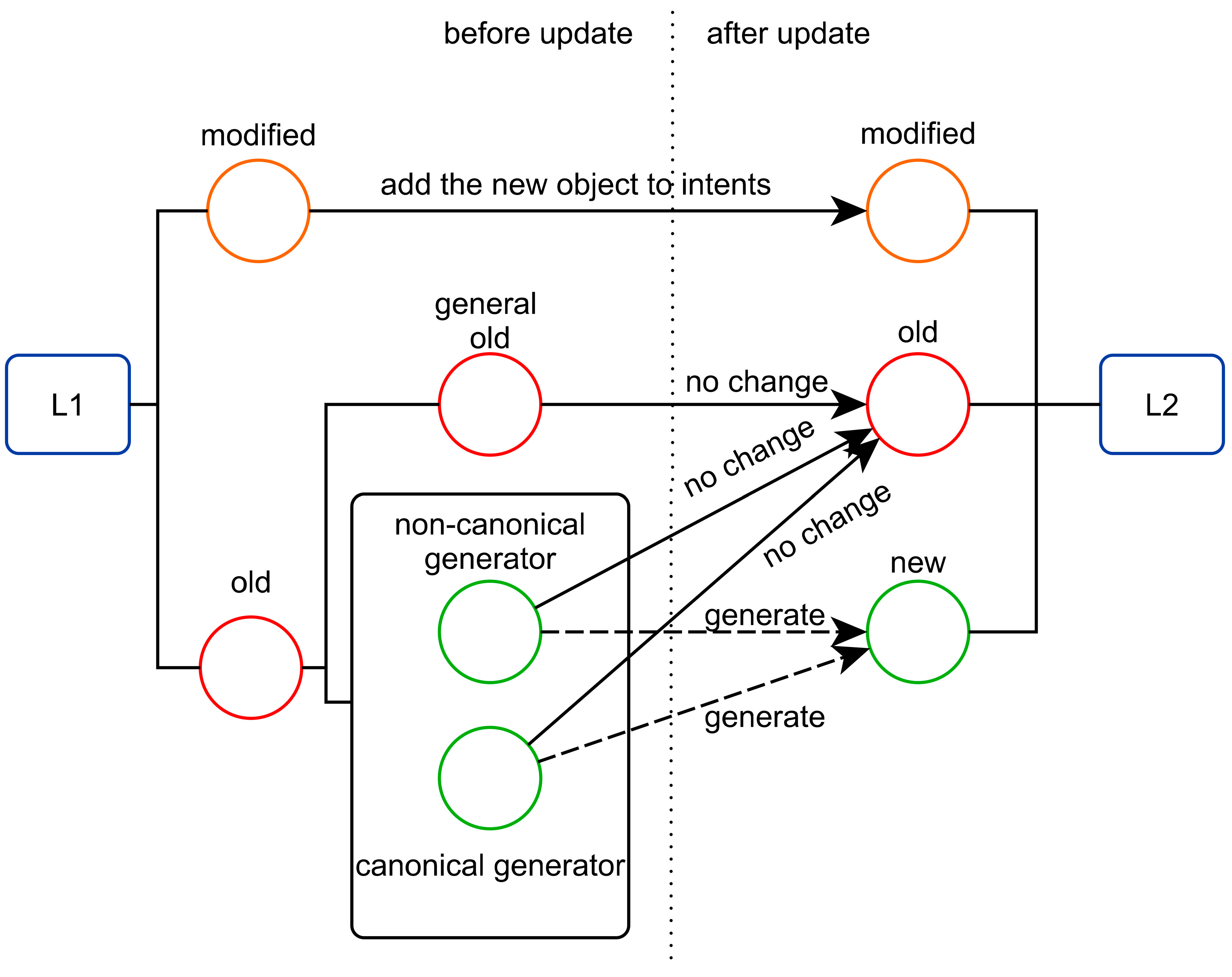
- (A, B) is a new concept if A is not an extent of any concept in L1,
- (2)
- (A, B) is a modified concept if A ⊆ m’ and A is an extent of one concept in L1,
- (3)
- If (A, B) is unchanged from L1 to L2, it is an old concept,
- (4)
- Assuming that (X, Y) is a new concept and (A, B) is an old concept, if they satisfy A∩m’ = X ≠ A, the concept (A, B) is the generator of the concept (X, Y). Otherwise, it is a general old concept.
3. Related Work
4. A New Rapid AddExtent Algorithm
4.1. The Overall Procedure
| Algorithm 1: Procedure FastAddExtent(extent, generatorConcept, L, n) {#} |
| 1: tempConcept = generatorConcept {*} |
| 2: generatorConcept = GetClosureConcept(extent, generatorConcept, L, n) |
| 3: tempConcept.doExtent = extent {*} |
| 4: tempConcept.MaximalConcept = generatorConcept {*} |
| 5: if generatorConcept.Extent == extent then |
| 6: return generatorConcept |
| 7: end if |
| 8: GeneratorChildren = generatorConcept.Children |
| 9: newChildren = ∅ |
| 10: for each candidate in GeneratorChildren |
| 11: meet = candidate.Extent ∩ extent |
| 12: if meet != candidate.Extent then |
| 13: if candidate.visited == n then {*} |
| 14: candidate = candidate.NewConcept {*} |
| 15: else |
| 16: if meet ∩ candidate.doExtent == meet then {*} |
| 17: candidate = candidate.MaximalConcept {*} |
| 18: end if |
| 19: NC = FastAddExtent(meet, candidate, L, n) {#} |
| 20: candidate.NewConcept = NC {*} |
| 21: candidate.visited = n {*} |
| 22: candidate = NC {*} |
| 23: end if |
| 24: end if |
| 25: addChild = true |
| 26: for each Child in NewChildren |
| 27: if Candidate.Extent ⊆ Child.Extent then |
| 28: addChild = false |
| 29: exit for |
| 30: else if Child.Extent ⊆ Candidate.Extent then |
| 31: remove Child from NewChildren |
| 32: end if |
| 33: end for |
| 34: if addChild then |
| 35: add Candidate to NewChildren |
| 36: end if |
| 37: end for |
| 38: newConcept = (extent, generatorConcept.Intent) |
| 39: L = L∪{newConcept} |
| 40: for each Child in NewChildren |
| 41: removeLink(Child, generatorConcept, L) |
| 42: SetLink(Child, newConcept, L) |
| 43: end for |
| 44: SetLink(newConcept, generatorConcept, L) |
| 45: generatorConcept.NewConcept = newConcept {*} |
| 46: return newConcept |
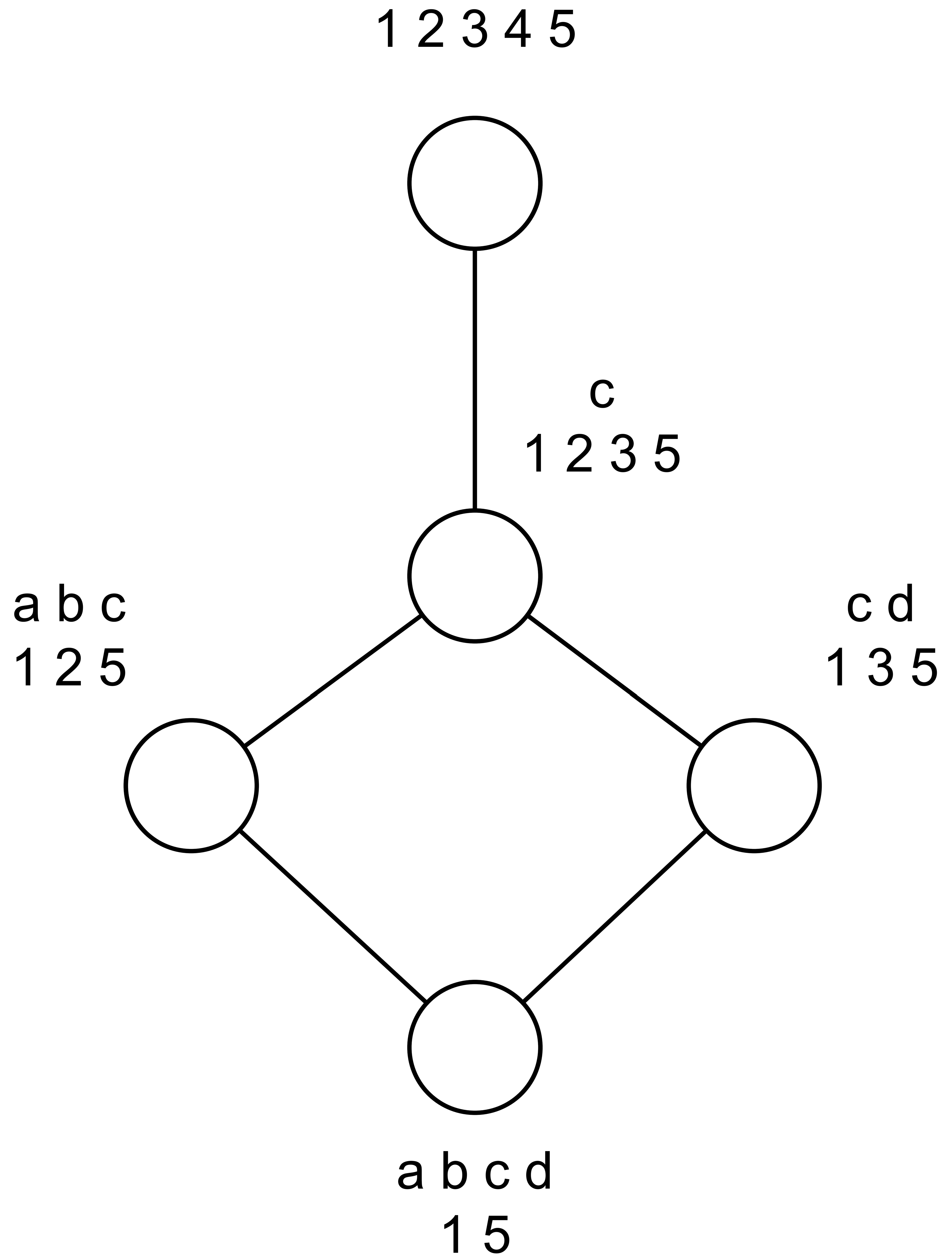
- c0 ({1, 2, 3, 4, 5}, ∅)
- c1 ({1, 2, 3, 5}, {c})
- c2 ({1, 2, 5}, {a, b, c})
- c3 ({1, 3, 5}, {c, d})
- c4 ({1, 5}, {a, b, c, d})
- c5 ({1, 2, 3}, {c, e})
- c6 ({1, 2}, {a, b, c, e})
- c7 ({1, 3}, {c, d, e})
- c8 ({1}, {a, b, c, d, e})
4.2. Find the Canonical Generator
| Algorithm 2: Procedure GetClosureConcept (extent, generator, L): |
| 1: extentConcept = L.Find(extent) |
| 2: if extentConcept ≠ ∅then |
| 3: return extentConcept |
| 4: end if |
| 5: childIsMinimal = true |
| 6: while childIsMinimal |
| 7: childIsMinimal = false |
| 8: Children = GetChildren(GeneratorConcept, L) |
| 9: for each Child in Children |
| 10: if extent ⊆ Child.Extent |
| 11: GeneratorConcept = Child |
| 12: childIsMinimal = true |
| 13: end if |
| 14: end for |
| 15: return GeneratorConcept |
| Algorithm 3: Procedure CreateLatticeIncrementally(G, M, I |
| 1: topConcept = (G, ∅) |
| 2: L = {topConcept} |
| 3: i = 0 |
| 4: for each m in M |
| 5: i++ |
| 6: propertyConcept = FastAddIntent(m′,topConcept, L, i) |
| 7: Add m to the intent of propertyConcept and all concepts above |
| 8: end for |
| 9: return L |
5. Complexity Issues
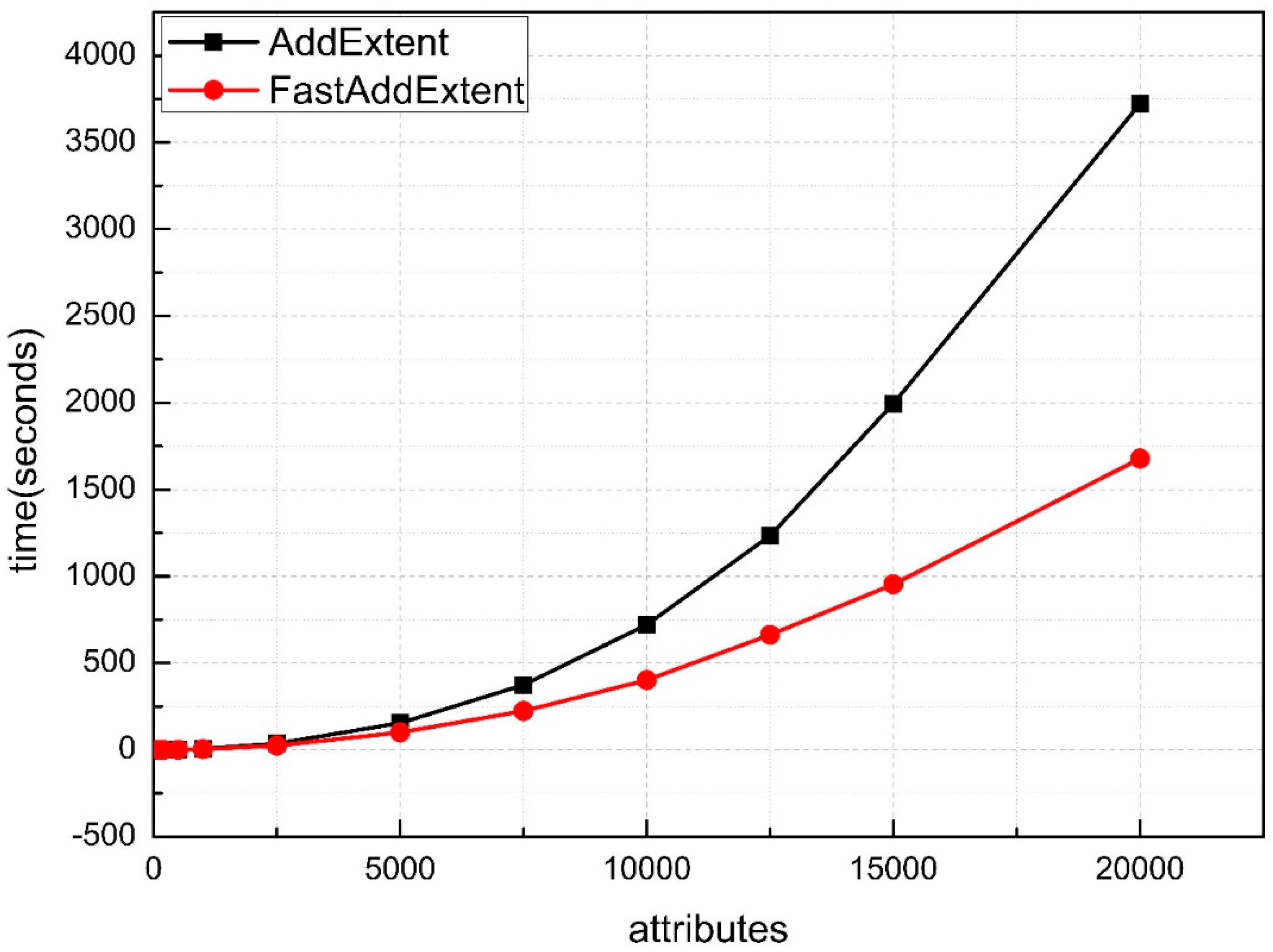
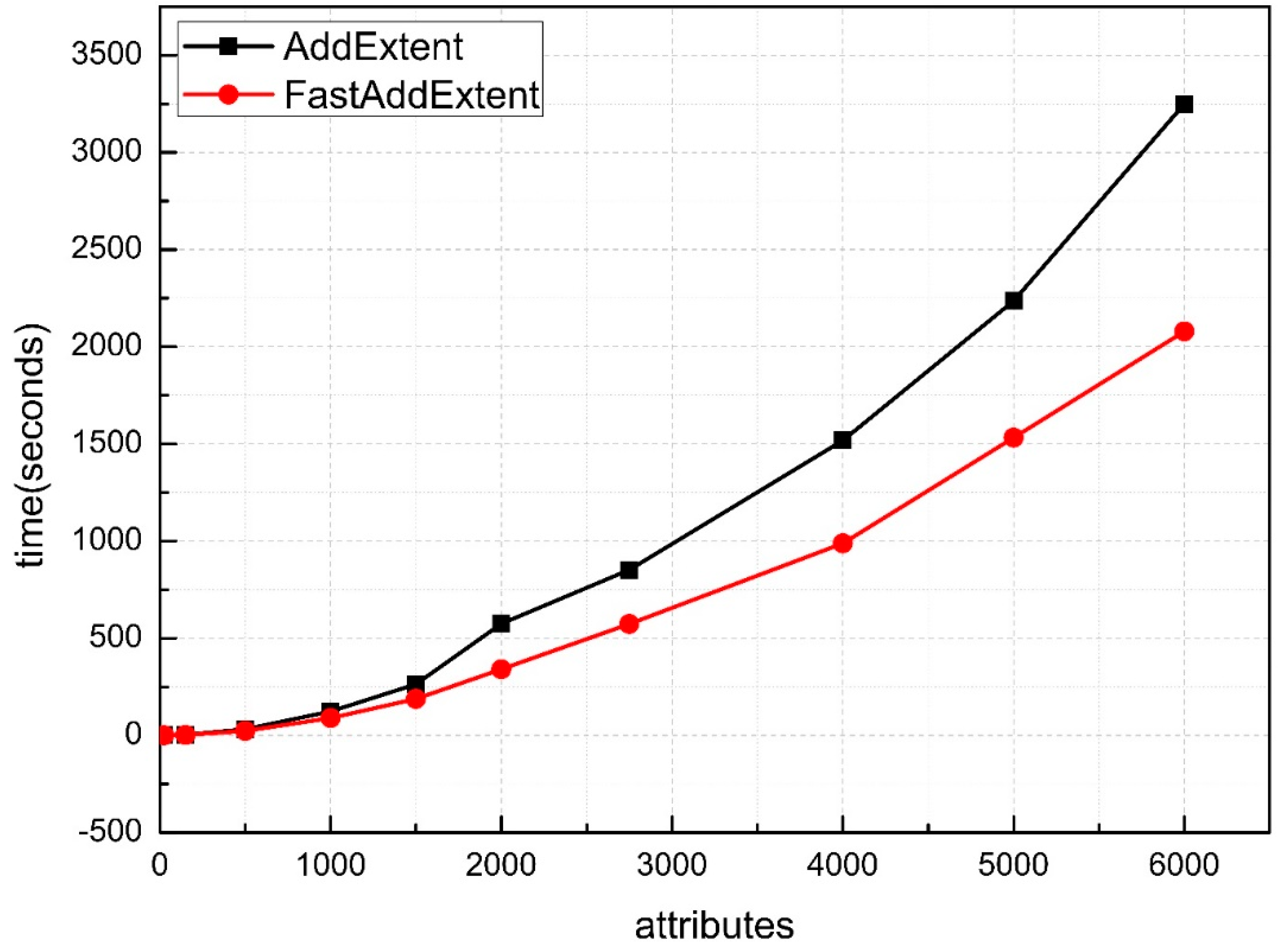
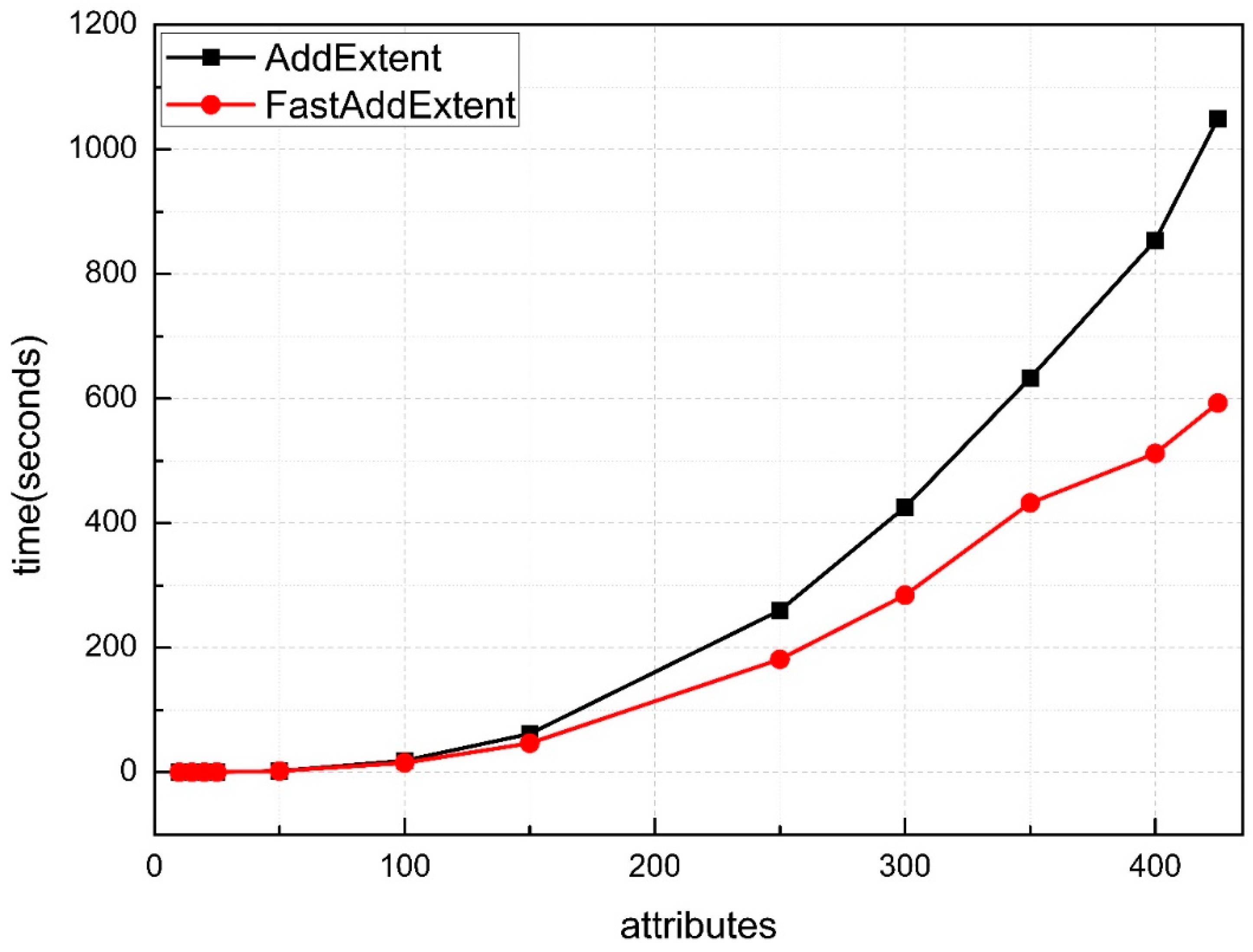
6. Experimental Evaluation and Analysis
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wille, R. Restructuring lattice theory: An approach based on hierarchies of concepts. In International Conference on Formal Concept Analysis; Springer: Berlin/Heidelberg, Germany, 2009; pp. 314–339. [Google Scholar]
- Ganter, B.; Wille, R. Formal Concept Analysis: Mathematical Foundations. (Translated from the German by Cornelia Franzke); Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Valtchev, P.; Missaoui, R. Building concept (Galois) lattices from parts: Generalizing the incremental methods. In International Conference on Conceptual Structures; Springer: Berlin/Heidelberg, Germany, 2001; pp. 290–303. [Google Scholar]
- Godin, R.; Missaoui, R.; Alaoui, H. Incremental concept formation algorithms based on Galois (concept) lattices. Comput. Intell. 1995, 11, 246–267. [Google Scholar] [CrossRef]
- Ganter, B. Two basic algorithms in concept analysis. In International Conference on Formal Concept Analysis; Springer: Berlin/Heidelberg, Germany, 2010; pp. 312–340. [Google Scholar]
- Bordat, J.-P. Calcul pratique du treillis de Galois d’une correspondance. Mathématiques et Sciences Humaines 1986, 96, 31–47. [Google Scholar]
- Norris, E.M. An algorithm for computing the maximal rectangles in a binary relation. Revue Roumaine de Mathématiques Pures et Appliquées 1978, 23, 243–250. [Google Scholar]
- Kuznetsov, S.O.; Obiedkov, S.A. Comparing performance of algorithms for generating concept lattices. J. Exp. Theor. Artif. Intell. 2002, 14, 189–216. [Google Scholar] [CrossRef]
- Zou, L.; Zhang, Z.; Long, J.; Zhang, H. A fast incremental algorithm for deleting objects from a concept lattice. Knowl.-Based Syst. 2015, 89, 411–419. [Google Scholar] [CrossRef]
- Zou, L.; Zhang, Z.; Long, J. An efficient algorithm for increasing the granularity levels of attributes in formal concept analysis. Expert Syst. Appl. 2016, 46, 224–235. [Google Scholar] [CrossRef]
- Wermelinger, M.; Yu, Y.; Strohmaier, M. Using formal concept analysis to construct and visualise hierarchies of socio-technical relations. In Proceedings of the 2009 31st International Conference on Software Engineering—Companion Volume, Vancouver, BC, Canada, 16–24 May 2009; pp. 327–330. [Google Scholar]
- Ganter, B.; Stumme, G.; Wille, R. Formal Concept Analysis: Foundations and Applications; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3626. [Google Scholar]
- Priss, U. Linguistic applications of formal concept analysis. In Formal Concept Analysis; Springer: Berlin/Heidelberg, Germany, 2005; pp. 149–160. [Google Scholar]
- Ghani, I.; Jeong, S.R. Software Climate Change and its Disruptive Weather: A Potential Shift from”Software Engineering” to Vibrant/Dynamic Softology. KSII Trans. Internet Inf. Syst. 2016, 10, 3925–3942. [Google Scholar]
- Dau, F.; Ducrou, J.; Eklund, P. Concept similarity and related categories in SearchSleuth. In International Conference on Conceptual Structures; Springer: Berlin/Heidelberg, Germany, 2008; pp. 255–268. [Google Scholar]
- Hong, S.-S.; Kong, J.-H.; Han, M.-M. The Adaptive SPAM Mail Detection System using Clustering based on Text Mining. KSII Trans. Internet Inf. Syst. 2014, 8, 2186–2196. [Google Scholar]
- De Maio, C.; Fenza, G.; Gaeta, M.; Loia, V.; Orciuoli, F.; Senatore, S. RSS-based e-learning recommendations exploiting fuzzy FCA for Knowledge Modeling. Appl. Soft Comput. 2012, 12, 113–124. [Google Scholar] [CrossRef]
- Ahmad, I.S. Text-based Image Indexing and Retrieval using Formal Concept Analysis. KSII Trans. Internet Inf. Syst. 2008, 2, 150–170. [Google Scholar] [CrossRef]
- Amin, I.I.; Kassim, S.K.; ella Hassanien, A.; Hefny, H.A. Using formal concept analysis for mining hyomethylated genes among breast cancer tumors subtypes. In Proceedings of the 2013 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Mysore, India, 22–25 August 2013; pp. 521–526. [Google Scholar]
- Viji Rajendran, V.; Swamynathan, S. Enhanced Cloud Service Discovery for Naïve users with Ontology based Representation. KSII Trans. Internet Inf. Syst. 2016, 10, 38–57. [Google Scholar]
- Poelmans, J.; Kuznetsov, S.O.; Ignatov, D.I.; Dedene, G. Formal Concept Analysis in knowledge processing: A survey on models and techniques. Expert Syst. Appl. 2013, 40, 6601–6623. [Google Scholar] [CrossRef]
- Ahn, B.; Abbas, E.; Park, J.A.; Choi, H.-J. Increasing Splicing Site Prediction by Training Gene Set Based on Species. KSII Trans. Internet Inf. Syst. 2012, 6, 2784–2799. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, B.; Sheng, J.; Hu, Y.; Wang, Y.; Shao, J. Identifying Influential Nodes in Complex Networks Based on Weighted Formal Concept Analysis. IEEE Access 2017, 5, 3777–3789. [Google Scholar] [CrossRef]
- Song, G.Y.; Cheon, Y.; Lee, K.; Park, K.M.; Rim, H.C. Inter-category Map: Building Cognition Network of General Customers through Big Data Mining. KSII Trans. Internet Inf. Syst. 2014, 8, 583–600. [Google Scholar]
- Lv, L.; Zhang, L.; Zhu, A.; Zhou, F. An improved addintent algorithm for building concept lattice. In Proceedings of the 2011 2nd International Conference on Intelligent Control and Information Processing (ICICIP), Harbin, China, 25–28 July 2011; pp. 161–165. [Google Scholar]
- Van Der Merwe, D.; Obiedkov, S.; Kourie, D. AddIntent: A new incremental algorithm for constructing concept lattices. In International Conference on Formal Concept Analysis; Springer: Berlin/Heidelberg, Germany, 2004; pp. 372–385. [Google Scholar]
- Kourie, D.G.; Obiedkov, S.; Watson, B.W.; van der Merwe, D. An incremental algorithm to construct a lattice of set intersections. Sci. Comput. Programm. 2009, 74, 128–142. [Google Scholar] [CrossRef]
- Outrata, J.; Vychodil, V. Fast algorithm for computing fixpoints of Galois connections induced by object-attribute relational data. Inf. Sci. 2012, 185, 114–127. [Google Scholar] [CrossRef]
- Kuznetsov, S.O. A fast algorithm for computing all intersections of objects from an arbitrary semilattice. Nauchno-Tekh. Informatsiya Ser. 2-Informatsionnye Protsessy I Sist. 1993, 1, 17–20. [Google Scholar]
- Valtchev, P.; Missaoui, R.; Godin, R. A framework for incremental generation of closed itemsets. Discret. Appl. Math. 2008, 156, 924–949. [Google Scholar] [CrossRef]
- Zou, L.; Zhang, Z.; Long, J. A fast incremental algorithm for constructing concept lattices. Expert Syst. Appl. 2015, 42, 4474–4481. [Google Scholar] [CrossRef]
- Van Der Merwe, F.; Kourie, D. AddAtom: An Incremental Algorithm for Constructing Concept Lattices and Concept Sublattices; Technical Report; Department of Computer Science, University of Pretoria: Pretoria, South Africa, 2002. [Google Scholar]

| a | b | c | d | e | |
|---|---|---|---|---|---|
| 1 | × | × | × | × | |
| 2 | × | × | × | ||
| 3 | × | × | |||
| 4 | |||||
| 5 | × | × | × | × |
| a | b | c | d | e | |
|---|---|---|---|---|---|
| 1 | × | × | × | × | × |
| 2 | × | × | × | × | |
| 3 | × | × | × | ||
| 4 | |||||
| 5 | × | × | × | × |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Liu, R.; Zou, L.; Zeng, L. A New Rapid Incremental Algorithm for Constructing Concept Lattices. Information 2019, 10, 78. https://doi.org/10.3390/info10020078
Zhang J, Liu R, Zou L, Zeng L. A New Rapid Incremental Algorithm for Constructing Concept Lattices. Information. 2019; 10(2):78. https://doi.org/10.3390/info10020078
Chicago/Turabian StyleZhang, Jingpu, Ronghui Liu, Ligeng Zou, and Licheng Zeng. 2019. "A New Rapid Incremental Algorithm for Constructing Concept Lattices" Information 10, no. 2: 78. https://doi.org/10.3390/info10020078
APA StyleZhang, J., Liu, R., Zou, L., & Zeng, L. (2019). A New Rapid Incremental Algorithm for Constructing Concept Lattices. Information, 10(2), 78. https://doi.org/10.3390/info10020078




