Crime Scene Shoeprint Retrieval Using Hybrid Features and Neighboring Images
Abstract
1. Introduction
2. Related Works
3. Method
3.1. Notations and Formulations
3.2. Solution
| Algorithm 1. Solution to the retrieval problem |
| Input: The affinity matrix , the initial ranking score list . Iteration number T, tuning parameter . |
| Output: The final ranking score list . |
| 1: Set , set , assign to . |
| 2: Compute the degree matrix and the Laplacian matrix |
| 3: Update ranking score |
| 4: Update using Equation (7). |
| 5: Let . If , quit iteration and output final ranking score list , otherwise go to 3. |
3.3. The Affinity Matrix Computation Mothod
4. Experiments
4.1. Experiment Configuration
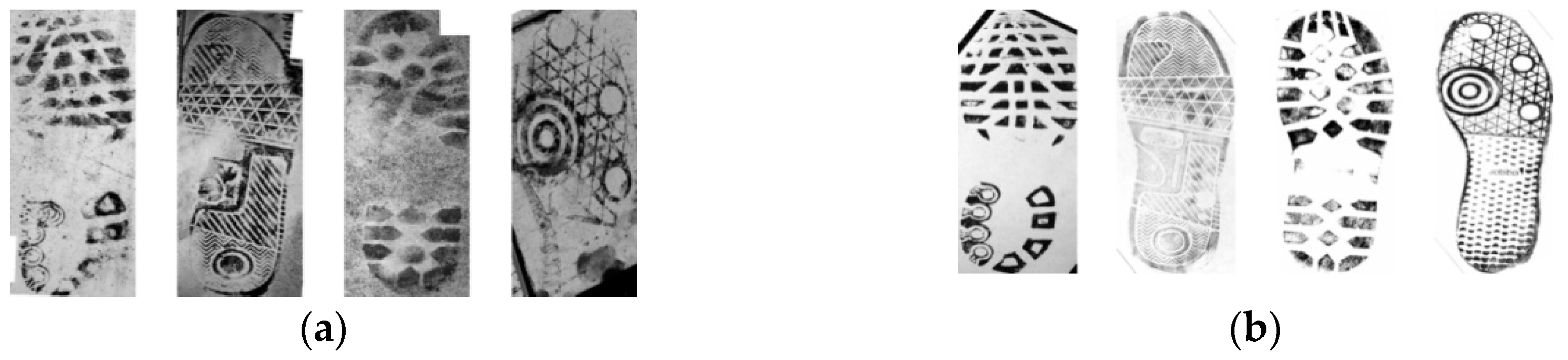
4.1.1. Dataset
4.1.2. Evaluation Metrics
4.2. Performance Evaluation
4.2.1. Performance Evaluation of the Proposed Hybrid Features and the Proposed NSE Method
4.2.2. Comparison with the Traditional Manifold Ranking Method
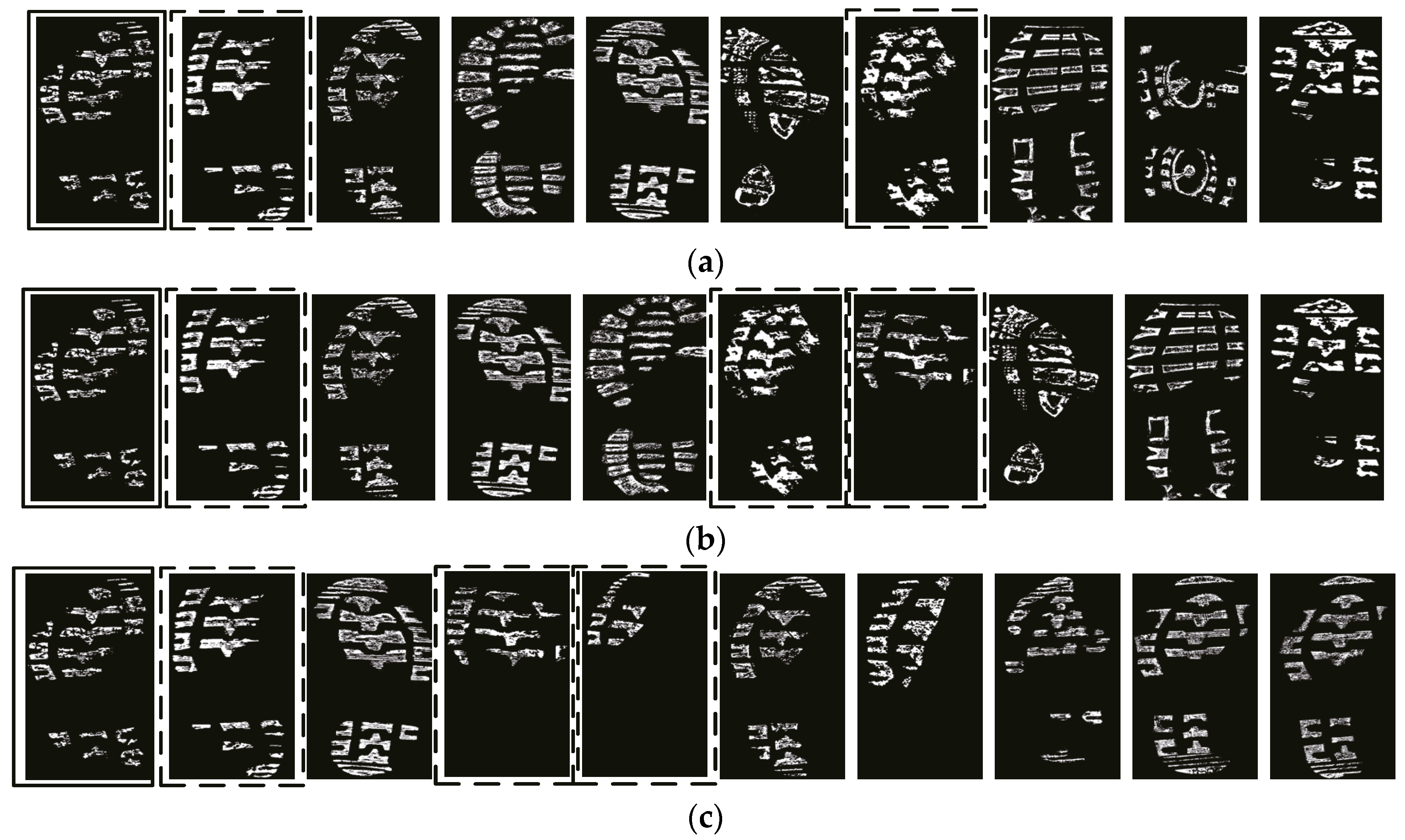
4.2.3. Comparison with the Manifold Ranking Based Shoeprint Retrieval Method
4.2.4. Comparison with the State-of-the-art Algorithms
4.3. Analysis and Discussion
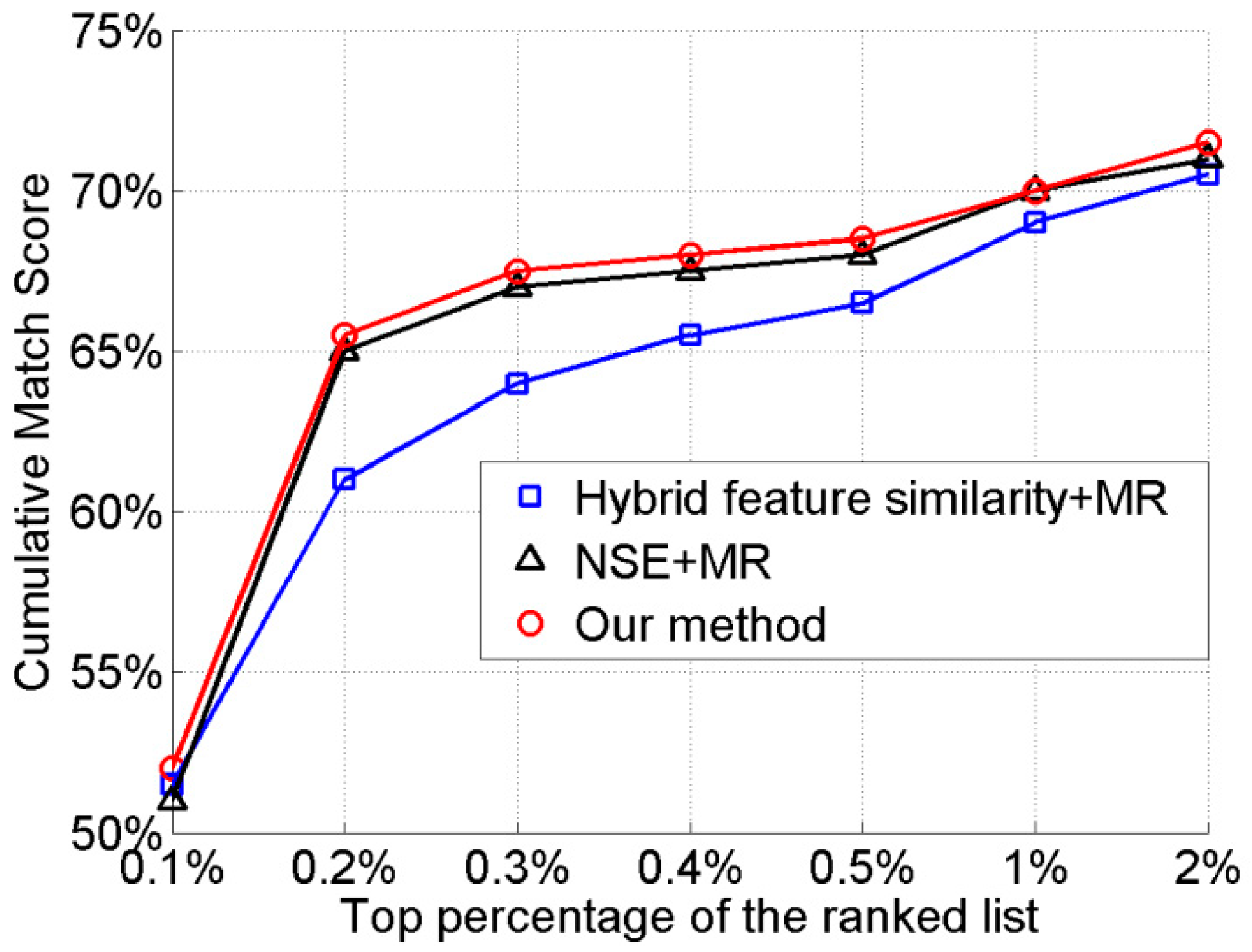
4.3.1. Effectiveness of the proposed NSE method and the hybrid feature similarity
4.3.2. Effectiveness of Each Kind of Low Level Feature
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bouridane, A.; Alexander, A.; Nibouche, M.; Crookes, D. Application of fractals to the detection and classification of shoeprints. In Proceedings of the International Conference on Image Processing, Vancouver, Canada, 10–13 September 2000; pp. 474–477. [Google Scholar] [CrossRef]
- Algarni, G.; Amiane, M. A novel technique for automatic shoeprint image retrieval. Forensic Sci. Int. 2008, 181, 10–14. [Google Scholar] [CrossRef] [PubMed]
- Wei, C.H.; Hsin, C.; Gwo, C.Y. Alignment of Core Point for Shoeprint Analysis and Retrieval. In Proceedings of the International Conference on Information Science, Electronics and Electrical Engineering (ISEEE), Sapporo, Japan, 26–28 April 2014; pp. 1069–1072. [Google Scholar] [CrossRef]
- Chazal, P.D.; Flynn, J.; Reilly, R.B. Automated processing of shoeprint images based on the Fourier transform for use in forensic science. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 341–350. [Google Scholar] [CrossRef] [PubMed]
- Gueham, M.; Bouridane, A.; Crookes, D. Automatic Classification of Partial Shoeprints Using Advanced Correlation Filters for Use in Forensic Science. In Proceedings of the International Conference on Pattern Recognition, Tampa, FL, USA, 8–11 December 2008; pp. 1–4. [Google Scholar] [CrossRef]
- Gueham, M.; Bouridane, A.; Crookes, D. Automatic recognition of partial shoeprints based on phase-only correlation. In Proceedings of the IEEE International Conference on Image Processing, San Antonio, TX, USA, 16 September–19 October 2007; pp. 441–444. [Google Scholar] [CrossRef]
- Cervelli, F.; Dardi, F.; Carrato, S. An automatic footwear retrieval system for shoe marks from real crime scenes. In Proceedings of the International Symposium on Image and Signal Processing and Analysis, Salzburg, Austria, 16–18 September 2009; pp. 668–672. [Google Scholar] [CrossRef]
- Cervelli, F.; Dardi, F.; Carrato, S. A texture based shoe retrieval system for shoe marks of real crime scenes. In Proceedings of the International Conference on Image Analysis and Processing, Catania, Italy, 8–11 September 2009; pp. 384–393. [Google Scholar] [CrossRef]
- Cervelli, F.; Dardi, F.; Carrato, S. A translational and rotational invariant descriptor for automatic footwear retrieval of real cases shoe marks. In Proceedings of the 18th European Signal Processing Conference, Aalborg, Denmark, 23–27 August 2010; pp. 1665–1669. [Google Scholar]
- Alizadeh, S.; Kose, C. Automatic retrieval of shoeprint images using blocked sparse representation. Forensic Sci. Int. 2017, 277, 103–114. [Google Scholar] [CrossRef] [PubMed]
- Richetelli, N.; Lee, M.C.; Lasky, C.A.; Gump, M.E.; Speir, J.A. Classification of footwear outsole patterns using Fourier transform and local interest points. Forensic Sci. Int. 2017, 275, 102–109. [Google Scholar] [CrossRef] [PubMed]
- Kong, B.; Supancic, J.; Ramanan, D.; Fowlkes, C. Cross-Domain Forensic Shoeprint Matching. In Proceedings of the 28th British Machine Vision Conference (BMVC), London, UK, 4–7 September 2017. [Google Scholar]
- Kong, B.; Supancic, J.; Ramanan, D.; Fowlkes, C. Cross-Domain Image Matching with Deep Feature Maps. arXiv, 2018; arXiv:1804.02367,2018. [Google Scholar]
- Patil, P.M.; Kulkarni, J.V. Rotation and intensity invariant shoeprint matching using Gabor transform with application to forensic science. Pattern Recognit. 2009, 42, 1308–1317. [Google Scholar] [CrossRef]
- Tang, Y.; Srihari, S.N.; Kasiviswanathan, H. Similarity and Clustering of Footwear Prints. In Proceedings of the 2010 IEEE International Conference on Granular Computing, San Jose, USA, 14–16 August 2010; pp. 459–464. [Google Scholar] [CrossRef]
- Tang, Y.; Srihari, S.N.; Kasiviswanathan, H.; Corso, J. Footwear print retrieval system for real crime scene marks. In Proceedings of the International Conference on Computational Forensics, Tokyo, Japan, 11–12 November 2010; pp. 88–100. [Google Scholar] [CrossRef]
- Pavlou, M.; Allinson, N.M. Automated encoding of footwear patterns for fast indexing. Image Vis. Comput. 2009, 27, 402–409. [Google Scholar] [CrossRef]
- Pavlou, M.; Allinson, N.M. Automatic extraction and classification of footwear patterns. In Proceedings of the 7th International Conference on Intelligent Data Engineering and Automated Learning, Burgos, Spain, 20–23 September 2006; pp. 721–728. [Google Scholar] [CrossRef]
- Kortylewski, A.; Albrecht, T.; Vetter, T. Unsupervised Footwear Impression Analysis and Retrieval from Crime Scene Data. In Proceedings of the Asian Conference on Computer Vision, Singapore, 1–5 November 2014; pp. 644–658. [Google Scholar] [CrossRef]
- Nibouche, O.; Bouridane, A.; Crookes, D.; Gueham, M.; Laadjel, M. Rotation invariant matching of partial shoeprints. In Proceedings of the International Machine Vision and Image Processing Conference, Dublin, Ireland, 2–4 September 2009; pp. 94–98. [Google Scholar] [CrossRef]
- Crookes, D.; Bouridane, A.; Su, H.; Gueham, M. Following the Footsteps of Others: Techniques for Automatic Shoeprint Classification. In Proceedings of the Second NASA/ESA Conference on Adaptive Hardware and Systems, Edinburgh, UK, 5–8 August 2007; pp. 67–74. [Google Scholar] [CrossRef]
- Su, H.; Crookes, D.; Bouridane, A.; Gueham, M. Local image features for shoeprint image retrieval. In Proceedings of the British Machine Vision Conference, University of Warwick, Coventry, UK, 10–13 September 2007; pp. 1–10. [Google Scholar]
- Wang, H.X.; Fan, J.H.; Li, Y. Research of shoeprint image matching based on SIFT algorithm. J. Comput. Methods Sci. Eng. 2016, 16, 349–359. [Google Scholar] [CrossRef]
- Almaadeed, S.; Bouridane, A.; Crookes, D.; Nibouche, O. Partial shoeprint retrieval using multiple point-of-interest detectors and SIFT descriptors. Integr. Comput. Aided Eng. 2015, 22, 41–58. [Google Scholar] [CrossRef]
- Luostarinen, T.; Lehmussola, A. Measuring the accuracy of automatic shoeprint recognition methods. J. Forensic Sci. 2014, 59, 1627–1634. [Google Scholar] [CrossRef] [PubMed]
- Kortylewski, A.; Vetter, T. Probabilistic Compositional Active Basis Models for Robust Pattern Recognition. In Proceedings of the 27th British Machine Vision Conference (BMVC), York, UK, 19–22 September 2016. [Google Scholar]
- Kortylewski, A. Model-based IMAGE Analysis for Forensic Shoe Print Recognition. Ph.D. Thesis, University of Basel, Basel, Switzerland, 2017. [Google Scholar]
- Wang, X.N.; Sun, H.H.; Yu, Q.; Zhang, C. Automatic Shoeprint Retrieval Algorithm for Real Crime Scenes. In Proceedings of the Asian Conference on Computer Vision, Singapore, 1–5 November 2014; pp. 399–413. [Google Scholar] [CrossRef]
- Wang, X.N.; Zhan, C.; Wu, Y.J.; Shu, Y.Y. A manifold ranking based method using hybrid features for crime scene shoeprint retrieval. Multimed. Tools Appl. 2016, 76, 21629–21649. [Google Scholar] [CrossRef]
- Reddy, B.S.; Chatterji, B.N. An FFT-based technique for translation, rotation, and scale-invariant image registration. IEEE Trans. Image Process. 1996, 5, 1266–1271. [Google Scholar] [CrossRef] [PubMed]
- Phillips, P.J.; Grother, P.; Micheals, R. Evaluation Methods in Face Recognition. In Handbook of Face Recognition; Jain Anil, K., Li Stan, Z., Eds.; Springer: New York, NY, USA, 2005; pp. 328–348. [Google Scholar]
- Zhou, D.; Weston, J.; Gretton, A.; Bousquet, O.; Scholkopf, B. Ranking on Data Manifolds. In Advances in Neural Information Processing Systems 16; Thrun, S., Saul, L.K., Schölkopf, B., Eds.; MIT Press: Cambridge, MA, USA, 2003; pp. 169–176. [Google Scholar]


| Approaches | The Cumulative Match Score of Top Percentage | ||||||
|---|---|---|---|---|---|---|---|
| 0.1% | 0.2% | 0.3% | 0.4% | 0.5% | 1% | 2% | |
| Holistic feature | 11.9% | 20.2% | 25.2% | 29.4% | 31.9% | 39.4% | 49.0% |
| Region feature [28] | 45.2% | 64.1% | 69.4% | 73.8% | 75.8% | 81.8% | 87.5% |
| Local feature | 11.3% | 17.1% | 19.0% | 20.2% | 21.2% | 26.8% | 32.7% |
| The proposed hybrid feature | 53.2% | 71.4% | 77.6% | 81.3% | 83.1% | 87.3% | 89.9% |
| The proposed NSE method | 53.8% | 80.0% | 84.1% | 84.7% | 86.1% | 89.7% | 92.3% |
| Approaches | The Cumulative Match Score of Top Percentage | ||||||
|---|---|---|---|---|---|---|---|
| 0.1% | 0.2% | 0.3% | 0.4% | 0.5% | 1% | 2% | |
| Manifold ranking method [32] | 52.4% | 79.6% | 83.9% | 85.1% | 86.3% | 89.5% | 91.9% |
| Our method | 53.6% | 81.0% | 84.7% | 85.9% | 86.7% | 89.5% | 92.5% |
| Approaches | The Cumulative Match Score of Top Percentage | ||||||
|---|---|---|---|---|---|---|---|
| 0.1% | 0.2% | 0.3% | 0.4% | 0.5% | 1% | 2% | |
| Wang et al. 2016 [29] | 52.6% | 76.0% | 81.8% | 84.5% | 85.5% | 90.1% | 93.5% |
| Our method | 54.6% | 81.7% | 86.5% | 87.9% | 88.9% | 90.9% | 94.8% |
| Methods | Performance Reported in the Literature | Performance on Our Dataset | ||
|---|---|---|---|---|
| Performance | Gallery Set Description | The Cumulative Match Score of Top 2% | Mean Average Running Time(ms) | |
| Kortylewski et al. 2014 [19] | 85.7%@20% | #R:1,175 | 38.64% | 0.5696 |
| Almaadeed et al. 2015 [24] | 68.5%@2.5% | #R:400 | 34.7% | 14.2 |
| Wang et al. 2014 [28] | 87.5%@2% | #S:10,096 | 87.5% | 17.8 |
| Wang et al. 2016 [29] | 93.5%@2% | #S:10,096 | 91.1% | 17.8238 |
| Kong et al. 2017 [12] | 92.5%@20% | #R:1,175 | 45.6% | 186.0 |
| Our method | _ | #S:10,096 | 92.5% | 18.2 |
| Method | The Cumulative Match Score of the Top Percentage | ||||
|---|---|---|---|---|---|
| 1% | 5% | 10% | 15% | 20% | |
| Kortylewski et al. 2016 [26] | 22.0% | 47.5% | 58.0% | 67.0% | 71.0% |
| Wang et al. 2016 [29] | 67.9% | 81.3% | 86.3% | 91.3% | 94.0% |
| Kong et al. 2017 [12] | 73.0% | 82.5% | 87.5% | 91.0% | 92.5% |
| Kortylewski 2017 [27] | 58.0% | 72.0% | 79.0% | 81.5% | 84.0% |
| Kong et al. 2018 [13] | 79.0% | 86.3% | 89.0% | 91.3% | 94.0% |
| Our method | 71.8% | 81.7% | 87.3% | 92.0% | 95.3% |
| Approaches | The Cumulative Match Score of Top Percentage | ||||||
|---|---|---|---|---|---|---|---|
| 0.1% | 0.2% | 0.3% | 0.4% | 0.5% | 1% | 2% | |
| Hybrid feature similarity+MR | 53.2% | 71.8% | 78.0% | 81.3% | 82.7% | 87.5% | 90.5% |
| NSE+MR | 52.4% | 79.6% | 83.9% | 85.1% | 86.3% | 89.5% | 91.9% |
| Our method (Hybrid feature similarity +NSE+ MR) | 53.6% | 81.0% | 84.7% | 85.9% | 86.7% | 89.5% | 92.5% |
| Approaches | The Cumulative Match Score of Top Percentage | ||||||
|---|---|---|---|---|---|---|---|
| 0.1% | 0.2% | 0.3% | 0.4% | 0.5% | 1% | 2% | |
| Hybrid feature of holistic and region | 48.8% | 73.0% | 76.6% | 80.4% | 81.3% | 86.7% | 89.3% |
| Hybrid feature of holistic and local | 33.9% | 44.4% | 50.2% | 54.4% | 56.7% | 70.4% | 77.2% |
| Hybrid feature of region and local | 48.6% | 72.2% | 75.8% | 78.8% | 83.9% | 88.5% | 89.5% |
| The proposed hybrid feature | 53.6% | 81.0% | 84.7% | 85.9% | 86.7% | 89.5% | 92.5% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Wang, X.; Zhang, T. Crime Scene Shoeprint Retrieval Using Hybrid Features and Neighboring Images. Information 2019, 10, 45. https://doi.org/10.3390/info10020045
Wu Y, Wang X, Zhang T. Crime Scene Shoeprint Retrieval Using Hybrid Features and Neighboring Images. Information. 2019; 10(2):45. https://doi.org/10.3390/info10020045
Chicago/Turabian StyleWu, Yanjun, Xinnian Wang, and Tao Zhang. 2019. "Crime Scene Shoeprint Retrieval Using Hybrid Features and Neighboring Images" Information 10, no. 2: 45. https://doi.org/10.3390/info10020045
APA StyleWu, Y., Wang, X., & Zhang, T. (2019). Crime Scene Shoeprint Retrieval Using Hybrid Features and Neighboring Images. Information, 10(2), 45. https://doi.org/10.3390/info10020045





