Hierarchical Data Decision Aided 2-Source BPSK H-MAC Channel Phase Estimator with Feed-Back Gradient Solver for WPNC Networks and Its Equivalent Model †
Abstract
1. Introduction
1.1. Background and Context
1.2. Goals and Contributions
1.3. Related Work
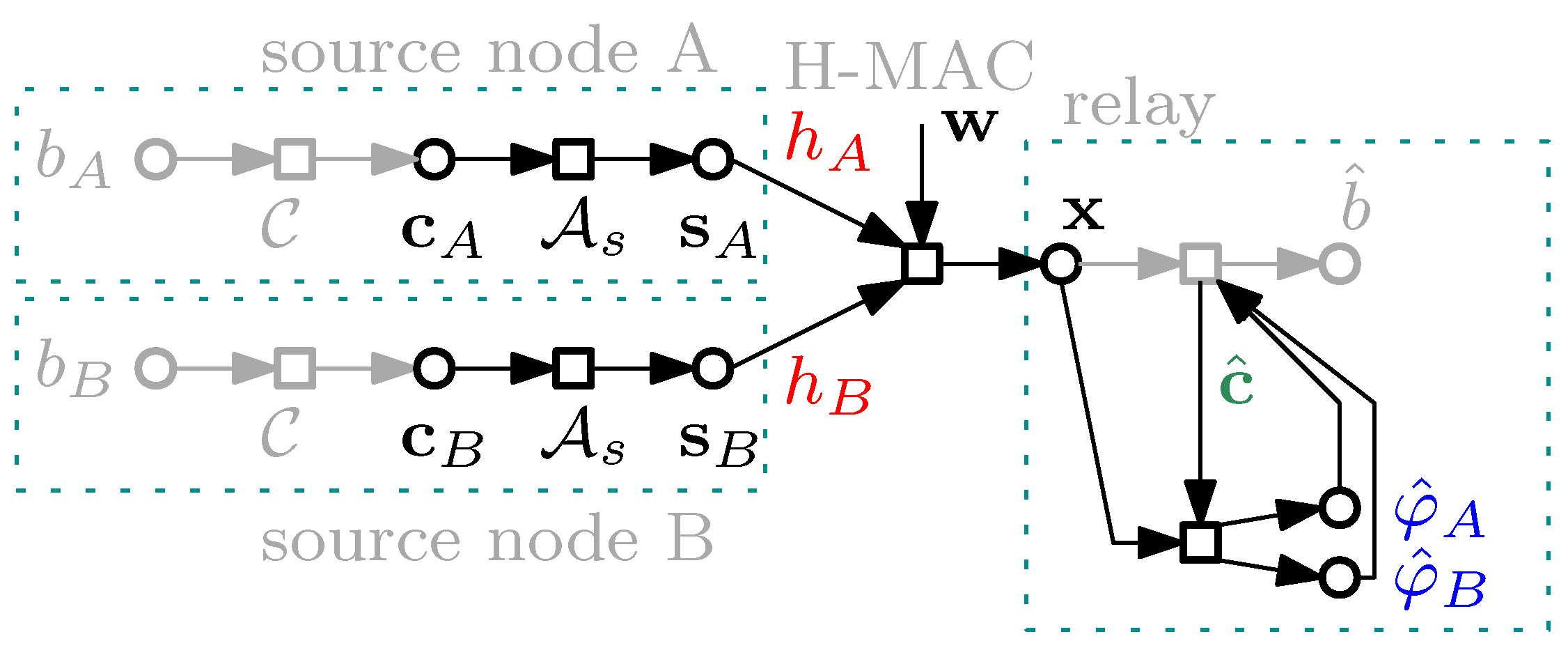
2. System Model
3. H-Data Decision Aided H-MAC CSE
3.1. H-Dispersion Marginalization for 2-Source BPSK
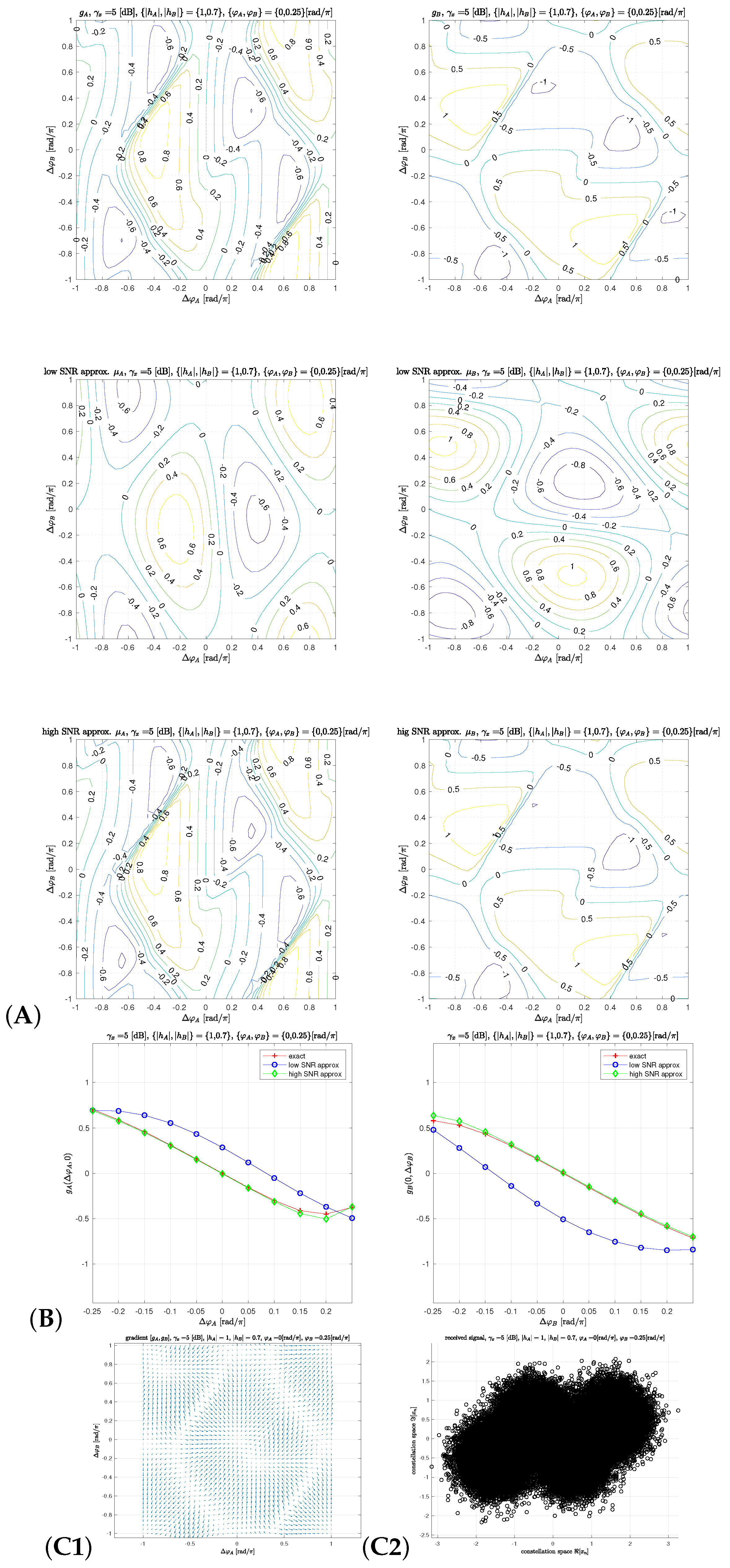
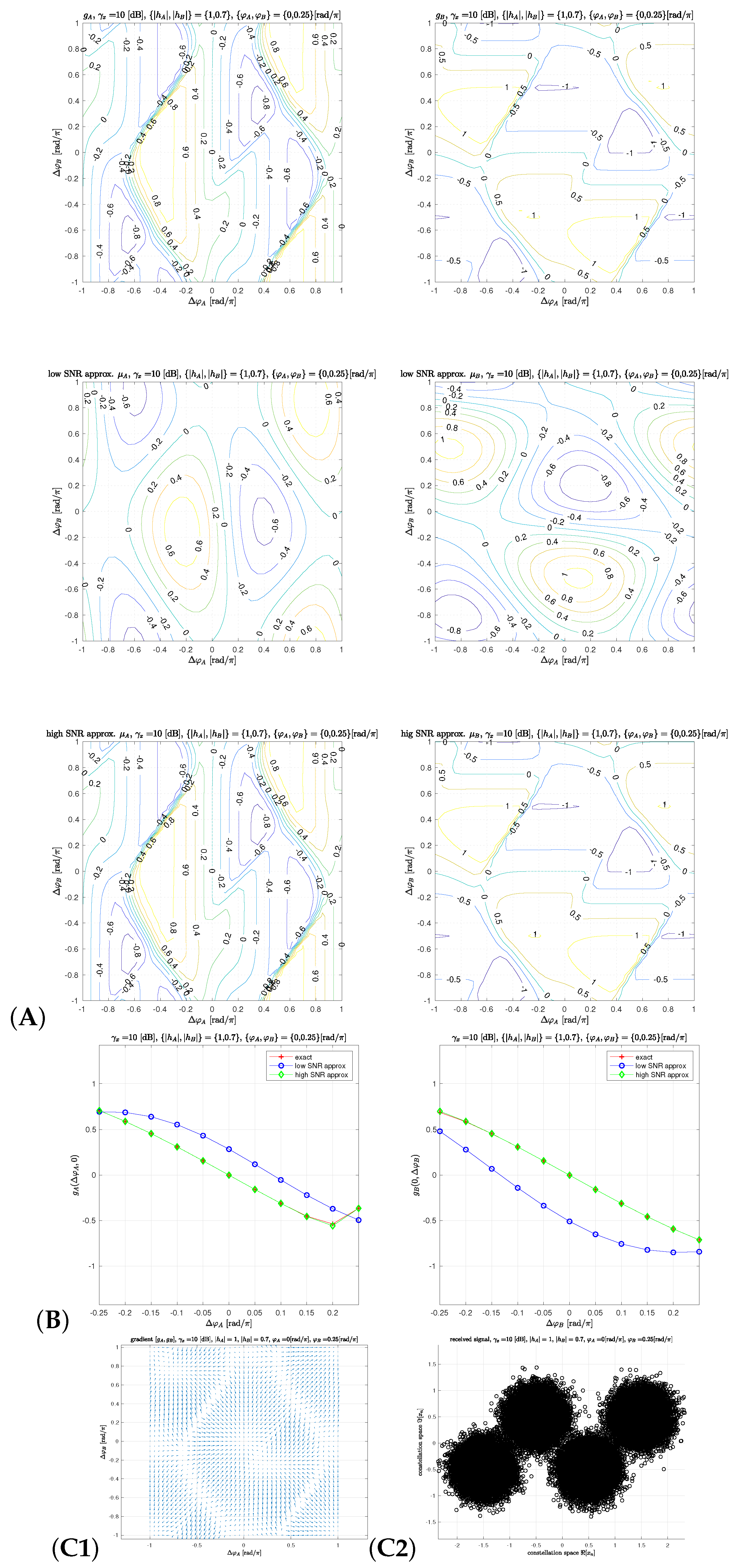
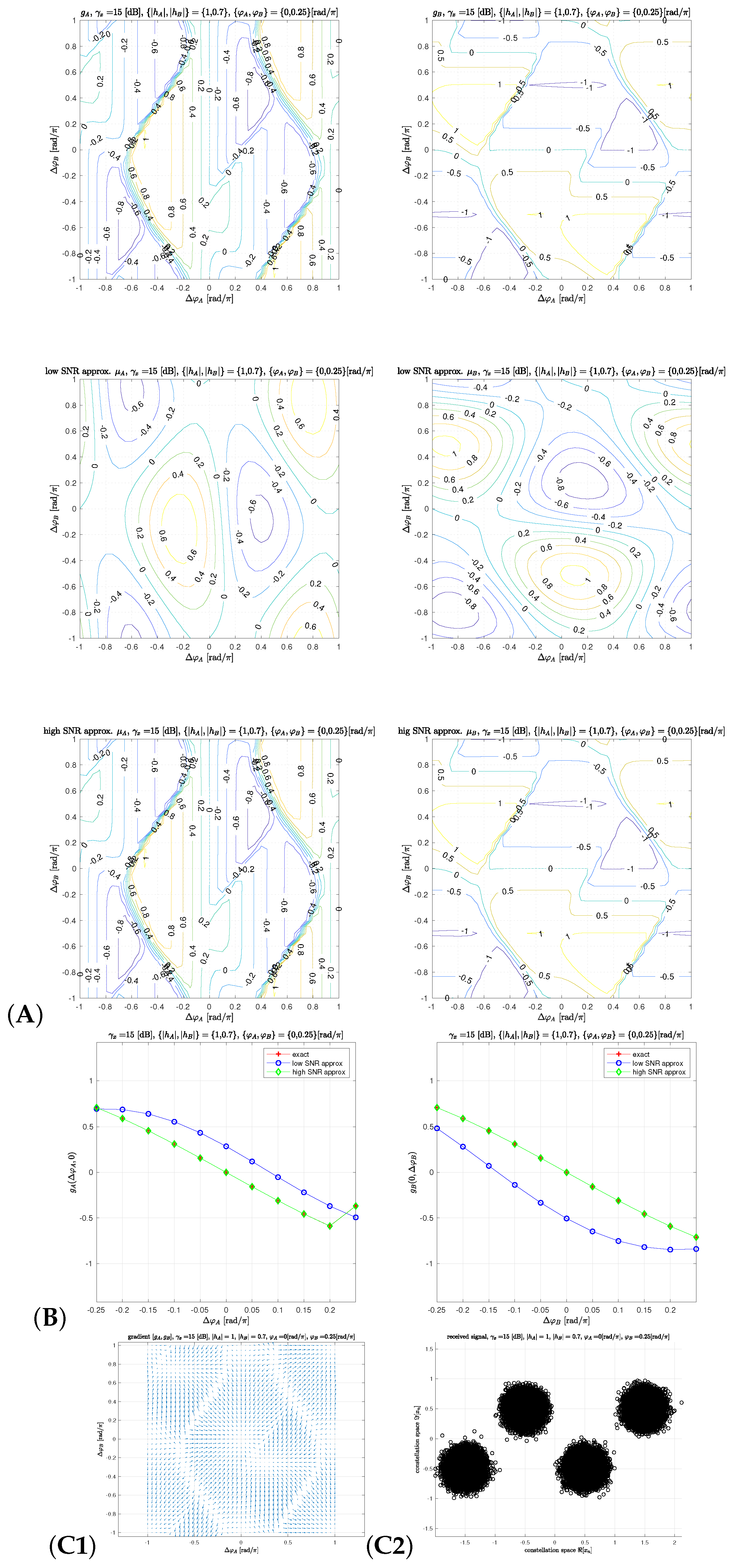
3.2. Feed-Back Gradient Solver
4. Equivalent Model of Feed-Back Solver
4.1. Equivalent Detector Characteristics
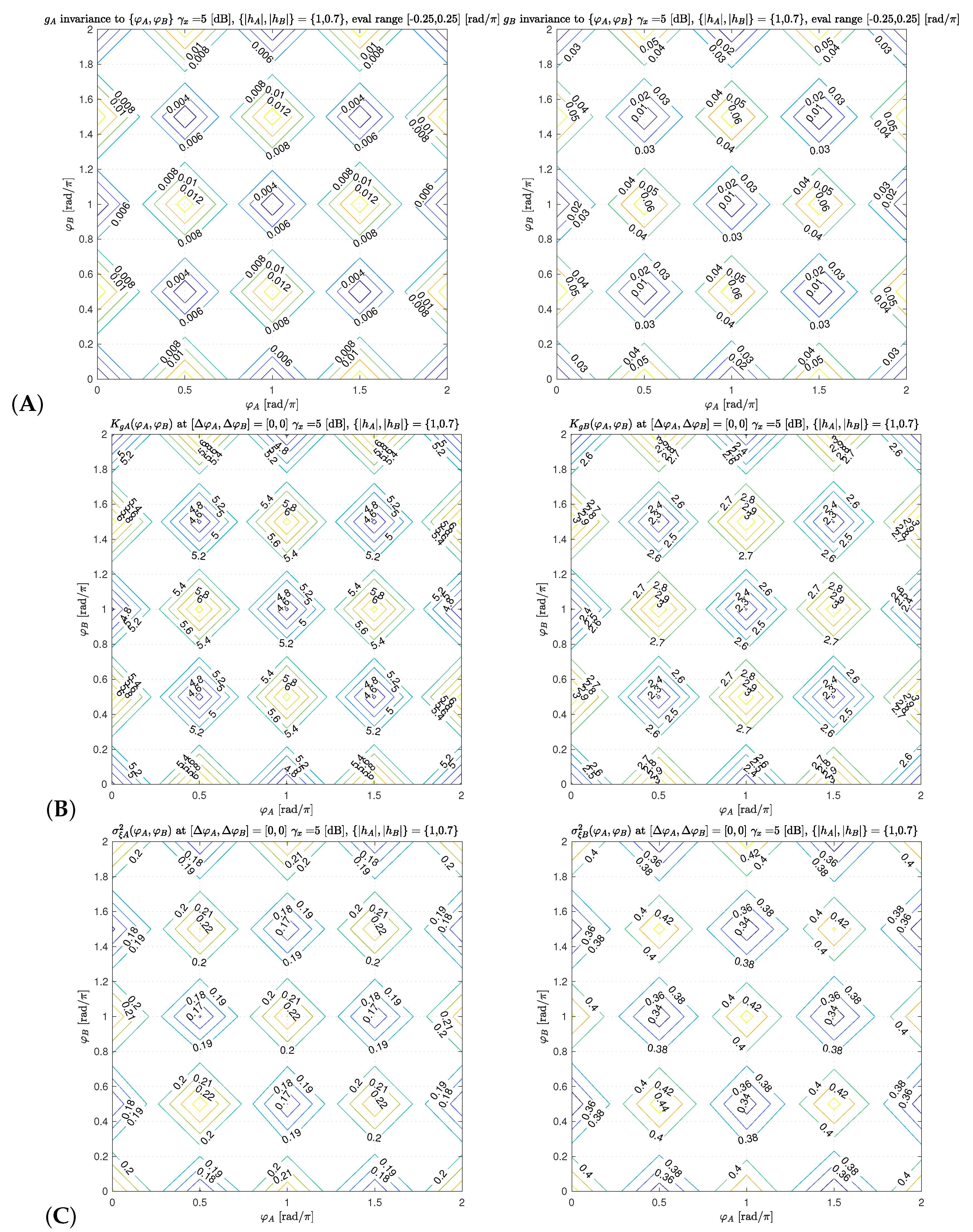
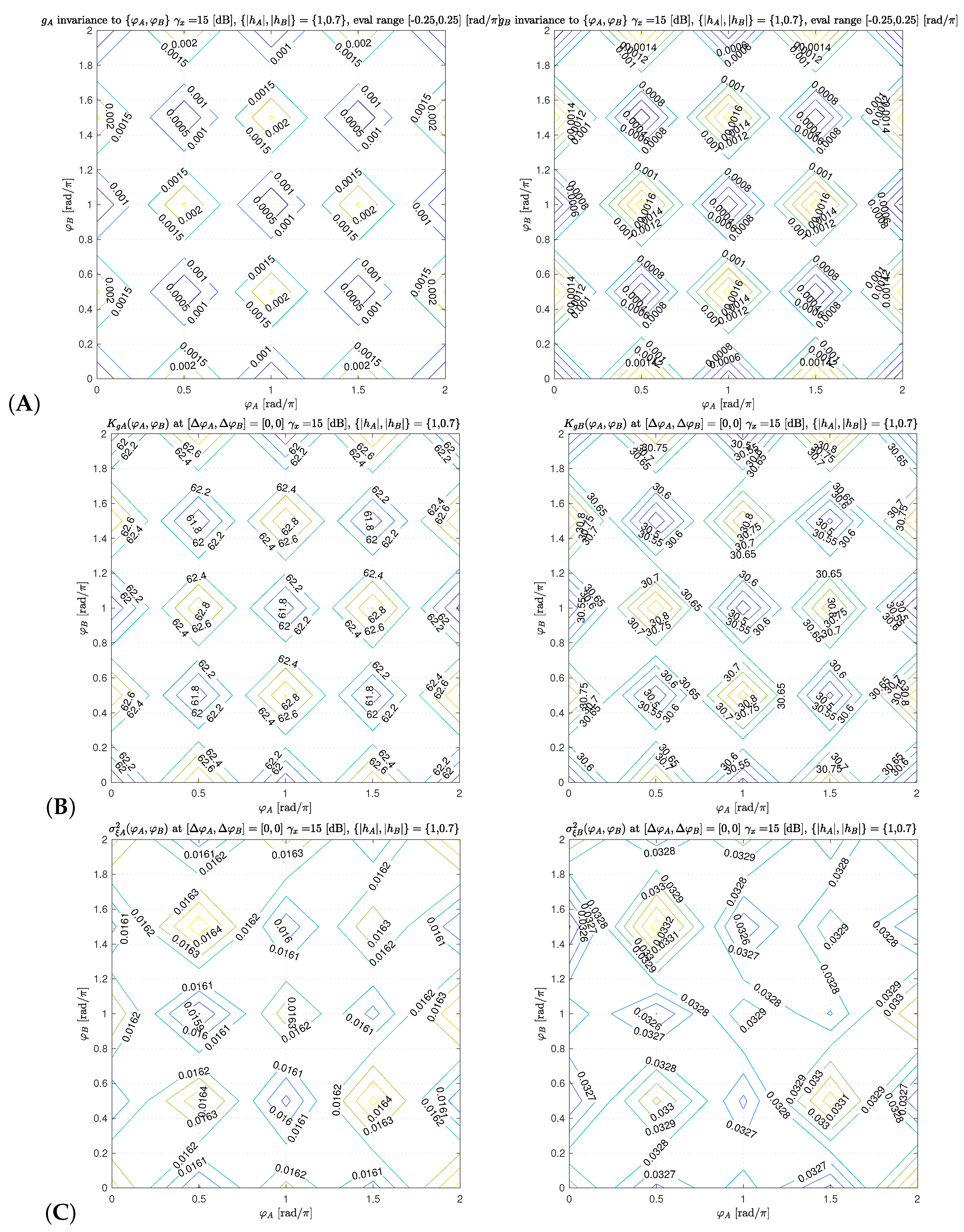
4.2. Invariance to Absolute Channel Component Phases
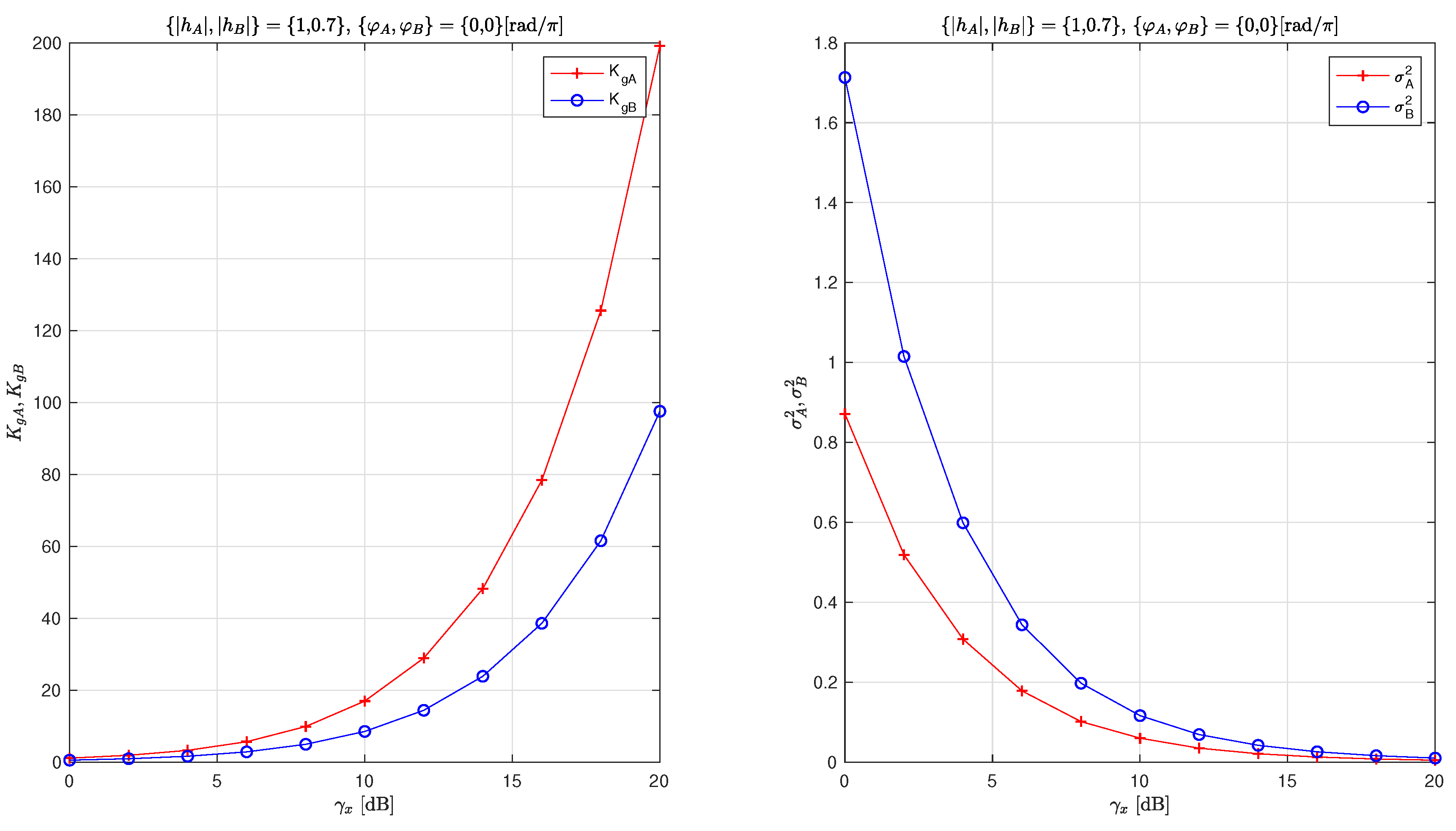
4.3. Detector Gain and Equivalent Noise
5. Discussion and Conclusions
5.1. H-Decision Aided H-MAC 2-Source Phase Estimator
5.2. Good Tracking Capabilities of Feed-Back Gradient Solver
5.3. Exact and Low/High SNR Approximation
5.4. Invariance to True Absolute Channel Phase
Funding
Conflicts of Interest
Abbreviations
| CSE | Channel State Estimation |
| WPNC | Wireless Physical Layer Network Coding |
| HDF | Hierarchical Decode and Forward |
| SNR | Signal to Noise Ratio |
References
- Sykora, J.; Burr, A. Wireless Physical Layer Network Coding; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Zhang, S.; Liew, S.C.; Lam, P.P. Hot Topic: Physical-Layer Network Coding. In Proceedings of the Twelfth Annual International Conference on Mobile Computing and Networking, Los Angeles, CA, USA, 23–29 September 2006. [Google Scholar]
- Koike-Akino, T.; Popovski, P.; Tarokh, V. Optimized Constellations for Two-Way Wireless Relaying with Physical Network Coding. IEEE J. Sel. Areas Commun. 2009, 27, 773–787. [Google Scholar] [CrossRef]
- Nazer, B.; Gastpar, M. Compute-and-Forward: Harnessing Interference Through Structured Codes. IEEE Trans. Inf. Theory 2011, 57, 6463–6486. [Google Scholar] [CrossRef]
- Sykora, J.; Burr, A. Layered Design of Hierarchical Exclusive Codebook and Its Capacity Regions for HDF Strategy in Parametric Wireless 2-WRC. IEEE Trans. Veh. Technol. 2011, 60, 3241–3252. [Google Scholar] [CrossRef]
- Minn, H.; Al-Dhahir, N. Optimal training signals for MIMO OFDM channel estimation. IEEE Trans. Wirel. Commun. 2006, 5, 1158–1168. [Google Scholar] [CrossRef]
- Haykin, S. Adaptive Filter Theory, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Spagnolini, U. Statistical Signal Processing in Engineering; John Wiley & Sons: Hoboken, NY, USA, 2017. [Google Scholar]
- Meyr, H.; Ascheid, G. Synchronization in Digital Communications; John Wiley & Sons: Hoboken, NY, USA, 1990. [Google Scholar]
- Meyr, H.; Moeneclaey, M.; Fechtel, S.A. Digital Communication Receivers, Synchronization Channel Estimation and Signal Processing; John Wiley & Sons: Hoboken, NY, USA, 1998. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sykora, J. Hierarchical Data Decision Aided 2-Source BPSK H-MAC Channel Phase Estimator with Feed-Back Gradient Solver for WPNC Networks and Its Equivalent Model. Information 2019, 10, 40. https://doi.org/10.3390/info10020040
Sykora J. Hierarchical Data Decision Aided 2-Source BPSK H-MAC Channel Phase Estimator with Feed-Back Gradient Solver for WPNC Networks and Its Equivalent Model. Information. 2019; 10(2):40. https://doi.org/10.3390/info10020040
Chicago/Turabian StyleSykora, Jan. 2019. "Hierarchical Data Decision Aided 2-Source BPSK H-MAC Channel Phase Estimator with Feed-Back Gradient Solver for WPNC Networks and Its Equivalent Model" Information 10, no. 2: 40. https://doi.org/10.3390/info10020040
APA StyleSykora, J. (2019). Hierarchical Data Decision Aided 2-Source BPSK H-MAC Channel Phase Estimator with Feed-Back Gradient Solver for WPNC Networks and Its Equivalent Model. Information, 10(2), 40. https://doi.org/10.3390/info10020040




