Choosing Mutation and Crossover Ratios for Genetic Algorithms—A Review with a New Dynamic Approach
Abstract
1. Introduction
1.1. Contributions
1.2. Organization
2. Review of GA Representations
- Binary encoding: Each chromosome in this technique is represented using strings of bits 0’s and 1’s. An example of the use of binary encoding is the knapsack problem.
- Permutation encoding: Each chromosome in this technique is represented as a string of numbers that represent a position in a sequence. This method is useful in ordering problems such as Traveling Salesman Problem (TSP).
- Value encoding: chromosomes are represented by using a sequence of some values such as real numbers, characters or objects. These values are possibly characters, real numbers, etc. [28].
- Tree encoding: Each chromosome is treated as a tree of certain items such as commands or functions. Tree encoding is good for evolving programs [28] used in genetic programming. The following outline summarizes how the GA works after the chromosomes are encoded [29].
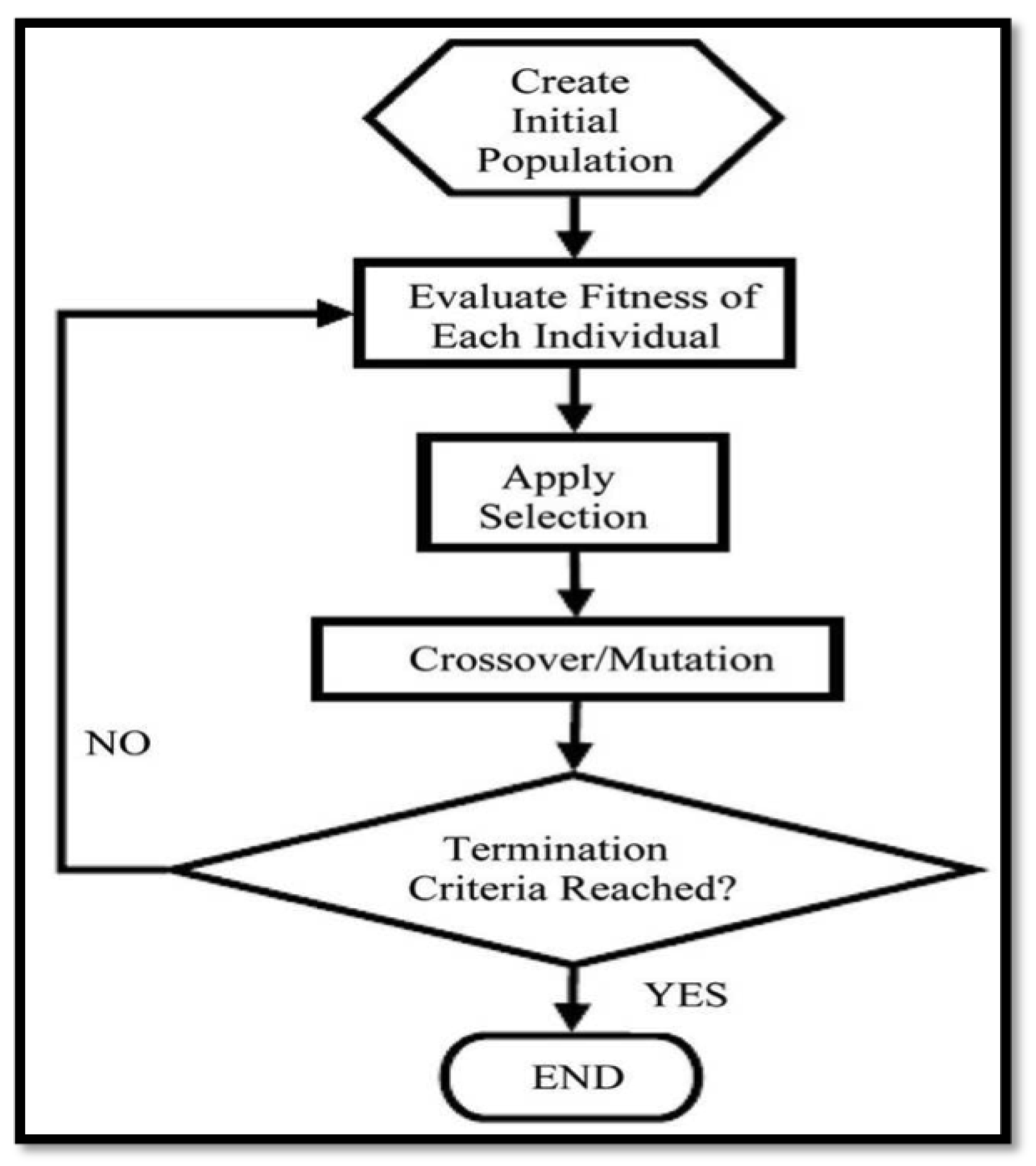
- Start: Generation of the beginning population of random individuals is the first step of any genetic algorithms. Each generated individual is then represented as a chromosome in a sequence of string with the length L, that aligns with the problem encoding. The step ends with creating a random population in “genotype” [1].
- Fitness: Next is to compute the fitness value of each individual in the present population. The evaluation process consists of choosing individuals for mating based on their fitness value (parents) and according to the desired values of each. The terms evaluation and fitness are usually used to mean the same thing but it is important to differentiate the evaluating and the fitness valuing as applied in GA. Evaluation function or objective function rates performance based on particular defined aspects. The performance measurement of the fitness function is transformed into a range of reproductive opportunities. [30].
- New population: Steps 4, 5 and 6 are repeated to create a new population up to completion.
- Selection (Reproduction): The selection process ascertains the chromosomes that are chosen for mating and reproduction as well as the number of offspring each chosen chromosome produces. The main purpose of the selection process is “the better an individual is; the higher its chance of being a parent” [31]. There exist various traditional selection mechanisms and user-specified-selection mechanisms that are applied in line with the problem in question. [32]. Selection strategies examples consist of:
- (a)
- Tournament Selection: This is arguably the most common selection technique in GA because of its efficiency and ease in implementation [33]. In tournament selection, the selection of individuals is done in a random manner starting with the larger population. Thereafter there is a competition amongst the selected individuals. The competition is used to determine the individual with the highest fitness value to be used in the generation of the new population. The individuals competing are usually set to two also called binary tournament or tournament size. Diversity is ensured in tournament selection as all the individuals have an equal chance to be chosen even though this may reduce the convergence speed. Some of tournament selection advantage includes proper time utilization mostly when the implementation is parallel with low susceptibility to being taken by dominant individuals, and no need for fitness scaling or sorting. [34].
- (b)
- (c)
- Rank Selection: Parent selection is done using a rank. Here, fitness value is used to rank individuals in the population where the best is ranked (n) and the worst-ranked (1). Every chromosome has a rank depending on its expected value [31].
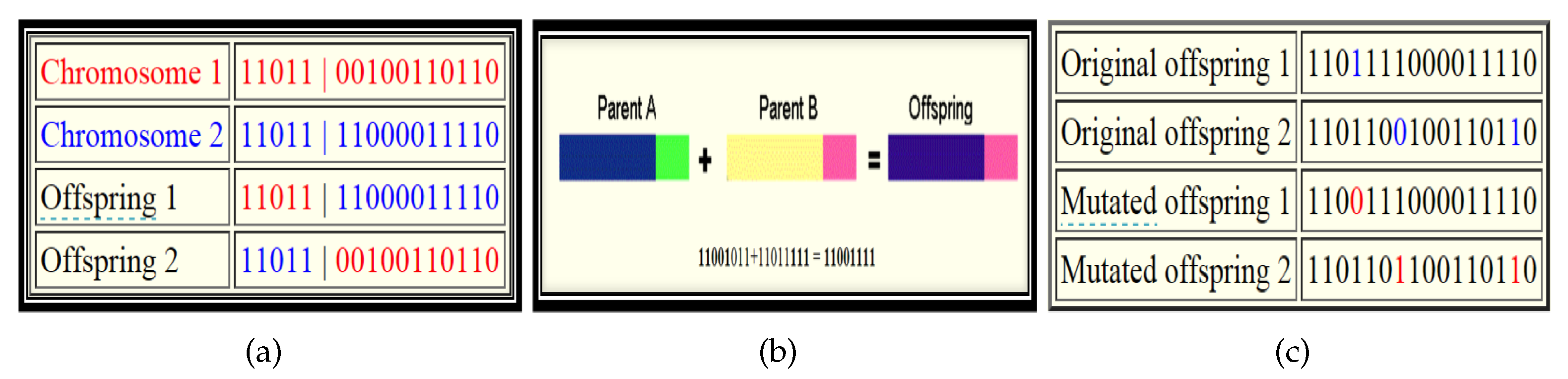
- Crossover: The use of the selection process determines the parents used in the crossover to produce a new offspring. Crossover is implemented by selecting a random point on the chromosome where the parents’ parts exchange happens. The crossover then brings up a new offspring based on the exchange point chosen with particular parts of the parents.There are different types of crossover namely: one-point crossover, two-point crossover, and multi-point crossover [39].There are some evolving techniques used to accommodate some situations. A brief definition of the two types are as follows:
- (a)
- One-point crossover: One-point crossover works when a crossover point along the chromosome is selected where genes are exchanged between the parents create two offspring (see Figure 2b).
- (b)
- Two-point crossover: Here, two points are selected on the parent chromosomes. There is then the exchange of genes between the two points for the production of two offspring. The crossover operator is used to avoid the exact duplication of the parents from the old population in the new offspring. This ensures that the new population being produced through crossover operation is able to survive in the next generation and also has the desirable parts or qualities of the parents [40].
- Mutation: Normally, mutation takes place after crossover is done. This operator applies the changes randomly to one or more “genes” to produce anew offspring, so it creates new adaptive solutions good avoid local optima. For example, in binary encoding, one or more randomly chosen bits can be switched from 0 to 1 or from 1 to 0; Figure 2c shows an example.Using the crossover operator alone to produce an offspring makes the GA stuck in the local optima, thus, the good parts of the parents survive in each generation, and the local optimal ones are to be found. This problem is called as the local-optima problem. The mutation operator is used to alleviate this problem by proving new offspring different from parents, and this encourages diversity in the population [41].
- Termination (stopping) criteria: GA at the end must stop to announce the best solution in hand, there are several termination conditions that are used [42], those include:
2.1. GA Parameters
- Crossover rate (probability): the number of times a crossover occurs for chromosomes in one generation, i.e., the chance that two chromosomes exchange some of their parts), crossover rate means that all offspring are made by crossover. If it is , then the complete new generation of individuals is to be exactly copied from the older population, except those resulted from the mutation process. Crossover rate is in the range of [43].
- Population size: the size of the population indicates the total number of the population’s inhabitants. Selection of population size is a sensitive issue; if the size of the population (search space) is small, this means little search space is available, and therefore it is possible to reach a local optimum. although, if the population size is very large, the area of search is increased and the computational load becomes high [45], therefore, the size of the population must be reasonable.
- Number of generations: It refers to the number of cycles before the termination. In some cases, hundreds of loops are sufficient, but in other cases we might need more, this depends on the problem type and complexity. Depending on the design of the GA, sometimes this parameter is not used, particularly if the termination of the GA depends on specific criteria.
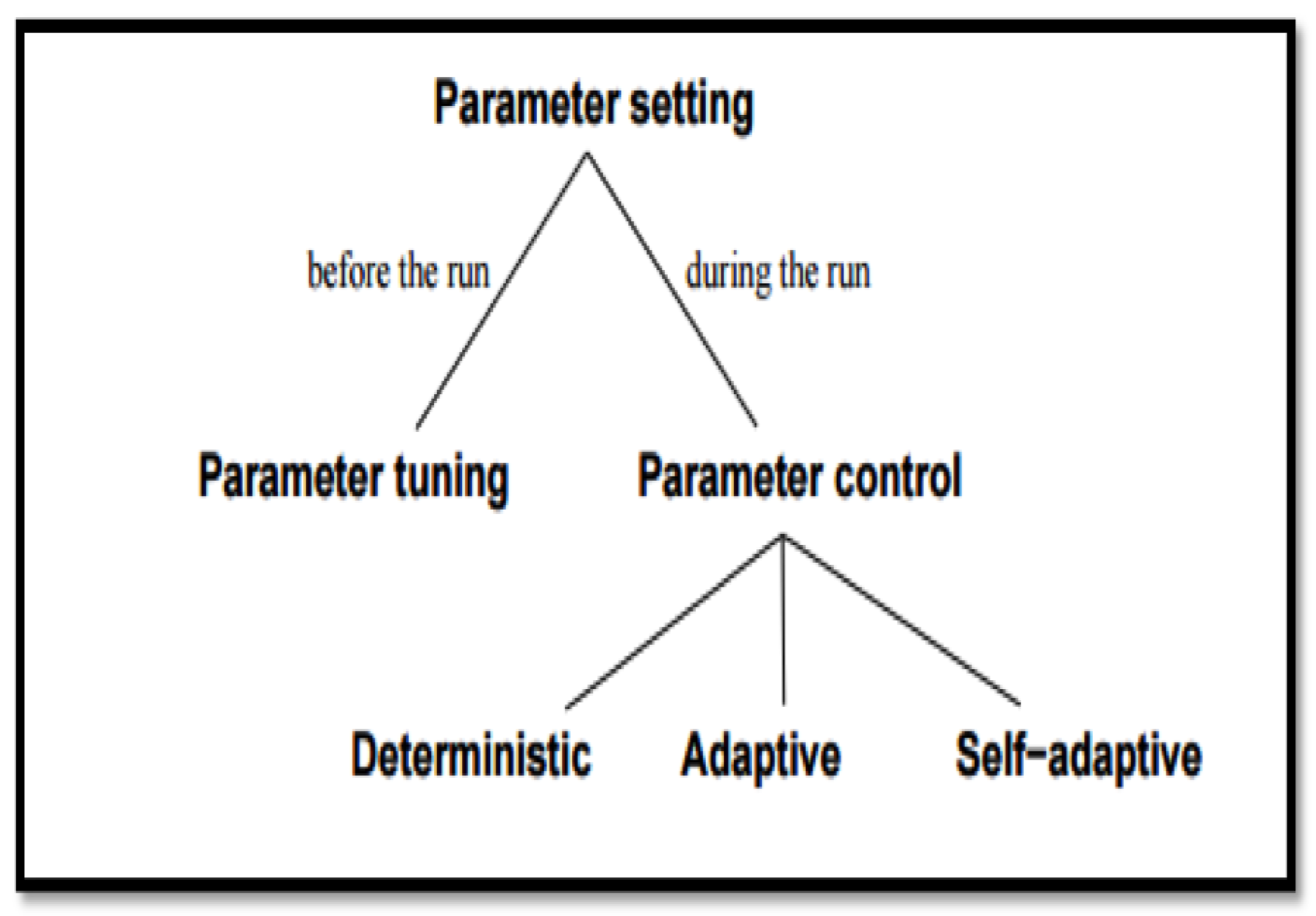
2.2. Crossover and Mutation Ratios
- Deterministic Parameter Control: used when the value of the parameter requires certain modifications using the same outcome rule. The parameter value is tuned to produce the same output without any results from the search process.
- Adaptive Parameter Control: applied when there is a particular kind of feedback required from the search option that assists in altering the parameter.
- Self-Adaptive Parameter Control. The GA here is allowed to develop its own parameters. The parameter values to be used are included in the individuals and go through mutation and crossover.
3. Literature Review for Parameter Selection in GAs
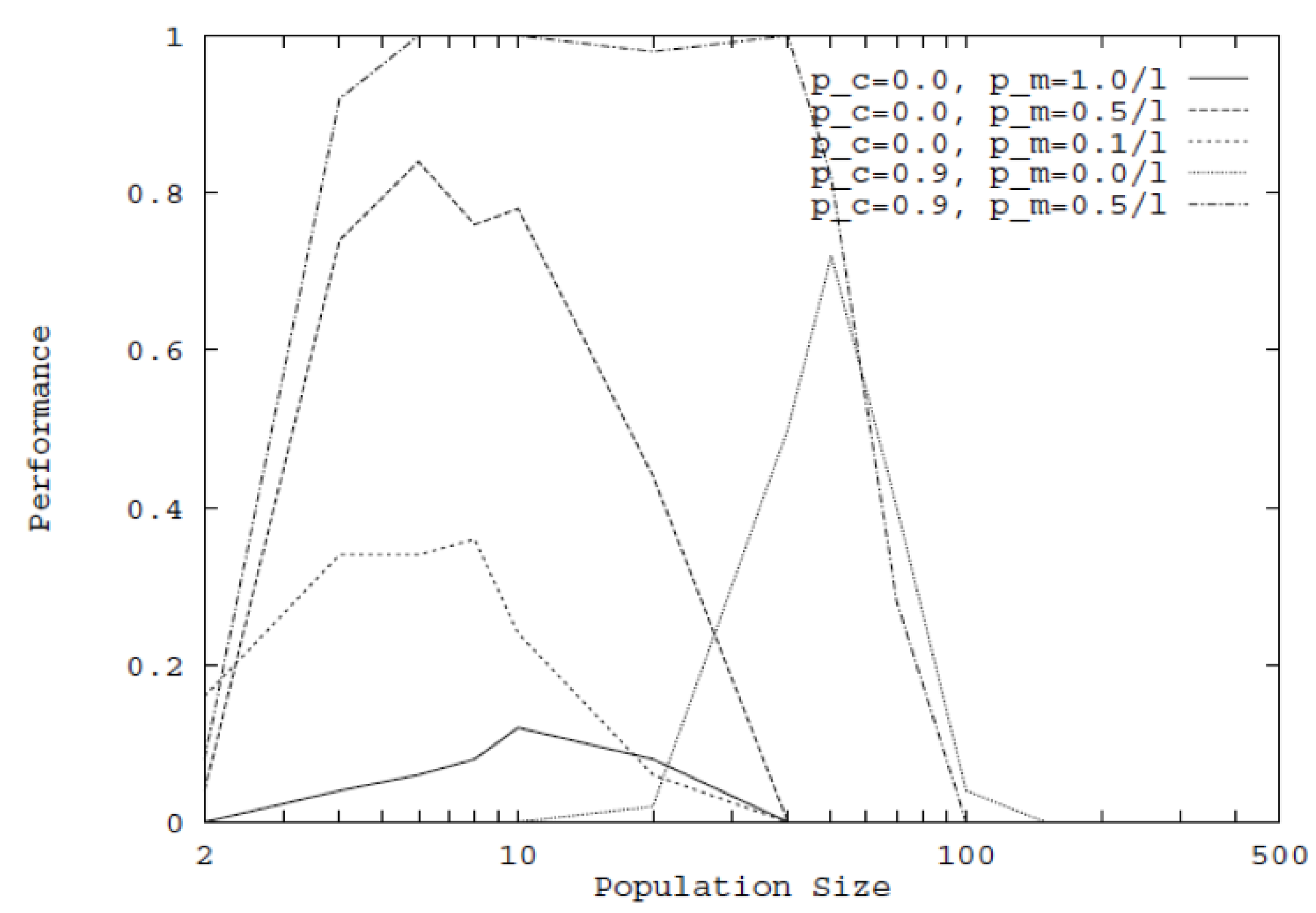
3.1. Crossover and Mutation Rates with Population Size
3.2. Traveling Salesman Problem (TSP)
4. Proposed Dynamic Approach
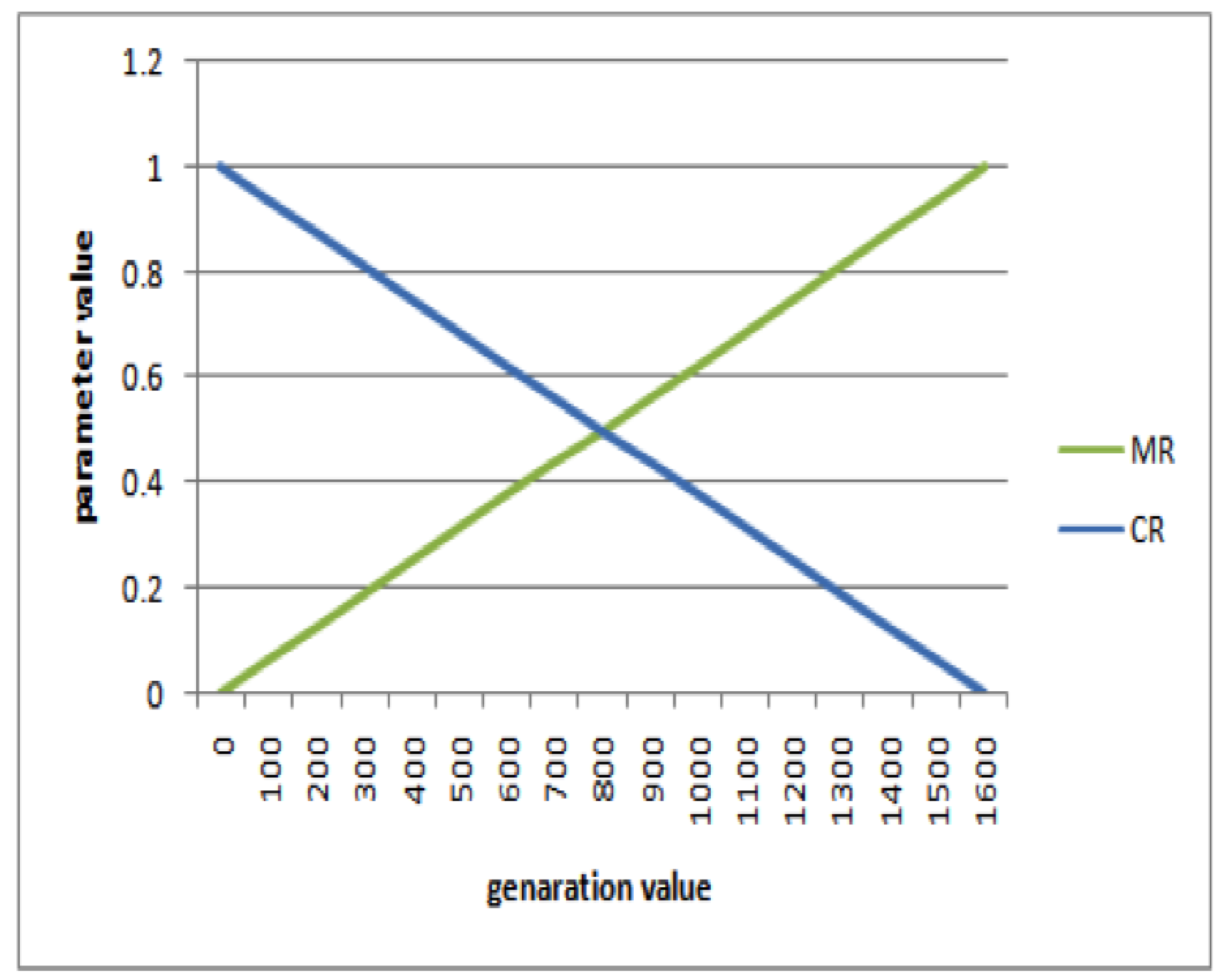
4.1. Dynamic Increasing of Low Mutation/Decreasing of High Crossover (ILM/DHC)
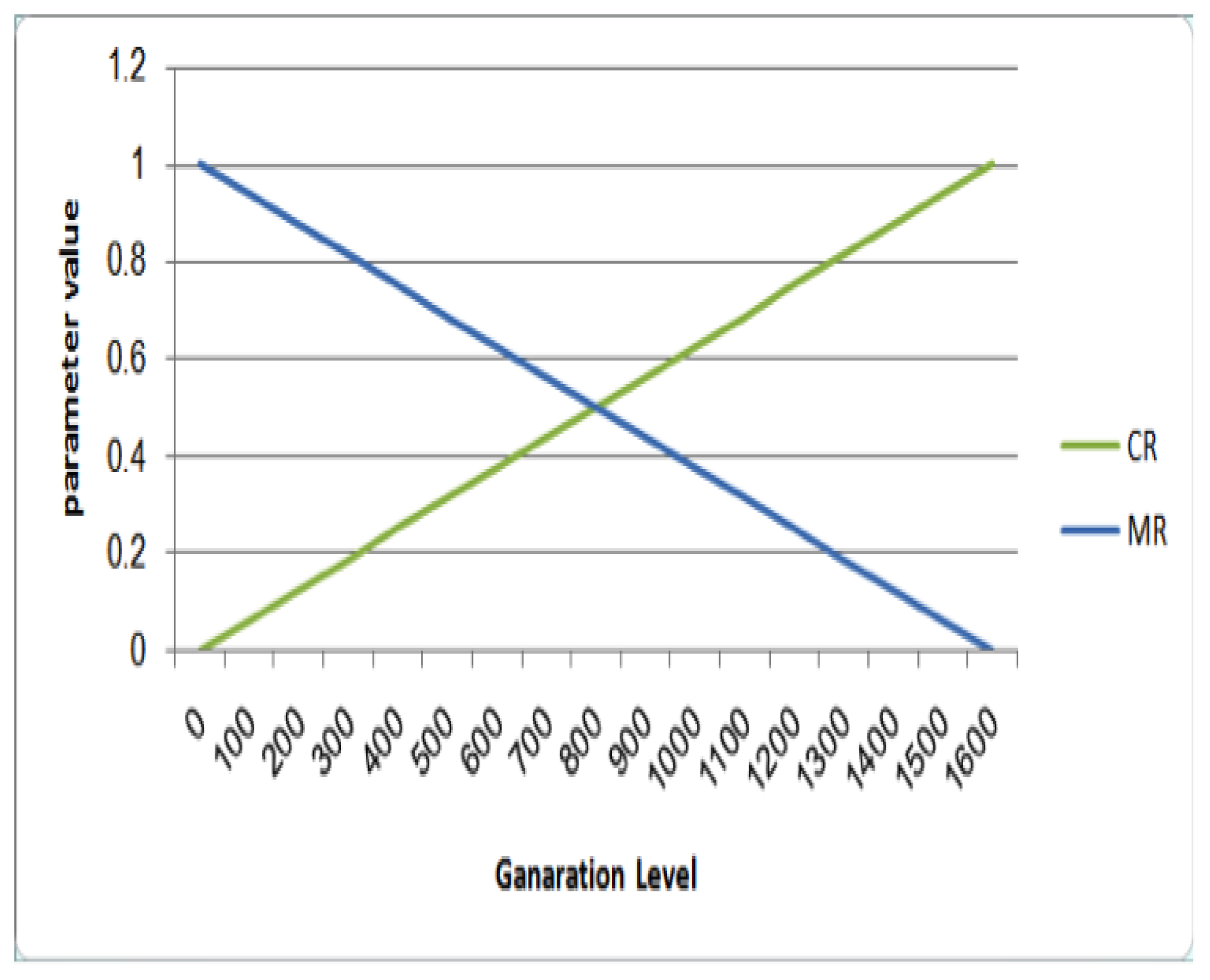
4.2. Dynamic Decreasing of High Mutation Rate/Increasing of Low Crossover Rate (DHM/ILC)
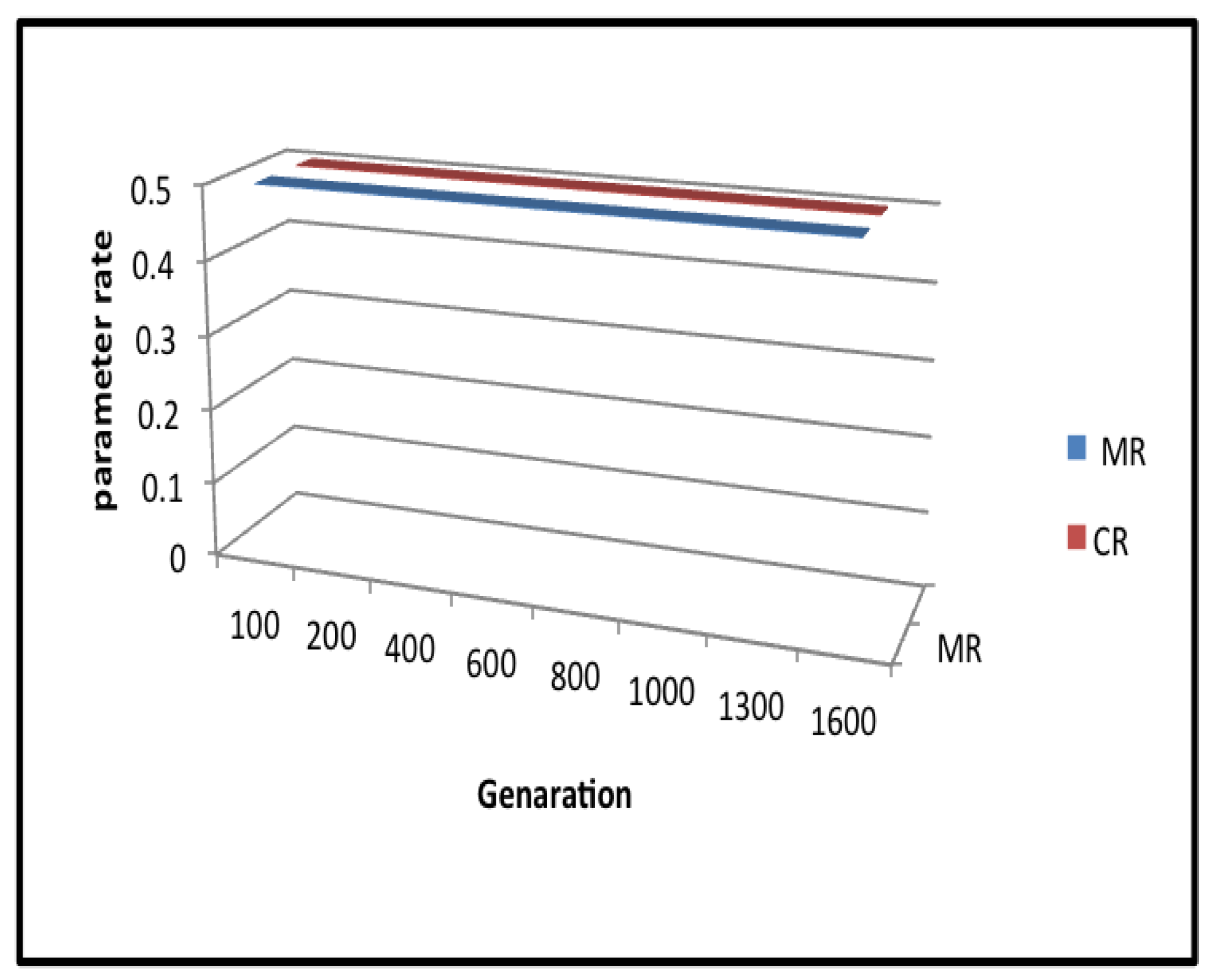
4.3. Fixed 50% for Mutation and Crossover Rates (FFMCR)
4.4. Parameter Tuning Method (0.03 Mutation, 0.9 Crossover) (0.03MR0.9CR)
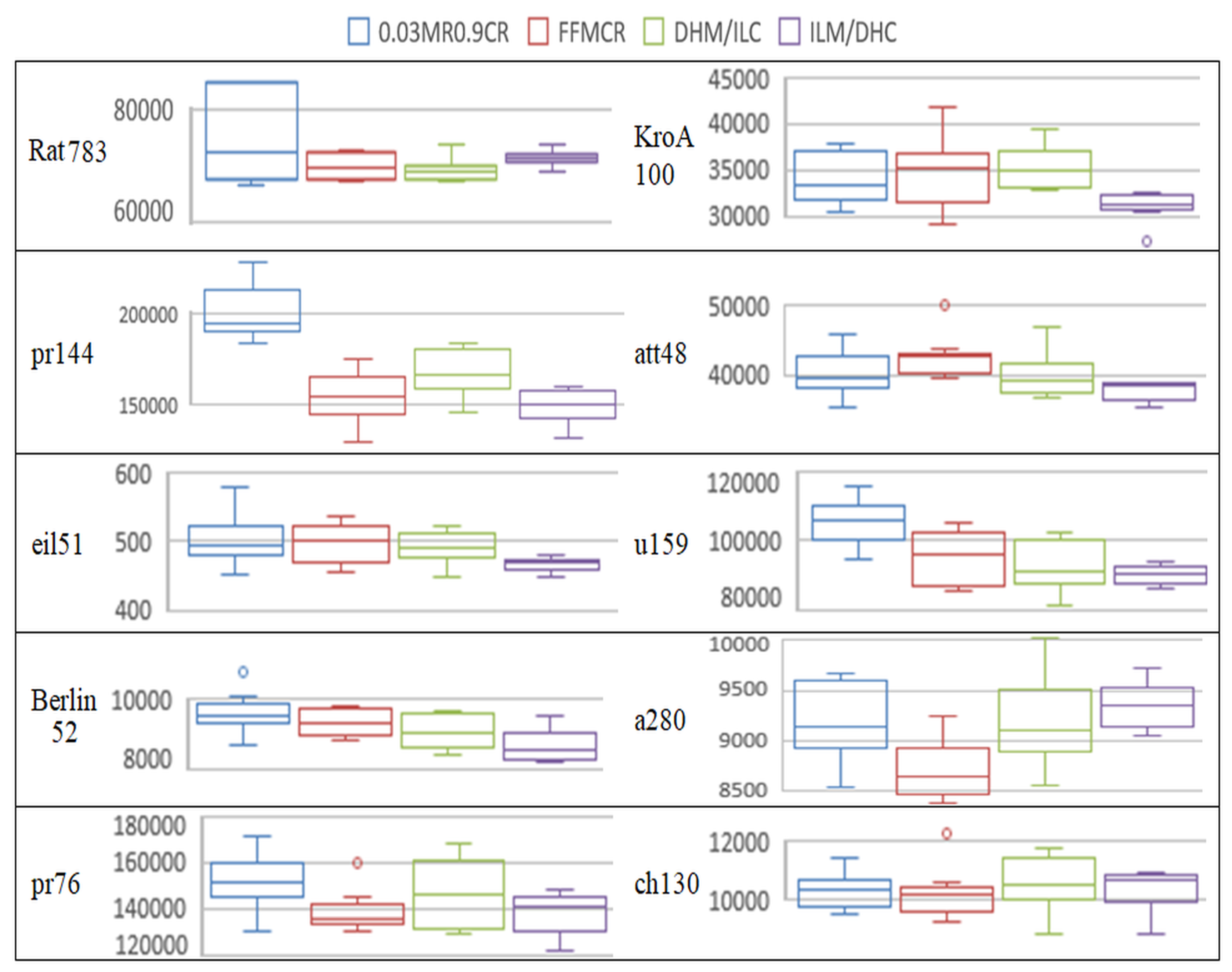
5. Experimental Results and Discussion
- (1)
- Small population size (25 and 50); sets 1 and 2.
- (2)
- Moderate population size (100 and 200); sets 3 and 4.
- (3)
- Large population size (300 and 400); sets 5 and 6.
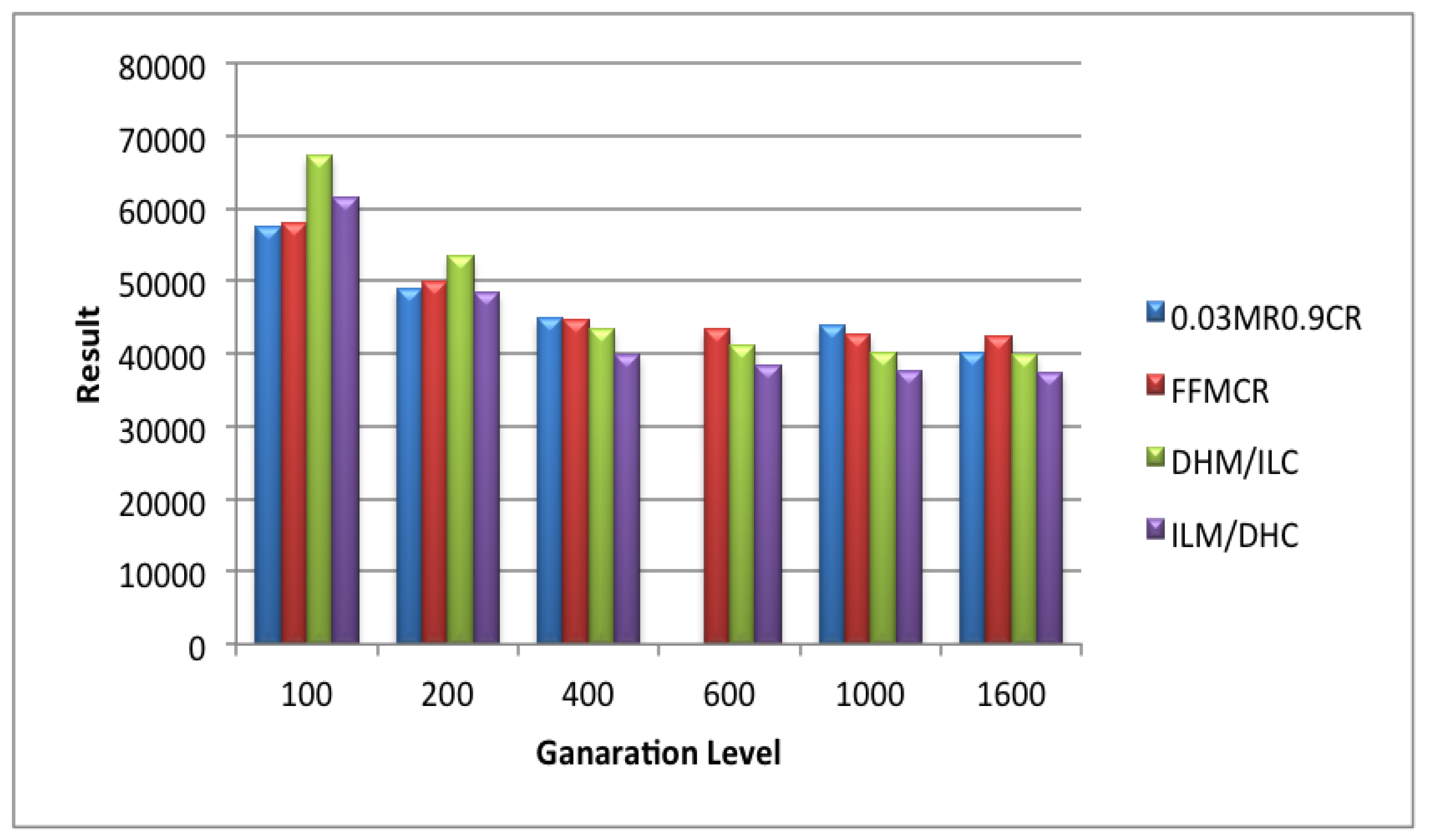
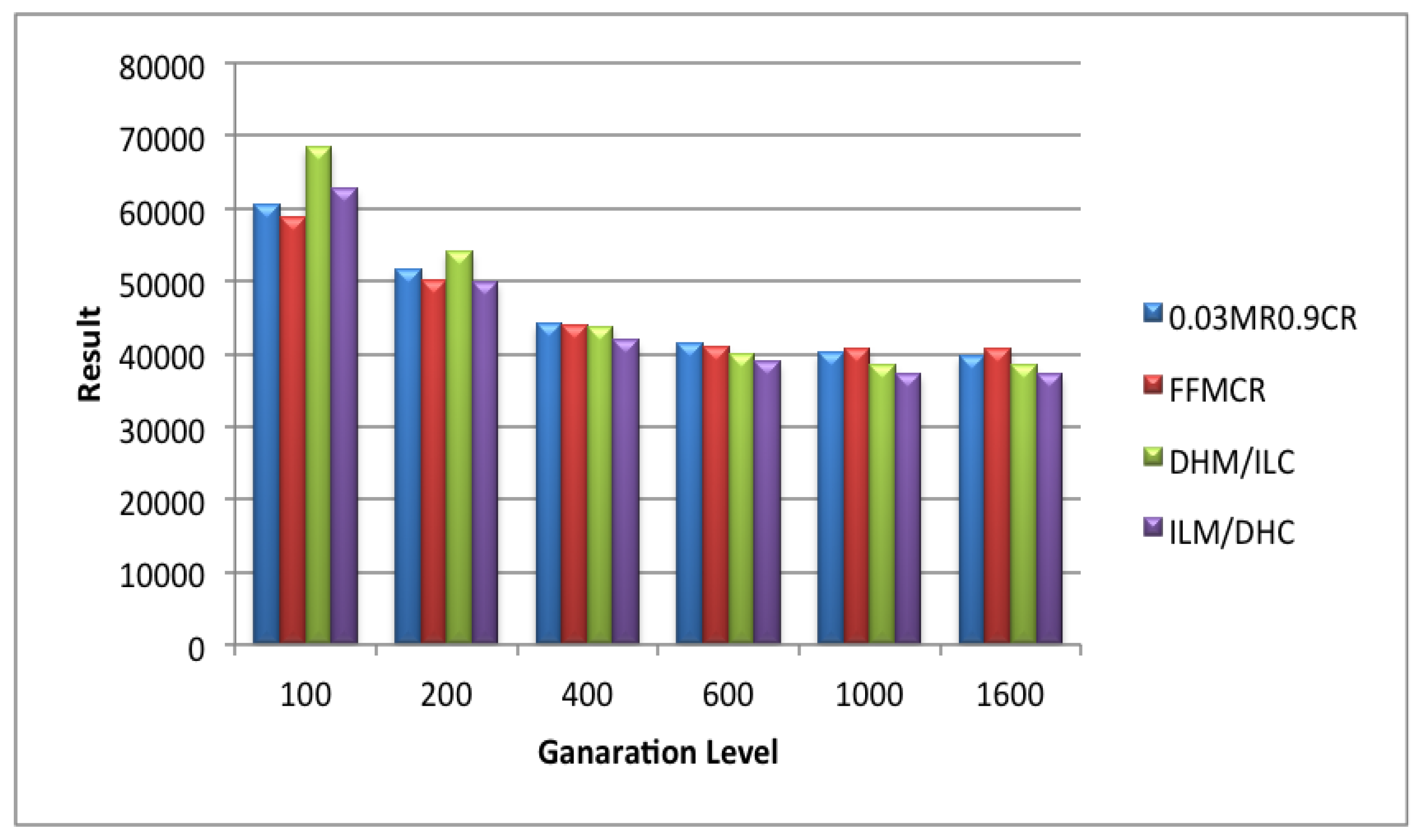
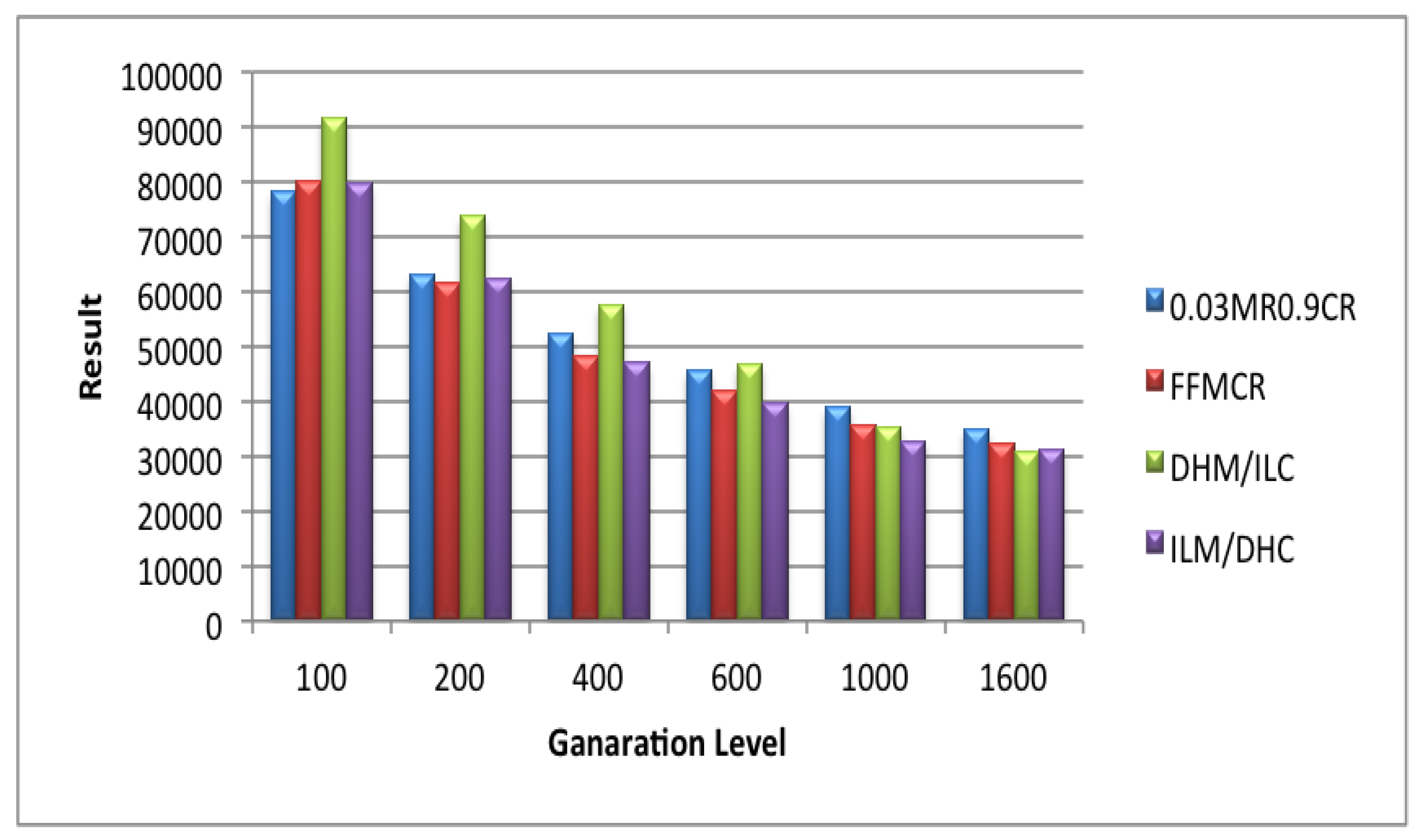
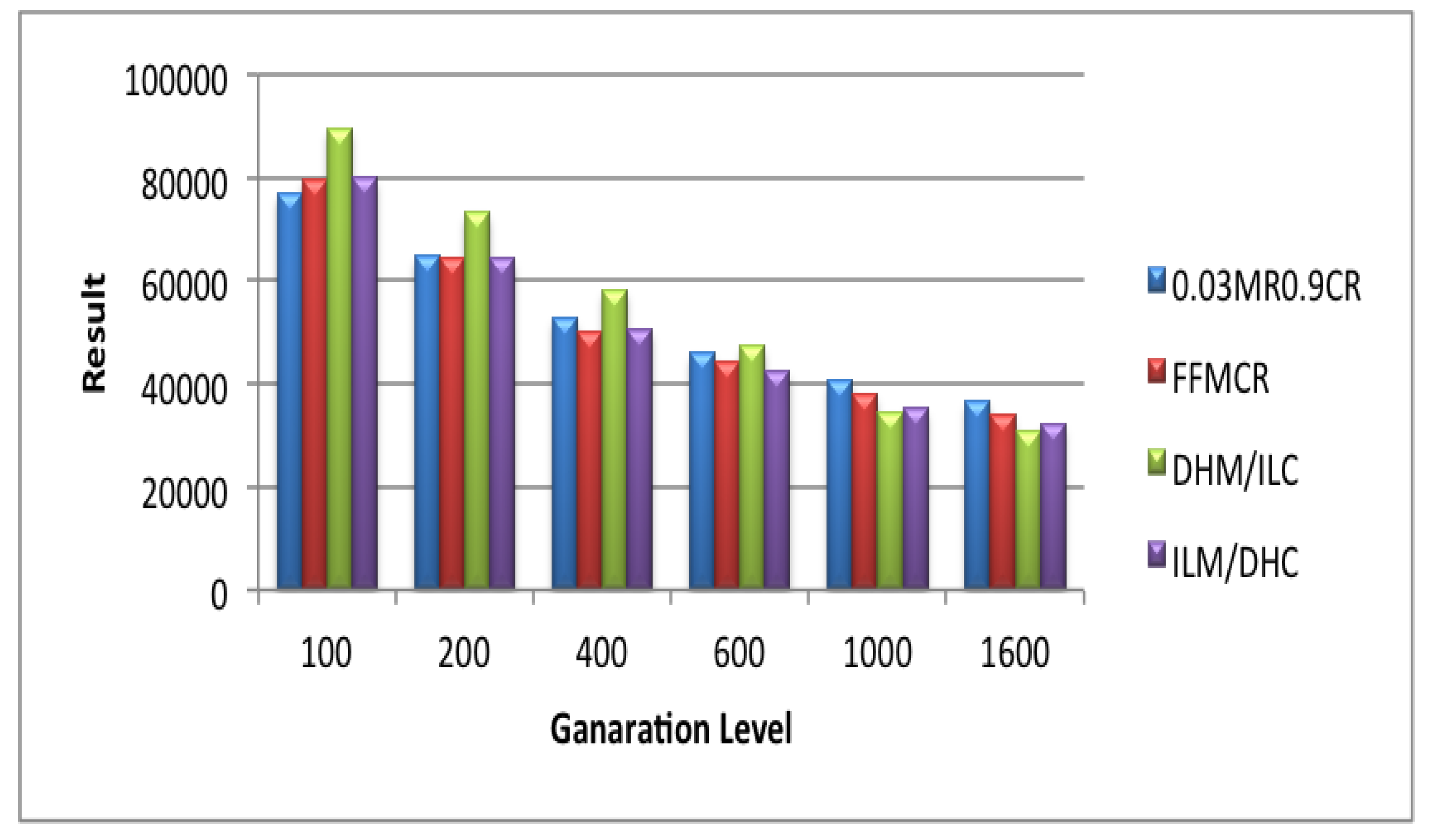
5.1. Set 1 of Experiments (Population Size = 25)
5.2. Set 2 of Experiments (Population Size = 50)
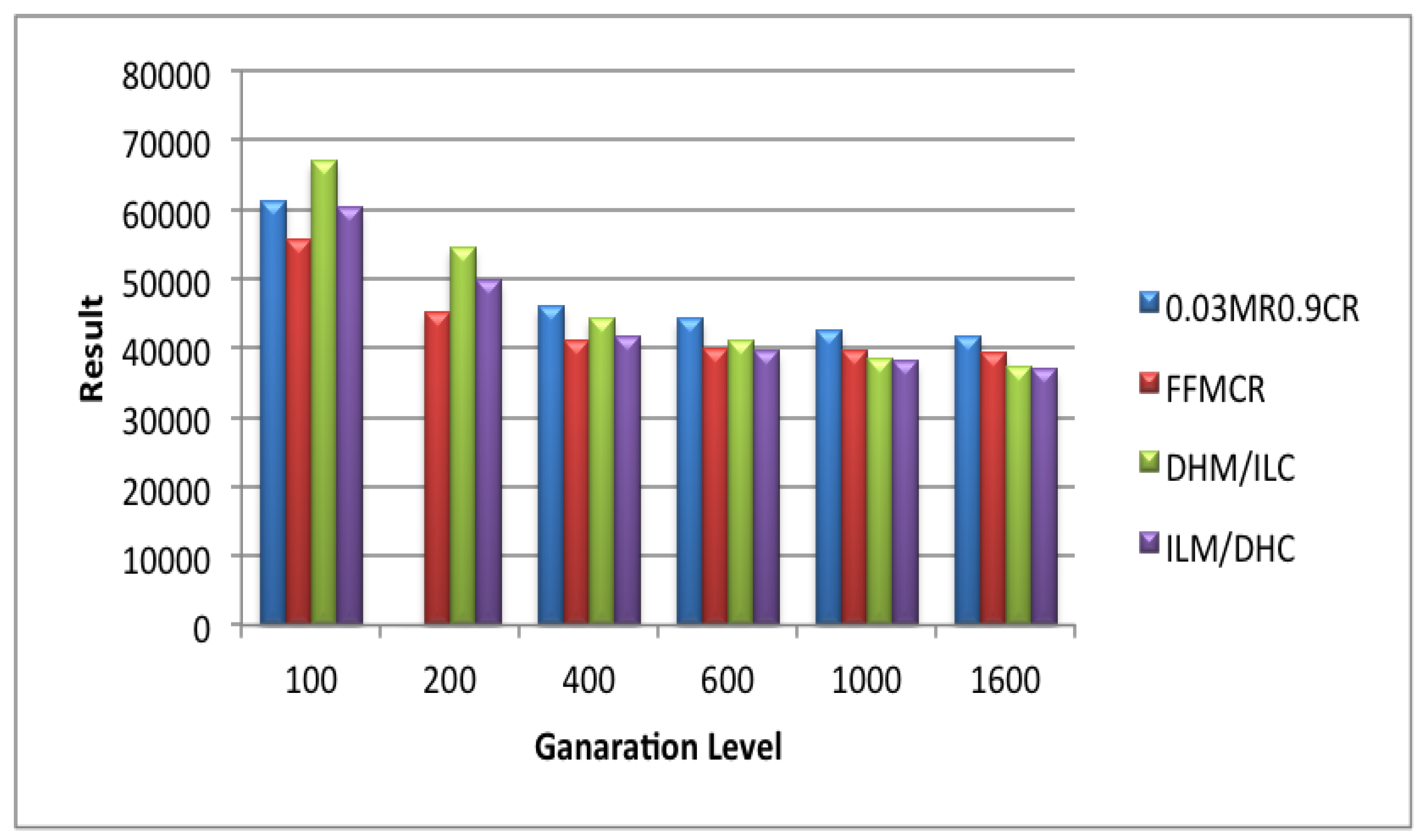
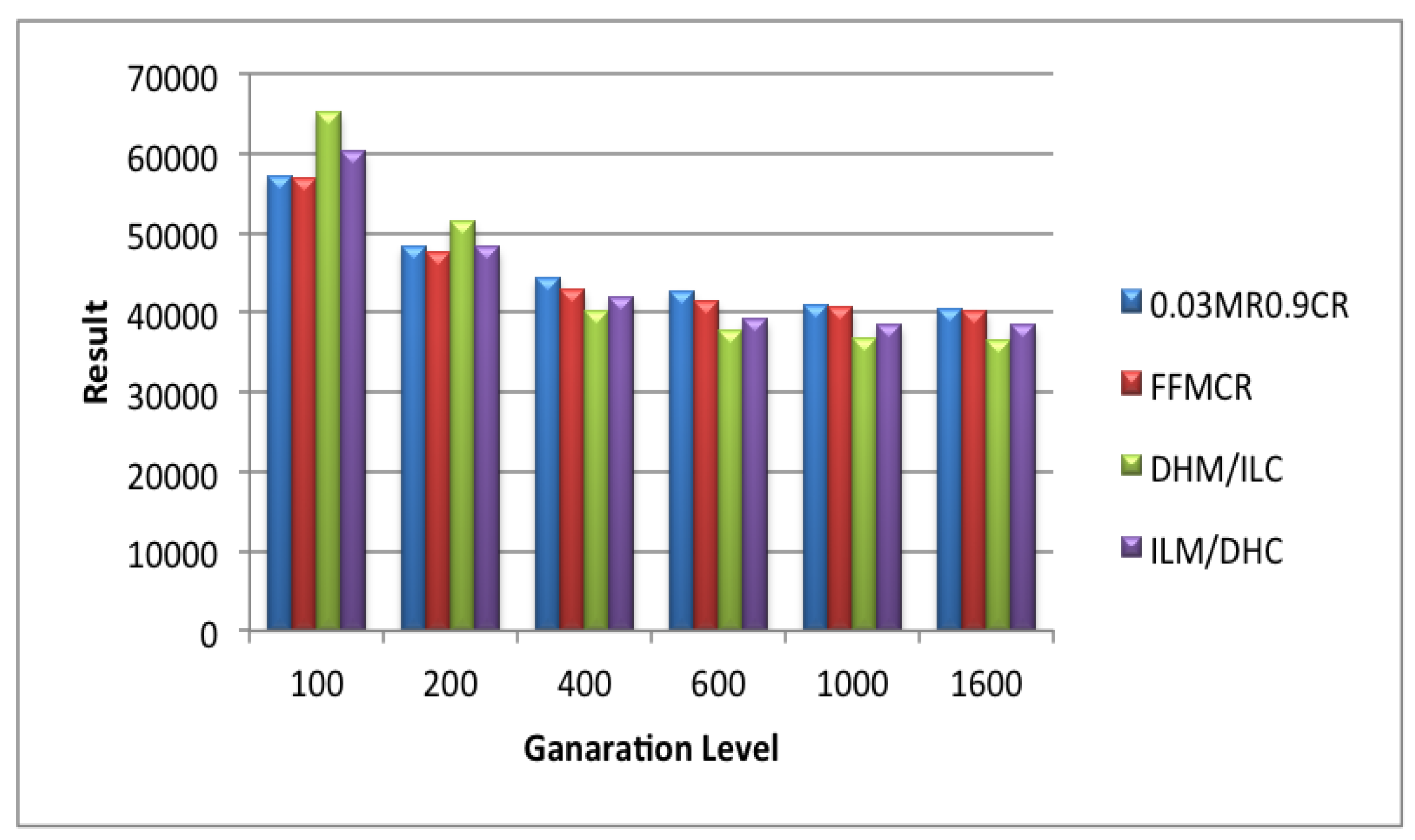
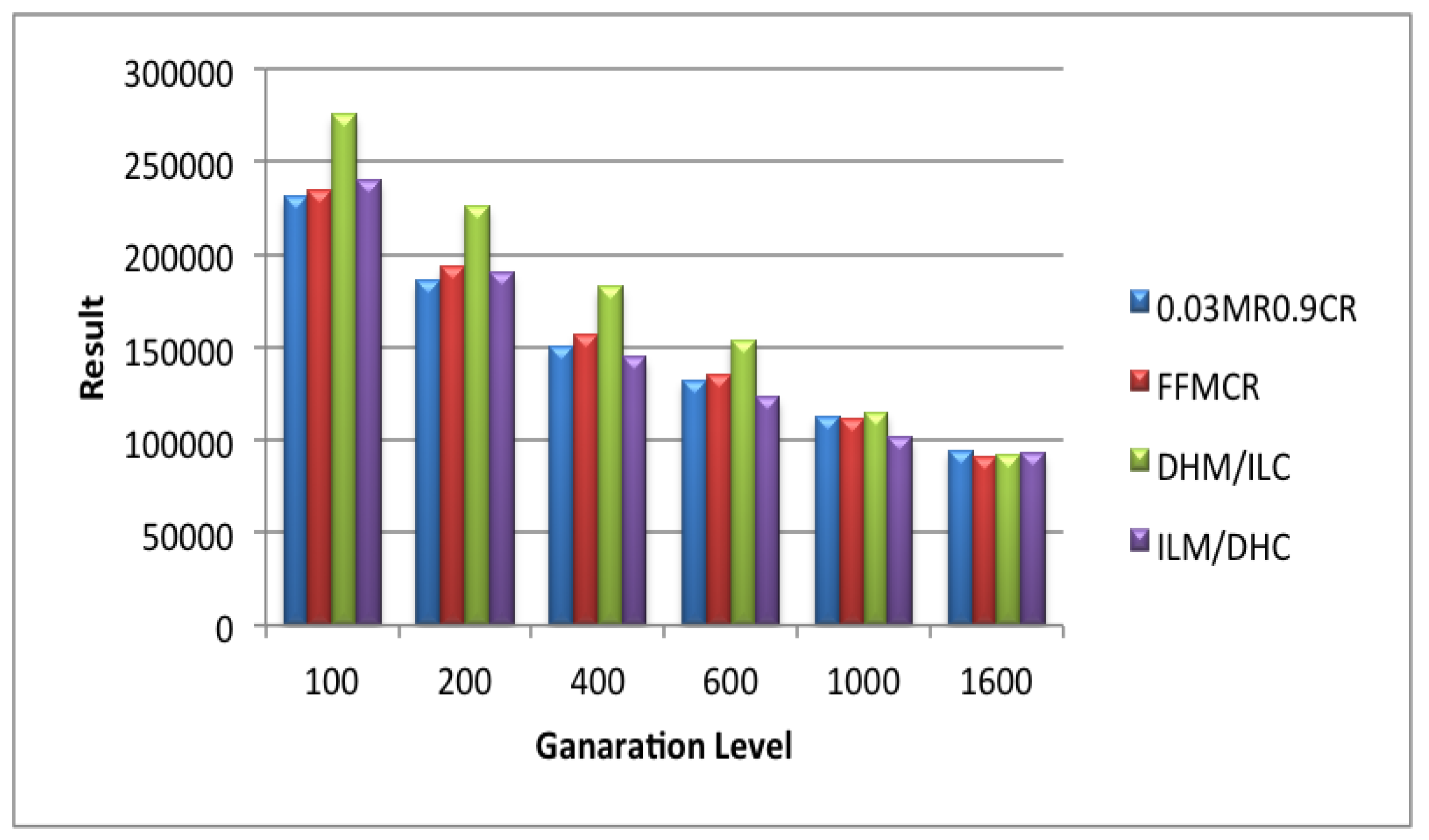
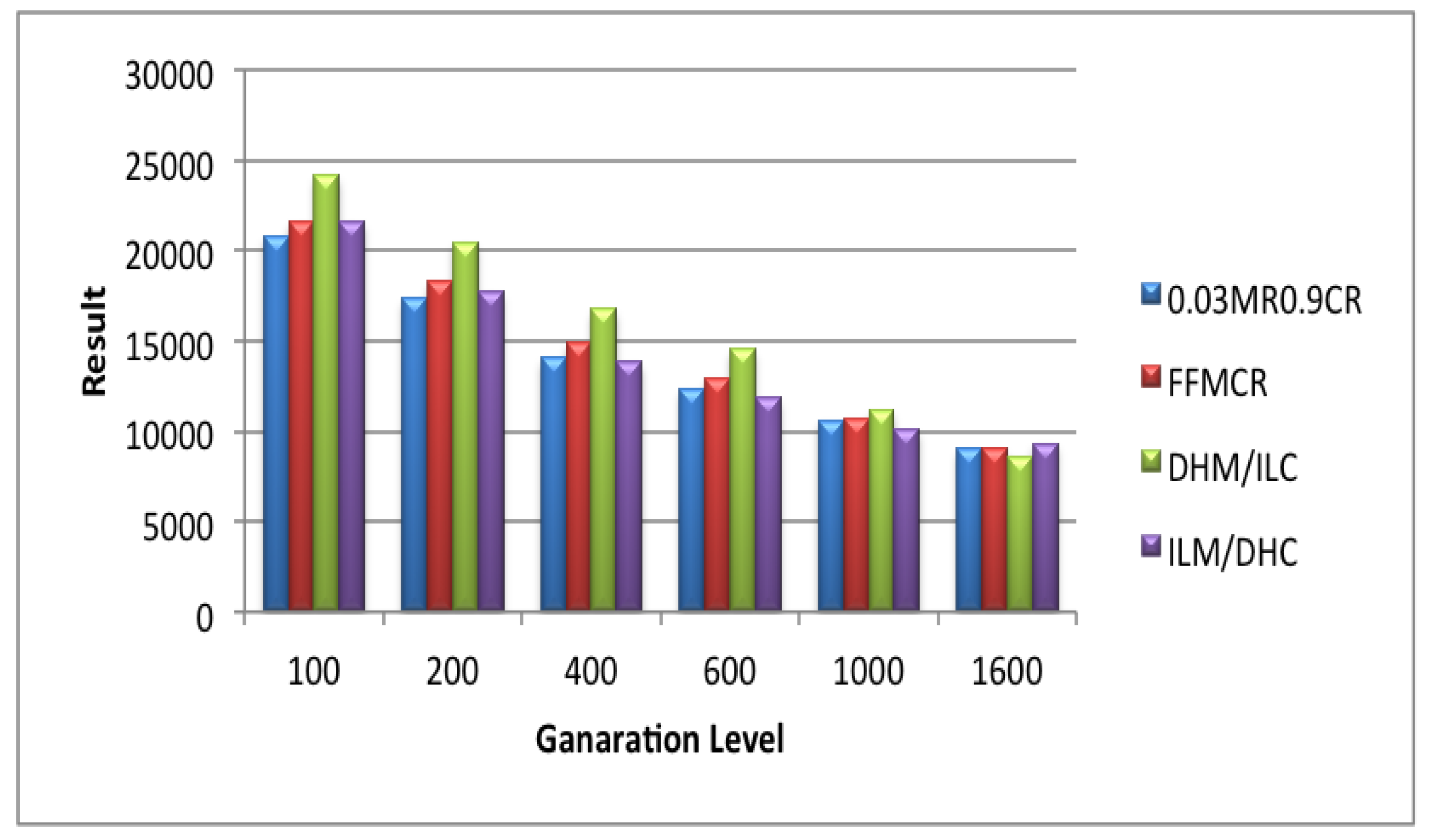
5.3. Set 3 of Experiments (Population Size = 100)
5.4. Set 4 of Experiments (Population Size = 200)
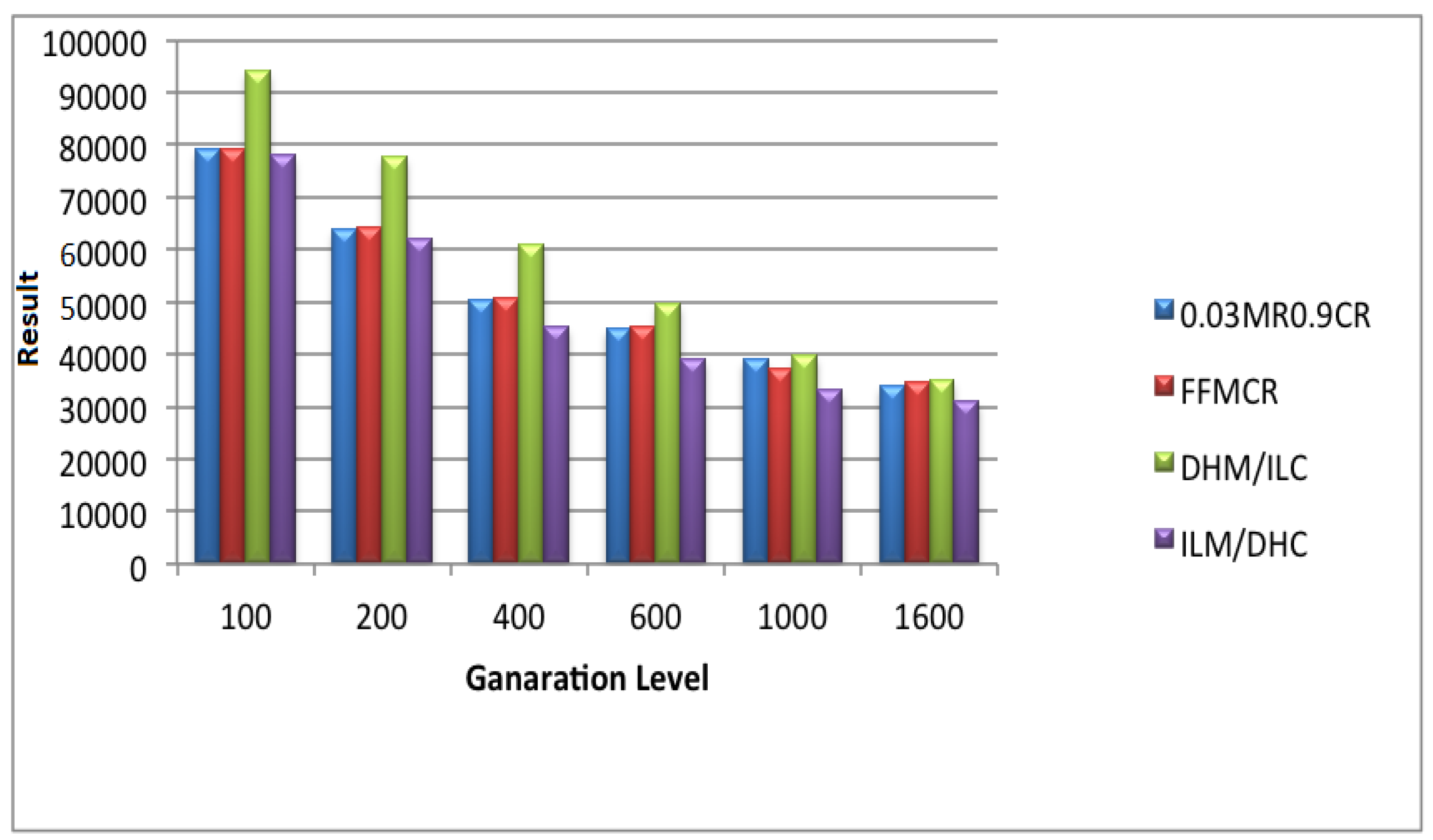
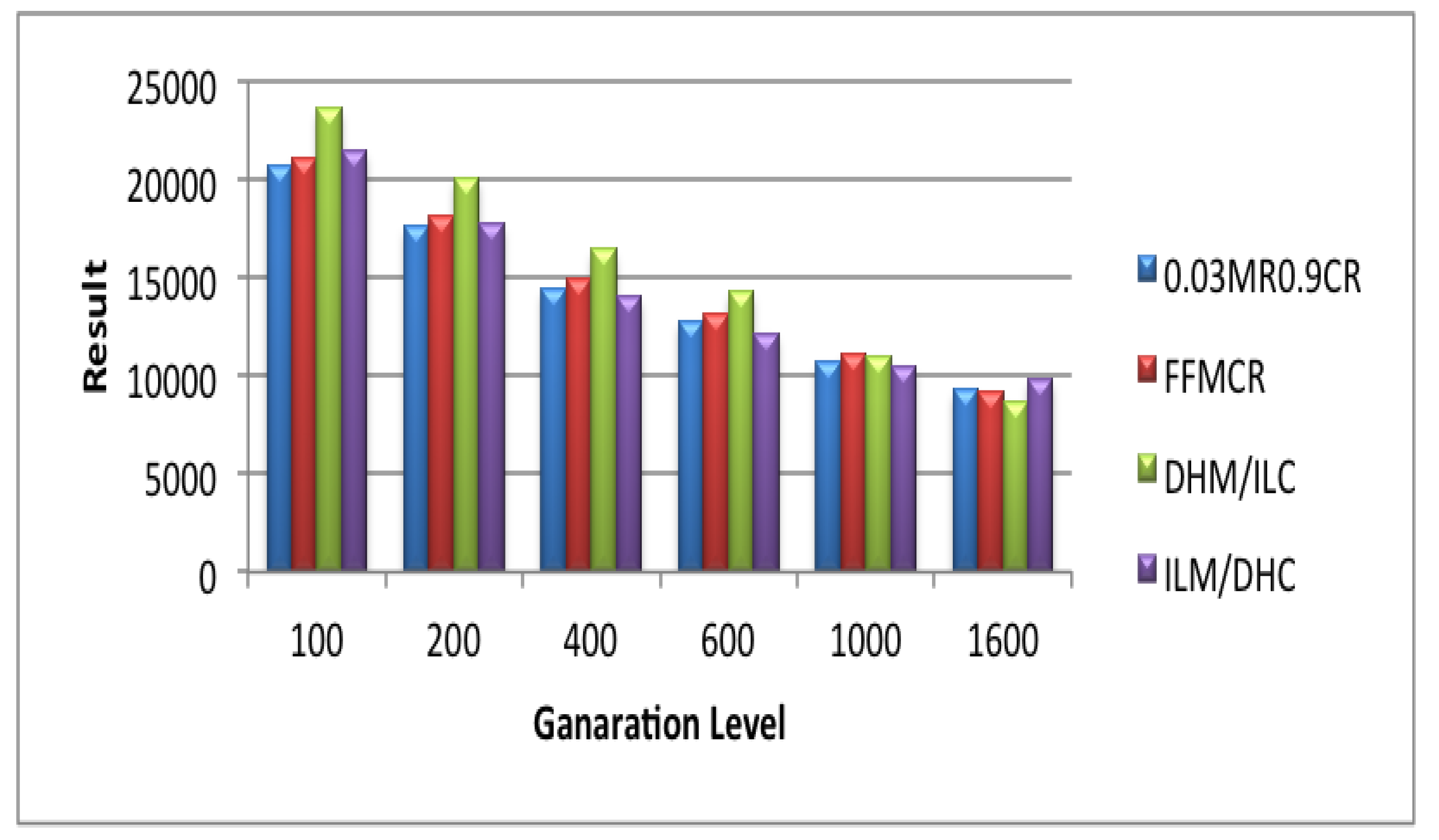
5.5. Set 5 of Experiments (Population Size = 300)
5.6. Set 6 of Experiments (Population Size = 400)
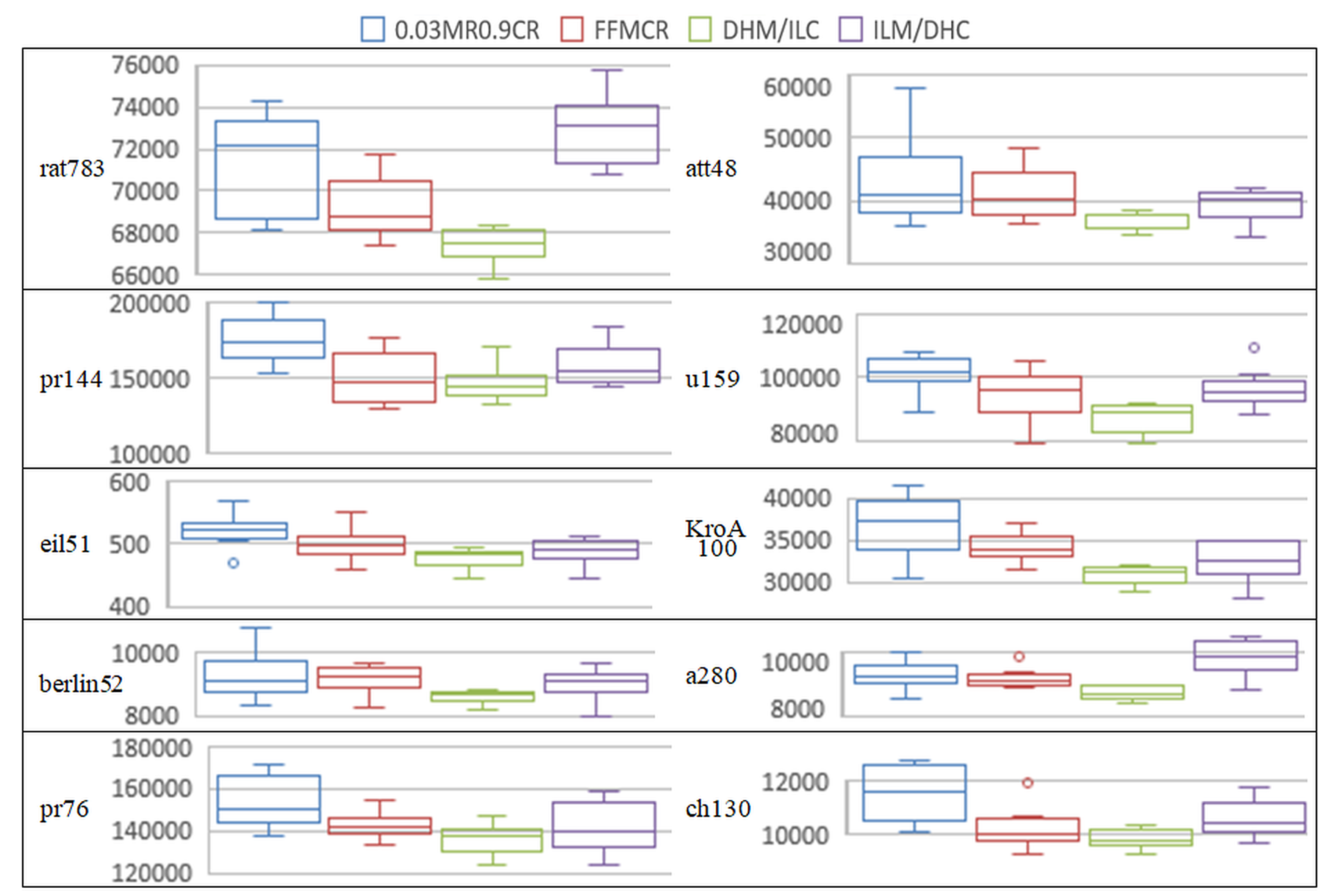
5.7. Time Complexity
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Results from the 6 Sets of Experiments Conducted for this Study
| Pop Size | Generation | Dynamic DHM/ILC | Dynamic ILM/DHC | 0.03MR0.9CR | FFMCR |
|---|---|---|---|---|---|
| 400 | 1600 | 8619.7 | 9166 | 9250.7 | 9167.6 |
| 300 | 1600 | 8790.7 | 9207 | 9642.6 | 9136.7 |
| 200 | 1600 | 9052.3 | 9526.9 | 9697.6 | 9397.8 |
| 100 | 1600 | 8782.5 | 8820.1 | 9200.3 | 8667.2 |
| 50 | 1600 | 9166.3 | 9024.5 | 9464 | 9155 |
| 25 | 1600 | 9068.2 | 8637.4 | 9606.1 | 9314.8 |
| Pop Size | Generation | Dynamic DHM/ILC | Dynamic ILM/DHC | 0.03MR0.9CR | FFMCR |
|---|---|---|---|---|---|
| 400 | 1600 | 135,876.6 | 141,485.1 | 152,704.2 | 142,986.3 |
| 300 | 1600 | 133,732.8 | 140,053.7 | 159,528.7 | 146,208.2 |
| 200 | 1600 | 139,640.5 | 142,065.1 | 151,172.8 | 149,717.8 |
| 100 | 1600 | 149,661.5 | 139,733.7 | 148,600.5 | 146,552.8 |
| 50 | 1600 | 139,644.6 | 135,316.6 | 155,182.4 | 140,766.9 |
| 25 | 1600 | 146,682.1 | 138,070.6 | 151,834.4 | 138,614.6 |
| Pop Size | Generation | Dynamic DHM/ILC | Dynamic ILM/DHC | 0.03MR0.9CR | FFMCR |
|---|---|---|---|---|---|
| 400 | 1600 | 30,804.1 | 32,291.9 | 36,751.3 | 34,094.3 |
| 300 | 1600 | 31,003.1 | 31,395 | 35,143 | 32,257.4 |
| 200 | 1600 | 32,754.5 | 32,435.6 | 34,587.6 | 35,331.6 |
| 100 | 1600 | 32,549.2 | 31,598.7 | 34,191 | 32,176.1 |
| 50 | 1600 | 32,058.6 | 31,630.6 | 39,674.8 | 32,730.7 |
| 25 | 1600 | 35,236.8 | 31,084.9 | 34,126.1 | 34,881.2 |
| Pop Size | Generation | Dynamic DHM/ILC | Dynamic ILM/DHC | 0.03MR0.9CR | FFMCR |
|---|---|---|---|---|---|
| 400 | 1600 | 87,507.6 | 96,255.1 | 101,313.2 | 94,858.3 |
| 300 | 1600 | 91,893.9 | 96,699.1 | 95,409.8 | 94,542.2 |
| 200 | 1600 | 91,861.1 | 92,766.4 | 94,578.1 | 91,125.4 |
| 100 | 1600 | 95,826.5 | 98,659 | 98,011.6 | 90,671.5 |
| 50 | 1600 | 95,642.6 | 93,439.5 | 101,332.3 | 93,621.9 |
| 25 | 1600 | 92,659.6 | 90,066.3 | 105,187.9 | 94,397.3 |
| Pop Size | Generation | Dynamic DHM/ILC | Dynamic ILM/DHC | 0.03MR0.9CR | FFMCR |
|---|---|---|---|---|---|
| 400 | 1600 | 9854.9 | 10,622 | 11,526.7 | 10,247.1 |
| 300 | 1600 | 9912 | 10,687 | 13,084.6 | 10,364.4 |
| 200 | 1600 | 10,687.2 | 10,213.4 | 10,442.9 | 10,238.1 |
| 100 | 1600 | 10,253.3 | 10,192.4 | 11,480 | 10,609.8 |
| 50 | 1600 | 10,383.2 | 10,178.5 | 11,455.4 | 10,231.1 |
| 25 | 1600 | 10,605 | 10,366.3 | 10,315.1 | 10,235.4 |
| Pop Size | Generation | Dynamic DHM/ILC | Dynamic ILM/DHC | 0.03MR0.9CR | FFMCR |
|---|---|---|---|---|---|
| 400 | 1600 | 8698.4 | 9862.1 | 9287.7 | 9177.3 |
| 300 | 1600 | 8645.6 | 9352.6 | 9017.8 | 9031.9 |
| 200 | 1600 | 9175.8 | 9425.4 | 9504.4 | 8912.6 |
| 100 | 1600 | 9134.1 | 9457.7 | 8957.1 | 8897 |
| 50 | 1600 | 9295.9 | 9067.3 | 9304.7 | 9264.5 |
| 25 | 1600 | 9176.5 | 9364.1 | 9180.7 | 8703.6 |
| Pop Size | Generation | Dynamic DHM/ILC | Dynamic ILM/DHC | 0.03MR0.9CR | FFMCR |
|---|---|---|---|---|---|
| 400 | 1600 | 36,854.5 | 39,310.4 | 43,077.1 | 41,121.3 |
| 300 | 1600 | 38,628.1 | 38,613.4 | 40,653.1 | 40,671.7 |
| 200 | 1600 | 36,502.1 | 38,514.7 | 40,504.6 | 40,272 |
| 100 | 1600 | 37,355.8 | 36,929.5 | 41,811.1 | 39,459.3 |
| 50 | 1600 | 38,448.1 | 37,244.2 | 39,872.2 | 40,686.3 |
| 25 | 1600 | 39,909.6 | 37,507.3 | 40,044.2 | 42,510.5 |
| Pop Size | Generation | Dynamic DHM/ILC | Dynamic ILM/DHC | 0.03MR0.9CR | FFMCR |
|---|---|---|---|---|---|
| 400 | 1600 | 476.6 | 485.4 | 519.6 | 498.7 |
| 300 | 1600 | 475.1 | 494.2 | 521.9 | 496.3 |
| 200 | 1600 | 468.5 | 481.6 | 501.5 | 490.7 |
| 100 | 1600 | 479 | 483.1 | 496.8 | 481.1 |
| 50 | 1600 | 486 | 472.5 | 511.1 | 488.4 |
| 25 | 1600 | 491.7 | 465.4 | 501 | 496.8 |
| Pop Size | Generation | Dynamic DHM/ILC | Dynamic ILM/DHC | 0.03MR0.9CR | FFMCR |
|---|---|---|---|---|---|
| 400 | 1600 | 146,385.7 | 158,169.1 | 174,357.6 | 149,038.5 |
| 300 | 1600 | 148,610.7 | 157,487.6 | 178,213.8 | 149,154.5 |
| 200 | 1600 | 155,994.3 | 165,080.7 | 169,101.1 | 177,072.5 |
| 100 | 1600 | 156,527.1 | 153,154.0 | 172,820.9 | 158,910.4 |
| 50 | 1600 | 157,446.3 | 151,455.1 | 175,095.8 | 151,072.1 |
| 25 | 1600 | 167,311.4 | 146,634.9 | 200,770.7 | 154,258.6 |
| Pop Size | Generation | Dynamic DHM/ILC | Dynamic ILM/DHC | 0.03MR0.9CR | FFMCR |
|---|---|---|---|---|---|
| 400 | 1600 | 67,424.3 | 73,022.8 | 71,517.6 | 69,253.6 |
| 300 | 1600 | 68,091.9 | 72,438.5 | 69,554.8 | 70,979.8 |
| 200 | 1600 | 67,399.3 | 71,571.3 | 70,486.3 | 71,100.3 |
| 100 | 1600 | 67,795.7 | 71,098.2 | 70,183.6 | 68,322.4 |
| 50 | 1600 | 68,424.3 | 71,127.7 | 76,428 | 67,791.5 |
| 25 | 1600 | 69,123.6 | 71,432.3 | 79,752 | 69,843.1 |
References
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Man, K.F.; Tang, K.S.; Kwong, S. Genetic algorithms: Concepts and applications. IEEE Trans. Ind. Electron. 1996, 43, 519–534. [Google Scholar] [CrossRef]
- Golberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Whitley, D. A genetic algorithm tutorial. Stat. Comput. 1994, 4, 65–85. [Google Scholar] [CrossRef]
- Tsang, P.W.M.; Au, A.T.S. A genetic algorithm for projective invariant object recognition. IEEE TENCON Digit. Signal Process. Appl. 1996, 1, 58–63. [Google Scholar]
- Mohammed, A.A.; Nagib, G. Optimal routing in ad-hoc network using genetic algorithm. Int. J. Adv. Netw. Appl. 2012, 03, 1323–1328. [Google Scholar]
- Srivastava, P.R.; Kim, T.H. Application of genetic algorithm in software testing. Int. J. Softw. Eng. Its Appl. 2009, 3, 87–96. [Google Scholar]
- Paulinas, M.; Ušinskas, A. A survey of genetic algorithms applications for image enhancement and segmentation. Inf. Technol. Control 2015, 36, 278–284. [Google Scholar]
- Hassanat, A.B.; Prasath, V.S.; Mseidein, K.I.; Al-Awadi, M.; Hammouri, A.M. A HybridWavelet-Shearlet Approach to Robust Digital ImageWatermarking. Informatica 2017, 41, 3–24. [Google Scholar]
- Benkhellat, Z.; Belmehdi, A. Genetic algorithms in speech recognition systems. In Proceedings of the International Conference on Industrial Engineering and Operations Management, Istanbul, Turkey, 3–6 July 2012; pp. 853–858. [Google Scholar]
- Gupta, H.; Wadhwa, D.S. Speech feature extraction and recognition using genetic algorithm. Int. J. Emerg. 2014, 4, 363–369. [Google Scholar]
- Aliakbarpour, H.; Prasath, V.B.S.; Dias, J. On optimal multi-sensor network configuration for 3D registration. J. Sens. Actuator Netw. 2015, 4, 293–314. [Google Scholar] [CrossRef]
- Papanna, N.; Reddy, A.R.M.; Seetha, M. EELAM: Energy efficient lifetime aware multicast route selection for mobile ad hoc networks. Appl. Comput. Inform. 2019, 15, 120–128. [Google Scholar] [CrossRef]
- Ashish, K.; Dasari, A.; Chattopadhyay, S.; Hui, N.B. Genetic-neuro-fuzzy system for grading depression. Appl. Comput. Inform. 2018, 14, 98–105. [Google Scholar] [CrossRef]
- Omisore, M.O.; Samuel, O.W.; Atajeromavwo, E.J. A Genetic-Neuro-Fuzzy inferential model for diagnosis of tuberculosis. Appl. Comput. Inform. 2017, 13, 27–37. [Google Scholar] [CrossRef]
- Hassanat, A.B.; Altarawneh, G.; Tarawneh, A.S.; Faris, H.; Alhasanat, M.B.; de Voogt, A.; Prasath, S.V. On Computerizing the Ancient Game of tāb. Int. J. Gaming Comput.-Mediat. Simul. (IJGCMS) 2018, 10, 20–40. [Google Scholar] [CrossRef]
- Guo, K.; Yang, M.; Zhu, H. Application research of improved genetic algorithm based on machine learning in production scheduling. In Neural Computing and Applications; Springer: London, UK, 2019; pp. 1–12. [Google Scholar]
- Wang, Y.M.; Yin, H.L. Cost-Optimization Problem with a Soft Time Window Based on an Improved Fuzzy Genetic Algorithm for Fresh Food Distribution. Math. Probl. Eng. 2018, 2018, 1–16. [Google Scholar] [CrossRef]
- Hendricks, D.; Wilcox, D.; Gebbie, T. High-speed detection of emergent market clustering via an unsupervised parallel genetic algorithm. arXiv 2014, arXiv:1403.4099. [Google Scholar]
- Mustafa, W. Optimization of production systems using genetic algorithms. Int. J. Comput. Intell. Appl. 2003, 3, 233–248. [Google Scholar] [CrossRef]
- Eiben, A.E.; Smith, J.E. Introduction to Evolutionary Computing; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Zhong, J.; Hu, X.; Gu, M.; Zhang, J. Comparison of performance between different selection strategies on simple genetic algorithms. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), Vienna, Austria, 28–30 November 2005; Volume 2, pp. 1115–1121. [Google Scholar]
- Eiben, A.E.; Michalewicz, Z.; Schoenauer, M.; Smith, J.E. Parameter control in evolutionary algorithms. In Parameter Setting in Evolutionary Algorithms; Springer: Berlin/Heidelberg, Germany, 2007; pp. 19–46. [Google Scholar]
- Hong, T.P.; Hong-Shung, W. A dynamic mutation genetic algorithm. IEEE Int. Conf. Syst. Man, Cybern. 1996, 3, 2000–2005. [Google Scholar]
- Gen, M.; Runwei, C. Genetic Algorithms and Engineering Optimization; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Deb, K.; Agrawal, S. Understanding interactions among genetic algorithm parameters. Found. Genet. Algorithms 1999, 5, 265–286. [Google Scholar]
- Pereira, G.C.; Oliveira, M.M.F.; Ebecken, N.F.F. Genetic Optimization of Artificial Neural Networks to Forecast Virioplankton Abundance from Cytometric Data. J. Intell. Learn. Syst. Appl. 2013, 5, 57–66. [Google Scholar] [CrossRef]
- Kumar, R. Novel encoding scheme in genetic algorithms for better fitness. Int. J. Eng. Adv. Technol. 2012, 1, 214–219. [Google Scholar]
- Shyr, W.J. Parameters Determination for Optimum Design by Evolutionary Algorithm; IntechOpen: Rijeka, Croatia, 2010. [Google Scholar]
- Alkafaween, E.O. Novel Methods for Enhancing the Performance of Genetic Algorithms. Master’s Thesis, Mu’tah University, Karak, Jordan, 2015. [Google Scholar]
- Shukla, A.; Pandey, H.M.; Mehrotra, D. Comparative review of selection techniques in genetic algorithm. In Proceedings of the International Conference on Futuristic Trends on Computational Analysis and Knowledge Management, Noida, India, 25–27 February 2015; pp. 515–519. [Google Scholar]
- Grefenstette, J. Optimization of control parameters for genetic algorithms. IEEE Trans. Syst. Man Cybern. 1986, 16, 122–128. [Google Scholar] [CrossRef]
- Razali, N.M.; Geraghty, J. Genetic algorithm performance with different selection strategies in solving TSP. In Proceedings of the world congress on engineering, London, UK, 6–8 July 2011; pp. 1–6. [Google Scholar]
- Oladele, R.O.; Sadiku, J.S. Genetic algorithm performance with different selection methods in solving multi-objective network design problem. Int. J. Comput. Appl. 2013, 70, 5–9. [Google Scholar] [CrossRef]
- Bäck, T. Evolutionary Algorithms in Theory and Practice; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Lipowski, A.; Lipowska, D. Roulette-wheel selection via stochastic acceptance. Phys. A Stat. Mech. Its Appl. 2012, 391, 2193–2196. [Google Scholar] [CrossRef]
- Srinivas, M.; Patnak, L.M. Adaptive probabilities of crossover and mutation in genetic algorithms. IEEE Trans. Syst. Man Cybern. 1994, 24, 656–667. [Google Scholar] [CrossRef]
- Obitko, M. Introduction to Genetic Algorithms; Czech Technical University: Prague, Czech Republic, 1998. [Google Scholar]
- Kaya, Y.; Uyar, M. A novel crossover operator for genetic algorithms: Ring crossover. arXiv 2011, arXiv:1105.0355. [Google Scholar]
- Bajpai, P.; Manoj, K. Genetic Algorithm—An Approach to Solve Global Optimization. Indian J. Comput. Sci. Eng. 2010, 1, 199–206. [Google Scholar]
- Korejo, I.; Yang, S.; Brohi, K.; Khuhro, Z.U. Multi-population methods with adaptive mutation for multi-modal optimization problems. Int. J. Soft Comput. Artif. Intell. Appl. 2013, 2, 19. [Google Scholar] [CrossRef]
- Safe, M.; Carballido, J.; Ponzoni, I.; Brignole, N. On stopping criteria for genetic algorithms. In Brazilian Symposium on Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2004; pp. 405–413. [Google Scholar]
- De Jong, K.; Spears, W. A formal analysis of the role of multi-point crossover. Ann. Math. Artif. Intell. 1992, 5, 1–26. [Google Scholar] [CrossRef]
- Lynch, M. Evolution of the mutation rate. Trends Genet. 2010, 26, 345–352. [Google Scholar] [CrossRef]
- Roeva, O.; Fidanova, S.; Paprzycki, M. Influence of the population size on the genetic algorithm performance in case of cultivation process modelling. In Proceedings of the IEEE Conference on Computer Science and Information Systems, Kraków, Poland, 8–11 September 2013; pp. 371–376. [Google Scholar]
- Tuson, A.L.; Ross, P. Adapting Operator Probabilities in Genetic Algorithms. Master’s Thesis, Department of Artificial Intelligence, Univeristy of Edinburgh, Edinburgh, UK, 1995. [Google Scholar]
- Davis, L. Handbook of Genetic Algorithms; Van Nostrand Reinhold Co.: New York, NY, USA, 1991. [Google Scholar]
- Munroe, R.D. Genetic programming: The ratio of crossover to mutation as a function of time. Res. Lett. Inf. Math. Sci. 2004, 6, 83–96. [Google Scholar]
- Bernard, T. Modeling, Control and Optimization of Water System; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Eiben, A.E.; Hinterding, R.; Michalewicz, Z. Parameter control in evolutionary algorithms. IEEE Trans. Evol. Comput. 1999, 3, 124–141. [Google Scholar] [CrossRef]
- Beasley, D.; Martin, R.R.; Bull, D.R. An overview of genetic algorithms: Part 1 Fundamentals. Univ. Comput. 1993, 15, 56–69. [Google Scholar]
- Beasley, D.; Bull, D.R.; Martin, R.R. An overview of genetic algorithms: Part 2 Research topics. Univ. Comput. 1993, 15, 170–181. [Google Scholar]
- Srinivas, M.; Patnaik, L.M. Genetic algorithms: A survey. Computer 1994, 27, 17–26. [Google Scholar] [CrossRef]
- DeJong, K. Analysis of the Behavior of a Class of Genetic Adaptive. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 1975. [Google Scholar]
- Schlierkamp-Voosen, D. Optimal interaction of mutation and crossover in the breeder genetic algorithm. In International Conference on Genetic Algorithms; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1993; 648p. [Google Scholar]
- Hong, T.P.; Wang, H.S.; Lin, W.Y.; Lee, W.Y. Evolution of appropriate crossover and mutation operators in a genetic process. Appl. Intell. 2002, 16, 7–17. [Google Scholar] [CrossRef]
- Pelikan, M.; Goldberg, D.E.; Cantú-Paz, E. Bayesian optimization algorithm, population sizing, and time to convergence. In Proceedings of the Annual Conference on Genetic and Evolutionary Computation, Las Vegas, NV, USA, 10–12 July 2000; pp. 275–282. [Google Scholar]
- Piszcz, A.; Soule, T. Genetic programming: Optimal population sizes for varying complexity problems. In Proceedings of the Annual Conference on Genetic and Evolutionary Computation, Seattle, WA, USA, 8–12 July 2006; pp. 953–954. [Google Scholar]
- Katsaras, V.; Koumousis, C.P. A sawtooth genetic algorithm combining the effects of variable population size and reinitialization to enhance performance. IEEE Trans. Evol. Comput. 2006, 10, 19–28. [Google Scholar]
- Lobo, G.; Goldberg, F. The parameterless genetic algorithm in practice. Inf. Sci. 2004, 167, 217–232. [Google Scholar] [CrossRef]
- Gotshall, S.; Rylander, B. Optimal population size and the genetic algorithm. Population 2002, 100, 900–904. [Google Scholar]
- Diaz-Gomez, P.A.; Hougen, D.F. Initial population for genetic algorithms: A metric approach. GEM 2007, 43–49. Available online: http://www.cameron.edu/ pdiaz-go/GAsPopMetric.pdf (accessed on 9 December 2019).
- Dong, M.; Wu, Y. Dynamic crossover and mutation genetic algorithm based on expansion sampling. In International Conference on Artificial Intelligence and Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2009; pp. 141–149. [Google Scholar]
- Abu Alfeilat, H.A.; Hassanat, A.B.; Lasassmeh, O.; Tarawneh, A.S.; Alhasanat, M.B.; Eyal Salman, H.S.; Prasath, V.S. Effects of Distance Measure Choice on K-Nearest Neighbor Classifier Performance: A Review. Big Data 2019, 7, 1–28. [Google Scholar] [CrossRef]
- Chiroma, H.; Abdulkareem, S.; Abubakar, A.; Zeki, A.; Gital, A.Y.; Usman, M.J. Correlation study of genetic algorithm operators: Crossover and mutation probabilities. In Proceedings of the International Symposium on Mathematical Sciences and Computing Research, Ipoh City, Malaysia, 6–7 December 2013; pp. 39–43. [Google Scholar]
- Huang, Y.; Shi, K. Genetic algorithms in the identification of fuzzy compensation system. In Proceedings of the 1996 IEEE International Conference on Systems, Man and Cybernetics. Information Intelligence and Systems (Cat. No.96CH35929), Beijing, China, 14–17 Octember 1996; pp. 1090–1095. [Google Scholar]
- Renders, J.; Flasse, S.P. Hybrid methods using genetic algorithms for global optimization. IEEE Trans. Syst. Man, Cybern. Part B Cybern. 1996, 26, 243–258. [Google Scholar] [CrossRef] [PubMed]
- Vavak, F.; Fogarty, C. Comparison of steady state and generational genetic algorithms for use in nonstationary environments. In Proceedings of the IEEE International Conference on Evolutionary Computation, Nagoya, Japan, 20–22 May 1996; pp. 192–195. [Google Scholar]
- Chaiyaratana, N.; Zalzala, A. Hybridisation of neural networks and genetic algorithms for time-optimal control. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999. [Google Scholar]
- Man, F.K.; Tang, S.K.; Kwong, S. Genetic Algorithms: Concepts and Designs; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Ammar, H.H.; Tao, Y. Fingerprint registration using genetic algorithms. In Proceedings of the 3rd IEEE Symposium on Application-Specific Systems and Software Engineering Technology, Richardson, TX, USA, 24–25 March 2000; pp. 148–154. [Google Scholar]
- Jareanpon, C.; Pensuwon, W.; Frank, R.J.; Dav, N. An adaptive RBF network optimised using a genetic algorithm applied to rainfall forecasting. In Proceedings of the IEEE International Symposium on Communications and Information Technology, Sapporo, Japan, 26–29 October 2004; pp. 1005–1010. [Google Scholar]
- Yu, X.; Meng, B. Research on dynamics in group decision support systems based on multi-objective genetic algorithms. In Proceedings of the IEEE International Conference on Service Systems and Service Management, Troyes, France, 25–27 October 2006; pp. 895–900. [Google Scholar]
- Alexandre, E.; Cuadra, L.; Rosa, M. Feature selection for sound classification in hearing aids through restricted search driven by genetic algorithms. IEEE Trans. Audio Speech Lang. Process. 2007, 15, 2249–2256. [Google Scholar] [CrossRef]
- Meng, X.; Song, B. Fast genetic algorithms used for PID parameter optimization. In Proceedings of the IEEE International Conference on Automation and Logistics, Jinan, China, 18–21 August 2007; pp. 2144–2148. [Google Scholar]
- Krawiec, K. Generative learning of visual concept using multi objective genetic programming. Pattern Recognit. Lett. 2007, 28, 2385–2400. [Google Scholar] [CrossRef][Green Version]
- Hamdan, M. A heterogeneous framework for the global parallelization of genetic algorithms. Int. Arab J. Inf. Technol. 2008, 5, 192–199. [Google Scholar]
- Liu, J. Application of fuzzy neural networks based on genetic algorithms in integrated navigation system. In Proceedings of the IEEE Conference on Intelligent Computation Technology and Automation, Changsha, China, 10–11 October 2009; pp. 656–659. [Google Scholar]
- Ka, Y.W.; Chi, L. Positioning weather systems from remote sensing data using genetic algorithms. In Computational Intelligence for Remote Sensing; Springer: Berlin/Heidelberg, Germany, 2008; pp. 217–243. [Google Scholar]
- Sorsa, A.; Peltokangas, R.; Leiviska, K. Real coded genetic algorithms and nonlinear parameter identification. In Proceedings of the IEEE International Conference on Intelligent System, Varna, Bulgaria, 6–8 September 2009; pp. 42–47. [Google Scholar]
- Ai, J.; Feng-Wen, H. Methods for optimizing weights of wavelet neural network based on adaptive annealing genetic algorithms. In Proceedings of the IEEE International Conference on Industrial Engineering and Engineering Management, Beijing, China, 21–23 October 2009; pp. 1744–1748. [Google Scholar]
- Krömer, P.; Platoš, J.; Snášel, V. Modeling permutation for genetic algorithms. In Proceedings of the IEEE International Conference on Soft Computing Pattern Recognition, Malacca, Malaysia, 4–7 December 2009; pp. 100–105. [Google Scholar]
- Lin, C. An adaptive genetic algorithms based on population diversity strategy. In Proceedings of the IEEE International Conference on Genetic and Evolutionary Computing, Guilin, China, 14–17 October 2009; pp. 93–96. [Google Scholar]
- Lizhe, Y.; Bo, X.; Xiangjie, W. BP network model optimized by adaptive genetic algorithms and the application on quality evaluation for class. In Proceedings of the IEEE International Conference on Future Computer and Communication, Wuhan, China, 21–24 May 2010; p. 273. [Google Scholar]
- Belevičius, R.; Ivanikovas, S.; Šešok, D.; Valenti, S. Optimal placement of piles in real grillages: Experimental comparison of optimization algorithms. Inf. Technol. Control 2011, 40, 123–132. [Google Scholar]
- Zhang, L.; Zhang, X. Measurement of the optical properties using genetic algorithms optimized neural networks. In Proceedings of the 2011 Symposium on Photonics and Optoelectronics (SOPO), Wuhan, China, 16–18 May 2011; pp. 1–4. [Google Scholar]
- Laboudi, Z.; Chikhi, S. Comparison of genetic algorithms and quantum genetic algorithms. Int. Arab J. Inf. Technol. 2012, 7, 243–249. [Google Scholar]
- Capraro, C.T.; Bradaric, I.; Capraro, G.; Kong, L. Using genetic algorithms for radar waveform selection. In Proceedings of the 2008 IEEE Radar Conference, Rome, Italy, 26–30 May 2008; pp. 1–6. [Google Scholar]
- Guo, F.; Qi, M. Application of Elman neural network based on improved niche adaptive genetic algorithm. IEEE Int. Conf. Intell. Control Inf. Process. 2011, 2, 660–664. [Google Scholar]
- Laporte, G. The traveling salesman problem: An overview of exact and approximate algorithms. Eur. J. Oper. Res. 1992, 59, 231–247. [Google Scholar] [CrossRef]
- Hassanat, A.B.; Alkafaween, E.; Al-Nawaiseh, N.A.; Abbadi, M.A.; Alkasassbeh, M.; Alhasanat, M.B. Enhancing genetic algorithms using multi mutations: Experimental results on the travelling salesman problem. Int. J. Comput. Sci. Inf. Secur. 2016, 14, 785–801. [Google Scholar]
- Hassanat, A.B.; Alkafaween, E. On enhancing genetic algorithms using new crossovers. Int. J. Comput. Appl. Technol. 2017, 55, 202–212. [Google Scholar] [CrossRef]
- Potvin, J.Y. Genetic algorithms for the traveling salesman problem. Ann. Oper. Res. 1996, 63, 337–370. [Google Scholar] [CrossRef]
- Reisleben, B.; Merz, P. A genetic local search algorithm for solving symmetric and asymmetric traveling salesman problems. In Proceedings of the IEEE International Conference on Evolutionary Computation, Nagoya, Japan, 20–22 May 1996; pp. 616–621. [Google Scholar]
- Larrañaga, P.; Kuijpers, C.M.; Murga, R.H.; Inza, I.; Dizdarevic, S. Genetic algorithms for the travelling salesman problem: A review of representations and operators. Artif. Intell. Rev. 1999, 13, 129–170. [Google Scholar] [CrossRef]
- Soni, N.; Kumar, T. Study of various mutation operators in genetic algorithms. Int. J. Comput. Sci. Inf. Technol. 2014, 5, 4519–4521. [Google Scholar]
- Hassanat, A.; Prasath, V.; Abbadi, M.; Abu-Qdari, S.; Faris, H. An improved genetic algorithm with a new initialization mechanism based on regression techniques. Information 2018, 9, 167. [Google Scholar] [CrossRef]
- Kaabi, J.; Harrath, Y. Permutation rules and genetic algorithm to solve the traveling salesman problem. Arab J. Basic Appl. Sci. 2019, 26, 283–291. [Google Scholar] [CrossRef]
- Gendreau, M.; Hertz, A.; Laporte, G. A tabu search heuristic for the vehicle routing problem. Manag. Sci. 1994, 40, 1276–1290. [Google Scholar] [CrossRef]
- Dorigo, M.; Gambardella, L.M. Ant colony system: A cooperative learning approach to the traveling salesman problem. IEEE Trans. Evol. Comput. 1997, 1, 53–66. [Google Scholar] [CrossRef]
- Shi, X.H.; Liang, Y.C.; Lee, H.P.; Lu, C.; Wang, Q.X. Particle swarm optimization-based algorithms for TSP and generalized TSP. Inf. Process. Lett. 2007, 103, 169–176. [Google Scholar] [CrossRef]
- Malek, M.; Guruswamy, M.; Pandya, M.; Owens, H. Serial and parallel simulated annealing and tabu search algorithms for the traveling salesman problem. Ann. Oper. Res. 1989, 21, 59–84. [Google Scholar] [CrossRef]
- Aarts, E.H.L.; Stehouwer, H.P. Neural networks and the travelling salesman problem. In Proceedings of the International Conference on Artificial Neural Networks, Amsterdam, The Netherlands, 13–16 September 1993; pp. 950–955. [Google Scholar]
- Durbin, R.; Szeliski, R.; Yuille, A. An analysis of the elastic net approach to the traveling salesman problem. Neural Comput. 1989, 1, 348–358. [Google Scholar] [CrossRef]
- Karkory, F.A.; Abudalmola, A.A. Implementation of heuristics for solving travelling salesman problem using nearest neighbour and minimum spanning tree algorithms. Int. J. Math. Comput. Phys. Electr. Comput. Eng. 2013, 7, 1524–1534. [Google Scholar]
- Singh, A.; Singh, R. Exploring travelling salesman problem using genetic algorithm. Int. J. Eng. Res. Technol. 2014, 3, 2032–2035. [Google Scholar]
- Ahmed, Z.H. Genetic algorithm for the traveling salesman problem using sequential constructive crossover operator. Int. J. Biom. Bioinform. 2010, 3, 96–105. [Google Scholar]
- Banzhaf, W. The “molecular” traveling salesman. Biol. Cybern. 1990, 64, 7–14. [Google Scholar] [CrossRef]
- Davis, L. Applying adaptive algorithms to epistatic domains. Int. Jt. Conf. Artif. Intell. 1985, 85, 162–164. [Google Scholar]
- Abdoun, O.; Abouchabaka, J.; Tajani, C. Analyzing the performance of mutation operators to solve the travelling salesman problem. Int. J. Emerg. Sci. 2012, 2, 61–77. [Google Scholar]
- Reinelt, G. TSPLIB—A traveling salesman problem library. ORSA J. Comput. 1991, 3, 376–384. [Google Scholar] [CrossRef]
- Hassanat, A. Furthest-Pair-Based Decision Trees: Experimental Results on Big Data Classification. Information 2018, 9, 284. [Google Scholar] [CrossRef]
- Hassanat, A. Norm-Based Binary Search Trees for Speeding Up KNN Big Data Classification. Computers 2018, 7, 54. [Google Scholar] [CrossRef]
- Hassanat, A.B. Two-point-based binary search trees for accelerating big data classification using KNN. PLoS ONE 2018, 13, e0207772. [Google Scholar] [CrossRef]
- Hassanat, A.B. Furthest-pair-based binary search tree for speeding big data classification using k-nearest neighbors. Big Data 2018, 6, 225–235. [Google Scholar] [CrossRef]
Sample Availability: TSP Data sets used in this work are available from the TSPLIB: http://elib.zib.de/pub/mp-testdata/tsp/tsplib/tsp/index.html. |


| Reference | PS | CP | MP |
|---|---|---|---|
| [66] | 30 | 0.95 | 0.01 |
| [66] | 80 | 0.45 | 0.01 |
| [67] | 100 | 0.9 | 1 |
| [68] | 100 | 0.8 | 0.005 |
| [69] | 50 | 0.9 | 0.03 |
| [69] | 50 | 1 | 0.03 |
| [70] | 50 | 0.8 | 0.01 |
| [71] | 15 | 0.7 | 0.05 |
| [72] | 100 | 1 | 0.003 |
| [73] | 30 | 0.8 | 0.07 |
| [74] | 100 | 0.8 | 0.01 |
| [75] | 500 | 0.8 | 0.2 |
| [76] | 40 | 0.6 | 0.1 |
| [77] | 100 | 0.8 | 0.3 |
| [78] | 100 | 0.6 | 0.02 |
| [79] | 30 | 0.6 | 0.05 |
| [80] | 76 | 0.8 | 0.05 |
| [67] | 4000 | 0.5 | 0.001 |
| [81] | 30 | 0.6 | 0.001 |
| [82] | 50 | 0.8 | 0.2 |
| [83] | 50 | 0.9 | 0.1 |
| [84] | 30 | 0.9 | 0.1 |
| [85] | 20 | 0.8 | 0.02 |
| [86] | 50 | 0.9 | 0.01 |
| [87] | 20 | 0.9 | 0.3 |
| [88] | 330 | 0.5 | 0.5 |
| [89] | 100 | 0.8 | 0.1 |
| Generation | ILM/DHC | |
|---|---|---|
| IMR | DCR | |
| 1 | 0 | 1 |
| 100 | 0.0625 | 0.9375 |
| 200 | 0.125 | 0.875 |
| 300 | 0.1875 | 0.8125 |
| 400 | 0.25 | 0.75 |
| 500 | 0.3125 | 0.6875 |
| 600 | 0.375 | 0.625 |
| 700 | 0.4375 | 0.5625 |
| 800 | 0.5 | 0.5 |
| 900 | 0.5625 | 0.4375 |
| 1000 | 0.625 | 0.375 |
| 1100 | 0.6875 | 0.3125 |
| 1200 | 0.75 | 0.25 |
| 1300 | 0.8125 | 0.1875 |
| 1400 | 0.875 | 0.125 |
| 1500 | 0.9375 | 0.0625 |
| 1600 | 1 | 0 |
| Generation | DHM/ILC | |
|---|---|---|
| DHM | ILC | |
| 1 | 1 | 0 |
| 100 | 0.9375 | 0.0625 |
| 200 | 0.875 | 0.125 |
| 300 | 0.8125 | 0.1875 |
| 400 | 0.75 | 0.25 |
| 500 | 0.6875 | 0.3125 |
| 600 | 0.625 | 0.375 |
| 700 | 0.5625 | 0.4375 |
| 800 | 0.5 | 0.5 |
| 900 | 0.4375 | 0.5625 |
| 1000 | 0.375 | 0.625 |
| 1100 | 0.3125 | 0.6875 |
| 1200 | 0.25 | 0.75 |
| 1300 | 0.1875 | 0.8125 |
| 1400 | 0.125 | 0.875 |
| 1500 | 0.0625 | 0.9375 |
| 1600 | 0 | 1 |
| Generation | Fifty-Fifty | |
|---|---|---|
| MR.5 | CR.5 | |
| 1 | 0.5 | 0.5 |
| 100 | 0.5 | 0.5 |
| 200 | 0.5 | 0.5 |
| 300 | 0.5 | 0.5 |
| 400 | 0.5 | 0.5 |
| 500 | 0.5 | 0.5 |
| 600 | 0.5 | 0.5 |
| 700 | 0.5 | 0.5 |
| 800 | 0.5 | 0.5 |
| 900 | 0.5 | 0.5 |
| 1000 | 0.5 | 0.5 |
| 1100 | 0.5 | 0.5 |
| 1200 | 0.5 | 0.5 |
| 1300 | 0.5 | 0.5 |
| 1400 | 0.5 | 0.5 |
| 1500 | 0.5 | 0.5 |
| 1600 | 0.5 | 0.5 |
| Problem | 0.03MR0.9CR | FFMCR | DHM/ILC | ILM/DHC |
|---|---|---|---|---|
| rat783 | 79,752/19,646 | 69,843/2280 | 69,124/1880 | 71,432/1295 |
| pr144 | 20,0771/14,306 | 154,259/14,668 | 167,311/12,273 | 149,060/9876 |
| eil51 | 501/35 | 497/29 | 492/24 | 465/10 |
| berlin52 | 9606/569 | 9315/377 | 9068/491 | 8637/457 |
| pr76 | 151,834/12,744 | 138,615/8629 | 146,682/14,217 | 138,071/8565 |
| KroA100 | 34,126/2847 | 34,881/3701 | 35,237/2236 | 31,085/1564 |
| att48 | 40,044/3113 | 42,511/3088 | 39,910/3261 | 37,507/1387 |
| u159 | 105,188/6624 | 94,397/7485 | 92,660/7017 | 90,066/2806 |
| a280 | 9181/379 | 8704/282 | 9177/440 | 9364/219 |
| ch130 | 10,315/594 | 10,235/829 | 10,605/904 | 10,366/717 |
| Problem | 0.03MR0.9CR | FFMCR | DHM/ILC | ILM/DHC |
|---|---|---|---|---|
| rat783 | 76,428 | 67,791.5 | 68,424.3 | 71,127.7 |
| pr144 | 175,095.8 | 151,072.1 | 157,446.3 | 151,455.1 |
| eil51 | 511.1 | 488.4 | 486 | 472.5 |
| berlin52 | 9464 | 9155 | 9166.3 | 9024.5 |
| pr76 | 155,182.4 | 140,766.9 | 139,644.6 | 135,316.6 |
| KroA100 | 39,674.8 | 32,730.7 | 32,058.6 | 31,630.6 |
| att48 | 39,872.2 | 40,686.3 | 38,448.1 | 37,244.2 |
| u159 | 101,332.3 | 93,621.9 | 95,642.6 | 93,439.5 |
| a280 | 9304.7 | 9264.5 | 9295.9 | 9067.3 |
| ch130 | 11,455.4 | 10,231.1 | 10,383.2 | 10,178.5 |
| Problem | 0.03MR0.9CR | FFMCR | DHM/ILC | ILM/DHC |
|---|---|---|---|---|
| rat783 | 70,183.6 | 68,322.4 | 67,795.7 | 71,098.2 |
| pr144 | 172,820.9 | 158,910.4 | 156,527.1 | 153,154 |
| eil51 | 496.8 | 481.1 | 479 | 483.1 |
| berlin52 | 9200.3 | 8667.2 | 8782.5 | 8820.1 |
| pr76 | 148,600.5 | 146,552.8 | 149,661.5 | 139,733.7 |
| KroA100 | 34,191 | 32,176.1 | 32,549.2 | 31,598.7 |
| att48 | 41,811.1 | 39,459.3 | 37,355.8 | 36,929.5 |
| u159 | 98,011.6 | 90,671.5 | 95,826.5 | 98,659 |
| a280 | 8957.1 | 8897 | 9134.1 | 9457.7 |
| ch130 | 11,480 | 10,609.8 | 10,253.3 | 10,192.4 |
| Problem | 0.03MR0.9CR | FFMCR | DHM/ILC | ILM/DHC |
|---|---|---|---|---|
| rat783 | 70,486.3 | 71,100.3 | 67,399.3 | 71,571.3 |
| pr144 | 169,101.1 | 177,072.5 | 155,994.3 | 165,080.7 |
| eil51 | 501.5 | 490.7 | 468.5 | 481.6 |
| berlin52 | 9697.6 | 9397.8 | 9052.3 | 9526.9 |
| pr76 | 151,172.8 | 149,717.8 | 139,640.5 | 142,065.1 |
| KroA100 | 34,587.6 | 35,331.6 | 32,754.5 | 32,435.6 |
| att48 | 40,504.6 | 40,272 | 36,502.1 | 38,514.7 |
| u159 | 94,578.1 | 91,125.4 | 91,861.1 | 92,766.4 |
| a280 | 9504.4 | 8912.6 | 9175.8 | 9425.4 |
| ch130 | 10,442.9 | 10,238.1 | 10,687.2 | 10,213.4 |
| Problem | 0.03MR0.9CR | FFMCR | DHM/ILC | ILM/DHC |
|---|---|---|---|---|
| rat783 | 69,554.8 | 70,979.8 | 68,091.9 | 72,438.5 |
| pr144 | 178,213.8 | 149,154.5 | 148,610.7 | 157,487.6 |
| eil51 | 521.9 | 496.3 | 475.1 | 494.2 |
| berlin52 | 9642.6 | 9136.7 | 8790.7 | 9207 |
| pr76 | 159,528.7 | 146,208.2 | 133,732.8 | 140,053.7 |
| KroA100 | 35,143 | 32,257.4 | 31,003.1 | 31,395 |
| att48 | 40,653.1 | 40,671.7 | 38628.1 | 38,613.4 |
| u159 | 95,409.8 | 94,542.2 | 91,893.9 | 96,699.1 |
| a280 | 9017.8 | 9031.9 | 8645.6 | 9352.6 |
| ch130 | 13,084.6 | 10,364.4 | 9912 | 10,687 |
| Problem | 0.03MR0.9CR | FFMCR | DHM/ILC | ILM/DHC |
|---|---|---|---|---|
| rat783 | 71,517.6 | 69,253.6 | 67,424.3 | 73,022.8 |
| pr144 | 174,357 | 149,038.5 | 146,385.7 | 158,169.1 |
| eil51 | 519.6 | 498.7 | 476.6 | 485.4 |
| berlin52 | 9250.7 | 9167.6 | 8619.7 | 9166 |
| pr76 | 152,704.2 | 142,986.3 | 135,876.6 | 141,485.1 |
| KroA100 | 36,751.3 | 34,094.3 | 30,804.1 | 32,291.9 |
| att48 | 43,077.1 | 41,121.3 | 36,854.5 | 39,310.4 |
| u159 | 101,313.2 | 94,858.3 | 87,507.6 | 96,255.1 |
| a280 | 9287.7 | 9177.3 | 8698.4 | 9862.1 |
| ch130 | 11,526.7 | 10,247.1 | 9854.9 | 10,622 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassanat, A.; Almohammadi, K.; Alkafaween, E.; Abunawas, E.; Hammouri, A.; Prasath, V.B.S. Choosing Mutation and Crossover Ratios for Genetic Algorithms—A Review with a New Dynamic Approach. Information 2019, 10, 390. https://doi.org/10.3390/info10120390
Hassanat A, Almohammadi K, Alkafaween E, Abunawas E, Hammouri A, Prasath VBS. Choosing Mutation and Crossover Ratios for Genetic Algorithms—A Review with a New Dynamic Approach. Information. 2019; 10(12):390. https://doi.org/10.3390/info10120390
Chicago/Turabian StyleHassanat, Ahmad, Khalid Almohammadi, Esra’a Alkafaween, Eman Abunawas, Awni Hammouri, and V. B. Surya Prasath. 2019. "Choosing Mutation and Crossover Ratios for Genetic Algorithms—A Review with a New Dynamic Approach" Information 10, no. 12: 390. https://doi.org/10.3390/info10120390
APA StyleHassanat, A., Almohammadi, K., Alkafaween, E., Abunawas, E., Hammouri, A., & Prasath, V. B. S. (2019). Choosing Mutation and Crossover Ratios for Genetic Algorithms—A Review with a New Dynamic Approach. Information, 10(12), 390. https://doi.org/10.3390/info10120390







