Identification of Insider Trading Using Extreme Gradient Boosting and Multi-Objective Optimization
Abstract
1. Introduction
2. Background
2.1. XGboost
2.2. NSGA-II
3. Proposed Approach
3.1. Structure of the Proposed Approach
3.2. Identification Indicators
- Stock market performance, including the excess return compared with same market (ERCSM), beta coefficient, sigma coefficient, etc.
- Financial performance: such as the current ratio and debt ratio.
- Share ownership structure and corporate governance, including the H5 index, Z index, etc.
4. Experiment Design
4.1. Data
4.2. XGboost Parameters for Optimization
4.3. Evaluation Measures and Multi-Objective Functions
- TNR is the ratio that the samples belong to insider trading cases are correctly identified. The calculation formula is:
- TPR is employed to measure the ratio that samples of non-insider trading cases are rightly classified. The calculation is:
- OIA is used to measure the ratio that the non-insider trading or insider trading samples are properly identified. It is calculated as:
- FPR is a ratio that samples do not have insider trading activities that are incorrectly identified as insider trading samples. It is calculated by:
- FNR is employed to evaluate the ratio that insider trading samples are wrongly classified as non-insider trading samples. The calculation formula is:
4.4. Benchmark Methods
5. Experimental Results
5.1. Identification Accuracy Results
5.2. Identification Efficiency Results
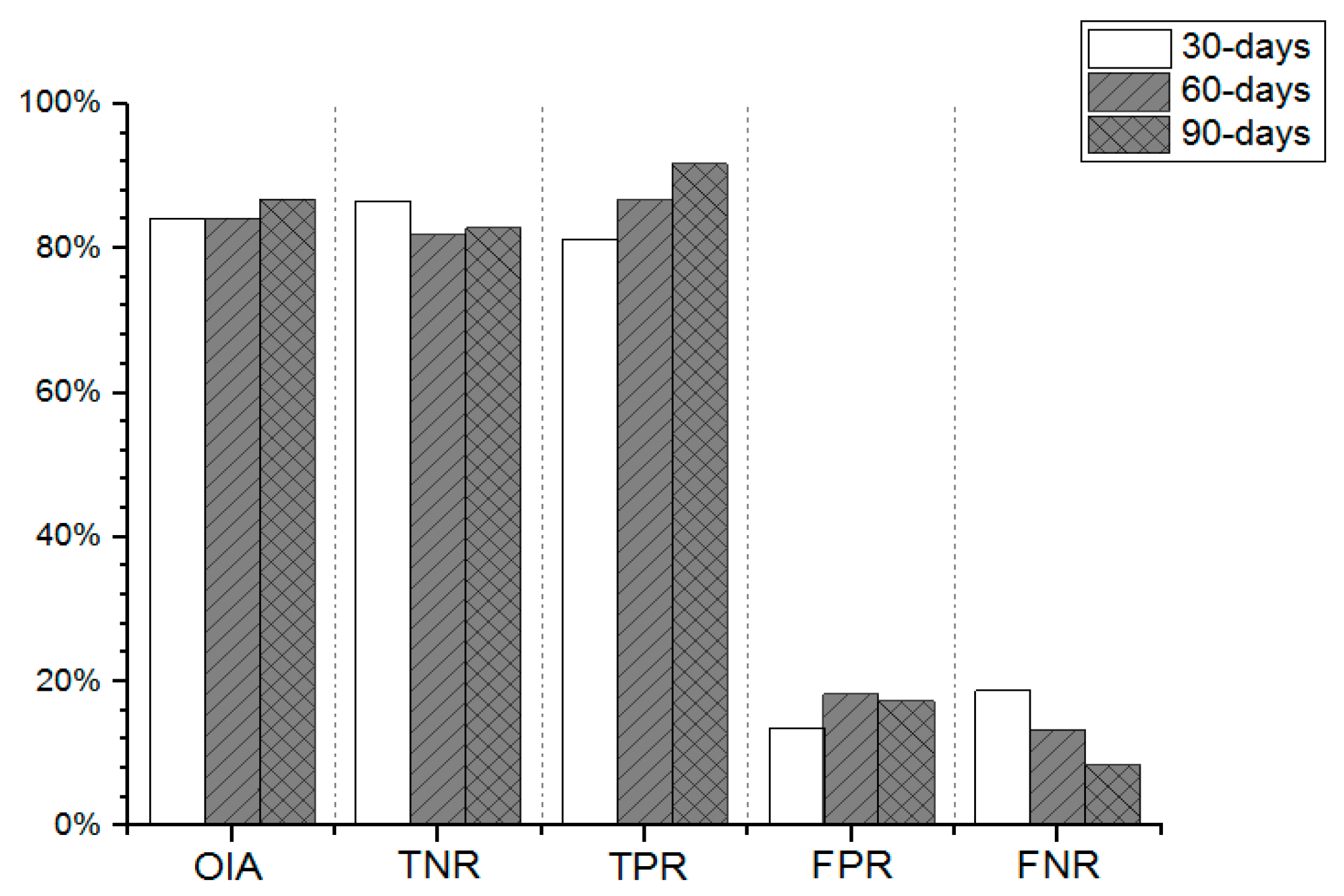
5.3. Performance of Different Time Window Length
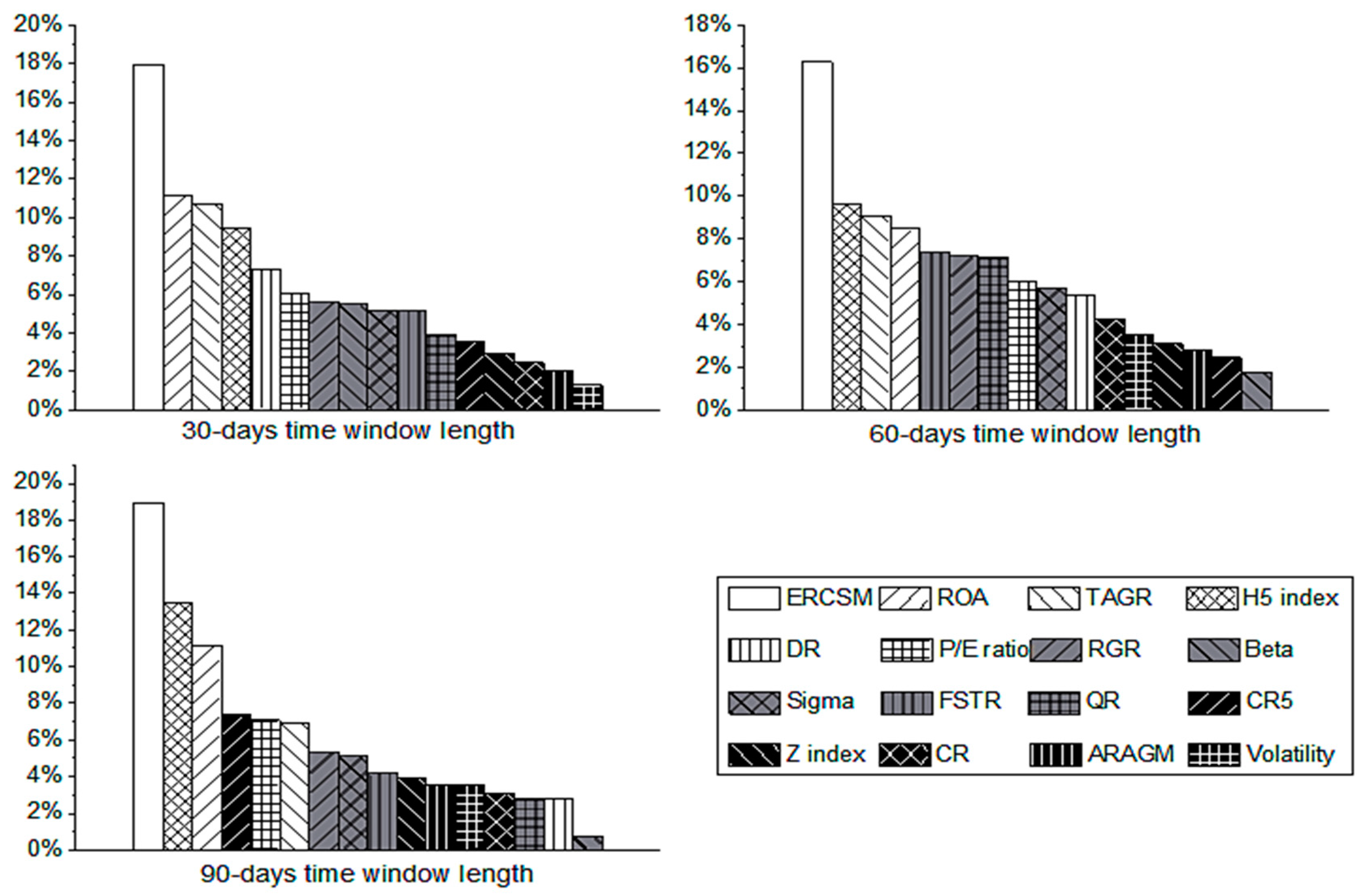
5.4. Importance of Indicators
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- Excess return compared with same market (ERCSM):This indicator estimates the excess return over the security market return. It is calculated by:
- Return on assets (ROA)The ROA is calculated to evaluate how much of the net income is yielded per unit of the total assets. It is calculated by:
- Total asset growth rate (TAGR)It is the ratio of the total asset growth in current year to the total assets at the start of current year, which reflects the asset growth ratio of the company in current year. It is calculated by:
- H5 indexThe H5 index is the sum of squares of the largest five stockholders’ share proportion. The closer of the H5 index to 1, the greater the share proportion difference between the largest five stockholders.
- Debt ratio (DR)It is a ratio of company total debts and total assets. The DR is calculated as:
- Price-earning ratio (P/E ratio)It is a ratio of a company’s stock price to the company’s earnings per share. The P/E ratio is often employed in stock price valuation. The calculation formula is:
- Revenue growth rate (RGR)It is the rate of the company increased revenue to the total revenue in the previous year. It is calculated by:
- Beta coefficientA stocks beta coefficient is the ratio of the product of the covariance of the stock’s returns and the benchmark’s returns to the product of the variance of the benchmark’s returns over a certain period.
- Sigma coefficientThe sigma coefficient is measured by using the standard deviation of a company’s stock prices in a certain length of period.
- Floating stock turnover rate (FSTR)The FSTR is generally used to evaluate the degree of the stock transfer frequency in a certain length of period. It is calculated as:
- Quick ratio (QR)It is the rate of a company’s quick asset to its current liability. The calculation formula is:
- CR5 IndexThe CR5 index is the total stock proportion of the largest five shareholders.
- Z indexIt is the ratio of the largest shareholder’s stock amount and the second-largest shareholder’s stock amount.
- Current Ratio (CR)The CR is the ratio of a company’s current assets to its current liabilities. It is often used to evaluate whether a company has enough current assets to meet its short-term obligations.
- Attendance ratio of the shareholders at the annual general meeting (ARAGM)The ARAGM is a ratio of what percentage of the company’s shareholders are attending at the annual general meeting.
- VolatilityIt is the degree of stock price variation of a company’s stock prices at a certain length of period that evaluated by standard deviation of logarithmic return.
References
- Cheung, Y.L.; Jiang, P.; Limpaphayom, P.; Lu, T. Does corporate governance matter in china? China Econ. Rev. 2008, 19, 460–479. [Google Scholar] [CrossRef]
- Howson, N.C. Enforcement without Foundation?—Insider Trading and China’s Administrative Law Crisis. Am. J. Comp. Law 2012, 60, 955–1002. [Google Scholar] [CrossRef]
- Meulbroek, L.K.; Hart, C. The Effect of Illegal Insider Trading on Takeover Premia. Rev. Financ. 2015, 1, 51–80. [Google Scholar] [CrossRef]
- Website of CSRC. Available online: http://www.csrc.gov.cn/pub/newsite/ (accessed on 1 October 2019).
- Islam, S.R.; Ghafoor, S.K.; Eberle, W. Mining Illegal Insider Trading of Stocks: A Proactive Approach. In Proceedings of the IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018. [Google Scholar]
- Zhang, G.; Patuwo, B.E.; Hu, M.Y. Forecasting with artificial neural networks: The state of the art. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Collins, M.; Schapire, R.E.; Singer, Y. Logistic Regression, AdaBoost and Bregman Distances. Mach. Learn. 2002, 48, 253–285. [Google Scholar] [CrossRef]
- Farooq, M.; Zheng, H.; Nagabhushana, A.; Roy, S.; Burkett, S.; Barkey, M.; Kotru, S.; Sazonov, E. Damage Detection and Identification in Smart Structures using SVM and ANN. In Proceedings of the Smart Sensor Phenomena, Technology, Networks, & Systems Integration, San Diego, CA, USA, 30 March 2012; Volume 8346, p. 40. [Google Scholar]
- Li, Z.X.; Yang, X.M. Damage identification for beams using ANN based on statistical property of structural responses. Comput. Struct. 2008, 86, 64–71. [Google Scholar] [CrossRef]
- Stoica, M.; Calangiu, G.A.; Sisak, F.; Sarkany, I. A method proposed for training an artificial neural network used for industrial robot programming by demonstration. In Proceedings of the International Conference on Optimization of Electrical & Electronic Equipment, Basov, Romania, 20–22 May 2010. [Google Scholar]
- Das, A.B.; Bhuiyan, M.I.H.; Alam, S.M.S. A statistical method for automatic detection of seizure and epilepsy in the dual tree complex wavelet transform domain. In Proceedings of the International Conference on Informatics, Dhaka, Bangladesh, 23–24 May 2014. [Google Scholar]
- ÇiMen, M.; KiSi, O. Comparison of two different data-driven techniques in modeling lake level fluctuations in Turkey. J. Hydrol. 2009, 378, 253–262. [Google Scholar] [CrossRef]
- Sun, H.; Xie, L. Recognition of a Sucker Rod’s Defect with ANN and SVM. In Proceedings of the International Joint Conference on Computational Sciences and Optimization, Sanya, China, 24–26 April 2009. [Google Scholar]
- Rodriguez-Martin, D.; Samà, A.; Perez-Lopez, C.; Català, A.; Cabestany, J.; Rodriguez-Molinero, A. SVM-based posture identification with a single waist-located triaxial accelerometer. Expert Syst. Appl. 2013, 40, 7203–7211. [Google Scholar] [CrossRef]
- Jiang, H.; Tang, F.; Zhang, X. Liver cancer identification based on PSO-SVM model. In Proceedings of the International Conference on Control Automation Robotics & Vision, Singapore, 7–10 December 2011. [Google Scholar]
- Amiri, S.; Rosen, D.V.; Zwanzig, S. The SVM approach for Box–Jenkins Models. Revstat-Stat. J. 2011, 7, 23–36. [Google Scholar]
- Liu, M. Fingerprint classification based on Adaboost learning from singularity features. Pattern Recogn. 2010, 43, 1062–1070. [Google Scholar] [CrossRef]
- Kim, D.; Philen, M. Damage classification using Adaboost machine learning for structural health monitoring. In Proceedings of the Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems, San Diego, CA, USA, 14 April 2011. [Google Scholar]
- Gutiérreztobal, G.C.; Álvarez, D.; Gómezpilar, J.; Campo, F.D.; Hornero, R. AdaBoost Classification to Detect Sleep Apnea from Airflow Recordings. In XIII Mediterranean Conference on Medical & Biological Engineering & Computing; Romero, L.M., Ed.; Springer: Cham, Switzerland, 2013; pp. 1829–1832. [Google Scholar]
- Liu, X.; Dai, Y.; Zhang, Y.; Yuan, Q.; Zhao, L. A preprocessing method of AdaBoost for mislabeled data classification. In Proceedings of the 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Deng, S.; Wang, C.; Cao, C.; Fan, Y. Identification of Insider Trading in Security Market Based on Random Forests. J. China Three Gorges Univ. Humanit. Soc. Sci. 2019, 41, 70–75. (In Chinese) [Google Scholar] [CrossRef]
- Murugan, A.; Nair, S.A.H.; Kumar, K.P.S. Detection of Skin Cancer Using SVM, Random Forest and KNN Classifiers. J. Med. Syst. 2019, 43, 269. [Google Scholar] [CrossRef] [PubMed]
- Choi, D.K. Data-Driven Materials Modeling with XGBoost Algorithm and Statistical Inference Analysis for Prediction of Fatigue Strength of Steels. Int. J. Precis. Eng. Manuf. 2019, 20, 129–138. [Google Scholar] [CrossRef]
- Nishio, M.; Nishizawa, M.; Sugiyama, O.; Kojima, R.; Yakami, M.; Kuroda, T.; Togashi, K. Computer-aided diagnosis of lung nodule using gradient tree boosting and Bayesian optimization. PLoS ONE 2017, 13, e0195875. [Google Scholar] [CrossRef]
- Mustapha, I.B.; Saeed, F. Bioactive Molecule Prediction Using Extreme Gradient Boosting. Molecules 2016, 21, 983. [Google Scholar] [CrossRef]
- Li, Y.Z.; Wang, Z.Y.; Zhou, Y.L.; Han, X.Z. The Improvement and Application of Xgboost Method Based on the Bayesian Optimization. J. Guangdong Univ. Technol. 2018, 35, 23–28. (In Chinese) [Google Scholar]
- Tamimi, A.; Naidu, D.S.; Kavianpour, S. An Intrusion Detection System Based on NSGA-II Algorithm. In Proceedings of the Fourth International Conference on Cyber Security, Cyber Warfare, and Digital Forensic (CyberSec), Jakarta, Indonesia, 29–31 October 2016. [Google Scholar]
- Lin, J.F.; Xu, Y.L.; Law, S.S. Structural damage detection-oriented multi-type sensor placement with multi-objective optimization. J. Sound Vib. 2018, 422, 568–589. [Google Scholar] [CrossRef]
- Guan, X.Z. Multi-objective PID Controller Based on NSGA-II Algorithm with Application to Main Steam Temperature Control. In Proceedings of the International Conference on Artificial Intelligence & Computational Intelligence, Shanghai, China, 7–8 November 2009. [Google Scholar]
- Li, C.; Liu, C.; Yang, L.; He, L.; Wu, T. Particle Swarm Optimization for Positioning the Coil of Transcranial Magnetic Stimulation. BioMed Res. Int. 2019, 2019, 946101. [Google Scholar] [CrossRef]
- Garg, H. A hybrid GSA-GA algorithm for constrained optimization problems. Inf. Sci. 2019, 478, 499–523. [Google Scholar] [CrossRef]
- Garg, H. A hybrid PSO-GA algorithm for constrained optimization problems. Appl. Math. Comput. 2016, 274, 292–305. [Google Scholar] [CrossRef]
- Alarifi, I.M.; Nguyen, H.M.; Bakhtiyari, A.N.; Asadi, A. Feasibility of ANFIS-PSO and ANFIS-GA Models in Predicting Thermophysical Properties of Al2O3-MWCNT/Oil Hybrid Nanofluid. Materials 2019, 12, 3628. [Google Scholar] [CrossRef] [PubMed]
- Chiang, C.H.; Chung, S.G.; Louis, H. Insider trading, stock return volatility, and the option market’s pricing of the information content of insider trading. J. Bank. Financ. 2017, 76, 65–73. [Google Scholar] [CrossRef]
- Jain, N.; Mirman, L.J. Effects of insider trading under different market structures. Q. Rev. Econ. Financ. 2004, 42, 19–39. [Google Scholar] [CrossRef]
- Jabbour, A.R.; Jalilvand, A.; Switzer, J.A. Pre-bid price run-ups and insider trading activity: Evidence from Canadian acquisitions. Int. Rev. Financ. Anal. 2004, 9, 21–43. [Google Scholar] [CrossRef]
- Dai, L.; Fu, R.; Kang, J.K.; Lee, I. Corporate governance and insider trading. SSRN Electron. J. 2013, 40, 235–253. [Google Scholar] [CrossRef][Green Version]
- Chronopoulos, D.K.; McMillan, D.G.; Papadimitriou, F.I.; Tavakoli, M. Insider trading and future stock returns in firms with concentrated ownership levels. Eur. J. Financ. 2018, 25, 139–154. [Google Scholar] [CrossRef]
- Lu, C.; Zhao, X.; Dai, J. Corporate Social Responsibility and Insider Trading: Evidence from China. Sustainability 2018, 10, 3163. [Google Scholar] [CrossRef]
- Chen, T.; He, T. XGBoost: eXtreme Gradient Boosting, R package version 04-2, 2015. Available online: https://cran.r-project.org/src/contrib/Archive/xgboost/ (accessed on 24 November 2019).
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Nebro, A.J.; Durillo, J.J.; Machín, M.; Coello, C.A.C.; Dorronsoro, B.A.J.; Dorronsoro, B. A Study of the Combination of Variation Operators in the NSGA-II Algorithm. In Advances in Artificial Intelligence; Springer: Berlin, Germany, 2013; pp. 269–278. [Google Scholar]
- CSMAR Database. Available online: http://www.gtafe.com/WebShow/ShowDataService/1 (accessed on 1 October 2019).
- RESSET Database. Available online: http://www.resset.cn/databases (accessed on 1 October 2019).
- Kalarani, P.; Brunda, S.S. An efficient approach for ensemble of SVM and ANN for sentiment classification. In Proceedings of the 2016 IEEE International Conference on Advances in Computer Applications (ICACA), Coimbatore, India, 24 October 2016. [Google Scholar]
- Ramaswamy, P.C.; Deconinck, G. Smart grid reconfiguration using simple genetic algorithm and NSGA-II. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT Europe), Berlin, Germany, 14–17 October 2012. [Google Scholar]
- Song, R.; Cui, M.; Liu, J. Single and multiple objective optimization of a natural gas liquefaction process. Energy 2017, 124, 19–28. [Google Scholar] [CrossRef]
- Eisinga, R.; Heskes, T.; Pelzer, B.; Grotenhuis, M.T. Exact p-values for pairwise comparison of friedman rank sums, with application to comparing classifiers. BMC Bioinform. 2017, 18, 68. [Google Scholar] [CrossRef] [PubMed]
- Meulbroek, L.K. An Empirical Analysis of Illegal Insider Trading. J. Financ. 1992, 47, 1661–1699. [Google Scholar] [CrossRef]
- Reynolds, J. Insider trading activities around the world: A case study in East Asia. Res. J. Financ. Account. 2010, 1. [Google Scholar]
- Klepáč, V.; Hampel, D. Prediction of Bankruptcy with SVM Classifiers Among Retail Business Companies in EU. Acta Univ. Agric. Silvic. Mendel. Brun. 2016, 64, 627–634. [Google Scholar] [CrossRef]
- Liu, K.; Yu, T. An Improved Support-Vector Network Model for Anti-Money Laundering. In Proceedings of the Fifth International Conference on Management of E-commerce & E-government, Wuhan, China, 5–6 November 2011. [Google Scholar]
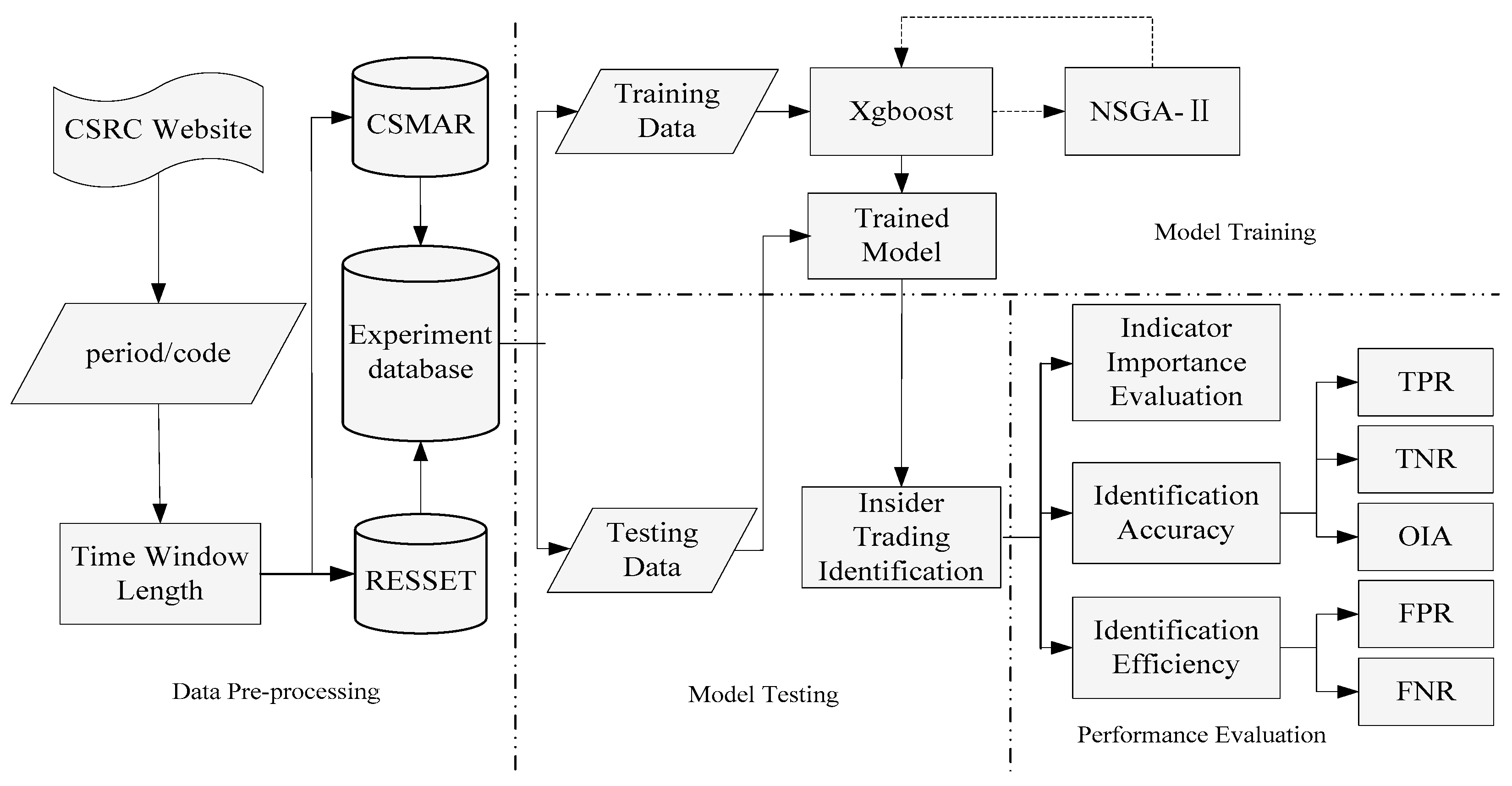
| Insider Trading Identification | Indicators |
|---|---|
| Market performance of the stock | excess return compared with same market (ERCSM); beta coefficient, sigma coefficient; floating stock turnover rate (FSTR); volatility |
| Financial performance | return on assets (ROA); debt ratio (DR); total asset growth rate (TAGR); Price-earning ratio (P/E ratio); revenue growth rate (RGR); quick ratio (QR); current ratio (CR) |
| Company ownership structure and governance | H5 index; CR5 index; Z index; attendance ratio of the shareholders at the annual general meeting (ARAGM) |
| No. | Parameters | Description |
|---|---|---|
| 1 | eta | After each boosting step, eta shrinks the feature weights to make the boosting process more conservative |
| 2 | max delta step | If the value is set to 0, it means there is no constraint. If it is set to a positive value, it can help to make the update step more conservative |
| 3 | gamma | The minimum loss reduction is required to make a further partition on a leaf node of the tree. The larger the gamma is, the more conservative of the XGboost algorithm |
| 4 | min child weight | It is the minimum sum of instance weight needed in a child. If the tree partition step results in a leaf node with the sum of instance weight less than this parameter value, then there will no further partition in the building process |
| 5 | colsample by tree | It is the subsample ratio of columns when constructing each tree. Subsampling occurs once for every tree constructed |
| 6 | colsample by level | It is the subsample ratio of columns for each level. Subsampling occurs once for every new depth level reached in a tree. Columns are subsampled from the set of columns chosen for the current tree |
| 7 | colsample by node | It is the subsample ratio of columns for each node (split). Subsampling occurs once every time a new split is evaluated. Columns are subsampled from the set of columns chosen for the current level |
| No | Evaluation Criteria | Calculation Formula |
|---|---|---|
| 1 | true negative rate (TNR) | |
| 2 | true positive rate (TPR) | |
| 3 | false positive rate (FPR) | |
| 4 | false negative rate (FNR) | |
| 5 | overall identification accuracy (OIA) |
| No | Method Name | Description |
|---|---|---|
| 1 | ANN | Identification model based on an ANN-based method |
| 2 | SVM | Identification model based on an SVM-based method |
| 3 | Adaboost | An Adaboost based approach for classification of illegal insider trading |
| 4 | RF | A random forest based approach for classification of illegal insider trading |
| 5 | XGboost | An XGboost based approach for identification of illegal insider trading |
| 6 | XGboost-GA | An XGboost based approach for identification of illegal insider trading. GA is adopted for initial parameter optimization of XGboost, and the fitness function is set to be the maximization of TPR |
| 7 | XGboost-NSGA-II | XGboost based classification approach for identification of insider trading. The NSGA-II is adopted for initial parameter optimization of XGboost. The fitness functions are designed to be the maximization of TPR and minimization of FNR |
| Window Length | ANN (%) | SVM (%) | Adaboost (%) | RF (%) | XGboost (%) | XGboost-GA (%) | XGboost-NSGA-II (%) |
|---|---|---|---|---|---|---|---|
| 30-days | 51.11 | 72.97 | 75 | 75.68 | 81.25 | 80.65 | 86.49 |
| 60-days | 80 | 74.07 | 75 | 76.92 | 82.61 | 82.14 | 81.82 |
| 90-days | 66.67 | 69.70 | 76.74 | 70.97 | 77.42 | 76.92 | 82.76 |
| Average | 65.93 | 72.25 | 75.58 | 74.52 | 80.43 | 79.90 | 83.69 |
| Window Length | ANN (%) | SVM (%) | Adaboost (%) | RF (%) | XGboost (%) | XGboost-GA (%) | XGboost-NSGA-II (%) |
|---|---|---|---|---|---|---|---|
| 30-days | 95.65 | 74.19 | 70.59 | 78.12 | 75 | 81.82 | 81.25 |
| 60-days | 55.81 | 79.41 | 76.47 | 78.12 | 72.41 | 80 | 86.67 |
| 90-days | 90.91 | 82.14 | 73.08 | 83.33 | 86.67 | 88.89 | 91.67 |
| Average | 80.79 | 78.58 | 73.38 | 79.86 | 78.03 | 83.57 | 86.53 |
| Window Length | ANN (%) | SVM (%) | Adaboost (%) | RF (%) | XGboost (%) | XGboost-GA (%) | XGboost-NSGA-II (%) |
|---|---|---|---|---|---|---|---|
| 30-days | 66.18 | 73.52 | 73.17 | 76.81 | 78.13 | 81.25 | 84.06 |
| 60-days | 66.67 | 77.05 | 75.71 | 77.59 | 76.92 | 81.03 | 84.13 |
| 90-days | 75.86 | 75.41 | 75.36 | 77.05 | 81.97 | 83.02 | 86.79 |
| Average | 69.57 | 75.33 | 74.75 | 77.15 | 79.01 | 81.77 | 84.99 |
| Compared Models | Significant Level α= 0.05 |
|---|---|
| Overall Identification Accuracy XGboost-NSGA-II vs. ANN XGboost-NSGA-II vs. SVM XGboost-NSGA-II vs. Adaboost XGboost-NSGA-II vs. RF XGboost-NSGA-II vs. XGboost XGboost-NSGA-II vs. XGboost-GA | H0: n1 = n2 = n3 = n4 = n5 = n6 = n7 F = 16.143 p = 0.013 (reject H0) |
| Window Length | ANN (%) | SVM (%) | Adaboost (%) | RF (%) | XGboost (%) | XGboost-GA (%) | XGboost-NSGA-II (%) |
|---|---|---|---|---|---|---|---|
| 30-days | 48.89 | 27.03 | 25 | 24.32 | 18.75 | 19.35 | 13.51 |
| 60-days | 20 | 25.93 | 25 | 23.08 | 17.39 | 17.86 | 18.18 |
| 90-days | 33.33 | 30.30 | 23.26 | 29.03 | 22.58 | 23.08 | 17.24 |
| Average | 34.07 | 27.75 | 24.42 | 25.48 | 19.57 | 20.10 | 16.31 |
| Window Length | ANN (%) | SVM (%) | Adaboost (%) | RF (%) | XGboost (%) | XGboost-GA (%) | XGboost-NSGA-II (%) |
|---|---|---|---|---|---|---|---|
| 30-days | 4.35 | 25.81 | 29.41 | 21.88 | 25 | 18.18 | 18.75 |
| 60-days | 44.19 | 20.59 | 23.53 | 21.88 | 27.59 | 20 | 13.33 |
| 90-days | 9.09 | 17.86 | 26.92 | 16.67 | 13.33 | 11.11 | 8.33 |
| Average | 19.21 | 21.42 | 26.62 | 20.14 | 21.97 | 16.43 | 13.47 |
| Window Length | OIA (%) | TNR (%) | TPR (%) | FPR (%) | FNR (%) |
|---|---|---|---|---|---|
| 30-day | 84.06 | 86.49 | 81.25 | 13.51 | 18.75 |
| 60-day | 84.13 | 81.82 | 86.67 | 18.18 | 13.33 |
| 90-day | 86.79 | 82.76 | 91.67 | 17.24 | 8.33 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, S.; Wang, C.; Li, J.; Yu, H.; Tian, H.; Zhang, Y.; Cui, Y.; Ma, F.; Yang, T. Identification of Insider Trading Using Extreme Gradient Boosting and Multi-Objective Optimization. Information 2019, 10, 367. https://doi.org/10.3390/info10120367
Deng S, Wang C, Li J, Yu H, Tian H, Zhang Y, Cui Y, Ma F, Yang T. Identification of Insider Trading Using Extreme Gradient Boosting and Multi-Objective Optimization. Information. 2019; 10(12):367. https://doi.org/10.3390/info10120367
Chicago/Turabian StyleDeng, Shangkun, Chenguang Wang, Jie Li, Haoran Yu, Hongyu Tian, Yu Zhang, Yong Cui, Fangjie Ma, and Tianxiang Yang. 2019. "Identification of Insider Trading Using Extreme Gradient Boosting and Multi-Objective Optimization" Information 10, no. 12: 367. https://doi.org/10.3390/info10120367
APA StyleDeng, S., Wang, C., Li, J., Yu, H., Tian, H., Zhang, Y., Cui, Y., Ma, F., & Yang, T. (2019). Identification of Insider Trading Using Extreme Gradient Boosting and Multi-Objective Optimization. Information, 10(12), 367. https://doi.org/10.3390/info10120367




