1. Introduction
Kriging is a geostatistical interpolation technique that predicts the value of observations in unknown locations based on previously collected data [
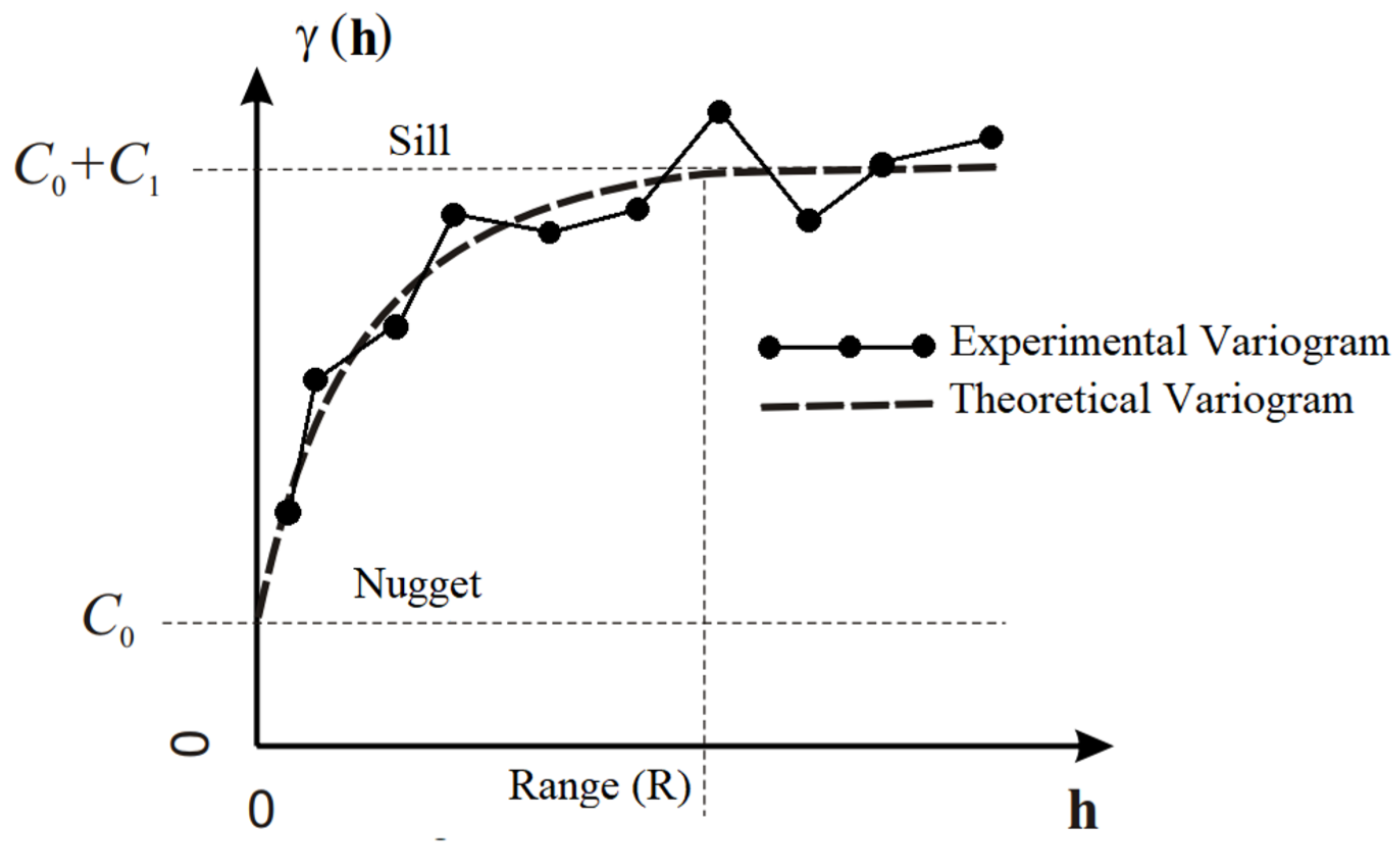
1]. The kriging error or interpolation error is minimized by studying and modelling the spatial distribution of points already obtained. This spatial distribution or spatial variation is expressed in the form of an experimental variogram.
The experimental variogram can be considered as a graphical representation of the data distribution and also expresses the data variance with the increment of the sampling distance. The variogram is the basis for the application of the kriging method. Thus, the kriging process is defined into three main steps. First, the experimental variogram is calculated. In the sequel, the theoretical variogram is modeled to represent the experimental variogram. Finally, the value of a new point is predicted using the built theoretical model [
2].
Despite advances in geostatistics and kriging areas, the task of modelling the theoretical variogram remains a challenge (step 2), which is mainly responsible for the interpolation accuracy. In order to model the theoretical variogram, it is necessary to estimate its parameters, which can be defined as an optimization problem [
3].
In recent years, artificial intelligence techniques have been used to improve the kriging process as shown in [
4,
5,
6,
7,
8,
9]. However, it is still a challenge to determine which method is better suited for a given database. As stated in [
6] and applied in [
7], bio-inspired algorithms, like Genetic Algorithms (GA), are suitable to help define the theoretical variogram parameters. Furthermore, these kinds of algorithms do not require a single initial seed value as input, but rather a minimum and maximum interval, different from classical methods such as Gauss–Newton [
3] and Levenberg–Marquardt [
10].
In an automated setting, these seeds and intervals must be determined based on data; however, this is a hard task since there is no well-defined heuristic to initialize them. In [
11], the authors applied a numerical minimization technique and proposed a heuristic to define the seed in the automatic structure of their method. The research presented in [
12] applied the Levenberg–Marquardt optimization technique with the least squares cost function. No heuristic was specified, but the authors tested several initial values in the optimization step. The work described in [
13] used an improved linear programming method in combination with the weighted polynomial, as well as the inverse of lag distance as the cost function to select the parameters for the theoretical variogram. In this scenario, we propose a heuristic to define the lower and upper bounds of the GA parameters’ intervals.
In [
14], the authors proposed a new method for kriging using the K-means clustering technique. The proposal consists in creating subsets of the database and predicting each given point using information from the subset of which it belongs. The proposed method presented better results than conventional kriging approaches. However, the authors used the same theoretical variogram model for all subsets, which could be improved, since the characteristics of each subset are different. In [
15], each subset has its own theoretical variogram model for interpolation. On the other hand, the researchers used non-spatial data, which do not have spatial coordinates, and did not detail how the parameters of the theoretical variogram model were defined.
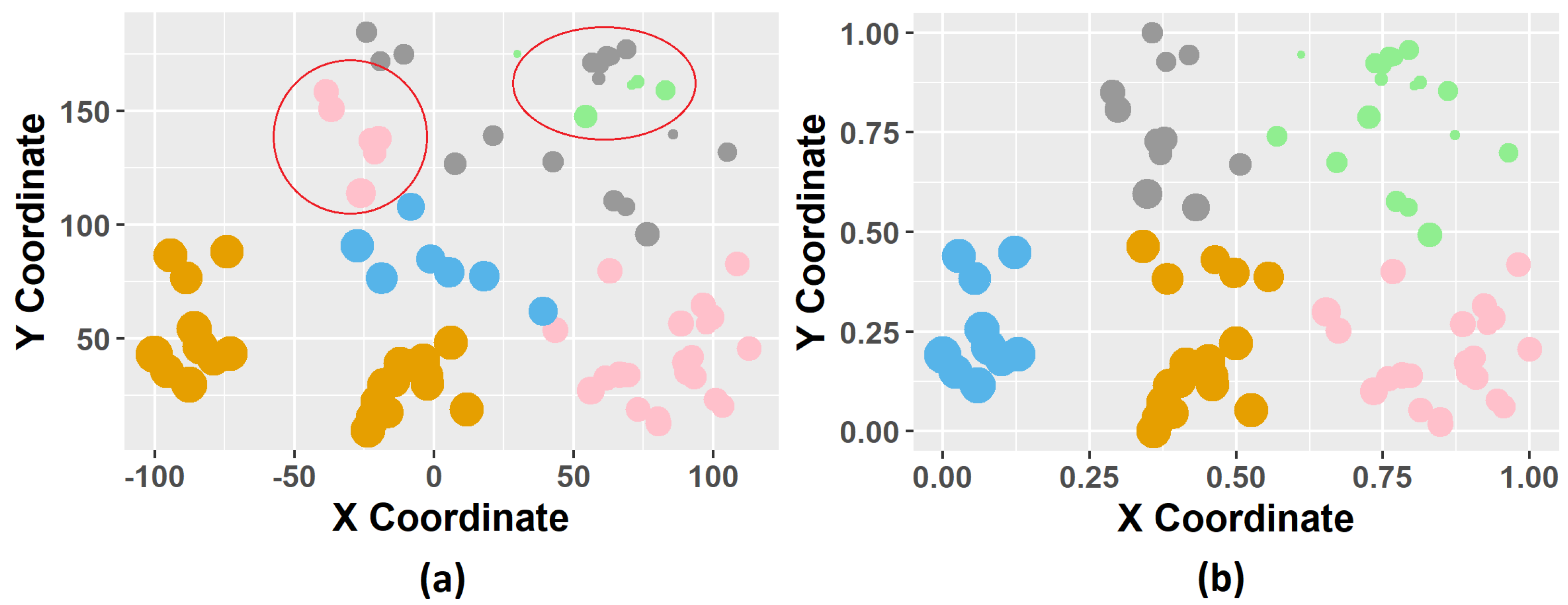
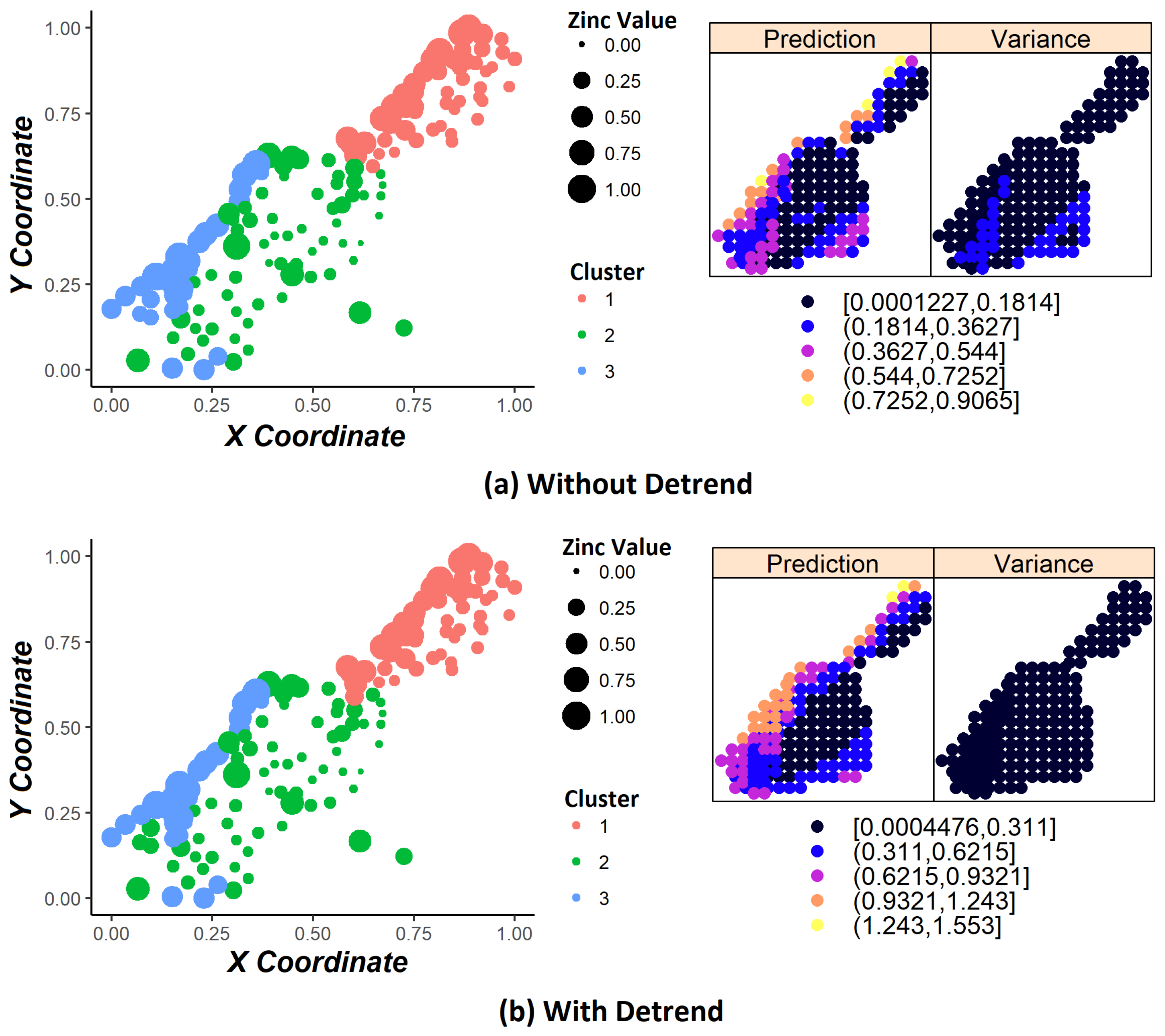
Data clustering techniques present some problems in spatial data, such as cluster overlapping. As stated in [
16], this behavior of creating spatially scattered clusters (cluster overlapping) is undesirable for many geostatistical applications, since it impacts the properties of spatial dependency over the study domain, and it is important to maintain the original characteristics of the database. Recently, some researchers seek to solve the cluster overlapping problem by developing methods that guarantee spatial contiguity where the groups created are uniform. For instance, in [
14], a normalization factor was used to minimize this problem. The method proposed in [
17] presented a new hierarchical clustering approach by applying weights to spatial and target variables, and Reference [
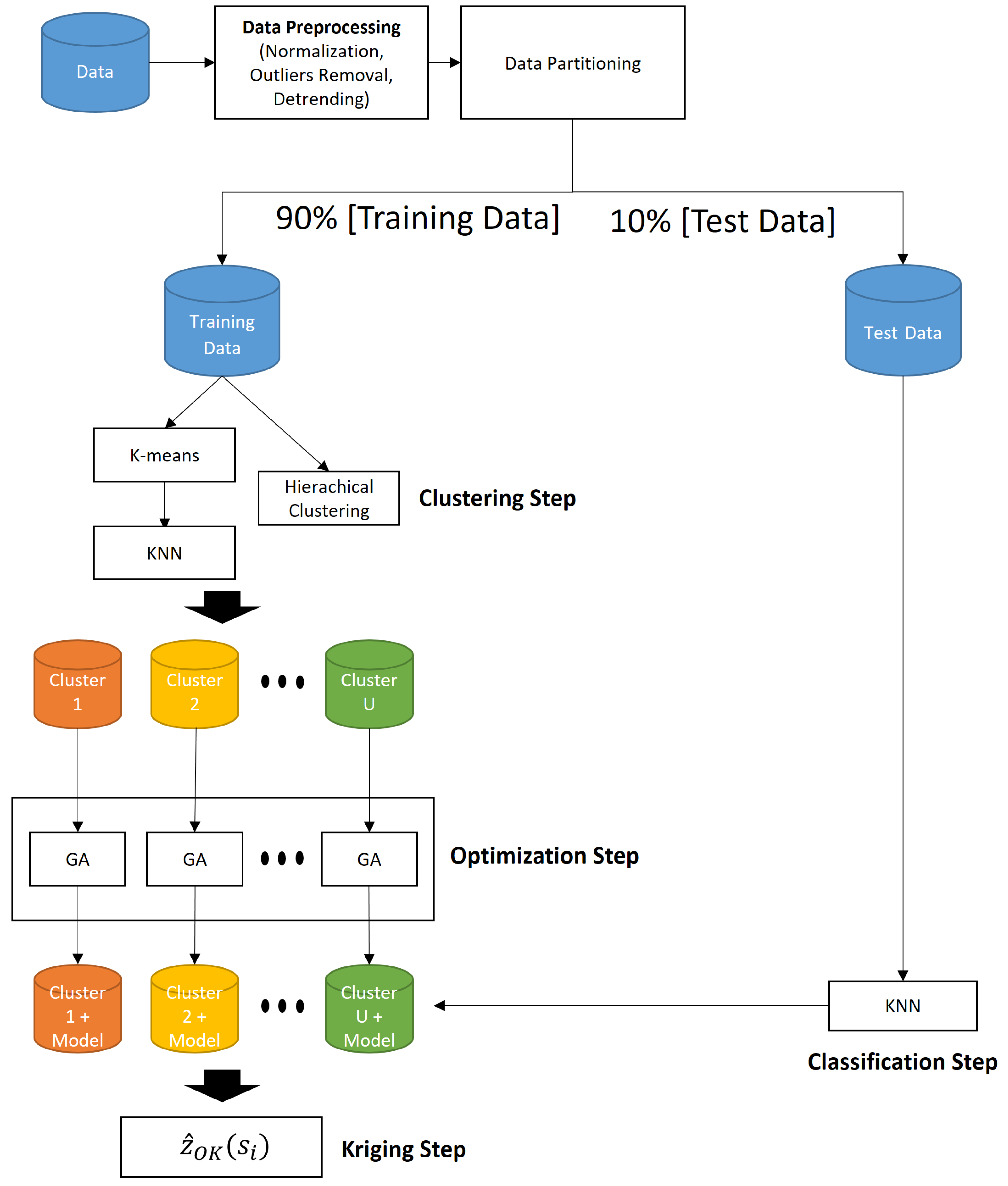
16] proposed a spectral clustering method to maintain the property of spatial contiguity. For this problem, we proposed a methodology using K-means clustering improved by the K-Nearest Neighbor (KNN) classifier.
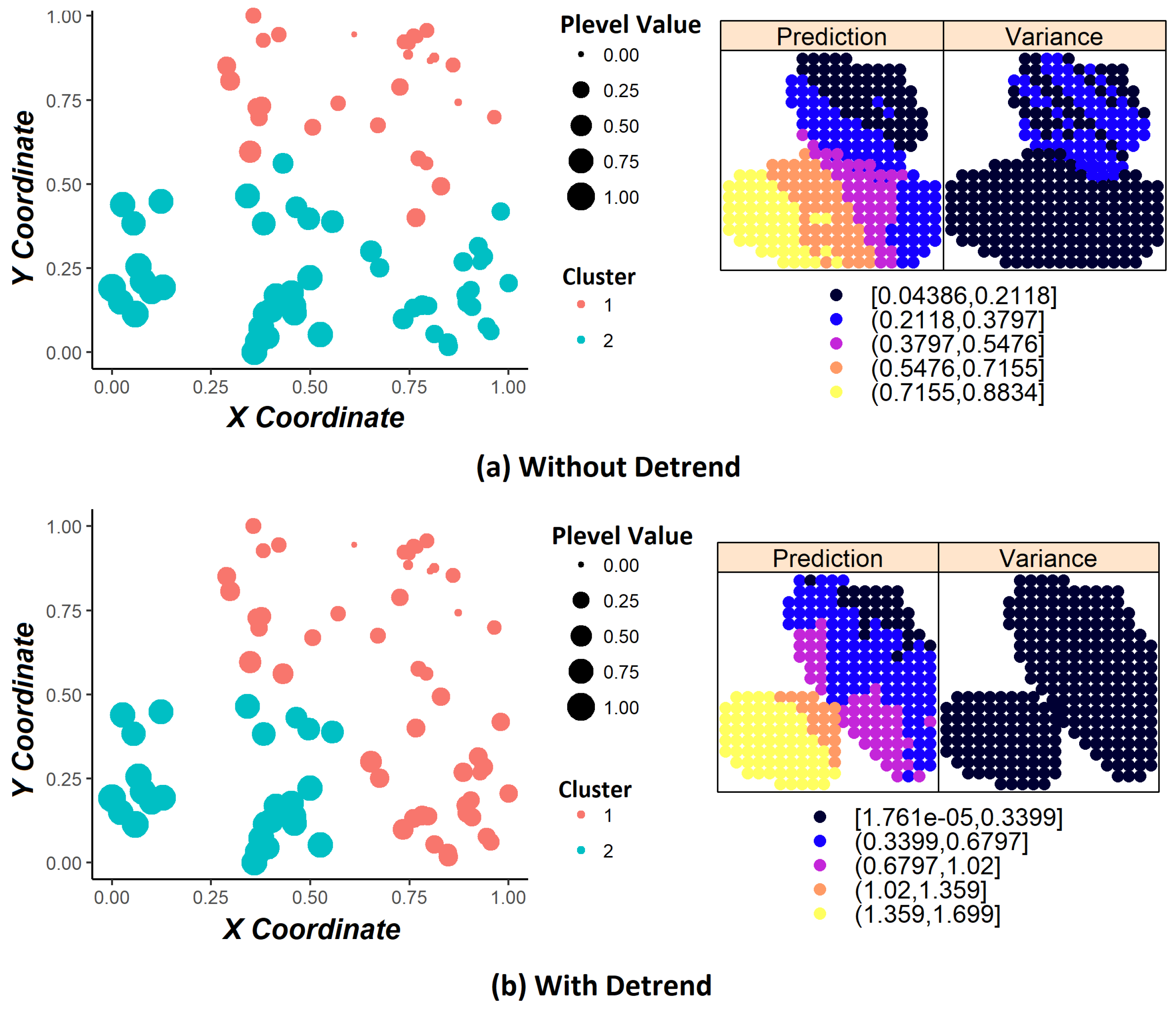
Another problem is that, when including coordinate variables in the clustering process, it does not guarantee the stationary hypothesis [
16]. Kriging requires that this hypothesis is satisfied [
1] that statistical properties such as mean, variance, among others, are all constant over the spatial domain; otherwise, we have the phenomenon called trend. According to [
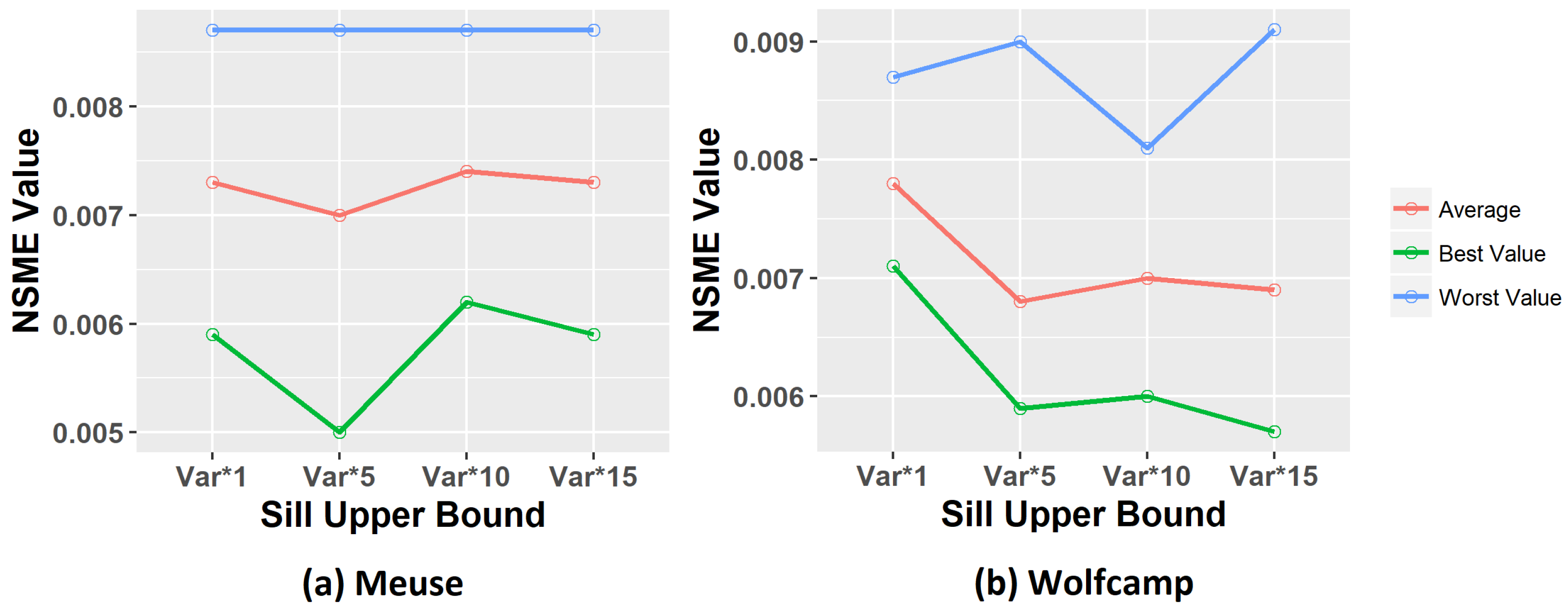
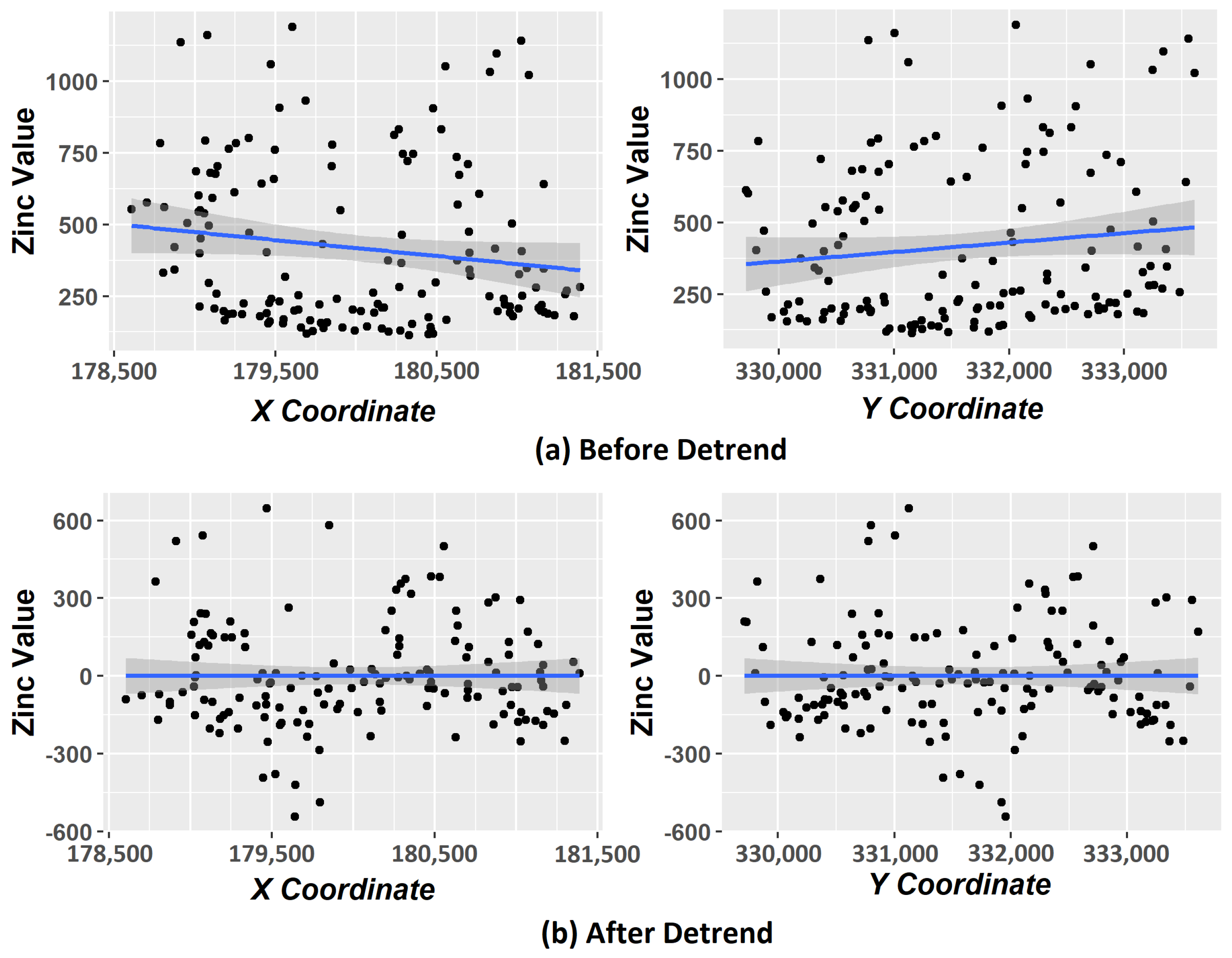
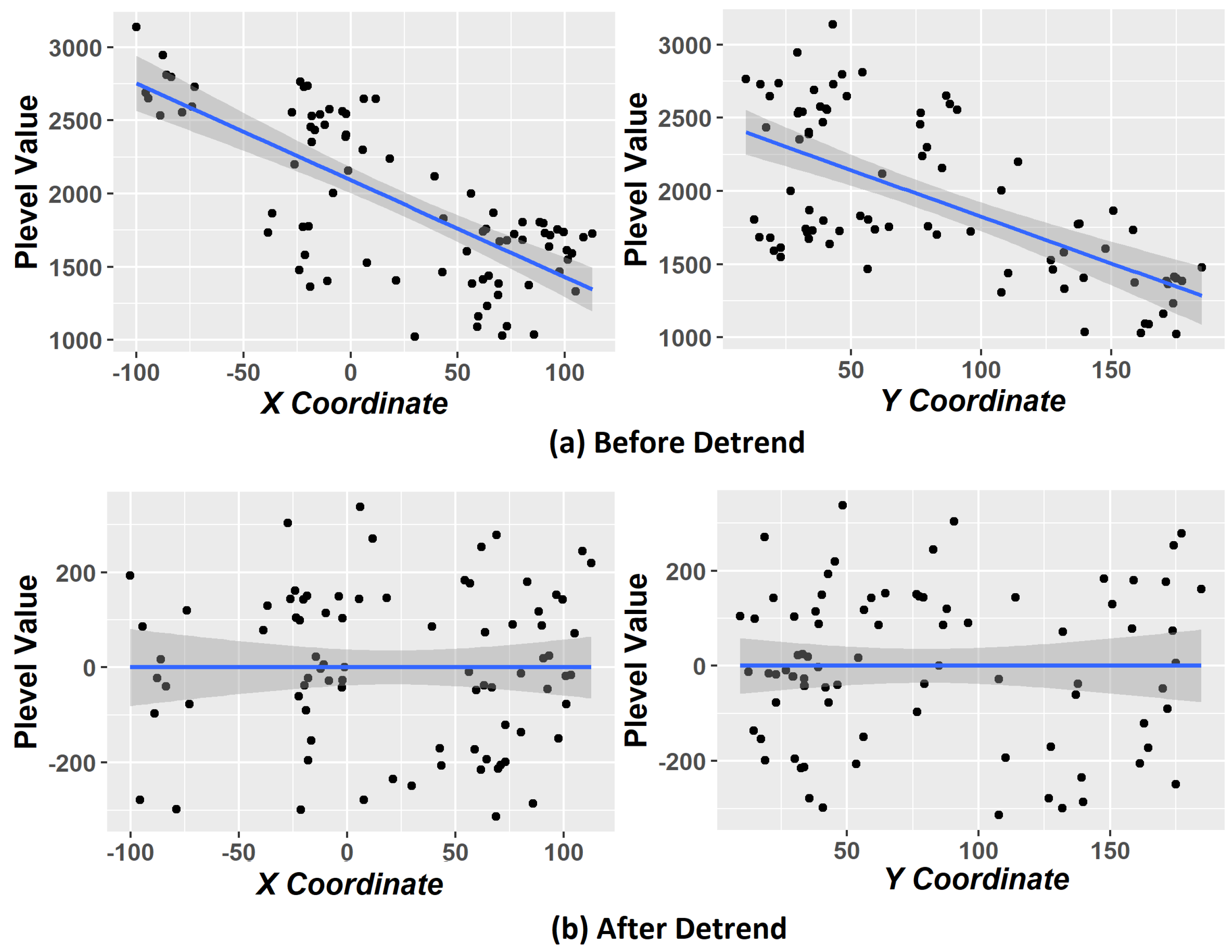
18], the trends removal procedure (also called detrending) ensures the stationary hypothesis on data. We carried out experiments with and without applying the detrending step in order to compare the results.
An important issue that has not been explored in the related works is when a new point in the spatial space needs to be interpolated. Since it must belong to a group, a mechanism to attach this new point to a cluster is needed. We explored this problem by proposing the application of the KNN algorithm to perform this allocation task.
In this context, a new methodology is proposed to improve kriging estimates, using concepts of preprocessing, data clustering, and optimization methods. In our approach, for comparison purposes, both K-means and Ward-Like Hierarchical [
17] clustering procedures were used to separate the data set in groups by similarity. The KNN algorithm performs the allocation task of new data in their respective cluster, and solves some problems occurred in the clustering step of the K-means method, such as cluster overlapping. In order to analyze the impacts on the stationary hypothesis, we applied the Mann–Kendall non-parametric test [
19] to evaluate the trend phenomenon. Finally, genetic algorithms were used to model a specific theoretical variogram to each group found in the clustering step, with the definition of the parameters’ bounds based on data of each group. Although GA is not considered nowadays as the state-of-the-art meta-heuristics, this technique was chosen in order to serve as a baseline for the proposed model, and also because it was applied in similar kriging methodologies, as can be seen in [
5,
7,
8,
20]. For instance, in [
20], the authors concluded that particle swarm optimization and genetic algorithms are statistically equivalent in the task of estimating the kriging parameters. The proposed methodology was evaluated using two publicly available databases and the results compared with other optimization techniques presented in the literature.
The remainder of the paper is organized as follows.
Section 2 presents the theoretical background.
Section 3 describes the proposed methodology steps.
Section 4 reports the used databases and the experimental setup. The baseline results are discussed in
Section 5. Finally,
Section 6 summarizes our conclusions and addresses future works.