Role-Engineering Optimization with Cardinality Constraints and User-Oriented Mutually Exclusive Constraints
Abstract
1. Introduction
- (1)
- Partitioning and compression are two important methods used to analyze clustering problems; they are widely used in scientific research and production practice because of their simple and accurate characteristics [29]. In order to reduce computational complexity and mining scale, we convert the basic role mining problem into a clustering problem, use partitioning and compressing technologies to eliminate redundancies, and evaluate the accuracy of the proposed method.
- (2)
- Role optimization that satisfies one cardinality constraint may violate another cardinality constraint. In order to limit the number of roles assigned to any user and/or a related permission, we present three role-optimization problems and their corresponding algorithms, and evaluate the effectiveness of the proposed method.
- (3)
- Mutually exclusive constraints, user-capability constraints, and cardinality constraints are critical to ensure authorization security. In order to satisfy these constraints, while maximizing the role assignments in the role-engineering system, we present a role-assignment algorithm and evaluate the efficiency of the proposed method.
2. Related Work and Preliminary Information
2.1. Methods of Role Optimization
2.2. Methods of Role Assignments
2.3. Preliminaries
2.3.1. Basic Components of Role Engineering
- (1)
- U, P, and R are the basic elements of RBAC; these elements denote a set of users, a set of permissions, and a set of roles, respectively;
- (2)
- , a many-to-many mapping of user-permission assignments in the non-RBAC model;
- (3)
- , a many-to-many mapping of user-role assignments in the RBAC model;
- (4)
- , a many-to-many mapping of role-permission assignments in the RBAC model;
- (5)
- , the mapping of user u onto a set of roles;
- (6)
- , the mapping of role r onto a set of users;
- (7)
- , the mapping of role r onto a set of permissions;
- (8)
- , the mapping of permission p onto a set of roles;
- (9)
- , the mapping of user u onto a set of permissions.
2.3.2. RBAC Constraints
2.3.3. Similarity and Dissimilarity in Clustering
- (1)
- ∀(Si,Sj)∈S; the similarity and dissimilarity between sample Si and sample Sj are, respectively, calculated as follows:
- (2)
- ∀(Si,Sj1,Sj2, …)∈S; the similarity and dissimilarity between sample Si and sample set {Sj1,Sj2,…} are, respectively, calculated as follows:
2.3.4. Basic RMP Problem and the Fast Miner Method
3. Proposed Method
3.1. Preprocessing for Basic RMP
| Algorithm 1. Initial role mining for basic RMP. |
| Input: the original matrix UPA Output: preprocessed matrices UA and PA and the initial set CR of the roles The Fast Miner and Boolean matrix decomposition are adopted to derive CR and configure RBAC, such that . |
3.1.1. Partitioning User Clusters
| Algorithm 2. Partitioning user clusters. |
| Input: user cluster CU and the k number of center points Output: center points and partitions 1. Randomly choose k users u1,u2,…,uk in CU as the initial center points; 2. for each center point ui in {u1,u2,…,uk} do 3. for each non-center point uj in associate(ui) do 4. 5. 6. if dis(uj,associate(ui)\{uj}∪{ui})<dis(ui,associate(ui)) then 7. associate(ui) = associate(ui)\{uj}∪{ui}; 8. swap(uj,ui) and divide CU into k partitions; 9. end if 10. end for 11. end for |
3.1.2. Compressing Cluster Partitions
| Algorithm 3. Compression cluster partitions. |
| Input: the initial set CR of the roles, the set VC of the compression points, the partition with center point ui, and threshold t Output: compressed matrix UPAcompressed 1. Initialize UPAcompressed = Φ, VC = Φ; 2. for each p in CR do 3. 4. if then 5. insert ui into VC; 6. UPAcompressed = UPAcompressed ∪ {(ui, p)}; 7. end if 8. end for |
3.2. Role Optimization Satisfying Cardinality Constraints
3.2.1. Role Optimization Satisfying UCC
| Algorithm 4. Role optimization satisfying UCC. |
| Input: preprocessed matrices UA and PA, the initial role set CR, and threshold MRCuser Output: the optimized matrices UA and PA 1. Define and compute count_user_roles(u) as the number of roles possessed by user u; 2. Define and compute count_role_users(r) as the number of users assigned to role r; 3. while ∃u∈U: count_user_roles(u) > MRCuser do 4. k = count_user_roles(u) − (MRCuser − 1); 5. Choose the top k roles from u with the highest count_role_users(r) values to constitute set S; 6. Merge the permissions of all the k roles and denote the union as set PS; 7. Create a new role rnr such that role_permissions(rnr) = PS; 8. for each pt in P do 9. if pt∈PS then 10. PA[nr][t] = 1; 11. else 12. PA[nr][t] = 0; 13. end if 14. end for 15. for each ui in U do 16. if ∀rj∈S: UA[i][j] = = 1 then 17. ∀rj∈S: UA[i][j] = 0; 18. UA[i][nr] = 1; 19. else 20. UA[i][nr] = 0; 21. end if 22. end for 23. Update count_user_roles(u) and count_role_users(r); 24. end while |
3.2.2. Role Optimization Satisfying PCC
| Algorithm 5. Role optimization satisfying PCC. |
| Input: the preprocessed matrices UA, PA, initial role set CR, and threshold MRCpermission Output: the optimized matrices UA and PA 1. Define and compute count_permission_roles(p) as the number of roles related to permission p; 2. Define and compute count_role_permissions(r) as the number of permissions assigned to role r; 3. while ∃p∈P: count_perm_roles(p)>MRCpermission do 4. k = count_perm_roles(p) − (MRCpermission − 1); 5. Choose the top k roles from p with the highest count_role_permissions(r) values to constitute set S; 6. Intersect the permissions of all the k roles and denote the intersection as set PS; 7. Create a new role rnr such that role_permissions(rnr) = PS; 8. for each ui in U do 9. if count_user_roles(ui)⊇rnr then 10. UA[i][nr] = 1; 11. else 12. UA[i][nr] = 0; 13. end if 14. end for 15. for each rj in S do 16. if ∀pt∈PS: PA[j][t] = = 1 then 17. ∀pt∈PS: PA[j][t] = 0; 18. PA[nr][t] = 1; 19. else 20. PA[nr][t] = 0; 21. end if 22. end for 23. Update count_perm_roles(p) and count_role_perms (r); 24. end while |
3.2.3. Role Optimization Satisfying both UCC and PCC
| Algorithm 6. Role optimization satisfying both UCC and PCC. |
| Input: preprocessed matrices UA, PA, initial role set CR, and thresholds MRCuser and MRCpermission Output: optimized matrices UA and PA 1. Define and compute count_user_roles(u), count_role_users(r), count_permission_roles(p), and count_role_permissions(r); 2. Identify RU, RI; 3. while (∃u∈U: count_user_roles(u) > MRCuser) or (∃p∈P: count_perm_roles(p) > MRCpermission) do 4. Choose violating users or violating permissions based on a heuristic strategy; 5. if user u is chosen then 6. k = count_user_roles(u) − (MRCuser − 1); 7. Choose the top k roles of u from RU with the highest count_role_users(r) values to constitute set S; 8. Merge the permissions of all the k roles and denote the union as set PS; 9. Create a new role rnr such that role_permissions(rnr) = PS; 10. Update the PA and UA with rnr according to Algorithm 4; 11. else 12. k = count_perm_roles(p) − (MRCpermission − 1); 13. Choose the top k roles of p from RI with the highest count_role_permissions(r) values to constitute set S; 14. Intersect the permissions of all the k roles and denote the intersection as set PS; 15. Create a new role rnr such that role_permissions(rnr) = PS; 16. Update the UA and PA with rnr according to Algorithm 5; 17. end if 18. end while |
3.3. Role Assignments Satisfying Multiple Constraints
| Algorithm 7. Role assignments satisfying multiple constraints. |
| Input: Set U for users, set R for roles, threshold MRCuser, matrix UC for user-capability constraints, and set C for t-t SMER constraints Output: user-role assignment matrix UA’ 1. for each UC[i][j] in UC do 2. if UC[i][j] = = 0 then 3. UA’[i][j] = 0; 4. else 5. UA’[i][j] = aij; 6. end if 7. end for 8. Create a new priority queue Q and insert all roles of R into Q; 9. Sort roles in Q according to the ascending order of their constraint degree. Role r, which has a lower smerC(r) value, has a higher priority; 10. while Q is not empty do 11. Choose role rj with the highest priority in Q; 12. for each ui in UC do 13. if UA’[i][j]≠ 0 then 14. for each smer<{r1,r2,…,rt},t> in C do 15. if (|{user_roles(ui) ∪ {rj}} ∩ {r1,r2,…,rt}|<t) and (count_user_roles(ui)≤ MRCuser − 1) then 16. UA’[i][j] = 1; 17. end if 18. end for 19. end if 20. end for 21. Remove rj from Q; 22. end while |
- (1)
- , ;
- (2)
- , .
4. Theoretical Analyses and Running Examples
4.1. Relationship between the Center Point and Compression Point
4.2. The Influencing Factors of Role Assignments
4.3. Relationship between the UCC and PCC
4.4. Running Examples
- (1)
- The matrix UC of user-capability constraints, which is shown in Table 10;
- (2)
- set C = {c1,c2,c3,c4} for the t-t SMER constraints, where c1 = smer<{r1,r3},2>, c2 = smer<{r2,r3},2>, c3 = smer<{r1,r2,r3},3>, and c4 = smer<{r4,r5},2>.
5. Experimental Evaluations
5.1. The Accuracy of the REO_CCUMEC
5.1.1. Experimental Setup
5.1.2. Evaluation Measures
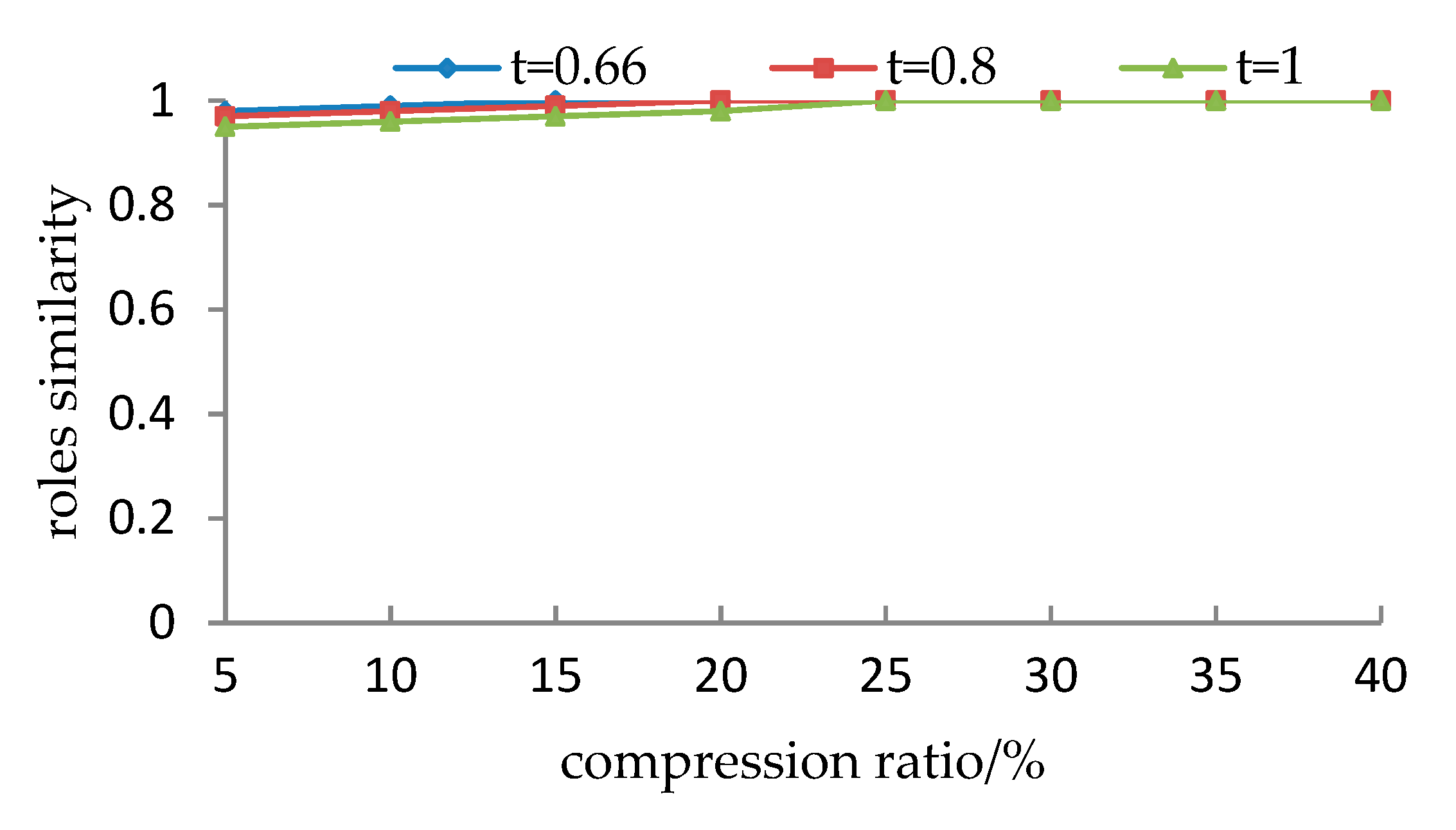
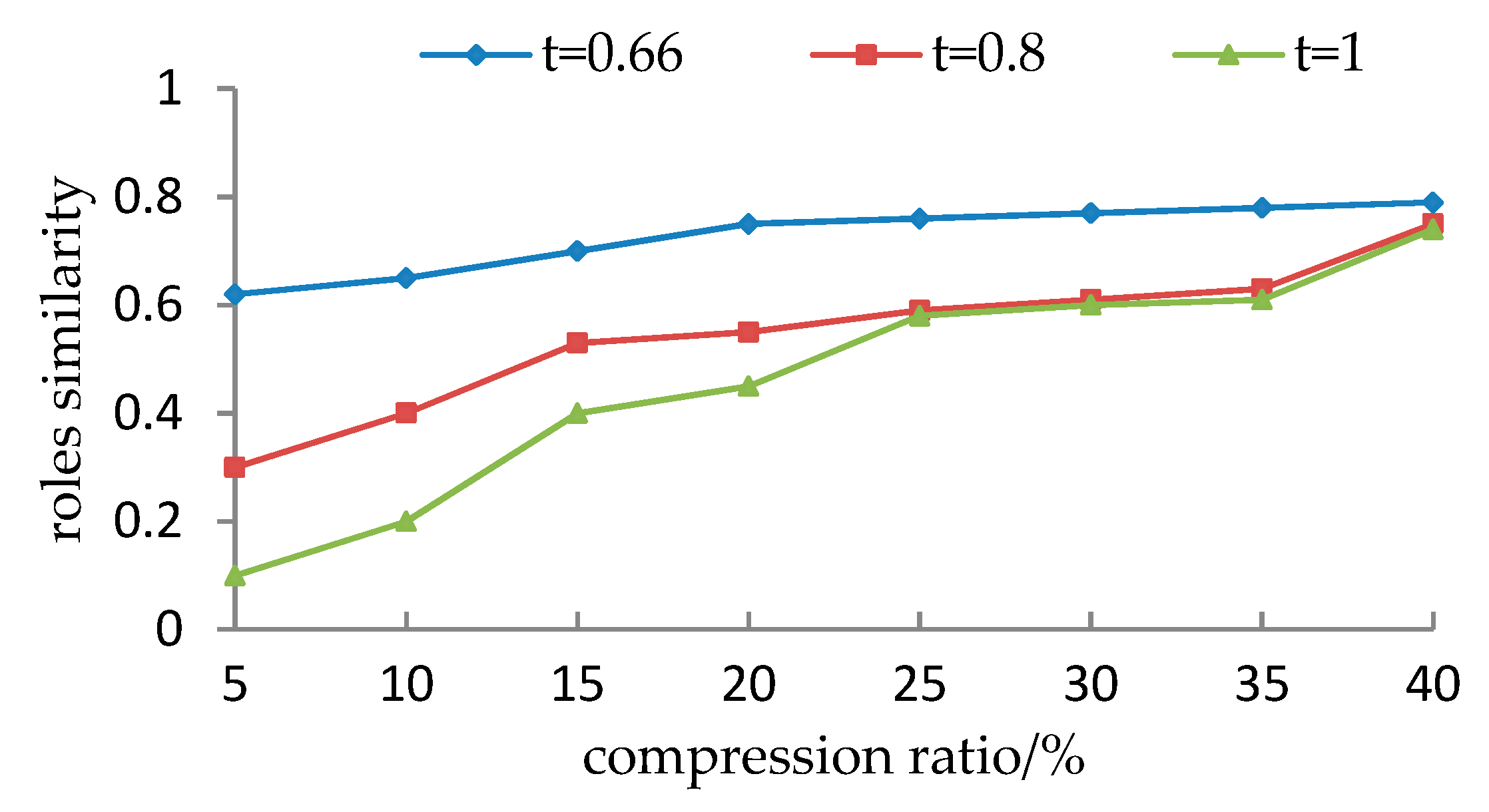
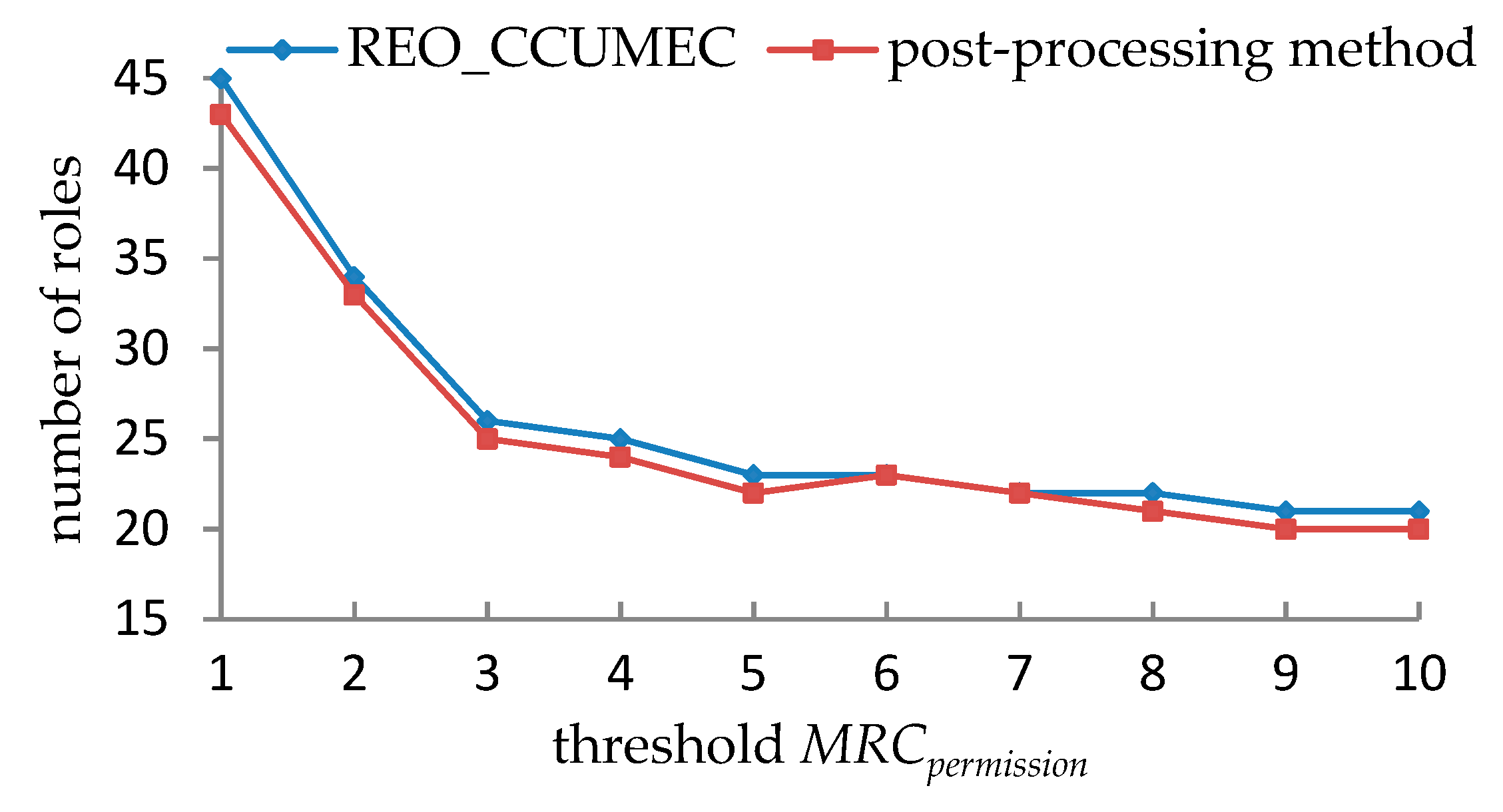
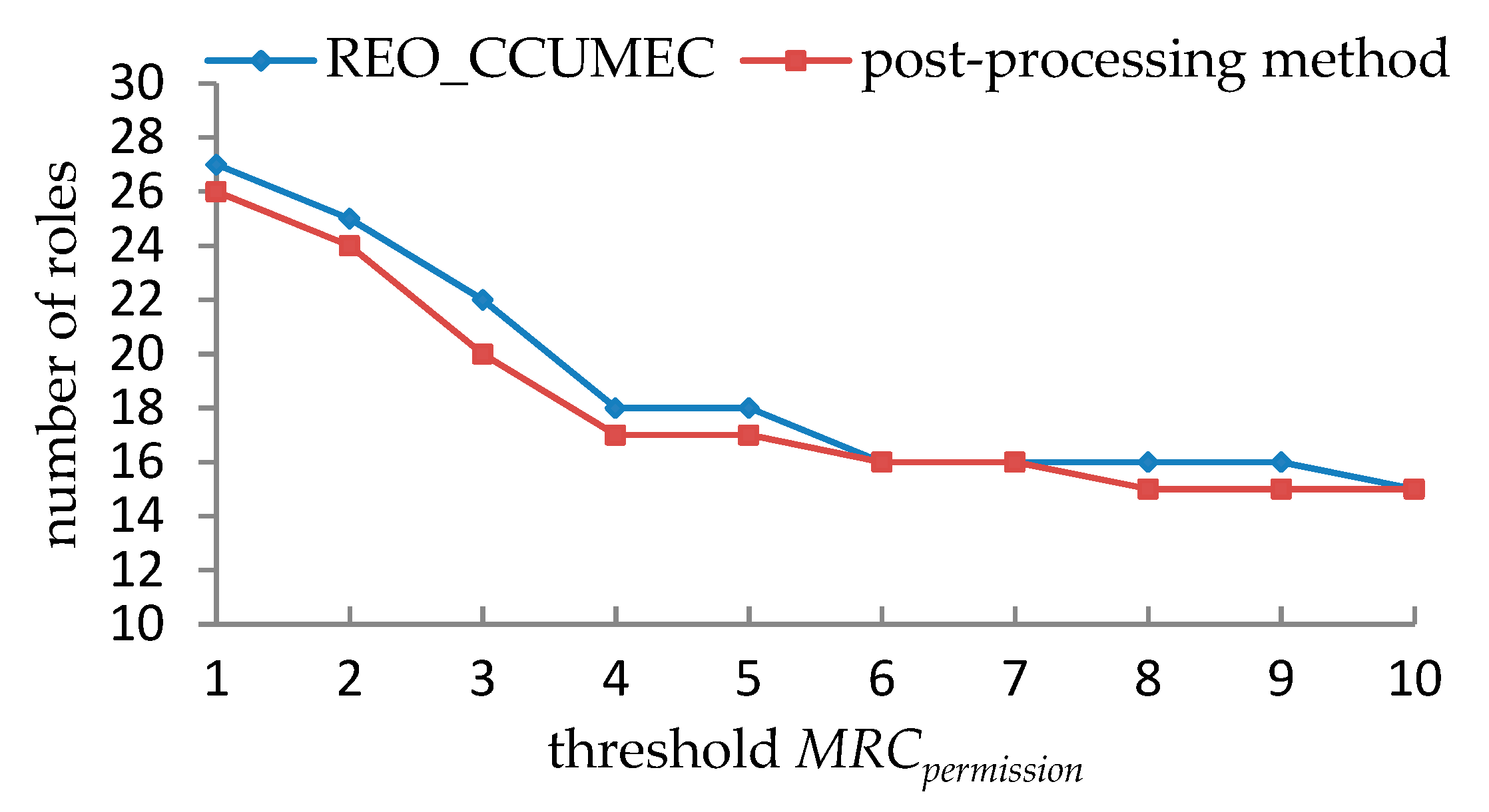
5.1.3. Experimental Results and Analyses
5.2. The Effectiveness of the REO_CCUMEC
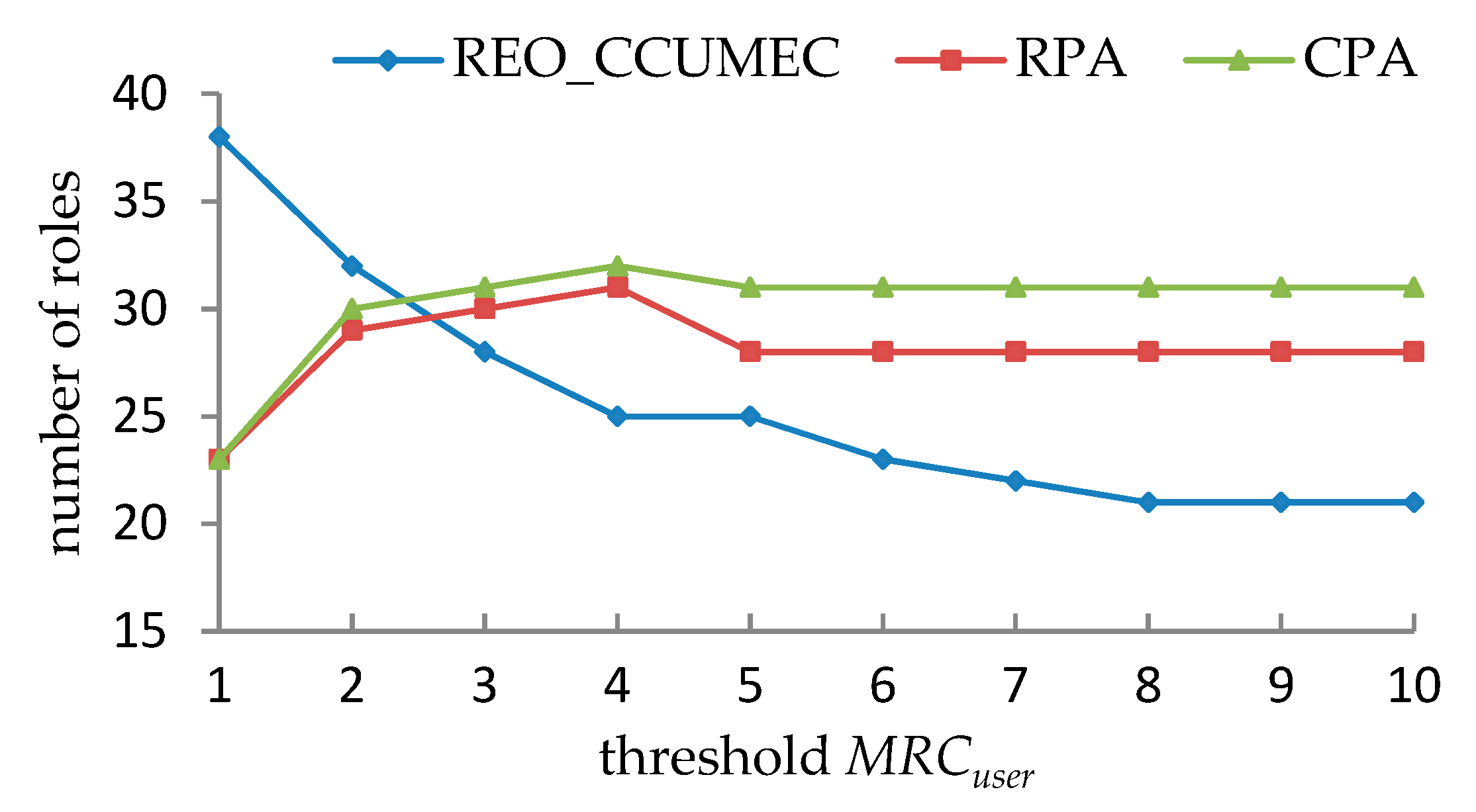
5.2.1. Performance Evaluations under a Single Constraint
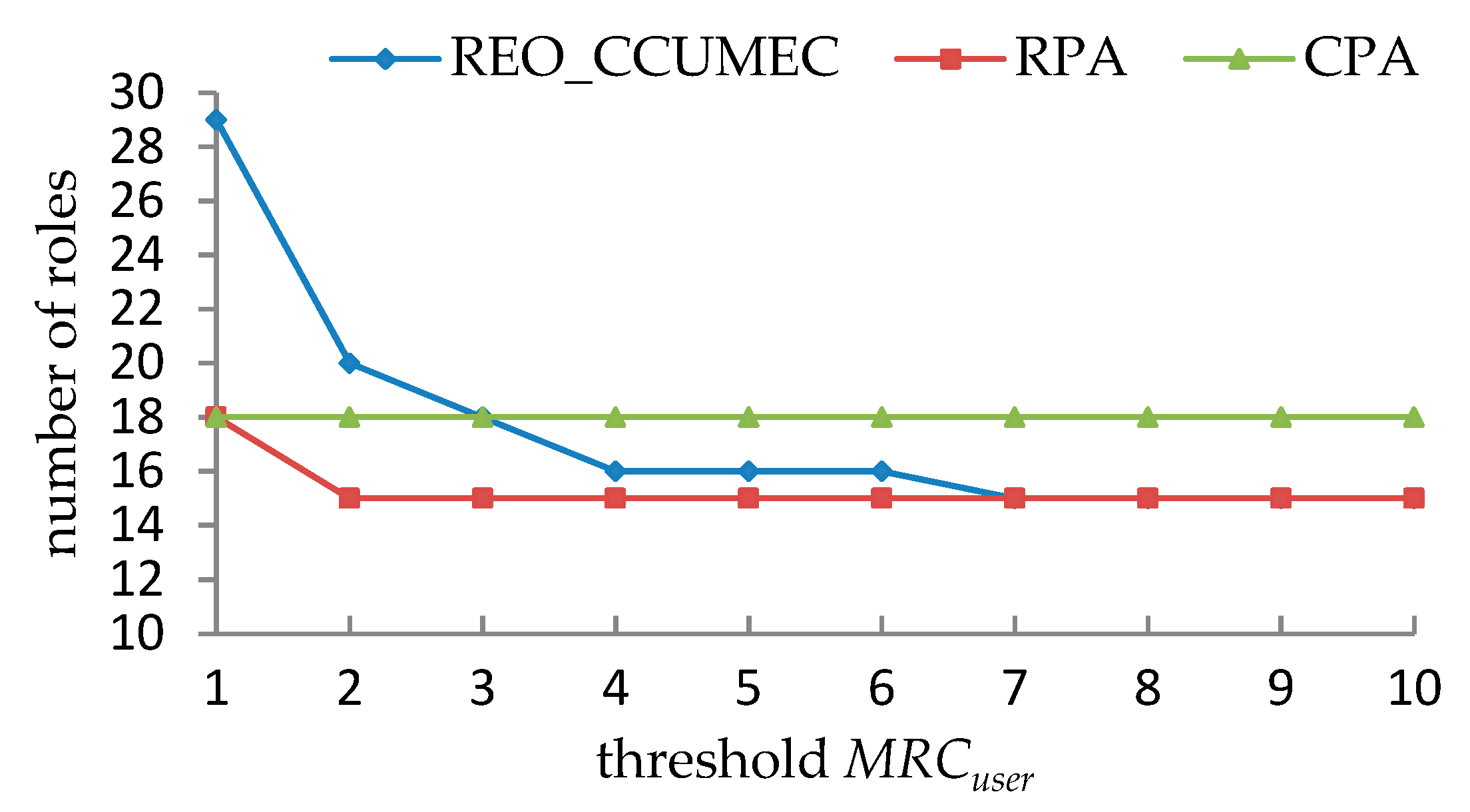
5.2.2. Performance Evaluations under the Double Constraints
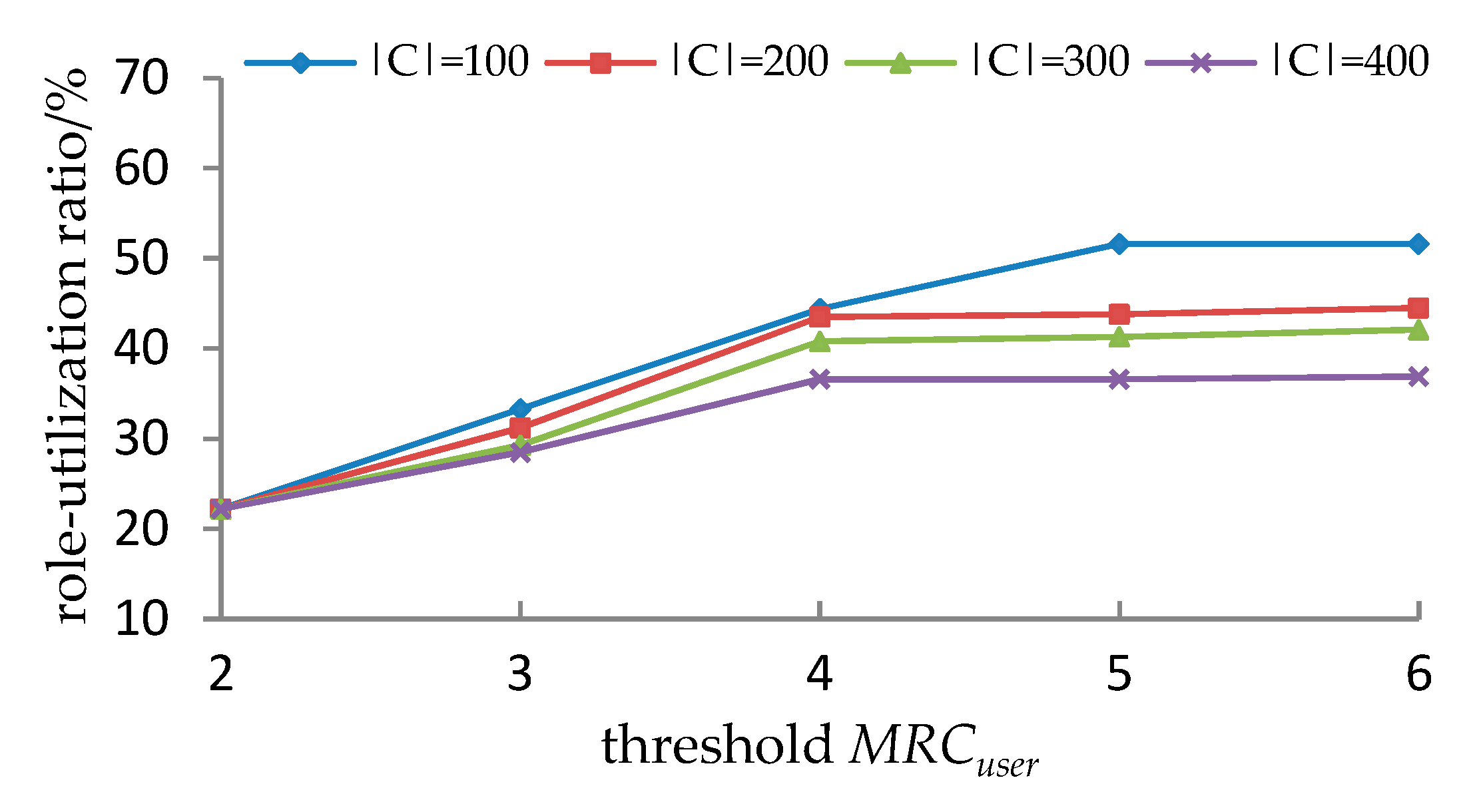
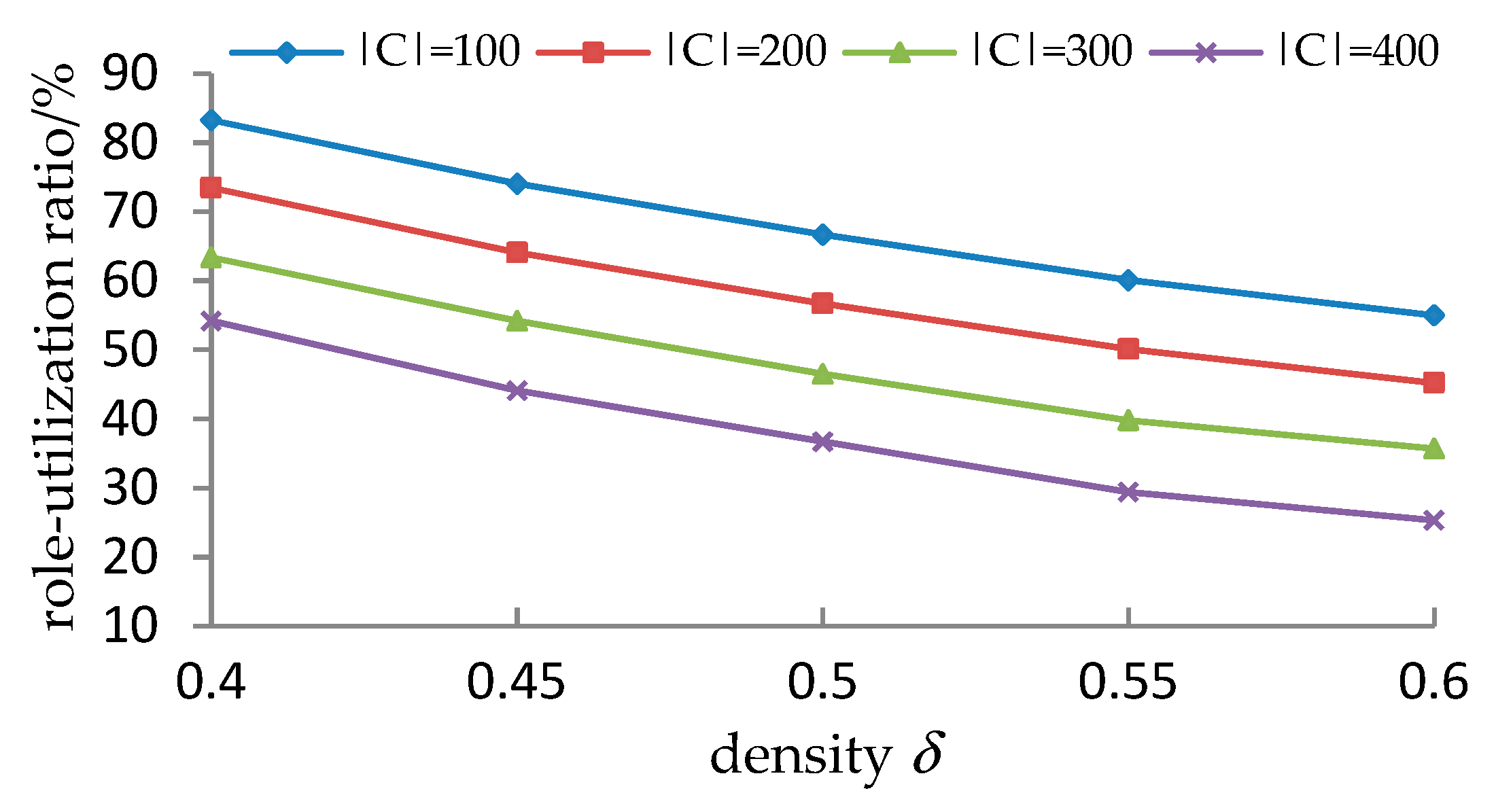
5.3. The Efficiency of the REO_CCUMEC
5.3.1. Experimental Setup
5.3.2. Evaluation Measure
5.3.3. Experimental Results and Analyses
5.4. Advantages and Limitations of the REO_CCUMEC
- (1)
- In the preprocessing phase, it can reduce the mining scale, while eliminating the redundancies of the mining roles by using partitioning and compressing technologies.
- (2)
- In the role optimization phase, REO_CCUMEC constructs a role-engineering system based on the mining results in the previous phase. Thus, it can satisfy two cardinality constraints simultaneously, and the problem of constraint conflicts between the UCC and PCC can be effectively solved.
- (3)
- In the role assignment phase, besides the cardinality constraints and the given user-capability constraints, we construct t-t SMER constraints using the existing mature methods. It is effective and efficient to implement the maximal role assignments, while satisfying all the constraints in the constructed RBAC system.
- (1)
- It is observed from Section 5.1.1 that for the given user cluster, how to set the parameters (including compression ratio and the threshold of the support degree) lacks a theoretical justification. Different parameters may cause different evaluation results. Although, the preprocessing roles are very similar to the initial roles from the viewpoint of simP(PAcompressed,PAinitial), they are less accurate from the viewpoint of simU(UAcompressed,UAinitial) when the threshold t exceeds a particular value.
- (2)
- It is observed in from Table 19, Table 20, Table 21 and Table 22 that the effective roles that can be generated as MRCuser and MRCpermission vary. However, certain combinations of the values of MRCuser and MRCpermission cannot produce a valid solution since the UCC and PCC are mutually exclusive, especially when MRCuser or MRCpermission becomes smaller.
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Xuan, H.; Wei, S.; Tong, W.; Liu, D.; Qi, C. Fault-tolerant scheduling algorithm with re-allocation for divisible task. IEEE Access 2018, 6, 73147–73157. [Google Scholar] [CrossRef]
- Batra, G.; Atluri, V.; Vaidya, J.; Sural, S. Deploying ABAC policies using RBAC systems. J. Comput. Secur. 2019, 27, 483–506. [Google Scholar] [CrossRef]
- Ghafoorian, M.; Abbasinezhad-Mood, D.; Shakeri, H. A Thorough Trust and Reputation Based RBAC Model for Secure Data Storage in the Cloud. IEEE Trans. Parallel Distrib. Syst. 2019, 30, 778–788. [Google Scholar] [CrossRef]
- Cruz, J.P.; Kaji, Y.; Yanai, N. Rbac-sc: Role-based access control using smart contract. IEEE Access 2018, 6, 12240–12251. [Google Scholar] [CrossRef]
- Pan, N.; Sun, L.; He, L.; Zhu, Z. An Approach for Hierarchical RBAC Reconfiguration with Minimal Perturbation. IEEE Access 2018, 6, 40389–40399. [Google Scholar] [CrossRef]
- Pan, N.; Zhu, Z.; He, L.; Sun, L. An efficiency approach for RBAC reconfiguration with minimal roles and perturbation. Concurr. Comput. Pract. Exp. 2018, 30, e4399. [Google Scholar] [CrossRef]
- Mitra, B.; Sural, S.; Vaidya, J.; Atluri, V. Migrating from RBAC to temporal RBAC. IET Inf. Secur. 2017, 11, 294–300. [Google Scholar] [CrossRef]
- Schefer-Wenzl, S.; Strembeck, M. Modeling Support for Role-Based Delegation in Process-Aware Information Systems. Bus. Inf. Syst. Eng. 2014, 6, 215–237. [Google Scholar] [CrossRef][Green Version]
- Baumgrass, A.; Strembeck, M. Bridging the gap between role mining and role engineering via migration guides. Inf. Sec. Tech. Rep. 2013, 17, 148–172. [Google Scholar] [CrossRef]
- Narouei, M.; Takabi, H. Towards an Automatic Top-down Role Engineering Approach Using Natural Language Processing Techniques. In Proceedings of the 20th ACM Symposium on Access Control Models and Technologies, Vienna, Austria, 1–3 June 2015; pp. 157–160. [Google Scholar]
- Gal-Oz, N.; Gonen, Y.; Gudes, E. Mining meaningful and rare roles from web application usage patterns. Comput. Secur. 2019, 82, 296–313. [Google Scholar] [CrossRef]
- Bai, W.; Pan, Z.; Guo, S.; Chen, Z. RMMDI: A Novel Framework for Role Mining Based on the Multi-Domain Information. Secur. Commun. Netw. 2019, 2019, 8085303. [Google Scholar] [CrossRef]
- Stoller, S.D.; Bui, T. Mining hierarchical temporal roles with multiple metrics. J. Comput. Secur. 2018, 26, 121–142. [Google Scholar] [CrossRef]
- Mitra, B.; Sural, S.; Vaidya, J.; Atluri, V. A Survey of Role Mining. ACM Comput. Surv. 2016, 48, 50. [Google Scholar] [CrossRef]
- Mitra, B.; Sural, S.; Vaidya, J.; Atluri, V. Mining temporal roles using many-valued concepts. Comput. Secur. 2016, 60, 79–94. [Google Scholar] [CrossRef]
- Vaidya, J.; Atluri, V.; Guo, Q. The role mining problem: A formal perspective. ACM Trans. Inf. Syst. Secur. 2010, 13, 27. [Google Scholar] [CrossRef]
- Vaidya, J.; Atluri, V.; Guo, Q. The role mining problem: Finding a minimal descriptive set of roles. In Proceedings of the 12th ACM Symposium on Access Control Models and Technologies, Sophia Antipolis, France, 20–22 June 2007; pp. 175–184. [Google Scholar]
- Lu, H.; Vaidya, J.; Atluri, V. Optimal boolean matrix decomposition: Application to role engineering. In Proceedings of the 24th International Conference on Data Engineering, Cancún, Mexico, 7–12 April 2008; pp. 297–306. [Google Scholar]
- Lu, H.; Vaidya, J.; Atluri, V. An optimization framework for role mining. J. Comput. Secur. 2014, 22, 1–31. [Google Scholar] [CrossRef]
- Lu, H.; Hong, Y.; Yang, Y.; Duan, L.; Badar, N. Towards user-oriented RBAC model. J. Comput. Secur. 2015, 23, 107–129. [Google Scholar] [CrossRef]
- Colantonio, A.; Pietro, R.D.; Ocello, A.; Verde, N.V. Mining Business-Relevant RBAC States through Decomposition. In Proceedings of the 25th IFIP TC-11 International Information Security Conference, Brisbane, Australia, 20–23 September 2010; pp. 19–30. [Google Scholar]
- Colantonio, A.; Pietro, R.D.; Ocello, A.; Verde, N.V. Taming role mining complexity in RBAC. Comput. Secur. 2010, 29, 548–564. [Google Scholar] [CrossRef]
- Lang, B.; Wang, J.; Liu, Y. Achieving flexible and self-contained data protection in cloud computing. IEEE Access 2017, 5, 1510–1523. [Google Scholar] [CrossRef]
- Ultra, J.D.; Pancho-Festin, S. A simple model of separation of duty for access control models. Comput. Secur. 2017, 68, 69–80. [Google Scholar] [CrossRef]
- Nazerian, F.; Motameni, H.; Nematzadeh, H. Emergency role-based access control (E-RBAC) and analysis of model specifications with alloy. J. Inf. Sec. Appl. 2019, 45, 131–142. [Google Scholar] [CrossRef]
- Ma, X.; Li, R.; Wang, H.; Li, H. Role mining based on permission cardinality constraint and user cardinality constraint. Secur. Commun. Netw. 2015, 8, 2317–2328. [Google Scholar] [CrossRef]
- Li, N.; Tripunitara, M.V.; Bizri, Z. On mutually exclusive roles and separation-of-duty. ACM Trans. Inf. Syst. Secur. 2007, 10, 5. [Google Scholar] [CrossRef]
- Roy, A.; Sural, S.; Majumdar, A.K.; Vaidya, J.; Atluri, V. On Optimal Employee Assignment in Constrained Role-Based Access Control Systems. ACM Trans. Manag. Inf. Syst. 2017, 7, 10. [Google Scholar] [CrossRef]
- Song, X.; Yang, Y.; Jiang, Y.; Jiang, K. Optimizing partitioning strategies for faster inverted index compression. Front. Comput. Sci. 2019, 13, 343–356. [Google Scholar] [CrossRef]
- Molloy, I.; Chen, H.; Li, T.; Wang, Q.; Li, N.; Bertino, E.; Calo, S.B.; Lobo, J. Mining roles with semantic meanings. In Proceedings of the 13th ACM Symposium on Access Control Models and Technologies, Estes Park, CO, USA, 11–13 June 2008; pp. 21–30. [Google Scholar]
- Zhang, D.; Ramamohanarao, K.; Ebringer, T. Role engineering using graph optimisation. In Proceedings of the 12th ACM Symposium on Access Control Models and Technologies, Sophia Antipolis, France, 20–22 June 2007; pp. 139–144. [Google Scholar]
- Ene, A.; Horne, W.G.; Milosavljevic, N.; Rao, P.; Schreiber, R.; Tarjan, R.E. Fast exact and heuristic methods for role minimization problems. In Proceedings of the 13th ACM Symposium on Access Control Models and Technologies, Estes Park, CO, USA, 11–13 June 2008; pp. 1–10. [Google Scholar]
- Colantonio, A.; Pietro, R.D.; Ocello, A.; Verde, N.V. Visual Role Mining: A Picture Is Worth a Thousand Roles. IEEE Trans. Knowl. Data Eng. 2012, 24, 1120–1133. [Google Scholar] [CrossRef]
- Verde, N.V.; Vaidya, J.; Atluri, V.; Colantonio, A. Role engineering: From theory to practice. In Proceedings of the Second ACM Conference on Data and Application Security and Privacy, San Antonio, TX, USA, 7–9 February 2012; pp. 181–192. [Google Scholar]
- Kumar, R.; Sural, S.; Gupta, A. Mining RBAC Roles under Cardinality Constraint. In Proceedings of the 6th International Conference on Information Systems Security, Gandhinagar, India, 17–19 December 2010; pp. 171–185. [Google Scholar]
- Blundo, C.; Cimato, S. Constrained Role Mining. In Proceedings of the Security and Trust Management—8th International Workshop, Pisa, Italy, 13–14 September 2012; pp. 289–304. [Google Scholar]
- Hingankar, M.; Sural, S. Towards role mining with restricted user-role assignment. In Proceedings of the 2nd International Conference on Wireless Communication, Vehicular Technology, Information Theory and Aerospace and Electronic Systems Technology, Chennai, India, 28 February–3 March 2011; pp. 1–5. [Google Scholar]
- John, J.C.; Sural, S.; Atluri, V.; Vaidya, J. Role Mining under Role-Usage Cardinality Constraint. In Proceedings of the 27th IFIP TC 11 Information Security and Privacy Conference on Information Security and Privacy Research, Heraklion, Crete, Greece, 4–6 June 2012; pp. 150–161. [Google Scholar]
- Harika, P.; Nagajyothi, M.; John, J.C.; Sural, S.; Vaidya, J.; Atluri, V. Meeting Cardinality Constraints in Role Mining. IEEE Trans. Depend. Sec. Comput. 2015, 12, 71–84. [Google Scholar] [CrossRef]
- Sarana, P.; Roy, A.; Sural, S.; Vaidya, J.; Atluri, V. Role Mining in the Presence of Separation of Duty Constraints. Inf. Syst. Secur. 2015, 9478, 98–117. [Google Scholar]
- Sun, W.; Wei, S.; Guo, H.; Liu, H. Role-Mining Optimization with Separation-of-Duty Constraints and Security Detections for Authorizations. Future Internet 2019, 11, 201. [Google Scholar] [CrossRef]
- Zhang, Y.; Joshi, J.B.D. Uaq: A framework for user authorization query processing in rbac extended with hybrid hierarchy and constraints. In Proceedings of the 13th ACM Symposium on Access Control Models and Technologies, Estes Park, CO, USA, 11–13 June 2008; pp. 83–92. [Google Scholar]
- Lu, J.; Xin, Y.; Zhang, Z.; Peng, H.; Han, J. Supporting user authorization queries in RBAC systems by role-permission reassignment. Future Gener. Comp. Syst. 2018, 88, 707–717. [Google Scholar] [CrossRef]
- Roy, A.; Sural, S.; Majumdar, A.K. Impact of Multiple t-t SMER Constraints on Minimum User Requirement inRBAC. Inf. Syst. Secur. 2014, 8880, 109–128. [Google Scholar]
- Roy, A.; Sural, S.; Majumdar, A.K.; Vaidya, J.; Atluri, V. Minimizing Organizational User Requirement while Meeting Security Constraints. ACM Trans. Manag. Inf. Syst. 2015, 6, 12. [Google Scholar] [CrossRef]
- Valsesia, D.; Fosson, S.M.; Ravazzi, C.; Bianchi, T.; Magli, E. Analysis of SparseHash: An efficient embedding of set-similarity via sparse projections. Pattern Recognit. Lett. 2019, 128, 93–99. [Google Scholar] [CrossRef]
- Li, Z.; Wang, G.; He, G. Milling tool wear state recognition based on partitioning around medoids (PAM) clustering. Int. J. Adv. Manuf. Technol. 2017, 88, 1203–1213. [Google Scholar] [CrossRef]
- Li, R.; Li, H.; Wei, W.; Ma, X.; Gu, X. RMiner: A tool set for role mining. In Proceedings of the 18th ACM Symposium on Access Control Models and Technologies, Amsterdam, The Netherlands, 12–14 June 2013; pp. 193–196. [Google Scholar]
| Symbol | Meaning |
|---|---|
| U,P,R,UA,PA,UPA | Basic components of RBAC |
| UCC | Limitation on the number of roles assigned to any user |
| MRCuser | Threshold of the UCC |
| PCC | Limitation the number of roles related to any permission |
| MRCpermission | Threshold of the PCC |
| SMER | Static mutually exclusive roles |
| smer<{r1,r2,…,rt},t> | t-t SMER constraint |
| C | Set of the t-t SMER constraints |
| UC | Matrix of the user-capability constraints |
| CU | Cluster of users |
| VC | Set of the compression points |
| RR | Role-utilization ratio |
| 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 0 | 1 | 1 | 1 |
| p1 | p2 | p3 | p4 | p5 | p6 | |
| u1 | 0 | 0 | 0 | 1 | 0 | 1 |
| u2 | 1 | 1 | 0 | 1 | 0 | 0 |
| u3 | 0 | 0 | 0 | 0 | 1 | 1 |
| u4 | 1 | 1 | 0 | 1 | 0 | 0 |
| u5 | 0 | 1 | 1 | 1 | 0 | 1 |
| u6 | 0 | 0 | 0 | 0 | 1 | 1 |
| u7 | 0 | 0 | 1 | 0 | 0 | 1 |
| u8 | 0 | 1 | 1 | 0 | 0 | 1 |
| u9 | 1 | 0 | 1 | 0 | 0 | 1 |
| u10 | 0 | 0 | 0 | 1 | 1 | 0 |
| u11 | 1 | 1 | 0 | 1 | 1 | 0 |
| u12 | 0 | 1 | 1 | 1 | 0 | 0 |
| u13 | 0 | 1 | 1 | 1 | 0 | 0 |
| u14 | 0 | 1 | 0 | 1 | 0 | 0 |
| u15 | 1 | 0 | 1 | 0 | 0 | 1 |
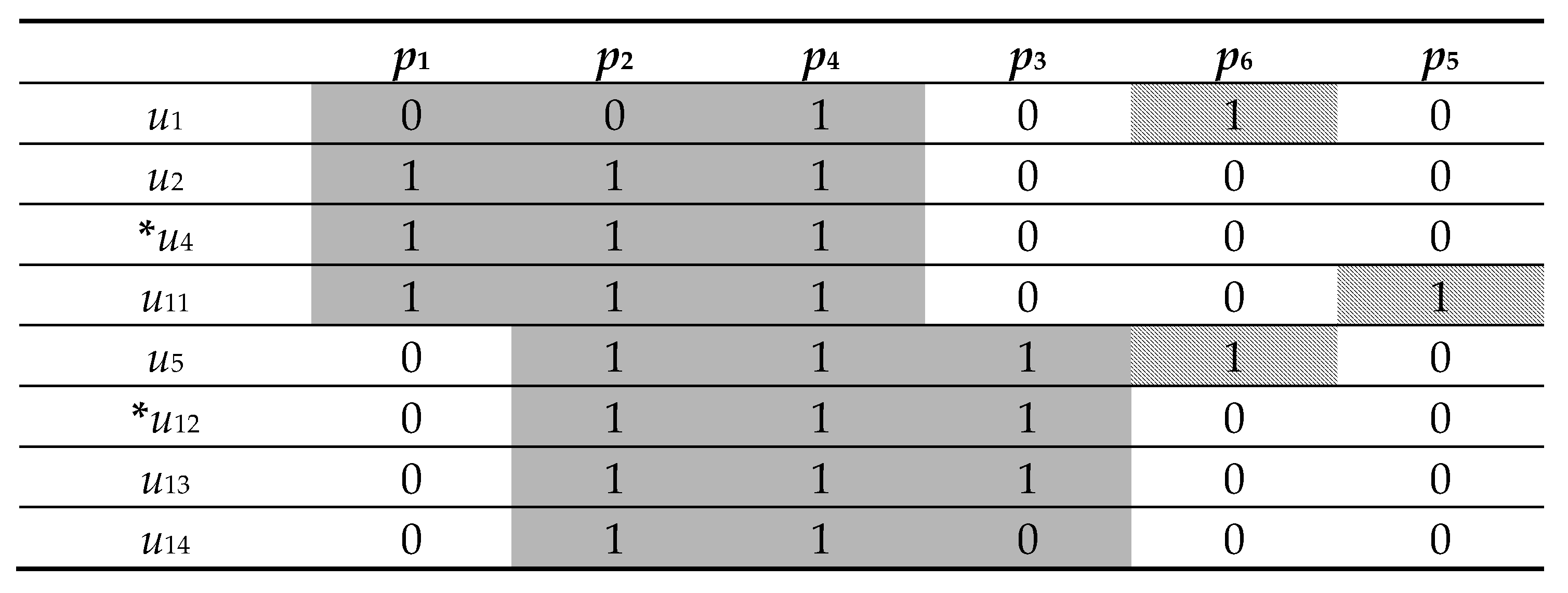
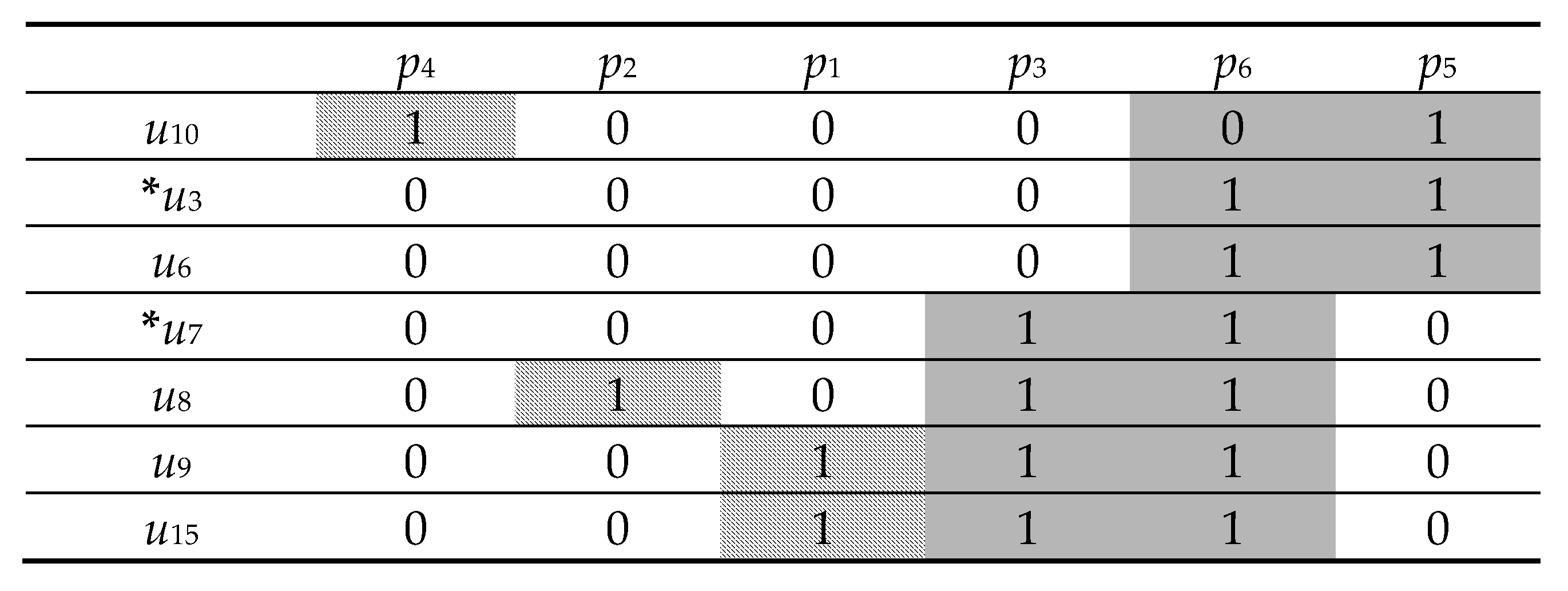
| p1 | p2 | p4 | p3 | p6 | p5 | |
| u1 | 0 | 0 | 1 | 0 | 0 | 0 |
| u4 | 1 | 1 | 1 | 0 | 0 | 0 |
| u12 | 0 | 1 | 1 | 1 | 0 | 0 |
| u14 | 0 | 1 | 1 | 0 | 0 | 0 |
| u3 | 0 | 0 | 0 | 0 | 1 | 1 |
| u7 | 0 | 0 | 0 | 1 | 1 | 0 |
| r1 | r2 | r3 | r4 | r5 | r6 | |
| u1 | 0 | 0 | 1 | 0 | 0 | 0 |
| u4 | 1 | 0 | 1 | 0 | 0 | 0 |
| u12 | 0 | 1 | 0 | 1 | 0 | 0 |
| u14 | 0 | 1 | 0 | 0 | 0 | 0 |
| u3 | 0 | 0 | 0 | 0 | 1 | 1 |
| u7 | 0 | 0 | 0 | 1 | 1 | 0 |
| p1 | p2 | p4 | p3 | p6 | p5 | |
| r1 | 1 | 1 | 0 | 0 | 0 | 0 |
| r2 | 0 | 1 | 1 | 0 | 0 | 0 |
| r3 | 0 | 0 | 1 | 0 | 0 | 0 |
| r4 | 0 | 0 | 0 | 1 | 0 | 0 |
| r5 | 0 | 0 | 0 | 0 | 1 | 0 |
| r6 | 0 | 0 | 0 | 0 | 0 | 1 |
| Role | Description |
|---|---|
| r1 | Software Designer |
| r2 | Software Developer |
| r3 | Software Tester |
| r4 | Accounts Manager |
| r5 | Financial Auditor |
| r1 | r2 | r3 | r4 | r5 | |
| u1 | 1 | 0 | 0 | 1 | 0 |
| u2 | 0 | 0 | 1 | 1 | 1 |
| u3 | 1 | 1 | 1 | 0 | 0 |
| u4 | 0 | 0 | 0 | 1 | 1 |
| u5 | 1 | 0 | 0 | 0 | 1 |
| u6 | 1 | 1 | 1 | 1 | 1 |
| r1 | r2 | r3 | r4 | r5 | |
| u1 | a11 | 0 | 0 | a14 | 0 |
| u2 | 0 | 0 | a23 | a24 | a25 |
| u3 | a31 | a32 | a33 | 0 | 0 |
| u4 | 0 | 0 | 0 | a44 | a45 |
| u5 | a51 | 0 | 0 | 0 | a55 |
| u6 | a61 | a62 | a63 | a64 | a65 |
| r1 | r2 | r3 | r4 | r5 | |
| u1 | a11 | 0 | 0 | 1 | 0 |
| u2 | 0 | 0 | a23 | 1 | 0 |
| u3 | a31 | a32 | a33 | 0 | 0 |
| u4 | 0 | 0 | 0 | 1 | 0 |
| u5 | a51 | 0 | 0 | 0 | a55 |
| u6 | a61 | a62 | a63 | 1 | 0 |
| r1 | r2 | r3 | r4 | r5 | |
| u1 | a11 | 0 | 0 | 1 | 0 |
| u2 | 0 | 0 | a23 | 1 | 0 |
| u3 | a31 | a32 | a33 | 0 | 0 |
| u4 | 0 | 0 | 0 | 1 | 0 |
| u5 | a51 | 0 | 0 | 0 | 1 |
| u6 | a61 | a62 | a63 | 1 | 0 |
| r1 | r2 | r3 | r4 | r5 | |
| u1 | 1 | 0 | 0 | 1 | 0 |
| u2 | 0 | 0 | a23 | 1 | 0 |
| u3 | 1 | a32 | 0 | 0 | 0 |
| u4 | 0 | 0 | 0 | 1 | 0 |
| u5 | 1 | 0 | 0 | 0 | 1 |
| u6 | 1 | a62 | 0 | 1 | 0 |
| r1 | r2 | r3 | r4 | r5 | |
| u1 | 1 | 0 | 0 | 1 | 0 |
| u2 | 0 | 0 | a23 | 1 | 0 |
| u3 | 1 | 1 | 0 | 0 | 0 |
| u4 | 0 | 0 | 0 | 1 | 0 |
| u5 | 1 | 0 | 0 | 0 | 1 |
| u6 | 1 | 0 | 0 | 1 | 0 |
| r1 | r2 | r3 | r4 | r5 | |
| u1 | 1 | 0 | 0 | 1 | 0 |
| u2 | 0 | 0 | 1 | 1 | 0 |
| u3 | 1 | 1 | 0 | 0 | 0 |
| u4 | 0 | 0 | 0 | 1 | 0 |
| u5 | 1 | 0 | 0 | 0 | 1 |
| u6 | 1 | 0 | 0 | 1 | 0 |
| Step | Candidate Role | Identified aij | Assigned Users | Updated Q |
|---|---|---|---|---|
| 1 | r4 | a14, a24, a44, a64, a25, a45, a65 | u1,u2,u4,u6 | {r5,r1,r2,r3} |
| 2 | r5 | a55 | u5 | {r1,r2,r3} |
| 3 | r1 | a11, a31, a51, a61, a33, a63 | u1,u3,u5,u6 | {r2,r3} |
| 4 | r2 | a32, a62 | u3 | {r3} |
| 5 (finish) | r3 | a23 | u2 | Φ |
| Dataset | |U| | |P| | |UPA| | Density | |CR| | Execution Time(s) |
|---|---|---|---|---|---|---|
| America-large | 3485 | 10,127 | 185,294 | 0.5% | 423 | 78.78 |
| America-small | 3477 | 1587 | 105,205 | 1.9% | 213 | 6.31 |
| Apj | 2044 | 1164 | 6841 | 0.3% | 456 | 5.60 |
| Customer | 10,961 | 284 | 45,427 | 1.5% | 276 | 4.66 |
| Domino | 79 | 231 | 730 | 4% | 20 | 0.01 |
| Emea | 35 | 3046 | 7,20 | 6.8% | 34 | 0.02 |
| Firewall1 | 365 | 709 | 31,951 | 12.3% | 69 | 0.11 |
| Firewall2 | 325 | 590 | 36,428 | 19% | 10 | 0.15 |
| Healthcare | 46 | 46 | 1486 | 70% | 15 | 0.01 |
| University1 | 493 | 56 | 3955 | 14.3% | 31 | 0.01 |
| University2 | 400 | 14 | 3073 | 54.9% | 15 | 0.01 |
| MRCpermission | MRCuser | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6 | 5 | 4 | 3 | |||||||||||||
| (1) | (2) | (3) | (4) | (1) | (2) | (3) | (4) | (1) | (2) | (3) | (4) | (1) | (2) | (3) | (4) | |
| 145 | 423 | 423 | 423 | 423 | 424 | 424 | 424 | 424 | 425 | 425 | 425 | 425 | x | x | x | x |
| 140 | 424 | 424 | 425 | 425 | 425 | 425 | 426 | 426 | 427 | 428 | 428 | 428 | x | x | x | x |
| 130 | 424 | 424 | 425 | 425 | 425 | 425 | 426 | 426 | 427 | 428 | 428 | 428 | x | x | x | x |
| 120 | 425 | 427 | 427 | 427 | 426 | 428 | 428 | 428 | 427 | 431 | 429 | 429 | x | x | x | x |
| 110 | 427 | 431 | 428 | 428 | 428 | 433 | 429 | 429 | 427 | 433 | 431 | 431 | x | x | x | x |
| 100 | 428 | 435 | 431 | 431 | 429 | 437 | 432 | 432 | 433 | 437 | 435 | 435 | x | x | x | x |
| MRCpermission | MRCuser | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 13 | 11 | 9 | 7 | |||||||||||||
| (1) | (2) | (3) | (4) | (1) | (2) | (3) | (4) | (1) | (2) | (3) | (4) | (1) | (2) | (3) | (4) | |
| 69 | 456 | 456 | 456 | 456 | 457 | 457 | 457 | 457 | 457 | 459 | 458 | 458 | 461 | 463 | 465 | 465 |
| 65 | 457 | 457 | 457 | 457 | 458 | 458 | 458 | 458 | 458 | 460 | 459 | 459 | 462 | 464 | 466 | 466 |
| 55 | 458 | 460 | 459 | 459 | 459 | 461 | 460 | 460 | 461 | 463 | 461 | 461 | x | x | 467 | 469 |
| 45 | 459 | 462 | 460 | 460 | 460 | 463 | 461 | 461 | 463 | 467 | 462 | 462 | x | x | x | x |
| 35 | 460 | 462 | 460 | 460 | 461 | 463 | 462 | 462 | x | 468 | x | x | x | x | x | x |
| 25 | 460 | 463 | 462 | 462 | 461 | 463 | 462 | 462 | x | 469 | x | x | x | x | x | x |
| MRCpermission | MRCuser | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 21 | 17 | 13 | 9 | |||||||||||||
| (1) | (2) | (3) | (4) | (1) | (2) | (3) | (4) | (1) | (2) | (3) | (4) | (1) | (2) | (3) | (4) | |
| 27 | 69 | 69 | 69 | 69 | 70 | 70 | 70 | 70 | 71 | 71 | 71 | 71 | 73 | 75 | 73 | 73 |
| 25 | 70 | 70 | 70 | 70 | 71 | 71 | 71 | 71 | 72 | 72 | 72 | 72 | 74 | 76 | 74 | 74 |
| 22 | 70 | 71 | 71 | 71 | 72 | 73 | 72 | 72 | 73 | 73 | 74 | 74 | x | 77 | 75 | 75 |
| 18 | 71 | 72 | 73 | 73 | 73 | 74 | 74 | 74 | 74 | 75 | 76 | 76 | x | x | x | x |
| 15 | 72 | 73 | 74 | 74 | 74 | 75 | 75 | 75 | 75 | 76 | 77 | 77 | x | x | x | x |
| 11 | 73 | 74 | 75 | 75 | 75 | 76 | 76 | 76 | x | 77 | 78 | 78 | x | x | x | x |
| MRCpermission | MRCuser | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9 | 8 | 7 | 6 | |||||||||||||
| (1) | (2) | (3) | (4) | (1) | (2) | (3) | (4) | (1) | (2) | (3) | (4) | (1) | (2) | (3) | (4) | |
| 3 | 10 | 10 | 10 | 10 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | x | x | x | x |
| 2 | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x |
| Characteristic | Kumar et al. [35] Blundo et al. [36] | Hingankar et al. [37] | John et al. [38] | Ma et al. [26] | Sarana et al. [40] | Harika et al. [39] | Roy et al. [28] | Proposed Method |
|---|---|---|---|---|---|---|---|---|
| UCC | √ | √ | √ | √ | ||||
| PCC | √ | √ | ||||||
| RUC | √ | √ | ||||||
| RPC | √ | √ | ||||||
| SMER | √ | √ | √ | |||||
| User-Capability Constraints | √ | √ | ||||||
| Unknown System Status | √ | √ | √ | √ | √ | √ | √ |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Su, H.; Liu, H. Role-Engineering Optimization with Cardinality Constraints and User-Oriented Mutually Exclusive Constraints. Information 2019, 10, 342. https://doi.org/10.3390/info10110342
Sun W, Su H, Liu H. Role-Engineering Optimization with Cardinality Constraints and User-Oriented Mutually Exclusive Constraints. Information. 2019; 10(11):342. https://doi.org/10.3390/info10110342
Chicago/Turabian StyleSun, Wei, Hui Su, and Hongbing Liu. 2019. "Role-Engineering Optimization with Cardinality Constraints and User-Oriented Mutually Exclusive Constraints" Information 10, no. 11: 342. https://doi.org/10.3390/info10110342
APA StyleSun, W., Su, H., & Liu, H. (2019). Role-Engineering Optimization with Cardinality Constraints and User-Oriented Mutually Exclusive Constraints. Information, 10(11), 342. https://doi.org/10.3390/info10110342





