Automatic Wireless Signal Classification: A Neural-Induced Support Vector Machine-Based Approach
Abstract
1. Introduction
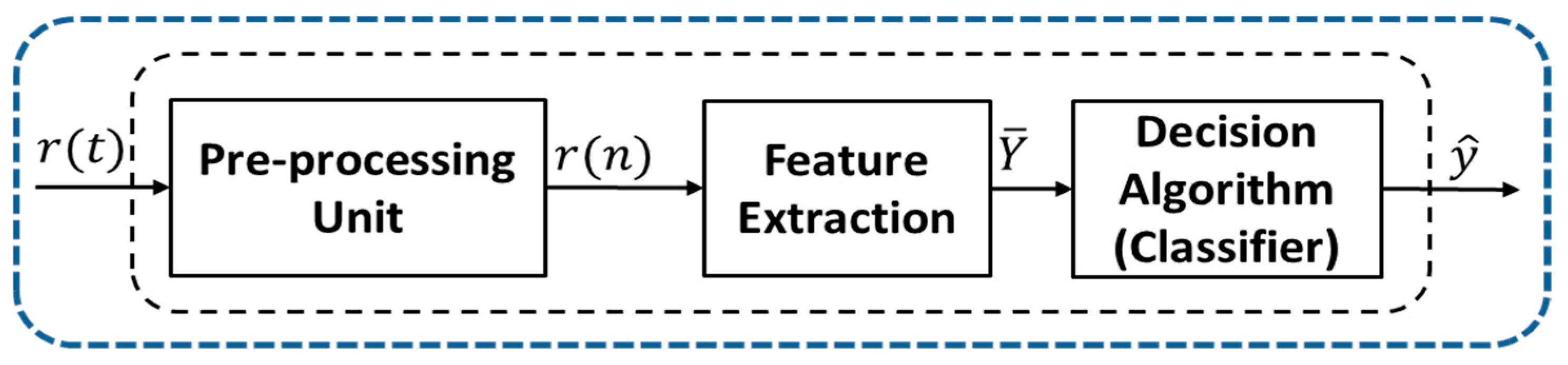
2. Signal Model and Problem Statement
3. Convolutional Neural Networks (CNN), Support Vector Machine (SVM) and Neural-Induced Support Vector Machine (NSVM)
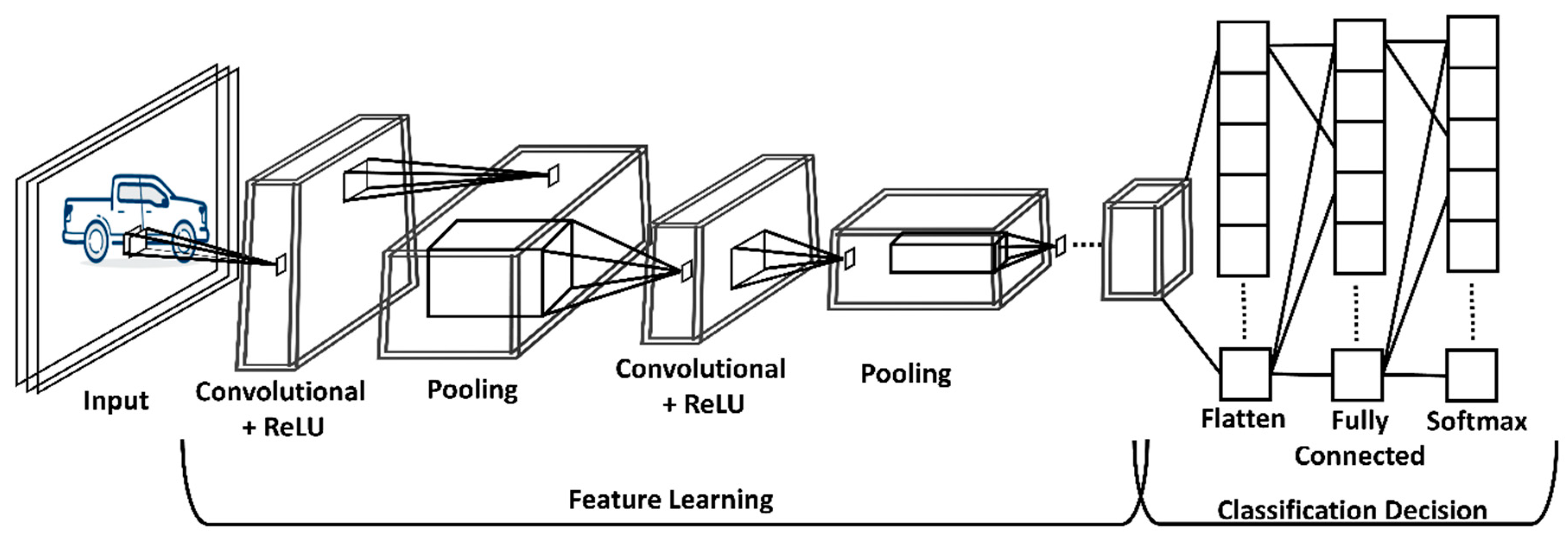
3.1. Convolutional Neural Networks
3.1.1. Input Layer
3.1.2. Convolutional Layer
3.1.3. Pooling Layer
3.1.4. Fully Connected Layer
3.1.5. SoftMax Layer
3.1.6. Loss Function
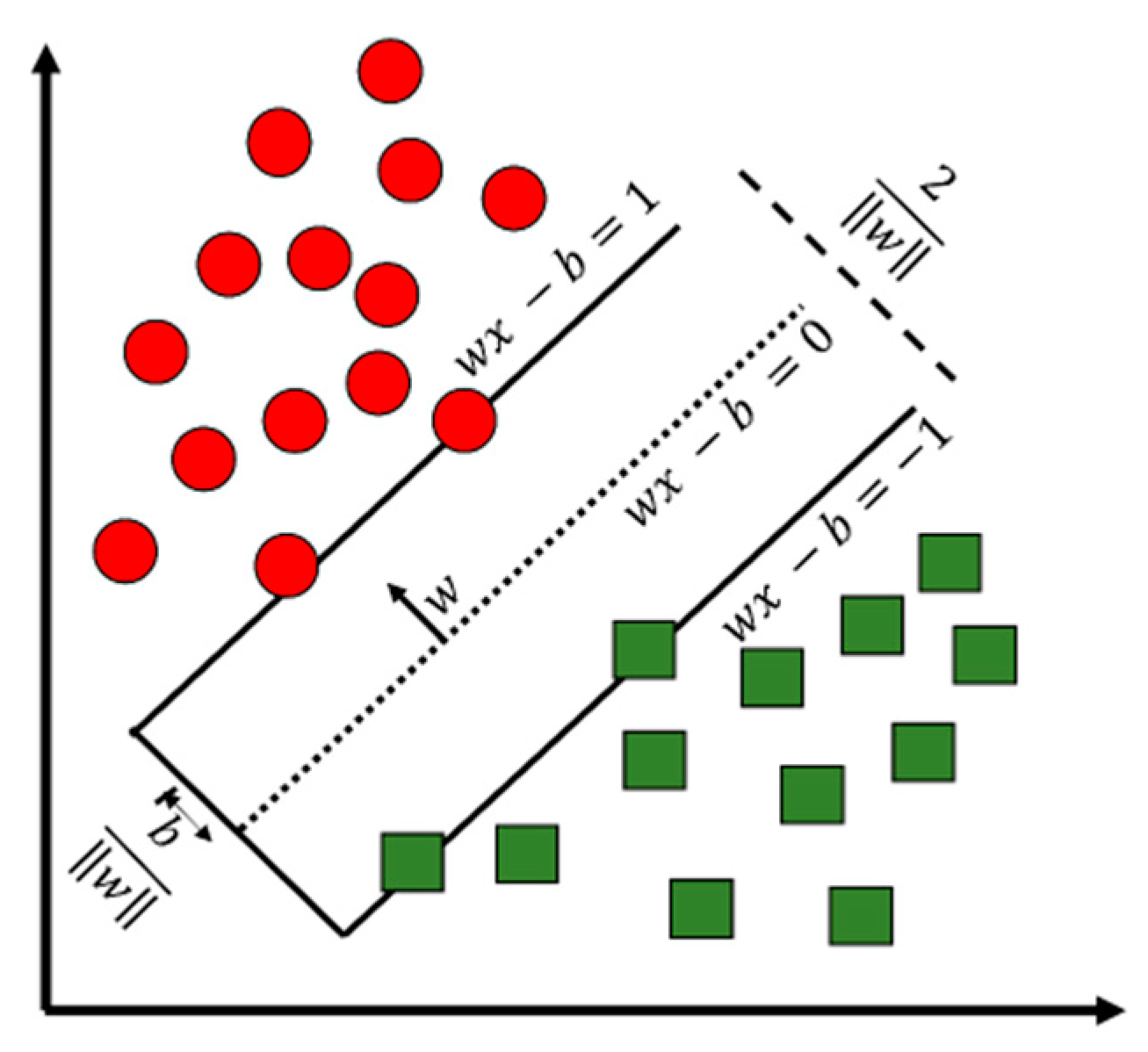
3.2. Support Vector Machine
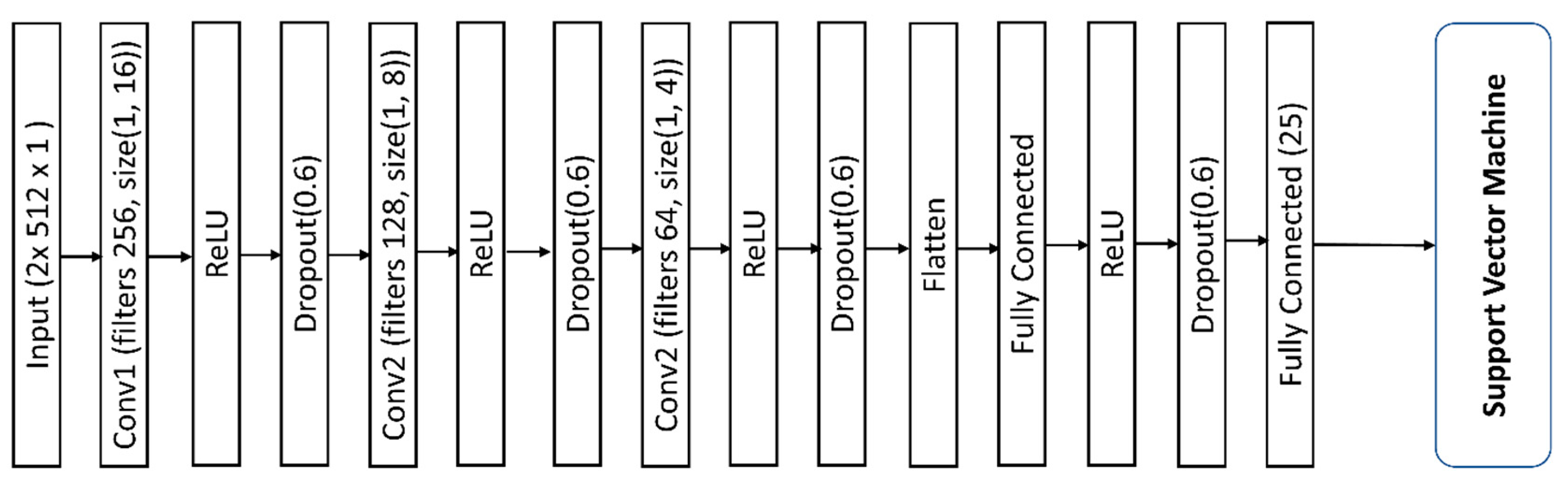
3.3. Neural-Induced Support Vector Machine (NSVM)
4. Simulation Results and Discussion
4.1. Dataset
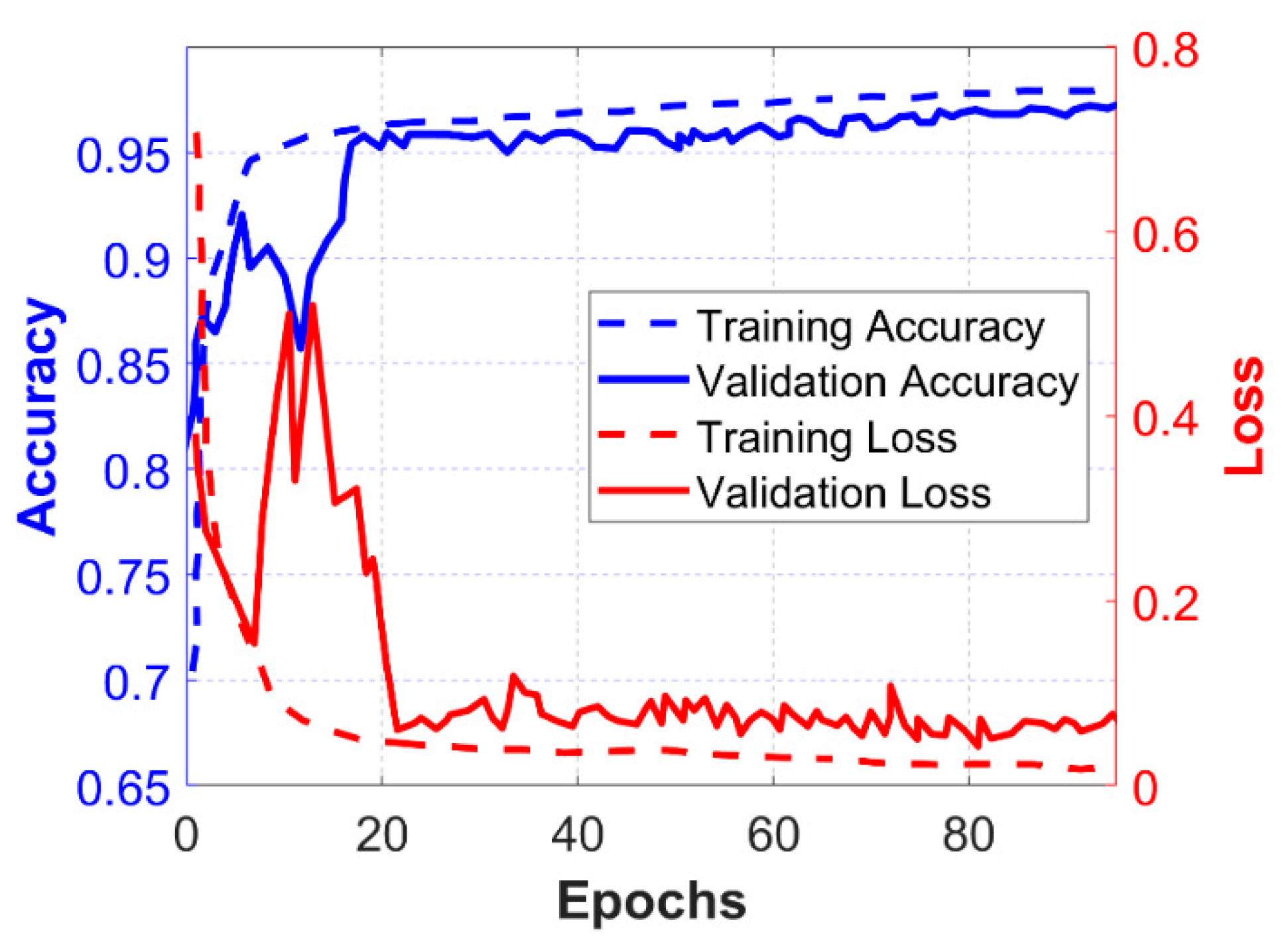
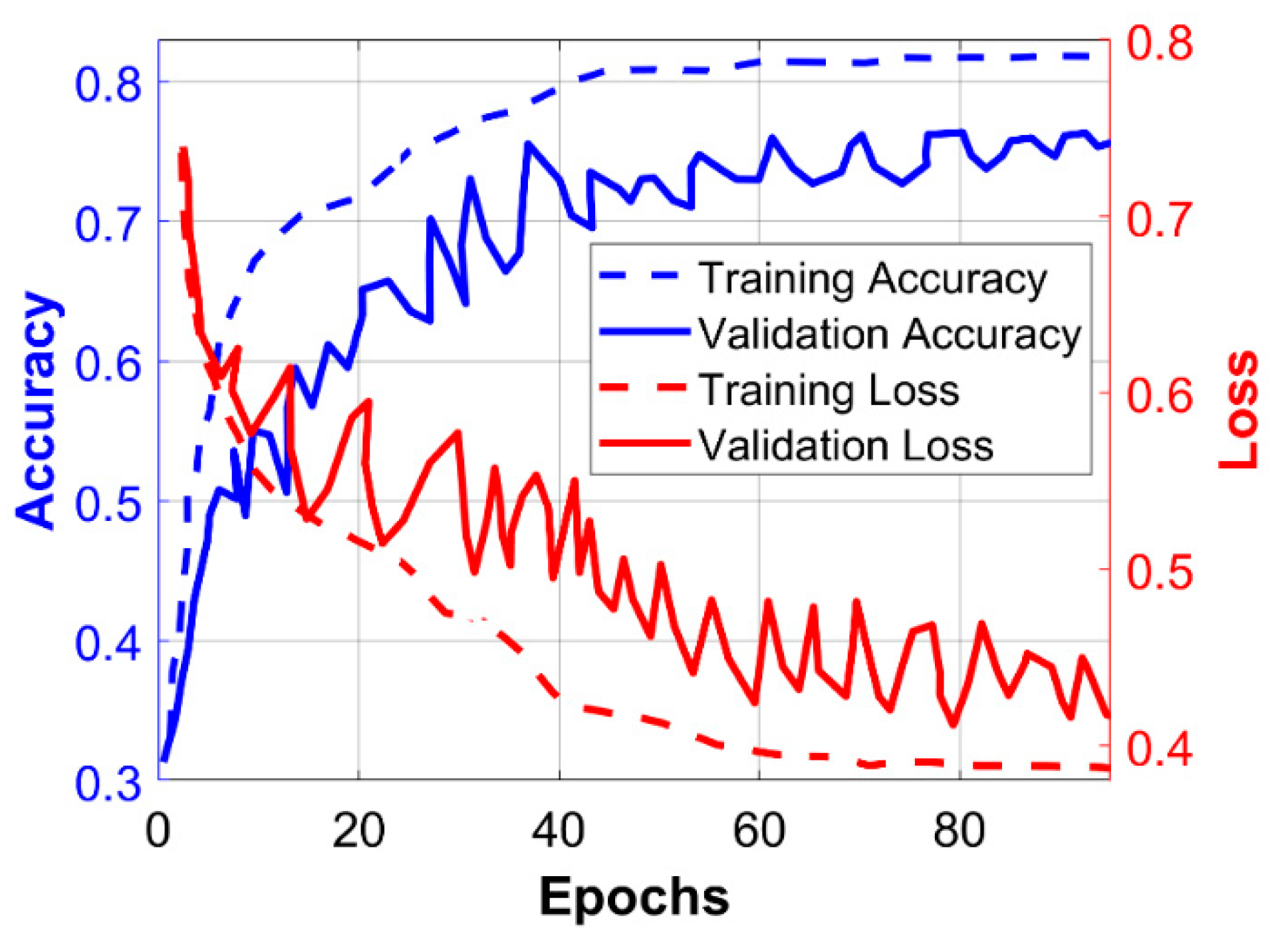
4.2. Training and Validation Performance
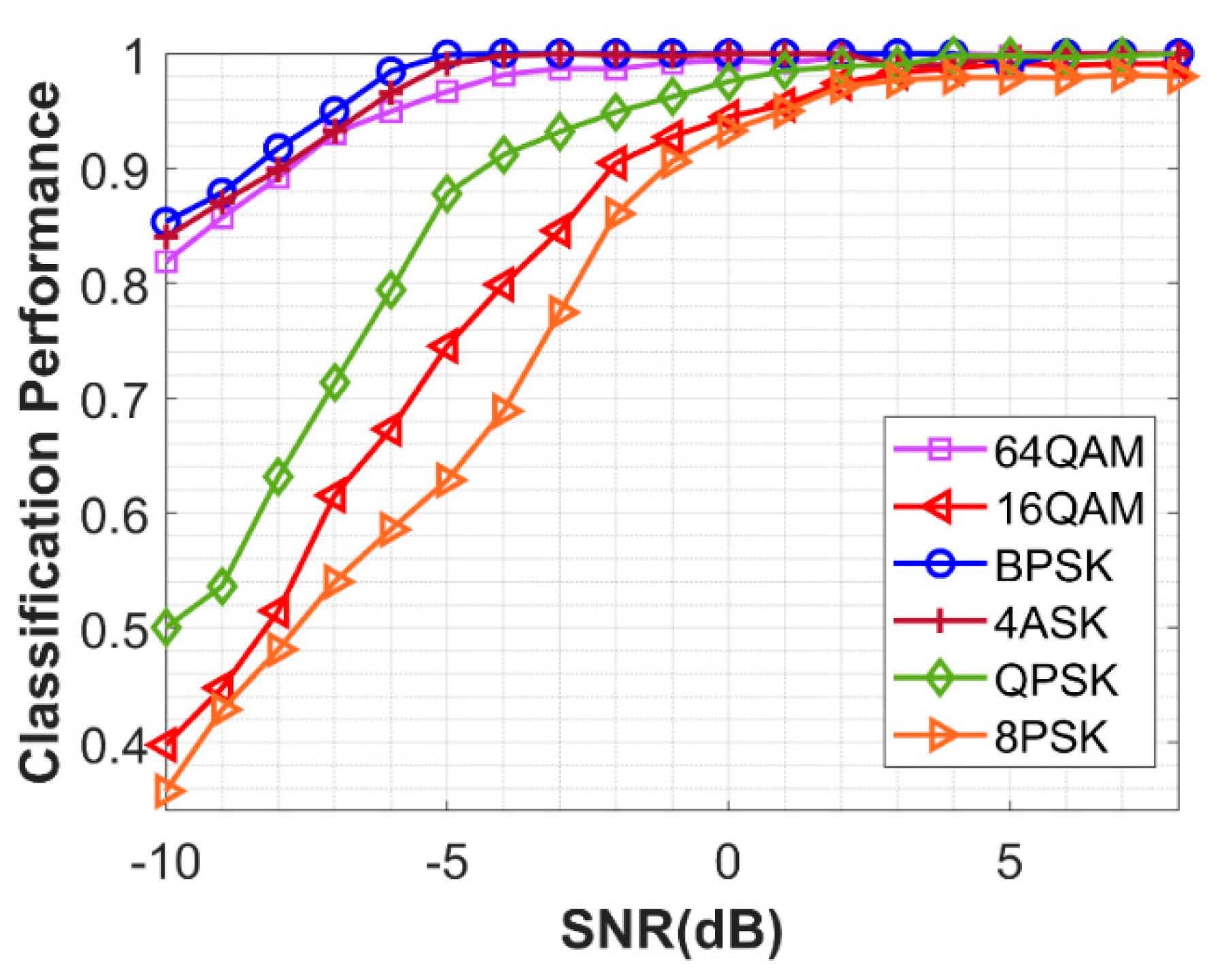
4.3. Basic Classification Performance
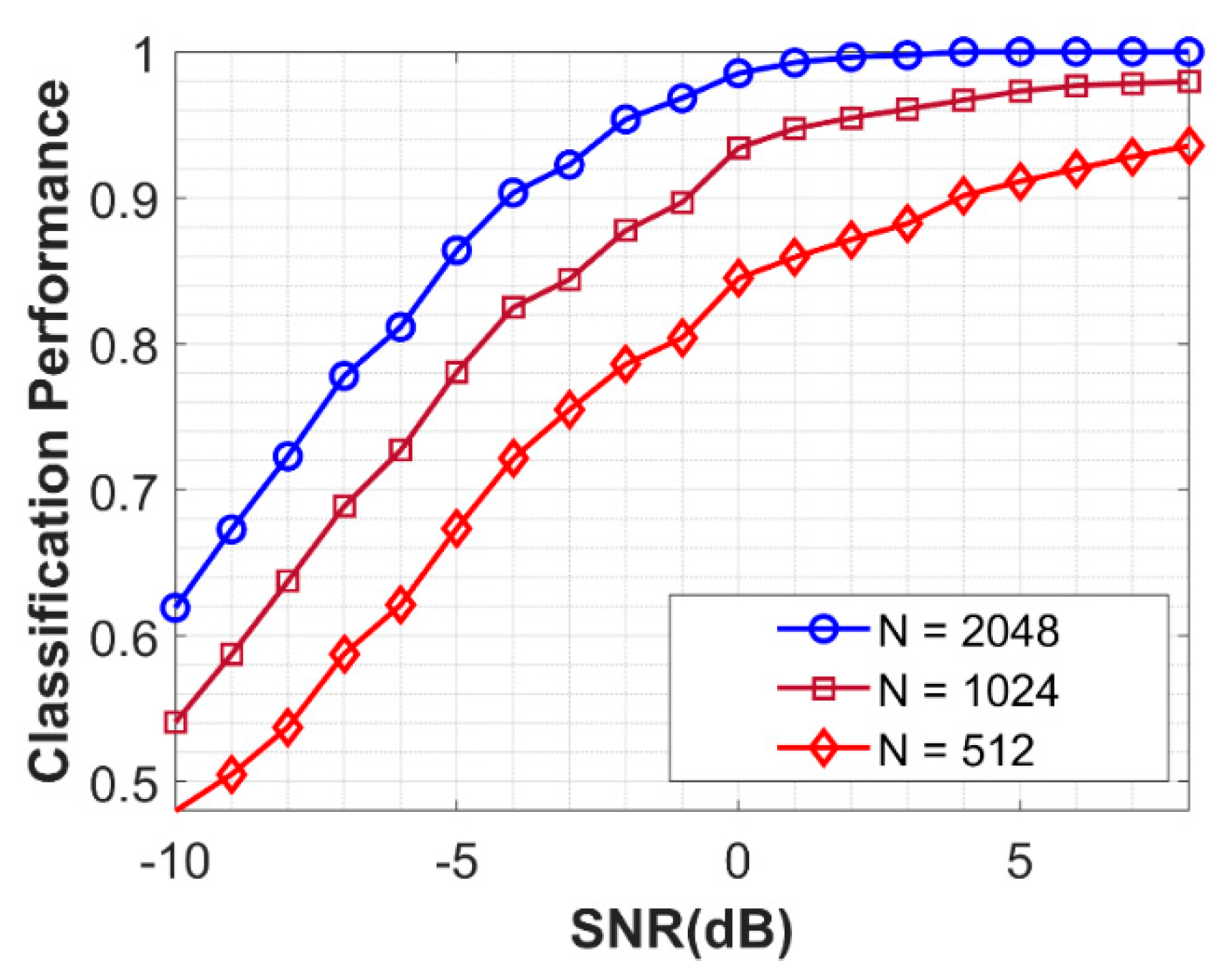
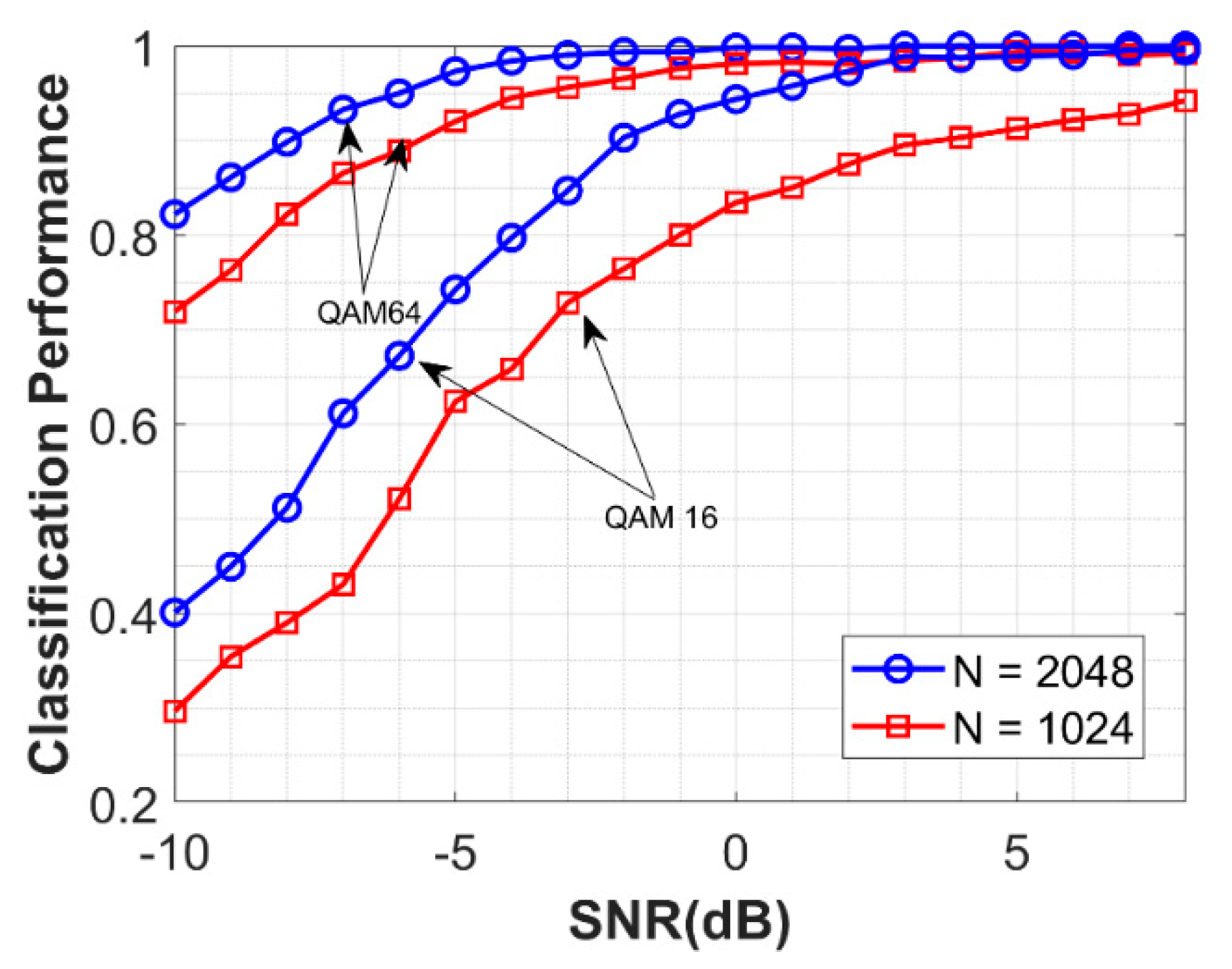
4.4. Performance of NSVM with Different N
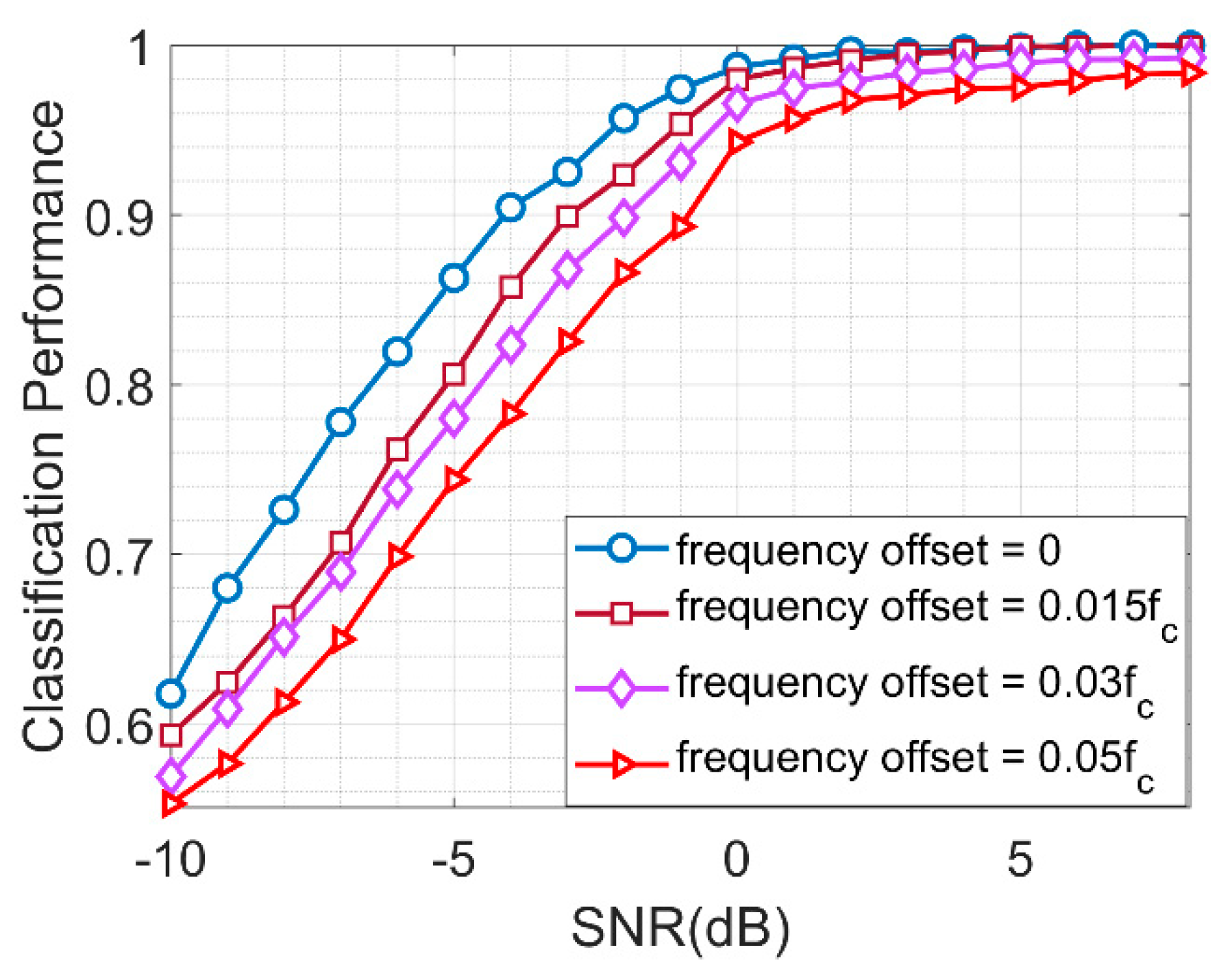
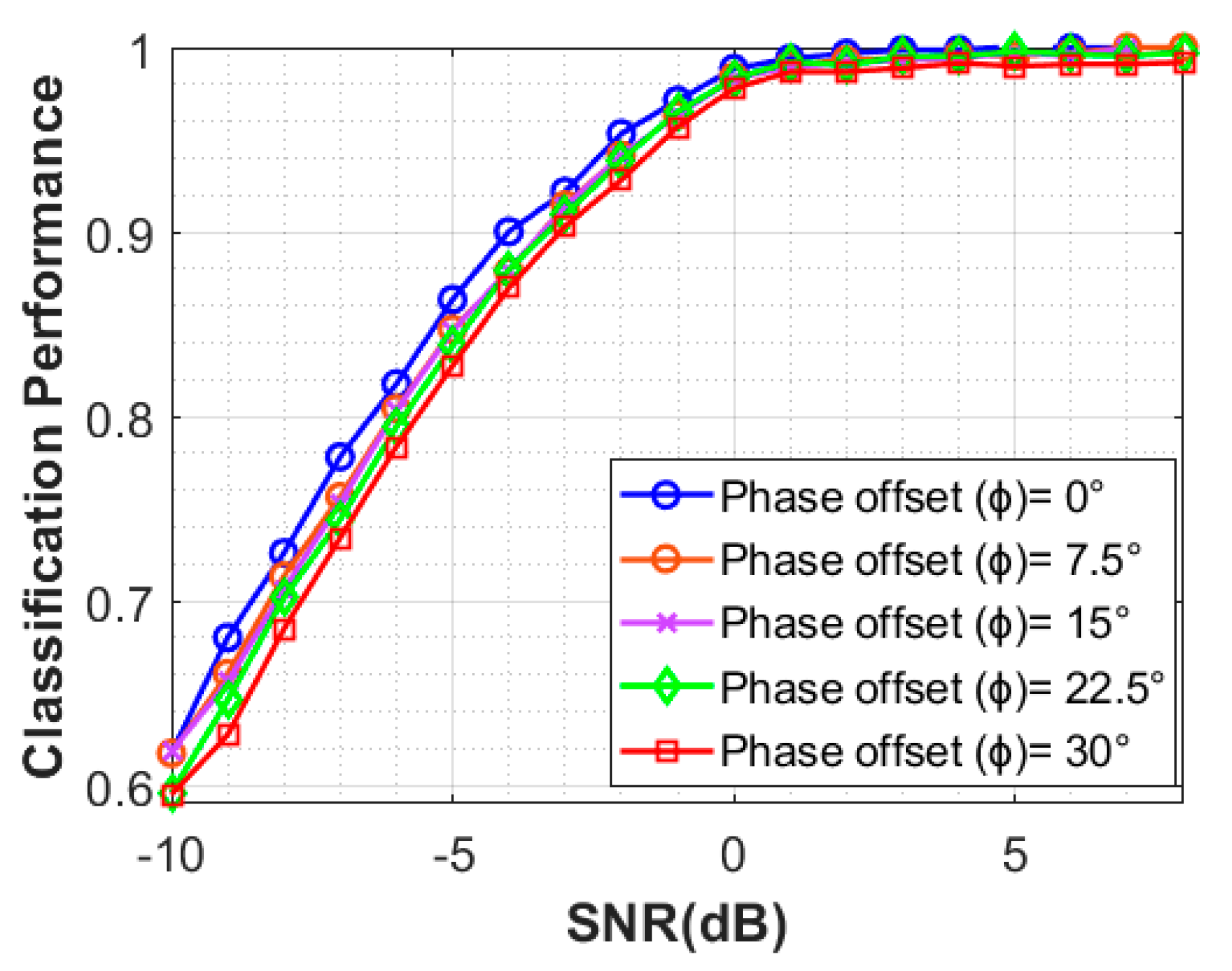
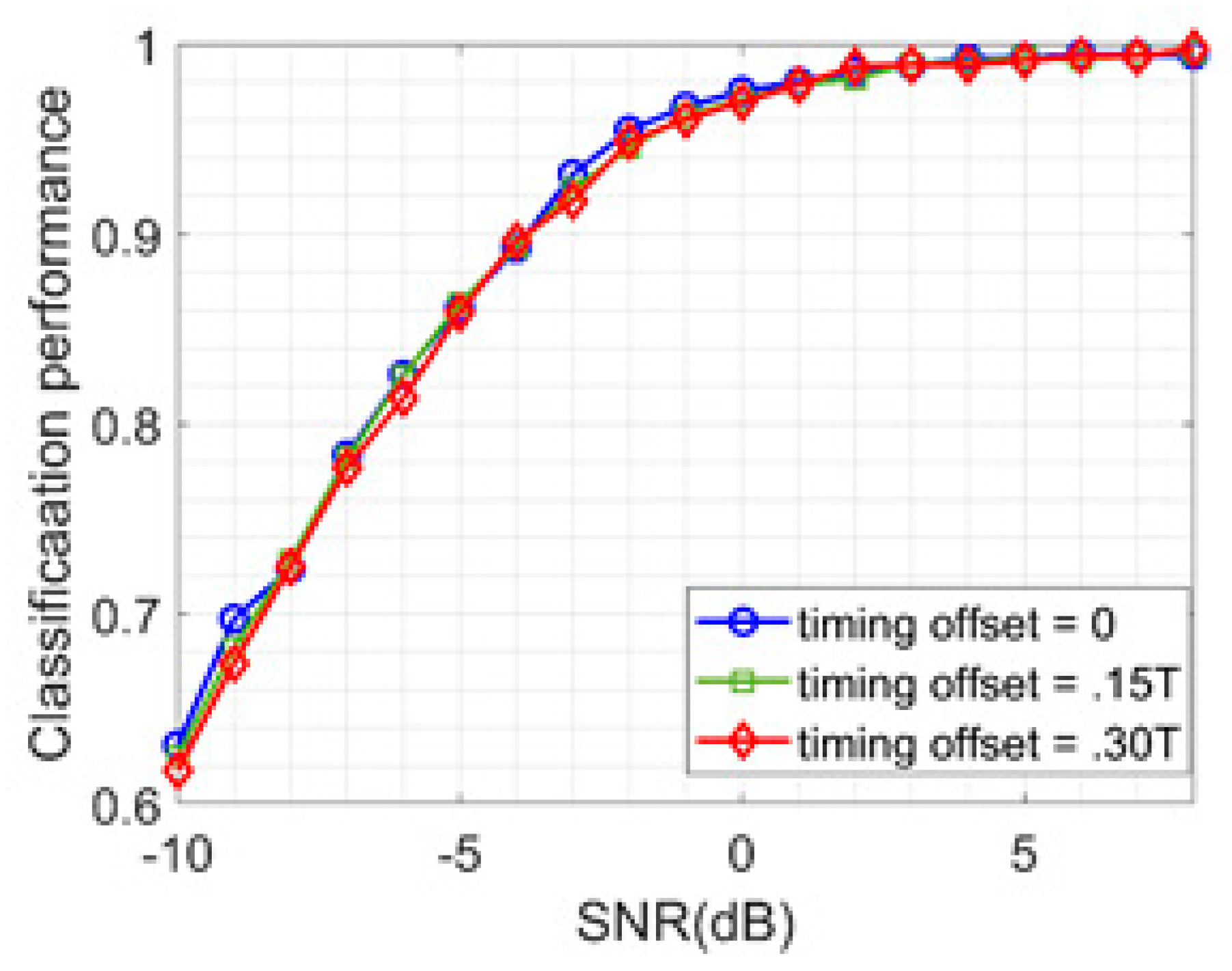
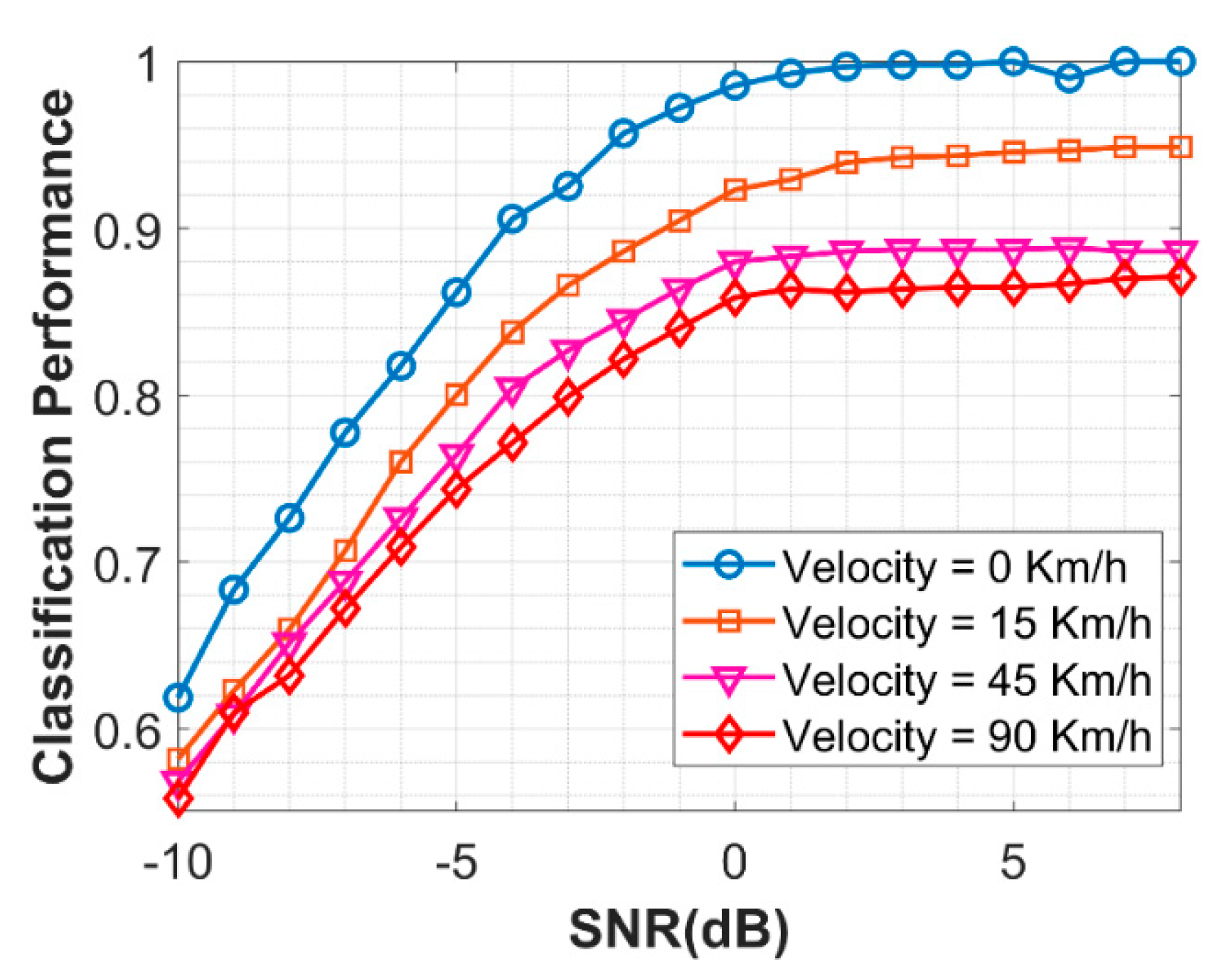
4.5. Performance of NSVM with Different Channel Impairments
4.6. Comparative Study of Related Works
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Qian, G.; Ruan, Z.; Lu, J. Joint modulation classification and user number detection for multiuser MIMO-STBC systems. Information 2016, 7, 70. [Google Scholar] [CrossRef]
- Dobre, O.A.; Abdi, A.; Bar-Ness, Y.; Su, W. Survey of automatic modulation classification techniques: Classical approaches and new trends. IET Commun. 2007, 1, 137–156. [Google Scholar] [CrossRef]
- Dobre, O.A.; Hameed, F. Likelihood-based algorithms for linear digital modulation classification in fading channels. In Proceedings of the 2006 Canadian Conference on Electrical and Computer Engineering, Ottawa, ON, Canada, 7–10 May 2006; pp. 1347–1350. [Google Scholar]
- Panagiotou, P.; Anastasopoulos, A.; Polydoros, A. Likelihood ratio tests for modulation classification. In Proceedings of the MILCOM 2000 Proceedings. 21st Century Military Communications. Architectures and Technologies for Information Superiority (Cat. No. 00CH37155), Los Angeles, CA, USA, 22–25 October 2000; pp. 670–674. [Google Scholar]
- Xu, J.L.; Su, W.; Zhou, M. Likelihood-ratio approaches to automatic modulation classification. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2010, 41, 455–469. [Google Scholar] [CrossRef]
- Azzouz, E.E.; Nandi, A.K. Automatic identification of digital modulation types. Signal Process. 1995, 47, 55–69. [Google Scholar] [CrossRef]
- Swami, A.; Sadler, B.M. Hierarchical digital modulation classification using cumulants. IEEE Trans. Commun. 2000, 48, 416–429. [Google Scholar] [CrossRef]
- Wang, Y.-E.; Zhang, T.-Q.; Bai, J.; Bao, R. Modulation recognition algorithms for communication signals based on particle swarm optimization and support vector machines. In Proceedings of the 2011 Seventh International Conference on Intelligent Information Hiding and Multimedia Signal Processing, Dalian, China, 14–16 October 2011; pp. 266–269. [Google Scholar]
- Yu, Z. Automatic Modulation Classification of Communication Signals. New Jersey Institute of Technology 2006. Available online: https://digitalcommons.njit.edu/cgi/viewcontent.cgi?article=1848&context=dissertations (accessed on 30 October 2019).
- Zhu, Z.; Nandi, A.K. Automatic Modulation Classification: Principles, Algorithms and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Gang, H.; Jiandong, L.; Donghua, L. Study of modulation recognition based on HOCs and SVM. In Proceedings of the 2004 IEEE 59th Vehicular Technology Conference, VTC 2004-Spring (IEEE Cat. No. 04CH37514), Milan, Italy, 17–19 May 2004; pp. 898–902. [Google Scholar]
- Aslam, M.W.; Zhu, Z.; Nandi, A.K. Automatic modulation classification using combination of genetic programming and KNN. IEEE Trans. Wirel. Commun. 2012, 11, 2742–2750. [Google Scholar]
- Berman, D.S.; Buczak, A.L.; Chavis, J.S.; Corbett, C.L. A survey of deep learning methods for cyber security. Information 2019, 10, 122. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Jarrett, K.; Kavukcuoglu, K.; Ranzato, M.A.; LeCun, Y. What is the best multi-stage architecture for object recognition? In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 2146–2153. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–8 December 2012; pp. 1097–1105. [Google Scholar]
- Jiao, Y.; Latifi, S.; Yang, M. Self error detection and correction for noisy labels based on error correcting output code in convolutional neural networks. In Proceedings of the 2019 IEEE 9th Annual Computing and Communication Workshop and Conference (CCWC 2019), Las Vegas, NV, USA, 7–9 January 2019; pp. 0311–0316. [Google Scholar]
- Dahl, G.E.; Yu, D.; Deng, L.; Acero, A. Context-dependent pre-trained deep neural networks for large-vocabulary speech recognition. IEEE Trans. Audio Speech Lang. Process. 2011, 20, 30–42. [Google Scholar] [CrossRef]
- Wallach, I.; Dzamba, M.; Heifets, A. AtomNet: A deep convolutional neural network for bioactivity prediction in structure-based drug discovery. arXiv 2015, arXiv:1510.02855. [Google Scholar]
- Amato, F.; Marrone, S.; Moscato, V.; Piantadosi, G.; Picariello, A.; Sansone, C. HOLMeS: Ehealth in the big data and deep learning era. Information 2019, 10, 34. [Google Scholar] [CrossRef]
- O’Shea, T.J.; Roy, T.; Clancy, T.C. Over-the-air deep learning based radio signal classification. IEEE J. Sel. Top. Signal Process. 2018, 12, 168–179. [Google Scholar] [CrossRef]
- O’Shea, T.; Hoydis, J. An introduction to deep learning for the physical layer. IEEE Trans. Cogn. Commun. Netw. 2017, 3, 563–575. [Google Scholar] [CrossRef]
- Li, M.; Li, O.; Liu, G.; Zhang, C. Generative adversarial networks-based semi-supervised automatic modulation recognition for cognitive radio networks. Sensors 2018, 18, 3913. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Wu, Z.; Ma, S.; Lu, S.; Zhang, H.; Ding, G.; Li, S. Deep learning for signal demodulation in physical layer wireless communications: Prototype platform, open dataset, and analytics. IEEE Access 2019, 7, 30792–30801. [Google Scholar] [CrossRef]
- Liang, Y.; Xiang, X.; Sun, Y.; Da, X.; Li, C.; Yin, L. Novel modulation recognition for WFRFT-based system using 4th-order cumulants. IEEE Access 2019, 7, 86018–86025. [Google Scholar] [CrossRef]
- Zhou, S.; Yin, Z.; Wu, Z.; Chen, Y.; Zhao, N.; Yang, Z. A robust modulation classification method using convolutional neural networks. EURASIP J. Adv. Signal Process. 2019, 2019, 21. [Google Scholar] [CrossRef]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Agarap, A.F. An architecture combining convolutional neural network (CNN) and support vector machine (SVM) for image classification. arXiv 2017, arXiv:1712.03541. [Google Scholar]
- Huang, F.-J.; LeCun, Y. Large-scale learning with svm and convolutional nets for generic object categorization. In Proceedings of the Proc. Computer Vision and Pattern Recognition Conference (CVPR’06), New York, NY, USA, 17–22 June 2006. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Zhang, M.; Diao, M.; Guo, L. Convolutional neural networks for automatic cognitive radio waveform recognition. IEEE Access 2017, 5, 11074–11082. [Google Scholar] [CrossRef]
| Parameters | Symbols | Values |
|---|---|---|
| Carrier Frequency | 10 MHz | |
| Number of Samples per input frame | N | 2048 |
| SNR | −10 dB to 8 dB | |
| Symbols per Frame | 256 | |
| Samples per Symbol | 8 |
| SNR = −4 dB | True Class | ||||||
|---|---|---|---|---|---|---|---|
| Predicted Class | BPSK | 4-ASK | QPSK | 16-QAM | 64-QAM | 8-PSK | |
| BPSK | 100 | ||||||
| 4-ASK | 100 | ||||||
| QPSK | 91.18 | 8.82 | |||||
| 16-QAM | 79.90 | 7.67 | 12.43 | ||||
| 64-QAM | 1.83 | 98.17 | |||||
| 8-PSK | 18.87 | 12.26 | 68.87 | ||||
| SNR = 0 dB | True Class | ||||||
|---|---|---|---|---|---|---|---|
| Predicted Class | BPSK | 4-ASK | QPSK | 16-QAM | 64-QAM | 8-PSK | |
| BPSK | 100 | ||||||
| 4-ASK | 100 | ||||||
| QPSK | 95.57 | 2.43 | |||||
| 16-QAM | 94.49 | 1.28 | 4.23 | ||||
| 64-QAM | 0.54 | 99.46 | |||||
| 8-PSK | 5.87 | 0.85 | 93.28 | ||||
| Classifier | Modulations | SNR | Accuracy |
|---|---|---|---|
| Artificial Neural Networks Based on spectral features [6] NSVM | BPSK, QPSK, 8PSK, QAM16, QAM 64 | −5 dB −5 dB | 83.7% 86.3% |
| Deep BeliefNetworks (DBN)-SVM [24], KNNAdaBoost [24] NSVM | BPSK, QPSK, QAM16, QAM 64 | 8 dB 8 dB 8 dB | 75.5% 89.9% 99.8% |
| Convolution Neural Networks [31] NSVM | 2FSK, DQPSK, 16AM, MSK, GMSK | 0 dB 0 dB | 83.5% 98.2% |
| GPKNN [12] NSVM | BPSK, QPSK, QAM16, QAM 64 | 10 dB 10 dB | 97% 99.9% |
| Convolutional Neural Networks with Cumulants [25] NSVM | BPSK, QPSK, 8PSK, 4ASK, QAM16, QAM 64 | 6 dB 6 dB | 90% 99% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wahla, A.H.; Chen, L.; Wang, Y.; Chen, R. Automatic Wireless Signal Classification: A Neural-Induced Support Vector Machine-Based Approach. Information 2019, 10, 338. https://doi.org/10.3390/info10110338
Wahla AH, Chen L, Wang Y, Chen R. Automatic Wireless Signal Classification: A Neural-Induced Support Vector Machine-Based Approach. Information. 2019; 10(11):338. https://doi.org/10.3390/info10110338
Chicago/Turabian StyleWahla, Arfan Haider, Lan Chen, Yali Wang, and Rong Chen. 2019. "Automatic Wireless Signal Classification: A Neural-Induced Support Vector Machine-Based Approach" Information 10, no. 11: 338. https://doi.org/10.3390/info10110338
APA StyleWahla, A. H., Chen, L., Wang, Y., & Chen, R. (2019). Automatic Wireless Signal Classification: A Neural-Induced Support Vector Machine-Based Approach. Information, 10(11), 338. https://doi.org/10.3390/info10110338





