Automatic Diagnosis of Neurodegenerative Diseases: An Evolutionary Approach for Facing the Interpretability Problem
Abstract
:1. Introduction
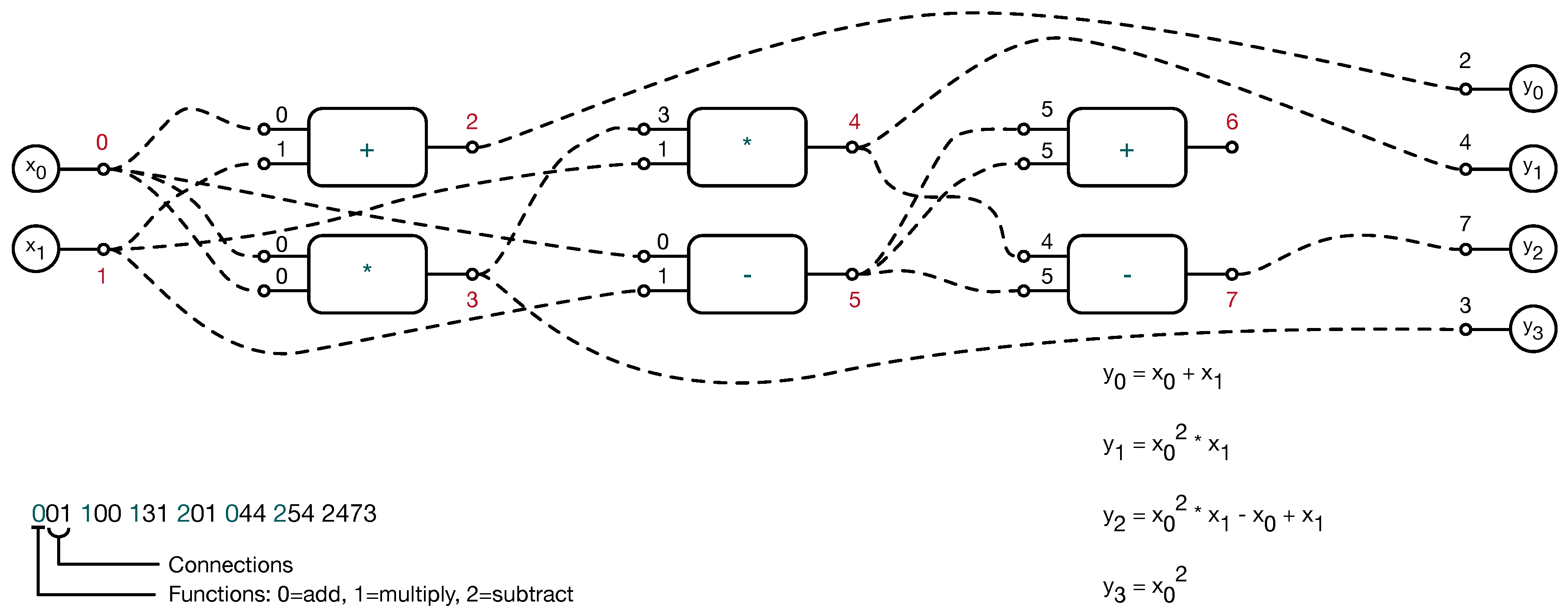
2. The Proposed Method
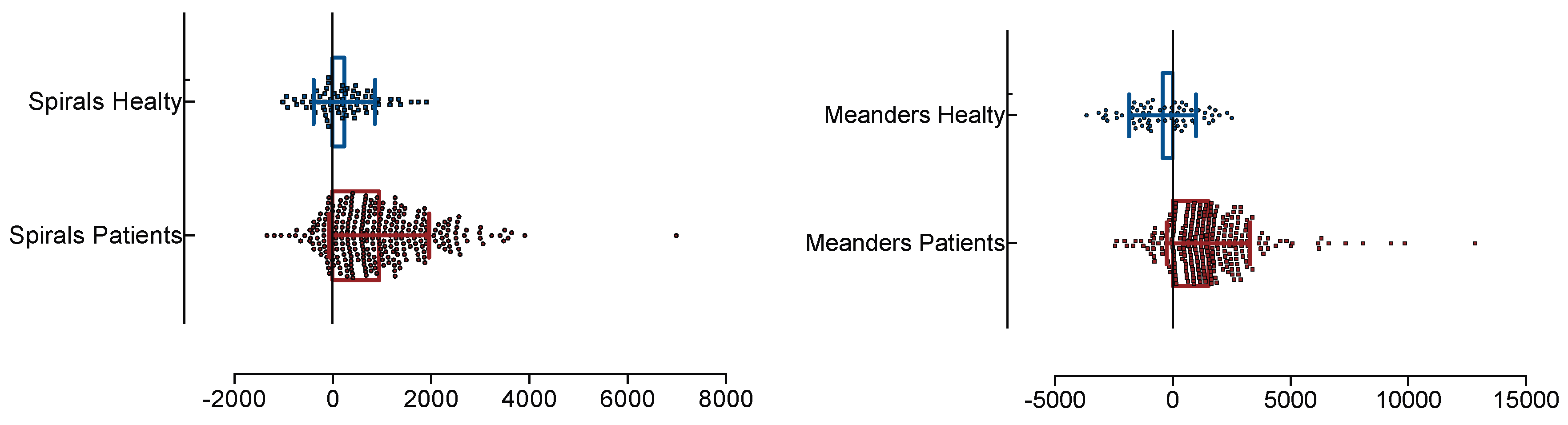
3. Experimental Results and Discussion
3.1. Parameter Settings
3.2. Results
3.3. Explicit Models of Classification Criteria
| Algorithm 1 The general model inferred by using all the best models at the end of each run. can contain both local and global features. |
| if then |
| output = ”control”; |
| else |
| output = ”patient”; |
| end if |
| Algorithm 2 The best performing model evolved by CGP among all the 20 runs. |
| if then |
| output = ”control”; |
| else |
| output = ”patient”; |
| end if |
| Algorithm 3 The simplest model evolved by CGP among all the 20 runs. |
| if then |
| output = ”control”; |
| else |
| output = ”patient”; |
| end if |
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jankovic, J. Parkinson’s disease: Clinical features and diagnosis. J. Neurol. Neurosurg. Psychiatry 2008. [Google Scholar] [CrossRef] [PubMed]
- Marsden, C.D. Slowness of movement in Parkinson’s disease. Mov. Disord. 1989, 4, S26–S37. [Google Scholar] [CrossRef] [PubMed]
- Sheridan, M.R.; Flowers, K.A.; Hurrell, J. Programming and execution of movement in parkinson’s disease. Brain 1987, 110, 1247–1271. [Google Scholar] [CrossRef] [PubMed]
- Stelmach, G.E.; Teasdale, N.; Phillips, J.; Worringham, C.J. Force production characteristics in Parkinson’s disease. Exp. Brain Res. 1989, 76, 165–172. [Google Scholar] [CrossRef] [PubMed]
- Senatore, R.; Marcelli, A. A neural scheme for procedural motor learning of handwriting. In Proceedings of the International Workshop on Frontiers in Handwriting Recognition (IWFHR), Bari, Italy, 18–20 September 2012. [Google Scholar] [CrossRef]
- McLennan, J.E.; Nakano, K.; Tyler, H.R.; Schwab, R.S. Micrographia in Parkinson’s disease. J. Neurol. Sci. 1972, 15, 141–152. [Google Scholar] [CrossRef]
- Teulings, H.; Contreras-Vidal, J.; Stelmach, G.; Adler, C. Parkinsonism reduces coordination of fingers, wrist, and arm in fine motor control. Exp. Neurol. 1997, 146, 159–170. [Google Scholar] [CrossRef] [PubMed]
- Van Gemmert, A.W.A.; Teulings, H.L.; Contreras-Vidal, J.L.; Stelmach, G.E. Parkinson’s disease and the control of size and speed in handwriting. Neuropsychologia 1999, 37, 685–694. [Google Scholar] [CrossRef]
- Teulings, H.; Stelmach, G.E. Control of stroke size, peak acceleration, and stroke duration in Parkinsonian handwriting. Hum. Mov. Sci. 1991, 10, 315–334. [Google Scholar] [CrossRef]
- De Stefano, C.; Marcelli, A.; Parziale, A.; Senatore, R. Reading cursive handwriting. In Proceedings of the 12th International Conference on Frontiers in Handwriting Recognition (ICFHR 2010), Kolkata, India, 16–18 November 2010. [Google Scholar] [CrossRef]
- Broderick, M.P.; Van Gemmert, A.W.A.; Shill, H.A.; Stelmach, G. Hypometria and bradykinesia during drawing movements in individuals with Parkinson’s disease. Exp. Brain Res. 2009, 197, 223–233. [Google Scholar] [CrossRef] [PubMed]
- Van Gemmert, A.W.A.; Adler, C.H.; Stelmach, G.E. Parkinson’s disease patients undershoot target size in handwriting and similar tasks. J. Neurol. Neurosurg. Psychiatry 2003, 74, 1502–1508. [Google Scholar] [CrossRef] [PubMed]
- Tucha, O.; Mecklinger, L.; Thome, J.; Reiter, A.; Alders, G.L.; Sartor, H.; Naumann, M.; Lange, K.W. Kinematic analysis of dopaminergic effects on skilled handwriting movements in Parkinson’s disease. J. Neural Transm. 2006, 113, 609–623. [Google Scholar] [CrossRef] [PubMed]
- Senatore, R.; Marcelli, A. A paradigm for emulating the early learning stage of handwriting: Performance comparison between healthy controls and Parkinson’s disease patients in drawing loop shapes. Hum. Mov. Sci. 2018. [Google Scholar] [CrossRef] [PubMed]
- Thomas, M.; Lenka, A.; Pal, P.K. Handwriting analysis in Parkinson’s disease: Current status and future directions. Mov. Disord. Clin. Prac. 2017. [Google Scholar] [CrossRef] [PubMed]
- Walton, J. Handwriting changes due to aging and Parkinson’s syndrome. Forensic Sci. Int. 1997, 88, 197–214. [Google Scholar] [CrossRef]
- Zham, P.; Arjunan, S.; Raghav, S.; Kumar, D.K. Efficacy of guided spiral drawing in the classification of Parkinson’s Disease. IEEE J. Biomed. Health Inf. 2017, 22, 1648–1652. [Google Scholar] [CrossRef] [PubMed]
- Rosenblum, S.; Samuel, M.; Zlotnik, S.; Erikh, I.; Schlesinger, I. Handwriting as an objective tool for Parkinson’s disease diagnosis. J. Neurol. 2013, 260, 2357–2361. [Google Scholar] [CrossRef] [PubMed]
- Drotár, P.; Mekyska, J.; Rektorová, I.; Masarová, L.; Smékal, Z.; Faundez-Zanuy, M. Analysis of in-air movement in handwriting: A novel marker for Parkinson’s disease. Comput. Methods Programs Biomed. 2014, 117, 405–411. [Google Scholar] [CrossRef] [PubMed]
- Pereira, C.R.; Weber, S.A.; Hook, C.; Rosa, G.H.; Papa, J.P. Deep learning-aided Parkinson’s disease diagnosis from handwritten dynamics. In Proceedings of the 2016 29th SIBGRAPI Conference on Graphics, Patterns and Images, Sao Paulo, Brazil, 4–7 October 2016. [Google Scholar] [CrossRef]
- Pereira, C.R.; Pereira, D.R.; Silva, F.A.; Masieiro, J.P.; Weber, S.A.; Hook, C.; Papa, J.P. A new computer vision-based approach to aid the diagnosis of Parkinson’s disease. Comput. Methods Programs Biomed. 2016, 136, 79–88. [Google Scholar] [CrossRef] [PubMed]
- Miller, J.F. Cartesian genetic programming. In Natural Computing Series; Springer: Berlin, Germany, 2011. [Google Scholar] [CrossRef]
- Smith, S.L. Medical Applications of Evolutionary Computation. In Proceedings of the Companion Publication of the 2015 Annual Conference on Genetic and Evolutionary Computation, Kyoto, Japan, 15–19 July 2018; ACM: New York, NY, USA, 2015; pp. 651–679. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992; Volume 1. [Google Scholar]
- De Falco, I.; Della Cioppa, A.; Tarantino, E.; Fontanella, F. A novel grammar-based genetic programming approach to clustering. In Proceedings of the ACM Symposium on Applied Computing, Santa Fe, NM, USA, 13–17 March 2005; Volume 2, pp. 928–932. [Google Scholar]
- De Falco, I.; Della Cioppa, A.; Tarantino, E.; Fontanella, F. An innovative approach to genetic programming-based clustering. In Advances in Soft Computing; Springer: Berlin, Germany, 2006; Volume 34, pp. 55–64. [Google Scholar]
- De Falco, I.; Della Cioppa, A.; Scafuri, U.; Tarantino, E. Accurate estimate of blood glucose through interstitial glucose by genetic programming. In Proceedings of the International Symposium on Computers and Communications, Heraklion, Greece, 3–6 July 2017; pp. 284–289. [Google Scholar]
- De Falco, I.; Della Cioppa, A.; Koutny, T.; Krcma, M.; Scafuri, U.; Tarantino, E. An evolutionary approach for estimating the blood glucose by exploiting interstitial glucose measurements. In Proceedings of the Eleventh International Joint Conference on Biomedical Engineering Systems and Technologies—HEALTHINF, Madeira, Portugal, 19–21 January 2018; Volume 5, pp. 625–632. [Google Scholar]
- Borrelli, A.; De Falco, I.; Della Cioppa, A.; Nicodemi, M.; Trautteur, G. Performance of genetic programming to extract the trend in noisy data series. Phys. A Stat. Mech. Its Appl. 2006, 370, 104–108. [Google Scholar] [CrossRef]
- Papa, J.P.; Falcão, A.X.; Suzuki, C.T. Supervised pattern classification based on optimum-path forest. Int. J. Imaging Syst. Technol. 2009, 19, 120–131. [Google Scholar] [CrossRef]
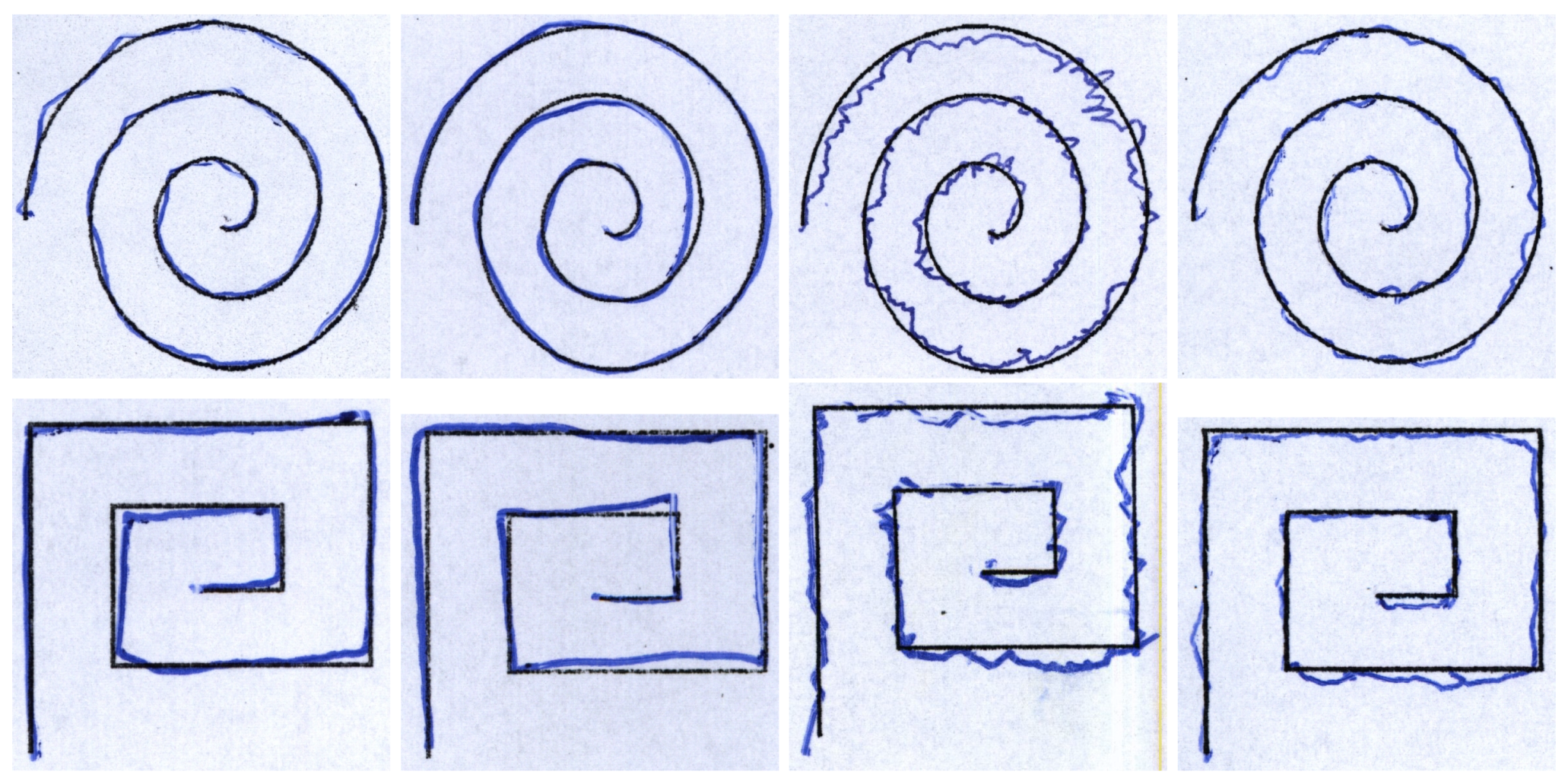
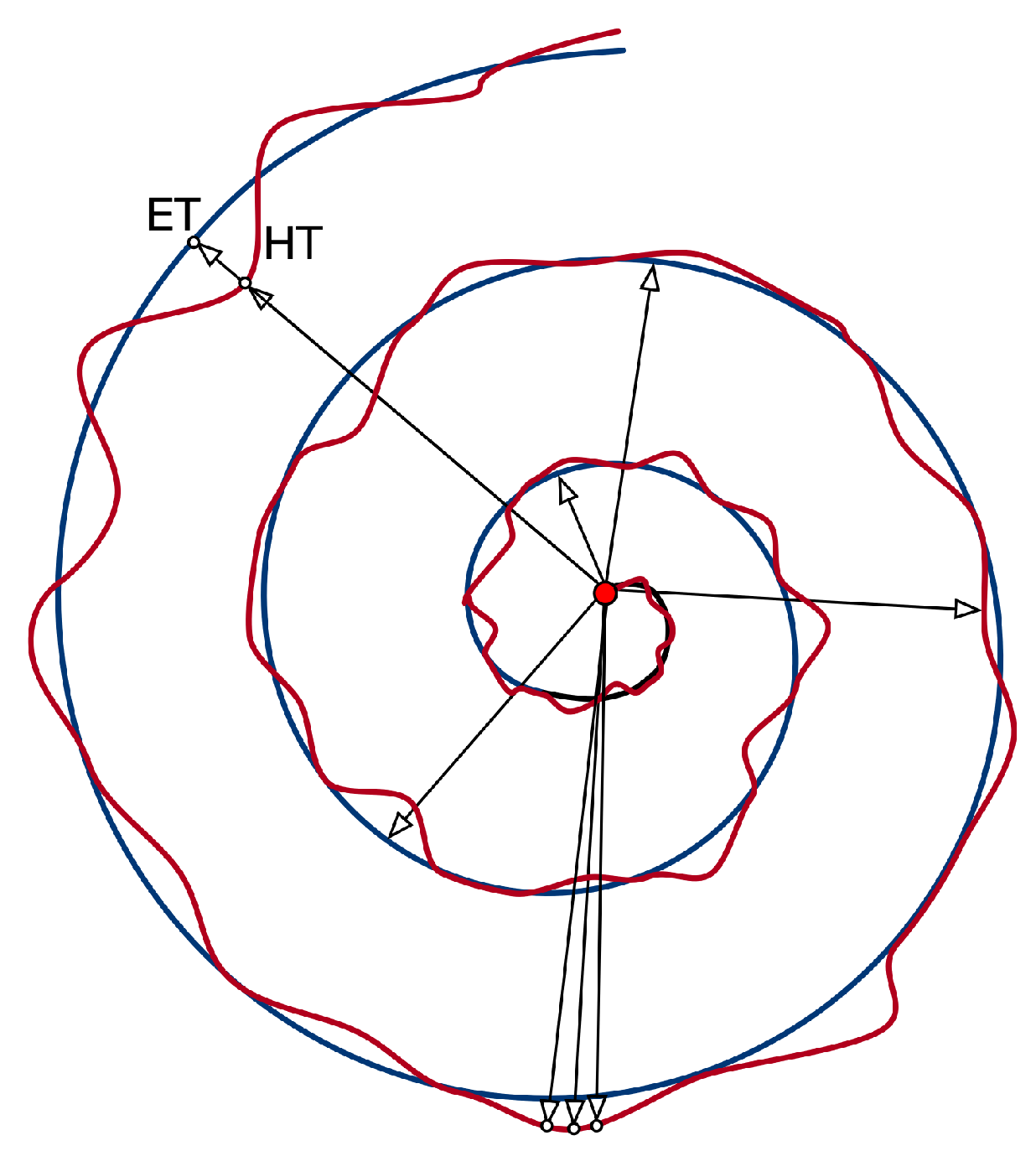
| Feature | Description |
|---|---|
| RMS of the difference between HT and ET radius | |
| Maximum difference between HT and ET radius | |
| Minimum difference between HT and ET radius | |
| Standard Deviation of the difference between HT and ET radius | |
| Mean Relative Tremor | |
| Maximum HT radius | |
| Minimum HT radius | |
| Standard Deviation of HT radius | |
| Number of times the difference between HT and ET radius changes sign |
| Parameter | Value | Analyzed Range |
|---|---|---|
| Row number | 2 | |
| Column number | 25 | |
| Node Configuration | ||
| Generation number | 50,000 | [1–60,000] : 10,000 |
| Levels-back | 25 | |
| Population | 15 | |
| Evolution Strategy | (, ) | |
| Mutation Rate | –20% : |
| Function | Definition | Arity |
|---|---|---|
| sum | 2 | |
| subtraction | 2 | |
| multiplication | 2 | |
| less | if () else | 2 |
| less or equal | if () else | 2 |
| greater | if () else | 2 |
| greater or equal | if () else | 2 |
| negation | 1 | |
| if-then-else | if () else | 3 |
| if-less-then-else | if () else | 3 |
| Healthy Subjects | PD Patients | Global | |
|---|---|---|---|
| CGP | |||
| NB | |||
| OPF | |||
| SVM |
| Healthy Subjects | PD Patients | Global | |
|---|---|---|---|
| CGP | |||
| NB | |||
| OPF | |||
| SVM |
| 100 | 95 | 10 | 30 | 65 | 100 | 50 | 60 | 40 |
| Healthy Subjects | PD Patients | Global | |
|---|---|---|---|
| CGP (all features) | |||
| CGP ( removed) | |||
| CGP ( and removed) |
| Healthy Subjects | PD Patients | Global |
|---|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Senatore, R.; Della Cioppa, A.; Marcelli, A. Automatic Diagnosis of Neurodegenerative Diseases: An Evolutionary Approach for Facing the Interpretability Problem. Information 2019, 10, 30. https://doi.org/10.3390/info10010030
Senatore R, Della Cioppa A, Marcelli A. Automatic Diagnosis of Neurodegenerative Diseases: An Evolutionary Approach for Facing the Interpretability Problem. Information. 2019; 10(1):30. https://doi.org/10.3390/info10010030
Chicago/Turabian StyleSenatore, Rosa, Antonio Della Cioppa, and Angelo Marcelli. 2019. "Automatic Diagnosis of Neurodegenerative Diseases: An Evolutionary Approach for Facing the Interpretability Problem" Information 10, no. 1: 30. https://doi.org/10.3390/info10010030
APA StyleSenatore, R., Della Cioppa, A., & Marcelli, A. (2019). Automatic Diagnosis of Neurodegenerative Diseases: An Evolutionary Approach for Facing the Interpretability Problem. Information, 10(1), 30. https://doi.org/10.3390/info10010030







