Full Support for Efficiently Mining Multi-Perspective Declarative Constraints from Process Logs †
Abstract
1. Introduction
- (i)
- We introduce algorithms and descriptions for the full set of commonly accepted types of MP-Declare constraints.
- (ii)
- The conceptual architecture of the implementation has been reworked such that new types of constraints can be easily defined and extracted by the user.
- (iii)
- We provide a more detailed description of the conceptual approach as well as the implemented protoype.
- (iv)
- Related work is discussed more thoroughly.
2. Related Work
3. Preliminaries
3.1. Multi-Perspective, Declarative Process Modelling
- Activation conditions: When a loan is requested and account balance > 4000 EUR, the loan must subsequently be granted.
- Correlation conditions: When a loan is requested, the loan must subsequently be granted and amount requested = amount granted.
- Target conditions: When a loan is requested, the loan must subsequently be granted by a specific member of the financial board.
- Temporal conditions: When a loan is requested, the loan must subsequently be granted within the next 30 days.
3.2. Metrics for Mining MP-Declare Models
3.3. MapReduce
3.3.1. Origin
3.3.2. Implementations
- MapReduce. Referring to Google’s original paper [42] or Hadoop [43], the open source de-facto standard implementation in Java, MapReduce, implies two functions, namely Map (a parallel transformation) and Reduce (a parallel aggregation). For the sake of performance with large datasets, these implementations include an intermediate shuffle or group phase.
- Map and Reduce in Functional Programming. Functional Programming languages or frameworks, such as Haskell, Java (includes functional concepts since Version 1.8) or Spark, also use the terms map and reduce, but are different from the MapReduce concepts mentioned above. For instance, in functional programming, users specify the semantic logic in a declarative way rather than the control flow [44].
3.3.3. Functionality
4. Map-Reduce for Declarative Process Mining
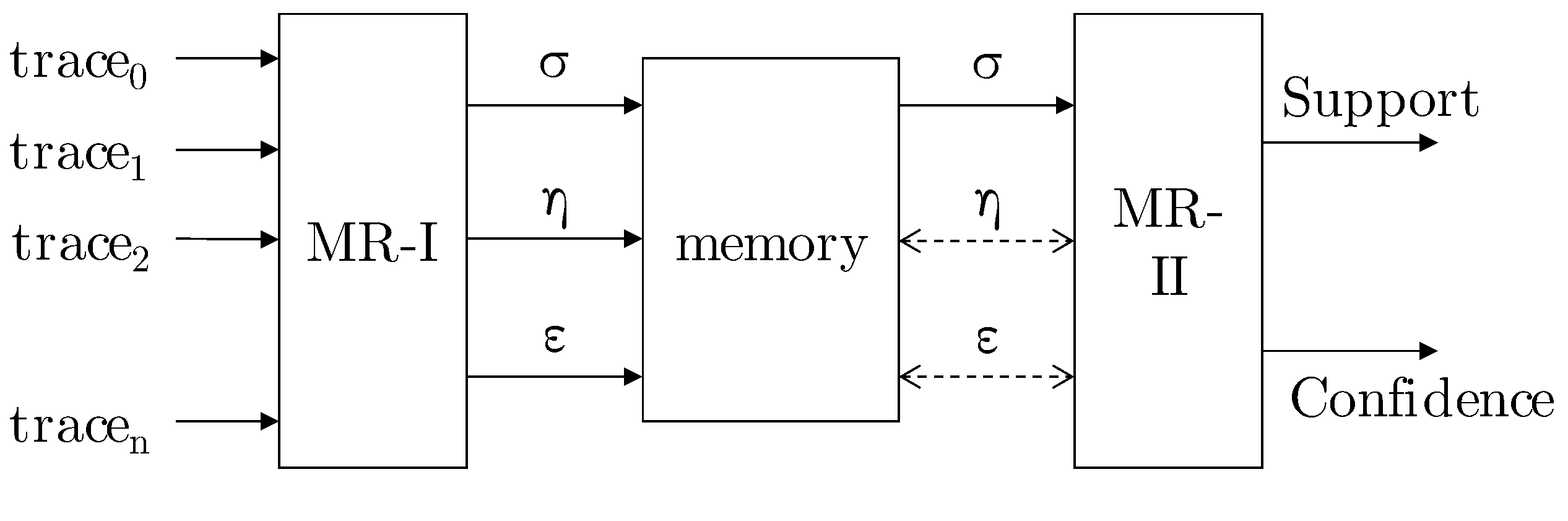
4.1. Architecture and Infrastructure
4.1.1. MR-I
-Function
-Function
-Function
4.1.2. MR-II
4.2. Mapping MP-Declare Templates to MapReduce
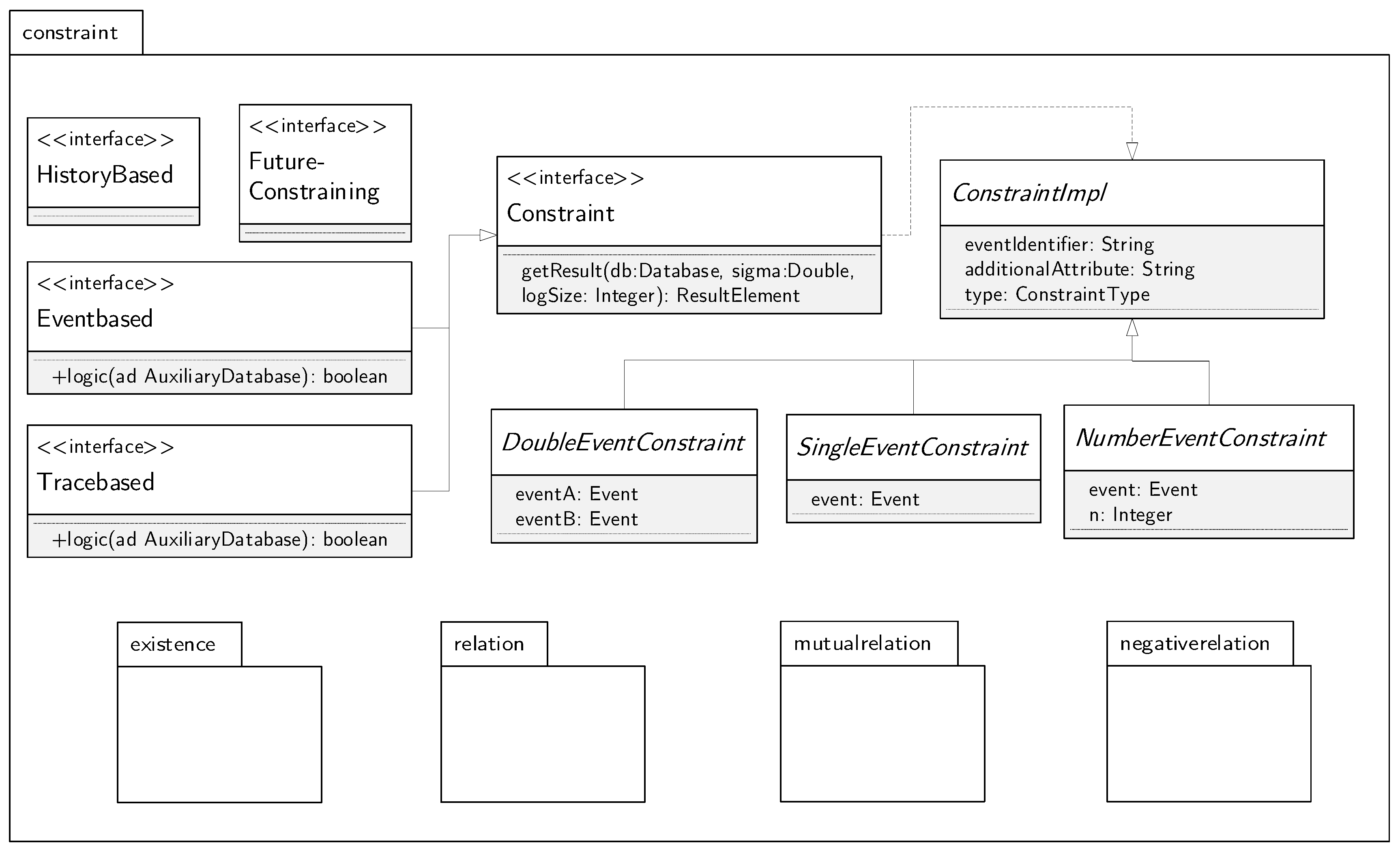
4.2.1. Existence Constraints
- ExistenceDescription. The future constraining constraint existence indicates that event e must occur at least n-times in the trace. The variable n takes an integer between 1 and the amount of occurrences of the event e in the trace, while e activates the constraint.Mining Trace-basedBeginning with the first trace, the constraint is fulfilled for each event e and variable n if the amount of occurrences of e in the trace is equal or greater than the value of n. By iterating through the trace, the fulfilled constraints are contemporaneously computed with the amount of occurrences of the respective event. As explained above, only activation constraints are take into account. The initial assignment of i is 0, while j is not considered, because of computing a trace-based constraint. Thus, the event is considered first and the amount of occurrences of is increased from 0 to 1 (cf. Table 5). The variable n takes the value of the up to this point computed amount of occurrences of the respective event in the trace. Thus, existence is investigated in this first case and is incremented by 1. In the case of , the amount of occurrences of event in the trace is increased from 1 to 2 and therefore existence is fulfilled.
- ParticipationDescription. The future constraining constraint participation indicates that event e occurs at least once in the trace. This constraint is equivalent to existence.MiningTrace-basedFor each event that occurs in the considered trace, the respective constraint is fulfilled. All traces that fulfil the constraint relating to a certain e are counted to receive the number of fulfillments in the whole log. That value is computed just as the corresponding value of .Because this constraint is classified as trace-based, only activation constraints are considered and there is no nested loop necessary. Similar to the existence constraint, i is initialised with 0 and the computation starts with . The constraint participation is fulfilled for each event that occurs in the trace, while each event is regarded by the iteration variable i. In the step with and , the -value must not be modified, as the constraint participation and were already activated and fulfilled with and and is stored only once per trace (cf. Table 6).
- AbsenceDescription. The future constraining constraint absence indicates that event e may occur at most in the trace. The variable n takes an integer between 2 and the size of the respective trace, while event e activates the constraint.MiningTrace-basedIn the first step, the amount of occurrences of each event in a trace is counted by iterating the trace with variable i. Since the absence constraint is limited by this amount, it has to be checked after counting the occurrences of all events. In a second step, two additional nested loops are added. The outer loop considers variable n reaching from 2 to the size of longest trace in the event log. The inner loop iterates all events in the trace and in each cycle, their amount of occurrences which were counted in the first step are compared to the recent value of n. Let be the variable for the inner loop that refers to the set of events in the trace, containing each event once in the order predetermined by the control variable i. The constraint is fulfilled for a certain event, if n is greater than the amount of occurrences of the respective event. If the constraint is fulfilled, it is implicitly fulfilled for all values bigger than n.For this constraint, only activation constraints are considered and so the event holds the additional condition. The initial assignment of is , hence absence is investigated in the first case. The constraint is not fulfilled, since occurs 2 times in the trace. In the next step, the -value needs to be incremented by 1, as the constraint absence is fulfilled. This constraint is also fulfilled for values of n greater than 2, represented by .. in Table 7.
- UniquenessDescription.The future constraining constraint uniqueness indicates that event e occurs at most once in the trace. This constraint is equivalent to absence(2,e).MiningTrace-basedThe computation for the uniqueness constraint is equal to the computation of the participation constraint. The only difference is the value of n. In the uniqueness constraint, n is fixed to the value 2 and thus the constraint is fulfilled for a certain event, if it does not occur in the trace or occurs only once in the trace. As described in the above section, we consider vacuously defined constraints. For this reason, uniqueness constraint is not fulfilled if the event does not occur in the trace.Since n is fixed, the additional nested loops are not necessary. As the uniqueness constraint is trace-based, only activation constraints are taken into account. In the case of and in Table 8, the referring constraints uniqueness and uniqueness are violated because the events and occur 2 times in the trace.
- InitDescription.The future constraining constraint init indicates that event e is the first event that occurs in the trace.MiningTrace-basedFor each trace, only the first event per trace is taken into account. Each of these events fulfil the constraint. Only the initial assignment of , and activation constraints are considered. The event is the first event in the trace and fulfils the constraint, while the fulfillment check for all over events in the trace to is skipped (cf. Table 9).
- EndDescription.The future constraining constraint end indicates that event e is the last event that occurs in the trace.MiningTrace-basedFor each trace, only the last event per trace is taken into account. Each of these events fulfil the constraint. Only the last assignment of i, which means , and activation constraints are considered. The event is the last event in the trace and fulfils the constraint, while the fulfillment check for all over events in the trace to is skipped (cf. Table 10).
4.2.2. Relation Constraints
- Responded ExistenceDescription.The future constraining and history-based constraint respondedExistence indicates that, if event a occurs in the trace, then event b occurs in the trace as well. Event a activates the constraint.MiningEvent-basedThe whole trace has to be considered to take all events into account that occur before or after the event that corresponds to the current value of the outer loop variable i. Therefore, the control variable of the inner loop j starts with 0 for each value of i. All pairs with fulfil the constraint while this pair occurs the first time for the activating event in the trace.The loop variables are initialised with , thus the event would be associated with itself. Such associations are not meaningful and since i and j have the same values, the fulfillment check is skipped. The next value for is and therefore the events and are considered. For activation constraints, the activating event holds the additional condition solely; hence, respondedExistence is investigated in this case. This constraint, activated with is fulfilled with and thus is incremented by 1. In addition, for , the value for is incremented. In the next step, i.e., , the must not be modified, as the constraint respondedExistence activated with the event was already fulfilled with (cf. in Table 11a). Cases – are similar.For target constraints such as respondedExistence, the additional condition appears on the right-hand side. That means, the events in the outer loops have to match the target template: . Referring to Table 11b, in Case , , respectively, must not be increased, as the constraint is also already fulfilled (with ). Cases – are similar.
- ResponseDescription.The future constraining constraint response indicates that, if event a occurs in the trace, then event b occurs after a. Event a activates the constraint.MiningEvent-basedSince the response constraint considers only events that occur after the activating event in a trace, the control variable of the inner loop j depends on the value of the outer loop variable i. Variable j starts with the value . All event pairs referring to fulfil the constraint while this pair occurs the first time for the activating event in the trace.The initial assignment of is . Since the assignment for the loop variables is never considered, the first column and last row that refer to the value are omitted in Table 12a. The events and are taken into account in the first step. If the activation conditions are considered, the first constraint is response. The constraint is activated with and fulfilled with . This leads to an incrementation of by 1. In the case of , the must not be modified, as the constraint response activated with the event was already fulfilled with . Cases – in Table 12a are similar.In terms of target conditions such as response, where the event on the right-hand side holds the additional condition, the value of must not be increased in the case of . The constraint is already fulfilled with . The same also applies to (cf. Table 12b).
- Alternate ResponseDescription.The future constraining constraint alternateResponse indicates that each time event a occurs in the trace, then event b occurs afterwards, before event a recurs. Event a activates the constraint.MiningEvent-basedFor this template, the loop variables i and j take the same values as explained for the response constraint. As additional restriction, the constraint alternate response is not fulfilled, if the set of events that occur between the events referring to i and j contains the event that correspond to i. In this case, the iteration is cancelled, i is incremented and the trace is taken into account with the new values.The alternateResponse template shares the pivot constellations for for already fulfilled constraints similar to the response template (cf. – in Table 13a). Similar to the response template, the initial assignment of is . As instance of an activation constraint, the alternate response in iteration from Table 13a is considered. In this case, the constraint is activated by and fulfilled with the event . Additional events b in the same iteration must be ignored (e.g., ).Besides the already-fulfilled-errors, another class of error type is introduced, which was already meant in a similar way in the uniqueness constraint: violations. Consider in Table 13a. In this case, the constraint alternate response is checked. Although this constellation has not occurred thus far for this activation, the value must not be modified, because it is violated by : The activating event recurs before a occurs. This is forbidden within the alternateResponse template. Note that the resource is also decisive, thus alternateResponse, activated with is fulfilled with , although the event b recurs. However, this is executed by x instead of y and so the constraint is not violated (marked with an asterisk in Table 13a).The analysis of the target constraints (cf. Table 13b) shows the following anomalies: and are excluded because of the already-fulfilled-case and cases – are excluded because of violations. For instance, – are activated with the event and as the first event in the inner loop is also b (represented with the activation template, i.e., the activity solely ), all constraints with succeeding events in the inner loop are violated.
- Chain ResponseDescription.The future constraining constraint chainResponse indicates that, each time event a occurs in the trace, event b occurs immediately afterwards. Event a activates the constraint.MiningEvent-basedFor each event referring to i in a trace, only the successive event referring to is considered. Therefore, the inner loop is skipped and j holds a fixed value depending on i.The initial assignment of is , thus the events and are considered. The corresponding activation constraint is chainResponse and the value of is incremented by 1. The target constraint for these values of i and j is chainResponse. In the next step with , the activation constraint chainResponse and target constraint chainResponse is considered (cf. Table 14).
- PrecedenceDescription.The history-based constraint precedence indicates that event b occurs only in the trace, if preceded by a. Event b activates the constraint.MiningEvent-basedIntuitively, one would iterate starting from the latest event for the history-based constraints, e.g., the first -tuple would be going on with , i.e., the constraints precedence and precedence, respectively.In the case of activation constraints, the former describes that, whenever a occurs and was executed by x, b has to precede. Referring to the latter, precedence describes that if event a occurs in a trace and was executed by x, then event d has to precede.For the sake of performance boost, we propose an algorithm, which handle the history-based constraints also by iterating through the events in a forward direction. To do so, the events of the outer loop fills the role of the target events and the events of the inner loop are now the activating events.Consider Table 15a and the assignment of with . The first constraint under investigation is precedence, activated with and fulfilled with . In the next step, precedence is considered. It is activated with and fulfilled with the same outer loop event .Interesting is the outer loop event (cf. third row in Table 15a). In the case of , the value for must not be modified . The reason is that this constraint, activated with is fulfilled with the outer loop event and thus, fulfilled in a future step (marked with an asterisk in Table 15a). Hence, the iteration of the inner loop is cancelled, if the event referring to the recent value of i in the outer loop is equal to the event referring to the recent value of j in the inner loop.The target constraints show similar behaviour. Whenever the event occurs also in the inner loop in , then the rest of the inner loop is neglected because the events are fulfilled afterwards. For example, precedence is fulfilled in the future in the asterisk-marked cell in Table 15b. Notice that, for precedence (third row in Table 15b), the value is incremented by 1, since the additional condition has to be considered and the preceding event b is executed by x instead of y.
- Alternate PrecedenceDescription.The history-based constraint alternatePrecedence indicates that, each time event b occurs in the trace, it is preceded by event a and no other event b can recur in between. Event b activates the constraint.MiningEvent-basedFor this template, the loop variables i and j take the same values as explained for the precedence constraint. As additional restriction, the constraint alternate precedence is not fulfilled, if the set of events that occur between the events referring to i and j contain the event that correspond to j. In this case, the iteration is cancelled, i is incremented and the trace is taken into account with the new values.As example for an activation constraint, consider alternatePrecedence in Table 16a. The marker indicates a violation of this constraint because of the reoccurrence of the activating event . Case is similar.In the case of , according to the constraint alternatePrecedence, must not be incremented there, because this constraint activated with is fulfilled with the event in the next run of the outer loop (note the asterisk in Table 16a). Cases – are similar.Table 16b shows the already-fulfilled-cases and violations of the exemplary trace in the case of target constraints. The constraints at – are violated, because of the reoccurrence of the events and in the events and .
- Chain PrecedenceDescription.The history-based constraint chainPrecedence indicates that, each time event b occurs in the trace, event a occurs immediately beforehand. Event b activates the constraint.MiningEvent-basedSince the precedence and all precedence-subsumed constraints are computed in a forward direction in our work, the inner loop is skipped similar to the chainResponse template and j holds a fixed value depending on i. For each event referring to in a trace, only its preceding event referring to i is considered.The initial assignment of is , thus the events and are considered. The corresponding activation constraint is chainPrecedence and the value of is incremented by 1. The target constraint for these values of i and j is chainPrecedence. In the next step with , the activation constraint chainPrecedence and target constraint chainPrecedence is considered (cf. Table 17).
4.2.3. Mutual Relation Constraints
- CoExistenceDescription.The future constraining and history-based constraint coExistence indicates that, if event b occurs in the trace, then event a occurs and vice versa. Event a and event b activate the constraint.MiningEvent-basedThe coExistence constraint is composed of two respondedExistence constraints. The second respondedExistence constraint considers the events of the first respondedExistence constraint in reversed order.The fulfillment of the two respondedExistence constraints is computed as described in the corresponding item above. The whole trace is considered and the loop variables are initialised with , while events that are associated with themselves are not considered. For example, take the event pair corresponding to into account. For activation constraints, e.g. coExistence, the constraints respondedExistence and respondedExistence are investigated in this case. The events are switched while the additional condition stays on the left-hand side.The first respondedExistence constraint, activated with , is fulfilled with and thus is incremented by 1. The second respondedExistence is activated with and fulfilled with leading to an incrementation of by 1. After iterating through the whole trace, the value of is 2 and the value of stays to 1. These values are summed up and is increased by 3. The same value is applied to . Table 18 is similar to Table 11a but marks the corresponding sigmas, which are summed up with same indices. The notation of the already-fulfilled-constraints (e.g., ) is taken over from Table 11a.For target constraints, e.g. coExistence, the constraints respondedExistence and respondedExistence have to be considered. Referring to Table 19, the final value of is 5. All fullfilments of this constraint are denoted as in the table.
- SuccessionDescription.The future constraining and history-based constraint succession indicates that event a occurs in the trace, if and only if it is followed by event b. Event a and event b activate the constraint.MiningEvent-basedThe succession constraint is composed of the response and the precedence constraint. The fulfillment of these two constraints is computed as described in the corresponding item above. The constraints are computed successively.The initial assignment of is . The events and are taken into account in the first step. If the activation conditions are considered, the constraints response and precedence would be investigated in the first step.To give an example how the Succession constraint is computed, consider = for the response constraint and = for the precedence constraint. According to Table 12a, the response constraint is activated with and fulfilled with . This leads to an incrementation of by 1. The precedence constraint is activated with and fulfilled with , leading to an incrementation of by 1 (cf. Table 15a). After iterating through the trace and calculating all fulfilled constraints, the values of and are summed up. Therefore, the number of fulfillments of the corresponding constraint succession is calculated, expressed by an incrementation of by 2. Another example is provided by = , where the response and precedence constraints are activated with the same additional condition z. In this case, and are incremented by 1. These both values are used to compute the number of fulfillments of constraint succession through incrementing by 2.If the target conditions are considered, the constraints response and precedence are investigated in the first step (cf. Table 12b and Table 15b). In the case = , the constraints response and precedence are fulfilled with the same additional condition x and the values of and are incremented by 1. The sum of these values leads to the number of fulfillments of the target constraint succession by incrementing by 2.
- AlternateSuccessionDescription.The future constraining and history-based constraint alternateSuccession indicates that event a and event b occur in the trace, if and only if the latter follows the former, and they alternate each other in the trace. Event a and event b activate the constraint.MiningEvent-basedThe alternateSuccession constraint is composed of the alternateResponse and the alternatePrecedence constraint. The fulfillment of these two constraints is computed as described in the corresponding item above. The constraints are computed successively.The initial assignment of is . The events and are taken into account in the first step.As example for an activation constraint, consider alternateSuccession. The respective constraints alternateResponse and alternatePrecedence have to be computed. As presented in Table 13a, the alternateResponse constraint is activated with and fulfilled with . Therefore, the value of is incremented by 1. The alternatePrecedence constraint is activated with and fulfilled with , leading to an incrementation of by 1 (cf. Table 16a). For both constraints, the value of is not incremented in the case of because the constraints are already fulfilled in the past for the alternateResponse constraint or will be fulfilled in the future for the alternatePrecedence constraint. Hence, the number of fulfillments of the composed constraint alternateSuccession is 2.For target constraints such as alternateSuccession, the number of fulfillments of the constraints alternateResponse and alternatePrecedence are computed and summed up. Since event a never occurs with the additional condition z, the value of is never incremented. This leads to the final value of .
- ChainSuccessionDescription.The future constraining and history-based constraint chainSuccession indicates that event a and event b occur in the trace, if and only if the latter immediately follows the former. Event a and event b activate the constraint.MiningEvent-basedFor the chainSuccession constraint, the computation of the constraints chainResponse and chainPrecedence are necessary. The fulfillment of these two constraints is computed like described in the corresponding item above. The constraints are computed successively.The initial assignment of is , while the inner loop is skipped and holds a fixed value depending on i. Therefore, the events and are considered. For activation constraints, chainSuccession including chainResponse and chainPrecedence is computed in the first step. For target constraints, chainSuccession and chainPrecedence are considered for the same values of i and j to calculate chainSuccession.
4.2.4. Negative Relation Constraints
- NotChainSuccessionDescription.The future constraining and history-based constraint notChainSuccession indicates that event a and event b occur in the trace, if and only if the latter does not immediately follow the former. Event a and event b activate the constraint.MiningEvent-basedThe notChainSuccession constraint is computed like the chainSuccession constraint for activation and target conditions. The only difference lies in the determination of the support value which is calculated by negating the support value of chainSuccession for each event pair. This negation is expressed formally as .
- NotSuccessionDescription.The future constraining and history-based constraint notSuccession indicates that event a can never occur before event b in the trace. Event a and event b activate the constraint.MiningEvent-basedThe notSuccession constraint is computed similar to the Succession constraint for activation and target conditions. Similar to the notChainSuccession constraint, the determination of the support value is calculated by negating the support value of Succession for each event pair. This negation is expressed formally as .
- NotCoExistenceDescription.The future constraining and history-based constraint notCoExistence indicates that event a and event b never occur together. Event a and event b activate the constraint.MiningEvent-basedThe notCoExistence constraint is computed similar to the coExistence constraint for activation and target conditions. Just as the two items above, the determination of the support value is calculated by negating the support value of coExistence for each event pair. This negation is expressed formally as .
4.3. Pivot Characteristics Overview
5. Implementation
5.1. An extendable Framework
5.2. MapReduce-Miner Library
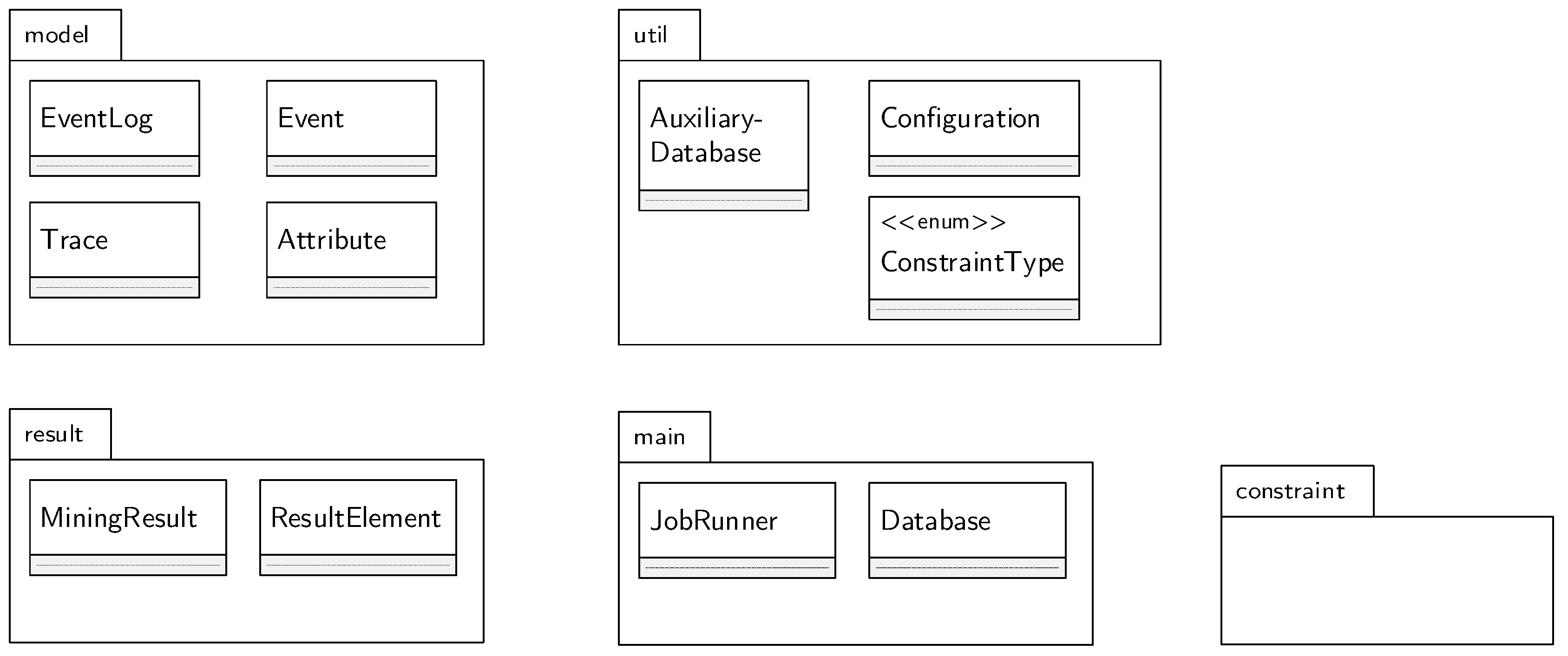
5.2.1. Package Model
5.2.2. JobRunner and Database as Centerpiece
| Algorithm 1: Setup of a mining job. |
| 1 Configuration configuration = new Configuration(); |
| 2 configuration |
| 3 .setEventIdentifier("task") |
| 4 .setAdditionalAttribute("resource") |
| 5 .addConstraint(Response.class) |
| 6 .allConstraintTypes(); |
| 7 JobRunner job = new JobRunner(eventLog, configuration); |
| 8 job.run(); |
| 9 job.getMiningResult(); |
| Algorithm 2: The run and map functions. |
| 1 publicvoid run() { |
| 2 // MR-I: produce Key–Value Pairs |
| 3 Database db = eventLog.getTraces().stream().map((trace) -> map(trace)) |
| 4 .reduce((accDb, currentDb) -> reduce(accDb, currentDb)).get(); |
| 5 // ’MR-II’: calculate Support and Confidence |
| 6 mrii(db); |
| 7 } |
| 8 publicvoid map(Trace trace) { |
| 9 Database database = new Database(configuration); |
| 10 AuxilaryDatabase ad = new AuxilaryDatabase(); |
| 11 for (int i = 0; i < trace.getEvents().size(); i++) { |
| 12 //… |
| 13 for (int j = 0; j < trace.getEvents().size(); j++) { |
| 14 for (Class<Constraint> c: getConfiguration().getConstraints()) { |
| 15 Constraint impl = instantiate(c, events.get(i), events.get(j), -1, ConstraintType.ACTIVATION); |
| 16 if (impl instanceof Eventbased) { |
| 17 Eventbased eventBasedImpl = (Eventbased) impl; |
| 18 if (eventBasedImpl.logic(ad)) |
| 19 database.addSigma(eventBasedImpl, 1); |
| 20 //… |
| 21 //Tracebased-Constraints… |
| 22 } |
5.2.3. Package Constraint
| Algorithm 3: Class Init. |
| 1 publicclassInitextendsSingleEventConstraintimplementsTracebased { |
| 2 @Override |
| 3 publicboolean logic(AuxilaryDatabase ad, int position, int size) { |
| 4 if(position == 0) |
| 5 return true; |
| 6 else |
| 7 return false; |
| 8 } |
| 9 @Override |
| 10 publicResultElement getResult(Database db, double sigma, int logSize) { |
| 11 returnnewResultElement( |
| 12 this.getClass().toString(), getEvent(), sigma/logSize, 0.0d, this.getType()); |
| 13 } |
| 14 } |
5.3. System Support
| Algorithm 4: Custom constraint WithinFiveSteps. |
| 1 publicclassWithinFiveStepsextendsDoubleEventConstraint |
| 2 implementsEventbased, FutureBased { |
| 3 @Override |
| 4 publicboolean logic(AuxiliaryDatabase ad) { |
| 5 CustomAuxiliaryDatabase cad = (CustomAuxiliaryDatabase) ad; |
| 6 if(cad.currentJ < cad.currentI+1) return false; |
| 7 if(cad.currentJ > cad.currentI+5) return false; |
| 8 if (!cad.tasksWithinFiveSteps.contains(super.getEventB())) { |
| 9 cad.tasksWithinFiveSteps.add(super.getEventB()); |
| 10 return true; |
| 11 } elsereturn false; } |
| 12 } |
| 13 } |
6. Evaluation
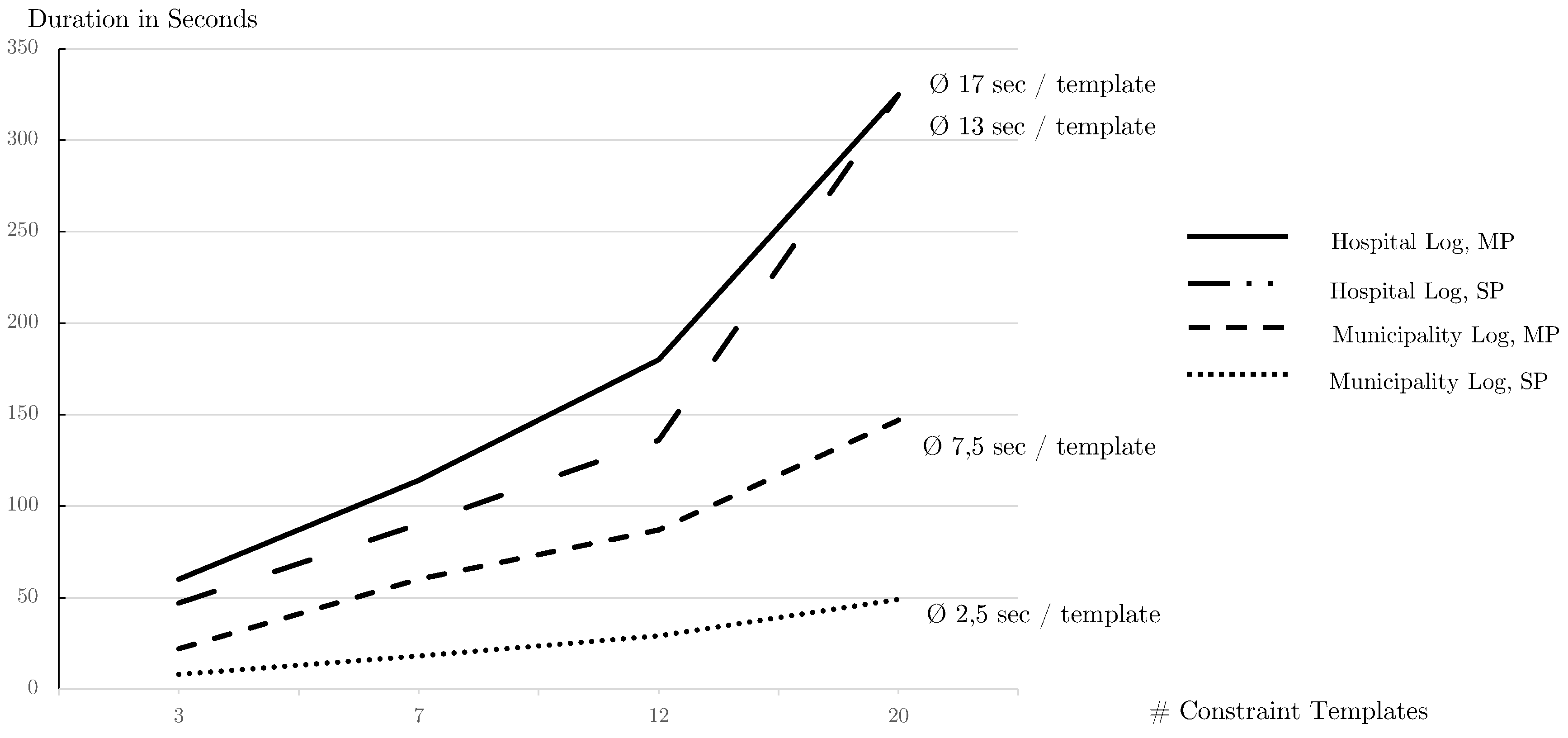
6.1. Quantitative Performance Analysis
6.2. Qualitative Evaluation
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schönig, S.; Zeising, M.; Jablonski, S. Supporting collaborative work by learning process models and patterns from cases. In Proceedings of the 9th IEEE International Conference on Collaborative Computing: Networking, Applications and Worksharing, Austin, TX, USA, 20–23 October 2013; pp. 60–69. [Google Scholar]
- Van der Aalst, W. Process Mining: Discovery, Conformance and Enhancement of Business Processes; Springer: Berlin, Germany, 2011. [Google Scholar]
- Pichler, P.; Weber, B.; Zugal, S.; Pinggera, J.; Mendling, J.; Reijers, H.A. Imperative versus Declarative Process Modeling Languages: An Empirical Investigation. In Proceedings of the International Conference on Business Process Management, Clermont-Ferrand, France, 29 August–2 September 2011; pp. 383–394. [Google Scholar]
- Pesic, M.; Schonenberg, H.; van der Aalst, W.M.P. DECLARE: Full Support for Loosely-Structured Processes. In Proceedings of the 11th IEEE International Enterprise Distributed Object Computing Conference (EDOC 2007), Annapolis, MD, USA, 15–19 October 2007; pp. 287–300. [Google Scholar]
- Zeising, M.; Schönig, S.; Jablonski, S. Towards a Common Platform for the Support of Routine and Agile Business Processes. In Proceedings of the Collaborative Computing: Networking, Applications and Worksharing, Miami, FL, USA, 22–25 October 2014. [Google Scholar]
- De Leoni, M.; van der Aalst, W.M.P.; Dees, M. A general process mining framework for correlating, predicting and clustering dynamic behavior based on event logs. Inf. Syst. 2016, 56, 235–257. [Google Scholar] [CrossRef]
- Burattin, A.; Maggi, F.M.; Sperduti, A. Conformance Checking Based on Multi-Perspective Declarative Process Models. arXiv, 2015; arXiv:1503.04957. [Google Scholar] [CrossRef]
- Augusto, A.; Conforti, R.; Dumas, M.; La Rosa, M.; Maggi, F.M.; Marrella, A.; Mecella, M.; Soo, A. Automated Discovery of Process Models from Event Logs: Review and Benchmark. CoRR 2017, arXiv:1705.02288. [Google Scholar] [CrossRef]
- Van der Aalst, W.M.P. Process Mining—Data Science in Action, 2nd ed.; Springer: Berlin, Germany, 2016. [Google Scholar]
- Leemans, S.J.J.; Fahland, D.; van der Aalst, W.M.P. Scalable process discovery and conformance checking. Softw. Syst. Model. 2018, 17, 599–631. [Google Scholar] [CrossRef] [PubMed]
- Di Ciccio, C.; Mecella, M. A Two-Step Fast Algorithm for the Automated Discovery of Declarative Workflows. In Proceedings of the 2013 IEEE Symposium on Computational Intelligence and Data Mining (CIDM), Singapore, 16–19 April 2013; pp. 135–142. [Google Scholar]
- Di Ciccio, C.; Mecella, M. On the Discovery of Declarative Control Flows for Artful Processes. ACM TMIS 2015, 5, 1–37. [Google Scholar] [CrossRef]
- Maggi, F.M. Declarative Process Mining with the Declare Component of ProM. In Proceedings of the Business Process Management Demos, Beijing, China, 26–30 August 2013. [Google Scholar]
- Schönig, S.; Rogge-Solti, A.; Cabanillas, C.; Jablonski, S.; Mendling, J. Efficient and Customisable Declarative Process Mining with SQL. In Proceedings of the International Conference on Advanced Information Systems Engineering, Tallinn, Estonia, 11–15 June 2016. [Google Scholar]
- Schönig, S.; Di Ciccio, C.; Maggi, F.M.; Mendling, J. Discovery of Multi-perspective Declarative Process Models. In Proceedings of the International Conference on Service-Oriented Computing, Hangzhou, China, 12–15 November 2016; pp. 87–103. [Google Scholar]
- Sturm, C.; Schönig, S.; Jablonski, S. A MapReduce Approach for Mining Multi-Perspective Declarative Process Models. In Proceedings of the 20th International Conference on Enterprise Information Systems, ICEIS 2018, Funchal, Portugal, 21–24 March 2018; pp. 585–595. [Google Scholar]
- Maggi, F.M.; Mooij, A.; van der Aalst, W. User-Guided Discovery of Declarative Process Models. In Proceedings of the 2011 IEEE Symposium on Computational Intelligence and Data Mining (CIDM), Paris, France, 11–15 April 2011; pp. 192–199. [Google Scholar]
- Di Ciccio, C.; Schouten, M.H.M.; de Leoni, M.; Mendling, J. Declarative Process Discovery with MINERful in ProM. In Proceedings of the Business Process Management Demos, Innsbruck, Austria, 31 August–3 September 2015; pp. 60–64. [Google Scholar]
- Westergaard, M.; Stahl, C.; Reijers, H. UnconstrainedMiner: Efficient Discovery of Generalized Declarative Process Models; BPM CR, No. BPM-13-28; BPM Center: Eindhoven, The Netherlands, 2013. [Google Scholar]
- Maggi, F.; Bose, R.; van der Aalst, W. A Knowledge-Based Integrated Approach for Discovering and Repairing Declare Maps. In Proceedings of the International Conference on Advanced Information Systems Engineering, Tallinn, Estonia, 11–15 June 2013. [Google Scholar]
- Di Ciccio, C.; Maggi, F.M.; Montali, M.; Mendling, J. Ensuring Model Consistency in Declarative Process Discovery. In Proceedings of the International Conference on Business Process Management, Innsbruck, Australia, 31 August–3 September 2015; pp. 144–159. [Google Scholar]
- Di Ciccio, C.; Maggi, F.M.; Montali, M.; Mendling, J. Resolving inconsistencies and redundancies in declarative process models. Inf. Syst. 2017, 64, 425–446. [Google Scholar] [CrossRef]
- Bose, J.C.; Maggi, F.M.; van der Aalst, W. Enhancing Declare Maps Based on Event Correlations. In Proceedings of the Business Process Management, Beijing, China, 26–30 August 2013; pp. 97–112. [Google Scholar]
- Vanden Broucke, S.K.L.M.; Vanthienen, J.; Baesens, B. Declarative process discovery with evolutionary computing. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; pp. 2412–2419. [Google Scholar] [CrossRef]
- Lamma, E.; Mello, P.; Montali, M.; Riguzzi, F.; Storari, S. Inducing Declarative Logic-Based Models from Labeled Traces. In Proceedings of the International Conference on Business Process Management, Brisbane, Australia, 24–28 September 2007; pp. 344–359. [Google Scholar]
- Chesani, F.; Lamma, E.; Mello, P.; Montali, M.; Riguzzi, F.; Storari, S. Exploiting Inductive Logic Programming Techniques for Declarative Process Mining. Trans. Petri Nets Other Models Concurrency 2009, 2, 278–295. [Google Scholar]
- Räim, M.; Di Ciccio, C.; Maggi, F.M.; Mecella, M.; Mendling, J. Log-Based Understanding of Business Processes through Temporal Logic Query Checking. In Proceedings of the OTM Confederated International Conferences “On the Move to Meaningful Internet Systems”, Amantea, Italy, 27–31 October 2014; pp. 75–92. [Google Scholar]
- Westergaard, M.; Maggi, F.M. Looking into the Future: Using Timed Automata to Provide A Priori Advice about Timed Declarative Process Models; OTM; LNCS; Springer: Berlin, Germany, 2012; Volume 7565, pp. 250–267. [Google Scholar]
- Maggi, F.M. Discovering Metric Temporal Business Constraints from Event Logs. In Proceedings of the International Conference on Business Informatics Research, Lund, Sweden, 22–24 September 2014; pp. 261–275. [Google Scholar]
- Schönig, S.; Cabanillas, C.; Jablonski, S.; Mendling, J. A Framework for Efficiently Mining the Organisational Perspective of Business Processes. Decis. Support Syst. 2016, 89, 87–97. [Google Scholar] [CrossRef]
- Cabanillas, C.; Schönig, S.; Sturm, C.; Mendling, J. Mining Expressive and Executable Resource-Aware Imperative Process Models. In Proceedings of the International Conference on Enterprise, Business-Process and Information Systems Modeling, Tallinn, Estonia, 11–12 June 2018; pp. 3–18. [Google Scholar]
- Schönig, S.; Cabanillas, C.; Ciccio, C.D.; Jablonski, S.; Mendling, J. Mining team compositions for collaborative work in business processes. Softw. Syst. Model. 2018, 17, 675–693. [Google Scholar] [CrossRef]
- Montali, M.; Chesani, F.; Mello, P.; Maggi, F.M. Towards data-aware constraints in declare. In Proceedings of the 28th Annual ACM Symposium on Applied Computing, Coimbra, Portugal, 18–22 March 2013; pp. 1391–1396. [Google Scholar]
- Maggi, F.M.; Dumas, M.; García-Bañuelos, L.; Montali, M. Discovering Data-Aware Declarative Process Models from Event Logs. In Proceedings of the Business Process Management 2013, Beijing, China, 26–30 August 2013; pp. 81–96. [Google Scholar] [CrossRef]
- Burattin, A.; Maggi, F.M.; Sperduti, A. Conformance checking based on multi-perspective declarative process models. Expert Syst. Appl. 2016, 65, 194–211. [Google Scholar] [CrossRef]
- Ackermann, L.; Schönig, S.; Jablonski, S. Simulation of Multi-perspective Declarative Process Models. In Proceedings of the Business Process Management Workshops—BPM 2016 International Workshops, Rio de Janeiro, Brazil, 19 September 2016; Revised Papers. pp. 61–73. [Google Scholar]
- Ackermann, L.; Schönig, S.; Petter, S.; Schützenmeier, N.; Jablonski, S. Execution of Multi-perspective Declarative Process Models. On the Move to Meaningful Internet Systems. In Proceedings of the OTM 2018 Conferences—Confederated International Conferences: CoopIS, C&TC, and ODBASE 2018, Valletta, Malta, 22–26 October 2018; pp. 154–172. [Google Scholar]
- Sturm, C.; Schönig, S.; Ciccio, C.D. Distributed Multi-Perspective Declare Discovery. In Proceedings of the BPM Workshops, Barcelona, Spain, 10–15 September 2017. [Google Scholar]
- Van der Aalst, W.; Pesic, M.; Schonenberg, H. Declarative Workflows: Balancing Between Flexibility and Support. Comput. Sci. Res. Dev. 2009, 23, 99–113. [Google Scholar] [CrossRef]
- Montali, M.; Pesic, M.; van der Aalst, W.M.P.; Chesani, F.; Mello, P.; Storari, S. Declarative Specification and Verification of Service Choreographies. ACM Trans. Web 2010, 4, 3. [Google Scholar] [CrossRef]
- Burattin, A.; Maggi, F.M.; van der Aalst, W.M.; Sperduti, A. Techniques for a Posteriori Analysis of Declarative Processes. In Proceedings of the 16th IEEE International Enterprise Distributed Object Computing Conference, EDOC 2012, Beijing, China, 10–14 September 2012; pp. 41–50. [Google Scholar]
- Dean, J.; Ghemawat, S. MapReduce: Simplified Data Processing on Large Clusters. Commun. ACM 2008, 51. [Google Scholar] [CrossRef]
- Foundation, A.S. Apache Hadoop. 2006. Available online: https://hadoop.apache.org/ (accessed on 5 January 2019).
- Wu, D.; Sakr, S.; Zhu, L. Big Data Programming Models. In Handbook of Big Data Technologies; Zomaya, A.Y., Sakr, S., Eds.; Springer International Publishing: Berlin, Germany, 2017; pp. 31–63. [Google Scholar]
- Boudewijn van Dongen, Real-Life Event Logs—Hospital Log. 2011. Available online: https://doi.org/10.4121/uuid:d9769f3d-0ab0-4fb8-803b-0d1120ffcf54 (accessed on 14 January 2019).
- Boudewijn van Dongen, BPI Challenge 2017. Available online: https://doi.org/10.4121/uuid:5f3067df-f10b-45da-b98b-86ae4c7a310b (accessed on 14 January 2019).
- Boudewijn van Dongen, BPI Challenge 2015. Available online: https://doi.org/10.4121/uuid:31a308ef-c844-48da-948c-305d167a0ec1 (accessed on 14 January 2019).

| Template | LTL Semantics |
|---|---|
| existence | |
| responded existence | |
| response | |
| alternate response | |
| chain response | |
| precedence | |
| alternate precedence | |
| chain precedence | |
| co existence | |
| succession | |
| alternate succession | |
| chain succession | |
| not responded existence | |
| not response | |
| not precedence | |
| not chain response | |
| not chain precedence | |
| not co existence | |
| not succession | |
| not chain succession |
| Trace | |||||
|---|---|---|---|---|---|
| a,b,b,c | ab,1 | bc,1 | ab,1 | a,1 | a,1 |
| ac,1 | bb,1 | b,1 | b,1 | ||
| bb,1 | bc,1 | b,1 | c,1 | ||
| bc,1 | c,1 | ||||
| a,c,d | ac,1 | ac,1 | a,1 | a,1 | |
| ad,1 | cd,1 | c,1 | c,1 | ||
| cd,1 | d,1 | d,1 | |||
| ab,1 | bc,2 | ab,1 | ac,1 | a,2 | a,2 |
| ac,2 | ad,1 | bb,1 | cd,1 | b,2 | b,1 |
| bb,1 | cd,1 | bc,1 | c,2 | c,2 | |
| d,1 | d,1 | ||||
| Constraint | Activated with | Fulfilled with | Trace-/Event-Based |
|---|---|---|---|
| 01. Existence | a | #a | Trace-based |
| 02. Participation | a | # | Trace-based |
| 03. Absence | a | # | Trace-based |
| 04. Uniqueness | a | # | Trace-based |
| 05. Init | a | Trace-based | |
| 06. End | a | Trace-based | |
| 07. Responded Existence | a | b | Event-based |
| 08. Response | a | b | Event-based |
| 09. AlternateResponse | a | b | Event-based |
| 10. ChainResponse | a | b | Event-based |
| 11. Precedence | b | a | Event-based |
| 12. AlternatePrecedence | b | a | Event-based |
| 13. ChainPrecedence | b | a | Event-based |
| 14. CoExistence | Event-based | ||
| 15. Succession | Event-based | ||
| 16. AlternateSuccession | Event-based | ||
| 17. ChainSuccession | Event-based | ||
| 18. NotChainSuccession | Event-based | ||
| 19. NotSuccession | Event-based | ||
| 20. NotCoExistence | Event-based |
| ax | cz | by | bx | dz | by | ax |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 2 | 2 |
| ax | cz | by | bx | dz | by | ax |
|---|---|---|---|---|---|---|
| ✓ | ✓ | ✓ | ✓ | ✓ |
| ax | cz | by | bx | dz |
|---|---|---|---|---|
| 3.. | 2.. | 3.. | 2.. | 2.. |
| ax | cz | by | bx | dz |
|---|---|---|---|---|
| ✓ | ✓ | ✓ |
| ax | cz | by | bx | dz | by | ax |
|---|---|---|---|---|---|---|
| ✓ |
| ax | cz | by | bx | dz | by | ax |
|---|---|---|---|---|---|---|
| ✓ |
| (a) | |||||||
|---|---|---|---|---|---|---|---|
| a | c | b | b | d | b | a | |
| ax | ✓ | ✓ | ✓ | ✓ | |||
| cz | ✓ | ✓ | ✓ | ||||
| by | ✓ | ✓ | ✓ | ✓ | |||
| bx | ✓ | ✓ | ✓ | ✓ | |||
| dz | ✓ | ✓ | ✓ | ||||
| by | ✓ | ✓ | ✓ | ✓ | |||
| ax | ✓ | ✓ | ✓ | ✓ | |||
| (b) | |||||||
| ax | cz | by | bx | dz | by | ax | |
| a | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| c | ✓ | ✓ | ✓ | ✓ | |||
| b | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| b | ✓ | ✓ | ✓ | ✓ | |||
| d | ✓ | ✓ | ✓ | ✓ | |||
| b | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| a | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| (a) | ||||||
|---|---|---|---|---|---|---|
| c | b | b | d | b | a | |
| ax | ✓ | ✓ | ✓ | ✓ | ||
| cz | ✓ | ✓ | ✓ | |||
| by | ✓ | ✓ | ✓ | |||
| bx | ✓ | ✓ | ✓ | |||
| dz | ✓ | ✓ | ||||
| by | ✓ | |||||
| (b) | ||||||
| cz | by | bx | dz | by | ax | |
| a | ✓ | ✓ | ✓ | ✓ | ✓ | |
| c | ✓ | ✓ | ✓ | ✓ | ||
| b | ✓ | ✓ | ✓ | ✓ | ||
| b | ✓ | ✓ | ✓ | |||
| d | ✓ | ✓ | ||||
| b | ✓ | |||||
| (a) | ||||||
|---|---|---|---|---|---|---|
| c(z) | b(y) | b(x) | d(z) | b(y) | a(x) | |
| ax | ✓ | ✓ | ✓ | ✓ | ||
| cz | ✓ | ✓ | ✓ | |||
| by | ✓ | ✓* | ||||
| bx | ✓ | ✓ | ✓ | |||
| dz | ✓ | ✓ | ||||
| by | ✓ | |||||
| (b) | ||||||
| cz | by | bx | dz | by | ax | |
| a | ✓ | ✓ | ✓ | ✓ | ✓ | |
| c | ✓ | ✓ | ✓ | ✓ | ||
| b | ✓ | |||||
| b | ✓ | ✓ | ||||
| d | ✓ | ✓ | ||||
| b | ✓ | |||||
| cz | by | bx | dz | by | ax | |
|---|---|---|---|---|---|---|
| ax | ✓ | |||||
| cz | ✓ | |||||
| by | ✓ | |||||
| bx | ✓ | |||||
| dz | ✓ | |||||
| by | ✓ |
| (a) | ||||||
|---|---|---|---|---|---|---|
| cz | by | bx | dz | by | ax | |
| a | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| c | ✓ | ✓ | ✓ | ✓ | ✓ | |
| b | ✓ | |||||
| b | ✓* | ✓ | ||||
| d | ✓ | ✓ | ||||
| b | ✓ | |||||
| (b) | ||||||
| c | b | b | d | b | a | |
| ax | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| cz | ✓ | ✓ | ✓ | ✓ | ✓ | |
| by | ✓ | ✓ | ✓ | |||
| bx | ✓ | ✓ | ✓ | |||
| dz | ✓ | ✓ | ||||
| by | ✓* | |||||
| (a) | ||||||
|---|---|---|---|---|---|---|
| cz | by | bx | dz | by | ax | |
| a | ✓ | ✓ | ✓ | ✓ | ✓ | |
| c | ✓ | ✓ | ✓ | ✓ | ||
| b | ✓ | |||||
| b | ✓* | ✓ | ||||
| d | ✓ | ✓ | ||||
| b | ✓ | |||||
| (b) | ||||||
| c | b | b | d | b | a | |
| ax | ✓ | ✓ | ✓ | ✓ | ||
| cz | ✓ | ✓ | ✓ | |||
| by | ✓ | ✓ | ||||
| bx | ✓ | ✓ | ✓ | |||
| dz | ✓ | ✓ | ||||
| by | ✓* | |||||
| cz | by | bx | dz | by | ax | |
|---|---|---|---|---|---|---|
| ax | ✓ | |||||
| cz | ✓ | |||||
| by | ✓ | |||||
| bx | ✓ | |||||
| dz | ✓ | |||||
| by | ✓ |
| a(x) | c(z) | b(y) | b(x) | d(z) | b(y) | a(x) | |
|---|---|---|---|---|---|---|---|
| ax | |||||||
| cz | |||||||
| by | |||||||
| bx | |||||||
| dz | |||||||
| by | |||||||
| ax |
| ax | cz | by | bx | dz | by | ax | |
|---|---|---|---|---|---|---|---|
| a(x) | |||||||
| c(z) | |||||||
| b(y) | |||||||
| b(x) | |||||||
| d(z) | |||||||
| b(y) | |||||||
| a(x) |
| Support | Confidence | ||
|---|---|---|---|
| Existence Constraints | Activation | ||
| Target | not defined | not defined | |
| Relation Constraints (forward constraining) | Activation | ||
| Target | |||
| Relation Constraints (history-based) | Activation | ||
| Target | |||
| Mutual Relation Constraints | Activation | ||
| Target | |||
| Negative Relation Constraints | Activation | ||
| Target |
| Single-Perspective * | Multi-Perspective ** | |||||||
|---|---|---|---|---|---|---|---|---|
| Financial Log | Hospital Log | Hospital Log | ||||||
| - | - | - | - | Activation | Target | |||
| Approach | seq. | par. | seq. | par. | seq. | par. | seq. | par. |
| SQLMiner [14,15] | 01:08 | - | 19:30 | - | 15:43 | - | 06:43:05 | - |
| MINERful [11,12] | 00:17 | - | 12:28 | - | - | - | - | - |
| MapReduce | 02:03 | 00:30 | 14:35 | 1:57 | 07:09 | 01:07 | 06:44 | 01:00 |
| MapReduce | MINERful | ||||
|---|---|---|---|---|---|
| Task A | Task B | Support | Confidence | Support | Confidence |
| a | a | 0.25 | 0.083 | - | - |
| a | b | 0.778 | 0.518 | 0.778 | 0.518 |
| a | c | 0.85714 | 0.85714 | 0.85714 | 0.85714 |
| a | d | 0.66 | 0.44 | 0.66 | 0.44 |
| b | a | 0.44 | 0.296 | 0.44 | 0.296 |
| b | b | 0.6 | 0.3997 | - | - |
| b | c | 0.375 | 0.25 | 0.375 | 0.25 |
| b | d | 0.428571 | 0.142857 | 0.428571 | 0.285714 |
| c | a | 0.285714 | 0.285714 | 0.285714 | 0.285714 |
| c | b | 0.5 | 0.33 | 0.5 | 0.33 |
| c | d | 0.8 | 0.533 | 0.8 | 0.5334 |
| d | a | 0.33 | 0.22 | 0.33 | 0.22 |
| d | b | 0.285714 | 0.095238 | 0.285714 | 0.190476 |
| MapReduce | SQLMiner | |||||
|---|---|---|---|---|---|---|
| Task A | Resource A | Task B | Support | Confidence | Support | Confidence |
| a | x | a | 0.33 | 0.22 | - | - |
| a | x | b | 0.66 | 0.44 | 0.66 | 0.44 |
| a | x | c | 0.66 | 0.44 | 0.66 | 0.44 |
| a | y | c | 1.0 | 0.33 | 1.0 | 0.33 |
| a | x | d | 0.33 | 0.22 | 0.33 | 0.22 |
| a | y | d | 1.0 | 0.33 | 1.0 | 0.33 |
| b | x | a | 0.5 | 0.33 | 0.5 | 0.33 |
| b | y | a | 0.66 | 0.44 | 0.66 | 0.44 |
| b | x | b | 1.0 | 0.66 | - | - |
| b | y | b | 0.33 | 0.22 | - | - |
| b | x | c | 0.5 | 0.33 | 0.5 | 0.33 |
| b | y | c | 0.33 | 0.22 | 0.33 | 0.22 |
| b | x | d | 0.5 | 0.33 | 0.5 | 0.33 |
| b | y | d | 0.33 | 0.22 | 0.33 | 0.22 |
| c | z | a | 1.0 | 0.33 | 1.0 | 0.33 |
| c | z | b | 1.0 | 0.33 | 1.0 | 0.33 |
| c | x | d | 0.5 | 0.33 | 0.5 | 0.33 |
| c | z | d | 1.0 | 0.33 | 1.0 | 0.33 |
| d | z | a | 1.0 | 0.33 | 1.0 | 0.33 |
| d | z | b | 1.0 | 0.33 | 1.0 | 0.33 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sturm, C.; Fichtner, M.; Schönig, S. Full Support for Efficiently Mining Multi-Perspective Declarative Constraints from Process Logs. Information 2019, 10, 29. https://doi.org/10.3390/info10010029
Sturm C, Fichtner M, Schönig S. Full Support for Efficiently Mining Multi-Perspective Declarative Constraints from Process Logs. Information. 2019; 10(1):29. https://doi.org/10.3390/info10010029
Chicago/Turabian StyleSturm, Christian, Myriel Fichtner, and Stefan Schönig. 2019. "Full Support for Efficiently Mining Multi-Perspective Declarative Constraints from Process Logs" Information 10, no. 1: 29. https://doi.org/10.3390/info10010029
APA StyleSturm, C., Fichtner, M., & Schönig, S. (2019). Full Support for Efficiently Mining Multi-Perspective Declarative Constraints from Process Logs. Information, 10(1), 29. https://doi.org/10.3390/info10010029





