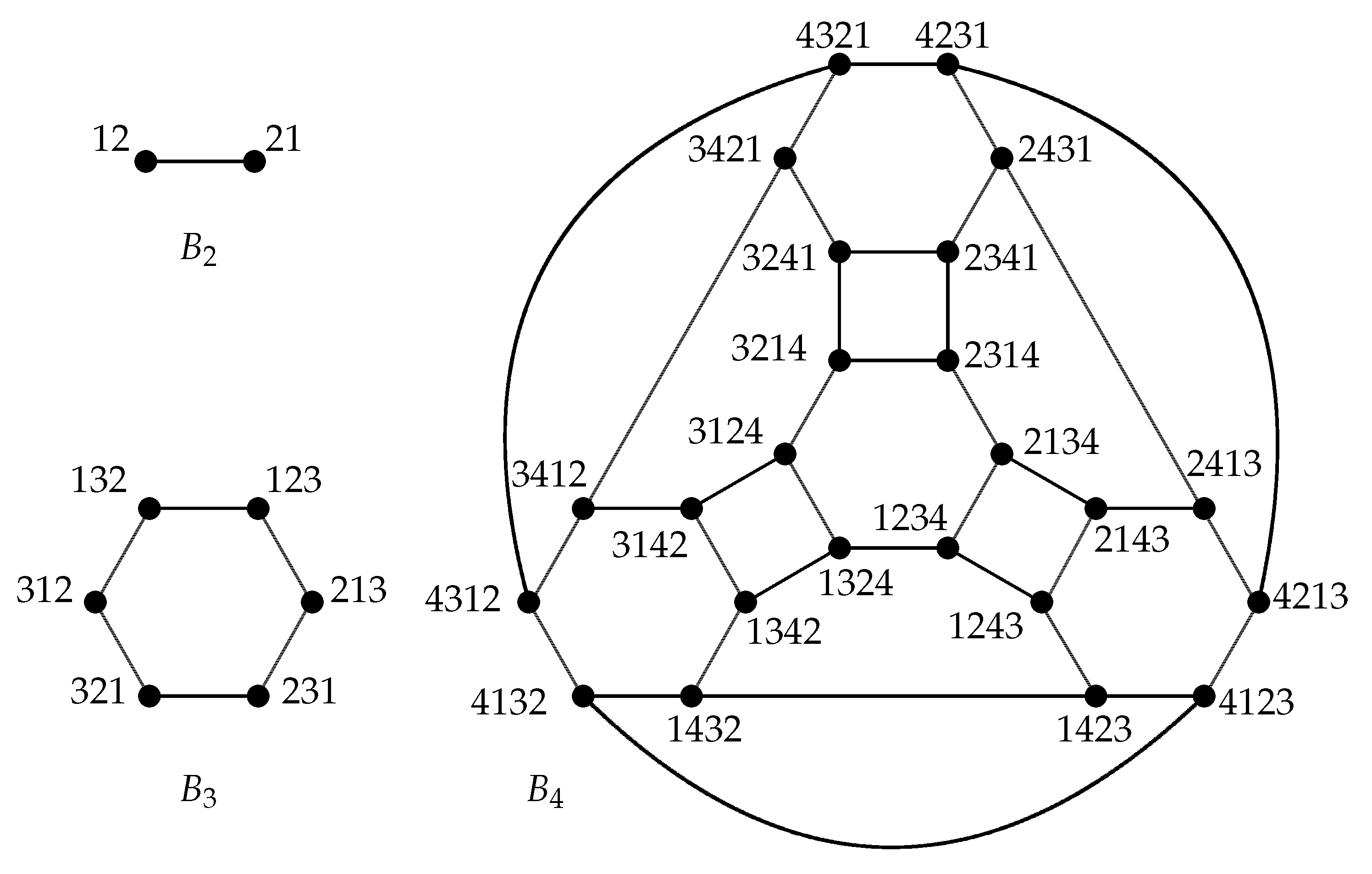
3. The Diagnosability of the Bubble-Sort Graph under the PMC Model
In this section, we shall show the g-good-neighbor diagnosability of the bubble-sort graph under the PMC model for .
Let
and
be two distinct subsets of
V for a system
. Define the symmetric difference
. Yuan et al. [
20] presented a sufficient and necessary condition for a system to be
g-good-neighbor
t-diagnosable under the PMC model.
Lemma 1 ([
20])
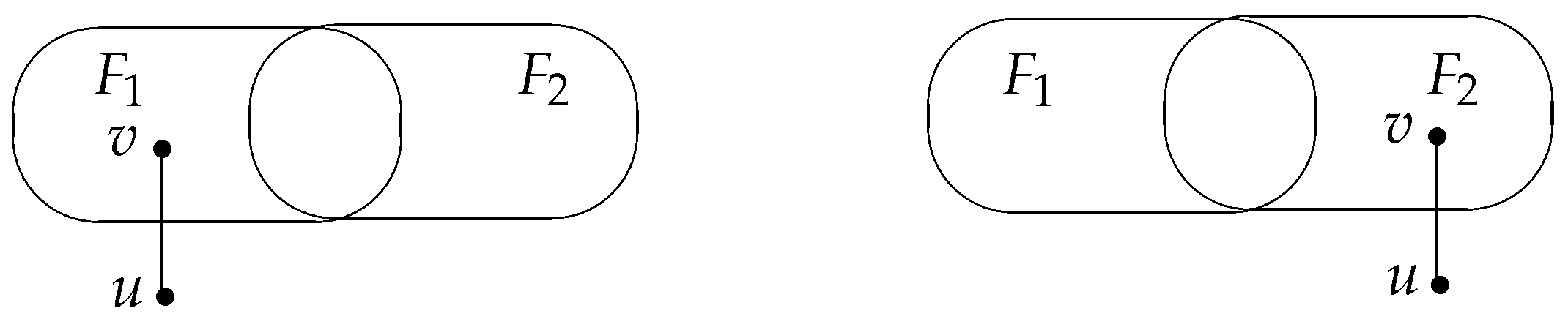
. A system is g-good-neighbor t-diagnosable under the model if and only if there is an edge with and for each distinct pair of g-good-neighbor faulty subsets and of V with and (See Figure 2). The g-good-neighbor diagnosability of G is the maximum value of t such that G is g-good-neighbor t-diagnosable under the PMC model. Theorem 6. The diagnosability of the bubble-sort graph is under the PMC model when .
Proof. Let . Then . Let and . Then and . Since and , there is no edge of between and . By Lemma 1, we show that is not n-diagnosable under the PMC model. Hence, by the definition of the diagnosability, we have that the diagnosability of is less than n-diagnosable, i.e., .
By the definition of the diagnosability, it is sufficient to show that is -diagnosable under the PMC model. By Lemma 1, to prove that is -diagnosable, it is equivalent to prove that there is an edge with and for each distinct pair of faulty subsets and of with and . We prove this statement by contradiction. Suppose that there are two distinct faulty subsets and of with and , but the vertex set pair is not satisfied with the condition in Theorem 1, i.e., there are no edges between and . Without loss of generality, assume that . Suppose . By the definition of , . It is obvious that for . Since , we have that , a contradiction. Therefore, . Since there are no edges between and , and and , we have that is a cut set. By Theorem 2, . Therefore, , which contradicts with that . So is -diagnosable. By the definition of , the diagnosability . □
Theorem 7. The 1-good-neighbor diagnosability of is under the PMC model when .
Proof. Let . By Proposition 2, . Let and . Then and . Let . By Proposition 4, and . By Proposition 2, and or and . Therefore, () in and is a 1-good-neighbor cut of . Since and , there is no edge of between and . By Lemma 1, we show that is not 1-good-neighbor -diagnosable under the PMC model. Hence, by the definition of the 1-good-neighbor diagnosability, we have that .
By the definition of the 1-good-neighbor diagnosability, it is sufficient to show that is 1-good-neighbor -diagnosable. By Lemma 1, to prove that is 1-good-neighbor -diagnosable, it is equivalent to prove that there is an edge with and for each distinct pair of 1-good-neighbor faulty subsets and of with and .
We prove this statement by contradiction. Suppose that there are two distinct 1-good-neighbor faulty subsets and of with and , but the vertex set pair is not satisfied with the condition in Lemma 1, i.e., there are no edges between and . Without loss of generality, assume that . Suppose . Since , we have that , a contradiction. Therefore, .
Since there are no edges between and , and is a 1-good-neighbor faulty set, has two parts and (for convenience). Thus, and . Similarly, when . Therefore, is also a 1-good-neighbor faulty set. When , is also a 1-good-neighbor faulty set. Since there are no edges between and , is a 1-good-neighbor cut. By Theorem 3, . Note that . Therefore, , which contradicts with that . So is 1-good-neighbor -diagnosable. By the definition of , . □
Lemma 2. Let . If , , , then , , , and .
Proof. By , we have that is a 4-cycle. By Propositions 3 and 4, . Thus from calculating, we have , .
Let and and . Let and . By Proposition 1, let . Then . By Proposition 2, there is no such that . Therefore, we consider only . We discuss the following cases.
Case 1. and , .
If , then a contradiction to . Therefore, . In this case, . Consider and , . Suppose . Since , . If , then . If , then, in , . If , then, in , . If , then . If , then, in , . If , then, or in , . Therefore, .
Case 2. and , .
Without loss of generality, let . Let . Then , . If , then . Note . Then . Suppose . Consider and , . If , then, by Theorem 1, . If , then . If , then, in , . If , then, or in , . If , then . If , then, in , . If , then, or in , . Therefore, .
By Cases 1 and 2, () in and is a 2-good-neighbor cut of . When , it is easy to verify that is a 2-good-neighbor cut of . □
Lemma 3. Let . Then the 2-good-neighbor diagnosability under the PMC model.
Proof. Let A be defined in Lemma 2, and let , . By Lemma 2, , , and . Therefore, and are both 2-good-neighbor faulty sets of with and . Since and , there is no edge of between and . By Lemma 1, we show that is not 2-good-neighbor -diagnosable under the PMC model. Hence, by the definition of 2-good-neighbor diagnosability, we conclude that the 2-good-neighbor diagnosability of is less than , i.e., . □
Lemma 4. Let H be a subgraph of such that . Then .
By the definition of , we have Lemma 4.
Lemma 5. Let . Then the 2-good-neighbor diagnosability under the PMC model.
Proof. By the definition of 2-good-neighbor diagnosability, it is sufficient to show that is 2-good-neighbor -diagnosable. By Theorem 1, to prove is 2-good-neighbor -diagnosable, it is equivalent to prove that there is an edge with and for each distinct pair of 2-good-neighbor faulty subsets and of with and .
We prove this statement by contradiction. Suppose that there are two distinct 2-good-neighbor faulty subsets and of with and , but the vertex set pair is not satisfied with the condition in Lemma 1, i.e., there are no edges between and . Without loss of generality, assume that . Suppose . By the definition of , . It is obvious that for . Since , we have that , a contradiction. Therefore, .
Since there are no edges between and , and is a 2-good-neighbor faulty set, has two parts and . Thus, and . Similarly, when . Therefore, is also a 2-good-neighbor faulty set. When , is also a 2-good-neighbor faulty set. Since there are no edges between and , is a 2-good-neighbor cut. Since , by Theorem 4, . By Lemma 4, . Therefore, , which contradicts with that . So is 2-good-neighbor -diagnosable. By the definition of , . □
Combining Lemmas 3 and 5, we have the following theorem.
Theorem 8. Let . Then the 2-good-neighbor diagnosability of the bubble-sort graph under the PMC model is .
Lemma 6. Let . If , , , then , , and .
Proof. By , we have that is 3-regular and .
Claim 1. for .
By Proposition 1, let . By Proposition 2, we consider only . Since , by Proposition 4, we have . The proof of Claim 1 is complete.
By Claim 1, . Thus from calculating, we have , . Let and and . Let and . By Proposition 1, let . Then . By Proposition 2, there is no such that . Therefore, we consider only .
Claim 2. .
Let . We discuss the following cases.
Case 1. and , .
If , then a contradiction to . Therefore, . Consider . If , then . Let .
Consider and , . Suppose . Since , . If , then . If , then, in , . If , then, in , . If , then . If , then, in , . If , then, or in , .
Consider and , . Suppose . Since , . If , then . If , then or in , . If , then or or (). When , in , . When , or in , . When , or in , .
Similarly, consider and . We have . Therefore, .
Case 2. and , .
Without loss of generality, let . Let . Then , . If , then . Note . Then . Suppose . Consider and , . If , then, by Theorem 1, . If , then . If , then, in , . If , then, or in , . If , then . If , then, or in , . If , then, or in , .
Consider and , . If , then, by Theorem 1, . If , then . If , then, in , . If , then, or in , . If , then . If , then, or in , . If , then, or in , . If , then . If , then, or in , . If , then, or in , .
Similarly, consider and . We have . Therefore, . The proof of Claim 2 is complete.
By Claim 2, () in and is a 3-good-neighbor cut of . □
Lemma 7. Let . Then the 3-good-neighbor diagnosability under the PMC model.
Proof. Let A be defined in Lemma 6, and let , . By Lemma 6, , , and . Therefore, and are both 3-good-neighbor faulty sets of with and . Since and , there is no edge of between and . By Lemma 1, we can deduce that is not 3-good-neighbor -diagnosable under the PMC model. Hence, by the definition of 3-good-neighbor diagnosability, we conclude that the 2-good-neighbor diagnosability of is less than , i.e., . □
Lemma 8. Let H be a subgraph of such that . Then .
Proof. Note that there is no subgraph of . Suppose, on the contrary, that there is a subgraph of such that and . Since is bipartite, let and , . By Proposition 1, let and . Since , , a contradiction to Proposition 4. Therefore, . □
Lemma 9. Let . Then the 3-good-neighbor diagnosability under the PMC model.
Proof. By the definition of 3-good-neighbor diagnosability, it is sufficient to show that is 3-good-neighbor -diagnosable. By Lemma 1, to prove is 3-good-neighbor -diagnosable, it is equivalent to prove that there is an edge with and for each distinct pair of 3-good-neighbor faulty subsets and of with and .
We prove this statement by contradiction. Suppose that there are two distinct 3-good-neighbor faulty subsets and of with and , but the vertex set pair is not satisfied with the condition in Lemma 1, i.e., there are no edges between and . Without loss of generality, assume that . Suppose . By the definition of , . It is obvious that for . Since , we have that , a contradiction. Therefore, .
Since there are no edges between and , and is a 3-good-neighbor faulty set, has two parts and . Thus, and . Similarly, when . Therefore, is also a 3-good-neighbor faulty set. When , is also a 3-good-neighbor faulty set. Since there are no edges between and , is a 3-good-neighbor cut. Since , by Theorem 5, . By Lemma 8, . Therefore, , which contradicts with that . So is 3-good-neighbor -diagnosable. By the definition of , . □
Combining Lemmas 7 and 9, we have the following theorem.
Theorem 9. Let . Then the 3-good-neighbor diagnosability of the bubble-sort graph under the PMC model is .
4. The Diagnosability of the Bubble-Sort Graph under the MM Model
Before discussing the diagnosability of the bubble-sort graph under the MM model, we first give an existing result.
Lemma 10 ([
4,
20])
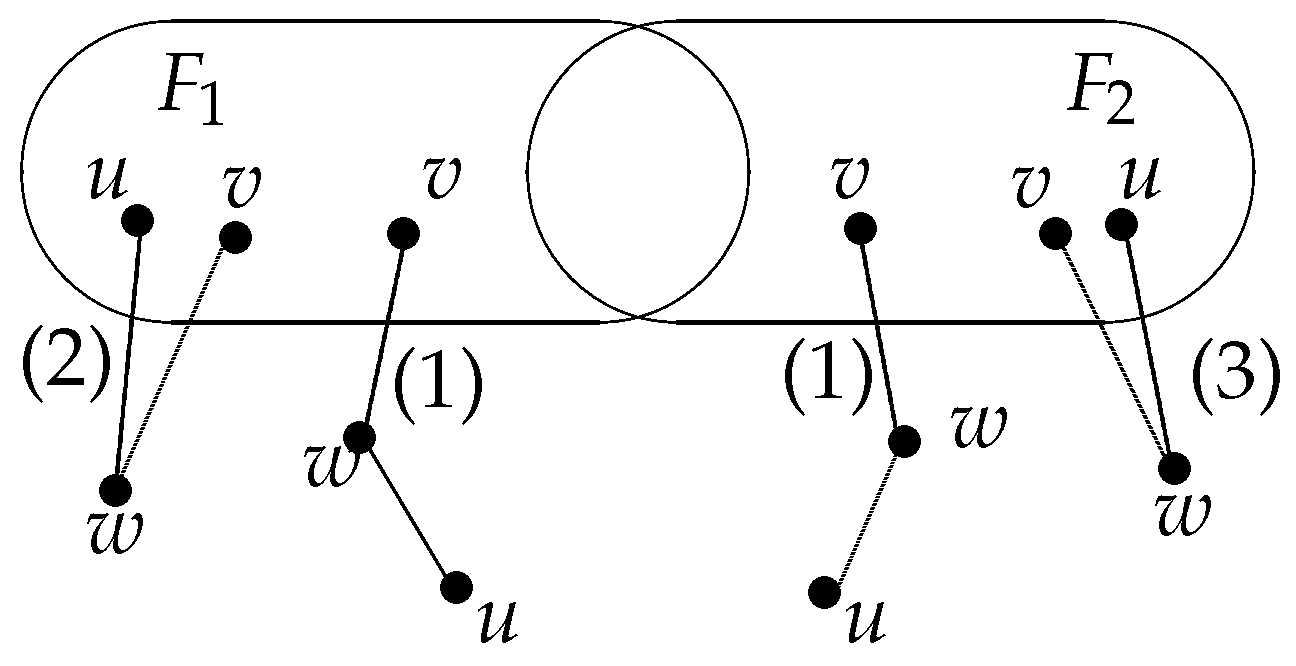
. A system is g-good-neighbor t-diagnosable under the model if and only if for each distinct pair of g-good-neighbor faulty subsets and of V with and satisfies one of the following conditions. (1) There are two vertices and there is a vertex such that and . (2) There are two vertices and there is a vertex such that and . (3) There are two vertices and there is a vertex such that and (See Figure 3). The g-good-neighbor diagnosability of G is the maximum value of t such that G is g-good-neighbor t-diagnosable under the MM model. Theorem 10 ([
12])
. The diagnosability of is under the MM model when . A component of a graph G is odd according as it has an odd number of vertices. We denote by the number of odd component of G.
Lemma 11 ([
22])
. A graph has a perfect matching if and only if for all . Lemma 12 ([
22])
. Let be an integer. Then every k-regular bipartite graph has k edge-disjoint perfect matchings. Since the bubble-sort graph is a regular bipartite graph, we have the following corollary by Lemma 12.
Corollary 1. The bubble-sort graph has a perfect matching.
Lemma 13. Let . Then the 1-good-neighbor diagnosability of the bubble-sort graph under the MM model is less than or equal to , i.e., .
Proof. Let and . Then u is adjacent to v. Let and . By Proposition 2, , . Let . By Proposition 4, and . By Proposition 2, if , then or if , then . Therefore, () in and is a 1-good-neighbor cut of . Since and , there is no edge of between and . By Lemma 10, we show that is not 1-good-neighbor -diagnosable under the MM model. Hence, by the definition of the 1-good-neighbor diagnosability, we have that . □
Lemma 14. Let . Then the 1-good-neighbor diagnosability of the bubble-sort graph under the MM model is more than or equal to , i.e., .
Proof. By the definition of 1-good-neighbor diagnosability, it is sufficient to show that is 1-good-neighbor -diagnosable. By Lemma 10, suppose, on the contrary, that there are two distinct 1-good-neighbor faulty subsets and of with and , but the vertex set pair is not satisfied with any one condition in Theorem 10. Without loss of generality, assume that Similarly to the discussion on in Theorem 3, we have .
Claim 1. has no isolated vertex.
Suppose, on the contrary, that has at least one isolated vertex w. Since is a 1-good-neighbor faulty set, there is a vertex such that u is adjacent to w. Since the vertex set pair is not satisfied with any one condition in Lemma 10, there is at most one vertex such that u is adjacent to w. Thus, there is just a vertex such that u is adjacent to w. Assume . Then . Since is a 1-good-neighbor faulty set, has no isolated vertex, a contradiction. Therefore, let as follows. Similarly, we can show that there is just a vertex such that v is adjacent to w. Let be the set of isolated vertices in , and let H be the subgraph induced by the vertex set . Then for any , there are neighbors in . By Corollary 1, has a perfect matching. By Lemma 11, . Assume . Note that . This is a contradiction to . So . Since the vertex set pair is not satisfied with the condition (1) of Theorem 10, and any vertex of is not isolated in H, we induce that there is no edge between and . Thus, is a vertex cut of and , i.e., is a 1-good-neighbor cut of . By Theorem 3, . Because and , and neither nor is empty, we have . Let and . Then for any vertex , w is adjacent to and . According to Proposition 4, there are at most three common neighbors for any pair of vertices in , it follows that there are at most two isolated vertices in , i.e., .
Suppose that there is exactly one isolated vertex v in . Let and be adjacent to v. Then . Note that has no 3-cycle. Thus, , , and and . Thus, . It follows that , which contradicts .
Suppose that there are exactly two isolated vertices v and w in . Let and be adjacent to v and w, respectively. Then , , , , and . , and . By Proposition 4, there are at most two common neighbors for any pair of vertices in . Thus, it follows that . Thus, . It follows that , which contradicts . The proof of Claim 1 is complete.
Let . By Claim 1, u has at least one neighbor in . Since the vertex set pair is not satisfied with any one condition in Lemma 10, by the condition (1) of Lemma 10, for any pair of adjacent vertices , there is no vertex such that and . It follows that u has no neighbor in . By the arbitrariness of u, there is no edge between and . Since and is a 1-good-neighbor faulty set, and hence . Since both and are 1-good-neighbor faulty sets, and there is no edge between and , is a 1-good-neighbor cut of . By Theorem 3, . Therefore, , which contradicts with that . So is 1-good-neighbor -diagnosable. By the definition of , . □
Combining Lemmas 13 and 14, we have the following theorem.
Theorem 11. Let . Then the 1-good-neighbor diagnosability of the bubble-sort graph under the MM model is .
Lemma 15. Let . Then the 2-good-neighbor diagnosability under the MM model.
Proof. Let A, and be defined in Lemma 2. By the Lemma 2, , , then , , , and . So both and are 2-good-neighbor faulty sets. By the definitions of and , . Note , and . Therefore, both and are not satisfied with any one condition in Lemma 10, and is not 2-good-neighbor -diagnosable. Hence, . The proof is complete. □
Lemma 16. Let . Then the 2-good-neighbor diagnosability under the MM model.
Proof. By the definition of 2-good-neighbor diagnosability, it is sufficient to show that is 2-good-neighbor -diagnosable. By Lemma 10, suppose, on the contrary, that there are two distinct 2-good-neighbor faulty subsets and of with and , but the vertex set pair is not satisfied with any one condition in Lemma 10. Without loss of generality, assume that Similarly to the discussion on in Lemma 5, we have .
Claim 1. has no isolated vertex.
Suppose, on the contrary, that has at least one isolated vertex w. Since is a 2-good neighbor faulty set, there are two vertices such that u and v are adjacent to w. Since the vertex set pair is not satisfied with any one condition in Lemma 10, this is a contradiction. Therefore, has no isolated vertex. The proof of Claim 1 is complete.
Let . By Claim 1, u has at least one neighbor in . Since the vertex set pair is not satisfied with any one condition in Theorem 10, by the condition (1) of Lemma 10, for any pair of adjacent vertices , there is no vertex such that and . It follows that u has no neighbor in . By the arbitrariness of u, there is no edge between and . Since and is a 2-good-neighbor faulty set, . By Lemma 4, . Since both and are 2-good-neighbor faulty sets, and there is no edge between and , is a 2-good-neighbor cut of . By Theorem 4, we have . Therefore, , which contradicts . Therefore, is 2-good-neighbor -diagnosable and . The proof is complete. □
Combining Lemmas 15 and 16, we have the following theorem.
Theorem 12. Let . Then the 2-good-neighbor diagnosability of the bubble-sort star graph under the model is .
We point out that
is the least bubble-sort graph satisfying the three sufficient conditions in Lemma 10. Because
is a cycle with six vertices which is isomorphic to the 3-dimensional star graph, by [
21]
is not 2-diagnosable.
Lemma 17. Let . Then the 3-good-neighbor diagnosability under the MM model.
Proof. Let A, and be defined in Lemma 6. By the Lemma 6, , , then , , , and . So both and are 3-good-neighbor faulty sets. By the definitions of and , . Note , and . Therefore, both and are not satisfied with any one condition in Lemma 10, and is not 3-good-neighbor -diagnosable. Hence, . The proof is complete. □
Lemma 18. Let . Then the 3-good-neighbor diagnosability under the MM model.
Proof. By the definition of 3-good-neighbor diagnosability, it is sufficient to show that is 3-good-neighbor -diagnosable. By Lemma 10, suppose, on the contrary, that there are two distinct 3-good-neighbor faulty subsets and of with and , but the vertex set pair is not satisfied with any one condition in Lemma 10. Without loss of generality, assume that Similarly to the discussion on in Lemma 9, we have .
Claim 1. has no isolated vertex.
Suppose, on the contrary, that has at least one isolated vertex w. Since is a 3-good neighbor faulty set, there are three vertices such that u, v and x are adjacent to w. Since the vertex set pair is not satisfied with any one condition in Lemma 10, this is a contradiction. Therefore, has no isolated vertex. The proof of Claim 1 is complete.
Let . By Claim 1, u has at least one neighbor in . Since the vertex set pair is not satisfied with any one condition in Theorem 10, by the condition (1) of Lemma 10, for any pair of adjacent vertices , there is no vertex such that and . It follows that u has no neighbor in . By the arbitrariness of u, there is no edge between and . Since and is a 3-good-neighbor faulty set, . By Lemma 8, . Since both and are 3-good-neighbor faulty sets, and there is no edge between and , is a 3-good-neighbor cut of . By Theorem 5, we have . Therefore, , which contradicts . Therefore, is 3-good-neighbor -diagnosable and . The proof is complete. □
Combining Lemmas 17 and 18, we have the following theorem.
Theorem 13. Let . Then the 3-good-neighbor diagnosability of the bubble-sort graph under the model is .