Comparative Study of Ant Colony Algorithms for Multi-Objective Optimization
Abstract
:1. Introduction
2. The Basic Process of Solving the Multi-Objective Optimization Problem (MOP) by the Ant Colony Algorithm
- (1)
- Initialization: initialize the parameters of the algorithm, the pheromone information and heuristic information.
- (2)
- Solution construction: for each ant i, construct a new solution by using a probabilistic rule to choose solution components. The rule is a function of the current solution to sub-problem i, pheromone and heuristic information.
- (3)
- Solution evaluation: evaluate the solution of each ant obtained in step 2, store the non-dominated solutions, and eliminate the dominated ones.
- (4)
- Update of pheromone matrices: update the pheromone matrix by using information extracted from the newly constructed solutions. The pheromone related with edges in a non-dominated solution will increase.
- (5)
- Termination: if a problem-specific stopping condition is met, such as the number of iterations and the running time, the algorithm stops and outputs the non-dominated solution set, otherwise go back to step 2.
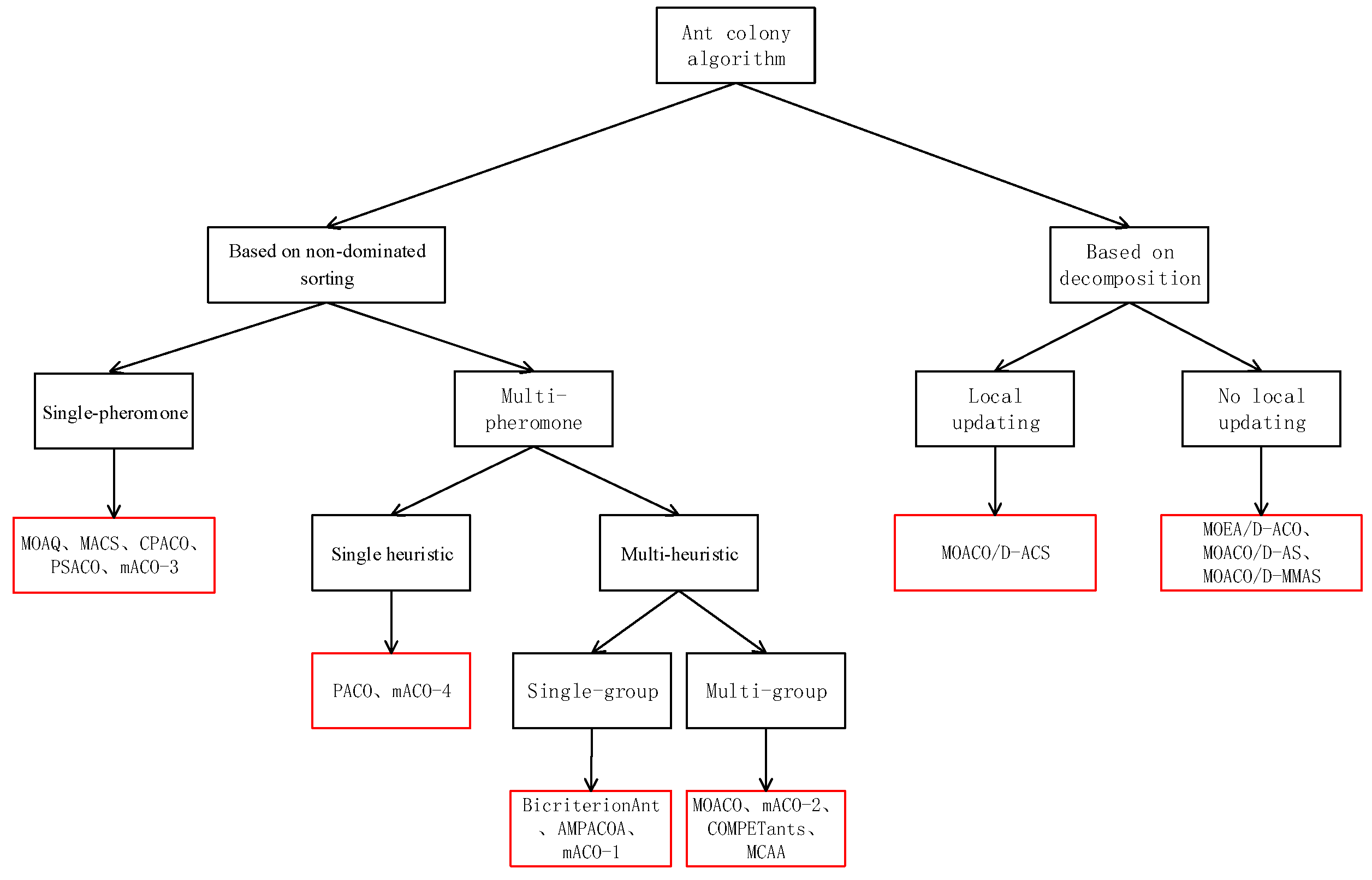
3. Classification of Multi-Objective Ant Colony Algorithms
3.1. Multi-Objective Ant Colony Algorithms Based on Non-Dominated Sorting
3.1.1. Single-Pheromone Matrix
3.1.2. Multi-Pheromone Matrix
- (1)
- Single-heuristic matrix: the single heuristic matrix means that all ants in the algorithm share a heuristic matrix in the process of constructing the solution, including PACO [42], mACO-4 [40] and so on. The PACO algorithm is updated in a special way, using the best solution and second-best solutions to update pheromone information. The pheromone aggregation method used in mACO-4 is the same as mACO-1, but mACO-4 uses only one heuristic information matrix.
- PACO algorithm: this algorithm uses many pheromone matrices and one heuristic matrix. All ants share this heuristic matrix. Each pheromone matrix is responsible for one objective. As with the MACS, each ant has a weight vector, and all pheromone matrices are aggregated by using the weighted sum. This algorithm uses the best solution and second-best solutions of each objective to update pheromone information. The non-dominated solutions generated by the single-heuristic matrix mainly approximate to the central part of the Pareto Front [35].
- (2)
- Multi-heuristic matrix: this kind of algorithm uses a number of pheromone matrices and many heuristic matrices. According to the number of groups, these algorithms are divided into single-group and multi-group.
- (a)
- Single-group: the representative algorithms for this kind of algorithms are BicriterionAnt [43], AMPACOA [44], mACO-1 [40] and so on. Each ant in BicriterionAnt has a weight vector to aggregate pheromone information and heuristic information. AMPACOA is based on the first generation ant colony algorithm AS, and its characteristic is its pheromone updating way. This algorithm assigns a weight to each non-dominated solution based on the length of time when the non-dominated solution added. The weight is used to compute the coefficients of this non-dominated solution, and the coefficient of each non-dominated solution is related to the pheromone increment. The mACO-1 uses many ant groups. Each ant group is responsible for one objective, and it also has an additional ant group. It aggregates pheromone information and heuristic information of each ant group randomly by the weighted sum. The best solution for each group is used to update the respective pheromone matrices. The optimal solution for each objective generated by the additional group is to update the pheromone matrices of other groups.
- BicriterionAnt algorithms: this algorithm uses many pheromone matrices and many heuristic matrices, all of which are aggregated by the weighted sum. The number of weights equals the ants’, and each ant has a weight vector. When constructing the solution, the ants first calculate the probability of each untapped city by aggregating pheromone information and heuristic information. Then select the next city to go by roulette wheel selection. This algorithm uses the non-dominated solution generated by the current iteration to update the pheromone information.
- (b)
- Multi-group: this kind of algorithm differs from the single group in using more than one ant groups, including MOACO [45], mACO-2 [40], COMPETants [46], MACC [47] and so on. The MOACO algorithm uses multiple weights, but if the number of weights is less than the number of ants, the same weight may be used by different ants. The pheromone used by mACO-2 is the sum of the pheromones of all groups, rather than the weighted sum method used by mACO-1. The COMPETants algorithm divides the ants into three groups, each with a weight w = {0,0.5,1}. Each group of ants uses its weight vector to aggregate pheromone matrices and heuristic matrix to construct solution. The MACC algorithm divides the ants into multiple groups. Each group is responsible for one objective, and has its heuristic information and pheromone information. The pheromone matrice of each group is updated based on the best solution generated in the current iteration.
- MOACO algorithm: the MOACO algorithm uses multiple pheromone matrices and more heuristic matrices. Each pheromone matrix and heuristic matrix is responsible for one objective. All the ants are divided into many groups. Each group has multiple weights, and each ant in the group has a weight vector. If the number of weights in the group is less than the number of ants, the extra ants are assigned weights from the beginning. That is, it is possible that two or more ants in a group may use the same weight vector. The ant uses its weight vector to aggregate the pheromone information and heuristic information by the weighted product method. It then calculates the probability of the unvisited city to move to, and chooses the next city to visit by wheel roulette selection to construct the solution. Finally, it uses the non-dominated solution generated by current iteration to update the pheromone information.
3.2. Multi-Objective Ant Colony Algorithms Based on Decomposition
3.2.1. Local Updating
3.2.2. No Local Updating
4. Experimental Comparisons of Typical Multi-Objective Ant Colony Algorithms
- Initialization: initialize the parameters of the algorithm, the pheromone information and heuristic information. Initialize the objective1, the objective2 and the pheromone τ on each edge. Such as edge (A, B) and initialize the parameters: α, β, λ, ρ etc. According to the weight λi, calculate the pheromone matrix τi and heuristic matrix ηi of each ant.
- Solution construction: each ant constructs a solution based on a probability function P consisting of pheromone information and heuristic information. Through the following probability function, each ant i constructs a path according to its τi and ηi.where C represents a set of all the cities that are connected with the city m and unvisited by the ant i.
- Solution evaluation: evaluate the solution of each ant in step 2. Store the non-dominated solution in the non-dominated solution set according to the relationship of dominance. Moreover eliminate the dominated solution.
- Update of pheromone matrices: updating pheromone information τ on all edges: If the edge is in the non-dominated solution, it is updated by pheromone increment. Otherwise, volatile the pheromone, that is, the pheromone increment is 0. The formula is as follows:where ρ is the volatilization factor and Δτ is the pheromone increment.
- Termination: determine the number of iterations whether met the max value or whether the runtime is over. If there is no end, return to step 2 to continue. Otherwise, output the set of non-dominated solutions, then the algorithm is ended.
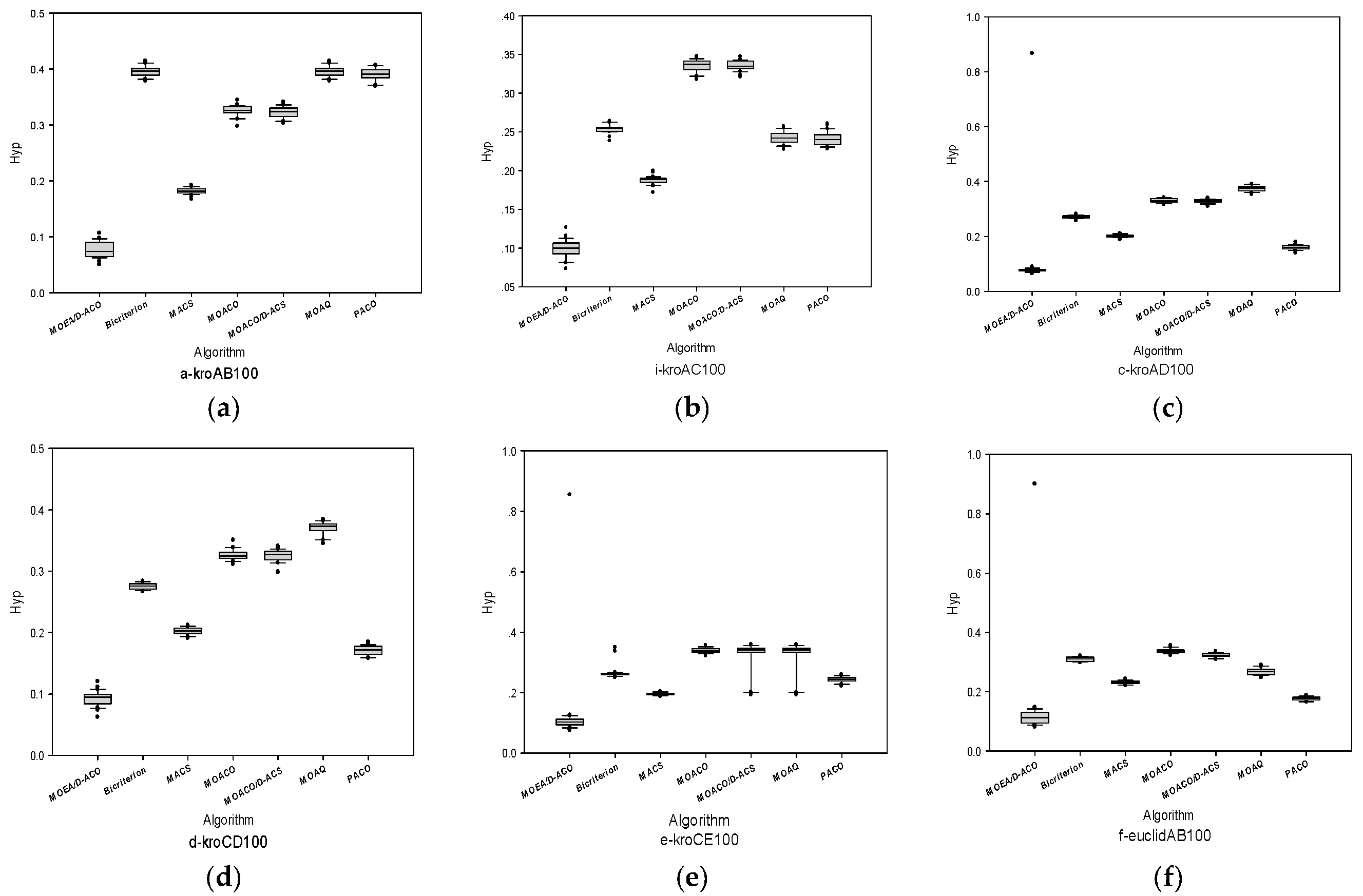
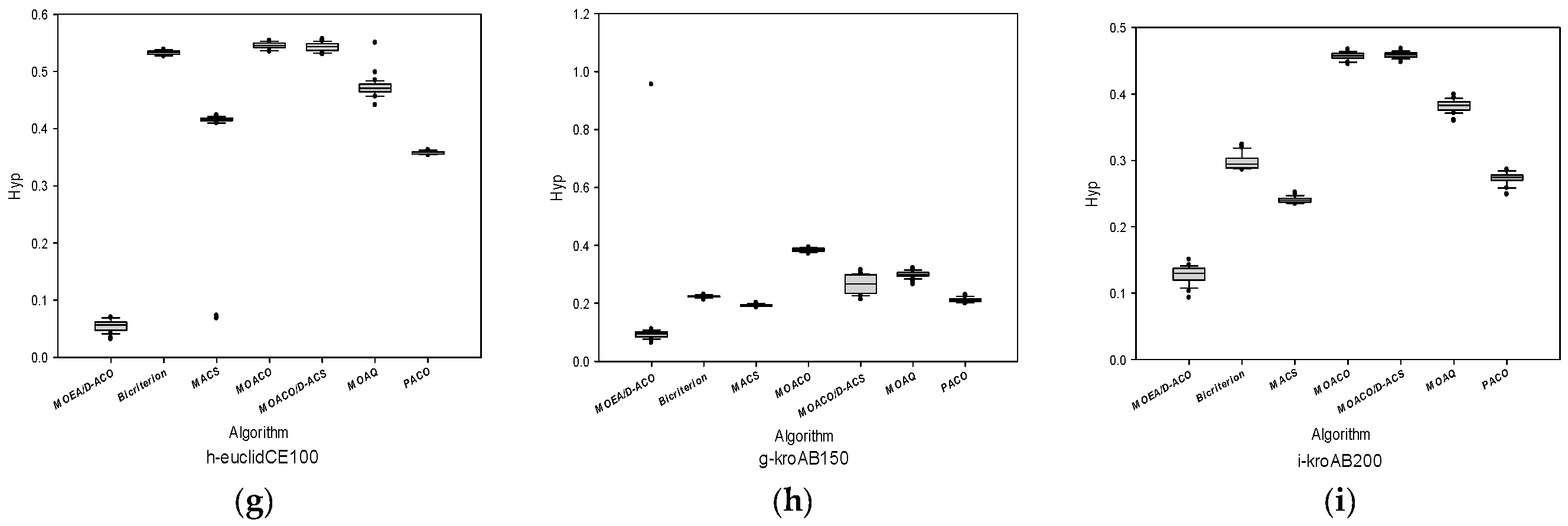
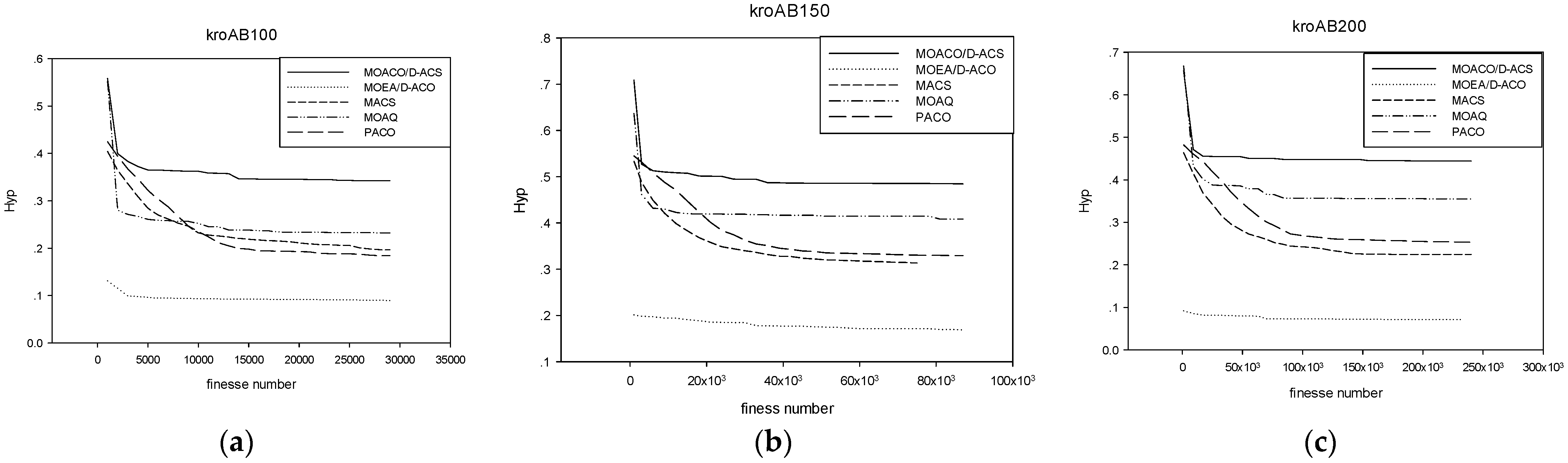
4.1. Comparison Based on H-Indicator
4.2. Convergence Analysis Based on H-indicator
4.3. Comparison of Hypothesis Testing
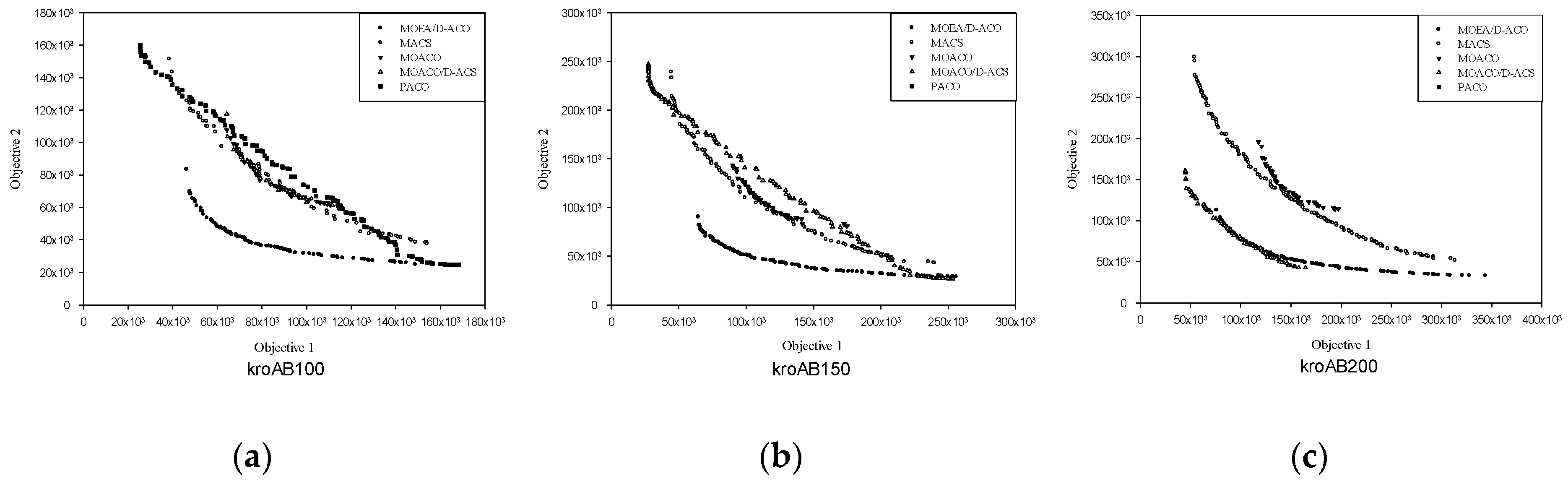
4.4. Approximate Pareto Front
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wei, W.; Ouyang, D.T.; Lv, S.; Feng, Y.X. Multiobjective Path Planning under Dynamic Uncertain Environment. Chin. J. Comput. 2011, 34, 836–846, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Kalyanmoy, D.; Himanshu, J. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Non-dominated Sorting Approach, Part I: Solving Problems with Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar]
- Wen, R.Q.; Zhong, S.B.; Yuan, H.Y.; Huang, Q.Y. Emergency Resource Multi-Objective Optimization Scheduling Model and Multi-Colony Ant Optimization Algorithm. J. Comput. Res. Dev. 2013, 50, 1464–1472, (In Chinese with English Abstract). [Google Scholar]
- He, Z.N.; Yen, G.G. Visualization and Performance Metric in Many-Objective Optimization. IEEE Trans. Evol. Comput. 2016, 20, 386–402. [Google Scholar] [CrossRef]
- Ganguly, S. Multi-objective planning for reactive power compensation of radial distribution networks with unified power quality conditioner allocation using particle swarm optimization. IEEE Trans. Power Syst. 2014, 29, 1801–1810. [Google Scholar] [CrossRef]
- Yu, X.; Chen, W.N.; Hu, X.M.; Zhang, J. A Set-based Comprehensive Learning Particle Swarm Optimization with Decomposition for Multi-objective Traveling Salesman Problem. In Proceedings of the 2015 Annual Conference on Genetic and Evolutionary Computation, Madrid, Spain, 11–15 July 2015; pp. 89–96. [Google Scholar]
- Horng, S.C. Combining artificial bee colony with ordinal optimization for stochastic economic lot scheduling problem. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 373–384. [Google Scholar] [CrossRef]
- Gao, W.F.; Huang, L.L.; Liu, S.Y.; Dai, C. Artificial bee colony algorithm based on information learning. IEEE Trans. Cybern. 2015, 45, 2827–2839. [Google Scholar] [CrossRef]
- Jara, E.C. Multi-Objective Optimization by Using Evolutionary Algorithms: The p-Optimality Criteria. IEEE Trans. Evol. Comput. 2014, 18, 167–179. [Google Scholar] [CrossRef]
- Cai, X.Y.; Li, Y.X.; Fan, Z.; Zhang, Q.F. An external archive guided multi-objective evolutionary algorithm based on decomposition for combinatorial optimization. IEEE Trans. Evol. Comput. 2015, 19, 508–523. [Google Scholar]
- Eldurssi, A.M.; O’Connell, R.M. A fast non-dominated sorting guided genetic algorithm for multi-objective power distribution system reconfiguration problem. IEEE Trans. Power Syst. 2015, 30, 593–601. [Google Scholar] [CrossRef]
- Cheng, Y.F.; Shao, W.; Zhang, S.J. An Improved Multi-Objective Genetic Algorithm for Large Planar Array Thinning. IEEE Trans. Magnet. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Zuo, L.Y.; Shu, L.; Dong, S.B.; Zhu, C.S.; Hara, T. A Multi-Objective Optimization Scheduling Method Based on the Ant Colony Algorithm in Cloud Computing. IEEE Access 2015, 3, 2687–2699. [Google Scholar] [CrossRef]
- Gao, L.R.; Gao, J.W.; Li, J.; Plaza, A.; Zhuang, L.; Sun, X.; Zhang, B. Multiple algorithm integration based on ant colony optimization for endmember extraction from hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 2569–2582. [Google Scholar] [CrossRef]
- Liu, Y.X.; Gao, C.; Zhang, Z.L.; Lu, Y.; Chen, S.; Liang, M.; Tao, L. Solving NP-hard problems with Physarum-based ant colony system. IEEE/ACM Trans. Comput. Biol. Bioinform. 2017, 14, 108–120. [Google Scholar] [CrossRef]
- Yu, Y.; Li, Y.; Li, J. Nonparametric modeling of magnetorheological elastomer base isolator based on artificial neural network optimized by ant colony algorithm. J. Intell. Mater. Syst. Struct. 2015, 26, 1789–1798. [Google Scholar] [CrossRef]
- Liu, Q.; Chen, H.; Zhang, Y.G.; Li, J.; Zhang, S.B. An Ant Colony Optimization Algorithm Based on Dynamic Evaporation Rate and Amended Heruistic. J. Comput. Res. Dev. 2012, 49, 620–627. [Google Scholar]
- Zeng, M.F.; Chen, S.Y.; Zhang, W.Q.; Nie, C.H. Generating covering arrays using ant colony optimization: Exploration and mining. Ruan Jian Xue Bao/J. Softw. 2016, 27, 855–878. Available online: http://www.jos.org.cn/1000-9825/4974.htm (accessed on 3 October 2017). (In Chinese with English Abstract).
- Lin, Z.Y.; Zou, Q.; Lai, Y.X.; Lin, C. Dynamic result optimization for keyword search over relational databases. Jian Xue Bao/J. Softw. 2014, 25, 528–546. Available online: http://www.jos.org.cn/1000-9825/4384.htm (accessed on 9 August 2017).
- Wen, Y.P.; Liu, J.X.; Chen, Z.G. Instance aspect handling-oriented scheduling optimization in workflows. Jian Xue Bao/J. Softw. 2015, 26, 574–583. Available online: http://www.jos.org.cn/1000-9825/4767.htm (accessed on 22 September 2017). (In Chinese with English Abstract).
- Wang, G.C.; Feng, P.; Wang, Z.; Peng, Y.; Huang, S.Q. Study on Engery Consumption Optimization Routing Strategy Based on Rate Adaptation. Chin. J. Comput. 2015, 38, 555–566. [Google Scholar]
- Wang, X.Y.; Choi, T.M.; Liu, H.K.; Yue, X.H. Novel Ant Colony Optimization Methods for Simplifying Solution Construction in Vehicle Routing Problems. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3132–3141. [Google Scholar] [CrossRef]
- Hajar, B.T.; Ali, M.H.; Rizwan, M. Simultaneous Reconfiguration, Optimal Placement of DSTATCOM and Photovoltaic Array in a Distribution System Based on Fuzzy-ACO Approach. IEEE Trans. Sustain. Energy 2015, 6, 210–218. [Google Scholar]
- Ariyasingha, I.D.I.D.; Fernando, T.G.I. Performance analysis of the multi-objective ant colony optimization algorithms for the traveling salesman problem. Swarm Evol. Comput. 2015, 23, 11–26. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Xing, H.L.; Li, T.R.; Yang, Y.; Qu, R.; Pan, Y. A Modified Ant Colony Optimization Algorithm for Network Coding Resource Minimization. IEEE Trans. Evol. Comput. 2016, 20, 325–342. [Google Scholar] [CrossRef]
- Juang, C.-F.; Jeng, T.-L.; Chang, Y.-C. An Interpretable Fuzzy System Learned Through Online Rule Generation and Multiobjective ACO with a Mobile Robot Control Application. IEEE Trans. Cybern. 2016, 46, 2706–2718. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.J.; Shen, J. Multi-Phase Ant Colony System for Multi-Party Data-Intensive Service Provision. IEEE Trans. Serv. Comput. 2016, 9, 264–276. [Google Scholar] [CrossRef]
- Chica, M.; Cordón, Ó.; Damas, S.; Bautista, J. Interactive preferences in multiobjective ant colony optimisation for assembly line balancing. Soft Comput. 2015, 19, 2891–2903. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, W.N.; Hu, X.; Zhang, J. An Ant Colony Optimizing Algorithm Based on Scheduling Preference for Maximizing Working Time of WSN. In Proceedings of the Genetic and Evolutionary Computation, Madrid, Spain, 11–15 July 2015; pp. 41–48. [Google Scholar]
- Xiao, J.; Gao, M.L.; Huang, M.M. Empirical Study of Multi-objective Ant Colony Optimization to Software Project Scheduling Problems. In Proceedings of the 2015 Annual Conference on Genetic and Evolutionary Computation, Madrid, Spain, 11–15 July 2015; pp. 759–766. [Google Scholar]
- Tsutsui, S.; Fujimoto, N. A Comparative Study of Synchronization of Parallel ACO on Multi-core Processor. In Proceedings of the 2015 Annual Conference on Genetic and Evolutionary Computation, Madrid, Spain, 11–15 July 2015; pp. 777–778. [Google Scholar]
- Krynicki, K.; Houle, M.E.; Jaen, J. An efficient ant colony optimization strategy for the resolution of multi-class queries. Knowl.-Based Syst. 2016, 105, 96–106. [Google Scholar] [CrossRef]
- Verdaguer, M.; Clara, N.; Monclús, H.; Poch, M. A step forward in the management of multiple wastewater streams by using an ant colony optimization-based method with bounded pheromone. Process Saf. Environ. Protect. 2016, 102, 799–809. [Google Scholar] [CrossRef]
- Kucukkoc, I.; Zhang, D.Z. Mixed-model parallel two-sided assembly line balancing problem: A flexible agent-based ant colony optimization approach. Comput. Ind. Eng. 2016, 97, 58–72. [Google Scholar] [CrossRef] [Green Version]
- López-Ibáñez, M.; Stützle, T. The impact of design choices of multiobjective antcolony optimization algorithms on performance: An experimental study on the biobjective TSP. In Proceedings of the 2015 Annual Conference on Genetic and Evolutionary Computation, Portland, OR, USA, 7–11 July 2010; pp. 71–78. [Google Scholar]
- García-Martínez, C.; Cordón, O.; Herrera, F. A taxonomy and an empirical analysis of multiple objective ant colony optimization algorithms for the bi-criteria TSP. Eur. J. Oper. Res. 2007, 180, 116–148. [Google Scholar] [CrossRef] [Green Version]
- Barán, B.; Schaerer, M. A Multiobjective Ant Colony System for Vehicle Routing Problem with Time Windows. In Proceedings of the 21st IASTED international Multi-Conference on Applid Informatics, Innsbruck, Austria, 10–13 February 2003; pp. 97–102. [Google Scholar]
- Angus, D. Crowding Population-based Ant Colony Optimisation for the Multi-objective Travelling Salesman Problem. In Proceedings of the 2007 IEEE Symposium on Computational Intelligence in Multi-Criteria Decision-Making, Honolulu, HI, USA, 1–5 April 2007; pp. 333–340. [Google Scholar]
- Thantulage, G.I.F. Ant Colony Optimization Based Simulation of 3D Automatic Hose/Pipe Routing; Brunel University: London, UK, 2009. [Google Scholar]
- Solnon, C. Ant colony optimization for multi-objective optimization problems. In Proceedings of the 19th IEEE International Conference on Tools with Artificial Intelligence (ICTAI 2007), Patras, Greece, 29–31 October 2007; Volume 1, pp. 450–457. [Google Scholar]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Doerner, K.; Gutjahr, W.J.; Hartl, R.F.; Strauss, C.; Stummer, C. Pareto ant colony optimization: A metaheuristic approach to multiobjective portfolio selection. Ann. Oper. Res. 2004, 131, 79–99. [Google Scholar] [CrossRef]
- Iredi, S.; Merkle, D.; Middendorf, M. Bi-criterion optimization with multi colony ant algorithms. In Proceedings of the Evolutionary Multi-Criterion Optimization, Zurich, Switzerland, 7–9 March 2001; Volume 8, pp. 359–372. [Google Scholar]
- Bui, L.T.; Whitacre, J.M.; Abbass, H.A. Performance analysis of elitism in multi-objective ant colony optimization algorithms. In Proceedings of the IEEE Congress on Evolutionary Computation, Hong Kong, China, 1–6 June 2008; pp. 1633–1640. [Google Scholar]
- López-Ibánez, M.; Stützle, T. The automatic design of multiobjective ant colony optimization algorithms. IEEE Trans. Evol. Comput. 2012, 16, 861–875. [Google Scholar] [CrossRef]
- Doerner, K.; Hartl, R.F.; Reimann, M. Are COMPETants More Competent for Problem Solving? The Case of a Multiple Objective Transportation Problem; Vienna University of Economics and Business: Vienna, Austria, 2001; p. 11. [Google Scholar]
- Shrivastava, R.; Singh, S.; Dubey, G.C. Multi objective optimization of time cost quality quantity using multi colony ant algorithm. Int. J. Contemp. Math. Sci. 2012, 7, 773–784. [Google Scholar]
- Cheng, J.X.; Zhang, G.X.; Li, Z.D.; Li, Y.Q. Multi-objective ant colony optimization based on decomposition for bi-objective traveling salesman problems. Soft Comput. 2012, 16, 597–614. [Google Scholar] [CrossRef]
- Zhang, Q.F.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Ke, L.; Zhang, Q.F.; Battiti, R. MOEA/D-ACO: A multi-objective evolutionary algorithm using decomposition and ant colony. IEEE Trans. Cybern. 2013, 43, 1845–1859. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- While, L.; Bradstreet, L.; Barone, L. A fast way of calculating exact hyper-volumes. IEEE Trans. Evol. Comput. 2012, 16, 86–95. [Google Scholar] [CrossRef]
- Basseur, M.; Zeng, R.Q.; Hao, J.K. Hyper-volume-based multi-objective local search. Neural Comput. Appl. 2012, 21, 1917–1929. [Google Scholar] [CrossRef]
- Nowak, K.; Märtens, M.; Izzo, D. Empirical performance of the approximation of the least hypervolume contributor. In Proceedings of the Parallel Problem Solving from Nature–PPSN XIII, Ljubljana, Slovenia, 13–17 September 2014; Volume 8672, pp. 662–671. [Google Scholar]

| Case | Algorithm | Max | Min | Mean | Standard |
|---|---|---|---|---|---|
| kroAB100 | MOEA/D-ACO | 0.1062 | 0.0505 | 0.0767 | 0.0144815 |
| MACS | 0.1924 | 0.1675 | 0.1823 | 0.0054743 | |
| MOACO/D-ACS | 0.3412 | 0.3037 | 0.3236 | 0.0105447 | |
| MOACO | 0.3452 | 0.2985 | 0.3254 | 0.0093617 | |
| PACO | 0.4076 | 0.3695 | 0.3912 | 0.011176 | |
| kroAC100 | MOEA/D-ACO | 0.1264 | 0.0734 | 0.0989 | 0.0115925 |
| MACS | 0.1995 | 0.1723 | 0.1885 | 0.0051235 | |
| MOACO/D-ACS | 0.3475 | 0.3211 | 0.3352 | 0.0063372 | |
| MOACO | 0.3472 | 0.3182 | 0.3352 | 0.0077542 | |
| PACO | 0.2612 | 0.2285 | 0.2413 | 0.0086281 | |
| kroAD100 | MOEA/D-ACO | 0.8672 | 0.0638 | 0.1035 | 0.1443142 |
| MACS | 0.2103 | 0.1881 | 0.2022 | 0.0050040 | |
| MOACO/D-ACS | 0.3404 | 0.3102 | 0.3283 | 0.0066690 | |
| MOACO | 0.3412 | 0.3173 | 0.3312 | 0.0074212 | |
| PACO | 0.1802 | 0.1401 | 0.1612 | 0.0089611 | |
| kroCD100 | MOEA/D-ACO | 0.1201 | 0.0624 | 0.0925 | 0.0122063 |
| MACS | 0.2123 | 0.1912 | 0.2021 | 0.0057761 | |
| MOACO/D-ACS | 0.3412 | 0.2971 | 0.3251 | 0.0103092 | |
| MOACO | 0.2121 | 0.1912 | 0.2021 | 0.0057761 | |
| PACO | 0.1853 | 0.1582 | 0.1713 | 0.0074041 | |
| kroCE100 | MOEA/D-ACO | 0.8363 | 0.0857 | 0.1337 | 0.1378296 |
| MACS | 0.2090 | 0.1932 | 0.2017 | 0.0040522 | |
| MOACO/D-ACS | 0.3828 | 0.3482 | 0.3601 | 0.0083833 | |
| MOACO | 0.3803 | 0.1986 | 0.3602 | 0.0509902 | |
| PACO | 0.2784 | 0.2451 | 0.2793 | 0.0072993 | |
| euclidAB100 | MOEA/D-ACO | 0.9044 | 0.0853 | 0.1427 | 0.1452584 |
| MACS | 0.2469 | 0.2254 | 0.2355 | 0.0054608 | |
| MOACO/D-ACS | 0.3359 | 0.3102 | 0.3236 | 0.0070820 | |
| MOACO | 0.3568 | 0.3224 | 0.3371 | 0.0074314 | |
| PACO | 0.1926 | 0.1693 | 0.1808 | 0.0066197 | |
| euclidCE100 | MOEA/D-ACO | 0.0703 | 0.0319 | 0.0548 | 0.0101184 |
| MACS | 0.4239 | 0.0681 | 0.3925 | 0.0924695 | |
| MOACO/D-ACS | 0.5572 | 0.5305 | 0.5432 | 0.0074305 | |
| MOACO | 0.5597 | 0.5352 | 0.5454 | 0.0055957 | |
| PACO | 0.3638 | 0.3543 | 0.3582 | 0.0026483 | |
| kroAB150 | MOEA/D-ACO | 0.9661 | 0.0797 | 0.1395 | 0.1555635 |
| MACS | 0.2010 | 0.1998 | 0.2086 | 0.0036208 | |
| MOACO/D-ACS | 0.4149 | 0.3901 | 0.4066 | 0.0309838 | |
| MOACO | 0.3102 | 0.2758 | 0.2913 | 0.0060745 | |
| PACO | 0.3061 | 0.2887 | 0.2976 | 0.0071204 | |
| kroAB200 | MOEA/D-ACO | 0.1673 | 0.0901 | 0.1387 | 0.0139102 |
| MACS | 0.2506 | 0.2333 | 0.2398 | 0.0042814 | |
| MOACO/D-ACS | 0.4664 | 0.4439 | 0.4566 | 0.0055929 | |
| MOACO | 0.4665 | 0.4455 | 0.4569 | 0.0044351 | |
| PACO | 0.2833 | 0.2459 | 0.2697 | 0.0095473 |
| Max | Min | Mean | Standard | Middle | Quality | |
|---|---|---|---|---|---|---|
| kroAB100 | MOEA/D-ACO | MOEA/D-ACO | MOEA/D-ACO | MACS | MOEA/D-ACO | MOEA/D-ACO |
| kroAC100 | MOEA/D-ACO | MOEA/D-ACO | MOEA/D-ACO | MACS | MOEA/D-ACO | MOEA/D-ACO |
| kroAD100 | PACO | MOEA/D-ACO | MOEA/D-ACO | MACS | MOEA/D-ACO | MOEA/D-ACO |
| kroCD100 | MOEA/D-ACO | MOEA/D-ACO | MOEA/D-ACO | BicriterionAnt | MOEA/D-ACO | MOEA/D-ACO |
| kroCE100 | MACS | MOEA/D-ACO | MOEA/D-ACO | BicriterionAnt | MOEA/D-ACO | MOEA/D-ACO |
| euclidAB100 | PACO | MOEA/D-ACO | MOEA/D-ACO | MACS | MOEA/D-ACO | MOEA/D-ACO |
| euclidCE100 | MOEA/D-ACO | MOEA/D-ACO | MOEA/D-ACO | PACO | MOEA/D-ACO | MOEA/D-ACO |
| kroAB150 | MACS | MOEA/D-ACO | MOEA/D-ACO | MACS | MOEA/D-ACO | MOEA/D-ACO |
| kroAB200 | MOEA/D-ACO | MOEA/D-ACO | MOEA/D-ACO | MACS | MOEA/D-ACO | MOEA/D-ACO |
| MOEA/D-ACO | MACS | MOACO | MOACO/D-ACS | P-ACO | |
|---|---|---|---|---|---|
| MOEA/D-ACO | - | 1.0 × 10−8 | 2.6 × 10−32 | 4.5 × 10−35 | 2.1 × 10−71 |
| MACS | >0.05 | - | 7.4 × 10−15 | 2.3 × 10−17 | 8.3 × 10−56 |
| MOACO | >0.05 | >0.05 | - | 1.9 × 10−5 | 7.5 × 10−31 |
| MOACO/D-ACS | >0.05 | >0.05 | 8.1 × 10−5 | - | 4.4 × 10−28 |
| P-ACO | >0.05 | >0.05 | >0.05 | >0.05 | - |
| kroAC100/H-Indicator | |||||||
|---|---|---|---|---|---|---|---|
| MOEA/D-ACO | BicriterionAnt | MACS | MOACO | MOACO/D-ACS | MOAQ | P-ACO | |
| MOEA/D-ACO | - | 7.8 × 10−66 | 1.1 × 10−10 | 1.3 × 10−93 | 6.3 × 10−93 | 6.1 × 10−45 | 1.0 × 10−42 |
| BicriterionAnt | >0.05 | - | >0.05 | 4.1 × 10−25 | 4.0 × 10−24 | >0.05 | >0.05 |
| MACS | >0.05 | 6.5 × 10−47 | - | 9.9 × 10−79 | 6.0 × 10−78 | 5.8 × 10−24 | 4.8 × 10−22 |
| MOACO | >0.05 | >0.05 | >0.05 | - | >0.05 | >0.05 | >0.05 |
| MOACO/D-ACS | >0.05 | >0.05 | >0.05 | >0.05 | - | >0.05 | >0.05 |
| MOAQ | >0.05 | 2.3 × 10−13 | >0.05 | 1.6 × 10−49 | 1.6 × 10−48 | - | >0.05 |
| P-ACO | >0.05 | 3.0 × 10−14 | >0.05 | 6.4 × 10−50 | 5.9 × 10−49 | >0.05 | - |
| MOEA/D-ACO | MACS | MOACO | MOACO/D-ACS | P-ACO | |
|---|---|---|---|---|---|
| MOEA/D-ACO | - | 5.5 × 10−24 | 3.7 × 10−72 | 1.0 × 10−69 | 7.4 × 10−7 |
| MACS | >0.05 | - | 3.8 × 10−40 | 3.6 × 10−37 | >0.05 |
| MOACO | >0.05 | >0.05 | - | >0.05 | >0.05 |
| MOACO/D-ACS | >0.05 | >0.05 | >0.05 | - | >0.05 |
| PACO | >0.05 | 3.6 × 10−10 | 4.2 × 10−59 | 2.1 × 10−56 | - |
| MOEA/D-ACO | MACS | MOACO | MOACO/D-ACS | P-ACO | |
|---|---|---|---|---|---|
| MOEA/D-ACO | - | 3.7 × 10−48 | 8.4 × 10−105 | 2.3 × 10−105 | 1.0 × 10−18 |
| MACS | >0.05 | - | 1.7 × 10−61 | 2.6 × 10−62 | >0.05 |
| MOACO | >0.05 | >0.05 | - | >0.05 | >0.05 |
| MOACO/D-ACS | >0.05 | >0.05 | >0.05 | - | >0.05 |
| PACO | >0.05 | 1.0 × 10−18 | 2.7 × 10−85 | 5.9 × 10−86 | - |
| MOEA/D-ACO | MACS | MOACO | MOACO/D-ACS | P-ACO | |
|---|---|---|---|---|---|
| MOEA/D-ACO | - | 2.3 × 10−16 | 3.5 × 10−66 | 1.7 × 10−66 | 7.7 × 10−5 |
| MACS | >0.05 | - | 1.0 × 10−39 | 2.2 × 10−41 | >0.05 |
| MOACO | >0.05 | >0.05 | - | >0.05 | >0.05 |
| MOACO/D-ACS | >0.05 | >0.05 | >0.05 | - | >0.05 |
| PACO | >0.05 | 6.9 × 10−7 | 4.0 × 10−55 | 5.5 × 10−56 | - |
| MOEA/D-ACO | MACS | MOACO | MOACO/D-ACS | P-ACO | |
|---|---|---|---|---|---|
| MOEA/D-ACO | - | 1.1 × 10−25 | 4.7 × 10−96 | 7.0 × 10−82 | 2.4 × 10−7 |
| MACS | >0.05 | - | 8.4 × 10−69 | 1.2 × 10−50 | >0.05 |
| MOACO | >0.05 | >0.05 | - | >0.05 | >0.05 |
| MOACO/D-ACS | >0.05 | >0.05 | 1.7 × 10−10 | - | >0.05 |
| PACO | >0.05 | 6.2 × 10−11 | 4.7 × 10−85 | 2.8 × 10−69 | - |
| MOEA/D-ACO | MACS | MOACO | MOACO/D-ACS | P-ACO | |
|---|---|---|---|---|---|
| MOEA/D-ACO | - | 2.8 × 10−16 | 2.0 × 10−47 | 5.1 × 10−102 | 8.0 × 10−8 |
| MACS | >0.05 | - | 1.4 × 10−23 | 8.6 × 10−72 | >0.05 |
| MOACO | >0.05 | >0.05 | - | >0.05 | >0.05 |
| MOACO/D-ACS | >0.05 | >0.05 | >0.05 | - | >0.05 |
| PACO | >0.05 | 4.2 × 10−7 | 3.0 × 10−32 | 2.7 × 10−76 | >0.05 |
| MOEA/D-ACO | MACS | MOACO | MOACO/D-ACS | P-ACO | |
|---|---|---|---|---|---|
| MOEA/D-ACO | - | 6.8 × 10−5 | 4.6 × 10−94 | 1.8 × 10−70 | 8.3 × 10−19 |
| MACS | >0.05 | - | 1.8 × 10−83 | 4.6 × 10−56 | 2.4 × 10−8 |
| MOACO | >0.05 | >0.05 | - | >0.05 | >0.05 |
| MOACO/D-ACS | >0.05 | >0.05 | >0.05 | - | >0.05 |
| PACO | >0.05 | >0.05 | 1.5 × 10−67 | 1.0 × 10−34 | - |
| MOEA/D-ACO | MACS | MOACO | MOACO/D-ACS | PACO | |
|---|---|---|---|---|---|
| MOEA/D-ACO | - | 4.4 × 10−16 | 1.7 × 10−115 | 8.1 × 10−117 | 4.6 × 10−44 |
| MACS | >0.05 | - | 2.7 × 10−103 | 7.2 × 10−105 | 1.3 × 10−18 |
| MOACO | >0.05 | >0.05 | - | >0.05 | >0.05 |
| MOACO/D-ACS | >0.05 | >0.05 | >0.05 | - | >0.05 |
| PACO | >0.05 | >0.05 | 4.4 × 10−84 | 5.3 × 10−86 | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ning, J.; Zhang, C.; Sun, P.; Feng, Y. Comparative Study of Ant Colony Algorithms for Multi-Objective Optimization. Information 2019, 10, 11. https://doi.org/10.3390/info10010011
Ning J, Zhang C, Sun P, Feng Y. Comparative Study of Ant Colony Algorithms for Multi-Objective Optimization. Information. 2019; 10(1):11. https://doi.org/10.3390/info10010011
Chicago/Turabian StyleNing, Jiaxu, Changsheng Zhang, Peng Sun, and Yunfei Feng. 2019. "Comparative Study of Ant Colony Algorithms for Multi-Objective Optimization" Information 10, no. 1: 11. https://doi.org/10.3390/info10010011
APA StyleNing, J., Zhang, C., Sun, P., & Feng, Y. (2019). Comparative Study of Ant Colony Algorithms for Multi-Objective Optimization. Information, 10(1), 11. https://doi.org/10.3390/info10010011





