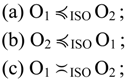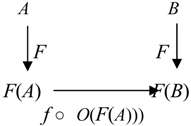3. The Phenomenological Stratum of the General Theory of Information
The general theory of information is constructed as an axiomatic theory and has three levels: Conceptual, methodological (also called meta-theoretical) and theoretical.
On the conceptual level, the essence of information as a dynamic object playing a pivotal role in all walks of reality is explicated. This allows clarifying a quantity of misconceptions, fallacies and illusions.
Methodological (meta-theoretical) level is based on two classes of principles and their relations. The first class contains ontological principles, which bring to light general properties and regularities of information and its functioning. Principles from the second class explain how to measure information and are called axiological principles.
On the theoretical level, axioms of theoretical structures and axioms reflecting features of information are introduced and utilized for building models of information and related phenomena, e.g., information flow or information processing. These models are employed in studies of information and various related systems and phenomena, e.g., information flow in society or information processing systems, such as computers and networks.
To clarify the concept of information, we consider here the basic ontological principles. The first of them separates local and global approaches to information definition, i.e., in what context information is defined.
Ontological Principle O1 (the Locality Principle). It is necessary to separate information in general from information (or a portion of information) for a system R.
In other words, empirically, it is possible to speak only about information (or a portion of information) for a system. In the mathematical model studied in this paper, portions of information are formalized as information operators in infological system representation spaces.
Definition 3.1. The system R with respect to which some information is considered is called the receiver, receptor or recipient of this information.
Such a receiver/recipient can be a person, community, class of students, audience in a theater, animal, bird, fish, computer, network, database and so on.
The Locality Principle explicates an important property of information, but does not answer the question “What is information?” The essence of information is described by the second ontological principle, which has several forms.
Ontological Principle O2 (the General Transformation Principle). In a broad sense, information for a system R is a capacity to cause changes in the system R.
Thus, we may understand information in a broad sense as a capacity (ability or potency) of things, both material and abstract, to change other things. Information exists in the form of portions of information. Informally, a portion of information is such information that can be separated from other information. Information is, as a rule, about something. What information is about is called the object of this information.
The Ontological Principle O2 has several consequences. First, it demonstrates that information is closely connected to transformation. Namely, it means that information and transformation are functionally similar because they both point to changes in a system. At the same time, they are different because information is potency for (or in some sense, cause of) change, while transformation is the change itself, or in other words, transformation is an operation, while information is what induces this operation.
Second, the Ontological Principle O2 explains
why information influences society and individuals all the time, as well as why this influence grows with the development of society. Namely, reception of information by individuals and social groups induces transformation. In this sense, information is similar to energy. Moreover, according to the Ontological Principle O2, energy is a kind of information in a broad sense. This well correlates with the von Weizsäcker's idea (
cf. [
3]) that
energy might in the end turn out to be information.
Third, the Ontological Principle O2 makes it possible to separate different kinds of information. For instance, people, as well as any computer, have many kinds of memory. It is even supposed that each part of the brain has several types of memory agencies that work in somewhat different ways to suit particular purposes [
28]. Thus, it is possible to consider each of these memory agencies as a separate system and to study differences between information that changes each type of memory. This might help to understand the interplay between stability and flexibility of mind, in general, and memory, in particular.
In essence, we can see that all kinds and types of information are encompassed by the Ontological Principle O2. In the most concise form, it is demonstrated in [
7].
However, the common usage of the word information does not imply such wide generalizations as the Ontological Principle O2 implies. Thus, we need a more restricted theoretical meaning because an adequate theory, whether of information or of anything else, must be in significant accord with our common ways of thinking and talking about what the theory is about, else there is the danger that theory is not about what it purports to be about.
Information in a proper sense is defined based on the concept of structural infological systems. In essence, any subsystem of a system may be considered as its infological system. However, information in a proper sense acts on structural infological systems. An infological system is structural if all its elements are structures. For example, systems of knowledge, which are paradigmatic infological systems, are structural because their elements are structures. Other examples of structural infological systems are: systems of beliefs, systems of values, systems of goals, and systems of ideas.
To achieve precision in the information definition, we do two conceptual steps. At first, we make the concept of information relative to the chosen infological system IF(
R) of the system
R and then we select a specific class of infological systems to specify information in the strict sense. That is why it is impossible and, as well as, counterproductive to give an exact and thus, too rigid and restricted definition of an infological system. Indeed, information is a very rich and widespread phenomenon to be reflected by a restricted rigid definition (
cf. for example, [
2,
7,
29,
30]).
Infological system plays the role of a free parameter in the general theory of information, providing for representation of different kinds and types of information in this theory. That is why the concept of infological system, in general, should not be limited by boundaries of exact definitions. A free parameter must really be free. Identifying an infological system IF(R) of a system R, we can define information relative to this system. This definition is expressed in the following principle.
Ontological Principle O2g (the Relativized Transformation Principle). Information for a system R relative to the infological system IF(R) is a capacity to cause changes in the system IF(R).
As a model example of an infological system IF(R) of an intelligent system R, we take the system of knowledge of R. In cybernetics, it is called the thesaurus Th(R) of the system R. Another example of an infological system is the memory of a computer. Such a memory is a place in which data and programs are stored and is a complex system of diverse components and processes.
Elements from IF(R) are called infological elements.
There is no exact definition of infological elements although there are various entities that are naturally considered as infological elements as they allow one to build theories of information that inherit conventional meanings of the word information. For instance, knowledge, data, images, ideas, algorithms, procedures, scenarios, schemas, values, goals, ideals, fantasies, abstractions, beliefs, and similar objects are standard examples of infological elements.
When we take a physical system D as the infological system and allow only for physical changes, information with respect to D coincides with energy.
Taking a mental system B as the infological system and considering only mental changes, we see that information with respect to B coincides with mental energy.
These ideas are crystallized in the following principle.
Ontological Principle O2a (the Special Transformation Principle). Information in the strict sense or proper information or, simply, information for a system R, is a capacity to change structural infological elements from an infological system IF(R) of the system R.
To better understand how infological systems can help explicating the concept of information in the strict (conventional) sense, we consider cognitive infological systems.
An infological system IF(R) of the system R is called cognitive if IF(R) contains (stores) elements or constituents of cognition, such as knowledge, data, ideas, fantasies, abstractions, beliefs, etc. A cognitive infological system of a system R is denoted by CIF(R) and is related to cognitive information.
In this case, it looks like it is possible to give an exact definition of a cognitive infological system. However, now cognitive sciences do not know all structural elements involved in cognition. A straightforward definition specifies cognition as an activity (process) that gives knowledge. At the same time, we know that knowledge, as a rule, comes through data and with data. So, data are also involved in cognition and thus, have to be included in cognitive infological systems. Besides, cognitive processes utilize such structures as ideas, algorithms, procedures, scenarios, images, beliefs, values, measures, problems, tasks, etc. Thus, to comprehensively represent cognitive information, it is imperative to include all such objects in cognitive infological systems.
For those who prefer to have an exact definition contrary to a broader perspective, it is possible to define a cognitive infological system as the system of knowledge. This approach was used by [
31,
32].
Cognitive infological systems are standard examples of infological systems, while their elements, such as knowledge, data, images, ideas, fantasies, abstractions, and beliefs, are standard examples of infological elements. Cognitive infological systems are very important, especially, for intelligent systems as the majority of researchers believe that information is intrinsically connected to knowledge.
Ontological Principle O2c (the Cognitive Transformation Principle). Cognitive information for a system R, is a capacity to cause changes in the cognitive infological system CIF(R) of the system R.
As the cognitive infological system contains knowledge of the system it belongs to, cognitive information is the source of knowledge changes.
It is useful to understand that in the definition of cognitive information, as well as of other types of information in the strict sense, it is assumed that an infological system IF(R) of the system R is a part (subsystem) of the system R. However, people have always tried to extend their cognitive tools using different things from their environment. In ancient times, people made marks on stones and sticks. Then they used paper. Now they use computers and computer networks.
There are two ways to take this peculiarity into consideration. In one approach, it is suggested to consider extended infological systems that do not completely belong to the primary system R that receives information. For instance, taking an individual A, it is possible to include in the extended cognitive infological system IF(A) of A not only the mind of A but also memory of the computer that A uses, books that A reads and cognitive objects used by A.
Another approach extends the primary system R as a cognitive object, including all objects used for cognitive purposes. In this case, when we regard an individual A as a cognitive system R, we have to include (in R) all cognitive tools used by A. The second approach does not demand to consider extended infological systems. In this case, all infological systems of R are parts (subsystems) of the primary system R.
As a result, we come to the situation where the concept of information is considered on three basic levels of generality:
Information in a broad sense is considered when there are no restrictions on the infological system (cf. Ontological Principle O2).
Information in the strict sense is considered when the infological system consists of structural elements (cf. Ontological Principle O2a).
Cognitive information is considered when the infological system consists of cognitive structures, such as knowledge, beliefs, ideas, images, etc. (cf. Ontological Principle O2c).
As a result, we come to three levels of information understanding:
Information in a broad sense for a system R is a capability (potential) to change (transform) this system in any way.
Information in the strict sense for a system
R is a capability (potential) to change (transform) structural components of this system, e.g., cognitive information changes knowledge of the system, affective information changes the state of the system, while effective information changes system orientation [
7].
Cognitive information for a system R is a capability (potential) to change (transform) the cognitive subsystem of this system.
Let us explicate other properties of information, taking into consideration a portion I of informationfor a system R.
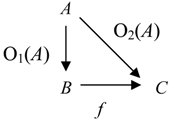
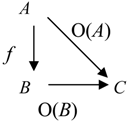
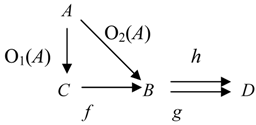
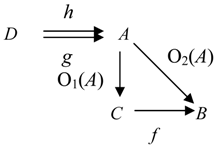
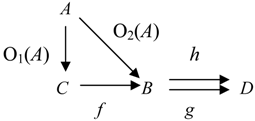
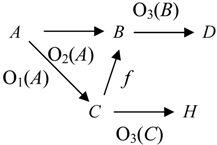
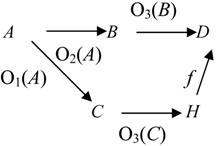
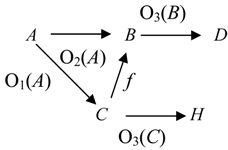
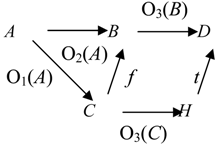
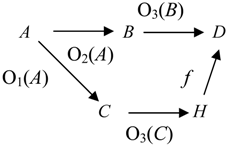
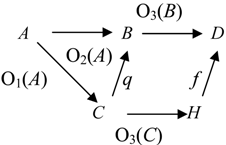
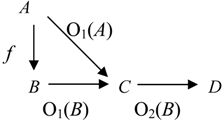
Ontological Principle O3 (the Embodiment Principle). For any portion of information I, there is always a carrier C of this portion of information for a system R.
People get information from books, magazines, TV and radio sets, computers, and from other people. To store information people use their brains, paper, tapes, and computer disks. All these entities are carriers of information.
For adherents of the materialistic approach, the Ontological Principle O3 must be changed to its stronger version.
Ontological Principle OM3 (the Material Embodiment Principle). For any portion of information I, there is some substance C that contains I.
The substance (material object) C that is a carrier of the portion of information I is called the physical, or material, carrier of I.
Ontological Principle O4 (the Representability Principle). For any portion of information I, there is always a representation C of this portion of information for a system R.
As any information representation is, in some sense, its carrier, the Ontological Principle O4 implies the Ontological Principle O3.
The first four ontological principles ((O1)-(O4) or (O1)-(OM4)) imply that information connects the carrier
C with the system
R and thus, information
I is a component of the following fundamental triad [
7],
People empirically observed that for information to become available, the carrier must interact with a receptor that was capable of detecting information the carrier contained. This empirical fact is represented by the following principle.
Ontological Principle O5 (the Interaction Principle). A transaction/transition/transmission of information goes on only in some interaction of C with R.
However, being necessary, interaction is not sufficient for information transmission. Thus, we need one more principle.
Ontological Principle O6 (the Actuality Principle). A system R accepts a portion of information Ionly if the transaction/transition/transmission causes corresponding transformations.
For instance, if after reading this paper, your knowledge remains the same, you do not accept cognitive information from this text. In a general case, when the recipient's knowledge structure was not changed, there is no cognitive information reception.
Ontological Principle O7 (the Multiplicity Principle). One and the same carrier C can contain different portions of information for one and the same system R.
Thus, all ontological principles form three groups:
- -
Ontological Principles O1 and O2 reflect intrinsic substantial properties of information.
- -
Ontological Principles O3, O4 and O7 reflect representation properties of information.
- -
Ontological Principles O5 and O6 reflect dynamic properties of information.
4. Categorical Representation of Information Dynamics
To build a categorical representation of information dynamics, i.e., of regularities of information processes, we start with constructing a categorical representation of the information receptor/receiver R because according to the Principles O1 and O2, information is determined by its action on the information receptor/receiver. When we are interested in information in the strict sense, we consider only an infological system IF(R) of R.
Let us take a category C. Objects from the category C can represent different infological systems IF, the same infological system IF in different states or different infological systems IF, the same infological system IF in different states. In all cases, the category C is called a categorical information space.
Definition 4.1. a) A categorical representation of the infological system IF(R) (or R) assigns objects from C to the states of IF(R) (correspondingly, R) and morphisms from C to transformations of IF(R) (or R).
b) A categorical representation of the infological system IF(R) (or R) is called complete if all states of IF(R) (correspondingly, R) are represented and each object in Ob C is a representation of some state of IF(R) (or R).
c) The category C is called a categorical information state space for the infological system IF(R) (for the system R).
In this case, MorIF(R) C (MorR C) denotes the set of all morphisms from C representing transformations of IF(R) (correspondingly, R) and if A, B ϵ Ob C, then HomIF(R)(A, B) = MorIF(R) C ∩ HomC(A, B) (HomR (A, B) = MorRC ∩ HomC(A, B)).
In what follows, we consider only complete representations.
Example 4.1. Objects of the category C are linear spaces, while morphisms are linear mappings (linear operators) of these spaces.
Example 4.2. Objects of the category
C are sets, e.g., sets of knowledge items, such as considered in [
31], or of propositions, such as in [
33,
34], while morphisms are mappings (transformations) of these sets.
Example 4.3. Words, or more generally, texts are information carriers, as well as information representations. Thus, it is natural to take words (texts) as objects of the category
C. Then morphisms of this category are computations that transform one word (system of words) into another one. These computations may be restricted to computations of some class of abstract automata, such as finite automata, Turing machines, inductive Turing machines or neural networks (
cf. e.g., [
35]. It is possible to consider information automata in the sense of Cooper [
36] as devices that perform computations.
Example 4.4. Thesaurus is a natural infological system [
7,
32]. An efficient representation of a thesaurus is a set of words, or more generally, of texts in some languages, which are information representations, as well as information carriers when these texts are in a material form, e.g., strings of symbols on paper or states of a computer memory [
32]. Thus, it is natural to take sets of words (or texts) as objects of the category
C. Then morphisms of this category are multiple computations ([
37]) performed by systems/automata from some class, e.g., Turing machines, inductive Turing machines or finite automata.
Example 4.5. Classifications, which are also infological systems used in a variety of areas, and their infomorphisms in the sense of [
38] form a category in which classifications are objects and infomorphism are morphisms.
Informally, a portion of information I is a potency to cause changes in (infological) systems, i.e., to change the state of this system. Assuming that all systems involved in such changes are represented in a category C, we see that a change in a system may by represented by a morphism from this category. This gives us a transformation of the system that receives information. As a result, the portion of information I is represented by a categorical information operator Op(I). When it does not cause misunderstanding, it is possible to denote the information portion I and the information operator Op(I) by the same letter I.
Definition 4.2. a) A pure categorical representation of a collection IF = { IF(Ri); i ϵ I } of infological systems assigns objects from C to the infological systems IF(Ri) and morphisms from C to transformations of one infological system into another.
b) A pure categorical representation of the collection IF is called complete if all systems from IF are represented and each object in Ob C is a representation of some system from IF.
c) The category C is called a pure categorical information system space for the collection IF.
In this case, MorIFC denotes the set of all morphisms from C represent transformations of systems from IF and if A, B ϵ Ob C, then HomIF(A, B) = MorIF C ∩ HomC(A, B).
In what follows we consider only complete representations.
Example 4.6. Information operators can represent information that changes DNA molecules to RNA molecules and RNA molecules to proteins.
Definition 4.3. a) An enriched categorical representation of the collection IF = { IF(Ri); i ϵ I) of marked infological systems assigns objects from C to the states of infological systems IF(Ri) and morphisms from C to transformations of one infological system in some state into another infological system in some state.
b) An enriched categorical representation of the collection IF is called complete if all systems from IF and all their states are represented and each object in Ob C is a representation of some system from IF and its state.
c) The category C is called an enriched categorical information extended system space for the collection IF.
Definitions 4.1 and 4.2 describe particular cases of categorical representations from the Definition 4.3 because a categorical representation of IF(R) is an enriched categorical representation of one infological system, while a pure categorical representation of a collection IF is enriched categorical representation of IF assuming that each infological system from IF has only one state.
In this case, objects from C represent pairs (IF(R), r) where r is a state of the infological system IF(R). MorIF(R)C (MorRC) denotes the set of all morphisms from C represent transformations of IF(R) (correspondingly, R) and if A, B ϵ Ob C, then HomIF(R)(A, B) = MorIF(R)C Ç HomC(A, B) (HomR (A, B) = MorRC Ç HomC(A, B)).
Note that two different states of a system may be considered as different systems. This allows us to reduce categorical representations from Definitions 4.1 and 4.3 to categorical representations from Definition 4.2. At the same time, it is also possible (at least formally) to consider different systems as the states of one universal system. This allows us to reduce categorical representations from Definitions 4.2 and 4.3 to categorical representations from Definition 4.1. It means that although Definition 4.3 looks as the most general, on the abstract level, it is possible to reduce it to any of the other two definitions.
In what follows we consider only complete representations.
Let us consider a categorical information space C.
Definition 4.4. A categorical information operator Op(I) over the categorical information space C is a mapping Op(I): Ob C → Mor C such that for any A ϵ Ob C, its image Op(I)(A) ϵ HomIF(R) (A, X) for some X ϵ Ob C. The morphism Op(I)(A) is called the component of the categorical information operator Op(I) at A.
Informally, a categorical information operator shows how each object (infological system) changes when a portion of information is received.
Categorical operators can be total or partial.
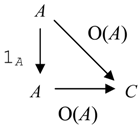
Note that it is possible that X coincides with the same object A. When Op(I)(A) = 1A , it means that the information portion I does not change A or the state of A.
Example 4.7. Taking the category
C from the Example 4.1, in which objects of the category
C are linear spaces and morphisms are linear operators in these spaces, we can build categorical information operators. These operators assign a linear operator to each linear space from
C. Such operators represent, for example, information extraction by measurement in physics (
cf. for example, [
39]).
Example 4.8. Taking the category C from the Example 4.3, in which words (or texts) are objects and morphisms are computations performed by automata from some class, e.g., Turing machines, inductive Turing machines or finite automata, we obtain computational information operators. These operators assign a computation to each word (text) where this word (text) is the input.
Example 4.9. Taking the category
C from the Example 4.4, in which an object is a thesaurus, e.g., represented by systems of words (or texts), and morphisms are transformations of these thesauruses, we obtain a cognitive information operator, which assigns to each thesaurus its transformation. There are different types of cognitive information operators:
computational cognitive information operators;
analytical cognitive information operators;
matrix cognitive information operators;
set-theoretical cognitive information operators;
named-set-theoretical cognitive information operators.
For instance, transformations of knowledge states studied by Mizzaro [
31] form set-theoretical cognitive information operators, while infomorphisms studied by Barwise and Seligman [
38] shape named-set-theoretical cognitive information operators and transformations studied by Shreider [
32] bring into being analytical cognitive information operators.
Information is often connected to meaning. Some researchers even cannot imagine information without meaning, understanding meaning in the conventional sense (
cf. for example, [
40]). However, it was demonstrated that meaning is not a necessary attribute of information (
cf. for example, [
41]). For instance, Shannon’s information theory is very useful although it ignores meaning
However, as the general theory of information (GTI) encompasses all other approaches in information theory, it also includes semantic theories of information (
cf. [
7]). As a result, the GTI allows us to reflect meaning of information by the following model. In a formal context, meaning is represented by formal structures, e.g., it is possible to represent meaning by propositions, by semantic networks or by frames. There are also other formal representations of meaning, such as the Universal grammar of Montague, Discourse Representation Semantics, and File Change Semantics. Formal structures that represent meaning for a given system
R constitute a semantic system
M. It is possible to take this semantic system
M as the infological system of the system
R. This incorporates semantic approach to information into the GTI framework.
In this formal context, acceptance of meaningful information I changes the semantic system M by integrating the meaning of I into M. When we employ a categorical model, representing states of the semantic system M by objects of a category C, information is naturally represented by a categorical operator, which changes the states of M, reflecting adaptation of the meaning of I.
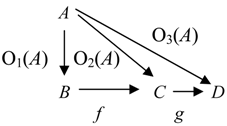
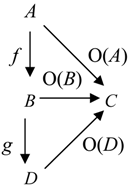
There are different operations with categorical information operators. One of the most important is sequential composition.
Definition 4.5. The sequential composition (often called simply composition) of categorical information operators O1 and O2 is a mapping O2 ○ O1: Ob C → Mor C such that for any A ϵ Ob C, if O1(A) ϵ HomC(A, B), then [O2 ○ O1](A) = O2(B) ○ O1(A).
By definition, the (sequential) composition of categorical information operators also is a categorical information operator. It models sequential reception of information by systems.
We do not use the shorter name composition instead of the name sequential composition because there other types of compositions of categorical information operators, for example, parallel composition of categorical information operators or concurrent composition of categorical information operators.
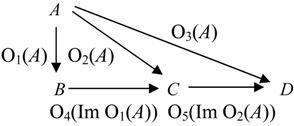
Let us consider some relations between categorical information operators.
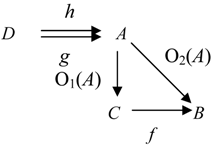
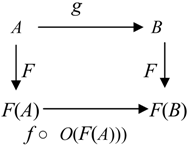
Definition 4.6. a) If O
1 and O
2 are categorical information operators, then O
1≼ O
2 (we say, O
1 is an
information suboperator of O
2) if for any object
A from
C, we have
This condition is equivalent to the following commutative diagram:
b) If O
1 and O
2 are categorical information operators and K is a class (type) of morphisms, e.g., K consists of all monomorphisms, then O
1 is a K-
uniform information suboperator of O
2 (O
1 ≼
K O
2) if for any object
A from
C, we have
c) If O
1 and O
2 are categorical information operators, then O
1 is an
information net suboperator of O
2 (O
1 ⊆ O
2) if for any object
A from
C, we have
d) If O1 and O2 are categorical information operators, then O1 ≍ O2 (we say, O1 is a equivalent to O2) if O1 ≼K O2 and O2 ≼K O1.
e) If O1 and O2 are categorical information operators and K is a class (type) of morphisms, then O1 ≍ K O2 (we say, O1 is a K-uniformly equivalent to O2) if O1 ≼K O2 and O2 ≼K O1 .
f) If O1 and O2 are categorical information operators, then O1 ≡ O2 (we say, O1 is a net equivalent to O2) if O1 ⊆ O2 and O2 ⊆ O1.
The concept of a information suboperator models the situation when one portion of information can be converted to another portion of information by transformations in the information space, i.e., O1 ≼ O2 means that information represented by the information operator O1 can be converted to information represented by the information operator O2.
The concept of a uniform information suboperator models the situation when one portion of information can be converted to another portion of information by transformations in the information space that belong to a given class of transformations, i.e., O1 ≼K O2 means that information represented by the information operator O1 can be converted to information represented by the information operator O2 by transformations that belong to the class K.
The concept of a net information suboperator models the situation when one portion of information can be converted to (complemented by) another portion of information by some information operator.
As it is usual in mathematics, all three relations generate corresponding equivalence relations: equivalence of information operators ≍, uniform equivalence of information operators ≍K and net equivalence of information operators ≡.
Example 4.10. Objects of the category
C are sets of well formed formulas of a logical calculus, e.g., sets of of propositions, such as considered in [
33,
34], while morphisms are finite deductions, which add deduced formulas to the initial set. It means that reception of information initiates some deductive process.
Let us assume that O1 and O2 are categorical information operators in C, while O1 ≼ O2. In this interpretation, the set B = Im O1(A) of well formed formulas is less than or equal to the set C = Im O2(A) of well formed formulas. It means that if O1 ≼ O2, then the categorical information operator O1(A) adds less formulas than the categorical information operator O1(A) does. This is true for all objects A from C, giving the meaning of the relation ≼.
Example 4.11. Objects of the category
C are sets of knowledge items, such as considered in [
31] or in [
7], while morphisms are transformations of these sets that only add new knowledge items but never delete them.
Let us assume that O1 and O2 are categorical information operators in C, while O1 ≼ O2. In this interpretation, the set B = Im O1(A) of knowledge items is less than or equal to the set C = Im O2(A) of knowledge items. It means that if O1 ≼ O2, then the categorical information operator O1(A) adds less knowledge items than the categorical information operator O1(A) does. This is true for all objects A from C, giving the meaning of the relation ≼.
Lemma 4.1. The relation ⊆ is stronger than the relation ≼, i.e., O1 ⊆ O2 implies O1 ≼ O2 for any categorical information operators O1 and O2.
Corllary 4.1. The relation ≡ is stronger than the relation ≍, i.e., O1 ≡ O2 implies O1 ≍ O2 for any categorical information operators O1 and O2.
Lemma 4.2. If the class K is closed with respect to all identity morphisms1A form Mor C, then the relation ≼K is reflexive.
Indeed, for any categorical information operator O, we have O ≼K O because for any object A from C, O(A) = 1B ○ O(A) where B = Im A (cf. Diagram (4.1)).
Lemma 4.3. If the class K is closed with respect to composition of morphisms, then the relation ≼K is transitive.
Proof. Let us consider categorical information operators O1, O2 and O3. If O1 ≼K O2 and O2 ≼K O3, then O2(A) = f ○ O1(A) for some morphism f from K and O3(A) = g ○ O2(A) for some morphism g form K.
These conditions are equivalent to the following commutative diagram:
where h = g ○ f belongs to K. Consequently, O1 ≼K O3.
Lemma is proved.
Lemmas 4.2 and 4.3 imply the following result.
Proposition 4.1. If the class K is closed with respect to composition of morphisms and all identity morphisms1A form Mor C, then the relation ≼K is a preorder on the class of all information operators, i.e., the relation ≼K is reflexive and transitive.
As the relation ≼ is a particular case of the relation ≼K when K = Mor C and the class Mor C is closed with respect to composition of morphisms, Proposition 4.1 implies the following result.
Corollary 4.2. The relation ≼ is a preorder on the class of all information operators, i.e., the relation ≼ is reflexive and transitive.
Proposition 4.2. If the class K is closed with respect to composition of morphisms and all identity morphisms1A form Mor C, then the relation ≍K is an equivalence on the class of all information operators, i.e., the relation ≍K is reflexive, symmetric and transitive.
Indeed, by definition, the relation ≍K is symmetric and by Proposition 4.1, it is reflexive and transitive.
As the relation ≍ is a particular case of the relation ≍K when K = Mor C and the class Mor C is closed with respect to composition of morphisms, Proposition 4.1 implies the following result.
Corollary 4.3. The relation ≍ is an equivalence relation on the class of all information operators, i.e., the relation ≍ is reflexive, symmetric and transitive.
Let us consider the class ISO of all isomorphisms of the category C.
Proposition 4.3. The relation ≼ISO is an equivalence relation on the class of all information operators, i.e., the relation ≼ISO is reflexive, symmetric and transitive.
Proof. By Proposition 4.1, the relation ≼
ISO is a preorder on the class of all information operators because any identity morphism 1
X is an isomorphism and composition of two isomorphisms is also an isomorphism [
27]. So, it is necessary to show that the relation ≼
ISO is symmetric.
Let us consider two categorical information operators O1 and O2 such that O1 ≼ISO O2. By Definition 4.6, it means that there is a commutative Diagram (4.1) in which f is an isomorphism. As f is an isomorphism, there is a morphism g: C → B, such that g ○ f = 1B.
Thus, for
A is an arbitrary object from the category
C, the relation O
1 ≼
ISO O
2 implies O
2(
A) =
f ○ O
1(
A), which in turn, implies the following sequence of equalities:
As A is an arbitrary object from the category C, it means that O2 ≼ISO O1, i.e., the relation ≼ISO is symmetric.
Proposition is proved.
Proposition 4.4. The relation ⊆ is a preorder on the class of all information operators, i.e., the relation is reflexive and transitive.
Proof. (a) For any categorical information operator O, we have O ⊆ O because there is the identity categorical information operator Id such that Id(A) = 1A for any object A from C and O1(A) = 1B ○ O1(A) = Id(B) ○ O(A) where B = Im O(A) (cf. Diagram (4.1)).
(b) Let us consider categorical information operators O1, O2 and O3 . If O1 ⊆ O2 and O2 ⊆ O3 , then O2(A) = O4(Im O1(A)) ○ O1(A) for some categorical information operators O4 and O3(A) = O5(Im O2(A)) ○ O2(A) for some categorical information operators O5 .
These conditions are equivalent to the following commutative diagram:
As Im O
4(Im O
1(
A)) = Im O
2(
A), we have
where
h = (O
5(Im O
4(Im O
1(
A)))) ○ O
4(Im O
1(
A))). Consequently, O
1⊆ O
3.
Proposition is proved.
Proposition 4.5. The relation ≡ is an equivalence relation on the class of all information operators, i.e., the relation ≡ is reflexive, symmetric and transitive.
Indeed, by definition, the relation ≡ is symmetric and by Proposition 4.4, it is reflexive and transitive.
Proposition 4.6. The following conditions are equivalent:
Proof. Let us consider two categorical information operators O1 and O2 such that O1 ≼ISO O2. By Definition 4.6, it means that there is a commutative Diagram (4.1) in which f is an isomorphism. As f is an isomorphism, there is a morphism g: C → B, such that g ○ f = 1B.
Thus, for
A is an arbitrary object from the category
C, the relation O
1 ≼
ISO O
2 implies O
2(
A) =
f ○ O
1(
A), which in turn, implies the following sequence of equalities:
As A is an arbitrary object from the category C, it means that O2 ≼ISO O1.
In a similar way, O2 ≼ISO O1 implies O1 ≼ISO O2 .
Consequently, each of the relations O1 ≼ISO O2 or O2 ≼ISO O1 implies O1 ≍ISO O2.
Proposition is proved.
Let us consider the class SEC of all sections and the class RET of all retractions of the category C.
Proposition 4.7. O1 ≼SEC O2 if and only if O2 ≼RET O1.
Proof.
Necessity. Let us consider two categorical information operators O
1 and O
2 such that O
1 ≼
SEC O
2. By Definition 4.6, it means that there is a commutative Diagram (4.1) in which
f:
B →
C is a section. As
f is a section (
cf. Section 2), there is a morphism
g:
C →
B, such that
g ○
f = 1
B. By Definition 2.2,
g is a retraction.
Thus, since an arbitrary object
A from the category
C, the relation O
1 ≼
SEC O
2 implies O
2(
A) =
f ○ O
1(
A), which in turn, implies the following sequence of equalities:
As A is an arbitrary object from the category C and g is a retraction, it means that O2 ≼RET O1.
Sufficiency. In a similar way, O2 ≼RET O1 implies O1 ≼SEC O2.
Proposition is proved.
Definition 4.7. a) If
A and
B are objects from the category
C and O is a categorical information operator, then
A ≤
O B (we say, an object
A is
less than or
equal to an object
B with respect to a categorical information operator O) if for any object
C from
C, there is a morphism
f such that the following diagram is commutative:
i.e., O(A) = O(B) ○ f .
b) an object A is O-equivalent to an object B ( A ≈O B ) if for any object C from C, there is an isomorphism f such that the diagram (4.4) is commutative.
Relations ≤O and ≈O are called O-relative order and O-relative equivalence, respectively.
Lemma 4.4. For any categorical information operator O, the relation ≤O is a partial preorder on the class of all objects in the category C.
Proof. (a) For any categorical information operator O and any object A from the category C, we have A ≤O A because for any object A from C, O(A) = O(A) ○ 1A (cf. Diagram (4.5)).
(b) If
A ≤
O B and
B ≤
O D, then O(
A) = O(
B) ○
f for some morphism
f and O(
B) = O(
D) ○
g for some morphism
g . This gives the following commutative diagram
Consequently, we have
where
h =
g ○
f. Consequently,
A ≤
O B.
Lemma is proved.
Proposition 4.8. The relation ≈O is an equivalence on the class Ob C of all objects from C, i.e., the relation ≈O is idempotent, symmetric and transitive.
Proof is similar to the proof of Proposition 4.1.
Definition 4.7 and Proposition 6.13 from [
27] imply the following result.
Proposition 4.9. If A ≤OB and O(A) is an epimorphism, then O(B) is also an epimorphism.
Definition 4.7 and Proposition 5.11 from [
27] imply the following result.
Proposition 4.10. If A ≤OB and O(A) is a retraction, then O(B) is also a retraction.
There are different types of categorical information operators.
Definition 4.8. A categorical information operator Op(
I) is called:
- a)
Monoperator if all morphisms Op(I)(A) with A ϵ Ob C are monomorphisms.
- b)
Epoperator if all morphisms Op(I)(A) with A ϵ Ob C are epimorphisms.
- c)
Bimoperator if all morphisms Op(I)(A) with A ϵ Ob C are bimorphisms.
- d)
Secoperator if all morphisms Op(I)(A) with A ϵ Ob C are sections.
- e)
Retroperator if all morphisms Op(I)(A) with A ϵ Ob C are retractions.
- f)
Isoperator if all morphisms Op(I)(A) with A ϵ Ob C are isomorphisms.
- g)
A constant operator if all morphisms Op(I)(A) with A ϵ Ob C are constants.
- h)
A co-constant operator if all morphisms Op(I)(A) with A ϵ Ob C are co-constants.
- i)
A zero operator if all morphisms Op(I)(A) with A ϵ Ob C are zeroes.
Informally, we have the following interpretation of the introduced types of information operators:
Information monoperators preserve distinctions between previously accepted information portions.
Information epoperators preserve distinctions between next coming information portions.
Information bimoperators are both information monoperators and information epoperators.
Information retroperators represent such information portions I the impact of which can be erased from system state by another information impact, i.e., there is another information portions J that moves the infological system IF(R) back to the previous state.
Information secoperators represent such information portions I that act like an eraser of some previously received information.
Information isooperators are both information retroperators and information secoperators.
Information zero operators represent such information portions I that erases all existed information reducing it to minimum.
Information constant operators represent such information portions I that equalize all previously received information.
Information co-constant operators represent such information portions I that equalize all further information.
Example 4.12. Taking a category C from Example 4.2 where objects are sets of propositions, or more generally, of knowledge items, and morphisms are transformations of these sets, we define the categorical information operator O so that for each set A of propositions, the corresponding morphism O(A) is a deduction in a monotone logic. As we know, deduction in a monotone logic only adds new propositions (knowledge items) to the initial set. Thus, O is a categorical information monoperator.
Example 4.13. Let us take a category C where objects are collections of books that some library L has at different periods of time and morphisms are transformations of these collections that go from time to time. Assuming that this library never discards books, we see that any categorical information operator O in C is a categorical information monoperator.
Example 4.14. Let us take a category C where objects are collections of software systems that some software depositary L has at different periods of time and morphisms are transformations of these collections that go from time to time. We define the categorical information operator O in the following way. For each set A of software systems, the corresponding morphism O(A) is validation of software systems from A, exclusion of invalid systems and elimination of copies of the same system. As software systems are never added by morphisms O(A), we see that any categorical information operator O in C is a categorical information epoperator.
Proposition 4.12. If O2 is a categorical information monoperator and O1 ≼ O2, then O1 is also a categorical information monoperator.
Proof. Let us take an object A from the category C and two morphisms h: D → A and g: D → A such that O1(A) ○ h = O1(A) ○ g (cf. Diagram (4.7)).
As O2 is a categorical information monoperator, O2(A) is a monomorphism. Consequently, h = g.
Proposition is proved because A is an arbitrary object from the category C and g and h are arbitrary morphisms into A.
Corollary 4.4. If O2 is a categorical information monoperator and O1 ⊆ O2, then O1 is also a categorical information monoperator.
Corollary 4.5. A categorical information operator equivalent to a categorical information monoperator is itself a categorical information monoperator.
Definition 4.6 and Proposition 5.5 from [
27] imply the following result.
Proposition 4.13. If O2 is a categorical information secoperator and O1 ≼ O2, then O1 is also a categorical information secoperator.
Proposition 4.14. If O1 is a categorical information epoperator and O1 ≼ISO O2, then O2 is also a categorical information epoperator.
Proof. Let us take an object A from the category C and two morphisms h: B → D and g: B → D such that O2(A): A → B, h ○ O2(A) = g ○ O2(A) (cf. Diagram (4.8)).
As O
1 is a categorical information epoperator, O
1(
A) is an epimorphism. Consequently,
h ○
f =
g ○
f. As
f is an isomorphism, there is a morphism
t:
B →
C such that
f ○
r = 1
B. Consequently,
As g and h are arbitrary morphisms from B, O2(A) is an epimorphism.
Proposition is proved because A is an arbitrary object from the category C and g and h are arbitrary morphisms from B.
Corollary 4.6. If O1 is a categorical information epoperator, O2 is a categorical information monoperator and O1 ≼ISO O2, then both O1 and O2 are categorical information bimoperators.
Corollary 4.7. A categorical information operator ISO-equivalent to a categorical information epoperator is itself a categorical information epoperator.
Corollary 4.8. A categorical information operator ISO-equivalent to a categorical information bimoperator is itself a categorical information bimoperator.
Proposition 4.15. If O1 is a constant categorical information operator and O1 ≼ O2, then O2 is also a constant categorical information operator.
Proof. Let us take an object A from the category C and two morphisms h: C → A and g: C → A (cf. Diagram (4.9)).
As O
1 is a constant categorical information operator, we have
O2 is also a constant categorical information operator because A is an arbitrary object from the category C and g and h are arbitrary morphisms into A.
Proposition is proved.
Corollary 4.9. If O1 is a constant categorical information operator and O1 ⊆ O2 , then O2 is also a constant categorical information operator.
Corollary 4.10. A categorical information operator equivalent to a constant categorical information operator is itself a constant categorical information operator.
Proposition 4.16. If O1 is a co-constant categorical information operator and O1 ≼ISO O2, then O2 is also a co-constant categorical information operator.
Proof. Let us take an object A from the category C and two morphisms h: B → D and g: B → D such that O2(A): A → B. As O1 ≼ISO O2, we have O2(A) = f ○ O1(A) for an isomorphism f (cf. Diagram (4.10)).
As O
1 is a co-constant categorical information operator, we have
O2 is a co-constant categorical information operator because A is an arbitrary object from the category C and g and h are arbitrary morphisms from B.
Proposition is proved.
Corollary 4.11. An information suboperator of a zero categorical information operator is itself a zero categorical information operator.
Corollary 4.12. An information operator equivalent to a zero categorical information operator is itself a zero categorical information operator.
Corollary 4.13. An information operator equivalent to a co-constant categorical information operator is itself a co-constant categorical information operator.
Corollary 4.14. If O1 is a constant (co-constant) categorical information operator and O1 ⊆ O2, then O2 is also a constant (co-constant) categorical information operator.
Information is a dynamic essence and its processing involves different operations with information and its representations and carriers. In the mathematical setting of categories, operations with information are represented by operations with information operators. One of the most important information operations is the (sequential) composition of categorical information operators.
Let us find some properties of the (sequential) composition of categorical information operators.
Proposition 4.17. The (sequential) composition of total categorical information operators is a total categorical information operator.
Proposition 4.18. If O3 is a categorical information secoperator, then O3 ○ O1 ≼ O3 ○ O2 if and only if O1 ≼ O2 .
Proof. 1. Let us assume that O
1 ≼ O
2. Then for an arbitrary object
A from the category
C, we have the commutative Diagram (4.11):
As O3 is a categorical information secoperator, the morphism O3(C) is a section. Consequently, there is a morphism g: H → C, such that g ○ O3(C) = 1C.
Thus, we have
where
t = O
3(
B) ○
f ○
g. As
A is an arbitrary object from the category
C, we have
2. Now let us assume that O
3 ○ O
1≼ O
3 ○ O
2. Then we have the commutative Diagram (4.12):
As O3 is a categorical information secoperator, the morphism O3(B) is a section. Consequently, there is a morphism g: H → C, such that g ○ O3(B) = 1B .
Thus, the equality
implies the equalities
where
q =
g ○
f ○ O
3(
C). As
A is an arbitrary object from the category
C, we have
Proposition is proved.
Corollary 4.15. If O3 is a categorical information secoperator, then O3 ○ O1≍ O3 ○ O2 if and only if O1≍ O2.
Proof. 1. Let us take categorical information operators O1, O2 and O3 and assume that O1≍ O2 and O3 is a categorical information secoperator. Then by Definition 4.6, we have O1≼ O2. Thus, by Proposition 4.18, O3 ○ O1≼ O3 ○ O2.
Besides, O1≍ O2 implies O2≼ O1. Thus, by Proposition 4.18, O3 ○ O2≼ O3 ○ O1. Then by Definition 4.6, we have O3 ○ O1≍ O3 ○ O2.
2. Let us take categorical information operators O1, O2 and O3 and assume that O3 ○ O1≍ O3 ○ O2 and O3 is a categorical information secoperator. Then by Definition 4.6, O3 ○ O1≼ O3 ○ O2. Thus, by Proposition 4.18, O1≼ O2.
Besides, O3 ○ O1≍ O3 ○ O2 implies O3 ○ O2≼ O3 ○ O1 . Thus, by Proposition 4.18, O2≼ O1. Then by Definition 4.6, O1≍ O2.
Corollary is proved.
Proposition 4.19. If O3 is a categorical information isoperator, then O3 ○ O1 ≼ISO O3 ○ O2 if and only if O1 ≼ISO O2.
Proof. 1. Let us take categorical information operators O
1, O
2 and O
3 and assume that O
1 ≼
ISO O
2 and O
3 is a categorical information isoperator. Then we have the commutative diagram (4.13) in which
f is an isomorphism:
By Proposition 4.18, it is possible to extend Diagram (4.13) to the commutative Diagram (4.14):
where
t = O
3(
B) ○
f ○
g and
g is the inverse to the morphism O
3(
C). As O
3 is a categorical information isooperator, O
3(
C) and O
3(
B) are isomorphisms. Consequently,
g is an isomorphism [
27]. As
f is an isomorphism, the morphism
t is also an isomorphism as the sequential composition of isomorphisms [
27]. It means that O
3(
B) ○ O
2(
A) =
t ○ O
3(
C) ○ O
1(
A) where
t is an isomorphism.
As
A is an arbitrary object from the category
C, we have
2. Let us take categorical information operators O
1, O
2 and O
3 and assume that O
3 ○ O
1 ≼
ISO O
3 ○ O
2 and O
3 is a categorical information isoperator. Then we have the commutative diagram (4.15) in which
f is an isomorphism:
By Proposition 4.18, it is possible to extend Diagram (4.15) to the commutative Diagram (4.16):
where
q =
g ○
f ○ O
3(
C). and
g is the inverse to the morphism O
3(
B). As O
3 is a categorical information isooperator, O
3(
C) and O
3(
B) are isomorphisms. Consequently,
g is an isomorphism [
27]. As
f is an isomorphism, the morphism
q is also an isomorphism as the sequential composition of isomorphisms [
27]. It means that O
2(
A) =
q ○ O
1(
A) where
q is an isomorphism.
As
A is an arbitrary object from the category
C, we have
Proposition is proved.
Let us take two categorical information spaces C and K.
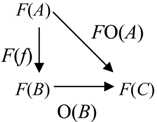
Theorem 4.1. A covariant functor F: C → K associates categorical information operators over K to categorical information operators over C and preserves their sequential composition.
Proof. Let us consider a covariant functor
F:
C → K. To each object
A from
C, the functor
F assigns the object
F(
A) from
K, and if O is a categorical information operator, then
F assigns the morphism
F(O(
A)) from Mor
K to each morphism O(
A) from
C. Assuming axiom of choice for the class Ob
C, it is possible to choose a unique object
DA from the class F
A = {
C;
C ϵ Ob
C and
F(
C) =
F(
A) }. Then we define
FO(
F(
A)) as the morphism
F(O(
DA)). Note that
F(
DA) =
F(
A). In such a way, we build a categorical information operator
FO over
K. By definition (
cf. Section 2), functors preserve sequential composition. Thus, sequential composition of categorical information operators is also preserved.
Theorem is proved.
Informally, functors are mapping of categorical information spaces that preserve the structure of information transformations. In particular, Theorem 4.1 shows that functors are mappings between categories of states of different infological systems that are compatible with actions of information. Functors allow one to study how the same information operates in different infological systems.
As we can see from the proof of Theorem 4.1, in a general case, it is possible to associate different categorical information operators over K to the same categorical information operator over C, i.e., correspondence between categorical information operators over K and categorical information operators over C is not a function. To make it a function, we need additional conditions on the functor F.
Theorem 4.2. If F is an embedding covariant functor, then a unique categorical information operator FO over K is associated to each categorical information operator O over C and if O is total, then FO is total.
Proof. Let us consider an embedding covariant functor
F:
C → K. To each object
A from
C, the functor
F assigns the object
F(
A) from
K, and if O is a categorical information operator, then
F assigns the morphism
F(O(
A)) from Mor
K to each morphism O(
A) from
C. Because
F is an embedding covariant functor, it defines a one-to-one correspondence between objects from
C and objects from
K [
27; Section 12]. Thus, there is only one object
X in the class Ob
C such that
F(
X) =
F(
A) and we define
FO(
F(
A)) as the morphism
F(O(
A)). In such a way, we build a unique categorical information operator
FO over
K. As O is total and
FObC: Ob
C→ Ob
K is a one-to-one correspondence, the operator
FO is also total.
Theorem is proved.
Theorem 4.3. A full dense covariant functor F: C → K maps categorical information operators over K into categorical information operators over C and preserves totality of categorical information operators.
Proof. Let us consider a full dense covariant functor
F:
C → K and a categorical information operator O over
K. To each object
D from
K, the operator O assigns the morphism O(
D) from
K. Besides, to each object
A from
C, the functor
F assigns the object
F(
A) from
K. If
C = Im O
F(
A), then there is an object
B from
C, such that
F(
B) is isomorphic to
C because
F is a dense functor,
i.e., there is an isomorphism
f:
C →
F(
B). This gives us the following diagram
Because
F is a full functor, there is a morphism
g:
A →
B such that
F(
g) =
f ○
O(
F(
A))). This gives us the following diagram
Thus, we define U(A) = g. This is done for each object A in the class Ob C, and such a way we obtain a categorical information operator U over C. As O is total and FObC: Ob C → Ob K is a one-to-one correspondence, the operator U is also total. We denote the categorical information operator U by F-1O.
Theorem is proved.
Let us take a property P of categorical information operators.
Definition 4.9. A functor F: C → K:
a) preserves the property P if for any categorical information operator A over C with the property P, its image F(A) is a categorical information operator over K with the property P.
a) reflects the property P if for any categorical information operator A over C, if its image F(A) has the property P, then A also has the property P.
For instance, by definition, a covariant functor preserves the property of a morphism to be a composition of other morphisms.
Proposition 4.20. Every covariant functor F: C → K preserves the relation ≼ between categorical information operators.
Indeed, if O
1 ≼ O
2 for categorical information operators O
1 and O
2, then by Definition 4.6, for any object
A from
C, we have
Because
F is a functor, we also have
As F(A) is an arbitrary object where categorical information operators FO1 and FO2 are defined, we have FO1 ≼ FO2 .
Proposition 4.20 and Proposition 12.2 from [
27] imply the following result.
Proposition 4.21. Every covariant functor F: C → K preserves relations ≼RET, ≼SEC, and ≼ISO between categorical information operators.
Proposition 4.22. IfA →OB, then FA →FO FB.
Indeed, the commutative Diagram 4.4 in the category C implies the commutative Diagram 4.19 in the category K.
Proposition 4.23. For any categorical information operators O1 and O2 over C, if A ≤O1 B, then A ≤O2 →O1 B.
Indeed, the commutative Diagram 4.4 implies the commutative Diagram 4.20.
Proposition 12.2 from [
27] implies the following result.
Theorem 4.4. Every covariant functor F: C → K preserves categorical information secoperators, categorical information retroperators, and categorical information isoperators over the category C.
Theorem 12.10 from [
27] implies the following result.
Theorem 4.5. Every dense full and faithful covariant functor F: C → K preserves categorical information monooperators, categorical information epoperators, categorical information bimoperators over the category C.
Propositions 12.8 and 12.9 from [
27] imply the following result.
Theorem 4.6. Every full faithful covariant functor F: C → K reflects categorical information secoperators, categorical information retroperators, categorical information monoperators, categorical information epoperators, categorical information bimoperators, constant categorical information operators, co-constant categorical information operators, zero categorical information operators, and categorical information isoperators over the category C.
In addition to sequential composition, it is possible to define concurrent and parallel compositions of categorical information operators.
Let us consider a category
C with pushouts [
27].
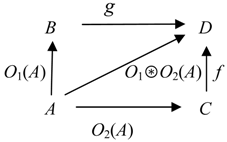
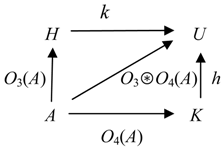
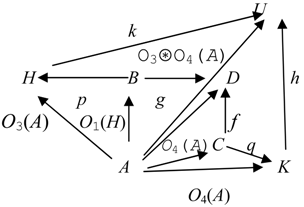
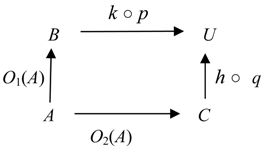
Definition 4.10. A categorical information operator O over C is called the free sum of categorical information operators O1 and O2 over C if for any A ϵ Ob C, there is the pushout (4.21) where q = g ○O1(A) = f ○O2(A) and O(A) = q.
The free sum of categorical information operators O1 and O2 over C is denoted by O1⊛O2.
By properties of pushouts [
27] the free sum of categorical information operators is defined uniquely up to an isomorphism.
On the level of information processes, the free sum of categorical information operators represents consistent integration of information. Now when people and databases receive information from diverse sources, information integration has become an extremely important cognitive operation. Information integration plays a mission critical role in a diversity of applications from life sciences to E-Commerce to ecology to disaster management. These applications rely on the ability to integrate information from multiple heterogeneous sources.
Operationally, Definition 4.3 means that the free sum of two categorical information operators O1 and O2 is constructed by taking pushouts for couples of actions of O1 and O2 on each object in C. It models concurrent information processing (e.g., integration and composition).
Theorem 4.7. The free sum of any two categorical information operators is a categorical information epoperator.
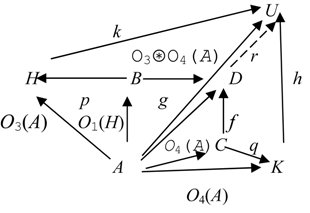
Proof. Let us take the free sum O of two categorical information operators O1 and O2 over C. Then for any object A ϵ Ob C, there is the pushout (4.21). To prove that O is a categorical information epoperator, we need to show that q always is an epimorphism.
Let us consider two morphisms
k,
h ϵ Hom
C(
D,
Q) such that
k○
q =
h○
q. Then we have
It gives us the commutative diagram (4.22).
By the definition of a pushout (
cf. for example, [
27]), we have a morphism
p:
D →
Q, which is defined in a unique way and for which
As the equality (4.23) is also true for morphisms k and h and morphism p is unique, we have k = h.
Theorem is proved because the object A ϵ Ob C and morphisms k and h were chosen in an arbitrary way.
The free sum preserves relations between categorical information operators.
Theorem 4.8. If O1 ≼ O3 and O2 ≼ O4 , then O1 ⊛ O2 ≼ O3 ⊛ O4 .
Proof. Let us take categorical information operators O1, O2, O3 and O4 and assume that O1 ≼ O3 and O2 ≼ O4. For each pair of them, we build their free sums O1 ⊛ O2 and O3 ⊛ O4, presented for an object A in diagrams (4.24) and (4.25).
As O
1 ≼ O
3 and O
2 ≼ O
4, by Definition 4.6, we have:
and
for some morphisms
f and
g.
This gives us the following commutative diagram
From Diagram (4.24), we obtain the following commutative square
As the commutative square in Diagram (4.24) is a pushout, there is a morphism
r:
D →
U, such that
k ○
p =
r ○
g and
h ○
q =
r ○
f. This gives us the following commutative diagram
From Diagram (4.28), we have
Thus, O1⊛ O2≼ O3⊛ O4.
Theorem is proved.
Definitions imply the following result.
Theorem 4.9. For any categorical information operators O1 and O2, we have O1 ≼ O1 ⊛ O2 and O2 ≼ O1 ⊛ O2.
Indeed, O1⊛O2(A) = g ○ O1(A) = f ○ O2(A) for any object A from the category C.