A Tourism Financial Conditions Index for Tourism Finance

Abstract

The paper uses monthly data on tourism related factors from April 2005–June 2016 for Taiwan that applies factor analysis and Chang’s (2015) novel approach for constructing a tourism financial indicator, namely the Tourism Financial Conditions Index (TFCI). The TFCI is an adaptation and extension of the widely-used Monetary Conditions Index (MCI) and Financial Conditions Index (FCI) to tourism stock data. However, the method of calculation of the TFCI is different from existing methods of constructing the MCI and FCI in that the weights are estimated empirically. The empirical findings show that TFCI is statistically significant using the estimated conditional mean of the tourism stock index returns (RTS). Granger Causality tests show that TFCI shows strong feedback on RTS. An interesting insight is that the empirical results show a significant negative correlation between F1_visitors (Foreign Visitor Arrivals) and RTS, implying that tourism authorities might promote travel by the “rich”, and not only on inbound visitor growth. The use of market returns on the tourism stock sub-index as the sole indicator of the tourism sector, as compared with the general activity of economic variables on tourism stocks, is shown to provide an exaggerated and excessively volatile explanation of tourism financial conditions.

1. Introduction

Despite political upheaval, economic uncertainty and natural disasters around the world in recent years, the global travel, tourism and hospitality industry, which is one of the world’s leading industries in both economic and financial terms, has experienced continued growth. According to the World Tourism Organization (UNWTO), international tourist arrivals worldwide have more than doubled since 1990, rising from 435 million to 675 million in 2000, to 940 million in 2010, growing by a further 4% in 2012 to reach 1.035 billion, and increasing by 4.4% in 2015 with a record of 1.184 billion. 2015 marks the sixth consecutive year of above-average growth, with international arrivals increasing by 4% or more every year since the post-crisis year of 2010 (UNWTO Annual Report 2015, World Tourism Organization, UNWTO/WWW2.unwto.org/About/Annual Report/UNWTO Annual Report 2015 http://www2.unwto.org/publication/unwto-annual-report-2015).

Results from the UNWTO Confidence Index remain largely positive for 2016, though at a slightly lower level as compared with the previous two years. Based on the current trend and this outlook, UNWTO projects international tourist arrivals to grow by 4% worldwide in 2016. These figures are in line with the UNWTO long term forecast for 2030, namely 3.8% increase per year, on average, between 2010 and 2020. Moreover, tourism arrivals are expected to increase by 3.3% each year from 2010 to 2030, representing 43 million additional international tourist arrivals annually, reaching a total of 1.8 billion arrivals by 2030.

The latest annual findings from the World Travel and Tourism Council (WTTC) and Oxford Economics show that Travel & Tourism’s contribution to GDP grew for the sixth consecutive year in 2015. The total contribution comprised 9.8% of global GDP (US $7.2 trillion) and generated over 284 million jobs, that is, 1 in 11 of global employment (WTTC, http://www.wttc.org/research/economic-research/economic-impact-analysis/Copyright @ WTTC 2016). With a stronger performance than the rest of the economy, the importance of the Travel & Tourism sector for economic growth and development is undisputed. In order to provide further support to enable accurate forecasts of the tourism and economic environments, a tourism index that is closely related to economic growth and development would be helpful to public and private decision makers, such as government, business executives and investors.

Recent years have shown increasing attention being paid to establishing tourism indexes for both the public and private sectors. For example, (i) the tourism industry stock index represents the performance of stocks of tourism-related firms listed on the stock market; (ii) the tourism index published by the World Economic Forum assesses the obstacles and drivers of Travel & Tourism development; (iii) the Travel and Tourism Competiveness Index (TTCI) (World Economic Forum, 2015, [1,2]); and (iv) the statistical information of tourism listed on Tourism Bureau Executive Information System available on the government’s website, are just a few of the available tourism-related indexes.

However, from the global economics viewpoint, in general, tourism is sensitive to the impacts of the international economic environment, such as price levels, exchange rates, and industry promotion policies, especially in the tourism industry. On the other hand, as foreign visitors who travel to a country will purchase that country’s tourist experience, the tourism industry is considered to be an export industry. The impacts arising from exchange rates affect the tourism and economic environments, such as the growth in international visitor arrivals, and domestic and international of business investment.

Therefore, a composite Tourism Conditions Indicator (TCI), taking account of both the economy and tourism environments as a whole, is desirable to assist in decision making for public and private policy makers. However, such an analysis pertaining to tourism indicators is limited. In order to incorporate greater information for purposes of forecasting future tourism and economic environments in a straightforward manner, this paper proposes a new tourism financial indicator, namely the Tourism Financial Conditions Index (TFCI).

The premise underlying the TFCI index is that it should be linked closely to both the economic and tourism environments. Therefore, three key components comprise the TFCI, namely the macro-economy, foreign visitor arrivals, and tourism related prices, respectively. The tourism industry stock index return (RTS), an observable variable, as a financial tourism performance indicator, is desirable to construct a lantern TFCI since RTS is closely linked to the components of the TFCI.

The foundation of the proposed the Tourism Financial Conditions Index (TFCI) is an application of the Financial Conditions Index (FCI), which is derived from the Monetary Conditions Index (MCI). As stated by the Bank of Canada, the MCI is an index number calculated from a linear combination of two variables, namely the short-run interest rate and an exchange rate, that are deemed relevant for monetary policy. Based on the MCI, the FCI takes account of an extra factor, namely real asset prices, such as house prices and stock prices, to assess the conditions of financial markets (see Beaton, Lalonde, and Luu, 2009, [3]; Brave and Butters, 2011, [4]; Ericsson, Jansen, Kerbeshian, and Nymoen, 1997, [5]; Freedman, 1994, [6], 1996a, [7], 1996b, [8]; Hatzius, Hooper, Mishkin, Schoenholtz, and Watson, 2010, [9]; Lin, 1999, [10]; Matheson, 2012, [11]; and Thompson, Eyden, and Gupta, 2015, [12]).

The aim of the paper is to construct a Tourism Financial Conditions Index (TFCI) to summarize current economy and tourism conditions into a single statistical index. There are two macro-economic indicators which represent the economic conditions, namely the composite leading indicator (LI) and composite coincident indicator (CI). The operations of the listed firms reflect the broader tourism industry in Taiwan, as these are the main stocks in terms of revenues and stock values. The components of the Trend-Adjusted Leading Indicators (LI) are the following: Building permits, Index of export orders (2011 = 100), TAIEX (Taiwan Capitalization Weighted Stock Index is a stock market index for companies traded on the Taiwan Stock Exchange) average closing price, the Taiwan manufacturing composite indicator, Net accession rate of employees on payrolls of industry and services, Real Monetary aggregates M1B, and SEMI book-to-bill ratio, a widely used metric in the semiconductor equipment sector (Council for Economic Planning and Development, Taiwan).

The components of the coincident indicators (CI) are the following: industrial production index (2006 = 100), electric power consumption (billion kWh), index of producer’s shipment for manufacturing (2006 = 100), sale index of wholesale retail and food services (2006 = 100), nonagricultural employment (1000), real customs-cleared exports (NT$ billion), and real machinery and electrical equipment import (NT$ billions) (Council for Economic Planning and Development, Taiwan). The data on foreign visitor arrivals, foreign visitor arrivals by pleasure, real effective exchange rates, and consumer price index represent the tourism conditions.

The remainder of the paper is structured as follows. Section 2 explains the proxy variables for analyzing the tourism and economic environments. Section 3 presents the model-based approach and estimation method for constructing the TFCI. Section 4 describes the data used in the analysis, and presents the descriptive and summary statistics. Section 5 discusses the empirical results. Section 6 concludes the paper by summarizing the key empirical results and findings.

2. Definitions and Construction of MCI and FCI

In this section, we describe the foundations of the Tourism Financial Conditions Index (TFCI), which is an adaptation and extension of the widely-used Financial Conditions Index (FCI). The FCI, in turn, is derived from the well-known Monetary Conditions Index (MCI). For an application of some of these ideas to daily data, including modelling the volatility that is inherent in daily data, see Chang (2015), [13].

2.1. MCI

Freedman (1994, [6], 1996a, [7], 1996b, [8]) discussed the units of measurement of the MCI in terms of real interest rate changes. The MCI is defined deterministically as:

$${\mathrm{MCI}}_t={\theta }_1\left(e_t-e_0\right)+{\theta }_2\left(r_t-r_0\right)$$

(1)

The subscripts t and 0 denote the current and base periods, respectively, and ${\theta }_1$ and ${\theta }_2$ are the weights attached to real effective exchange rates (e) (in logarithms) and real interest rates (r), respectively. The presentation of MCI in Equation (1) is linear, though this is not essential. The weights on the components of the MCI (that is, ${\theta }_1$ and ${\theta }_2$) are the results of empirical studies that estimate the effect on real aggregate demand over six to eight quarters of changes in real exchange rates and real interest rates.

Typically, in analyzing the constructed values of MCI, there is no allowance made for the fact that the weights in Equation (1) are estimated from other studies, and hence contain sampling variation. If the weights are altered, the index would also be altered. The sensitivity of the indexes to such changes has not been discussed in the literature. An exception to the general rule is Chang (2015), [13], who analyses the conditional volatility in daily economic and financial data series.

Based on Equation (1), the MCI may be interpreted as the percentage point change in monetary conditions arising from the combined change in real exchange rates and real interest rates from the base period. As the MCI is measured relative to a given base period, subtracting the MCI at two points in time gives a measure of the degree of tightening or easing between these two points. Lack (2003), [14], discusses the experience of various countries that have used the MCI as an operating target, such as Canada and New Zealand.

2.2. FCI

Owing to the recent high volatility in stock and property prices, the influence of asset prices on monetary policy has drawn greater attention of policy makers. Significant efforts have been made recently to extend additional asset variables, such as stocks and housing prices into the MCI as a new indicator, namely the Financial Conditions Index (FCI) (see Goodhart and Hofmann (2001), [15], for the G7 countries, Mayes and Virén (2001), [16], for 11 European countries, and Lack (2003), [14], for Canada and New Zealand).

Just as in the case of MCI, the FCI reveals the offsetting influences among real effective exchange rates, real interest rates, and real asset prices. The FCI is defined deterministically as:

$${\mathrm{FCI}}_t={\theta }_1\left(e_t-e_0\right)+{\theta }_2\left(r_t-r_0\right)+{\theta }_3\left(a_t-a_0\right).$$

(2)

As in the case of the MCI, the subscripts t and 0 denote the current and base periods, respectively, and ${\theta }_1$, ${\theta }_2,$ and ${\theta }_3$ are the weights attached to real effective exchange rates (e) (in logarithms), real interest rates (r), and real assets (a) (in logarithms), respectively. Furthermore, the relative weights on the components of the FCI, namely ${\theta }_1$, ${\theta }_2$, and ${\theta }_3$, are the outcomes of empirical estimation. The presentation of FCI in Equation (2) is linear, though this is not essential. As in the case of MCI, when analyzing the alternative constructed values of FCI, there is no allowance made for the fact that the weights in Equation (2) are estimated from other studies, and hence contain sampling variation. If the weights are altered, the index would also be altered. The sensitivity of the indexes to such changes has not been discussed in the literature. The exception to the general rule would seem to be the analysis in Chang (2015), [13], who analyses the conditional volatility in daily economic and financial data series.

3. Model-Based TFCI

The MCI and FCI are constructed in such a way that the respective weights are first obtained from a separate empirical model, and are then used to construct a data series using the definitions given in Equations (1) and (2), respectively. This is in marked contrast to the approach taken in this paper, whereby model-based estimates of the TFCI are calculated directly from empirical data. Such a contrast is explained in greater detail in this section. It is worth noting that changes in the weights, whether for MCI, FCI, or the estimated TFCI, would alter the respective indexes. The sensitivity of the indexes to such changes has not been discussed in the literature. However, it is worth emphasizing that, in the estimation of TFCI, explicit allowance can be made for the sampling variation in the parameter estimates.

3.1. TFCI

The Tourism Financial Conditions Index (TFCI) proposed in the paper focuses on economic activities related to the tourism industry. Unlike the construction of the MCI and FCI, where the weights are based on a wide range of considerations rather than using direct model-based estimates, the TFCI is based on estimation of a linear regression model. The model-based weights for the components will be estimated by OLS.

As the models to be estimated below are linear in the variables, with the appropriate weights to be estimated empirically, the percentage change in a variable is used to denote simple returns rather than logarithmic differences (or log returns). The latter would be more appropriate for calculating continuously compounded returns.

Accordingly, TFCI is defined as:

$${\mathrm{TFCI}}_t=c+{\theta }_{1}Factor1+{\theta }_{2}Factor2+{\theta }_3 Factor3+\dots +u_t, u_t~ D\left(0, {\sigma }_u^2\right)$$

(3)

where c denotes the constant term, and $u$ denotes the shocks to TFCI, which need not be independently or identically distributed. The parameters ${\theta }_1, {\theta }_2,\mathrm{and} {\theta }_3$ are the weights attached to the various Factors. Unlike the standard approach to estimating MCI and FCI, in this paper the weights will be estimated empirically and explicit allowance can be made for the sampling variation in the parameter estimates. To state the obvious, changing the sample period would lead to changes in the estimates of the associated parameters, and hence also in the estimate of TFCI. However, explicit allowance can be made for the sampling variation in the parameter estimates, which is a strong argument in favour of estimating the weights, and hence in estimating TFCI.

3.2. RTS

As TFCI is unobservable, it is necessary to relate TFCI to observable data. The unobservable variable is defined as being the conditional mean of an observable variable, namely the returns on a Tourism Stock Index (RTS), which reflects the tourism industry stock sub-index that is listed on the Taiwan Stock Exchange (specifically, the Taiwan Stock Exchange Tourism Sub-index), as follows:

$${\mathrm{RTS}}_t={\mathrm{TFCI}}_t+ v_t, v_t~ D\left(0, {\sigma }_v^2\right)$$

(4)

where RTS is observed, TFCI is not observed, and the measurement error in RTS is denoted by $v$, which need not be independently or identically distributed.

As mentioned above, RTS, a financial tourism performance indicator, an observable variable, combines both impacts from tourism supply and tourism demand, including lag effects. It is necessary and desirable to construct a latent tourism financial indicator (TFCI) based on RTS. Six attributes which are related to the tourism industry are examined (see

Table 1. Description of variables.

Variables	Description
RTS	Monthly returns on Taiwan Stock Exchange Tourism Subindex
REE	Monthly change rate on Real Effective Exchange Rates
RTCPI	Monthly change rate on the Taiwan Consumer Price Index
RLTCC	Monthly change rate on the Taiwan Composite Coincident Index with a one period of lag
RLTCL	Monthly change rate on the Taiwan Composite Leading Index with a one period of lag
RLTVA	Monthly change rate on the Taiwan’s Visitors Arrival with a one period of lag
RLTVAP	Monthly change rate on the Taiwan’s Visitors Arrival by Pleasure with a one period of lag
TFCI (OLS)	OLS estimates of monthly Tourism Financial Conditions Index

), including lagged effects of the predictor which are distributed across one time period.

A function of RTS is shown as:

$$\mathrm{RTS}=f\left(\mathrm{REE}, \mathrm{RTCPI}, \mathrm{RLTCL}, \mathrm{RLTCC}, \mathrm{RLTVA}, \mathrm{RLTVAP}\right)$$

where REE, RTCPI, RLTCL, RLTCC, RLTVA, and RLTVAP denote the rate of change in real effective exchange rates, rate of change in the consumer price index, rate of change in the composite coincident index (lag1), rate of change in the composite leading index (lag1), rate of change in visitor arrivals (lag1), and rate of change in visitor arrivals by pleasure (lag1). These variables represent tourism arrival costs, the macro-economy, and tourism arrival demand conditions, respectively.

For estimating the variables that influence RTS the most, the paper examined the six attributes perceived as determinants of RTS by factor analysis. Factor scores are estimated and then regressed against RTS. A test of statistical significance of the extracted factors was used in constructing RTS.

3.3. Results of Factor Analysis

As mentioned above, the paper categorized six variables into three groups by factor analysis (the details are in the Appendix A,

Table A1. Factor analysis.

Rotation Method: Orthogonal Varimax
Factor: Untitled
Initial loadings: Unrotated
Convergence achieved after 7 iterations
Rotated loadings: L * inv (T)’
REE	−0.118	0.2196	0.5572
RTCPI	0.0091	0.0648	0.5459
RLTCL	0.01823	0.9070	−0.0303
RLTCC	0.00161	0.9057	0.1570
RLTVA	0.9699	0.0187	−0.0228
RLTVAP	0.9700	−0.0032	−0.0188

Note: Kaiser’s measure of sampling adequacy (MSA) = 0.512.

), as follows:

(1)

Factor 1 is related to Foreign Visitor Arrivals, namely F1_visitors: two factors, RLTVA, RLTVAP, are grouped into F1_visitors. According to the fundamental equation in tourism finance (see McAleer (2015), [17]), the primary purpose of tourism authorities in the public and private sectors is to achieve high daily returns on total tourism. Therefore, foreign visitor arrivals should be an important factor for RTS.

(2)

Factor 2 is related to the index of the macro-economy, namely F2_macro: two factors, RLTCL, RLTCC, that are designed to explain the nation’s macroeconomic situation, are included in the group. Tang and Tan (2015), [18], indicated that tourism Granger-causes economic growth in the short- and long-run, and policies to promote inbound tourism could effectively stimulate economic growth. Pratt (2015), [19], also mentioned that tourism provides economic benefits for Small Island Developing States (SIDS). Kasimati (2016), [20], analyzed and confirmed the contribution of tourism to the economic growth in Greece.

(3)

Factor 3 is related to the own price of tourism, namely F3_price: two variables, REE, RTCPI, are categorized into one group to test whether the factors of the “own price of tourism” has any significant influence on RTS. Song and Witt (2006), [21], mentioned that, in theory, the “own price of tourism” should contain two components, namely the cost of living for tourists at the destination and the travel cost to the destination. Previous research, such as Dritsakis (2004), [22], Lim and McAleer (2001, [23], 2002, [24]), Qiu and Zhang (1995), [25], Song and Witt (2006), [26], and Witt and Witt (1992), [27], shows that the cost of living in the destination is normally measured by the destination consumer price index (CPI) relative to the origin CPI, and travel costs to the destination are measured by the exchange rate between the origin country and destination country currencies.

3.4. RTS and TFCI

Given the zero mean assumption for $v$, the means of RTS and TFCI will be identical, as will their estimates. Using Equations (3) and (4), the empirical model for estimating the weights for TFCI is given as:

$${\mathrm{RTS}}_t=c+{\theta }_{1}F1\_visitors+{\theta }_{2}F{2}_{macro}+{\theta }_{3}F{3}_{price}+ u_{t }+v_t,{\epsilon }_t=u_t+v_t~D\left(0,{\sigma }_{\epsilon }^2\right)$$

(5)

where ${\epsilon }_t= u_t+v_t$ need not be independently or identically distributed.

The parameters in Equation (5) can be estimated by OLS to yield unbiased and consistent estimates of RTS. In view of the definition in Equation (4), the unbiased and consistent estimates of RTS will also be unbiased and consistent estimates of the unobservable TFCI.

This paper proposes unbiased and consistent estimation of TFCI in Equations (3) and (5) by Ordinary Least Squares (OLS), with consistent Newey-West HAC standard errors to accommodate the possibility of serial correlation and heteroskedasticity in the errors in Equation (5).

4. Data

In this section, we present the data used for the empirical analysis. Monthly data are used from April 2005 to June 2016. The sources of data are the Taiwan Stock Exchange (TWSE), Taipei Foreign Exchange Market Development Foundation for the tourism industry stock index, and the real effective exchange rate, respectively.

As discussed in Section 3 above, six observable variables that will be used to estimate the unobservable monthly TFCI are as follows (see Table 1):

(1)

rate of change in real effective exchange rates (REE);

(2)

rate of change in the Taiwan Consumer Price Index (RTCPI);

(3)

rate of change in the Taiwan Composite Leading Index Lagged 1 (RLTCL);

(4)

rate of change in the Taiwan Composite Coincident Index, Lagged 1 (RLTCC);

(5)

rate of change in Taiwan’s Visitor Arrivals, Lagged 1 (RLTVA);

(6)

rate of change in Taiwan’s Visitor Arrivals by Pleasure, Lagged 1 (RLTVAP).

This paper categorizes six observable variables into three groups by factor analysis. After the factor scores are estimated, the data will be used in the regression of RTS in Equation (5) by OLS. The estimates of monthly RTS in Equation (5), which are equivalent to the estimates of monthly TFCI, are defined as TFCI (OLS).

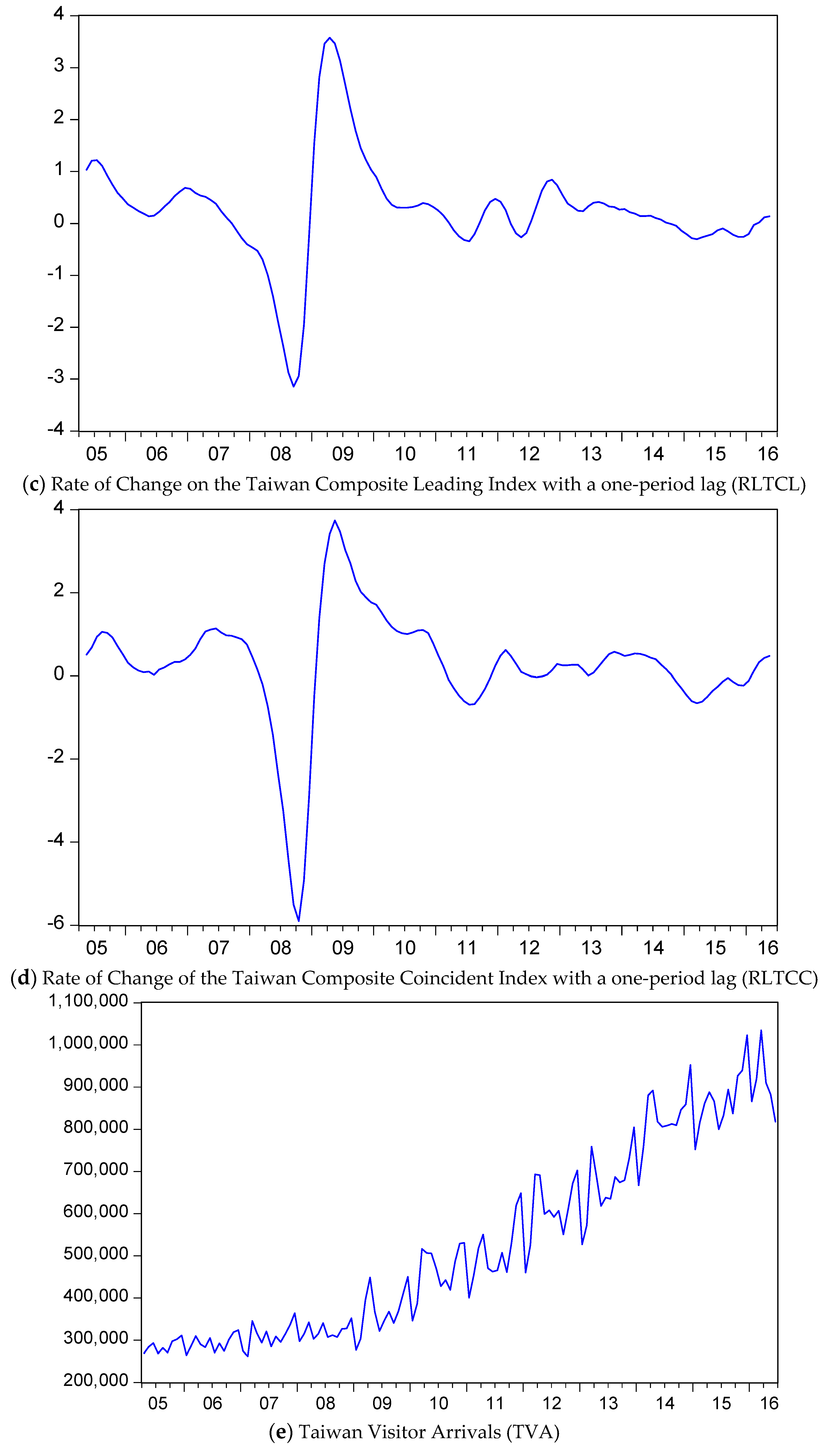
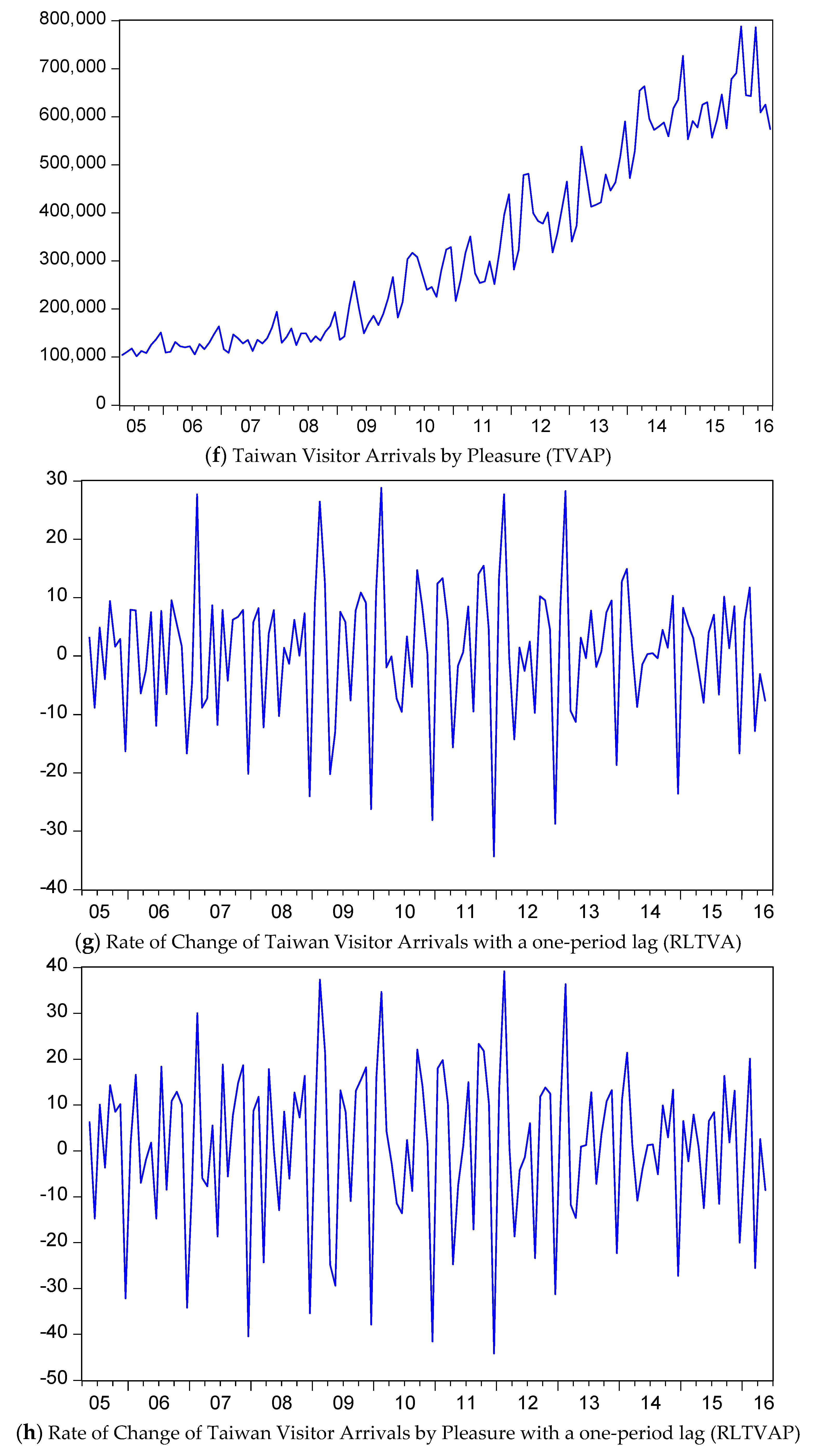
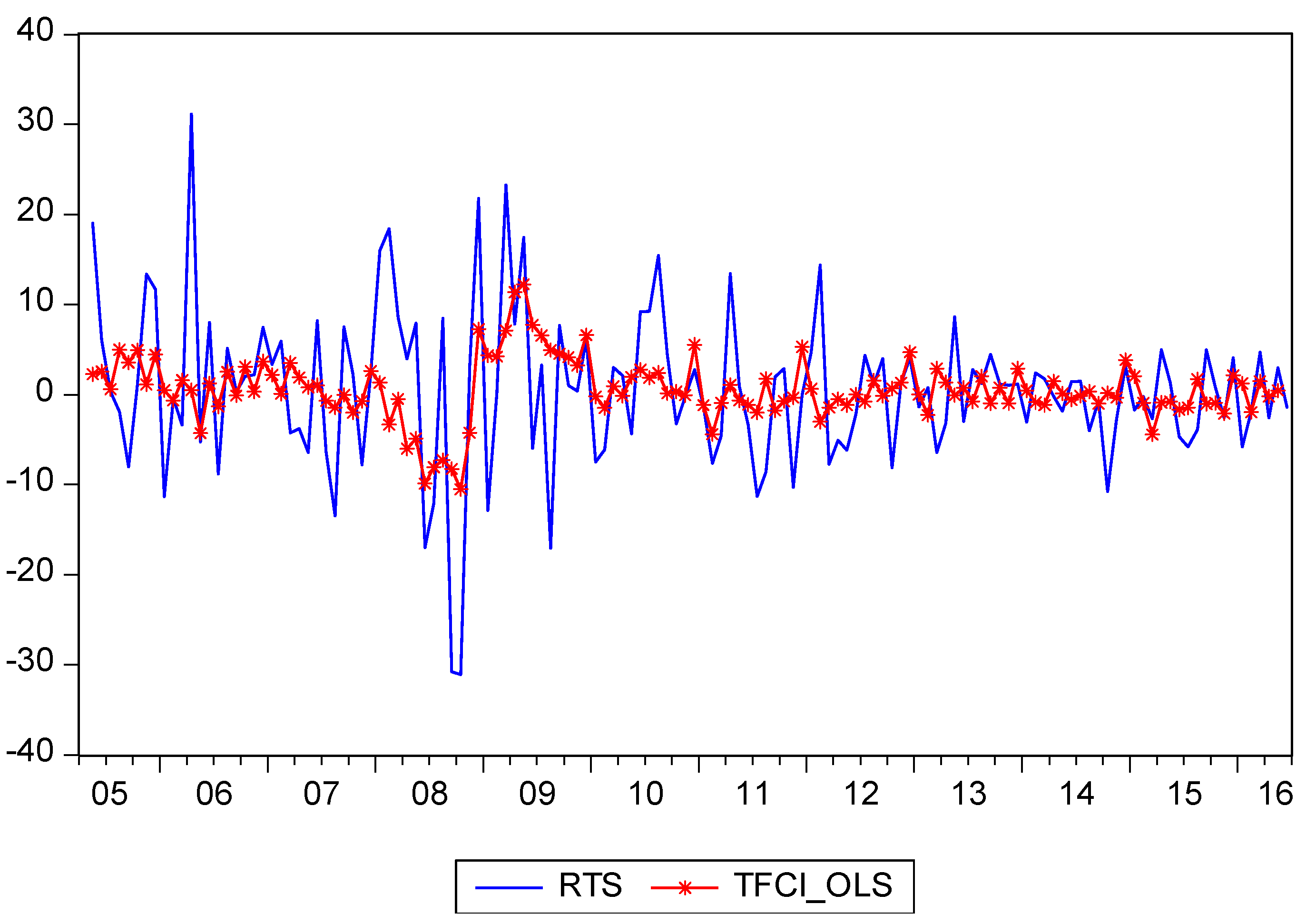
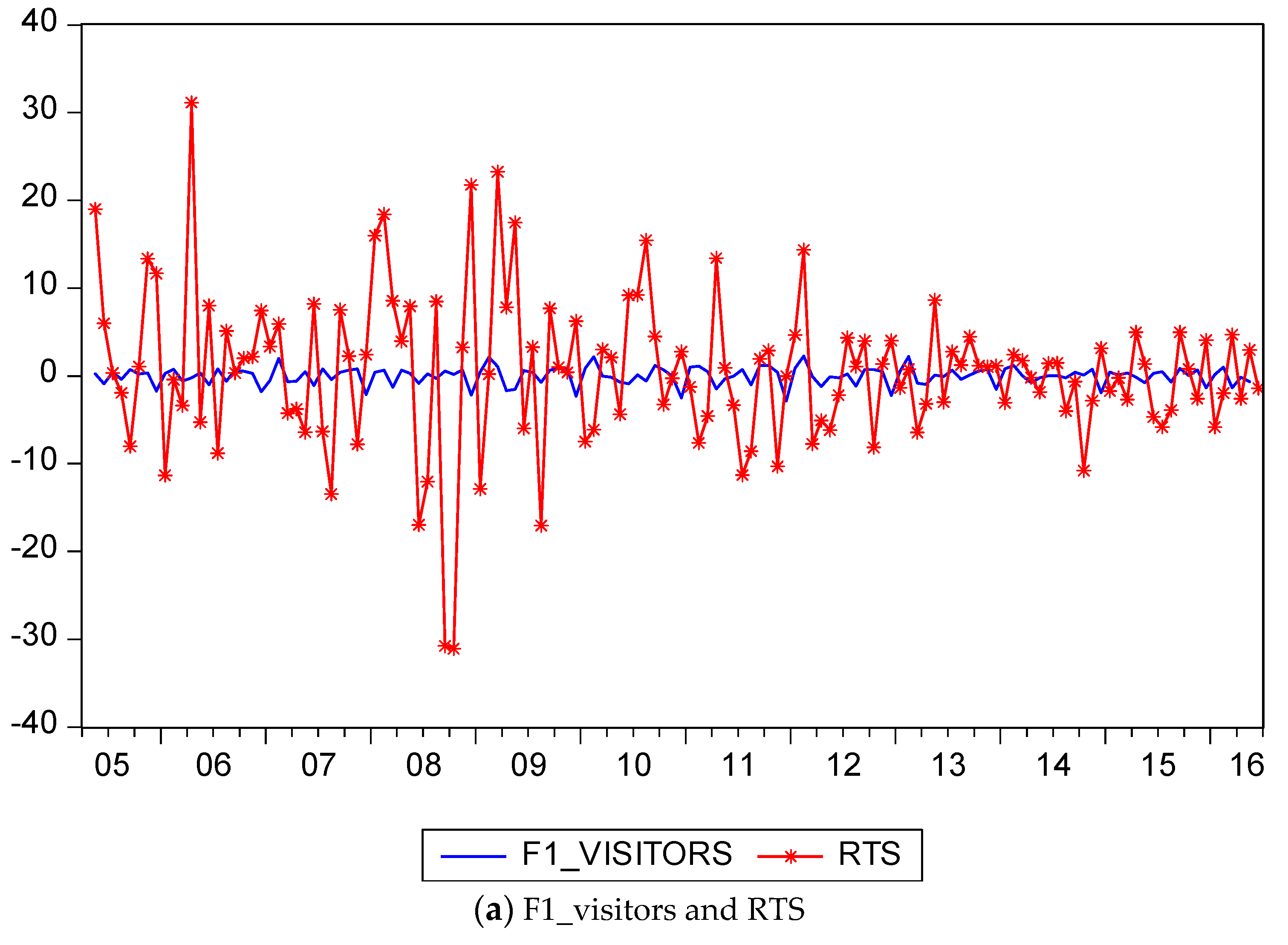
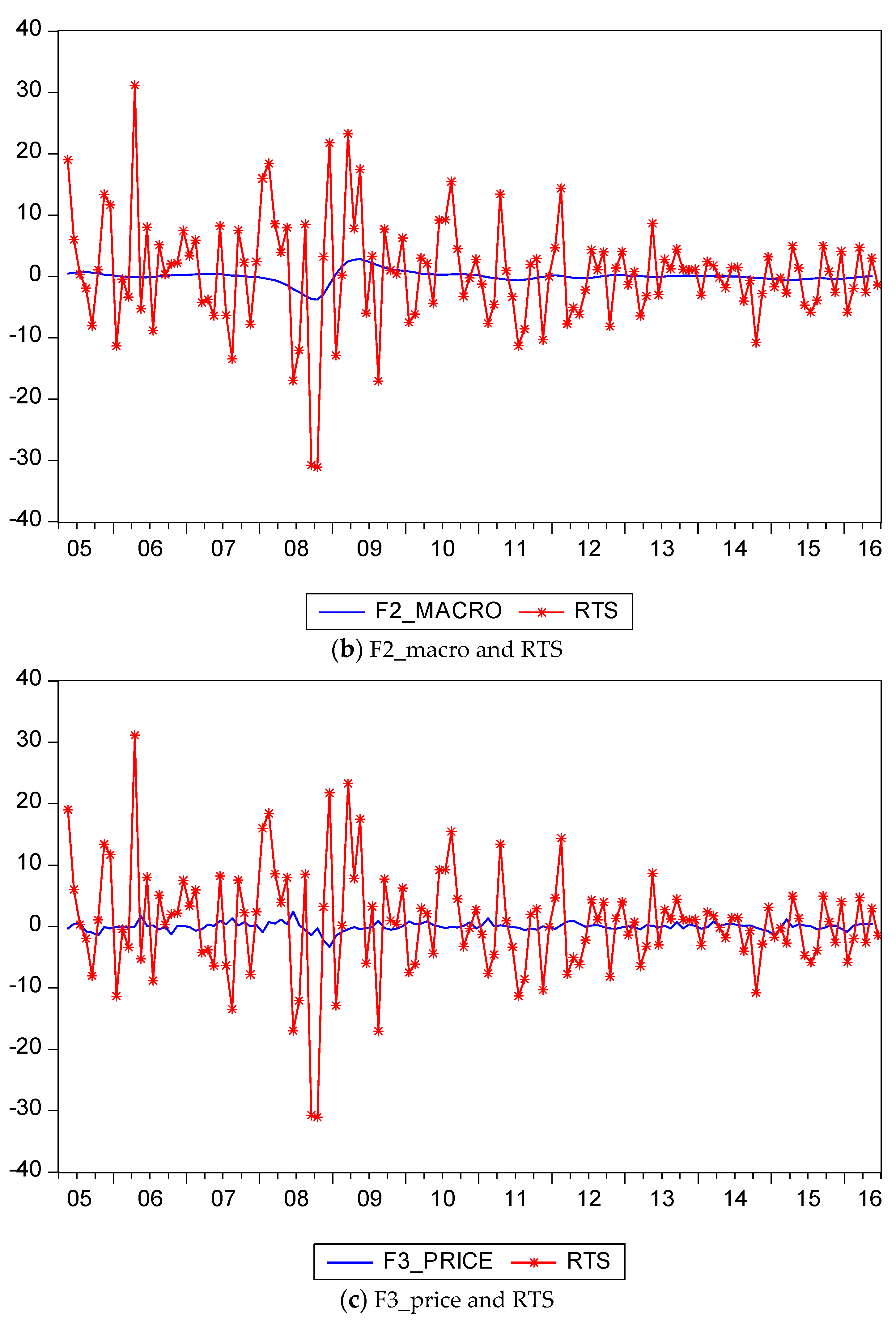
The time series plots in Figure 1 are instructive. The returns on the tourism stock index, RTS, exhibit standard stock market returns, with some volatility clustering, namely periods of relatively high volatility interspersed with periods of relatively low volatility. The lowest value of RTS occurs at the end of 2008. The rate of change in real effective exchange rates, REE, exhibit similar patterns of variation to those of RTS, with some periods of relatively high volatility mixed with periods of relatively low volatility. Both variables, the rate of change in the Taiwan composite coincident index (lag 1), RLTCC, and the rate of change in the Taiwan Composite leading index (lag 1), RLTCL, are reasonably smooth throughout the sample period, apart from a sharp fall at the end of 2008, followed by an even larger positive correction during 2009.

However, both the rate of change in Taiwan Visitor Arrivals, TVA, and the rate of change in Taiwan Visitor Arrivals by Pleasure, TVAP, show a strong increasing trend, with strong seasonality. There is no evidence of any cyclical behavior.

The descriptive statistics of the variables that are used to estimate the parameters in Equation (5) are given in

Table 2. Descriptive statistics of variables for April 2005–June 2016.

Variables	RTS	F1_Visitors	F2_Macro	F3_Price	TFCI (OLS)
Mean	0.5380	4.67 × 1017	1.25 × 1017	6.68 × 1017	0.5526
Median	0.9590	0.1760	0.0294	0.0284	0.3245
Maximum	31.1559	2.2789	2.8293	2.4543	12.2306
Minimum	−31.0804	−2.8514	−3.7720	−3.3111	−10.4946
Std. Dev.	8.6865	0.9837	0.9410	0.6873	3.4082
Skewness	−0.0706	−0.4881	−0.8188	−0.7351	−0.0313
Kurtosis	5.7145	3.3795	8.4540	7.9237	5.2995
Jarque-Bera	41.25	6.08	179.71	146.32	29.33
Prob-value	0	0.0479	0	0	0
Sum	72.0952	4.00 × 1015	8.40 × 1016	9.16 × 1015	73.5002
Sum Sq. Dev.	10,035.48	127.72	116.89	62.35	1533.29
Observations	134	133	133	133	133

Notes: RTS is return on Taiwan Stock Exchange Tourism Subindex. F1_visitors, F2_visitors, and F3_price are factor scores. TFCI (OLS) denotes OLS estimates of the monthly Tourism Financial Conditions Index.

. There are 134 monthly observations in total (133 for factor scores). The means and medians of the four variables are reasonably close to zero.

Estimation of TFCI, as defined in Table 1, will be examined in the next section to determine an unbiased estimate of TFCI for purposes of sensible public and private policy considerations that focus on economic activities that are related to the tourism industry, using factor scores based on the results of factor analysis.

5. Empirical Results

This section discusses the construction of the monthly TFCI based on the regression model in Equation (5) which estimates RTS on F1_visitors, F2_macro, and F3_price. Estimation of the model in Equation (5) by OLS is undertaken using the EViews econometric software package.

The descriptive statistics of the estimated monthly TFCI from Equation (5) are given in the last column of Table 2, where the fitted value (that is, the estimates) from the regression model are given as TFCI (OLS). The OLS estimates of TFCI are given in Figure 2. The mean of TFCI (OLS) is identical to that of RTS, as expected, but the medians are different. The range, or difference between the largest and smallest TFCI estimates, is much smaller for TFCI (OLS) than for RTS. The distribution of TFCI (OLS) is found to be significantly different from the normal distribution, as shown by the Jarque-Bera Lagrange multiplier test of normality. The departure from symmetry is relatively small, but the kurtosis suggests a significant departure from what would be expected under normality.

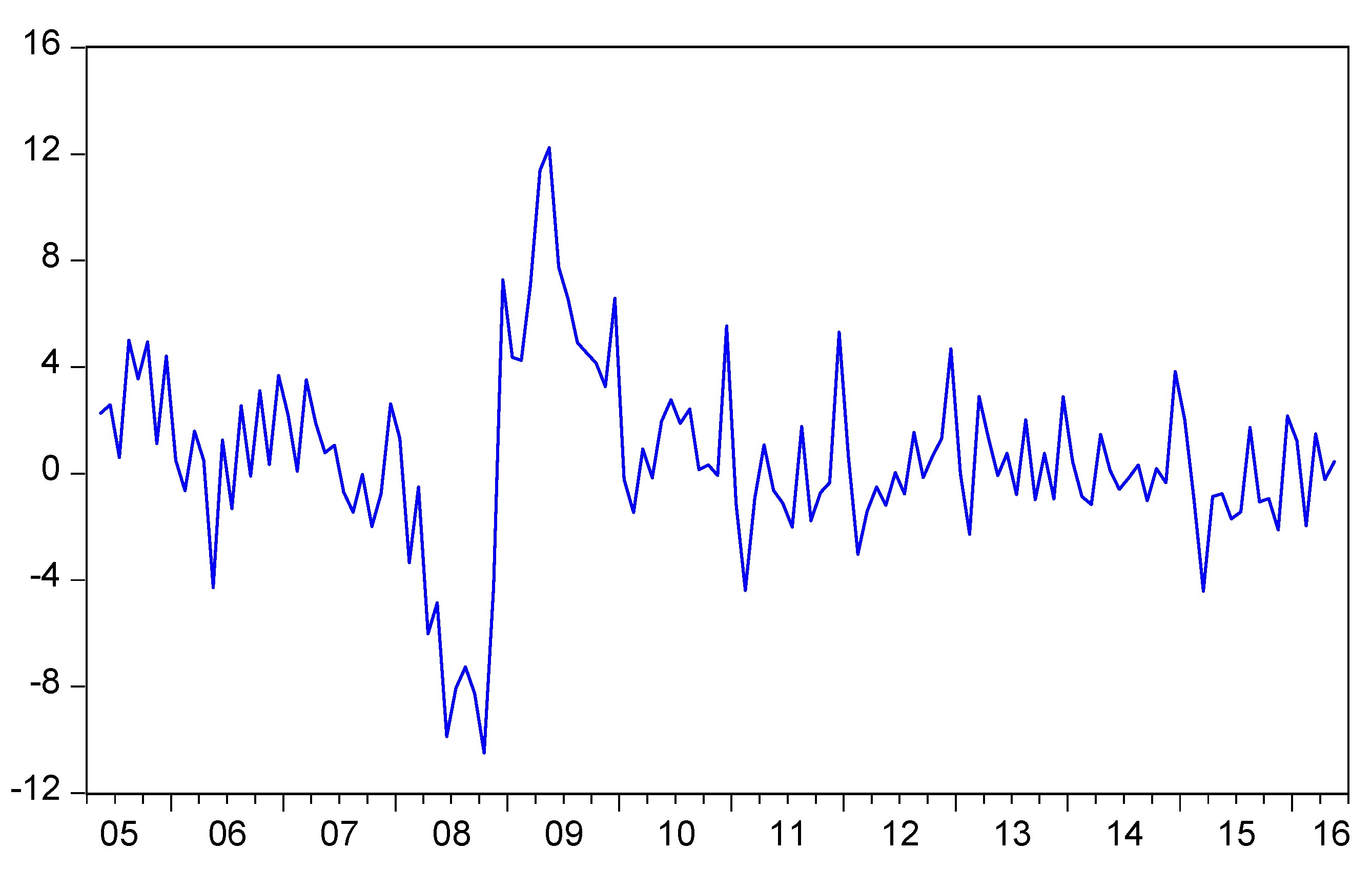
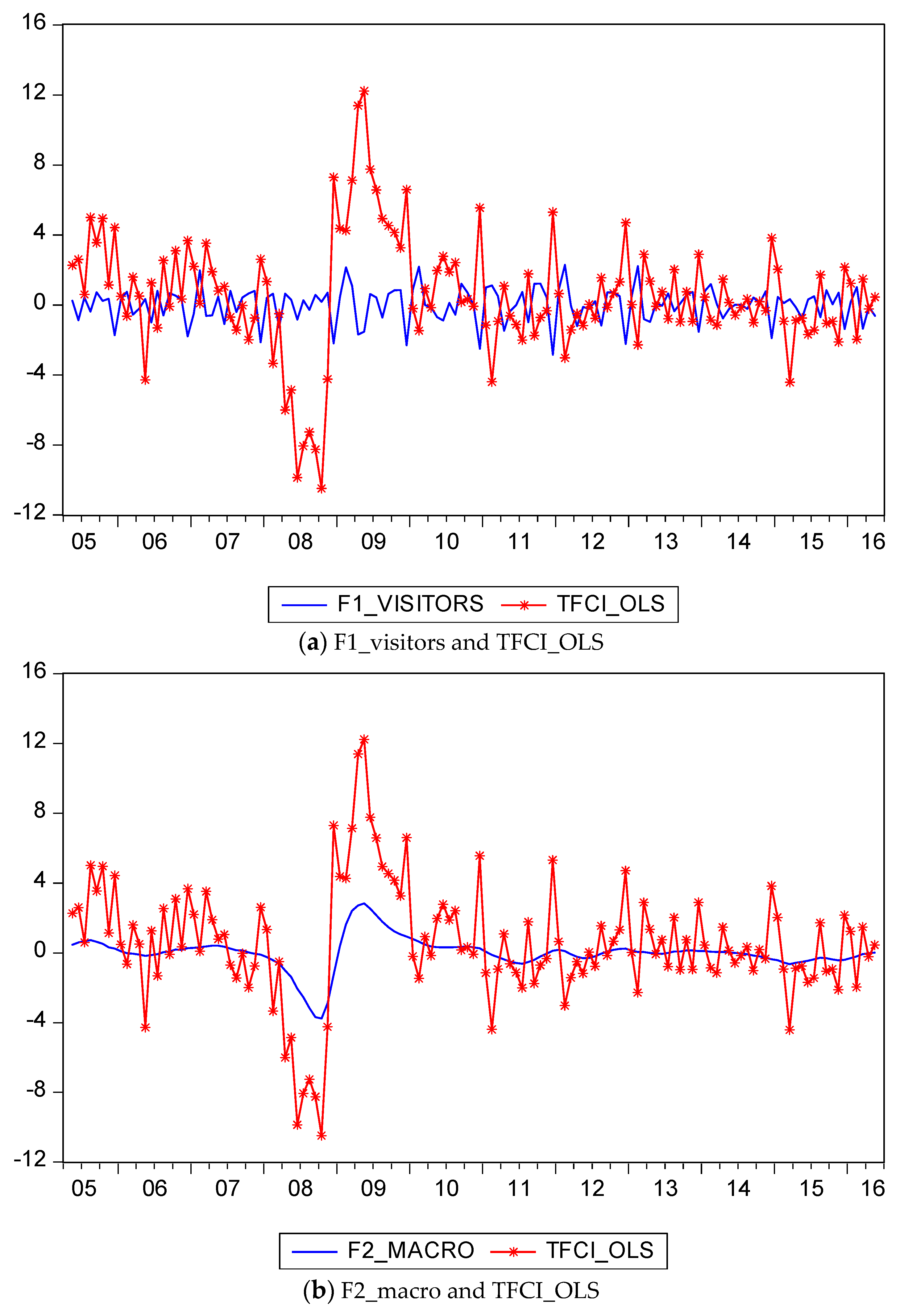
The time series plots of the OLS estimates of TFCI, TFCI (OLS), resemble the plots of F1_visitors. These two variables are given in Figure 3, where it is clear that the overall pattern of TFCI (OLS), though not the extreme values observed in 2008 and 2009, are tracked reasonably well by of the variations in F1_visitors.

The OLS estimates of TFCI obtained from Equation (5) are given in

Table 3. OLS estimates of TFCI for April 2005–June 2016.

Parameters	OLS
Constant	0.553
	(0.434)
	[0.704]
θ1	−1.446
	(0.046) **
	[0.718]
θ2	3.011
	(0.0001) ***
	[0.753]
θ3	−2.216
	(0.034) **
	[1.031] *
Diagnostics
Adjusted R2	0.133
F-statistic	7.758 ***
Jarque-Bera	20.120 ***

Notes: The dependent variable is RTS, the returns on the Taiwan Stock Exchange Over the Counter Tourism Subindex. The numbers in parentheses (brackets) are standard OLS (robust Newey-West HAC) standard errors. ***, **, and * denote the estimated coefficients are statistically significant at the 1%, 5%, and 10% levels, respectively.

. The F1_visitors have a negative and significant impact on the estimated TFCI, while F2_macro has a significant positive effect. The F3_price has a significant and negative effect on the estimated TFCI, using both the OLS and robust Newy-West HAC standard errors. It is not surprising that F2_macro should have a statistically significant impact on the tourism stock index returns as F2_macro is based on the industrial production index, electric power consumption, index of producer’s shipment for manufacturing, sale index of wholesale retail and food services, nonagricultural employment, real customs-cleared exports, and real machinery and electrical equipment import. Finally, the Jarque-Bera Lagrange multiplier statistic for normality indicates that the residuals from the OLS regression are not normally distributed.

It is interesting that the empirical results show a significantly negative correlation between F1_visistors and RTS, implying the tourism authorities might promote travel by the “rich”, and not only on inbound visitor growth.

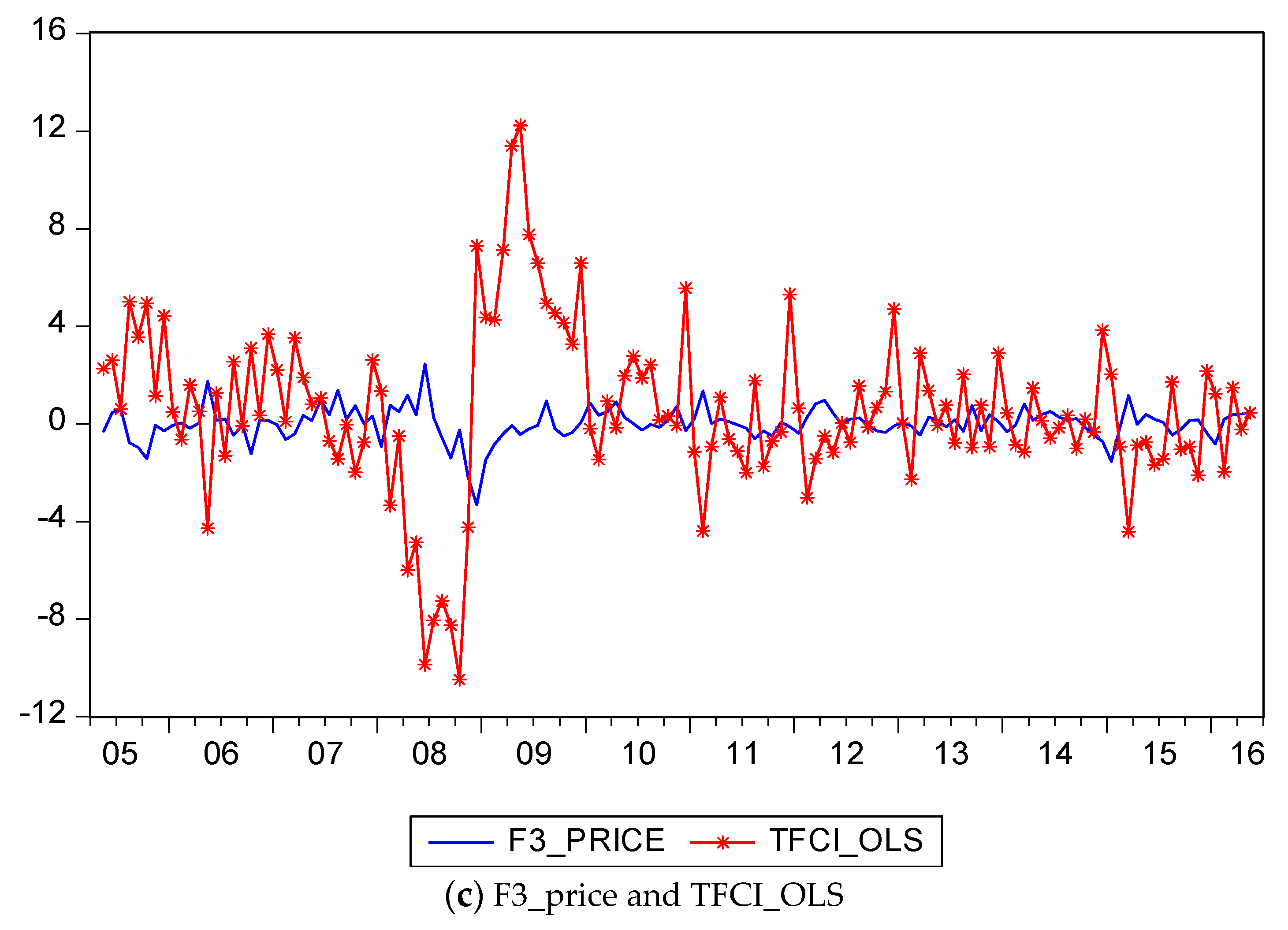
The differences in the magnitudes of RTS and the OLS estimates of TFCI, TFCI (OLS), which is equivalently an estimate of RTS from Equation (5), indicate the importance of the model-based estimates of TFCI in discussing the tourism sector. The use of RTS as the sole indicator of the tourism sector, as compared with the general activity of the economic variables on the tourism stock variable, would seem to provide an exaggerated and excessively volatile explanation of tourism financial conditions. The use of the estimated TFCI, TFCI (OLS), exhibits far less volatility than does RTS, as can be seen clearly in Figure 4.

This paper used the Granger causality test between a latent variable, TFCI, and an observable variable, RTC. Empirical data indicate that TFCI shows strong feedback on RTS, while RTS reveals slight feedback on TFCI (see Figure 5 and

Table 4. Granger causality tests on TFCI and RTS for April 2005–June 2016.

Null Hypothesis	F-Statistic	Prob.
TFCI does not Granger Cause RTS	4.225 **	0.0168
RTS does not Granger Cause TFCI	2.396 *	0.0952

Notes: ** and * denote the estimated coefficients are statistically significant at the 5% and 10% levels, respectively.

). The empirical findings suggest that Granger causality is bi-directional, that is, runs both ways between TFCI and RTS.

6. Conclusions

The paper used monthly rates of change of data on the composite coincident index (lag1), composite leading index (lag1), foreign visitor arrival (lag1), foreign visitors by pleasure (lag1), real effective exchange rates and consumer price index from April 2005 to June 2016 for Taiwan to construct a novel monthly tourism financial indicator, namely the Tourism Financial Conditions Index (TFCI).

The TFCI is an adaptation and extension of the widely-used Monetary Conditions Index (MCI) and Financial Conditions Index (FCI) to the tourism industry stock data that is listed on the Taiwan Stock Exchange (specifically, the Taiwan Stock Exchange Tourism Sub-index). However, the method of calculation of the monthly TFCI is different from existing methods of constructing the MCI and FCI in that the weights are estimated empirically from a regression model using publicly available data. The empirical results showed that TFCI can be estimated quite accurately using a regression model to explain the tourism stock index returns.

The monthly TFCI is straightforward to use and interpret, and provides interesting insights in predicting the current economic and financial environment for tourism stock index returns. The use of returns on the tourism stock index as the sole indicator of the tourism sector, as compared with the general activity of the economic variables on the tourism stock variable, was shown to provide an exaggerated and excessively volatile explanation of tourism financial conditions.

It is worth emphasizing that, as noted in Shiller (1981), [27], stock prices appear to vary far more than would be justified from a dividend discount model perspective. Accordingly, it could be argued that the fact that the TFCI varies far less than returns tourism industry stocks is useful and informative. This interpretation presumes that the aim of the index is to model the underlying financial conditions facing the industry, rather than current stock market investor expectations of the net present value of future dividends from listed tourism companies. Such an interpretation is appropriate for the model developed in the paper.

It is interesting that the empirical results show a significantly negative correlation between F1_visistors and RTS, implying the tourism authorities might promote travel by the “rich”, and not only on inbound growth of visitors. Using the Granger causality test, the empirical finding indicate that TFCI shows strong feedback on RTS, and also a slight feedback on TFCI.

Overall, the empirical findings should be helpful for public and private decision makers, such as government, business executives and investors, as the TFCI provides useful insights that can be based on straightforward calculations and interpretations of publicly available information.

The TFCI was related to the fundamental equation in tourism finance, whereby the primary purpose of tourism authorities in the public and private sectors is to achieve high daily returns on total tourism.