Offshore Structural Reliability Assessment by Probabilistic Procedures—A Review
Abstract
:1. Introduction
2. Overview of the Offshore Structural Assessment
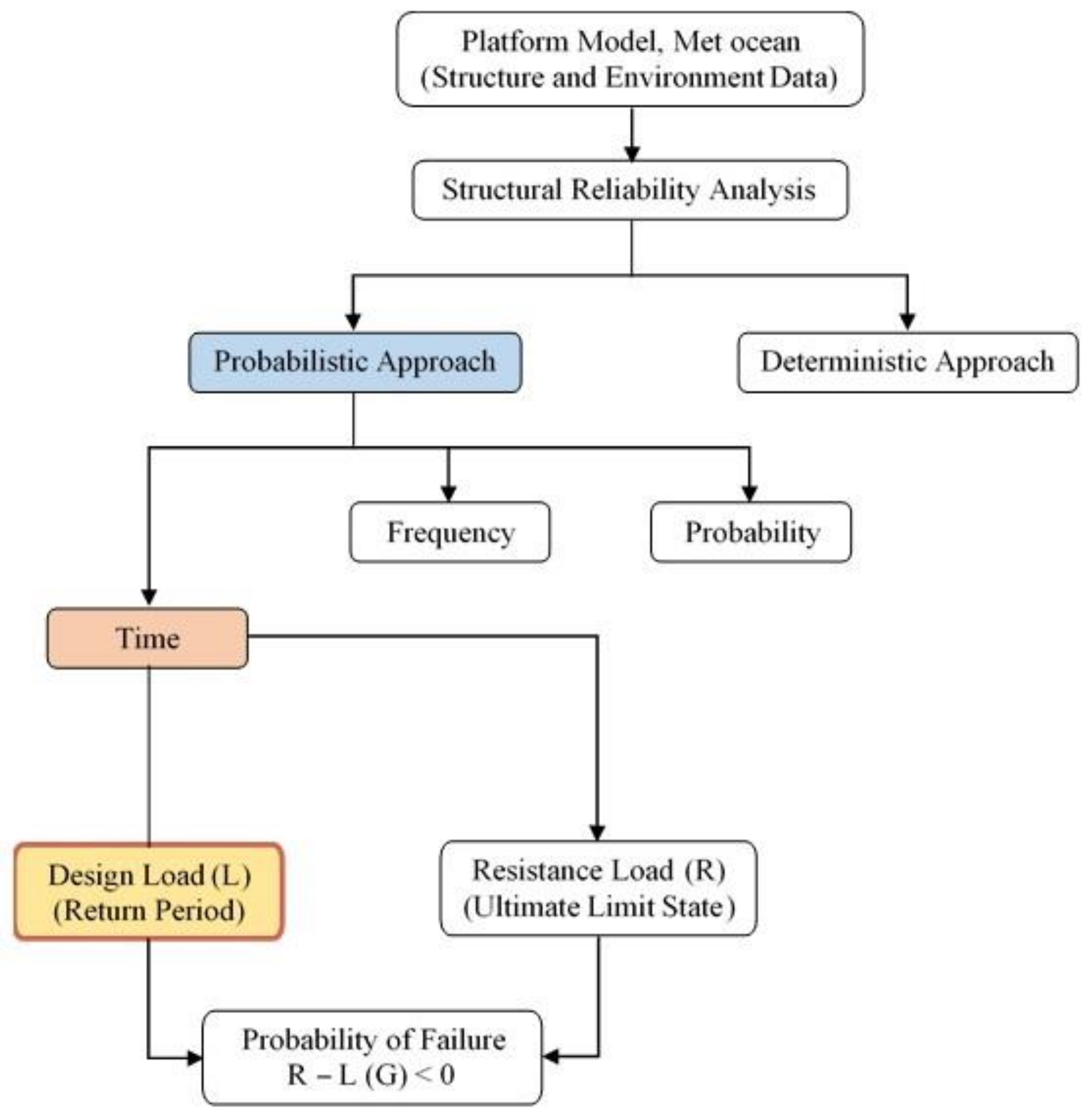
2.1. Structural Reliability Analysis for Fixed Offshore Platforms
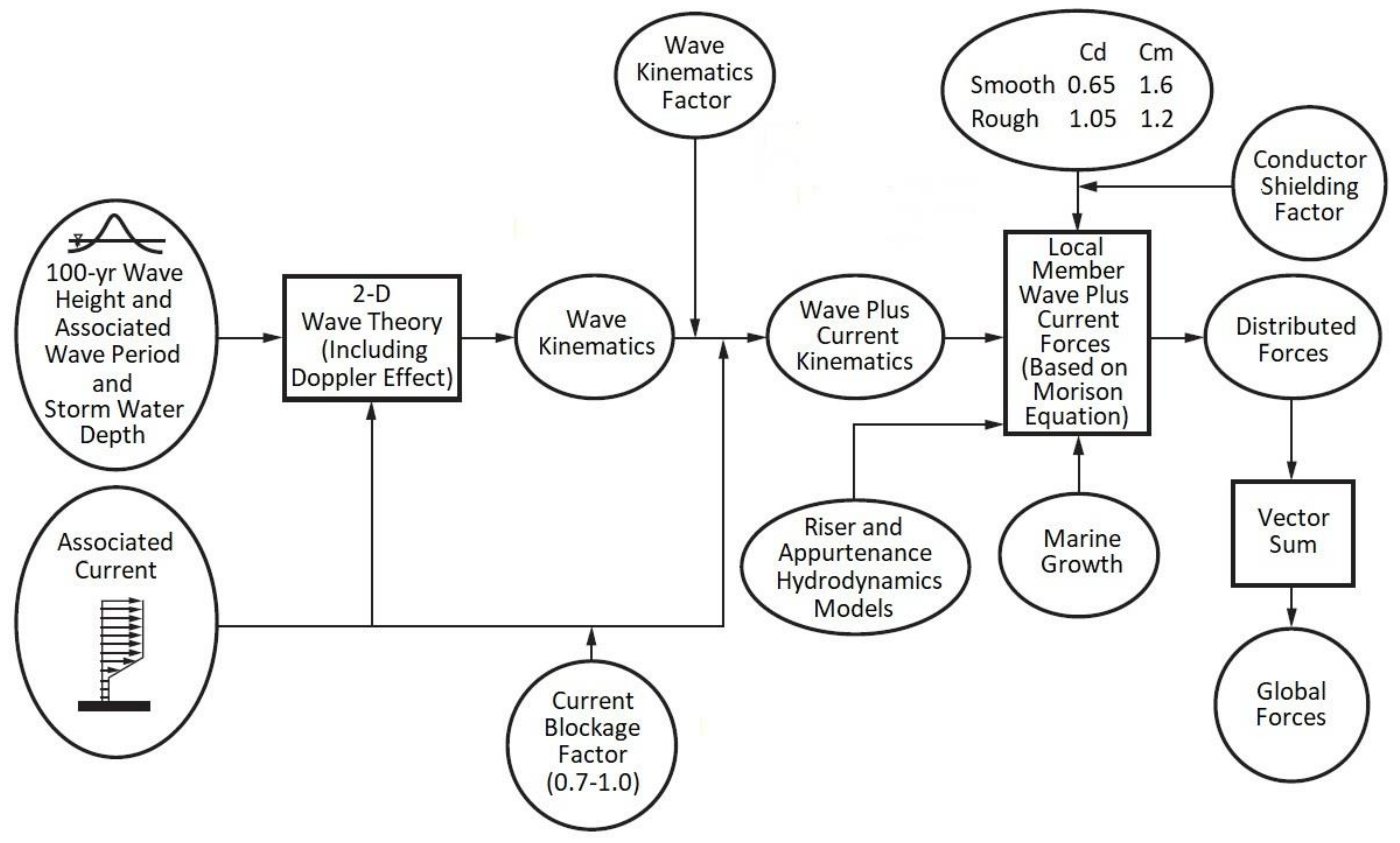
2.2. Determination on the Wave Force Procedure
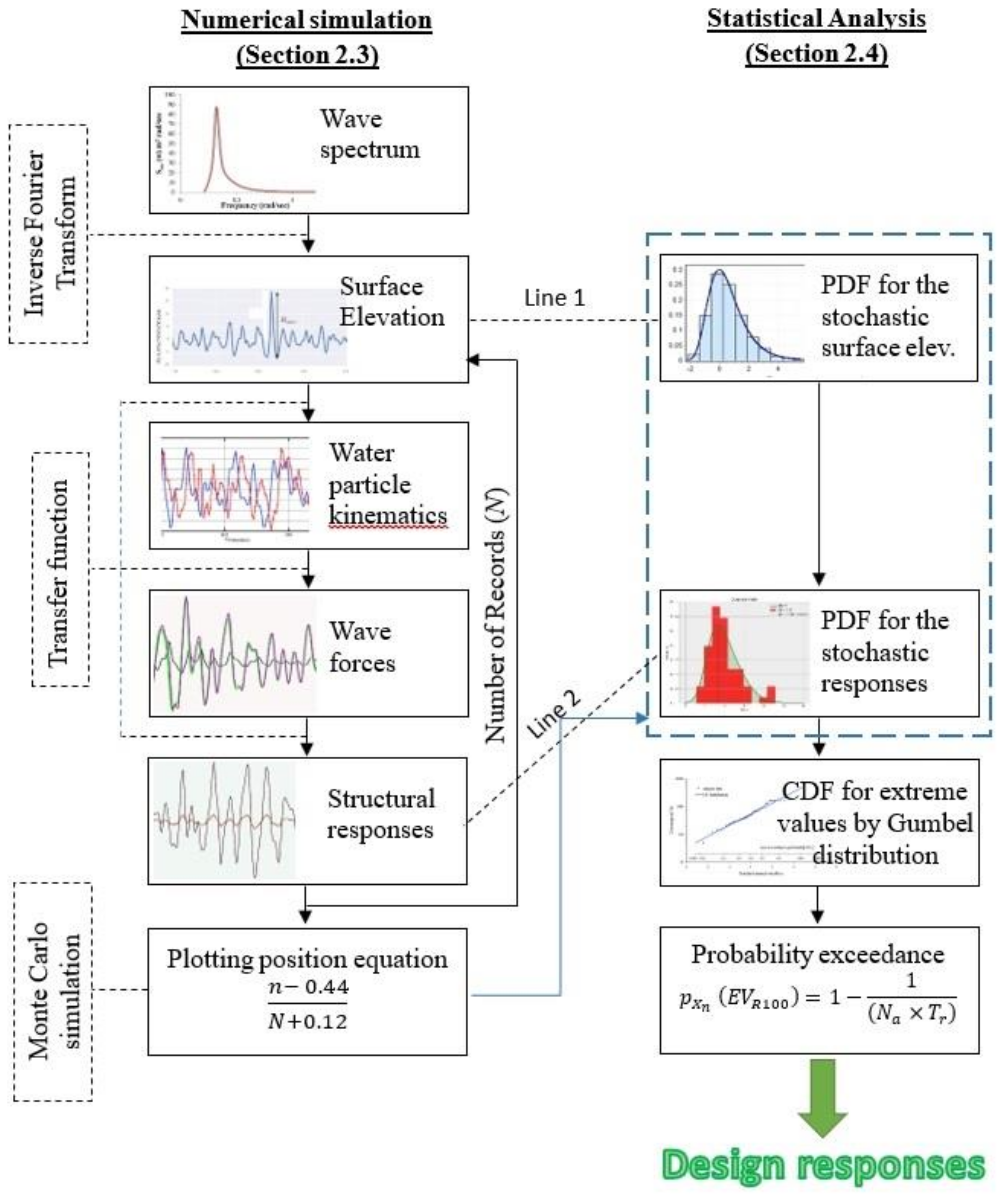
2.3. Analysing Hydrodynamic Wave Load-Induced Offshore Structural Responses
2.3.1. Numerical Simulation Analysis
2.3.2. Short-Term and Long-Term Analysis
3. Probabilistic Approaches for Fixed Offshore Structural Response Analyses
3.1. Probability Domain Methods
3.2. Frequency Domain Methods
3.3. Time Domain Methods
4. Overall Review of the Probabilistic Domains on Offshore Structural Assessment
5. Conclusions
- The fundamental principle of the design and analysis of offshore structures is that it enables their stability over design life to be maintained. It follows from the non-linear behaviourof fixed offshore platforms that they involve a considerable number of major uncertainties pertaining to the techniques of structural analysis, the mathematical models for the structural behaviour, the loading mechanism, and the response to the parameters concerned.
- The probabilistic approach has been shown to have several benefits compared to the deterministic approach. It offers, in particular, a clear framework for calibrating code design practices like the evolving load and resistance factor design (LRFD) methods. This will explain a decrease in the safety factors associated with the individual components through a clear reflection of the distinctive aspect of the wave environments and hydrodynamic response.
- There are three fields in which the response properties can be built on the basis of the probabilistic method;the probability, frequency, and time domain. The principal challenge in probabilistic analysis is the randomness of stochastic waves. An exact model for predicting extreme responses is important as awareness is necessary if the structural design of the offshore is to be optimised.
- With regard to design structural analysis, establishing a practicable technique that combines the latest short-term and long-term non-linear analysis methods with the conventional design wave methods seems desirable in a manner compatible with the reliability analysis.
- The long-term probability distribution, which is then required to analyse fatigue concerning the structural extreme during its service life, is needed to analyse the first excursion failure. It can be accomplished by transforming their respective short-term distributions into a long-term wave environment.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| API | American Petroleum Institute |
| API RP 2A | API Standard according to the Recommended Practice (RP) of 2A |
| CPU | Computer Processing Unit |
| EVR100 | 100-Year Extreme Responses |
| FFTrf and FFTrfa | Randomization of Wave Component Frequency |
| FFT | Fast Fourier Transform |
| HAWC2 | Horizontal Axis Wind Turbine Simulation Code 2nd Generation |
| PM | Pierson-Moskowitz Spectrum |
| POF | Probability of Failure |
| RSR | Reserve Strength Ratio |
| SACS | Structural Analysis Computer Software |
| SRA | Structural Reliability Analysis |
| USFOS | Ultimate Strength for Offshore Structural Software |
Nomenclature
| peak frequency | Hz | |
| function of failure | – | |
| wave height | m | |
| significant wave height | m | |
| load distribution (model) | N or Nm | |
| the smallest simulated extreme value | – | |
| total number of simulation records (simulated responses) | – | |
| annual average number of sample data | – | |
| probability distribution (model) | – | |
| cumulative probability of return periods | – | |
| resistance distribution (model) | N or Nm | |
| wave period | s | |
| zero up-crossing wave period | s | |
| specific return periods | – |
References
- Hübler, C.J. Efficient Probabilistic Analysis of Offshore Wind Turbines Based on Time-Domain Simulations. Ph.D. Thesis, Leibniz Universität, Hannover, Germany, 2019. [Google Scholar]
- Folley, M. The Wave Energy Resource. In Handbook of Ocean Wave Energy; Pecher, A., Kofoed, J.P., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 43–79. [Google Scholar] [CrossRef] [Green Version]
- Vanem, E. Joint Statistical Models for Significant Wave Height and Wave Period in a Changing Climate. Mar. Struct. 2016, 49, 180–205. [Google Scholar] [CrossRef]
- Baarholm, G.S.; Haver, S.; Økland, O.D. Combining Contours of Significant Wave Height and Peak Period with Platform Response Distributions for Predicting Design Response. Mar. Struct. 2010, 23, 147–163. [Google Scholar] [CrossRef]
- Vanem, E.; Fazeres-Ferradosa, T.; Rosa-Santos, P.; Taveira-Pinto, F. Statistical Description and Modelling of Extreme Ocean Wave Conditions. Proc. Inst. Civ. Eng.-Marit. Eng. 2019, 172, 124–132. [Google Scholar] [CrossRef]
- Lin, P. Numerical Modeling of Water Waves; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Morooka, C.K.; Yokoo, I.H. Numerical Simulation and Spectral Analysis of Irregular Sea Waves. Int. J. Offshore Polar Eng. 1997, 7, ISOPE-97-07-3-189c. [Google Scholar]
- Dimitrov, N. Comparative Analysis of Methods for Modelling the Short-Term Probability Distribution of Extreme Wind Turbine Loads. Wind Energy 2016, 19, 717–737. [Google Scholar] [CrossRef]
- Benstock, D.; Cegla, F. Extreme Value Analysis (EVA) of Inspection Data and Its Uncertainties. NDT E Int. 2017, 87, 68–77. [Google Scholar] [CrossRef] [Green Version]
- Raheem, S.E.A. Nonlinear Response of Fixed Jacket Offshore Platform Under Structural and Wave Loads. Coupled Syst. Mech. 2013, 2, 111–126. [Google Scholar] [CrossRef] [Green Version]
- Abdel Raheem, S.E. Nonlinear behaviour of steel fixed offshore platform under environmental loads. Ships Offshore Struct. 2016, 11, 1–15. [Google Scholar] [CrossRef]
- Petrauskas, C.; Heideman, J.C.; Berek, E.P. Extreme Wave-Force Calculation Procedure for 20th Edition of API-RP-2A. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 3–6 May 1993; p. 11. [Google Scholar]
- Nallayarasu, S. Offshore Structures—Analisys and Design. Ph.D. Thesis, Indian Instritute of Technology Madras, Chennai, India, 1981. [Google Scholar]
- Stewart, G. Reassessment of Fixed Offshore Structures. Encycl. Marit. Offshore Eng. 2017, 1–17. [Google Scholar] [CrossRef]
- Bea, R.G. Structural Reliability: Design and Requalification of Offshore Platforms. In Proceedings of the Reliability of Offshore Operations, Proceedings, International Workshop, Building and Fire Research Laboratory, Berkeley, CA, USA, 1–3 April 1992; pp. 41–67. [Google Scholar]
- Sadeghi, K.; Dilek, H. An Introduction to the Design of Offshore Structures. Acad. Res. Int. 2019, 10, 19–27. [Google Scholar]
- Wei, K.; Liu, Q.; Qin, S. Nonlinear Assessment of Offshore Steel Trestle Subjected to Wave and Current Loads. Ships Offshore Struct. 2019, 15, 479–491. [Google Scholar] [CrossRef]
- Kharade, A.; Kapadiya, S. Offshore Engineering: An Overview of Types and Loadings on Structures. Int. J. Struct. Civ. Eng. Res. 2014, 3, 16–28. [Google Scholar]
- El-Reedy, M.A. Offshore Structures: Design, Construction and Maintenance; Gulf Professional Publishing: Houston, TX, USA, 2019. [Google Scholar]
- Melchers, R.E.; Beck, A.T. Structural Reliability Analysis and Prediction; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Chandrasekaran, S. Environmental forces. In Dynamic Analysis and Design of Offshore Structures; Springer: Berlin/Heidelberg, Germany, 2018; pp. 63–125. [Google Scholar]
- Connor, J.J.; Faraji, S. Fundamentals of Structural Engineering, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Slåke, T. Analysis of Jacket Type Fixed Platforms–Effect of Various Mass Modelling Approaches for Topsides on Structural Response. Master’s Thesis, University of Stavanger, Stavanger, Norway, 2016. [Google Scholar]
- Kolios, A.; Brennan, F. Reliability Based Design of Novel Offshore Structures. In Proceedings of the 3rd International Conference on Integrity, Chengdu, China, 20–24 July 2009. [Google Scholar]
- Hørte, T.; Sigurdsson, G. On the Application of Structural Reliability Analysis. In Proceedings of the 36th International Conference on Ocean, Offshore and Arctic Engineering, Trondheim, Norway, 25–30 June 2017. [Google Scholar]
- Moan, T. Safety of Offshore Structures; National University of Singapore: Singapore, 2005. [Google Scholar]
- Wouts, M.; van der Graaf, J.; Vrouwenvelder, A. Fatigue Reliability Analyses of Fixed Offshore Structures. In Proceedings of the European Petroleum Conference, London, UK, 16–19 October 1988. [Google Scholar]
- Mukherjee, D.; Mahadevan, S. Reliability-based Structural Design. In Proceedings of the Annual Reliability and Maintainability Symposium, Washington, DC, USA, 16–19 January 1995; pp. 207–212. [Google Scholar]
- Jiang, Z.; Hu, W.; Dong, W.; Gao, Z.; Ren, Z. Structural reliability analysis of wind turbines: A review. Energies 2017, 10, 2099. [Google Scholar] [CrossRef] [Green Version]
- San Tint, A. Reliability Analysis of the Final Design of a Fixed Offshore Jacket. Master’s Thesis, Asian Institute of Technology, Khlong Nueng, Thailand, 2015. [Google Scholar]
- Ayyub, B.M.; McCuen, R.H. Probability, Statistics, and Reliability for Engineers and Scientists; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Lotsberg, I.; Sigurdsson, G.; Fjeldstad, A.; Moan, T. Probabilistic Methods for Planning of Inspection for Fatigue Cracks in Offshore Structures. Mar. Struct. 2016, 46, 167–192. [Google Scholar] [CrossRef]
- Mat Soom, E.; Abu Husain, M.K.; Mohd Zaki, N.I.; Azman, N.U.; Najafian, G. Reliability-Based Design and Assessment for Lifetime Extension of Ageing Offshore Structures. In Proceedings of the 35th International Conference on Ocean, Offshore and Arctic Engineering, Busan, Korea, 19–24 June 2016; p. V003T002A044. [Google Scholar]
- Mat Soom, E.; Abu Husain, M.K.; Mohd Zaki, N.I.; Mohd Nor, K.; Ayob, M.S.; Najafian, G. Lifetime Extension of Ageing Offshore Structures by Global Ultimate Strength Assessment (GUSA). Malays. J. Civ. Eng. 2018, 30, 1. [Google Scholar] [CrossRef] [Green Version]
- Zeinoddini, M.; Golpour, H.; Khalili, H.; Matin Nikoo, H.; Ahmadi, I. Sensitivity Analysis of Selected Random Variables of Existing Offshore Jacket Structures in Persian Gulf. Int. J. Coast. Offshore Eng. 2017, 5, 7–16. [Google Scholar]
- Mirzadeh, J.; Kimiaei, M.; Cassidy, M.J. A Framework to Efficiently Calculate the Probability of Failure of Dynamically Sensitive Structures in A Random Sea. Ocean. Eng. 2015, 110, 215–226. [Google Scholar] [CrossRef]
- Mat Soom, E.; Abu Husain, M.K.; Mohd Zaki, N.I.; Azman, N.U.; Structural Reliability Analysis for Fixed Offshore Platforms. Jurutera 2019. Available online: http://103.86.130.60/xmlui/bitstream/handle/123456789/62313/Structural%20reliability%20analysis%20for%20fixed%20offshore%20platforms.pdf?sequence=1 (accessed on 7 September 2021).
- van Os, J.; Caires, S.; van Gent, M. Guidelines for Metocean Data Analysis. In Proceedings of the Twenty-First International Offshore and Polar Engineering Conference, Beijing, China, 20–25 June 2010. [Google Scholar]
- Li, P.; Zhu, Q.; Zhou, C.; Li, L.; Li, H. Metocean Design Criteria Considerations in South China Sea by Adopting Multivariate Extreme Value Theory. In Proceedings of the 36th International Conference on Ocean, Offshore and Arctic Engineering, Trondheim, Norway, 25–30 June 2017. [Google Scholar]
- Cremona, C. Structural Performance: Probability-Based Assessment; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Czujko, J.; Bayatfar, A.; Smith, M.; Xu, M.; Wang, D.; Lützen, M.; Saad-Eldeen, S.; Yanagihara, D.; Notaro, G.; Qian, X.; et al. Committee III. 1: Ultimate Strength. In Proceedings of the 20th International Ship and Offshore Structures Congress (ISSC 2018), Liege, Belgium; Amsterdam, The Netherlands, 9–14 September 2018; pp. 381–390. [Google Scholar]
- Fjeld, S. Reliability of Offshore Structures. J. Pet. Technol. 1978, 30, 1486–1496. [Google Scholar] [CrossRef]
- Chen, J.; Gilbert, R.B. Offshore Pile System Model Biases and Reliability. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2017, 11, 55–69. [Google Scholar] [CrossRef]
- Low, B. Insights from Reliability-Based Design to Complement Load And Resistance Factor Design Approach. J. Geotech. Geoenvironmental Eng. 2017, 143, 04017089. [Google Scholar] [CrossRef]
- Stewart, G.; Manzocchi, M. Recent Developments in Probabilistic Pushover Models for The Reliability Re-Assessment of Fixed Offshore Structures. Saf. Reliab. 2018, 38, 3–31. [Google Scholar] [CrossRef]
- Mat Soom, E. Efficient Load Coefficient Method for Structural Reliability Assessment of Ageing Offshore Platforms. Ph.D. Thesis, Universiti Teknologi Malaysia, Johor Bahru, Malaysia, 2018. [Google Scholar]
- Nava-Viveros, I.; Heredia-Zavoni, E. Assessment of Statistical Parameter Uncertainty in The Reliability Analysis of Jacket Platforms. In Proceedings of the Ocean Engineering, Hong Kong, China, 13–14 October 2016; pp. 370–379. [Google Scholar]
- Shittu, A.A.; Mehmanparast, A.; Wang, L.; Salonitis, K.; Kolios, A. Comparative study of structural reliability assessment methods for offshore wind turbine jacket support structures. Appl. Sci. 2020, 10, 860. [Google Scholar] [CrossRef] [Green Version]
- Mat Soom, E.; Abu Husain, M.K.; Mohd Zaki, N.I.; Azman, N.U. A Reliable Approach for Fixed Offshore Structures Probability of Failure Determination. Int. J. Adv. Res. Eng. Technol. (IJARET) 2020, 11, 469–475. [Google Scholar]
- API. Recommended Practice for Planning, Designing and Constructing Fixed Offshore Platforms—Working Stress Design; American Petroleum Institute: Washington, DC, USA, 1993. [Google Scholar]
- Şen, Z. Probability and Statistical Methods. In Flood Modeling, Prediction and Mitigation; Springer: Berlin/Heidelberg, Germany, 2018; pp. 245–301. [Google Scholar]
- Zhang, B.; Shang, Z.-Q.; Wang, T.; Wang, Z. Hydrodynamic Load Analysis and Experimental Study of Grouting Clamp under Wave and Ocean Current. J. Mar. Sci. Eng. 2020, 8, 512. [Google Scholar] [CrossRef]
- Zhao, Y.; Guan, C.; Bi, C.; Liu, H.; Cui, Y. Experimental investigations on hydrodynamic responses of a semi-submersible offshore fish farm in waves. J. Mar. Sci. Eng. 2019, 7, 238. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Benoit, M.; Kimmoun, O.; Chabchoub, A.; Hsu, H.-C. Statistics of Extreme Waves in Coastal Waters: Large Scale Experiments and Advanced Numerical Simulations. Fluids 2019, 4, 99. [Google Scholar] [CrossRef] [Green Version]
- Kareem, A.; Kijewski, T. Time-Frequency Analysis of Wind Effects On Structures. J. Wind. Eng. Ind. Aerodyn. 2002, 90, 1435–1452. [Google Scholar] [CrossRef]
- Phillips, O.M. The Equilibrium Range in The Spectrum of Wind-Generated Waves. J. Fluid Mech. 1958, 4, 426–434. [Google Scholar] [CrossRef]
- Faltinsen, O.M. Sea Loads on Ships and Offshore Structures; Cambridge University Press: New York, NY, USA, 1990; Volume 1. [Google Scholar]
- Colagrossi, A.; Landrini, M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics. J. Comput. Phys. 2003, 191, 448–475. [Google Scholar] [CrossRef]
- Bateman, W.J.; Swan, C.; Taylor, P.H. On The Efficient Numerical Simulation of Directionally Spread Surface Water Waves. J. Comput. Phys. 2001, 174, 277–305. [Google Scholar] [CrossRef]
- Zheng, X.Y.; Moan, T.; Quek, S.T. Numerical Simulation of Non-Gaussian Wave Elevation and Kinematics Based on Two-Dimensional Fourier Transform. In Proceedings of the 25th International Conference on Offshore Mechanics and Arctic Engineering, Hamburg, Germany, 4–9 June 2006; pp. 7–16. [Google Scholar]
- Abu Husain, M.K.; Mohd Zaki, N.I.; Johari, M.B.; Najafian, G. Extreme Response Prediction for Fixed Offshore Structures by Monte Carlo Time Simulation Technique. In Proceedings of the 35th International Conference on Ocean, Offshore and Arctic Engineering, Busan, Korea, 19–24 June 2016; p. V003T002A037. [Google Scholar]
- Najafian, G. Local Hydrodynamic Force Coefficients from Field Data and Probabilistic Analysis of Offshore Structures Exposed to Random Wave Loading. Ph.D. Thesis, University of Liverpool, Liverpool, UK, 1991. [Google Scholar]
- Azarhoushang, A. Dynamic Response of Fixed Offshore Platforms to Environmental Loads. Master’s Thesis, Curtin University of Technology, Perth, Australia, 2010. [Google Scholar]
- He, Y.; Bi, J.; Haritos, N. Hydrodynamic forces and interactions of multiple circular cylindrical structure-fluid-soil systems. Appl. Ocean Res. 1992, 14, 231–239. [Google Scholar] [CrossRef]
- Schmucker, D.G. Near-Failure Behavior of Jacket-Type Offshore Platforms in the Extreme Wave Environment. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1997. [Google Scholar]
- Iraninejad, B. Dynamic Analysis of Fixed Offshore Platforms Subject to Nonlinear Hydrodynamic Loading. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1989. [Google Scholar]
- Ang, A.H.-S.; Tang, W.H. Probability Concepts in Engineering Planning and Design; John Wiley & Sons: Hoboken, NJ, USA, 1984. [Google Scholar]
- Najafian, G.; Burrows, R.; Tickell, R. A Review of the Probabilistic Description of Morison Wave Loading and Response of Fixed Offshore Structures. J. Fluids Struct. 1995, 9, 585–616. [Google Scholar] [CrossRef]
- Wang, Y.; Mallahzadeh, H.; Abu Husain, M.K.; Mohd Zaki, N.I.; Najafian, G. Probabilistic Modelling of Extreme Offshore Structural Response Due to Random Wave Loading. In Proceedings of the 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013; p. V02BT02A007. [Google Scholar]
- Bitner-Gregersen, E.M.; Dong, S.; Fu, T.; Ma, N.; Maisondieu, C.; Miyake, R.; Rychlik, I. Sea State Conditions for Marine Structures’ Analysis and Model Tests. Ocean Eng. 2016, 119, 309–322. [Google Scholar] [CrossRef] [Green Version]
- Taylor, R.E.; Jefferys, E. Variability of Hydrodynamic Load Predictions for A Tension Leg Platform. Ocean Eng. 1986, 13, 449–490. [Google Scholar] [CrossRef]
- Suyuthi, A.; Haver, S.K. Extreme Loads Due to Wave Breaking Against Platform Column. In Proceedings of the Nineteenth International Offshore and Polar Engineering Conference, Osaka, Japan, 21–26 July 2009. [Google Scholar]
- Ha, Y.-J.; Kim, K.-H.; Nam, B.W.; Hong, S.Y. Experimental Study of Wave Impact Loads on Circular Cylinder by Breaking Waves. In Proceedings of the 28th International Ocean and Polar Engineering Conference, Sapporo, Japan, 10–15 June 2018. [Google Scholar]
- Karadeniz, H. Uncertainty Modeling in The Fatigue Reliability Calculation of Offshore Structures. Reliab. Eng. Syst. Saf. 2001, 74, 323–335. [Google Scholar] [CrossRef]
- Reid, S.; Naess, A. Influence on Structural Reliability of Uncertain Extreme Value Estimates. In Proceedings of the 36th International Conference on Ocean, Offshore and Arctic Engineering, Trondheim, Norway, 25–30 June 2017; p. V009T012A037. [Google Scholar]
- Moon, M.-Y.; Kim, H.-S.; Lee, K.; Park, B.; Choi, K. Uncertainty Quantification and Statistical Model Validation for an Offshore Jacket Structure Panel Given Limited Test Data and Simulation Model. Struct. Multidiscip. Optim. 2020, 61, 2305–2318. [Google Scholar] [CrossRef]
- Oumeraci, H.; Kortenhaus, A.; Allsop, W.; de Groot, M.; Crouch, R.; Vrijling, H.; Voortman, H. Probabilistic Design Tools for Vertical Breakwaters; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Bruserud, K.; Haver, S. Uncertainties in Current Measurements in The Northern North Sea. J. Atmos. Ocean. Technol. 2017, 34, 855–876. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.-T.; Burnside, O.; Cruse, T. Probabilistic Methods for Structural Response Analysis. In Proceedings of the ASME/SES Applied Mechanics and Engineering Sciences Conference, San Antonio, TX, USA, 20–22 June 1988. [Google Scholar]
- Kirchsteiger, C. On The Use of Probabilistic and Deterministic Methods in Risk Analysis. J. Loss Prev. Process. Ind. 1999, 12, 399–419. [Google Scholar] [CrossRef]
- Sundararajan, C.R. Probabilistic Structural Mechanics Handbook: Theory and Industrial Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Holmes, P.; Tickell, R.; Burrows, R. Prediction of Long-Term Wave Loading On Offshore Structures. UK Rep. Dep. Energy 1978, 7823–7824. Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=b22eaf3499bdc560735a45667483ac40&site=xueshu_se (accessed on 7 September 2021).
- Price, R. A Useful Theorem for Nonlinear Devices Having Gaussian Inputs. IRE Trans. Inf. Theory 1958, 4, 69–72. [Google Scholar] [CrossRef]
- Tickell, R. Continuous Random Wave Loading on Structural Members. Structural Engineer 1977, 55, 209–222. [Google Scholar]
- Papoulis, A.; Pillai, S.U. Probability, Random Variables, and Stochastic Processes; Tata McGraw-Hill Education: New York, NY, USA, 2002. [Google Scholar]
- Burrows, R. Probabilistic Description of the Response of Offshore Structures to Random Wave Loading. In Mechanics of Wave Induced Forces on Cylinders; Shaw, T.L., Ed.; Pitman Publishing: London, UK, 1979; pp. 577–595. [Google Scholar]
- Burrows, R. Quasi-Static Response of Offshore Structures Using Probabilistic Methods. Appl. Math. Model. 1977, 1, 325–332. [Google Scholar] [CrossRef]
- Burrows, R. Expected Value Analysis for the Quasi-Static Response of Offshore Structures. Appl. Math. Model. 1983, 7, 317–328. [Google Scholar] [CrossRef]
- Najafian, G.; Burrows, R.; Tickell, R. Probabilistic Description of the Response of Offshore Structures to Wave Loading Via Random Sampling Technique. In Proceedings of the Ninth International Offshore and Polar Engineering Conference, Brest, France, 30 May–4 June 1999. [Google Scholar]
- Najafian, G.; Burrows, R.; Tickell, R.G.; Metcalfe, A.V. Higher-Order Statistical Moments of Wave-Induced Response of Offshore Structures Via Efficient Sampling Techniques. In Proceedings of the Twelfth International Offshore and Polar Engineering Conference, Kitakyushu, Japan, 26–31 May 2002. [Google Scholar]
- Najafian, G. Derivation of Statistical Properties of Wave-Induced Offshore Structural Response by Principal Component Technique. Ocean Eng. 2007, 34, 987–999. [Google Scholar] [CrossRef]
- Glisic, A.; Ferraz, G.T. Stochastic Variables in Modelling of the Wave Loads on Offshore Wind Turbine Structures. In Proceedings of the CESARE’17 International Conference, Dead Sea, Jordan, 3–8 May 2017. [Google Scholar]
- Ameryoun, H.; Schoefs, F.; Barillé, L.; Thomas, Y. Stochastic Modeling of Forces on Jacket-Type Offshore Structures Colonized by Marine Growth. J. Mar. Sci. Eng. 2019, 7, 158. [Google Scholar] [CrossRef] [Green Version]
- Ziegler, L.; Voormeeren, S.; Schafhirt, S.; Muskulus, M. Design Clustering of Offshore Wind Turbines Using Probabilistic Fatigue Load Estimation. Renew. Energy 2016, 91, 425–433. [Google Scholar] [CrossRef]
- Goryunova, M.; Kuleshova, L.; Khakimova, A. Application of Signal Analysis for Diagnostics. In Proceedings of the International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), Petersburg, Russia, 16–19 May 2017; pp. 1–5. [Google Scholar]
- Olagnon, M.; Prevosto, M.; Joubert, P. Nonlinear Spectral Computation of the Dynamic Response of a Single Cylinder. J. Offshore Mech. Arct. Eng. 1988, 110, 278–281. [Google Scholar] [CrossRef]
- Li, X.-M.; Quek, S.-T.; Koh, C.-G. Stochastic Response of Offshore Platforms by Statistical Cubicization. J. Eng. Mech. 1995, 121, 1056–1068. [Google Scholar] [CrossRef]
- Tognarelli, M.A.; Zhao, J.; Rao, K.B.; Kareem, A. Equivalent Statistical Quadratization and Cubicization for Nonlinear Systems. J. Eng. Mech. 1997, 123, 512–523. [Google Scholar] [CrossRef]
- Bendat, J.S. Nonlinear System Analysis and Identification from Random Data; Wiley-Interscience: Hoboken, NJ, USA, 1990. [Google Scholar]
- Bouyssy, V.; Rackwitz, R. Polynomial Approximation of Morison Wave Loading. J. Offshore Mech. Arct. Eng. 1997, 119, 30–36. [Google Scholar] [CrossRef]
- Naess, A.; Pisano, A. Frequency Domain Analysis of Dynamic Response of Drag Dominated Offshore Structures. Appl. Ocean Res. 1997, 19, 251–262. [Google Scholar] [CrossRef]
- Kareem, A.; Hsieh, C.; Tognarelli, M. Frequency-Domain Analysis of Offshore Platform in Non-Gaussian Seas. J. Eng. Mech. 1998, 124, 668–683. [Google Scholar] [CrossRef]
- Zheng, X.; Liaw, C. Response Cumulant Analysis of a Linear Oscillator Driven by Morison Force. Appl. Ocean Res. 2004, 26, 154–161. [Google Scholar] [CrossRef]
- Ersdal, G. Assessment of Existing Offshore Structures for Life Extension. Ph.D. Thesis, University of Stavanger, Stavanger, Norway, 2005. [Google Scholar]
- Puskar, F.; Spong, R.; Ku, A.; Gilbert, R.; Choi, Y. Assessment of fixed offshore platform performance in Hurricane Ivan. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 1–4 May 2006. [Google Scholar]
- Marzocca, P.; Nichols, J.; Milanese, A.; Seaver, M.; Trickey, S. Second-order spectra for quadratic nonlinear systems by Volterra functional series: Analytical description and numerical simulation. Mech. Syst. Signal Process. 2008, 22, 1882–1895. [Google Scholar] [CrossRef]
- Carassale, L.; Kareem, A. Modeling Nonlinear Systems by Volterra Series. J. Eng. Mech. 2009, 136, 801–818. [Google Scholar] [CrossRef]
- Agarwal, P.; Manuel, L. Incorporating irregular nonlinear waves in coupled simulation and reliability studies of offshore wind turbines. Appl. Ocean Res. 2011, 33, 215–227. [Google Scholar] [CrossRef]
- Norouzi, M.; Nikolaidis, E. Efficient Estimation of First Excursion Failure of Dynamic Systems by Probabilistic Re-analysis. In Proceedings of the 12th AIAA Aviation Technology Integration and Operations (ATIO) Conference and 14th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Indianapolis, IN, USA, 17–19 September 2012; p. 5664. [Google Scholar]
- Ebrahimian, H.; Jalayer, F.; De Dominicis, R.; Manfredi, G. Probability-Based Assessment of Jacket-Type Offshore. In Proceedings of the 7th EUROpean Conference on STEEL and Composite Structures (EUROSTEEL), Naples, Italy, 10–12 September 2014. [Google Scholar]
- Chen, J. Non-linear Wave Loads on Offshore Wind Support Structure. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2014. [Google Scholar]
- Alberello, A.; Chabchoub, A.; Gramstad, O.; Babanin, A.; Toffoli, A. Statistics of Wave Orbital Velocities in Random Directional Sea States. Statistics 2014, 8, 11. [Google Scholar]
- Kim, Y. Prediction of The Dynamic Response of a Slender Marine Structure Under an Irregular Ocean Wave Using the NARX-Based Quadratic Volterra Series. Appl. Ocean Res. 2015, 49, 42–56. [Google Scholar] [CrossRef]
- Saeedfar, S.; Abd Wahab, A. An Evaluation of the Depth of Similarity between Linear and Non-linear Wave Theories. In Proceedings of the 3rd International Conference on Water Resources, Sanya, China, 2–4 December 2011; pp. 1–11. [Google Scholar]
- Mérigaud, A.; Ringwood, J.V. A Nonlinear Frequency-Domain Approach for Numerical Simulation of Wave Energy Converters. IEEE Trans. Sustain. Energy 2017, 9, 86–94. [Google Scholar] [CrossRef]
- Kühn, M.J. Dynamics and Design Optimisation of Offshore Wind Energy Conversion Systems; DUWIND, Delft University Wind Energy Research Institute: Delft, The Netherlands, 2001. [Google Scholar]
- Van Der Tempel, J. Design of Support Structures for Offshore Wind Turbines. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2006. [Google Scholar]
- Seidel, M. Wave Induced Fatigue Loads: Insights from Frequency Domain Calculations. Stahlbau 2014, 83, 535–541. [Google Scholar] [CrossRef]
- Kang, H.; Kim, M. Time-Domain Hydroelastic Analysis with Efficient Load Estimation for Random Waves. Int. J. Nav. Archit. Ocean Eng. 2017, 9, 266–281. [Google Scholar] [CrossRef] [Green Version]
- Mohammadi, S.; Galgoul, N.; Starossek, U. Comparison of Time Domain and Spectral Fatigue Analyses of an Offshore Jacket Structure. In Proceedings of the 26th International Ocean and Polar Engineering Conference, Rhodes, Greece, 26 June–2 July 2016. [Google Scholar]
- Orkin, G.L.; Folck, R.L.; Startzman, R.A. Monte Carlo Simulation of Offshore Terminal Operations. In Proceedings of the SPE California Regional Meeting, San Francisco, CA, USA, 12–14 April 1978. [Google Scholar]
- Nikolaidis, E.; Mourelatos, Z.P.; Pandey, V. Design Decisions under Uncertainty with Limited Information: Structures and Infrastructures Book Series; CRC Press: Boca Raton, FL, USA, 2011; Volume 7. [Google Scholar]
- Tromans, P.S.; Anaturk, A.R.; Hagemeijer, P. A New Model for The Kinematics of Large Ocean Waves-Application as a Design Wave. In Proceedings of the First International Offshore and Polar Engineering Conference, Edinburgh, UK, 11–16 August 1991. [Google Scholar]
- Bar-Avi, P. Nonlinear Dynamics of Compliant Offshore Structures; Routledge: Oxfordshire, UK, 2017. [Google Scholar]
- Fedele, F.; Brennan, J.; De León, S.P.; Dudley, J.; Dias, F. Real World Ocean Rogue Waves Explained Without the Modulational Instability. Sci. Rep. 2016, 6, 27715. [Google Scholar] [CrossRef]
- Sclavounos, P.D.; Zhang, Y.; Ma, Y.; Larson, D.F. Offshore Wind Turbine Nonlinear Wave Loads and Their Statistics. J. Offshore Mech. Arct. Eng. 2019, 141, 031904. [Google Scholar] [CrossRef]
- Cassidy, M.; Taylor, R.E.; Houlsby, G. Analysis of Jack-Up Units Using a Constrained Newwave Methodology. Appl. Ocean. Res. 2001, 23, 221–234. [Google Scholar] [CrossRef]
- Cassidy, M.; Taylor, P.; Taylor, R.E.; Houlsby, G. Evaluation of Long-Term Extreme Response Statistics of Jack-Up Platforms. Ocean Eng. 2002, 29, 1603–1631. [Google Scholar] [CrossRef]
- Naess, A.; Gaidai, O.; Haver, S. Efficient Estimation of Extreme Response of Drag-Dominated Offshore Structures by Monte Carlo Simulation. Ocean Eng. 2007, 34, 2188–2197. [Google Scholar] [CrossRef]
- Najafian, G. Application of System Identification Techniques in Efficient Modelling of Offshore Structural Response. Part I: Model Development. Appl. Ocean Res. 2007, 29, 1–16. [Google Scholar] [CrossRef]
- Najafian, G. Application of System Identification Techniques in Efficient Modelling of Offshore Structural Response. Part II: Model Validation. Appl. Ocean Res. 2007, 29, 17–36. [Google Scholar] [CrossRef]
- Najafian, G.; Zaki, N. Finite-Memory Nonlinear System Modelling of Offshore Structures. In Proceedings of the 27th International Conference on Offshore Mechanics and Arctic Engineering, Estoril, Portugal, 15–20 June 2008; pp. 743–752. [Google Scholar]
- Mohd Zaki, N.I.; Abu Husain, M.K.; Wang, Y.; Najafian, G. Short-term distribution of the extreme values of offshore structural response by modified finite-memory nonlinear system modeling. In Proceedings of the 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013. [Google Scholar]
- Abu Husain, M.K.; Najafian, G. An Efficient Monte Carlo Simulation Technique for Derivation of the Probability Distribution of the Extreme Values of Offshore Structural Response. In Proceedings of the 29th International Conference on Ocean, Offshore and Arctic Engineering, Shanghai, China, 6–11 June 2010; pp. 369–375. [Google Scholar]
- Lambert, L.A.; Najafian, G.; Cooper, J.E.; Abu Husain, M.K.; Mohd Zaki, N.I. Efficient Estimation of Offshore Structural Response Based on Threshold Upcrossing Rates. In Proceedings of the 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013; pp. 9–14. [Google Scholar]
- Mallahzadeh, H.; Wang, Y.; Abu Husain, M.K.; Mohd Zaki, N.I.; Najafian, G. Efficient Derivation of the Probability Distribution of Extreme Responses Due to Random Wave Loading from The Probability Distribution of Extreme Surface Elevations. In Proceedings of the 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013. [Google Scholar]
- Mallahzadeh, H.; Wang, Y.; Abu Husain, M.K.; Mohd Zaki, N.I.; Najafian, G. Accurate Estimation of The 100-Year Responses from The Probability Distribution of Extreme Surface Elevations. In Proceedings of the 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014; pp. 8–13. [Google Scholar]
- Mallahzadeh, H.; Najafian, G.; Husain, M.; Zaki, N.M. Derivation of Probability Distribution of Extreme Offshore Structural Response due to Combined Wave and Current Loading from the Probability Distribution of Extreme Surface Elevations. In Proceedings of the 7th International ASRANet Conference, Glasgow, UK, 18–20 August 2014. [Google Scholar]
- Naess, A.; Leira, B.; Batsevych, O. System Reliability Analysis by Enhanced Monte Carlo Simulation. Struct. Saf. 2009, 31, 349–355. [Google Scholar] [CrossRef]
- Gaspar, B.; Naess, A.; Leira, B.J.; Soares, C.G. System Reliability Analysis by Monte Carlo Based Method and Finite Element Structural Models. J. Offshore Mech. Arct. Eng. 2014, 136, 031603. [Google Scholar] [CrossRef] [Green Version]
- Aarland, Y. Time-Domain Simulation of Marine Structures in Irregular Seas. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2015. [Google Scholar]
- Johari, M.B. Optimisation Of Efficient Time Simulation Method For The Prediction Of Extreme Offshore Structural Response. Master’s Thesis, Universiti Teknologi Malaysia, Johor Bahru, Malaysia, 2016. [Google Scholar]
- Mukhlas, N.A. Efficient Derivation of Extreme Non-Gaussian Stochastic Structural Response. Ph.D. Thesis, Universiti Teknologi Malaysia, Johor Bahru, Malaysia, 2020. [Google Scholar]
- Zakikhani, K.; Nasiri, F.; Zayed, T. A Review of Failure Prediction Models for Oil and Gas Pipelines. J. Pipeline Syst. Eng. Pract. 2020, 11, 03119001. [Google Scholar] [CrossRef]
- Zhao, Y.; Dong, S.; Jiang, F.; Soares, C.G. System Reliability Analysis of an Offshore Jacket Platform. J. Ocean Univ. China 2020, 19, 47–59. [Google Scholar] [CrossRef]
- Li, X.; Chen, G.; Zhu, H. Quantitative Risk Analysis On Leakage Failure of Submarine Oil and Gas Pipelines Using Bayesian Network. Process Saf. Environ. Prot. 2016, 103, 163–173. [Google Scholar] [CrossRef]
- He, R.; Li, X.; Chen, G.; Wang, Y.; Jiang, S.; Zhi, C. A Quantitative Risk Analysis Model Considering Uncertain Information. Process Saf. Environ. Prot. 2018, 118, 361–370. [Google Scholar] [CrossRef]
- Moan, T. Life Cycle Structural Integrity Management of Offshore Structures. Struct. Infrastruct. Eng. 2018, 14, 911–927. [Google Scholar] [CrossRef] [Green Version]
- Helder, J.A.; Bunnik, T. Deterministic Breaking Wave Simulation for Offshore Applications. In Proceedings of the SNAME 21st Offshore Symposium, Houston, TX, USA, 16 February 2016. [Google Scholar]
- Klein, M.; Dudek, M.; Clauss, G.F.; Ehlers, S.; Behrendt, J.; Hoffmann, N.; Onorato, M. On the Deterministic Prediction of Water Waves. Fluids 2020, 5, 9. [Google Scholar] [CrossRef] [Green Version]
- Burrows, R. Wave Loading on Offshore Structures: A Probabilistic Approach. Ph.D. Thesis, University of Liverpool, Liverpool, UK, 1982. [Google Scholar]
- Jurado, A.M.P.; Borg, M.; Bredmose, H. An Efficient Frequency-Domain Model for Quick Load Analysis of Floating Offshore Wind Turbines. Wind Energy Sci. 2018, 3, 693–712. [Google Scholar] [CrossRef] [Green Version]
- Ziegler, L.S. Probabilistic Estimation of Fatigue Loads on Monopile-based Offshore Wind Turbines. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2015. [Google Scholar]
- Abhishek, A.; Metrikine, A.V.; Male, P.v.d.; Dalen, K.N.v. Reduction of Fatigue Computational Time for Offshore Wind Turbine Jacket Foundations: Investigation of Lumping Methods for Correlated Wind-Wave Data and Frequency-Domain Approach. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2018. [Google Scholar]
- Moan, T.; Zheng, X.Y.; Quek, S.T. Frequency-Domain Analysis of Non-Linear Wave Effects On Offshore Platform Responses. Int. J. Non-Linear Mech. 2007, 42, 555–565. [Google Scholar] [CrossRef]
- Lim, D.-H.; Kim, Y. Probabilistic Analysis of Air Gap of Tension-Leg Platforms by A Nonlinear Stochastic Approach. Ocean Eng. 2019, 177, 49–59. [Google Scholar] [CrossRef]
- Somayajula, A.; Falzarano, J. Large-Amplitude Time-Domain Simulation Tool for Marine and Offshore Motion Prediction. Mar. Syst. Ocean Technol. 2015, 10, 1–17. [Google Scholar] [CrossRef]
- Guha, A.; Somayajula, A.; Falzarano, J. Time Domain Simulation of Large Amplitude Motions in Shallow Water. In Proceedings of the 21st SNAME Offshore Symposium, Society of Naval Architects and Marine Engineers, Houston, TX, USA, 16 February 2016; pp. 1–20. [Google Scholar]
- Romolo, A.; Malara, G.; Laface, V.; Arena, F. Space–Time Long-Term Statistics of Ocean Storms. Probabilistic Eng. Mech. 2016, 44, 150–162. [Google Scholar] [CrossRef]
- Ding, W.; Pang, L. Structural Fatigue Assessment of Offshore Platform Considering the Effect of Nonlinear Drag Force. In Proceedings of the 35th International Conference on Ocean, Offshore and Arctic Engineering, Busan, Korea, 18–24 June 2016. [Google Scholar]
- Faulkner, D.; Cowling, M.; Incecik, A. Integrity of Offshore Structures; CRC Press: Boca Raton, FL, USA, 1991. [Google Scholar]
- Mansour, A.E.; Ertekin, R.C. Ships and Offshore Structures. In Proceedings of the 15th International Ship and Offshore Structures Congress: 3-Volume Set, San Diego, CA, USA, 11–15 August 2003. [Google Scholar]
- Natarajan, A. Influence of second-order random wave kinematics on the design loads of offshore wind turbine support structures. Renew. Energy 2014, 68, 829–841. [Google Scholar]

| Author (Year) | Method | Findings | Limitations |
|---|---|---|---|
| Burrows R. (1977 & 1983) | Second and Fourth Statistical Moment (SFSM) |
|
|
| Najafian G., Burrows R., Tickell R.G., Metcalfe A.V. (2002) | An efficient sampling technique known as Simple Sampling Techniques (SST) |
|
|
| Najafian G. (2007) | Principal Component Techniques (PCT) |
|
|
| Author (Year) | Method | Findings | Limitations |
|---|---|---|---|
| Olagnon M., Prevosto M., Joubert P. (1988) | Non-linear spectral calculation based on Volterra kernels |
|
|
| Li X.-M., Quek S.-T., Koh C.-G. (1995) | Volterra series |
|
|
| Tognarelli M.A., Zhao J., Rao K.B., Kareem A. (1997) | Volterra functional series |
|
|
| Naess and Pisano (1997) | Exact computation of probability density functions |
|
|
| Kareem A., Hsieh C.C., Tognarelli M.A. (1998) | Stokes’ perturbation expansion solution |
|
|
| Zheng X.Y., Liaw C.Y. (2004) | Cumulant spectral analysis |
|
|
| Ersdal G. (2005) | Stokes’ analysis + USFOS |
|
|
| Marzocca P. Nicholsb J.M., Milanesea A., Seaverb M., Trickeyb S.T., (2008) | Volterra functional series-spectrum analysis |
|
|
| Carassale and Kareem (2009) | Improved version of Volterra frequency-response functions |
|
|
| Agarwal and Manuel (2011) | Second-order wave analysis + FAST software |
|
|
| Norouzi M., Nikolaidis E. (2012) | Extended probabilistic re-analysis method |
|
|
| Ebrahimian (2014) | Probability incremental wave analysis (PIWA) |
|
|
| Chen (2014) | Second-order wave analysis |
|
|
| Natarajan (2014) | Second-order wave analysis + HAWC2 Software |
|
|
| Kim O. (2015) | NARX-based quadratic Volterra series |
|
|
| Merigaud A., Ringwood J.V. (2016) | Nonlinear frequency-domain (NLFD) |
|
|
| Author (Year) | Method | Findings | Limitations |
|---|---|---|---|
| Orkin, G., Folck, R., Startzman, R. (1978) | The Conventional Time Simulation (CTS) or so-called Monte Carlo Time Simulation (MCTS) |
|
|
| Tromans, P. S., Anaturk, A. R., Hagemeijer, P. (1991) | New Wave Theory |
|
|
| Taylor P. H., Jonathan P., Harland L. A. (1997) | Constrained time domain simulation |
|
|
| Cassidy M.J., Taylor, P.H., Taylor, RE., Houlsby, G. T. (2001 & 2002) | Constrained New Wave (CNW) |
|
|
| Naess, A., Gaidai, O., Haver, S. (2007) | Linear extrapolation technique |
|
|
| Najafian G. (2007a & 2007b) | Finite-memory nonlinear system (FMNS) |
|
|
| Mohd Zaki N.I., Najafian G. (2008) | Finite-memory nonlinear system (FMNS) |
|
|
| Abu Husain M.K., Najafian G. (2010) | Efficient time simulation (ETS) |
|
|
| Mohd Zaki N.I., Abu Husain M.K., Mallahzadeh H., Najafian G. (2013) | Modified Finite-Memory Nonlinear System Modelling (FMNS) |
|
|
| Lambert L L.A., Najafian G., Copper J.E., Abu Husain M.K., Mohd Zaki N.I. (2013) | Efficient Threshold Upcrossing (ETU) |
|
|
| Mallahzadeh H., Wang Y., Abu Husain M.K., Mohd Zaki N.I., Najafian G. (2014) | ETS-Relationship (ETS-RTS) |
|
|
| Gaspar B., Naess A., Leira B.J., Soares C.G. (2014) | Montel Carlo Based Method & Finite Element Structural Models |
|
|
| Aarland Y (2015) | An equal area principle (EAP) to generate waves instead of FFT method |
|
|
| Johari M. B., Abu Husain M.K. (2017) | Optimization of ETS |
|
|
| Mukhlas N. A., Mohd Zaki N.I., Abu Husain M.K. (2020) | FMNS using non-linear wave theory |
|
|
| Syed Ahmad, S.Z.A, Abu Husain M.K., Mohd Zaki N.I. (2021) | ETS-Regression Procedure |
|
|
| Domains | Authors (Year) | Methods | Wave Model | Structural Analysis | Time Period | Current Impact | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| L | NL | RQS | RDYN | ST | LT | P | NP | |||
| Probability | Burrows R. (1977; 1983) | Second and fourth statistical moment | / | / | / | / | / | |||
| Najafian et. al. (2002) | Simple sampling techniques | / | / | / | / | |||||
| Najafian (2007) | Principle component techniques | / | / | / | / | |||||
| Frequency | Olagnon et. al. (1988) | Nonlinear spectral calculation based on Volterra kernels | / | / | ||||||
| Li et. al. (1995) | Volterra series (VS) | / | / | / | ||||||
| Tognarelli et. al. (1997) | Volterra functional series | / | / | |||||||
| Naess and Pisano (1997) | Exact computation of Probability Density Functions | / | / | / | / | / | ||||
| Kareem et. al. (1998) | Stokes’ perturbation expansion solution | / | / | / | / | / | / | |||
| Zheng and Liaw (2004) | Cumulant spectral analysis | / | / | / | ||||||
| Ersdal (2005) | Stokes’ analysis + USFOS | / | / | / | / | / | ||||
| Carassale and Kareem (2009) | Improved version of Volterra frequency-response functions | / | ||||||||
| Agarwal & Manuel (2011) | Second-order wave analysis + FAST software | / | / | / | / | |||||
| Norouzi and Nikolaidis (2012) | Extended Probabilistic Re-analysis method | / | / | / | / | |||||
| Ebrahimian (2014) | Probability incremental wave analysis | / | ||||||||
| Chen (2014) | Second-order wave analysis | / | / | / | / | |||||
| Natarajan (2014) | Second-order wave analysis + HAWC2 Software | / | / | / | / | |||||
| Kim (2015) | NARX-based quadratic VS | / | / | / | / | |||||
| Merigaud and Ringwood (2016) | Nonlinear frequency-domain (NLFD) | / | / | / | ||||||
| Time | Orkin et. al. (1978) | Monte Carlo Time Simulation | / | / | ||||||
| Tromans et. al. (1991) | NewWave Theory | / | / | |||||||
| Taylor et. al. (1997) | Constrained time domain simulation | / | / | / | / | |||||
| Cassidy et. al. (2001 and 2002) | Constrained New Wave (CNW) | / | / | / | / | / | / | / | / | |
| Naess et. al. (2007) | Linear extrapolation technique | / | / | |||||||
| Time | Najafian (2007) and Mohd Zaki and Najafian (2008) | Finite-memory nonlinear system (FMNS) | / | / | / | / | / | / | / | |
| Abu Husain and Najafian (2010) | Efficient Time Simulation (ETS) | / | / | / | / | / | / | / | ||
| Mohd Zaki et. al. (2013) | Modified FMNS | / | / | / | / | / | / | / | ||
| Lambert et. al. (2013) | Efficient Threshold Upcrossing (ETU) | / | / | |||||||
| Mallazadeh et. al. (2014) | ETS–Relationship Time Simulation (ETS-RTS) | / | / | |||||||
| Gaspar et. al. (2014) | Montel Carlo Based Metho–Finite Element Models | / | / | / | ||||||
| Aarland (2015) | Preferring EAP to generate waves instead of FFT method | / | / | |||||||
| Johari (2017) | Optimization of ETS | / | / | / | / | / | ||||
| Mukhlas et al. (2020) | FMNS using nonlinear wave theory | / | / | / | / | / | / | / | ||
| Syed Ahmad et al. (2021) | ETS-Regression Procedure | / | / | / | / | / | / | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Syed Ahmad, S.Z.A.; Abu Husain, M.K.; Mohd Zaki, N.I.; Mukhlas, N.A.; Mat Soom, E.; Azman, N.U.; Najafian, G. Offshore Structural Reliability Assessment by Probabilistic Procedures—A Review. J. Mar. Sci. Eng. 2021, 9, 998. https://doi.org/10.3390/jmse9090998
Syed Ahmad SZA, Abu Husain MK, Mohd Zaki NI, Mukhlas NA, Mat Soom E, Azman NU, Najafian G. Offshore Structural Reliability Assessment by Probabilistic Procedures—A Review. Journal of Marine Science and Engineering. 2021; 9(9):998. https://doi.org/10.3390/jmse9090998
Chicago/Turabian StyleSyed Ahmad, Sayyid Zainal Abidin, Mohd Khairi Abu Husain, Noor Irza Mohd Zaki, Nurul Azizah Mukhlas, Ezanizam Mat Soom, Nurul Uyun Azman, and Gholamhossein Najafian. 2021. "Offshore Structural Reliability Assessment by Probabilistic Procedures—A Review" Journal of Marine Science and Engineering 9, no. 9: 998. https://doi.org/10.3390/jmse9090998
APA StyleSyed Ahmad, S. Z. A., Abu Husain, M. K., Mohd Zaki, N. I., Mukhlas, N. A., Mat Soom, E., Azman, N. U., & Najafian, G. (2021). Offshore Structural Reliability Assessment by Probabilistic Procedures—A Review. Journal of Marine Science and Engineering, 9(9), 998. https://doi.org/10.3390/jmse9090998






