VPP Coupling High-Fidelity Analyses and Analytical Formulations for Multihulls Sails and Appendages Optimization
Abstract
1. Introduction
2. Performance Prediction Model
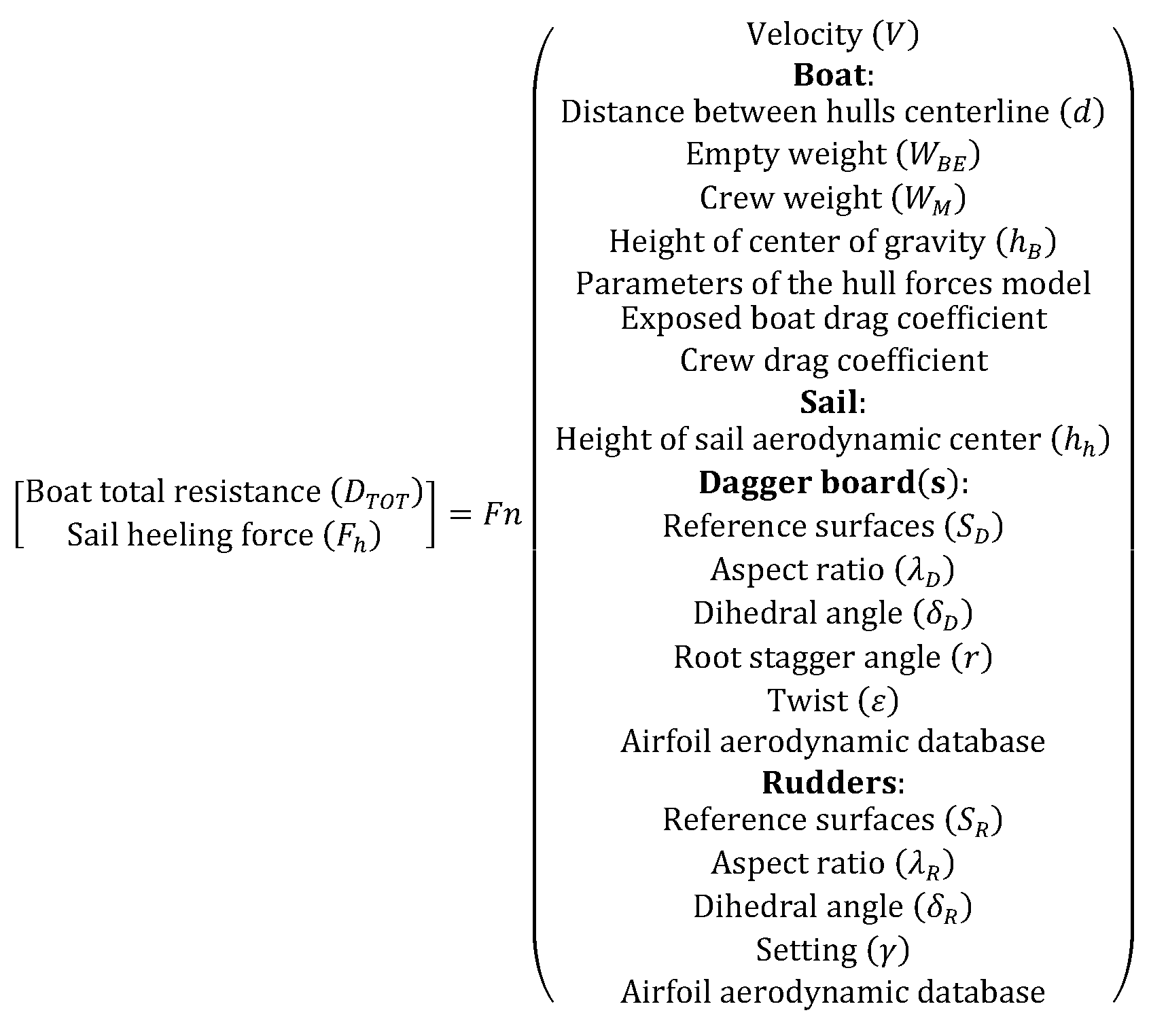
2.1. Boat Global Forces and Moment Equilibrium
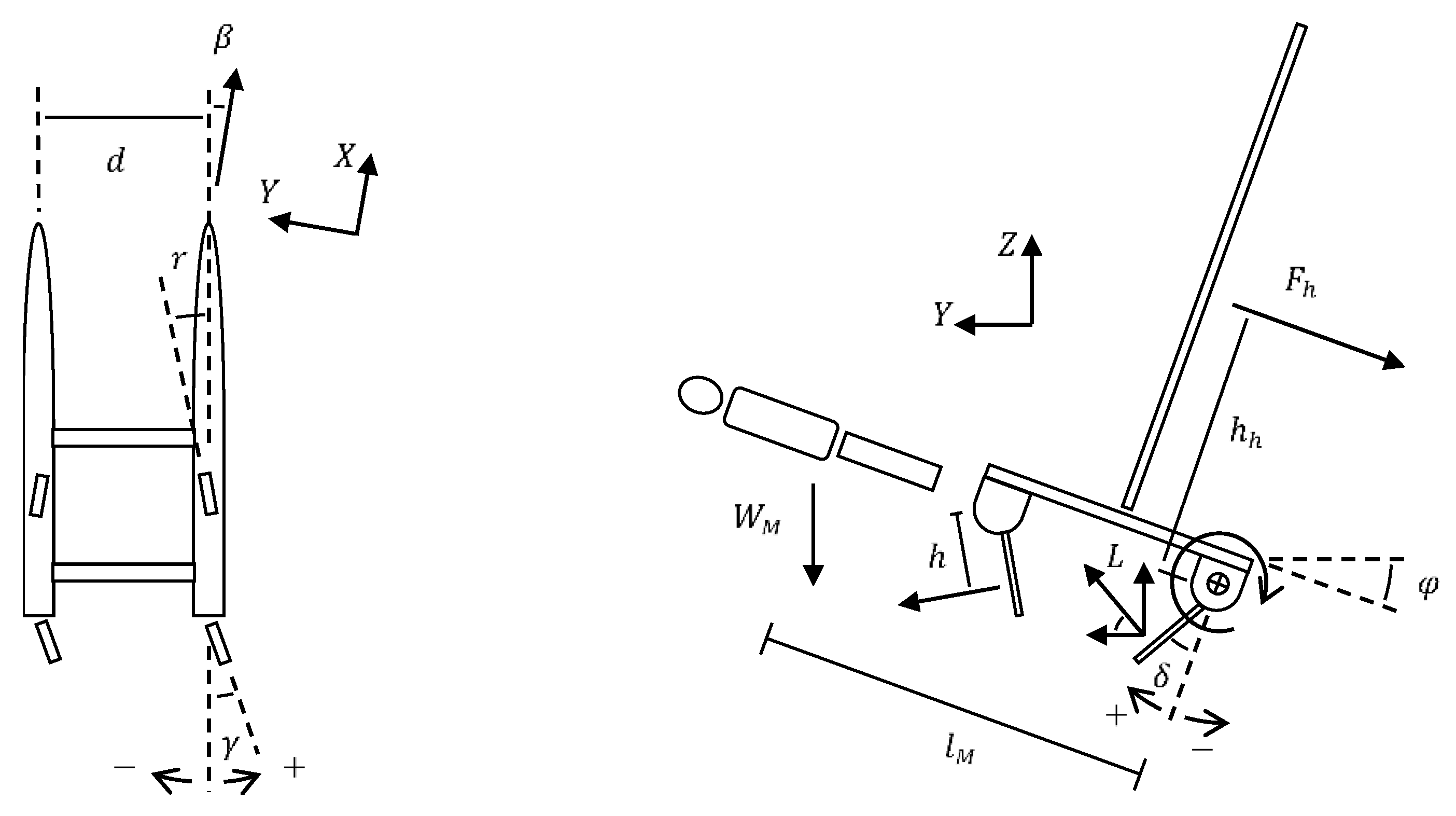
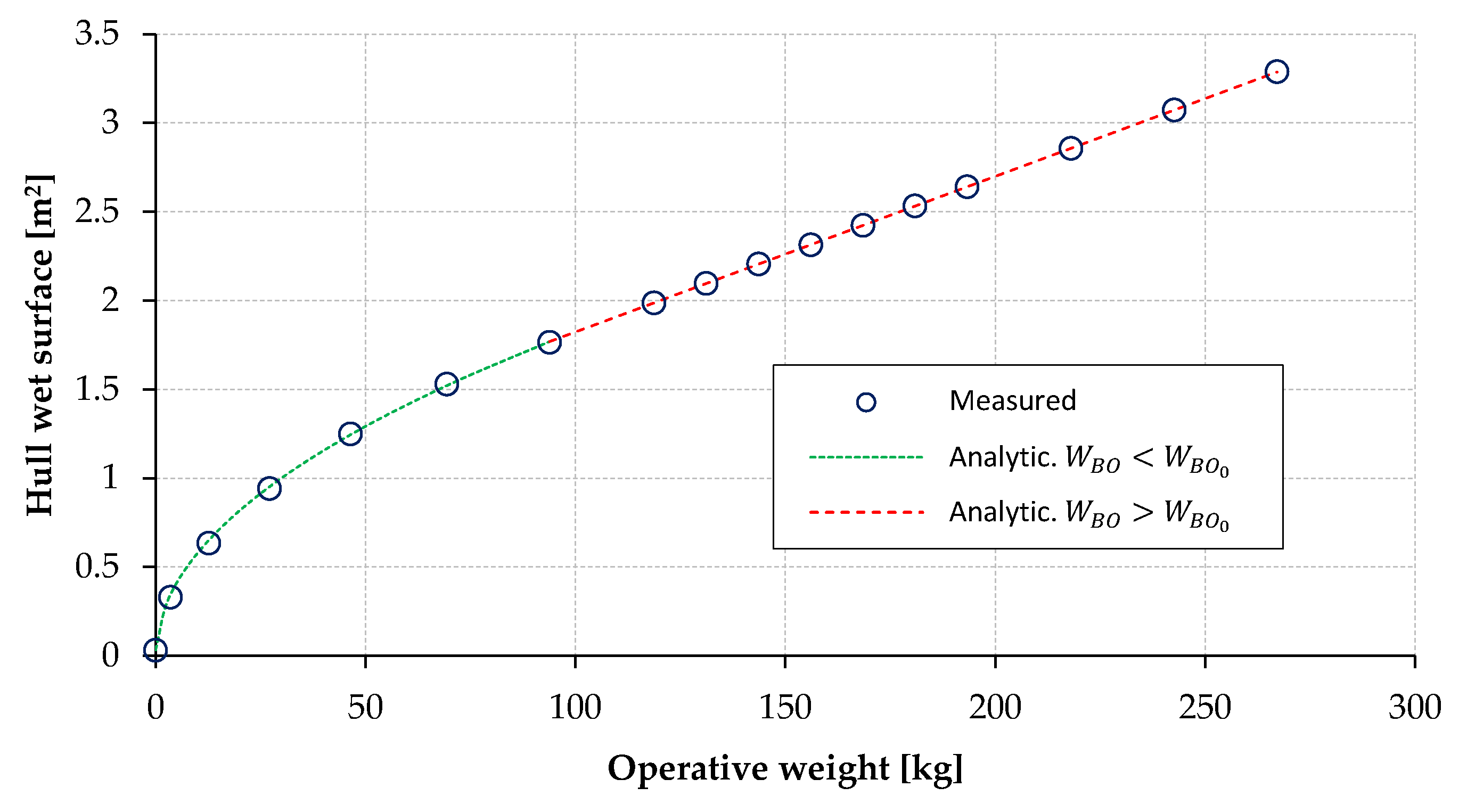
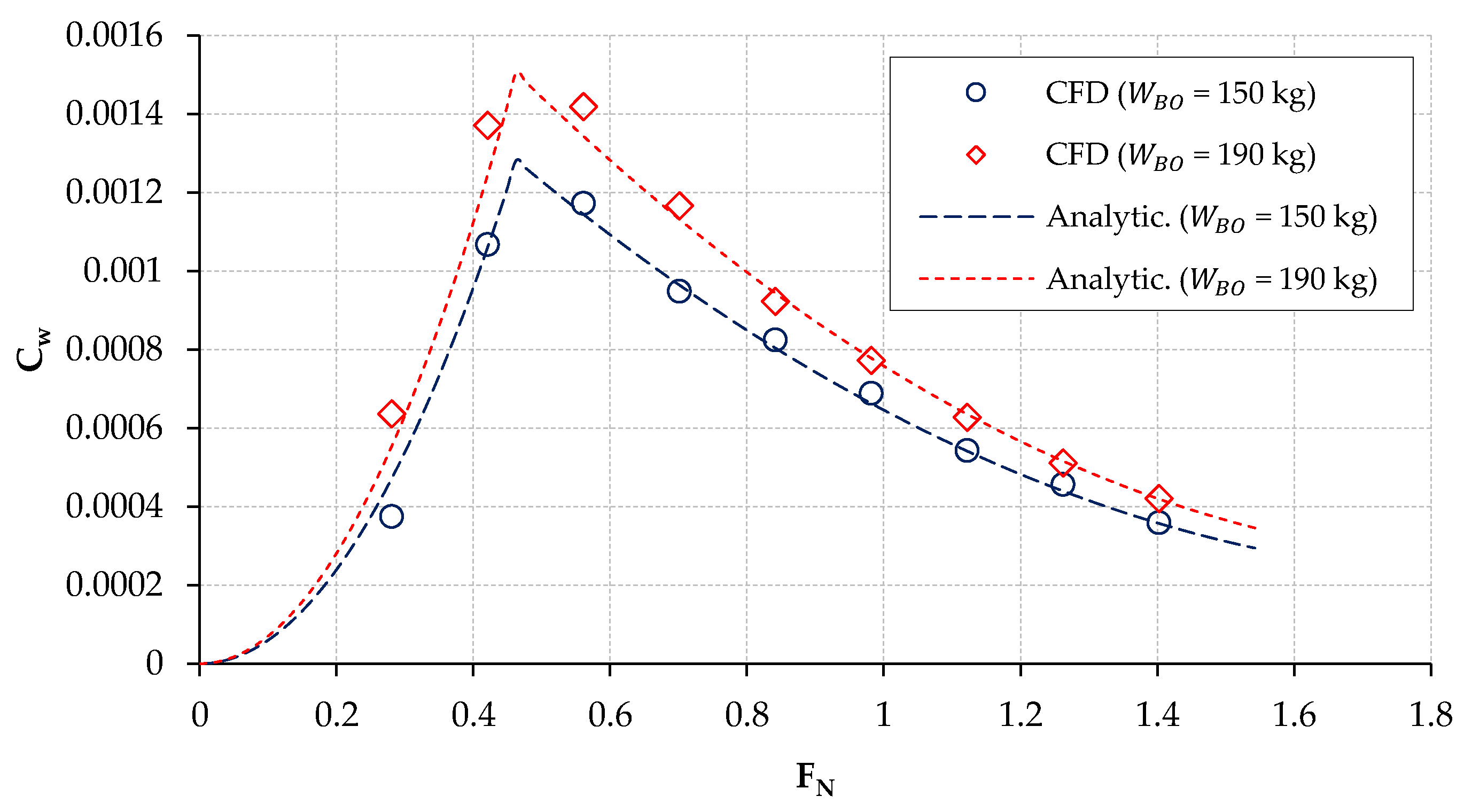
2.1.1. Hull Forces Modelling
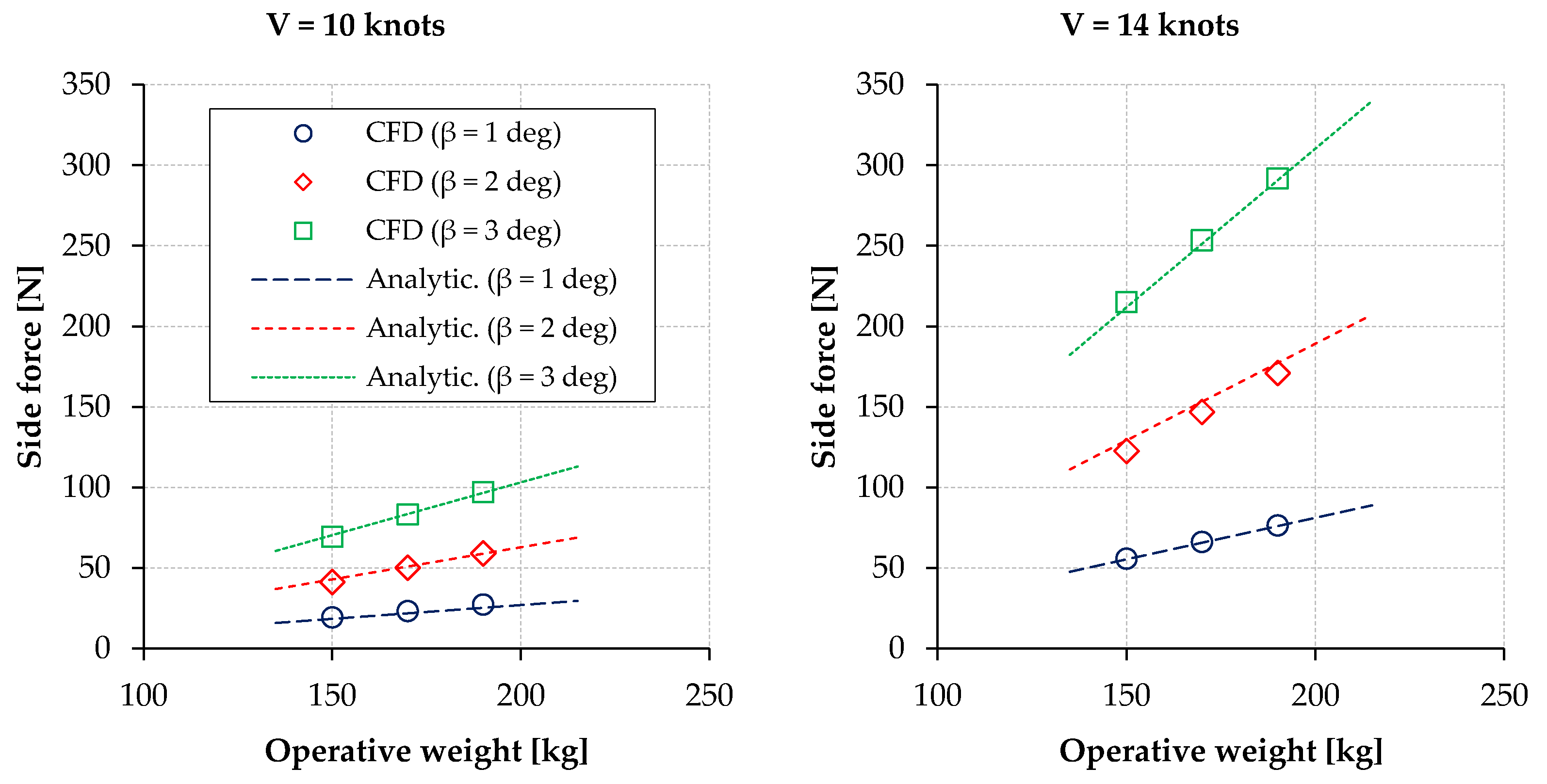
2.1.2. Appendages Forces Modelling
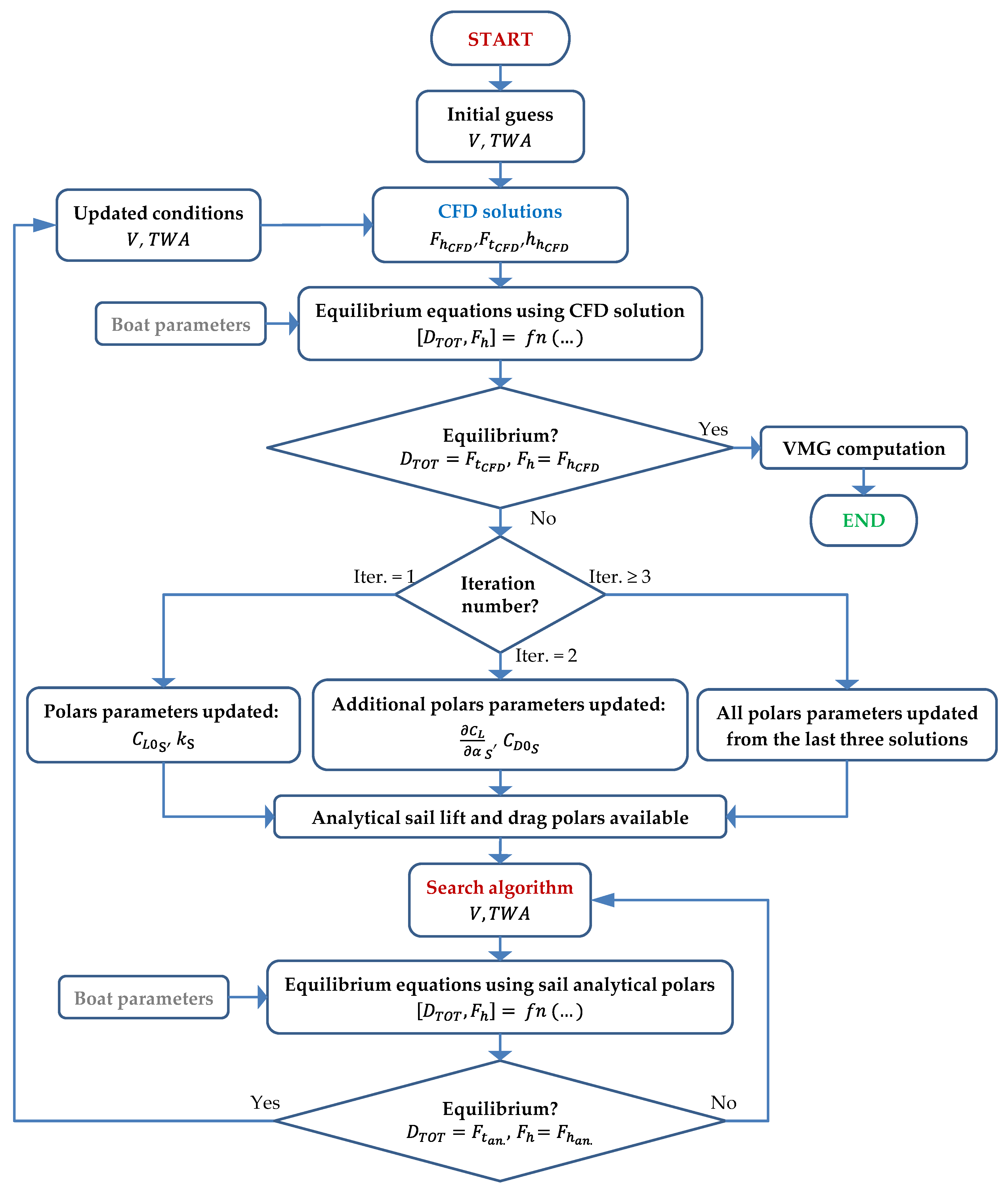
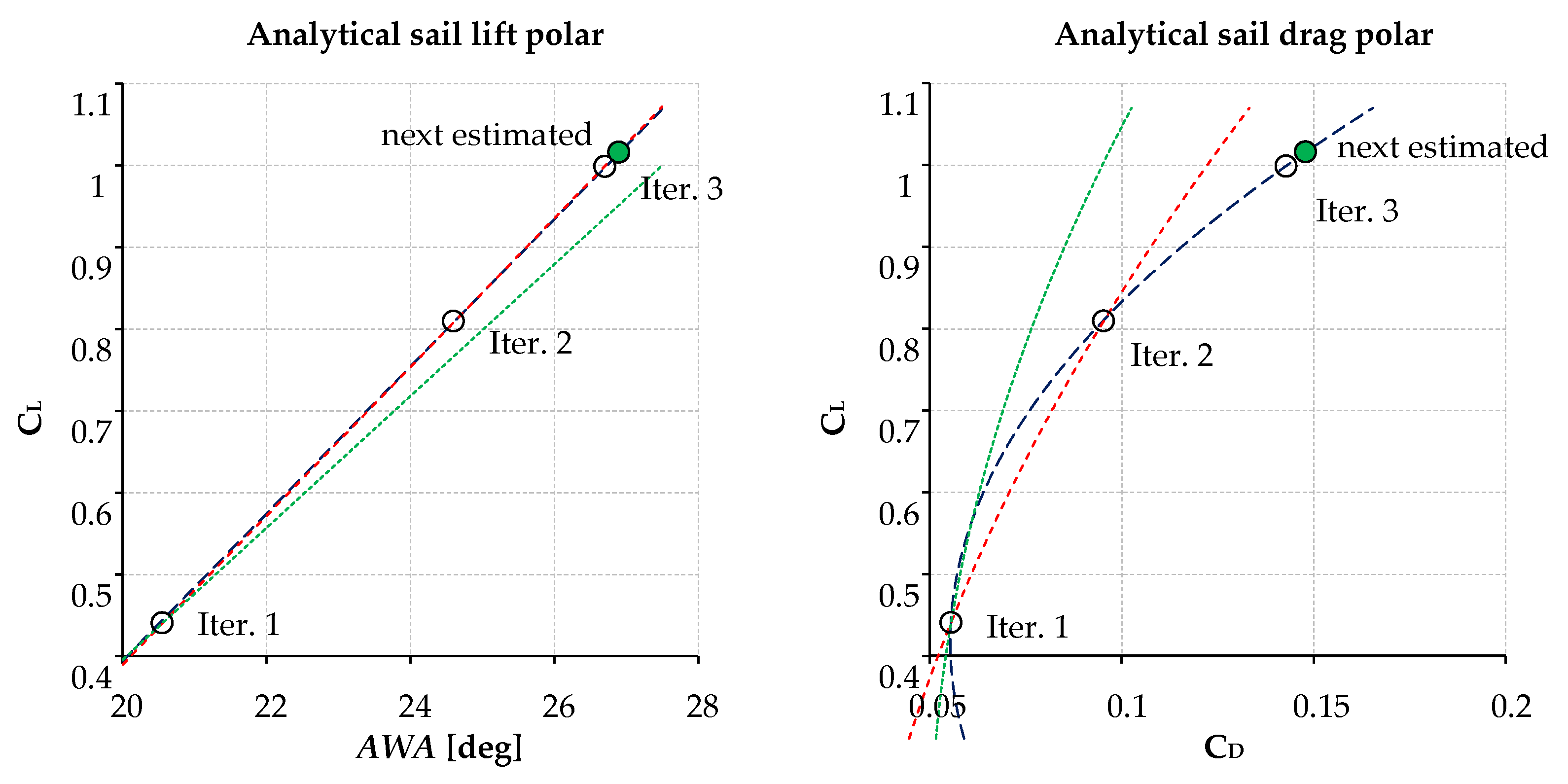
2.2. Closure of the Performance Solution Problem
- In the first iteration the sail lift curve slope and the induced drag factor are estimated from literature as function of sail aspect and taper ratio. The value of zero-lift drag coefficient is roughly guessed. The sail lift and drag coefficients and , obtained from the CFD analysis, are used to estimate from Equation (25) and from Equation (26).
- In the second iteration the additional CFD solution is used to complete the analytical lift curve formulation adjusting the values of the lift curve slope and zero-incidence lift coefficient . The parameters updated in the polar curve are and while the value of is still guessed.
- In the third iteration the analytical drag polar formulation is completed with the computation of the induced drag factor which is last unknown parameter. The lift curve is updated connecting a quadratic formulation to the previous computed linear part.
- In all the following iterations the sailing condition estimation are performed modelling the polars regions under investigation updating both curves by a generic quadratic formulation using the closest three solutions.
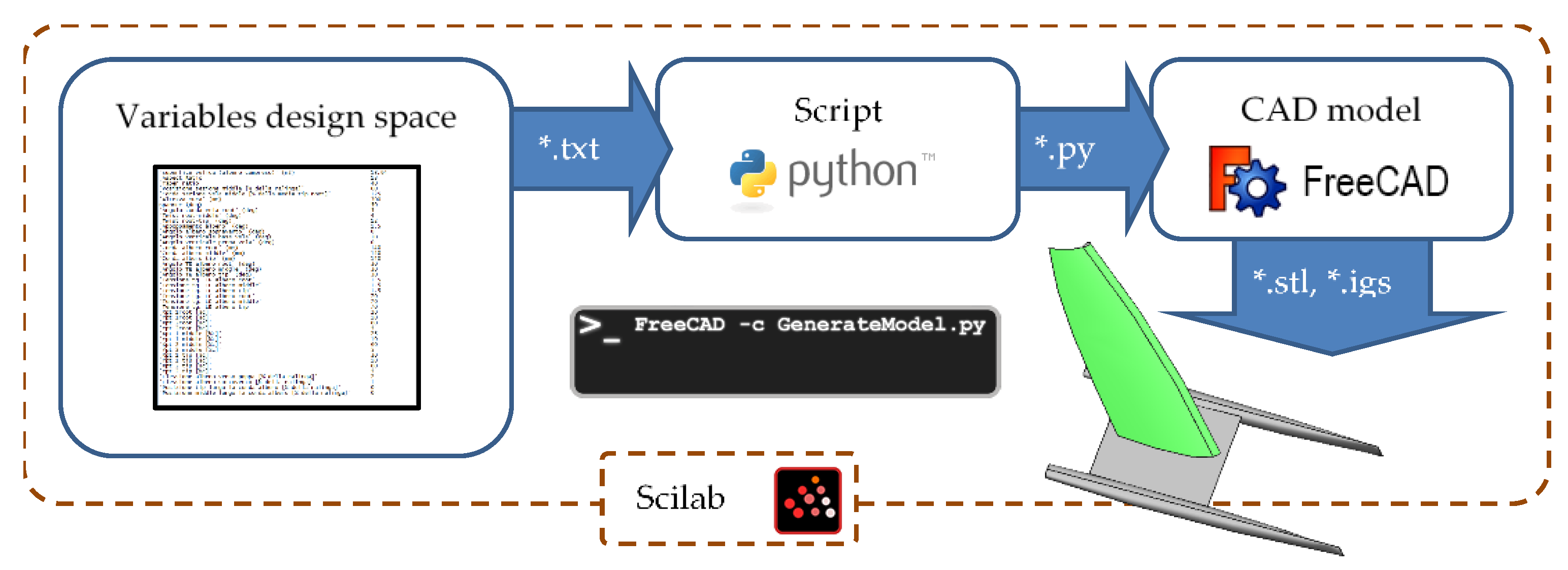
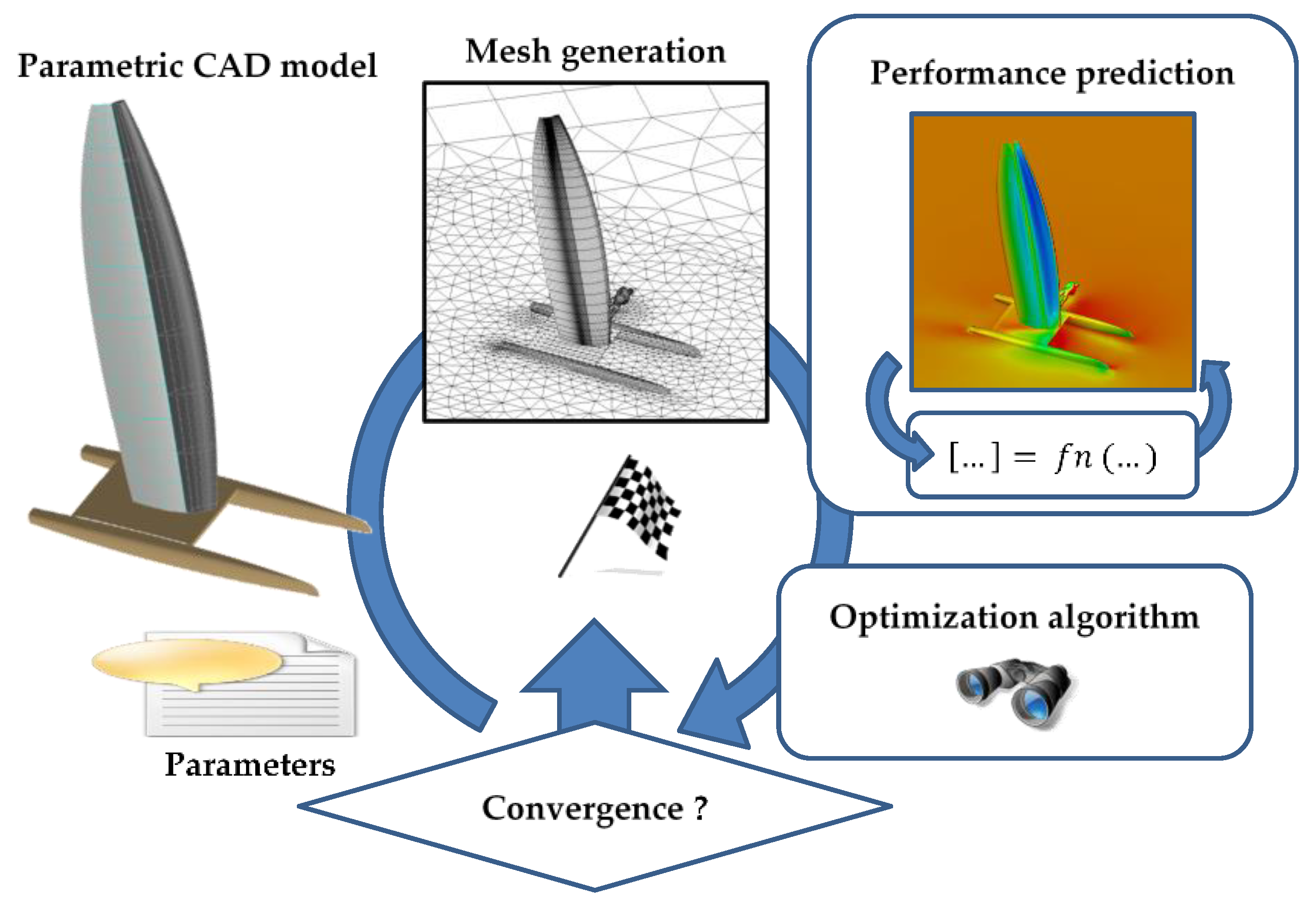
3. Optimization Environment
3.1. Sail Parametric Geometric Module
3.2. Sail CFD Analysis Module Implemented Adopting Commercial Software
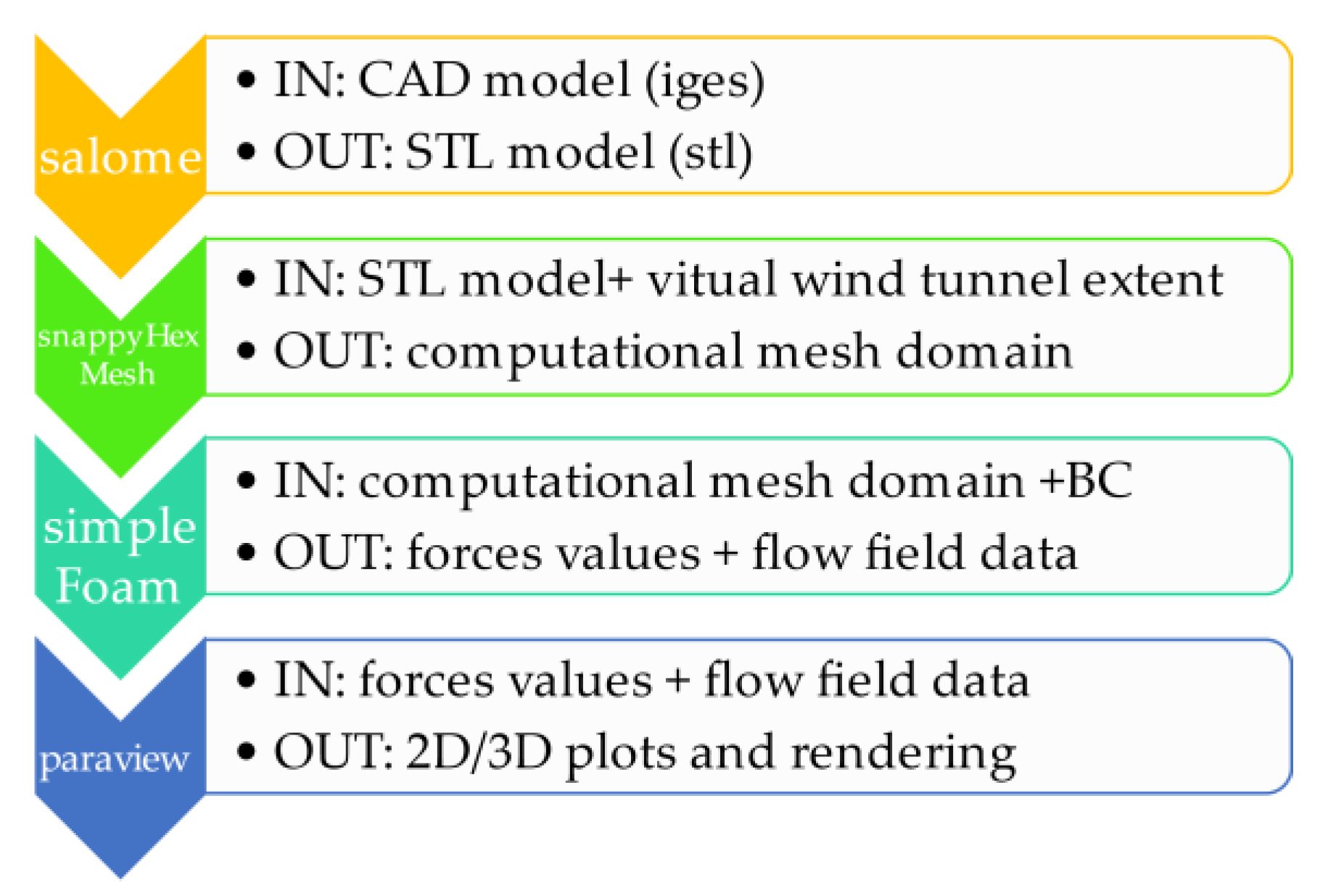
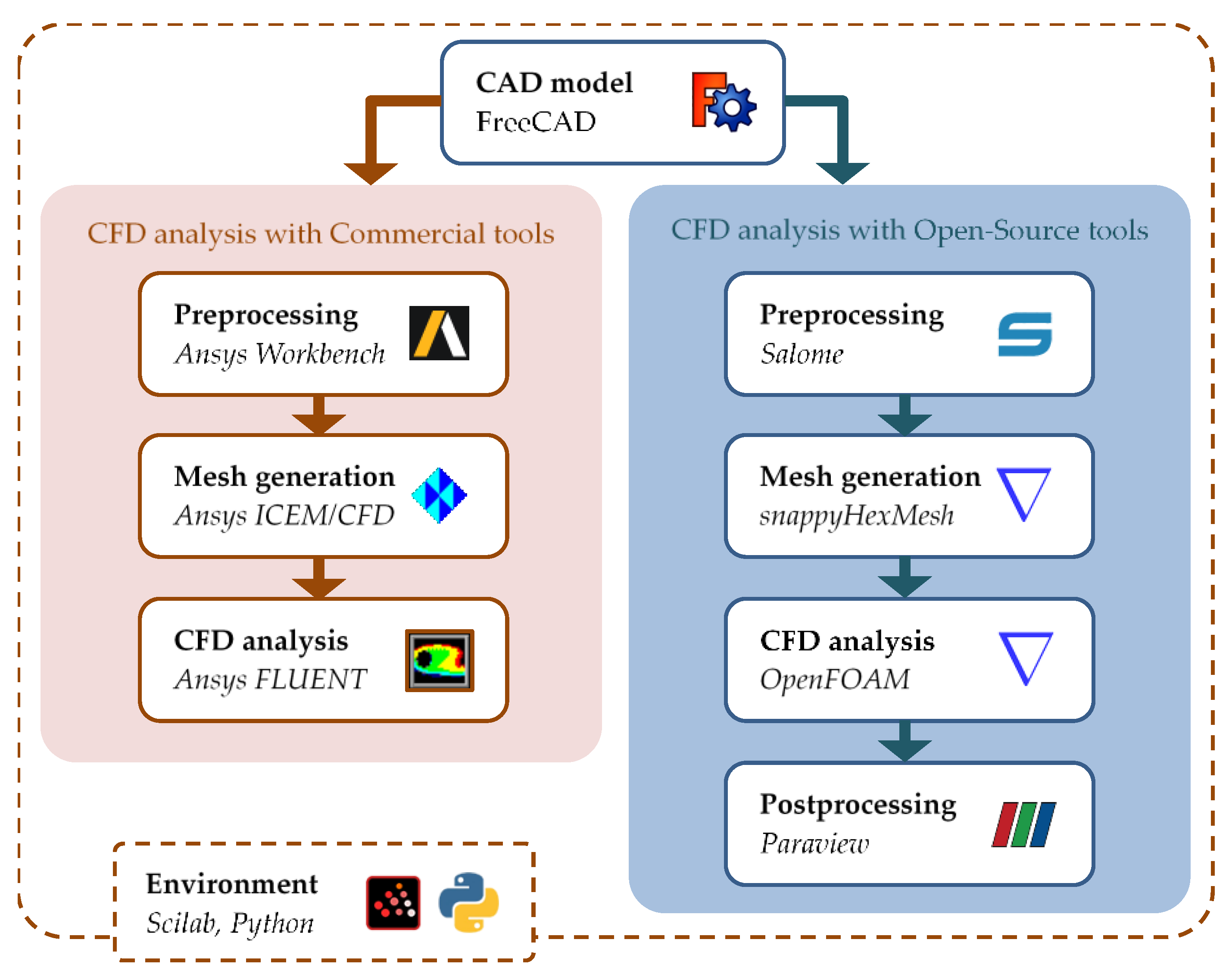
3.3. CFD Analysis Module Based on Open-Source Tools
- CAD import and pre-processing;
- Geometry meshing;
- Flow field solving;
- Data visualisation and post-processing.
- Conversion from CAD to STL;
- Mesh generation and CFD configuration update;
- CFD run and solutions export;
- Post-processing and results extraction.
3.4. Implementation of the Optimization Environment
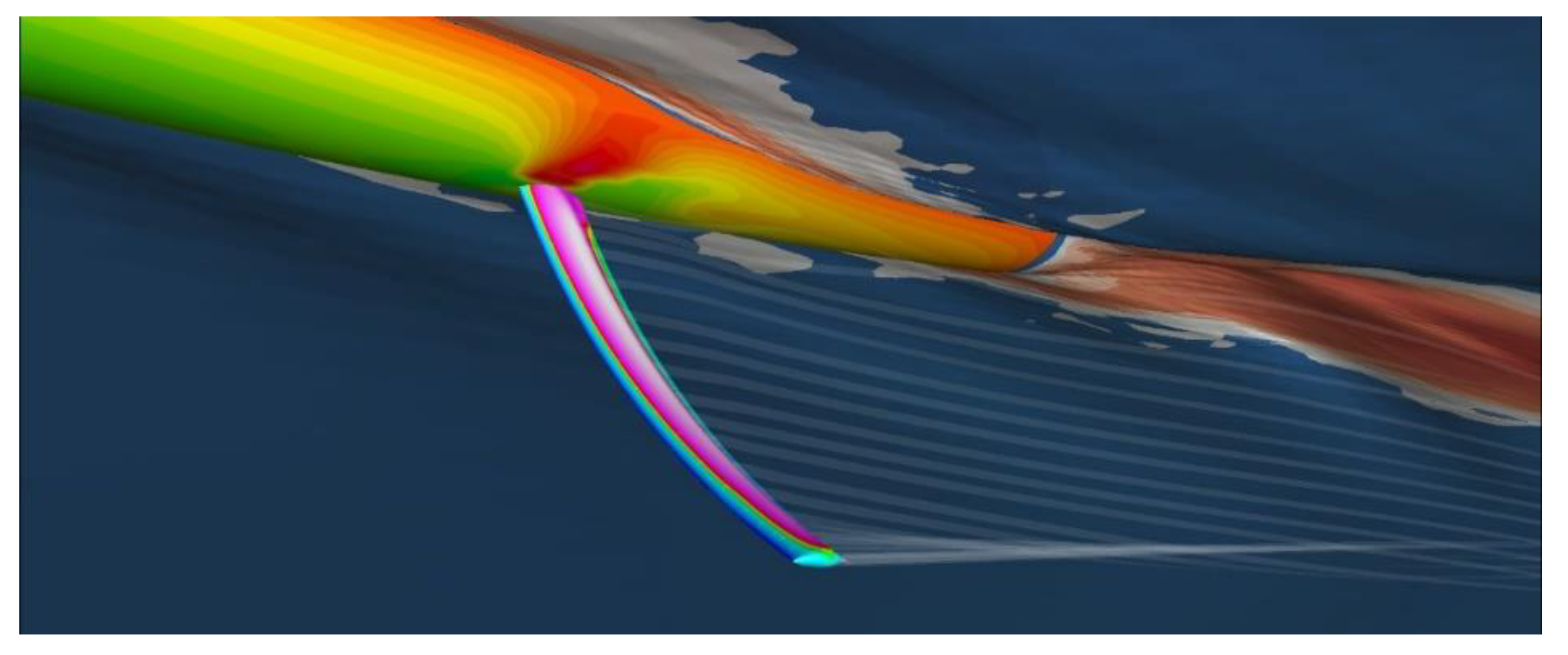
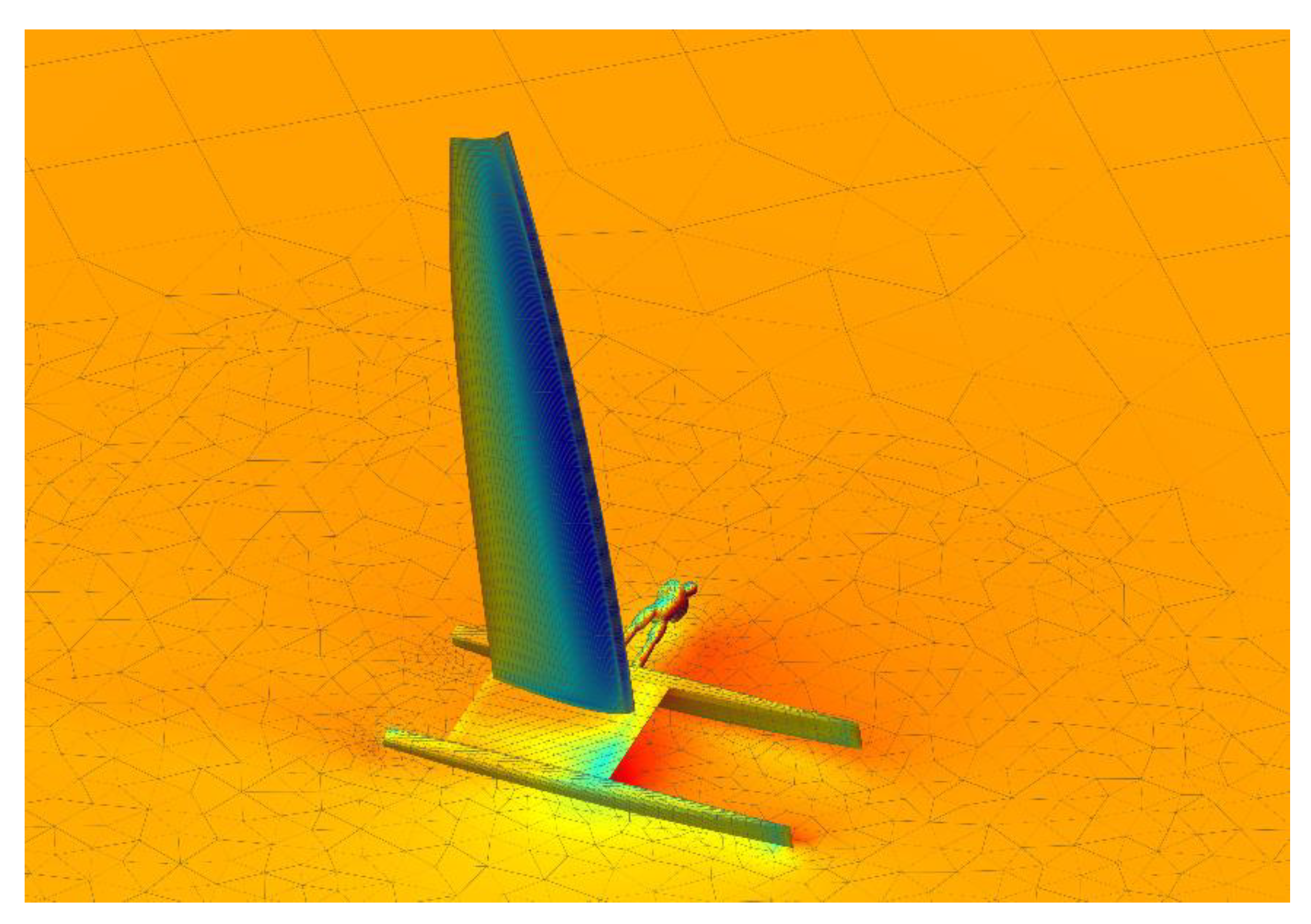
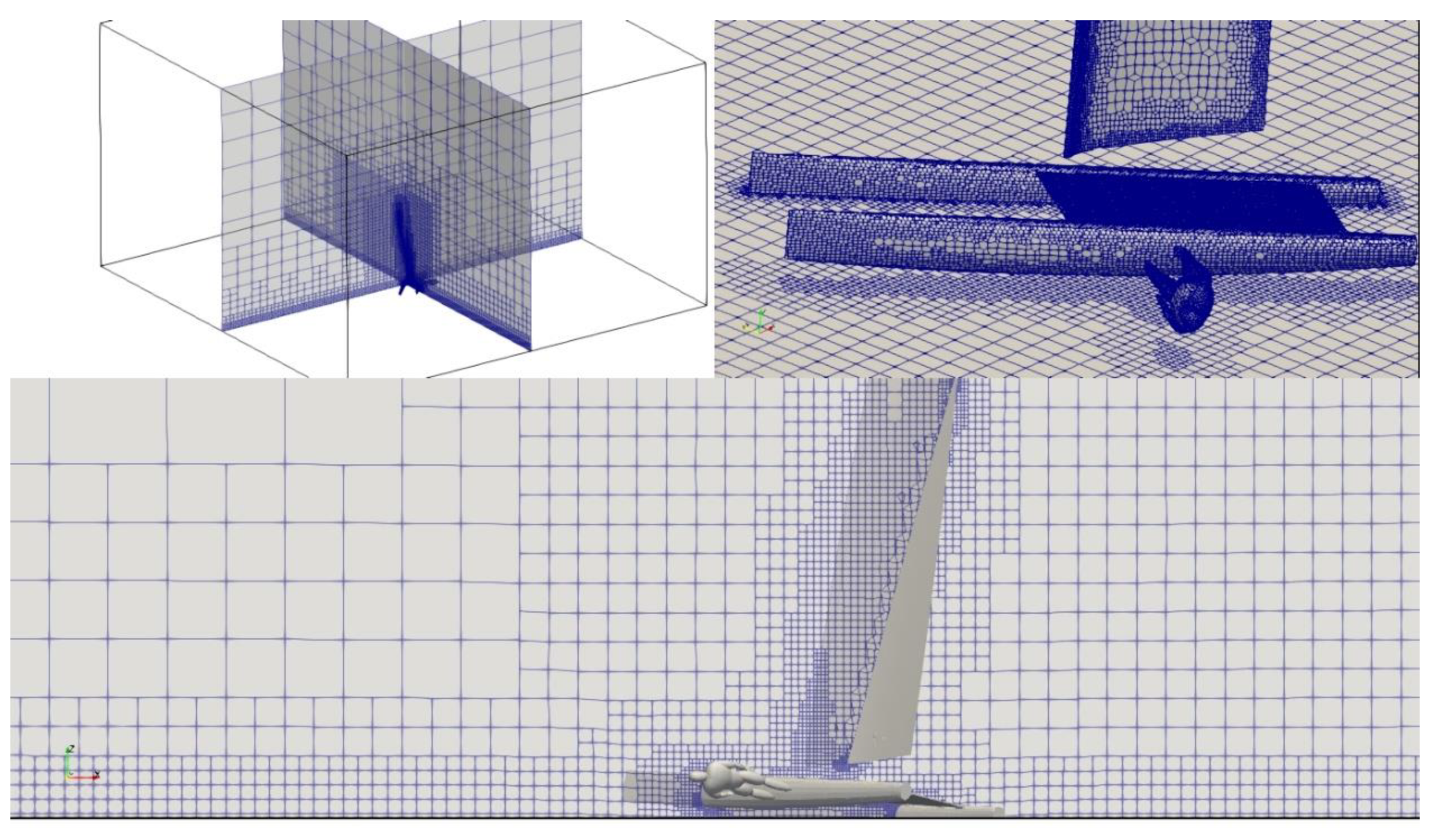
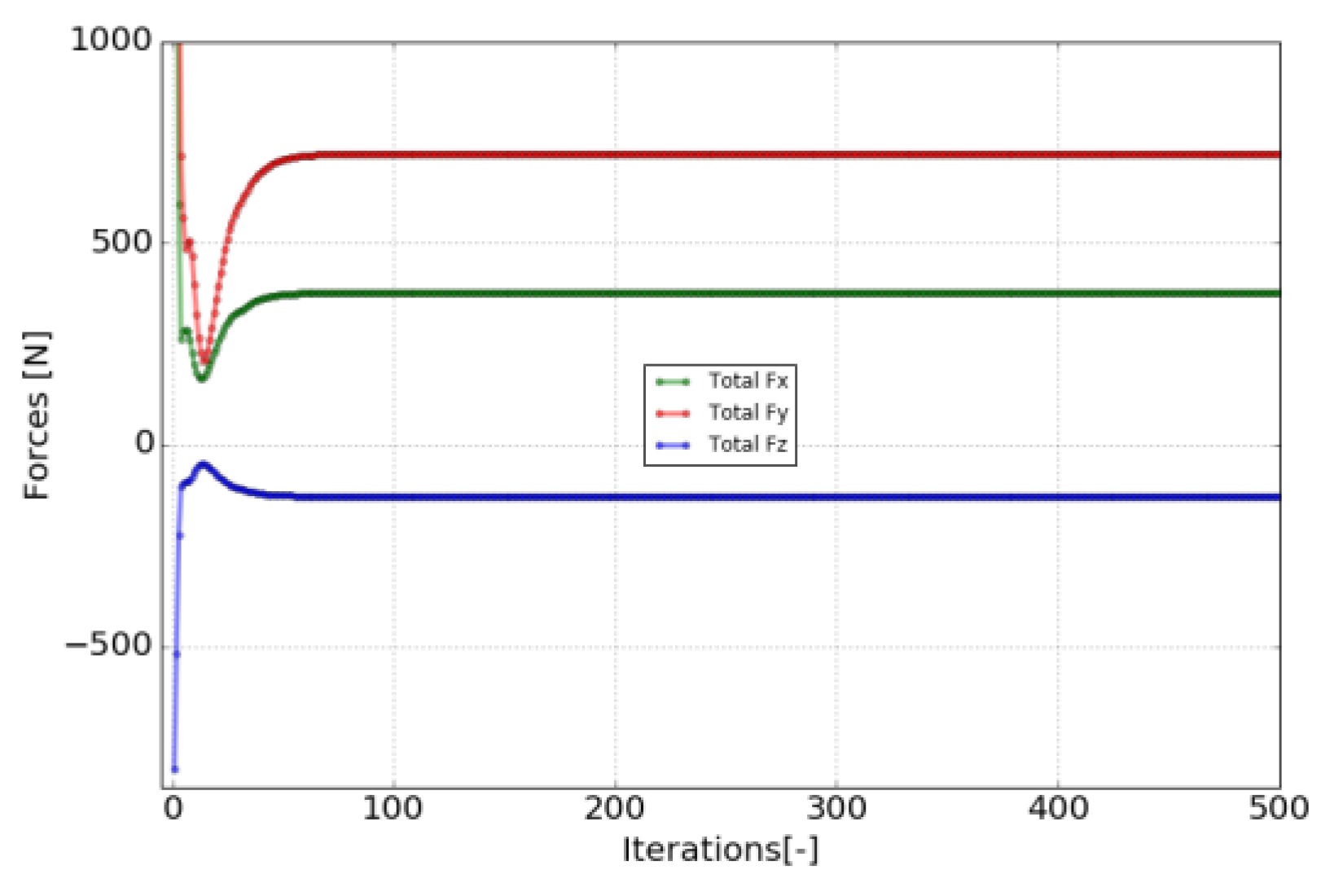
4. Test of the Analysis Modules
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Angle of incidence | |
| Leeway angle | |
| Rudder angle | |
| Appendage dihedral angle | |
| Aspect ratio | |
| Heeling angle | |
| Sea water density | |
| Apparent wind angle | |
| Apparent wind speed | |
| Draft of appendage | |
| Distance between hulls centrelines | |
| Drag coefficient | |
| Drag coefficient at zero incidence | |
| Friction drag coefficient | |
| Lift coefficient | |
| Lift coefficient at zero incidence | |
| Wave drag coefficient | |
| Drag | |
| component of the boat aerodynamic drag | |
| component of the boat aerodynamic drag | |
| Hull drag | |
| component of the crew aerodynamic drag | |
| component of the crew aerodynamic drag | |
| Oswald efficiency factor | |
| Sail heeling force | |
| Sail thrust force | |
| Appendage aerodynamic centre | |
| Height of boat centre of gravity | |
| Height of sail centre of effort | |
| Height of the boat centre of gravity | |
| Lift | |
| Hull side force (parallel to the sea plane) | |
| Arm of crew righting moment | |
| perimeter of the appendage (excluded root) | |
| Daggerboard stagger angle | |
| Reynolds number | |
| Reference surface | |
| True wind angle | |
| True wind speed | |
| Boat speed | |
| Boat empty weight | |
| Boat operative weight | |
| Crew weight |
References
- Fossati, F. Aero-Hydrodynamics and the Performance of Sailing Yachts: The Science behind Sailing Yachts and Their Design; A&C Black: London, UK, 2009. [Google Scholar]
- Lasher, W. The determination of aerodynamic forces on sails—Challenges and status. In Atmospheric Turbulence, Meteorological Modelingand Aerodynamics; Nova Science Publishers: Hauppauge, NY, USA, 2011; pp. 487–504. [Google Scholar]
- Day, A.H.; Cameron, P.; Dai, S. Hydrodynamic Testing of a High Performance Skiff at Model and Full Scale. J. Sail. Technol. 2019, 4, 17–44. [Google Scholar] [CrossRef]
- Graf, K.; Boehm, C. Coupling of ranse-CFD with VPP methods: From the numerical tank to virtual boat testing. In Proceedings of the 2nd International Conference on Innovation in High Performance Sailing Yachts, Lorient, France, 30 June–1 July 2010. [Google Scholar]
- Lasher, W.C.; Richards, P.J. Validation of Reynolds-Averaged Navier-Stokes Simulations for International America’s Cup Class Spinnaker Force Coefficients in an Atmospheric Boundary Layer. J. Ship Res. 2007, 51, 22–38. [Google Scholar] [CrossRef]
- Peart, T.; Aubin, N.; Nava, S.; Cater, J.; Norris, S. Multi-Fidelity Surrogate Models for VPP Aerodynamic Input Data. J. Sail. Technol. 2021, 6, 21–43. [Google Scholar] [CrossRef]
- Fossati, F.; Muggiasca, S.; Viola, I.M. An investigation of aerodynamic force modelling for IMS rule using wind tunnel techniques. In Proceedings of the 19th International HISWA Symposium on Yacht Design and Yacht Construction, Amsterdam, The Netherlands, 13–14 November 2006. [Google Scholar]
- Graf, K.; Freiheit, O.; Schlockermann, P.; Mense, J.C. VPP-Driven Sail and Foil Trim Optimization for the Olympic NACRA 17 Foiling Catamaran. J. Sail. Technol. 2020, 5, 61–81. [Google Scholar] [CrossRef]
- Findlay, M.W.; Turnock, S.R. Investigation of the effects of hydrofoil set-up on the performance of an international moth dinghy using a dynamic VPP. In Proceedings of the Innovation in High Performance Sailing Yachts, Lorient, France, 29–30 May 2008. [Google Scholar]
- Bagué, A.; Degroote, J.; Demeester, T.; Lataire, E. Dynamic Stability Analysis of a Hydrofoiling Sailing Boat using CFD. J. Sail. Technol. 2021, 6, 58–72. [Google Scholar] [CrossRef]
- Cella, U.; Salvadore, F.; Ponzini, R. Coupled Sail and Appendage Design Method for Multihull Based on Numerical Optimisation; EU SHAPE Project Final Report; PRACE: Bruxelles, Belgium, 2016. [Google Scholar]
- Gomez, C.; Bunks, C.; Chancelier, J.P.; Delebecque, F.; Goursat, M.; Nikoukhah, R.; Steer, S. Engineering and Scientific Computing with Scilab; Gomez, C., Ed.; Birkhäuser: Basel, Switzerland, 1999. [Google Scholar]
- Gerritsma, J.; Onnink, R.; Versluis, A. Geometry, resistance and stability of the Delft systematic yacht hull series. Int. Shipbuild. Prog. 1981, 28, 276–297. [Google Scholar] [CrossRef]
- Keuning, L.J.; Katgert, M. A bare hull resistance prediction method derived from the results of The Delft Systematic Yacht Hull Series to higher speeds. In Proceedings of the Innovation in High Performance Sailing Yachts, Lorient, France, 29–30 May 2008. [Google Scholar]
- Kerdraon, P.; Horel, B.; Bot, P.; Letourneur, A.; le Touzé, D. High Froude Number Experimental Investigation of the 2 DOF Behavior of a Multihull Float in Head Waves. J. Sail. Technol. 2021, 6, 1–20. [Google Scholar] [CrossRef]
- Molland, A.F.; Turnock, S.R.; Hudson, D.A. Ship Resistance and Propulsion; Cambridge University Press: New York, NY, USA, 2011. [Google Scholar]
- de Luca, F.; Mancini, S.; Miranda, S.; Pensa, C. An Extended Verification and Validation Study of CFD Simulations for Planing Hulls. J. Ship Res. 2016, 60, 101–118. [Google Scholar] [CrossRef]
- Zou, L.; Larsson, L. CFD Verification and Validation in Practice—A Study Based on Resistance Submissions to the Gothenburg 2010 Workshop on Numerical Ship Hydrodynamics. In Proceedings of the 30th Symposium on Naval Hydrodynamics, Hobart, Australia, 2–7 November 2014. [Google Scholar]
- Insel, M.; Molland, A. An Investigation into the Resistance Components of High Speed Displacement Catamarans; RINA: Genoa, Italy, 1992. [Google Scholar]
- Hoerner, S.F. Fluid-Dynamic Drag; Hoerner Fluid Dynamics: Brick Town, NJ, USA, 1965. [Google Scholar]
- ITTC. Resistance Uncertainty Analysis, Example for Resistance Test. In Proceedings of the ITTC International Towing Tank Conference, Recommended Procedures, Venice, Italy, 14–16 January 2002. [Google Scholar]
- Losito, V. Fondamenti di Aeronautica Generale; Accademia Aeronautica Pozzuoli: Pozzuoli, Italy, 1991. [Google Scholar]
- Roskam, J. Airplane Aerodynamics and Performance; DARcorporation: Lawrence, KS, USA, 1997. [Google Scholar]
- Drela, M. XFoil—An Analysis and Design System for Low Reynolds Number Airfoils. In Low Reynolds Number Aerodynamics. Lecture Notes in Engineering; Springer: Berlin/Heidelberg, Germany, 1989; Volume 54, pp. 1–12. [Google Scholar]
- Abbott, A.H.; von Doenhoff, A.E. Theory of Wing Sections; Dover Publications: Mineola, NY, USA, 1959. [Google Scholar]
- Perkins, C.D.; Hage, R.E. Airplane Performance Stability and Control; John Wiley & Sons: New York, NY, USA, 1949. [Google Scholar]
- Larsson, L.; Eliasson, R. Principle of Sailing Yacht Design; Adlard Coles Nautical: London, UK, 1997. [Google Scholar]
- Claughton, A.; Wellicome, J.; Shenoi, A. Sailing Yacht Design: Theory; Longman: London, UK, 1998. [Google Scholar]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Biancolini, M.E.; Viola, I.M.; Riotte, M. Sails trim optimisation using CFD and RBF mesh morphing. Comput. Fluids 2014, 93, 46–60. [Google Scholar] [CrossRef]
- Cella, U.; Cucinotta, F.; Sfravara, F. Sail Plan Parametric CAD Model for an A–Class Catamaran Numerical Optimization Procedure Using Open Source Tools. In Advances on Mechanics, Design Engineering and Manufacturing; Lecture Notes Series in Mechanical Engineering; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Cella, U.; Romano, D.G. Winglets design and assessment of optimization algorithms. In Proceedings of the CAE Technologies International Conference, Bergamo, Italy, 1–2 October 2009. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Musker, A.J. Explicit Expression for the Smooth Wall Velocity Distribution in a Turbulent Boundary Layer. AIAA J. 1979, 17, 655–657. [Google Scholar] [CrossRef]


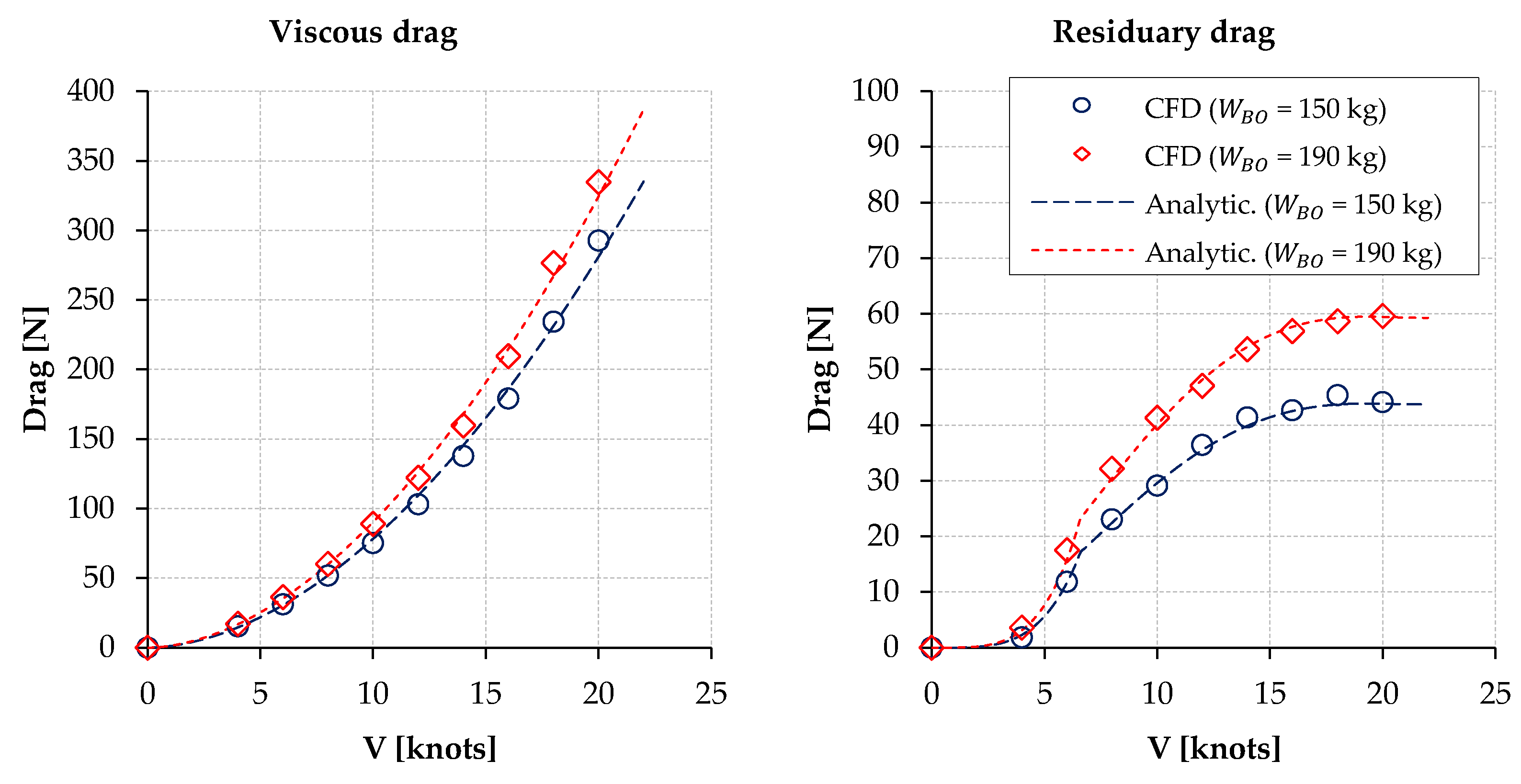

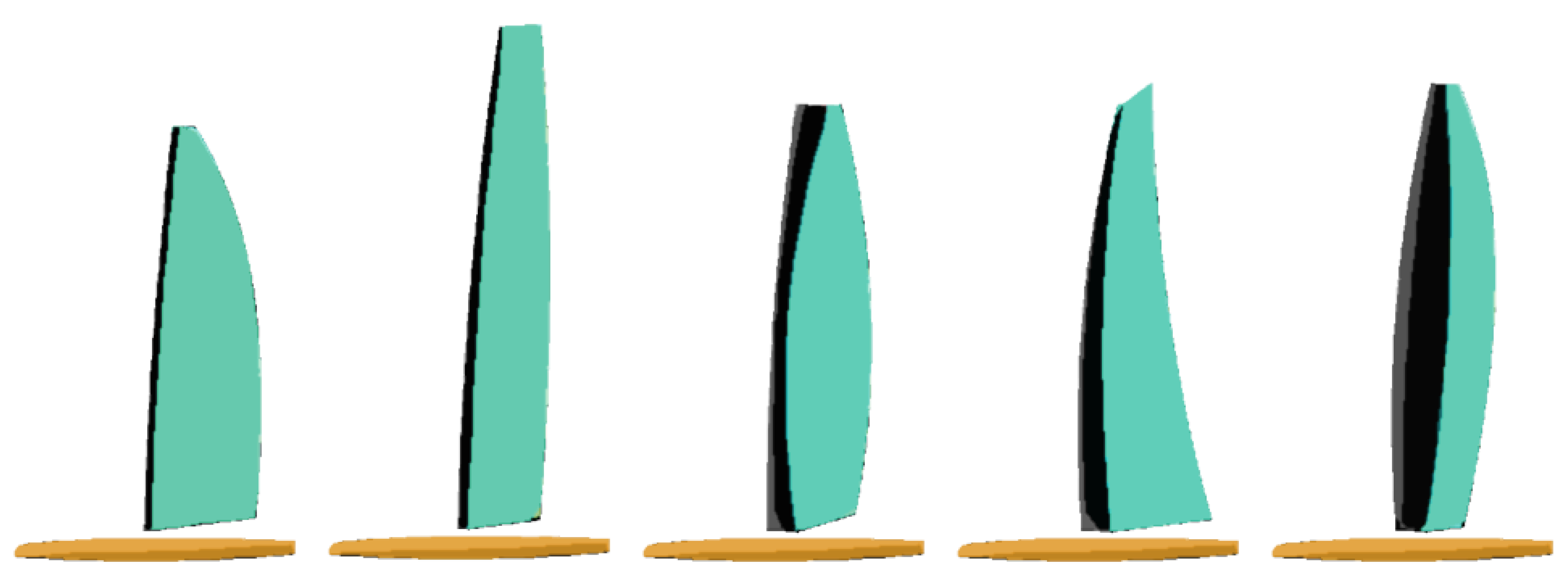


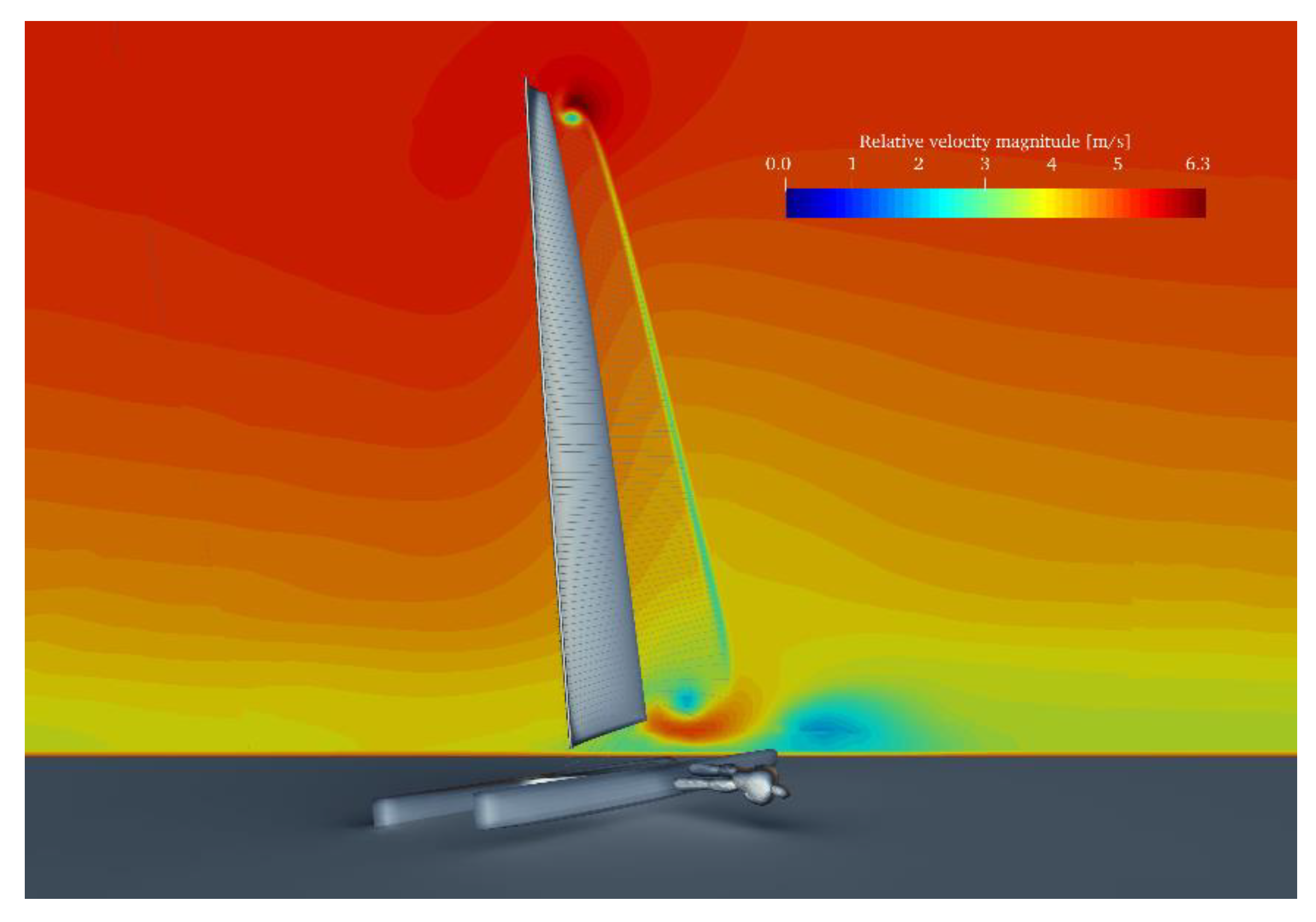
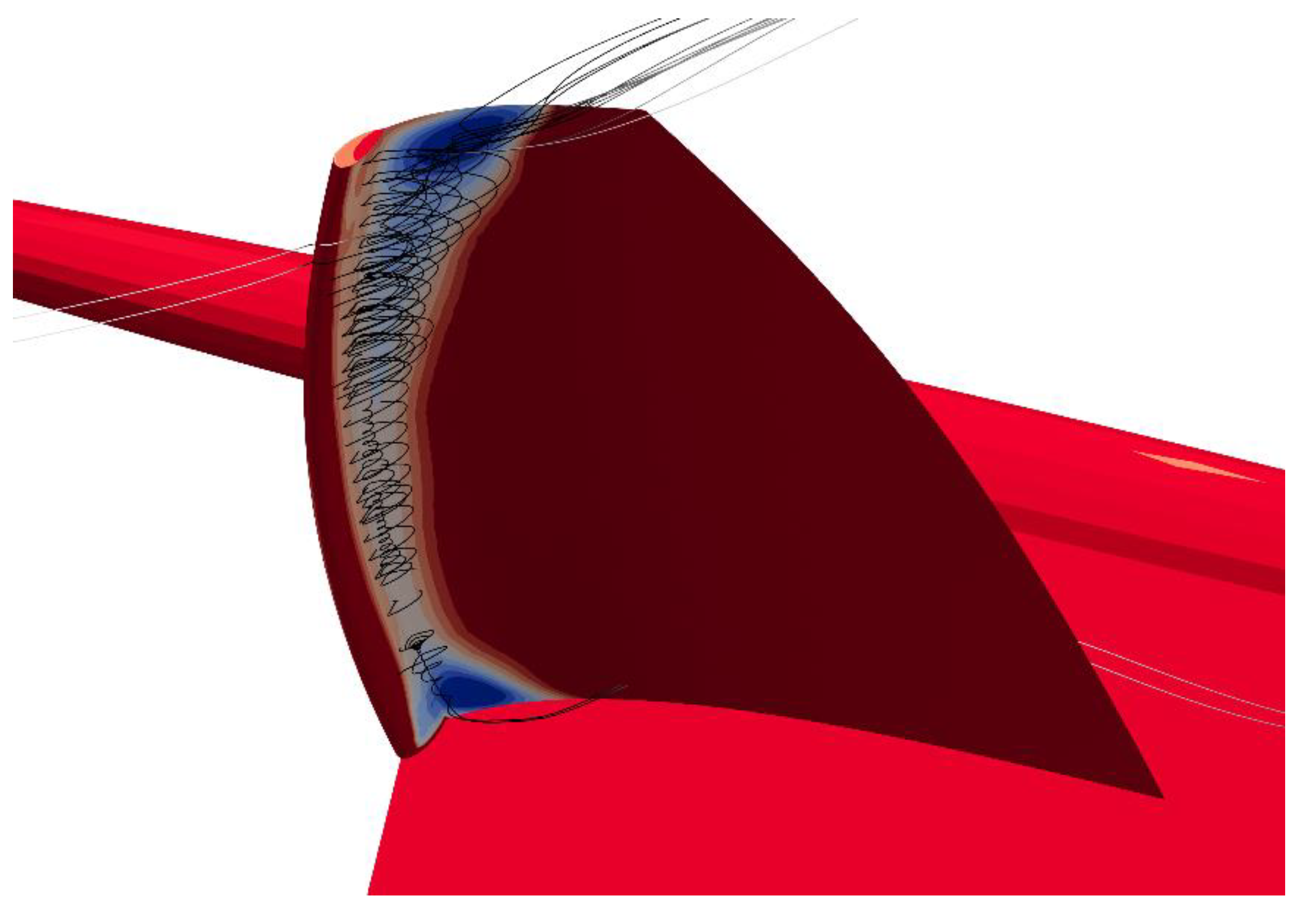
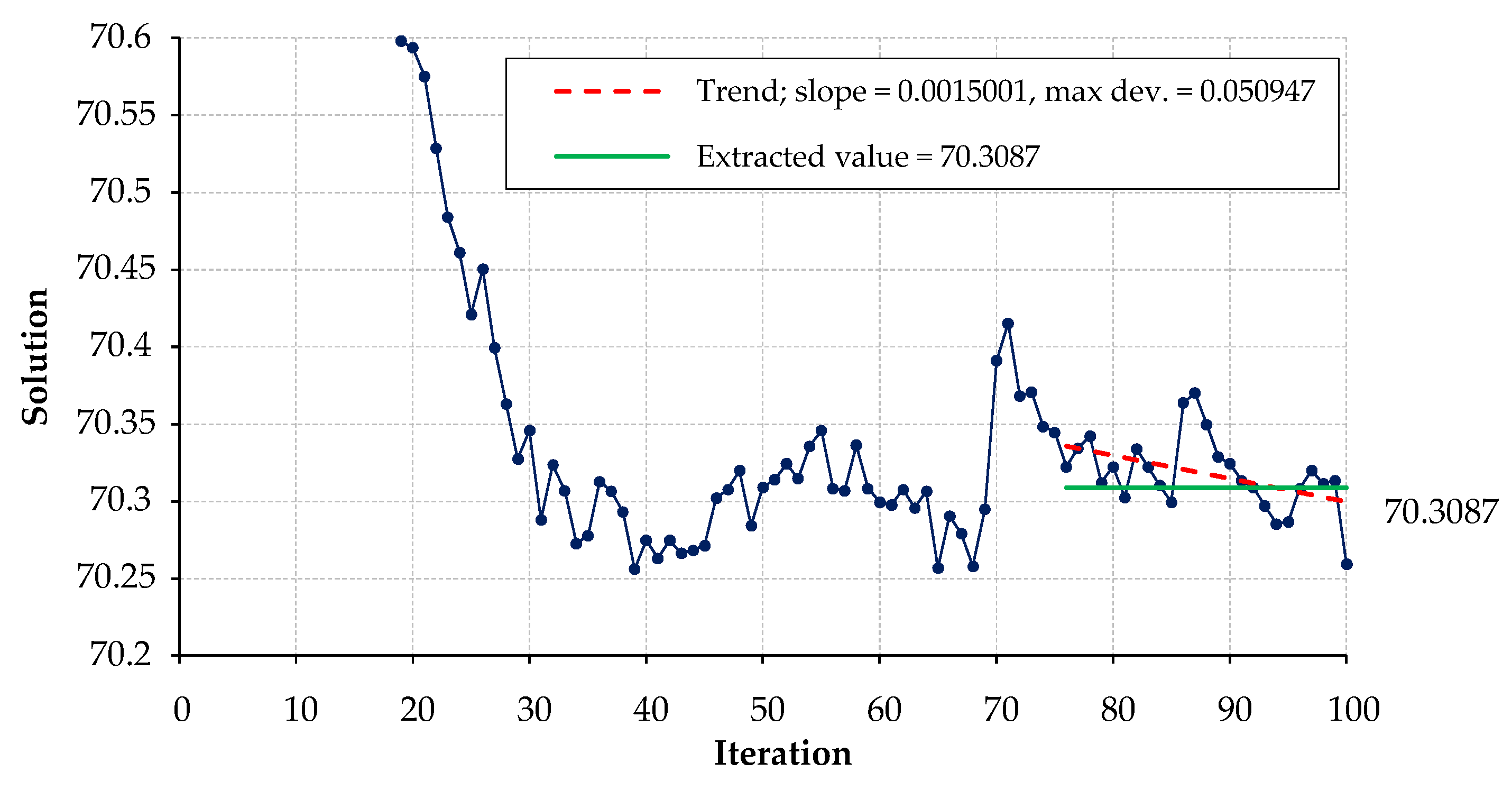
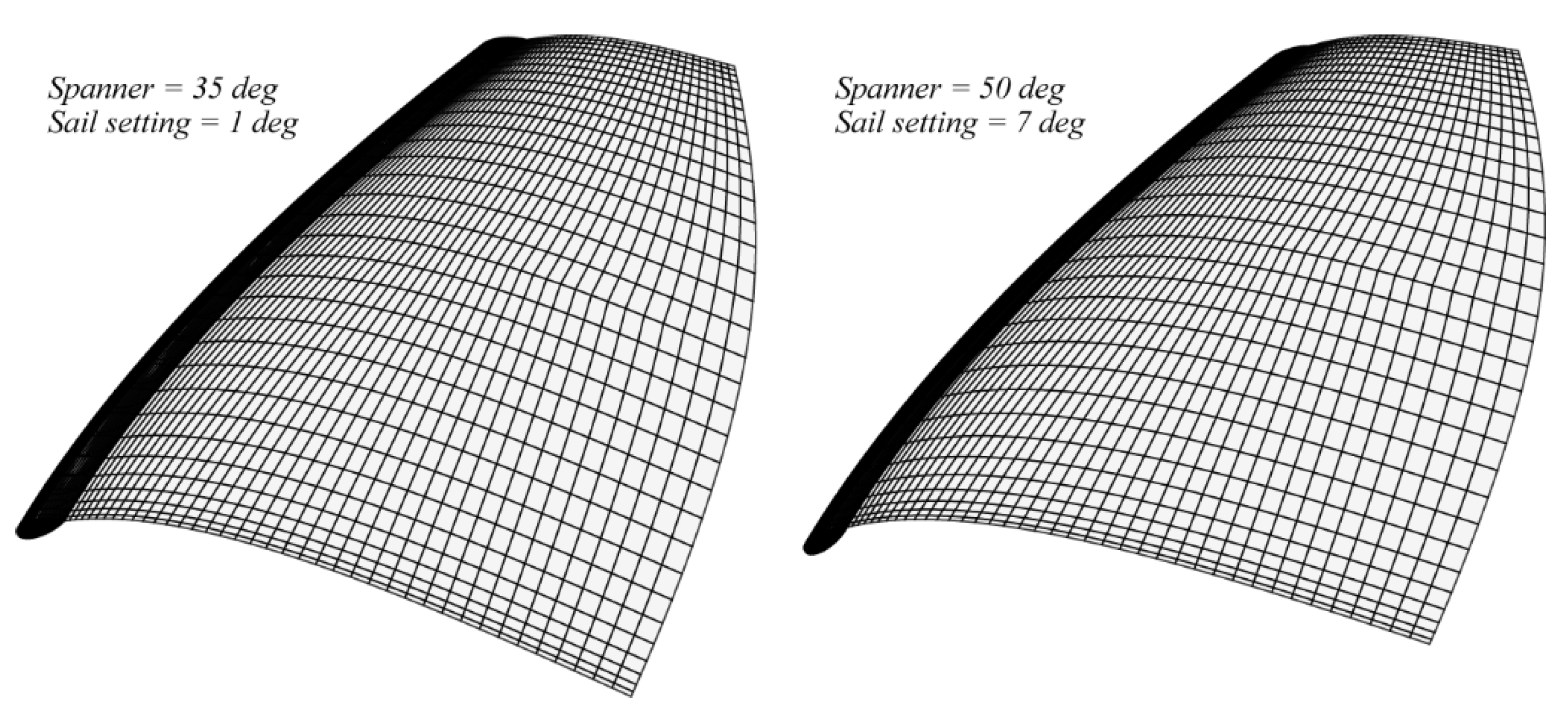
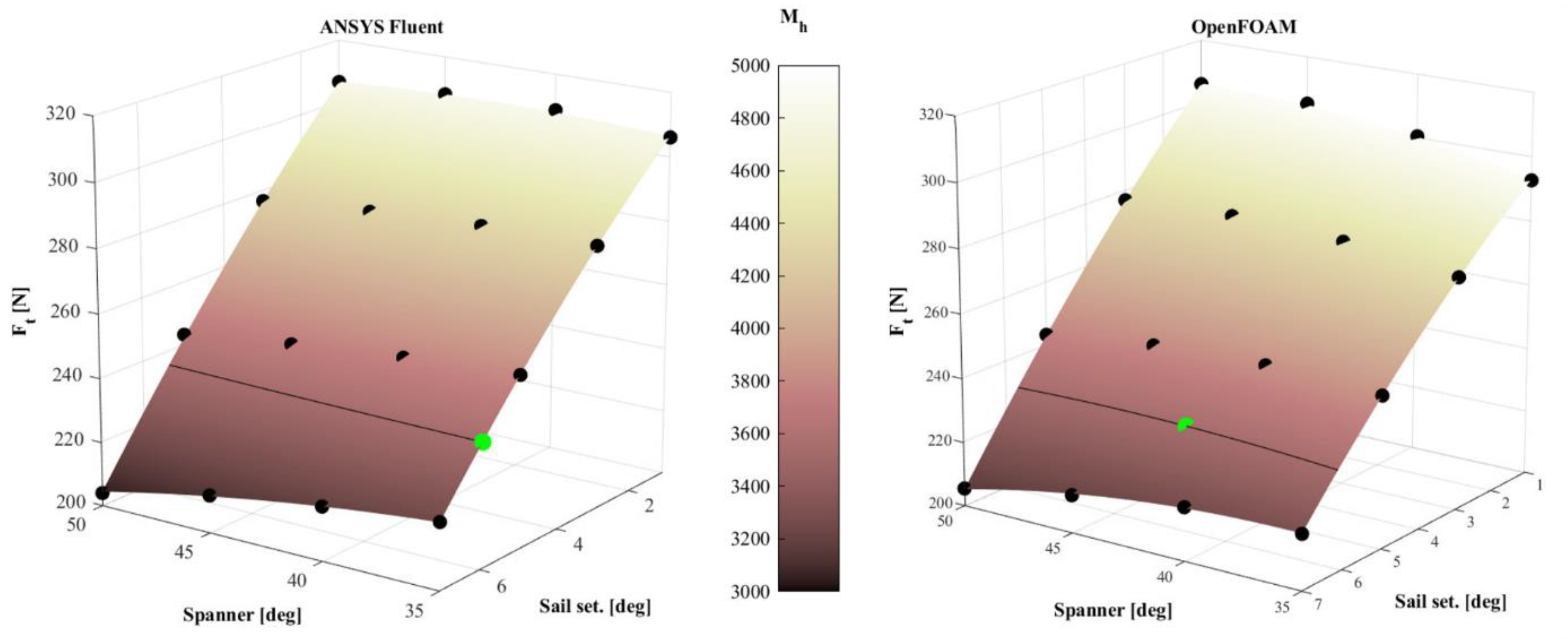
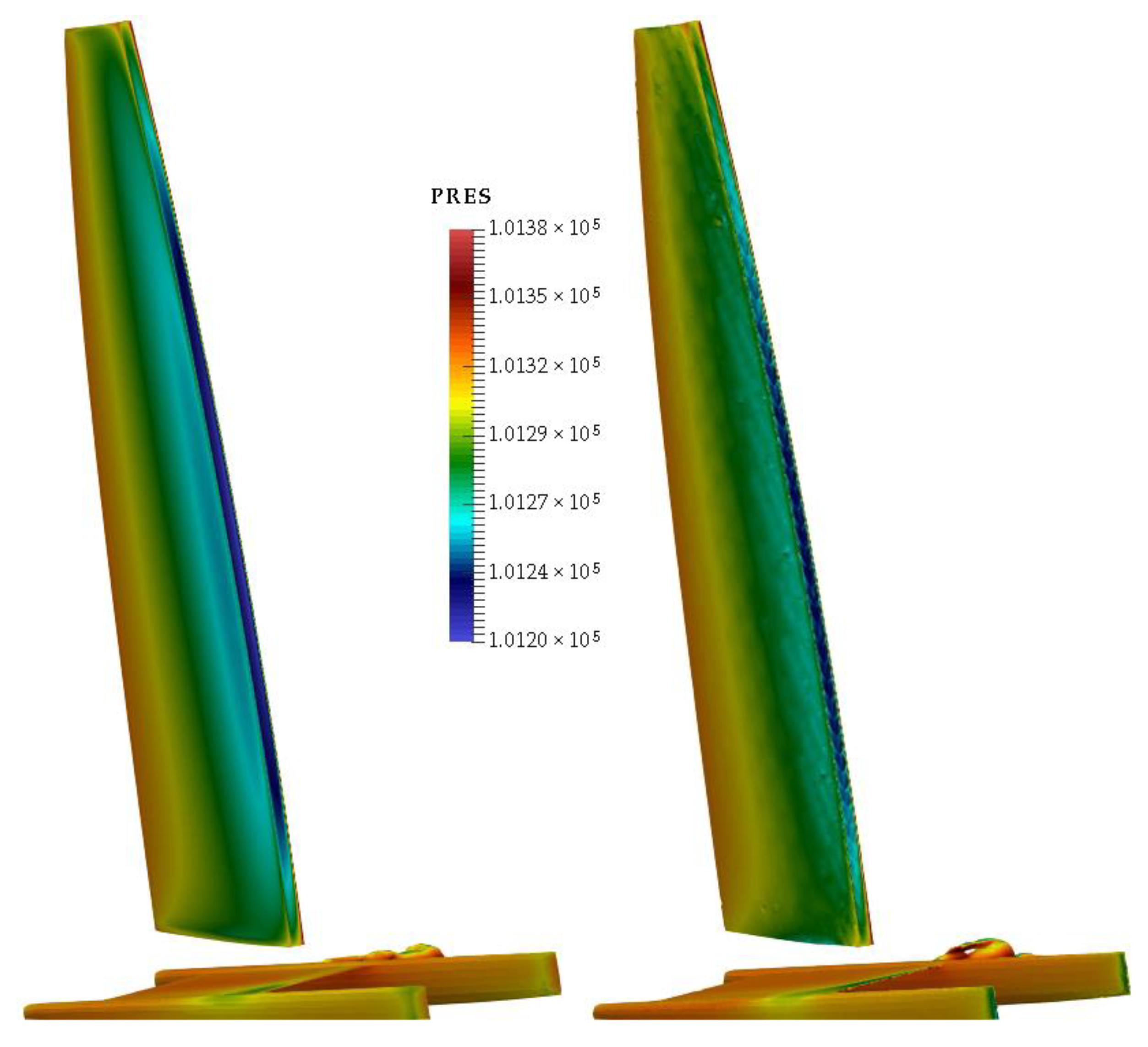
| Reference Surfaces | Side Force | Wave Drag | Leeway Drag |
|---|---|---|---|
| = 0.00437 | = 6 × 10−7 | = 80 kg | = 2 × 10−6 |
| = 0.07 | = 1.3 × 10−4 | = 2.16 × 10−6 | = 1.5 |
| = 0.83 | = 1.3 | = −8.3 × 10−6 | = 400 kg |
| = 0.00876 | = 0.2 | = 9 × 10−6 | |
| = 0.95 | |||
| = 0.5 | shape factor = 0.01 | ||
| = 94 kg | |||
| ANSYS Fluent | OpenFOAM | |
|---|---|---|
| Spanner | 35 deg | 41.7 deg |
| Sail setting | 5.9 deg | 6 deg |
| Thrust force | 238.2 N | 232.5 N |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cella, U.; Salvadore, F.; Ponzini, R.; Biancolini, M.E. VPP Coupling High-Fidelity Analyses and Analytical Formulations for Multihulls Sails and Appendages Optimization. J. Mar. Sci. Eng. 2021, 9, 607. https://doi.org/10.3390/jmse9060607
Cella U, Salvadore F, Ponzini R, Biancolini ME. VPP Coupling High-Fidelity Analyses and Analytical Formulations for Multihulls Sails and Appendages Optimization. Journal of Marine Science and Engineering. 2021; 9(6):607. https://doi.org/10.3390/jmse9060607
Chicago/Turabian StyleCella, Ubaldo, Francesco Salvadore, Raffaele Ponzini, and Marco Evangelos Biancolini. 2021. "VPP Coupling High-Fidelity Analyses and Analytical Formulations for Multihulls Sails and Appendages Optimization" Journal of Marine Science and Engineering 9, no. 6: 607. https://doi.org/10.3390/jmse9060607
APA StyleCella, U., Salvadore, F., Ponzini, R., & Biancolini, M. E. (2021). VPP Coupling High-Fidelity Analyses and Analytical Formulations for Multihulls Sails and Appendages Optimization. Journal of Marine Science and Engineering, 9(6), 607. https://doi.org/10.3390/jmse9060607






