1. Introduction
Great circle (GC) navigation is used for the calculation of large distances in marine and aero navigation [
1,
2]. Composite navigation is used when the great circle vertex exceeds the high-latitude areas. In certain cases, it is acceptable to approximate the Earth as a sphere. This approach is applicable to electronic navigation because the differences between great circle, great ellipse (GE), or geodetic sailing (GS) are minor [
3]. In [
4], the authors presented the differences between GC and GE, confirming measurable discrepancies in calculated distances while using the GC for the initial calculation of courses. The findings presented in our work refer to the spherical geometry and respective formulations; therefore, geodetic and elliptical approaches were not considered.
In [
5], the author notes that “the only safe way to use computer software for the solution of navigation problems is with a full background, navigational knowledge and understanding of the basic equation”, and the authors in [
6] ask “Can anyone suggest a neater and more elegant solution—without using the spherical trig?”. Perhaps there is a means to use spherical trigonometry with validated expressions and established axioms? The authors of [
7] note that “Although the follow-up studies claim that some new formulae which they proposed are the direct approach, they still have to calculate the initial great circle course angle first”. These statements highlight the importance of a reliable means to accurately calculate a vessel’s course, without mistakes that may arise from the trigonometry. Each of the statements quoted above relates to the occurrence of the same error, rather than noting the difference between the calculated angle and the vessel’s true course.
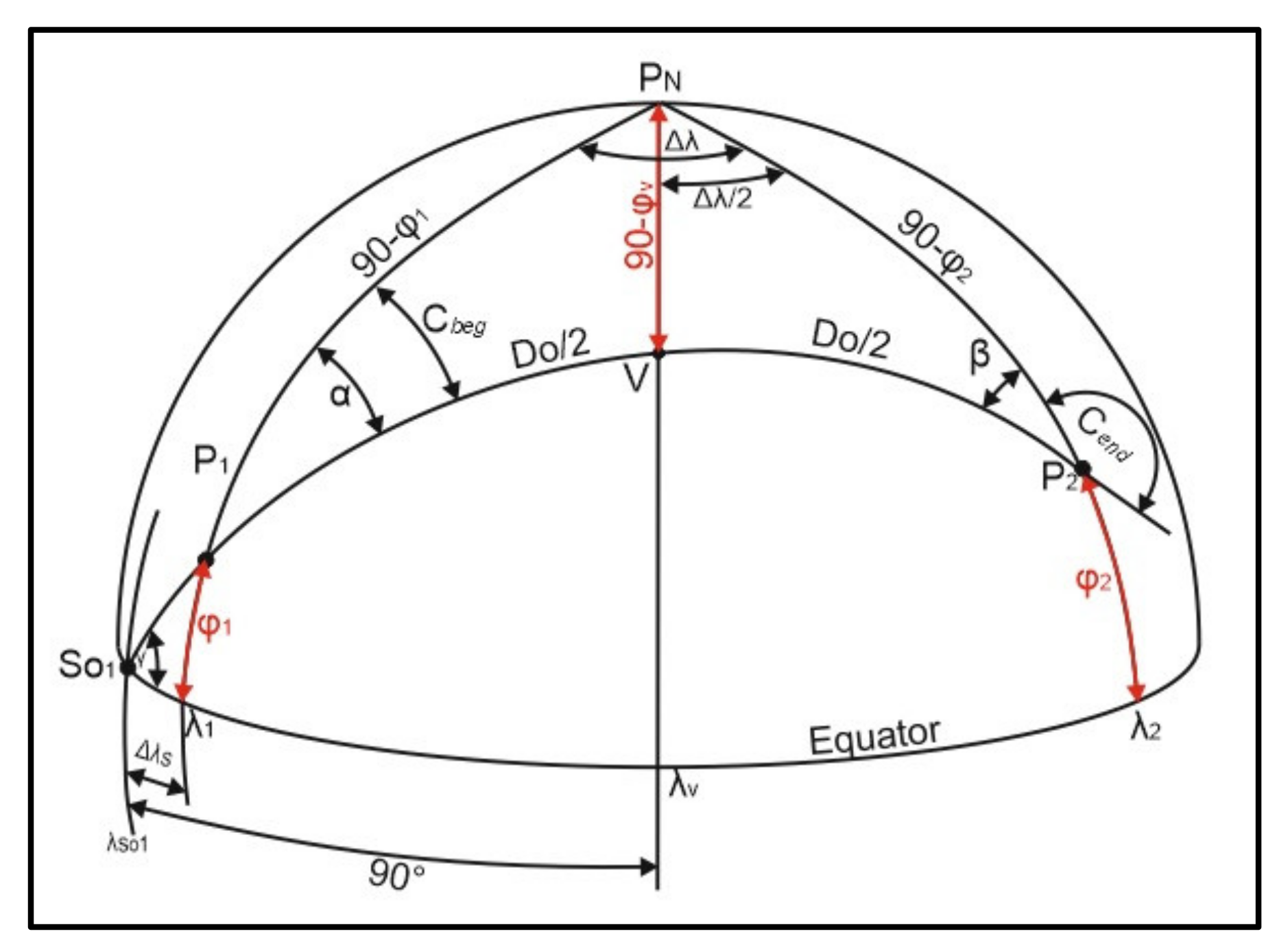
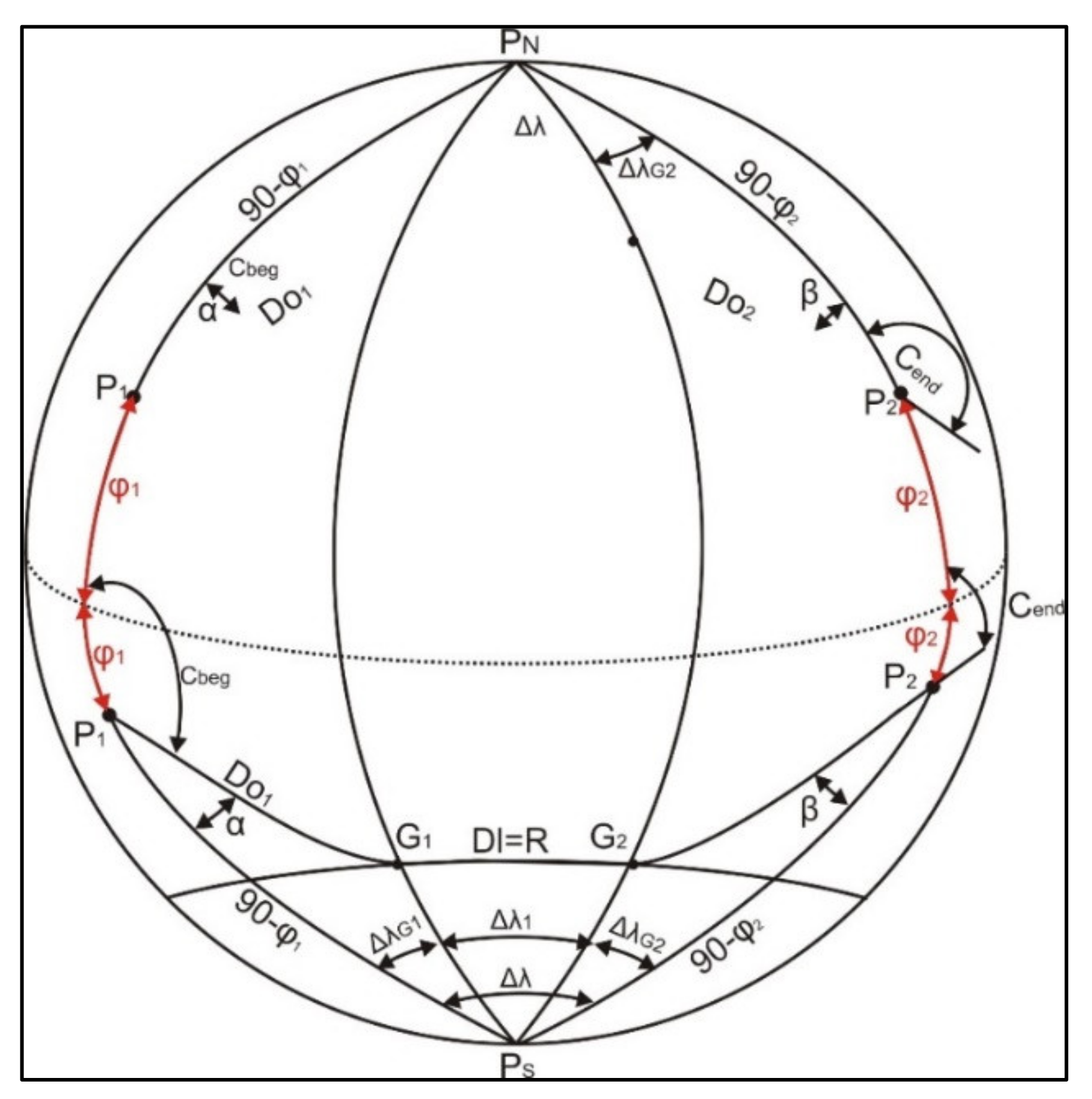
In this paper, attention is drawn to a vessel’s course at the beginning and end of the great circle navigation. In certain cases, the calculated angles do not represent the true course, and transformation of the angles is needed. To address this problem, a transformation axiom is proposed. Angles α and β (
Figure 1) are auxiliary angles used to calculate the true vessel’s course at the beginning (C
beg) and end (C
end) of the route, respectively.
This can be performed using navigational quadrants or by following the axiom rules:
(1) When sailing eastbound, courses can be calculated using:
(2) When sailing westbound, courses can be calculated using:
The same axiom can be used in composite GC navigation. The sole purpose of the proposed axiom is to enable the navigator to easily and quickly transform the auxiliary angles into the vessel’s true course. In this paper, well-known expressions used in course calculation are summarized and analyzed, followed by a recommendation of expressions that can be safely used. This enables unification of expressions and elimination of mistakes during the calculations.
2. Course Calculation Methods and Expressions
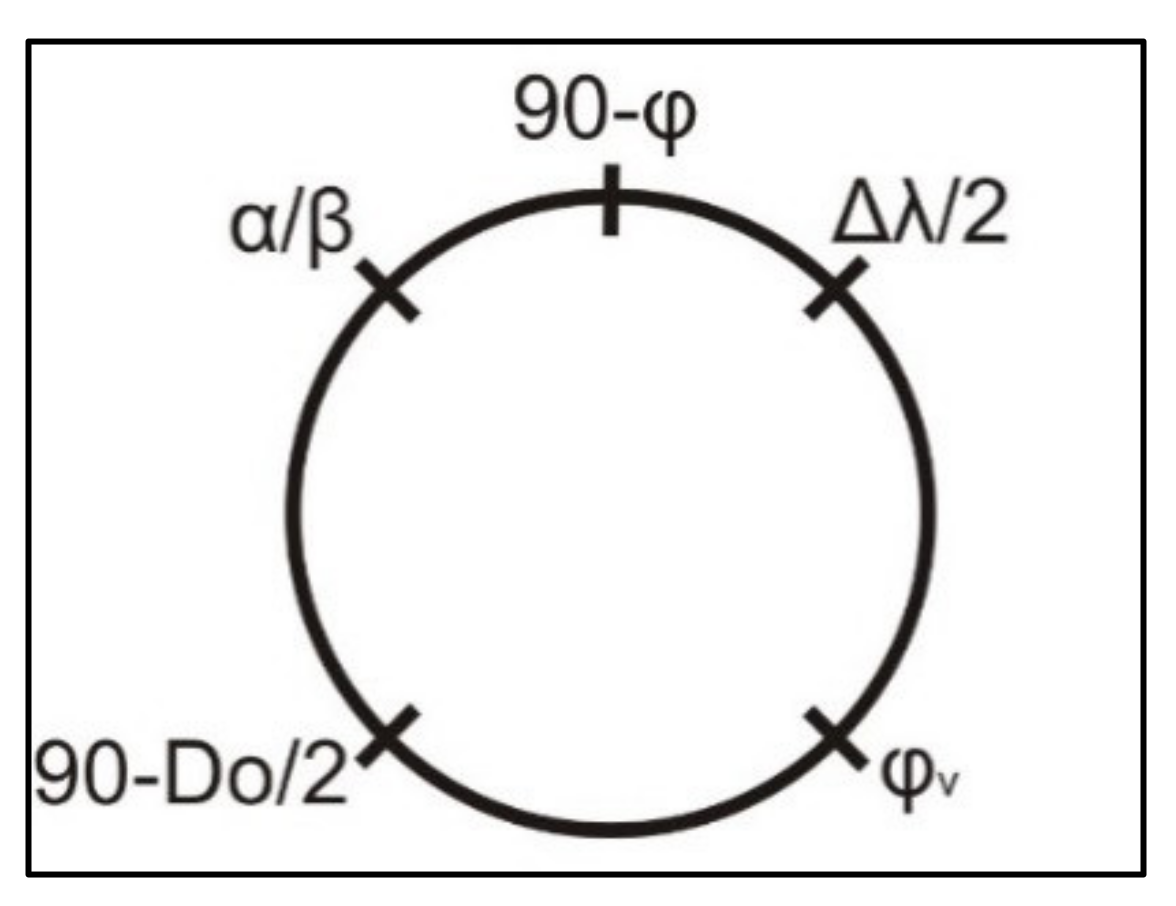
Angles α and β represent the auxiliary angles which are used in great circle and composite navigation course calculation. To calculate these angles, the Napier wheel [
8] is used on a rectangular spherical triangle (
Figure 1: P
N, P
1 or P
2, V) with the following rules: at the top of the wheel is the side of the triangle which is opposite to a right angle (90−φ); fitting angles (α or β and Δλ/2) are at both sides of the wheel; and at the bottom are latter angles opposing the sides in complement (90−D
O and φ
V) (
Figure 2).
To calculate values, the cosine of each element is equal to the product of the sine of the two farther elements, or the cotangent of the two closer elements, respectively. Therefore, auxiliary angles can be calculated as follows:
In addition to using the Napier wheel, these elements can be calculated using the spherical sine and cosine theorem, or the four-part formula. When the sine theorem is used, the angles can be calculated using the following expression:
when using the cosine theorem, the angles
α and
β are calculated using the following equations:
When the same angles are calculated using the four-part formula, the following equations can be used:
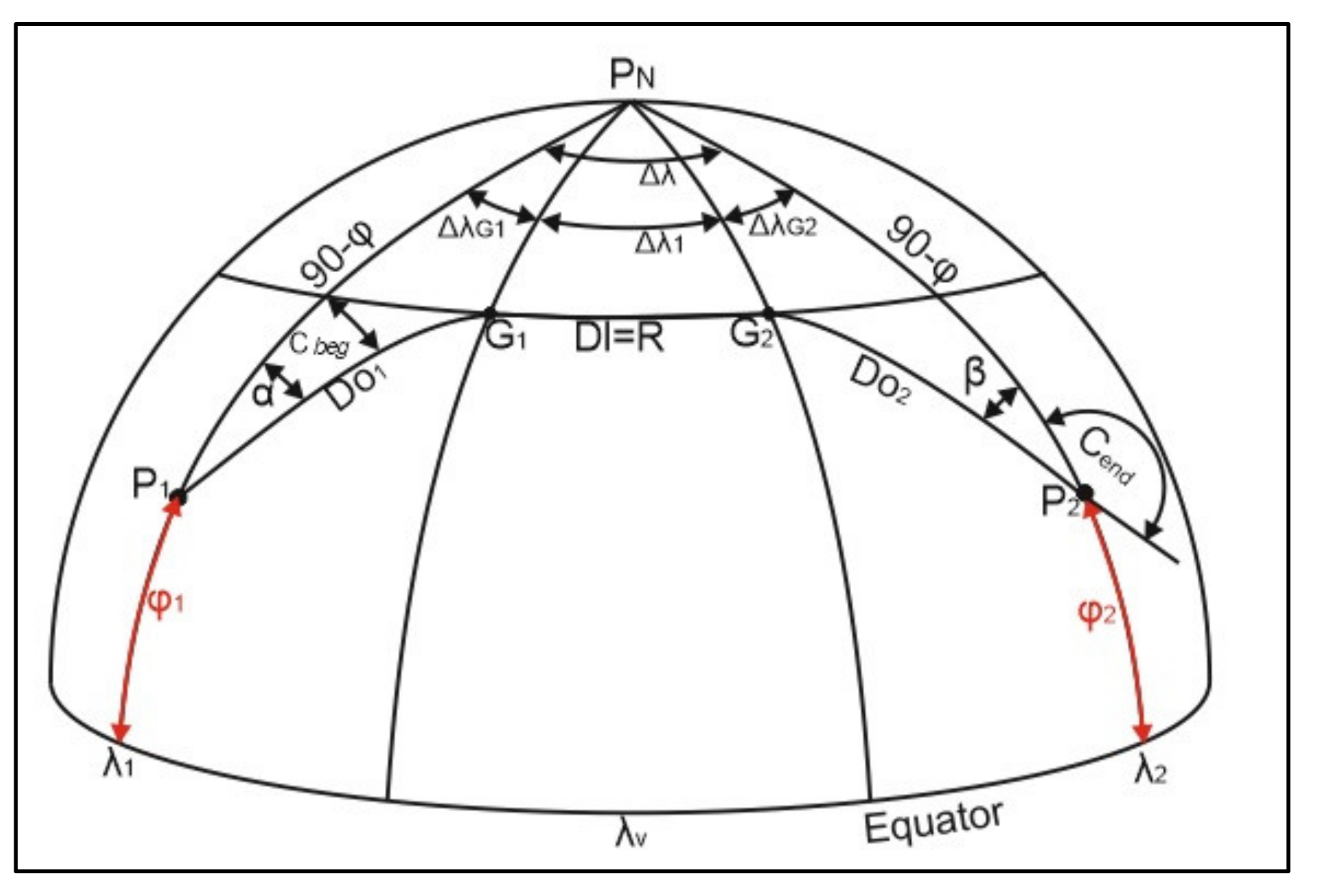
In
Figure 3, composite great circle navigation with the defined limiting parallel is presented.
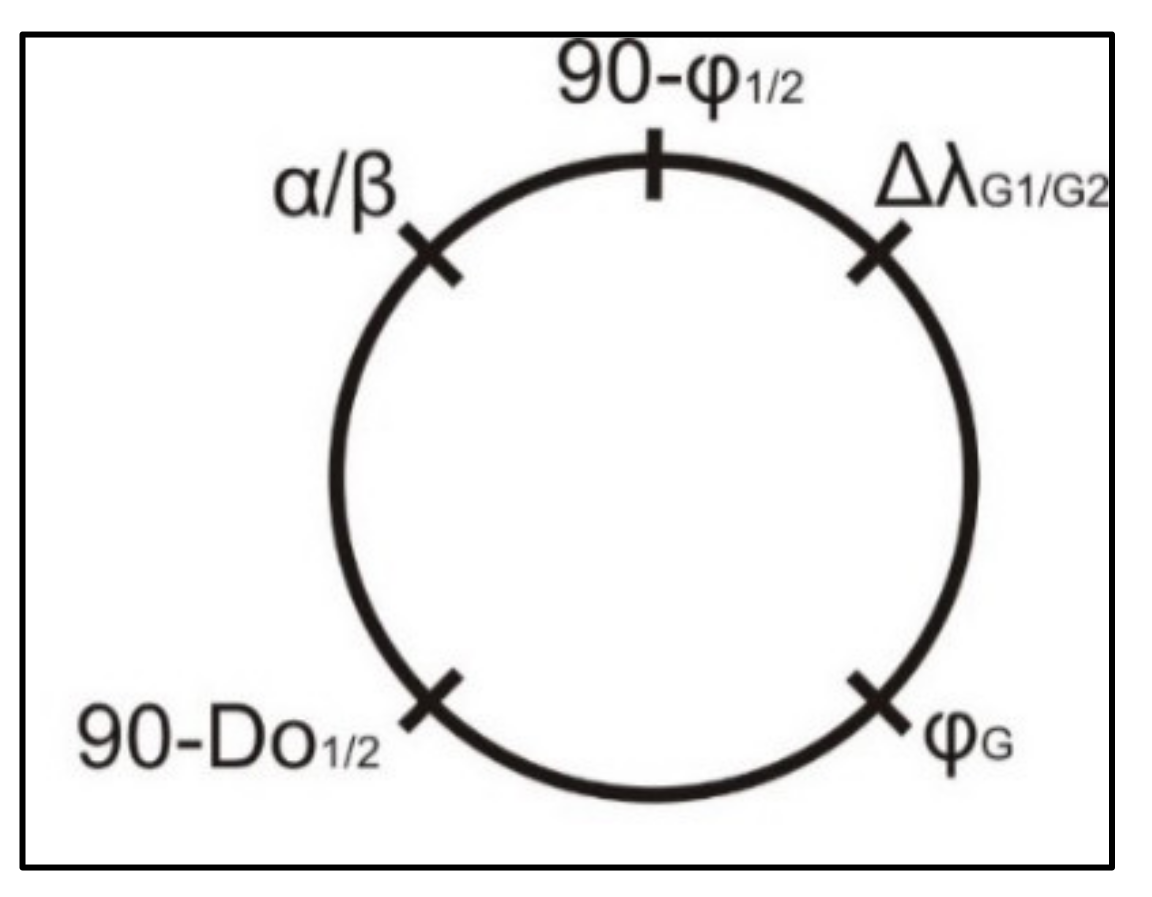
Here, the auxiliary angles are also calculated using the Napier wheel, in addition to the previously described theorems. In such cases, the rectangular triangle with vertexes P
N, P
1(P
2) and G
1(G
2), or P
2, V is used. The Napier wheel is constructed with the value of (90−φ
1) or (90−φ
2) at the top, values of α or β and Δλ
G1 or Δλ
G2 at the sides, and finally, (90−D
O1) or (90−D
O2) and φ
G at the bottom (
Figure 4).
Using the described rules, auxiliary angles can be derived as follows:
or:
Using the sine theorem, auxiliary angles can be calculated as:
Using the cosine theorem, the angles can be calculated using the following equations:
These equations can be used in the calculation of auxiliary angles α and β; however, certain equations are not compliant with these axioms to determine the vessel’s true course. This problem is discussed in the following sections.
3. Calculation of Auxiliary Angles α and β
Depending on the used equations, auxiliary angles may differ due to the limitations of the trigonometric functions. This can lead to misinterpretation, resulting in erroneous calculation of a vessel’s course. This is particularly the case when similar axioms are used, e.g., without additional navigational tools or software. The analysis and determination of accurate equations were conducted as follows.
In the testing phase, several geographical pairs of positions were used, with reference to their relative locations, hemisphere, and the required distance to justifiably apply the trigonometric functions. Four pairs were selected, two of which were situated in the northern hemisphere and two in the southern hemisphere (
Table 1). Routes crossing the equator were not analyzed.
To review the differences between theorems, auxiliary angles α and β for all routes were calculated (eastbound and westbound), including the elements of composite navigation, and using equations from the previous sections. The numbers of corresponding theorems are placed in parentheses. The results of calculated angles are presented in
Table 2.
The selected routes, i.e., pairs of locations, can be considered to be representative because suitable distances from various sources, e.g., [
9], resulted in the same outcomes. The coordinate pairs refer to the WGS84 geodetic datum. Although slight differences are caused by the lengths of axes and inverse flattening coefficients (
Table 3), the type of geodetic datum does not affect the calculation of the elaborated parameters, i.e., great circle angles and distances.
Furthermore, the geodetic parameters should be considered when observed positions do not refer to the same reference system, which was not the case in the proposed study.
From
Table 2, it can be seen that angles differ due to the theorem used and the respective hemisphere, because the south and west longitudes have negative signs. These differences between angles that otherwise appear the same were also explained using the spherical trigonometry approach. The equations which are not influenced by coordinate signs are recommended for usage with the proposed axiom.
4. Comparison and Analysis of Theorems
When calculating auxiliary angles, differences appear with the southern hemisphere pairs. This occurs due to the incorrect mathematical formulation, in addition to the sine theorem itself.
Usually, in the calculation of great circle navigation auxiliary angles it is recommended to use the cosine theorem with Equation (5) and Equation (6); however, some studies use sine theorem expressions. In handbooks [
11,
12], Equation (3) is recommended. In handbook [
13], the cosine theorem is used, but always with positive latitudes, even in the southern hemisphere case. As can be seen in
Table 2, auxiliary angles α and β differ, indicating that different angles are calculated and different rules for course calculation have to be followed.
Furthermore, for composite navigation, Equations (9) and (10) are recommended [
14,
15,
16,
17].
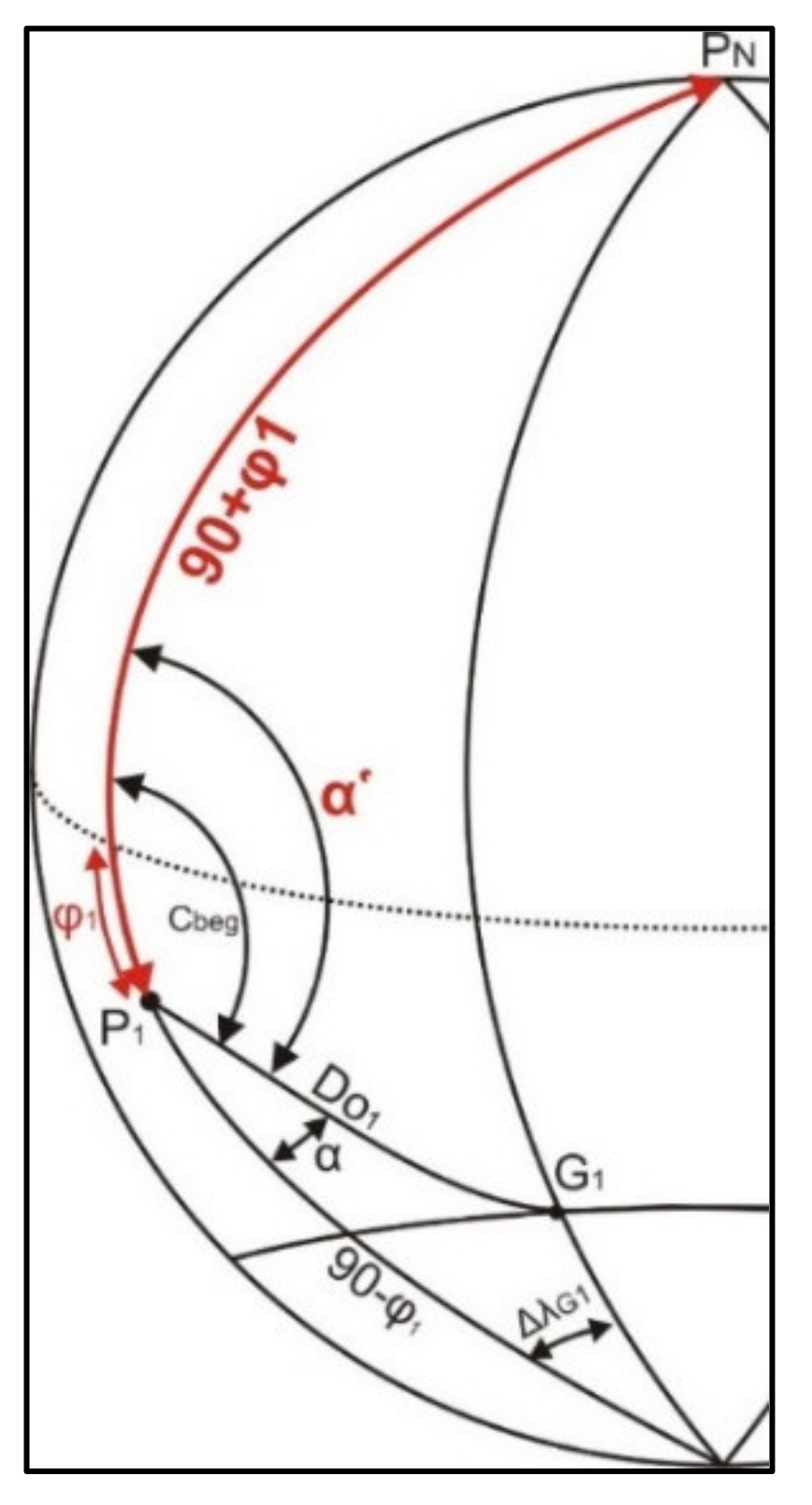
Equation (9) and Equation (10) use the sine-derived Napier wheel theorem, whereas Equation (13) and Equation (14) are derived using the sine theorem (
Table 2), resulting in differences between the calculated results. These differences are caused by improper mathematical inscription. For great circle navigation, in the southern hemisphere the auxiliary angle α lies between sides D
O1 and (90−φ
1), whereas angle β is situated between sides D
O2 and (90−φ
2) (
Figure 5). In the case of composite navigation, the angle α lies between sides D
O1 and (90−φ
1), and angle β lies between sides D
O2 and (90−φ
2). In both cases, the resulting angle is not α or β. For calculation purposes, the geographical latitude in the southern hemisphere has a negative sign. One of the sides of both angles is (90−φ); if this side is correctly written mathematically, the outcome is (90− (−φ)), which results in (90−φ). This side is the opposite of that required in triangle P
S, P
1, and P
2, and the final results are angles α’ and β’ (
Figure 6).
The other problem occurs due to the sine theorem itself. As explained previously, angles α’ and β’ are greater than 90° in the southern hemisphere. The sine theorem results in an arcus of angles between −90° and +90°.
Greater and lower angles result in a misleading arcus, and consequently, the wrong angle. The sine values of 135° and 45° are the same (
Figure 7, green line); thus, when used for course calculation, the arcus sine shows a value of 45° rather than 135°. The cosine theorem results in an arcus of angles between 0° and 180°. Therefore, the arcus cosine will always show values between 0° and 180° (
Figure 7, yellow line). This is confirmed in
Table 2. The cosine theorem yields stable results in both the northern and southern hemispheres.
5. Conclusions
Most of the described equations are derived using the northern hemisphere navigation routes. The results calculated for the southern hemisphere are adjusted due to the navigational quadrant. This is particularly pronounced in composite navigation, in which navigators experience difficulties with the equations, and in the calculation of the vessel’s true course. Substantial errors may arise by selecting the wrong quadrant in cases in which the great circle vertex is placed outside the pairs of positions. In the present paper, the possibility of erroneous calculations was identified, their presence was noted, and their causes explained. The main goal of the presented calculations and analysis was to select equations that provide navigators with a straightforward calculation using the proposed axiom, considering the spherical trigonometry approach and assuming the uniform geodetic datum for all geographic coordinates. When calculating the vessel’s course, using the proposed axiom, the most suitable equations for great circle navigation are Equation (5) and Equation (6), and Equation (11), Equation (12), Equation (15), and Equation (16) refer to composite navigation. The proposed axiom is simple to use and provides correct results, including at the vessel’s starting and ending point.
Author Contributions
Conceptualization, M.B. and M.K.; methodology, M.B.; validation, M.B., M.K. and D.B.; formal analysis, D.B.; investigation, R.J.; data curation, D.B. and M.B.; writing—original draft preparation, R.J. and M.B.; writing—review and editing, D.B.; visualization, M.B. and D.B.; supervision, D.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
There is power in good people, they are strong even after death. They live onwards, by their words and acts, but mostly by the kindness of their heart. In loving memory of our friend and colleague Roko Jelic (1985−2020).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nastro, V.; Tancredi, U. Great Circle Navigation with Vectorial Methods. J. Navig. 2010, 63, 557–563. [Google Scholar] [CrossRef]
- Chen, C.L. A Systematic Approach for Solving the Great Circle Track Problems based on Vector Algebra. Pol. Marit. Res. 2016, 2, 3–13. [Google Scholar] [CrossRef][Green Version]
- Tseng, W.K.; Lee, H.S. Navigation on a great ellipse. J. Mar. Sci. Technol. 2010, 18, 369–375. [Google Scholar]
- Tseng, W.K.; Guo, J.L.; Liu, C.P. A comparison of great circle, great ellipse and geodesic sailing. J. Mar. Sci. Technol. 2013, 21, 287–299. [Google Scholar]
- Chen, C.L.; Hsu, T.P.; Chang, J.R. A novel approach to great circle sailings: The great circle equation. J. Navig. 2004, 57, 311–325. [Google Scholar] [CrossRef]
- Hickley, P. Great circle versus rhumb line cross-track distance at mid-longitude. J. Navig. 2004, 57, 320–325. [Google Scholar] [CrossRef]
- Hsieh, T.H.; Wang, S.; Liu, W.; Zhao, J. New Formulae for Combined Spherical Triangles. J. Navig. 2019, 72, 503–512. [Google Scholar] [CrossRef]
- Napier, J. The Construction of the Wonderful Cannon of Logarithms; W. Blackwood and Sons: London, UK, 1889. [Google Scholar]
- British Admiralty. Admiralty Distance Tables, Indian Ocean; British Admiralty: London, UK, 2008; Volume 2. [Google Scholar]
- Lu, Z.; Qu, Y.; Qiao, S. Geodesy; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Kos, S.; Zorović, D.; Vranić, D. Terestrička i Elektronička Navigacija; Faculty of Maritime Studies, University of Rijeka: Rijeka, Croatia, 2010; pp. 37–39. [Google Scholar]
- Radulić, R. Terestrička Navigacija; Profil International: Zadar, Croatia, 2003. [Google Scholar]
- Truong, K.M. The Vessel Officer’s Handbook; Asoka Publishing Company: Jaipur, India, 2011. [Google Scholar]
- Anwar, N. Navigation Advanced Mates/Masters; Witherby Publishing: Livingston, UK, 2015. [Google Scholar]
- Lušić, Z. Terestrička Navigacija; Maritime Faculty of Maritime Studies, University of Split: Split, Croatia, 2012. [Google Scholar]
- Brown´s Nautical Almanac; Brown, Son & Ferguson, Ltd.: Glasgow, UK, 2021.
- Practical Navigation—The Sailings; Blackpool and The Fylde College Fleetwood Nautical Campus: Fleetwood, UK, 2006.
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).