Installation of Large-Diameter Monopiles: Introducing Wave Dispersion and Non-Local Soil Reaction
Abstract
1. Introduction
2. Modelling of Pile Driving
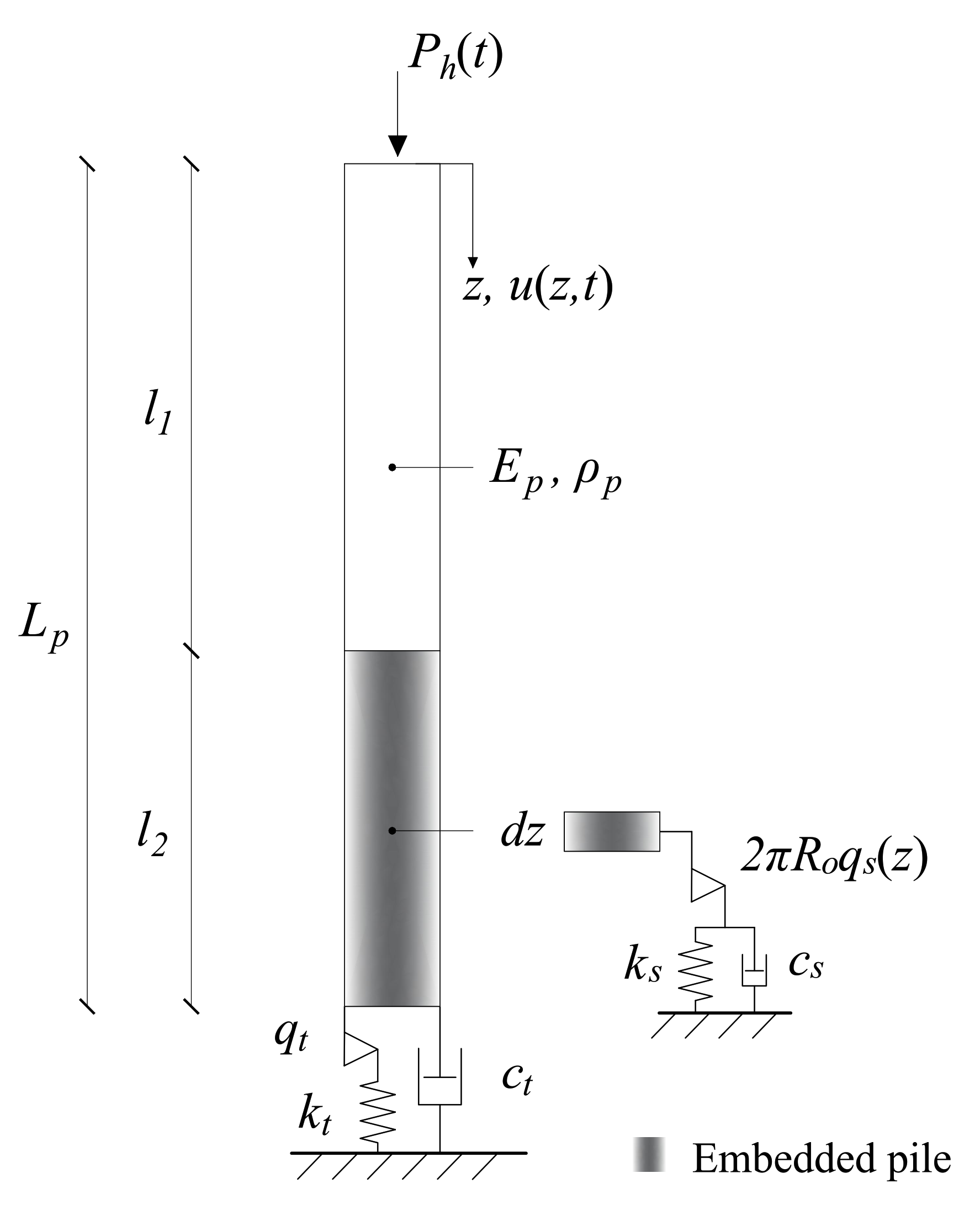
2.1. One-Dimensional Pile Driving Model
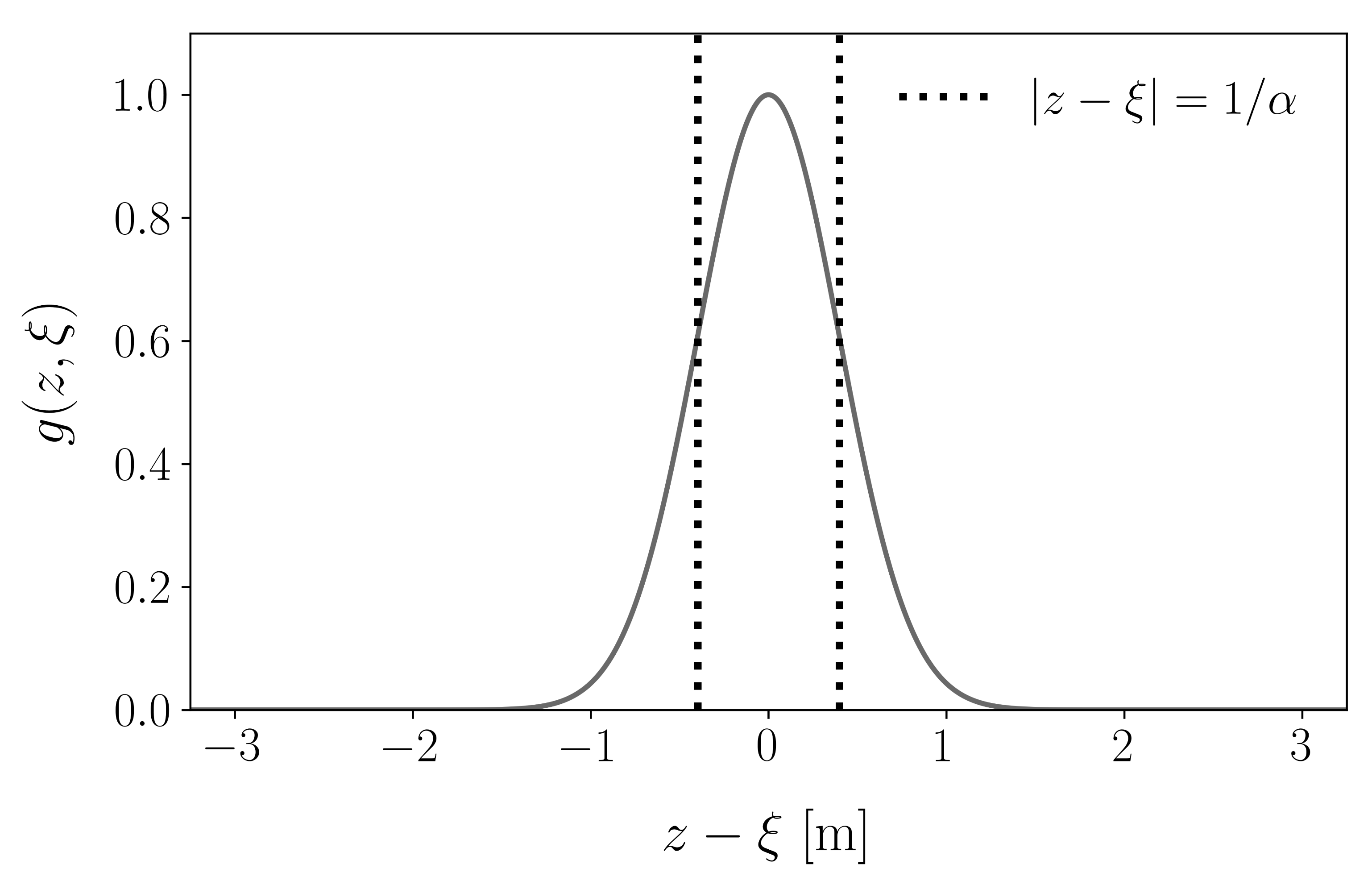
2.2. Non-Local Three-Dimensional Axisymmetric Pile Driving Model
2.3. Numerical Solution
3. Results
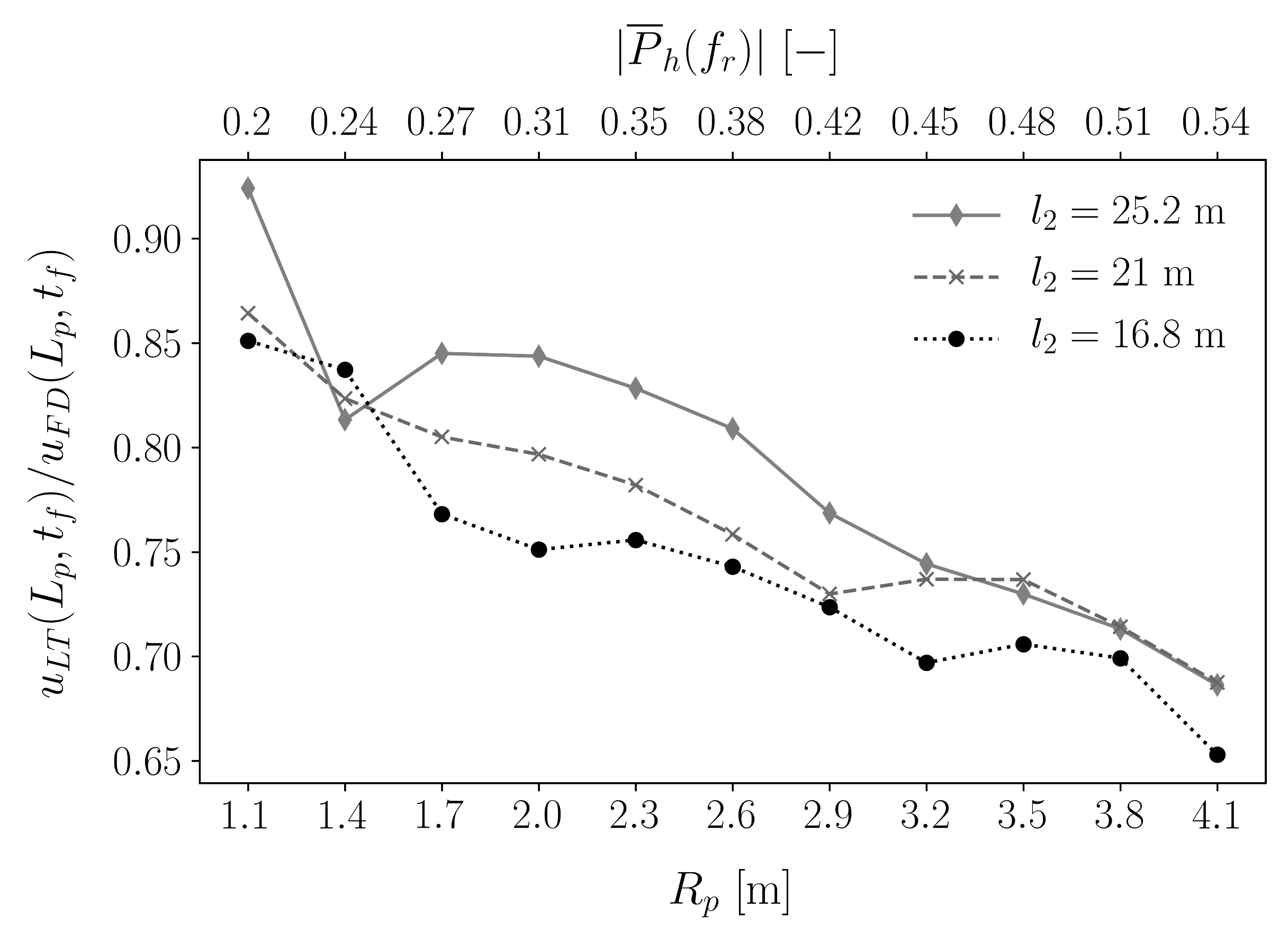
3.1. Validation of the 3-d LT Model
3.2. Influence of Wave Dispersion
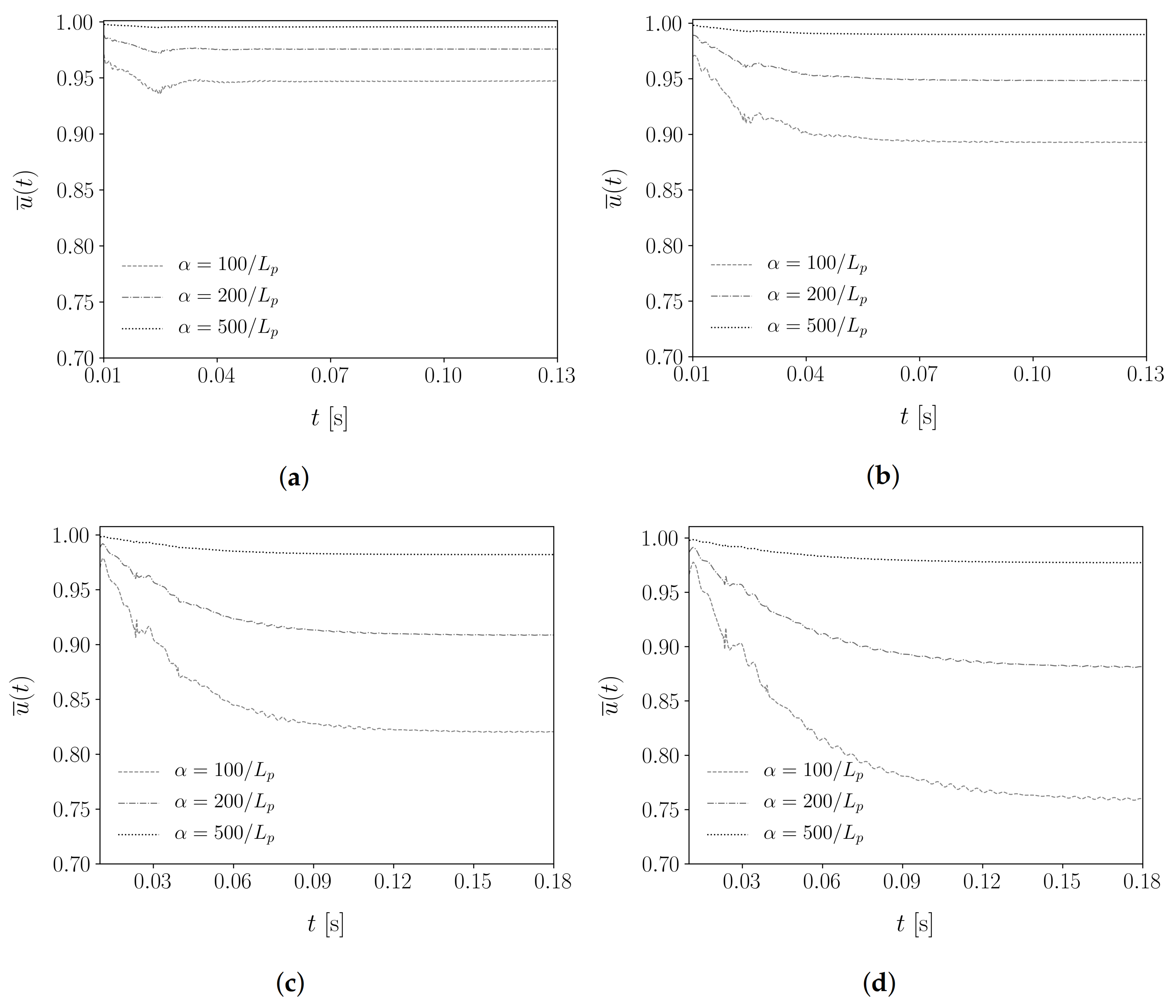
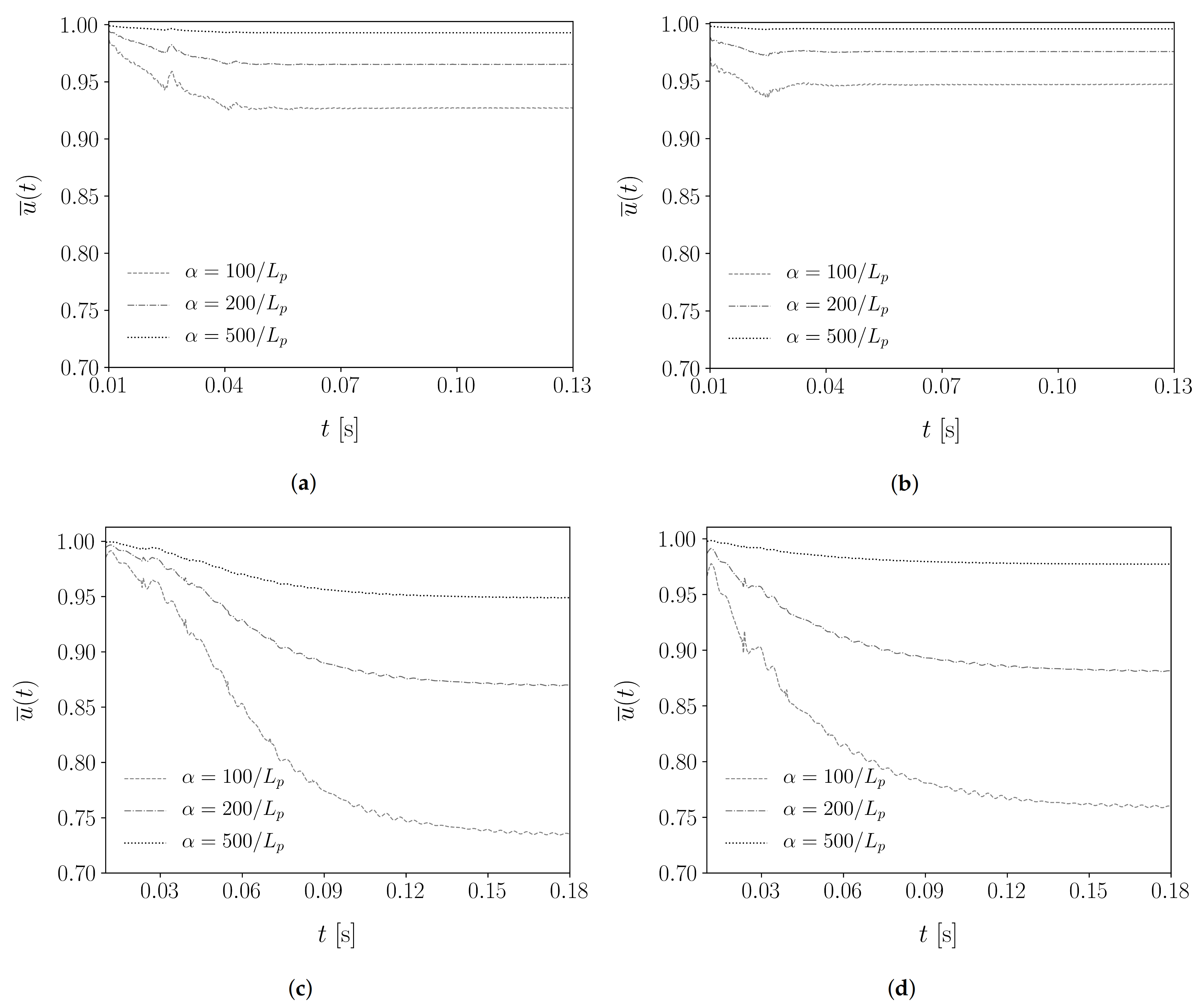
3.3. Influence of Non-Local Soil Reaction
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Poudineh, R.; Brown, C.; Foley, B. Economics of Offshore Wind Power: Challenges and Policy Considerations; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Sánchez, S.; López-Gutiérrez, J.S.; Negro, V.; Esteban, M.D. Foundations in offshore wind farms: Evolution, characteristics and range of use. Analysis of main dimensional parameters in monopile foundations. J. Mar. Sci. Eng. 2019, 7, 441. [Google Scholar] [CrossRef]
- Asgarpour, M. Assembly, transportation, installation and commissioning of offshore wind farms. In Offshore Wind Farms; Elsevier: Amsterdam, The Netherlands, 2016; pp. 527–541. [Google Scholar]
- Wu, X.; Hu, Y.; Li, Y.; Yang, J.; Duan, L.; Wang, T.; Adcock, T.; Jiang, Z.; Gao, Z.; Lin, Z.; et al. Foundations of offshore wind turbines: A review. Renew. Sustain. Energy Rev. 2019, 104, 379–393. [Google Scholar] [CrossRef]
- Sa, L.; Yinghui, T.; Yangrui, Z.; Baofan, J.; Jinbiao, W. Premature refusal of large-diameter, deep-penetration piles on an offshore platform. Appl. Ocean Res. 2013, 42, 55–59. [Google Scholar] [CrossRef]
- Ramírez, L.; Fraile, D.; Brindley, G. Offshore Wind in Europe: Key Trends and Statistics 2019; Technical Report; WindEurope: Brussels, Belgium, 2020. [Google Scholar]
- Gerwick, B.C., Jr. Construction of Marine and Offshore Structures; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Smith, E.A. Pile-driving analysis by the wave equation. Am. Soc. Civ. Eng. Trans. 1962, 127, 1145–1170. [Google Scholar] [CrossRef]
- Randolph, M.F.; Simons, H.A. An improved soil model for one-dimensional pile driving analysis. In Proceedings of the 3rd International Conference on Numerical Methods in Offshore Piling, Nantes, France, 21–22 May 1986; pp. 1–17. [Google Scholar]
- Lee, S.; Chow, Y.; Karunaratne, G.; Wong, K. Rational wave equation model for pile-driving analysis. J. Geotech. Eng. 1988, 114, 306–325. [Google Scholar] [CrossRef]
- Novak, M. Vertical vibration of floating piles. J. Eng. Mech. Div. 1977, 103, 153–168. [Google Scholar] [CrossRef]
- Novak, M.; Aboul-Ella, F.; Nogami, T. Dynamic soil reactions for plane strain case. J. Eng. Mech. Div. 1978, 104, 953–959. [Google Scholar] [CrossRef]
- Byrne, T.; Doherty, P.; Gavin, K.; Overy, R. Comparison of pile driveability methods in North Sea sand. In Offshore Site Investigation and Geotechnics: Integrated Technologies-Present and Future; Society of Underwater Technology: London, UK, 2012. [Google Scholar]
- Anusic, I.; Eiksund, G.R.; Liingaard, M.A. Comparison of pile driveability methods based on a case study from an offshore wind farm in North Sea. In Proceedings of the 17th Nordic Geotechnical Meeting Challenges in Nordic Geotechnic, Reykjavik, Iceland, 25–28 May 2016. [Google Scholar]
- Byrne, T.; Gavin, K.; Prendergast, L.; Cachim, P.; Doherty, P.; Pulukul, S.C. Performance of CPT-based methods to assess monopile driveability in North Sea sands. Ocean Eng. 2018, 166, 76–91. [Google Scholar] [CrossRef]
- Deng, Q.; Jiang, W.; Zhang, W. Theoretical investigation of the effects of the cushion on reducing underwater noise from offshore pile driving. J. Acoust. Soc. Am. 2016, 140, 2780–2793. [Google Scholar] [CrossRef]
- Meijers, P.; Tsouvalas, A.; Metrikine, A. The effect of stress wave dispersion on the drivability analysis of Large-Diameter monopiles. Procedia Eng. 2017, 199, 2390–2395. [Google Scholar] [CrossRef]
- Paliwal, D.; Pandey, R.K.; Nath, T. Free vibrations of circular cylindrical shell on Winkler and Pasternak foundations. Int. J. Press. Vessel. Pip. 1996, 69, 79–89. [Google Scholar] [CrossRef]
- De Nicola, A.; Randolph, M.F. Tensile and compressive shaft capacity of piles in sand. J. Geotech. Eng. 1993, 119, 1952–1973. [Google Scholar] [CrossRef]
- Deeks, A.J.; Randolph, M.F. Axisymmetric time-domain transmitting boundaries. J. Eng. Mech. 1994, 120, 25–42. [Google Scholar] [CrossRef]
- Liyanapathirana, D.; Deeks, A.; Randolph, M. Numerical analysis of soil plug behaviour inside open-ended piles during driving. Int. J. Numer. Anal. Methods Geomech. 1998, 22, 303–322. [Google Scholar] [CrossRef]
- Deeks, A.; Randolph, M. Analytical modelling of hammer impact for pile driving. Int. J. Numer. Anal. Methods Geomech. 1993, 17, 279–302. [Google Scholar] [CrossRef]
- Egorov, K. Calculation of bed for foundation with ring footing. In Proceedings of the 6th International Conference of Soil Mechanics and Foundation Engineering, Montreal, QC, Canada, 8–15 September 1965; Volume 2, pp. 41–45. [Google Scholar]
- Poulos, H.G.; Davis, E.H. Pile Foundation Analysis and Design; Number Monograph; Wiley: Hoboken, NJ, USA, 1980. [Google Scholar]
- Kumar, J.; Chakraborty, M. Bearing capacity factors for ring foundations. J. Geotech. Geoenviron. Eng. 2015, 141, 06015007. [Google Scholar] [CrossRef]
- Leissa, A.W. Vibration of Shells; Scientific and Technical Information Office, National Aeronautics and Space Administration: Hampton, VA, USA, 1973; Volume 288. [Google Scholar]
- Tsouvalas, A.; Metrikine, A. A semi-analytical model for the prediction of underwater noise from offshore pile driving. J. Sound Vib. 2013, 332, 3232–3257. [Google Scholar] [CrossRef]
- Graff, K. Wave Motion in Elastic Solids; Oxford University Press: Oxford, UK, 1975. [Google Scholar]
- Greenspon, J.E. Vibrations of a Thick-Walled Cylindrical Shell—Comparison of the Exact Theory with Approximate Theories. J. Acoust. Soc. Am. 1960, 32, 571–578. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Reismann, H.; Padlog, J. Forced, axisymmetric motions of cylindrical shells. J. Frankl. Inst. 1967, 284, 308–319. [Google Scholar] [CrossRef]
- Buckley, R.; Kontoe, S.; Jardine, R.; Maron, M.; Schroeder, F.; Barbosa, P. Common pitfalls of pile driving resistance analysis—A case study of the wikinger offshore windfarm. In Offshore Site Investigation Geotechnics, Proceedings of the 8th International Conference, London, UK, 12–14 September 2017; Society for Underwater Technology: London, UK, 2017; Volume 1246, pp. 1246–1253. [Google Scholar]
- Friswell, M.I.; Adhikari, S.; Lei, Y. Vibration analysis of beams with non-local foundations using the finite element method. Int. J. Numer. Methods Eng. 2007, 71, 1365–1386. [Google Scholar] [CrossRef]
- Versteijlen, W.; de Oliveira Barbosa, J.; van Dalen, K.; Metrikine, A. Dynamic soil stiffness for foundation piles: Capturing 3D continuum effects in an effective, non-local 1D model. Int. J. Solids Struct. 2018, 134, 272–282. [Google Scholar] [CrossRef]
- Lei, Y.; Friswell, M.I.; Adhikari, S. A Galerkin method for distributed systems with non-local damping. Int. J. Solids Struct. 2006, 43, 3381–3400. [Google Scholar] [CrossRef]
- Ames, W.F. Numerical Methods for Partial Differential Equations; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Fletcher, C.A. Computational Galerkin Methods; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Lowe, R.L.; Yu, S.T.J.; Yang, L.; Bechtel, S.E. Modal and characteristics-based approaches for modeling elastic waves induced by time-dependent boundary conditions. J. Sound Vib. 2014, 333, 873–886. [Google Scholar] [CrossRef]
- Dormand, J.R.; Prince, P.J. A family of embedded Runge-Kutta formulae. J. Comput. Appl. Math. 1980, 6, 19–26. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures; Prentice Hall: Upper Saddle River, NJ, USA, 2014. [Google Scholar]







| Pile | Young’s modulus | 210 GPa | |
| Mass density | 7850 kg/m | ||
| Poisson’s ratio | 0.3 | ||
| Length | 42 m | ||
| Radius | 1.1 m | ||
| Wall thickness | 0.03 m | ||
| Initial embedment depth | 25.2 m | ||
| Soil | Shear modulus | 18.52 MPa | |
| Mass density | 1900 kg/m | ||
| Poisson’s ratio | 0.35 | ||
| Friction angle | 35 | ||
| Soil-pile interface friction angle | 31.5 | ||
| Hammer | Ram mass | 10,000 kg | |
| Anvil mass | 1000 kg | ||
| Cushion stiffness | 70.87 × kN/m | ||
| Ram impact velocity | 5 m/s |
| 1.1 m | 1.4 m | 1.7 m | 2.0 m | 2.3 m | 2.6 m | 2.9 m | 3.2 m | 3.5 m | 3.8 m | 4.1 m | |
| 0.03 m | 0.03 m | 0.03 m | 0.04 m | 0.04 m | 0.04 m | 0.04 m | 0.05 m | 0.05 m | 0.05 m | 0.05 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsetas, A.; Tsouvalas, A.; Metrikine, A.V. Installation of Large-Diameter Monopiles: Introducing Wave Dispersion and Non-Local Soil Reaction. J. Mar. Sci. Eng. 2021, 9, 313. https://doi.org/10.3390/jmse9030313
Tsetas A, Tsouvalas A, Metrikine AV. Installation of Large-Diameter Monopiles: Introducing Wave Dispersion and Non-Local Soil Reaction. Journal of Marine Science and Engineering. 2021; 9(3):313. https://doi.org/10.3390/jmse9030313
Chicago/Turabian StyleTsetas, Athanasios, Apostolos Tsouvalas, and Andrei V. Metrikine. 2021. "Installation of Large-Diameter Monopiles: Introducing Wave Dispersion and Non-Local Soil Reaction" Journal of Marine Science and Engineering 9, no. 3: 313. https://doi.org/10.3390/jmse9030313
APA StyleTsetas, A., Tsouvalas, A., & Metrikine, A. V. (2021). Installation of Large-Diameter Monopiles: Introducing Wave Dispersion and Non-Local Soil Reaction. Journal of Marine Science and Engineering, 9(3), 313. https://doi.org/10.3390/jmse9030313







