Wave Propagation Studies in Numerical Wave Tanks with Weakly Compressible Smoothed Particle Hydrodynamics
Abstract
1. Introduction
2. Smoothed Particle Hydrodynamics Formulation
2.1. WCSPH Numerical Model
2.2. Numerical Dissipation Chemes
2.2.1. Artificial Viscosity
2.2.2. Density Reinitialization
2.2.3. δ-SPH Scheme
2.3. The Smoothing Kernel Functions
2.4. Boundary Handling
3. Validation Studies
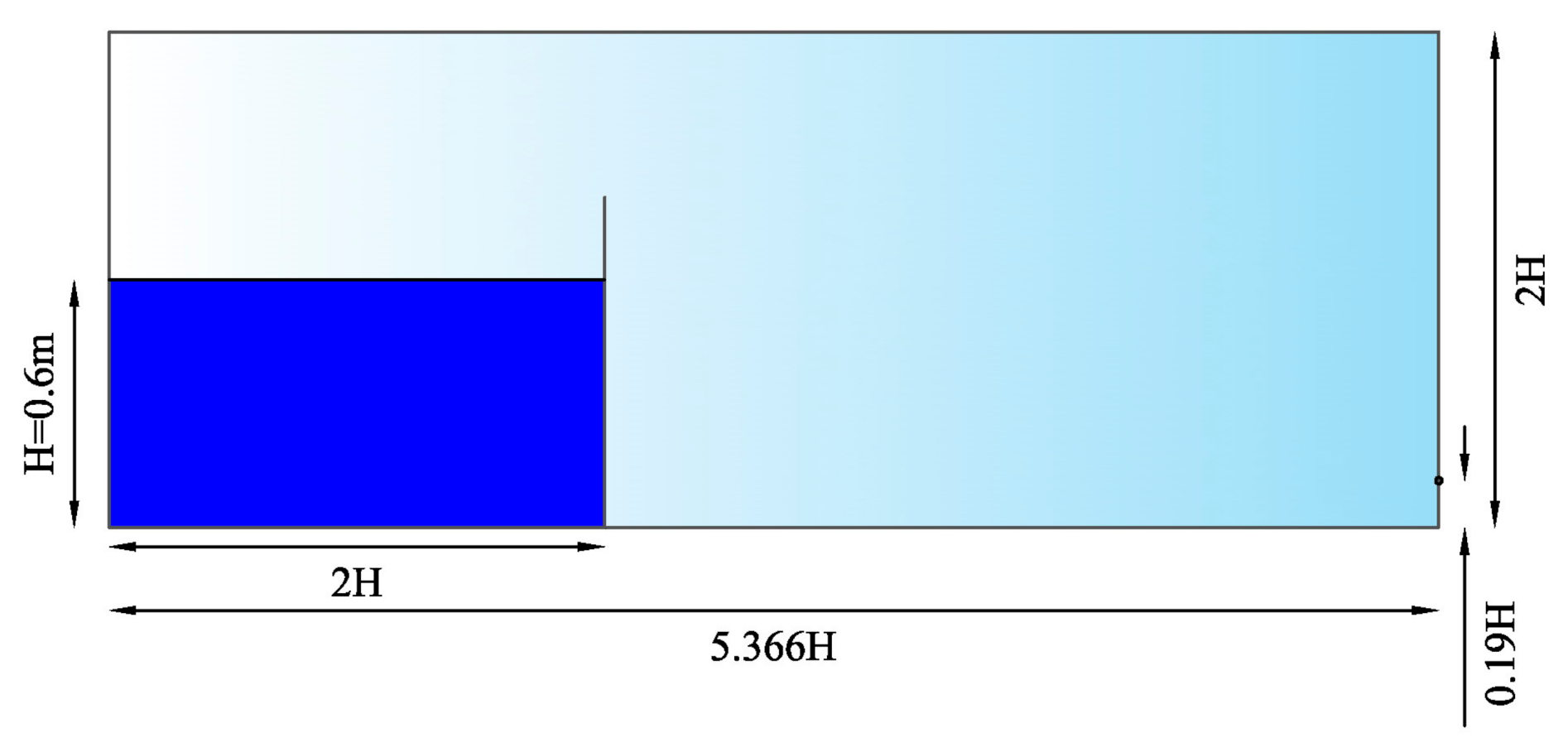
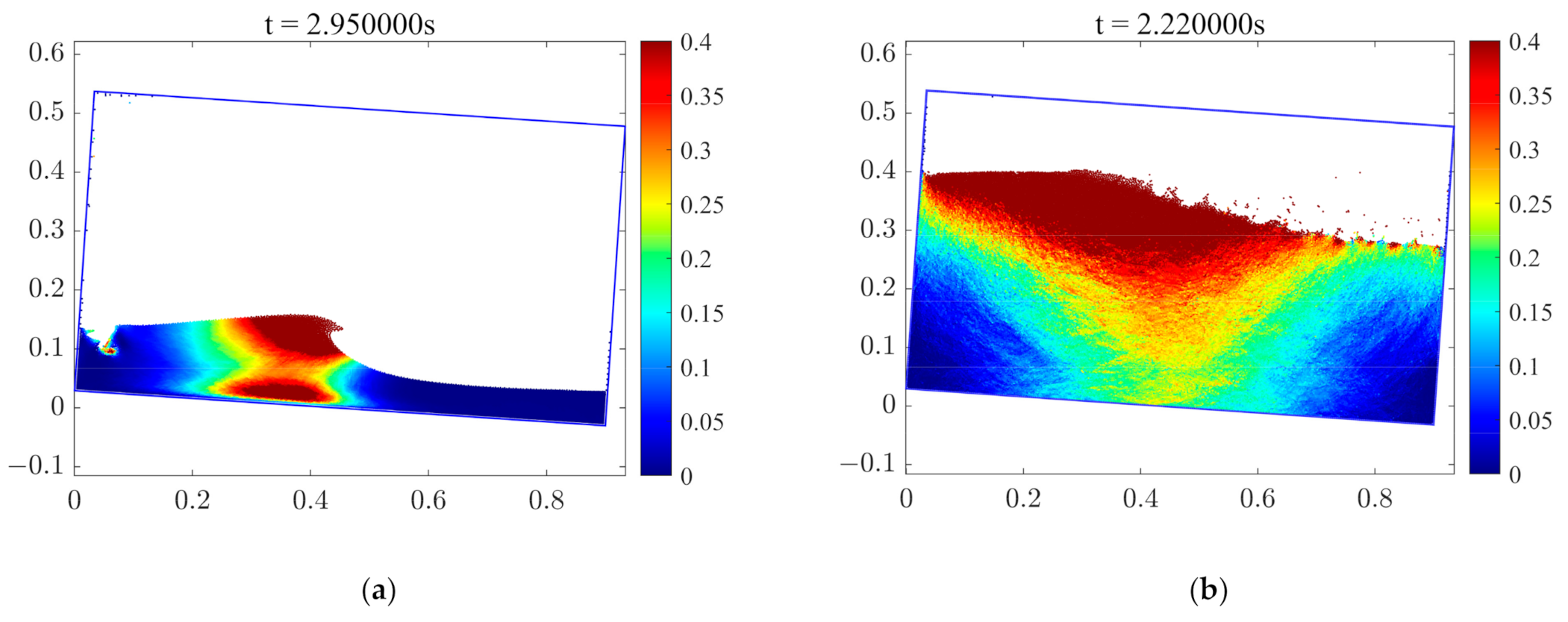
3.1. Dam-Break Simulations
3.2. Sloshing Simulations
4. Numerical Wave Tank Experiments
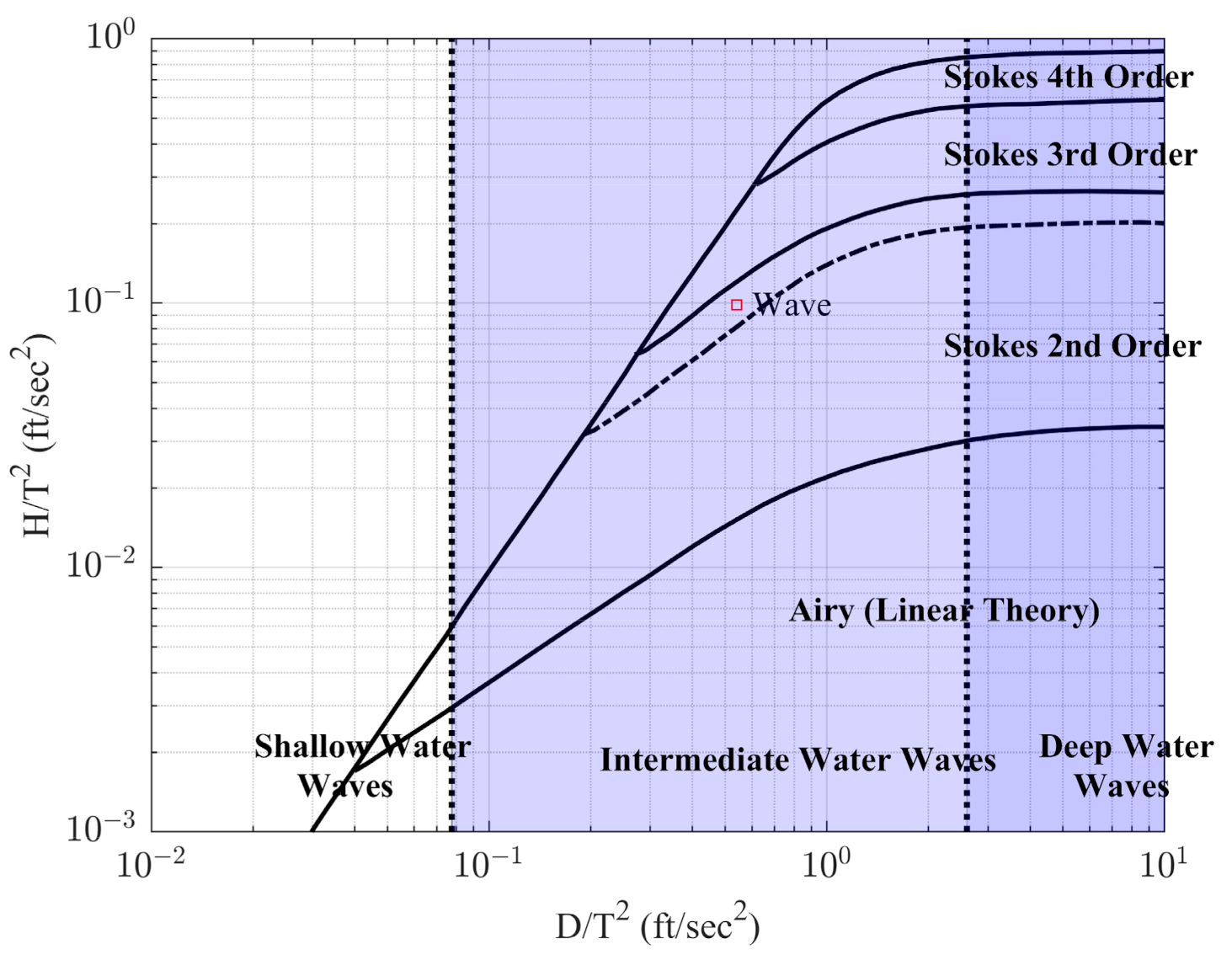
4.1. Wave Generation and Propagation
4.2. Results and Discussion
4.2.1. Hydrostatic Pressure Initialization
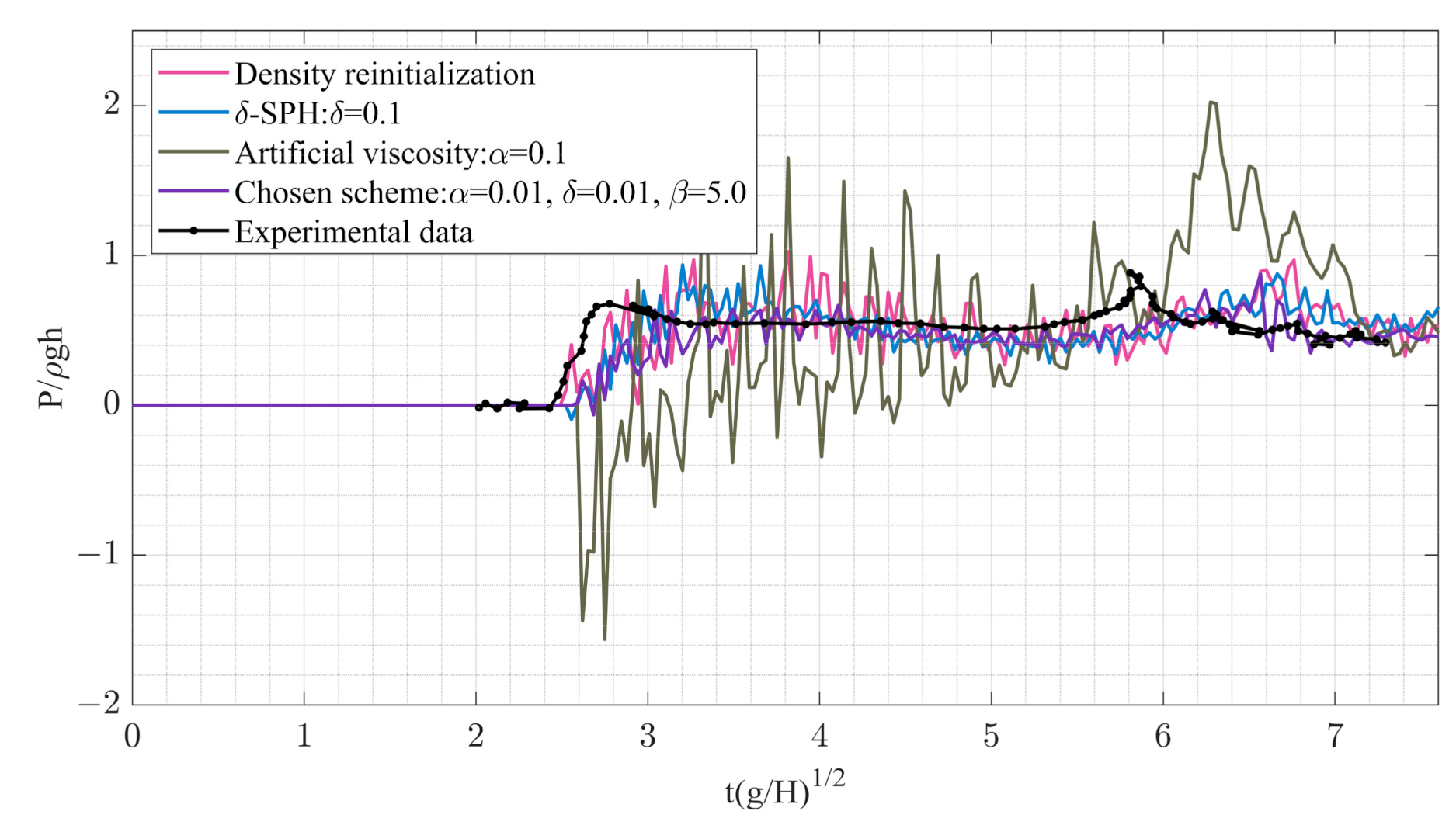
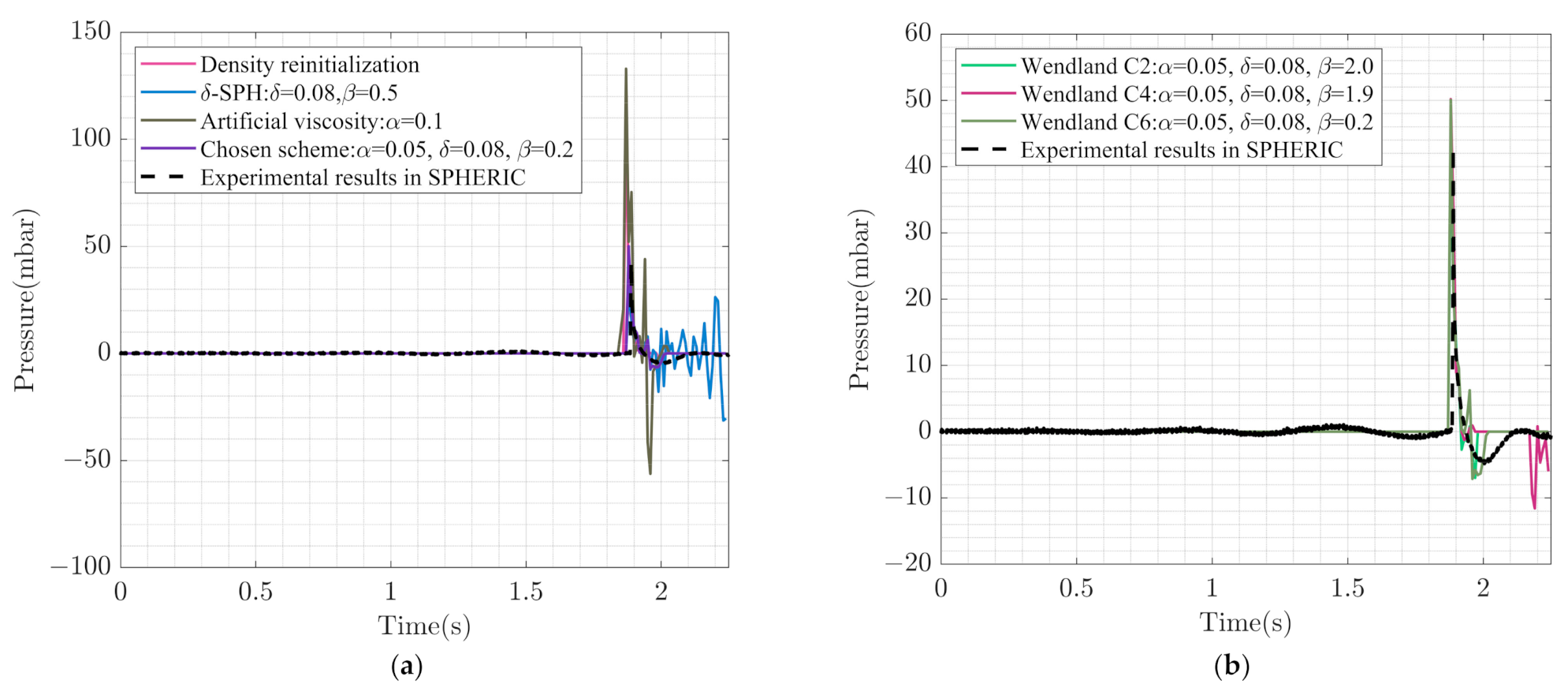
4.2.2. Comparisons with Different Dissipation Schemes
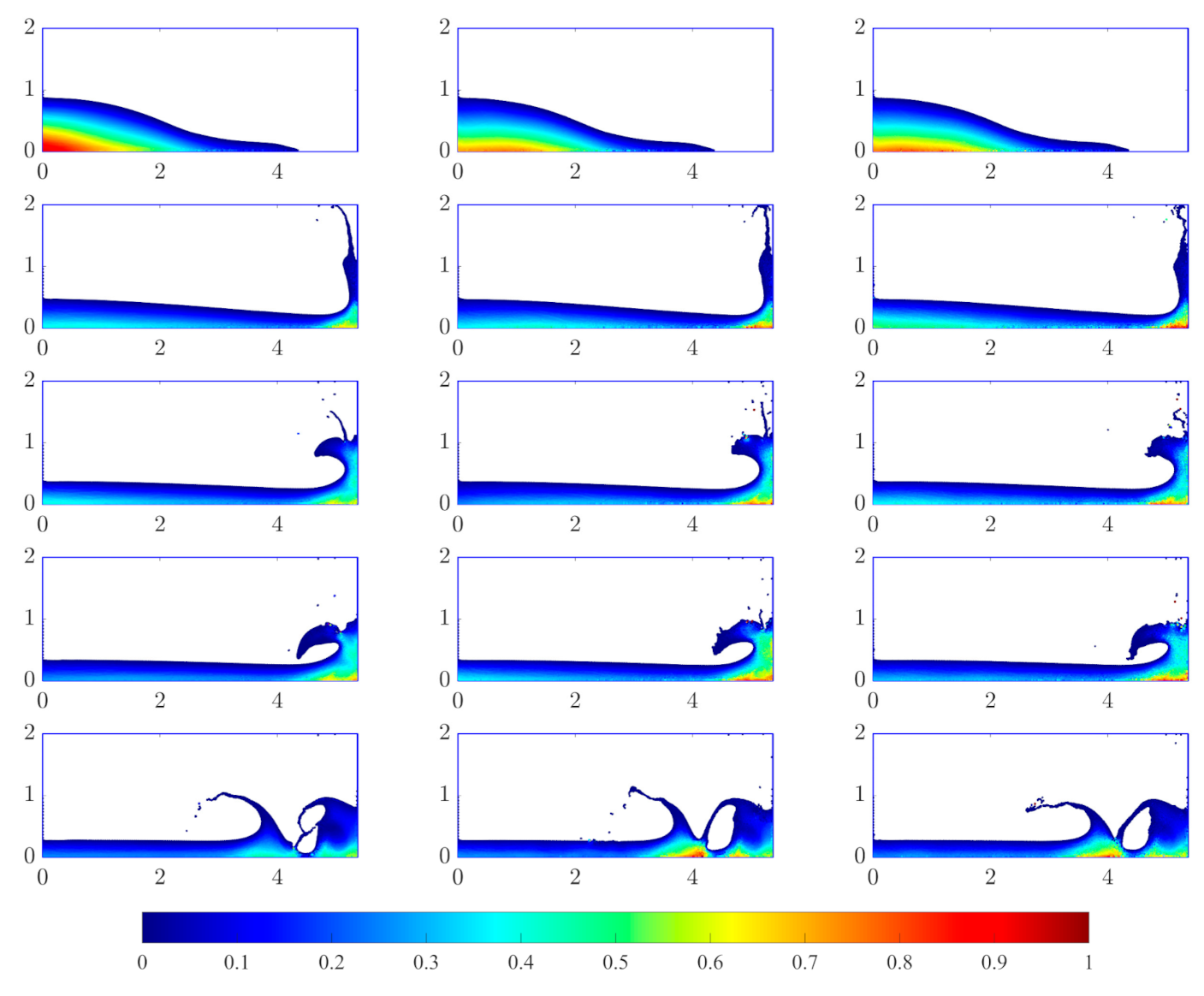
4.2.3. Particle Resolution Study
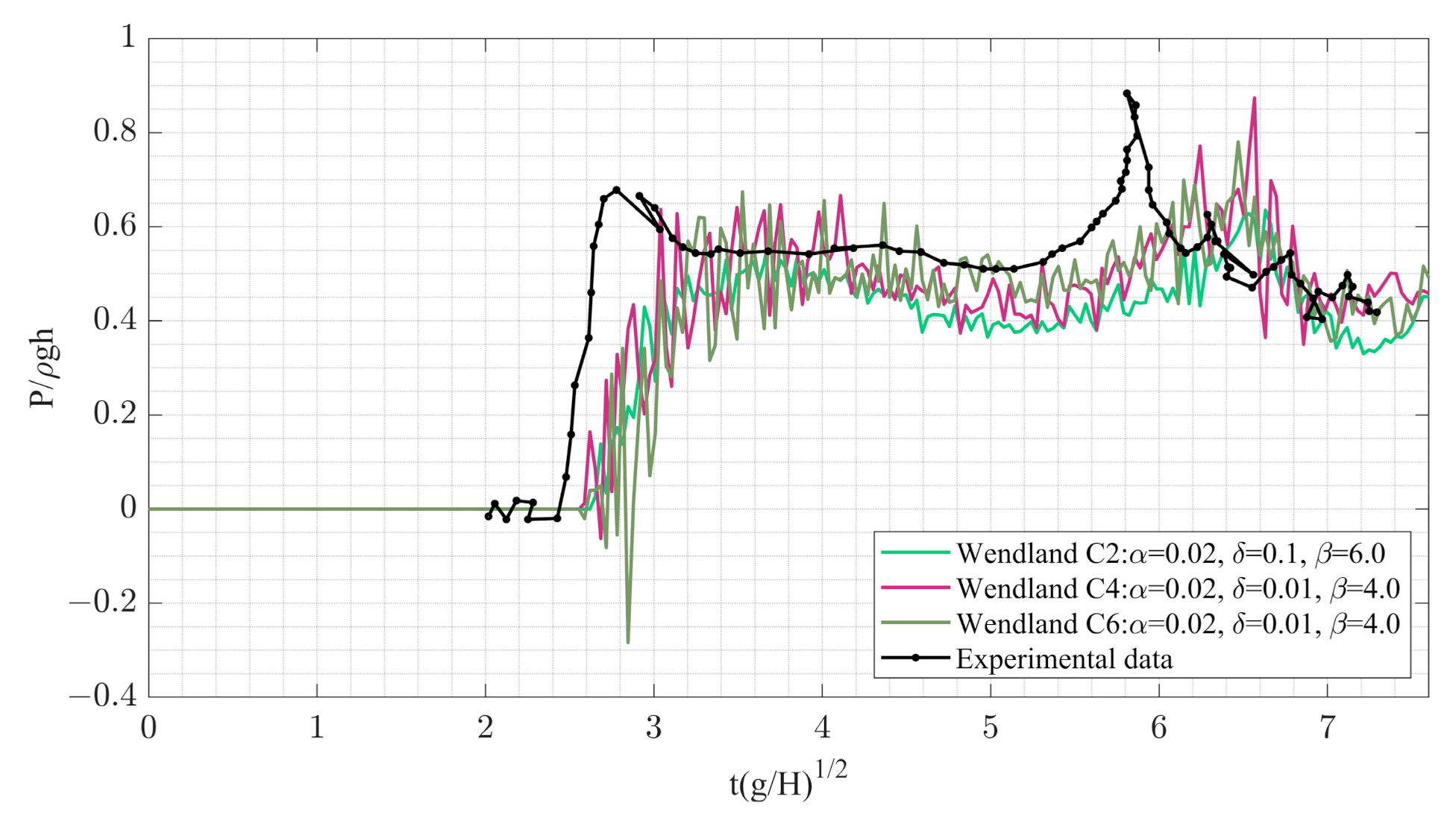
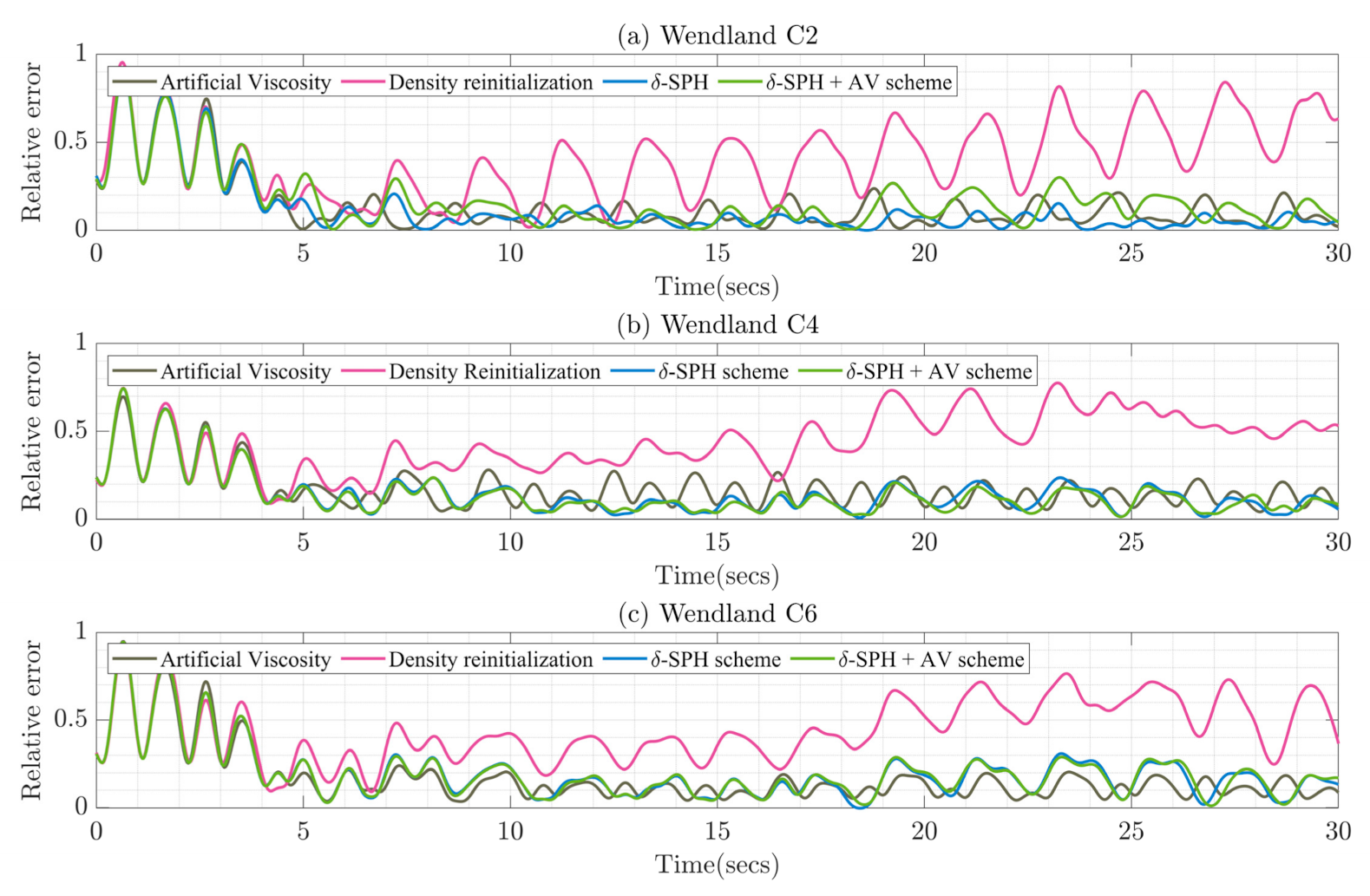
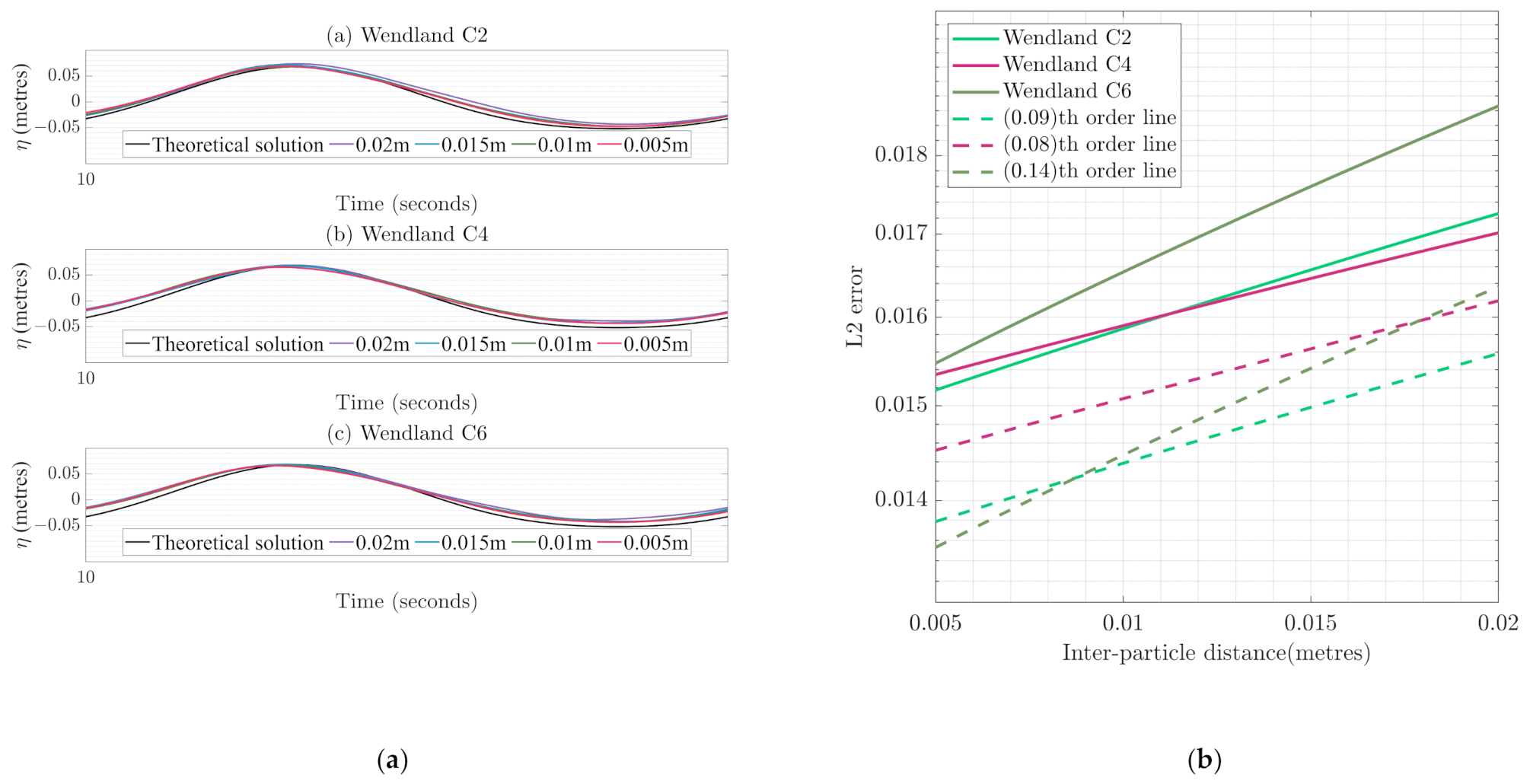
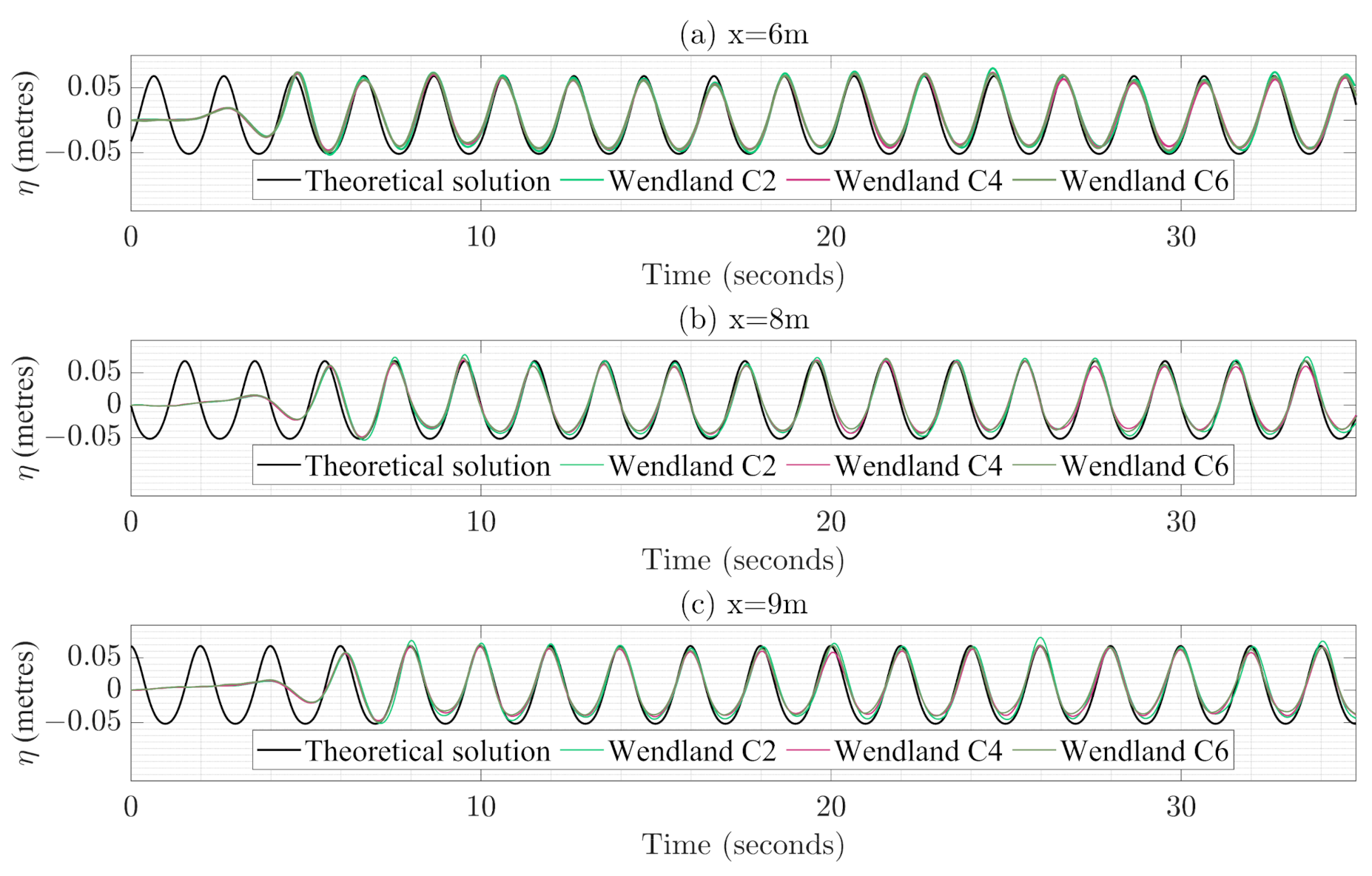
4.2.4. Effect of Kernels on Numerical Dissipation
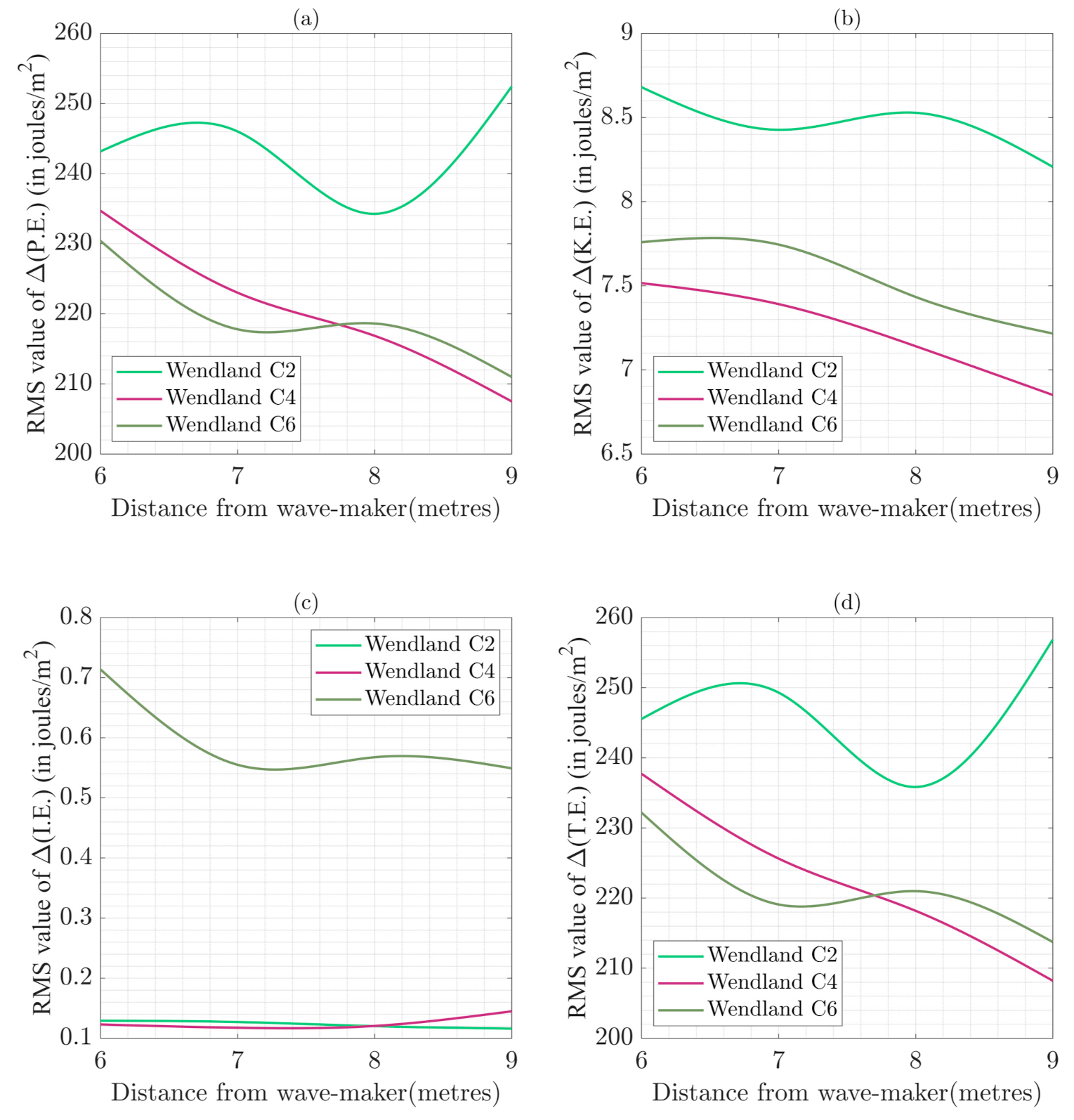
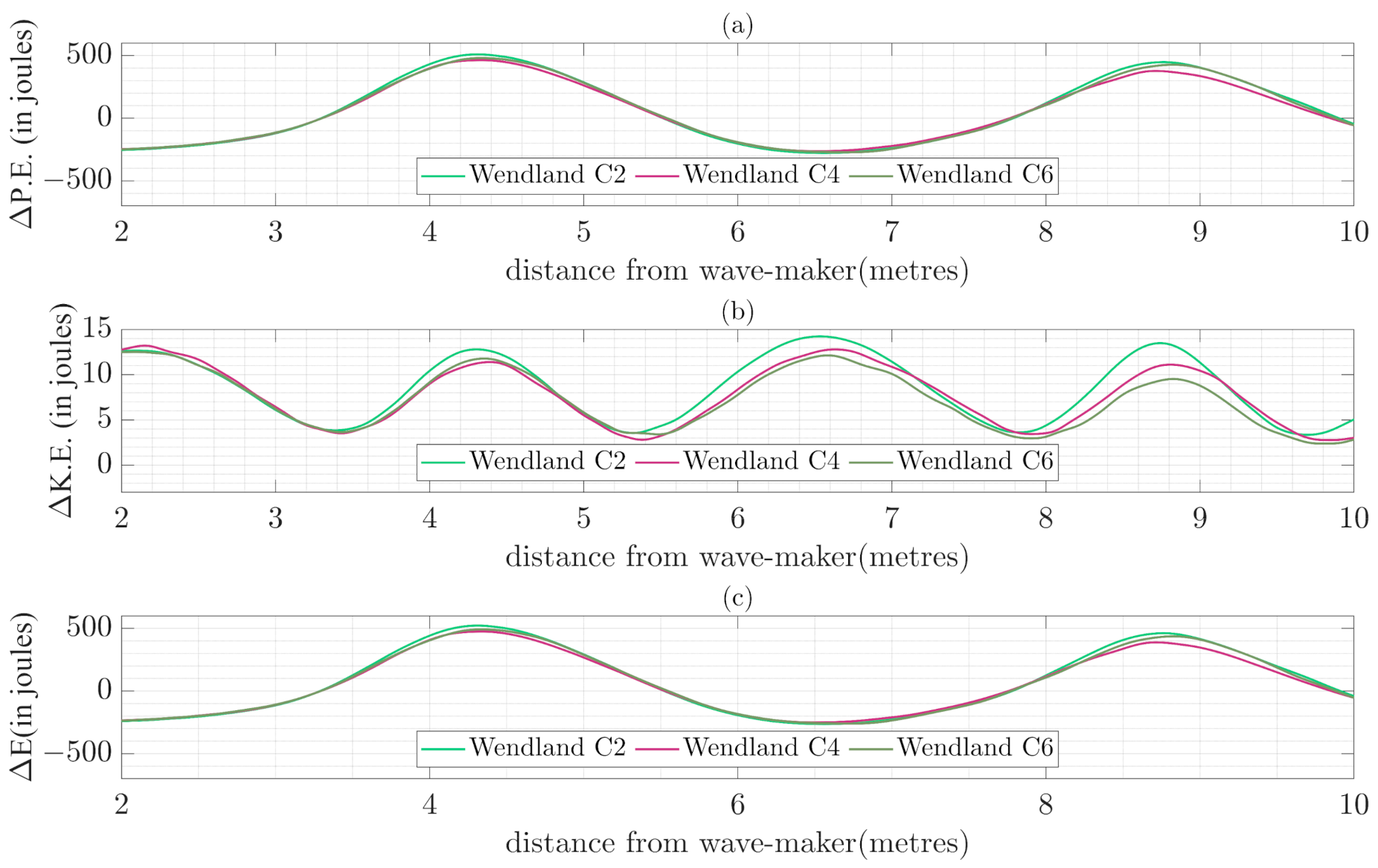
5. Variation of Parameters in WCSPH Simulations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lucy, L.B. A Numerical Approach to the Testing of the Fission Hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed Particle Hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 110, 543–574. [Google Scholar] [CrossRef]
- Higuera, P.; Lara, J.L.; Losada, I.J. Realistic Wave Generation and Active Wave Absorption for Navier-Stokes models. Application to OpenFOAM®. Coast. Eng. 2013, 71, 102–118. [Google Scholar] [CrossRef]
- Liu, P.L.-F.; Lin, P.; Chang, K.-A.; Sakakiyama, T. Numerical Modelling of Wave Interaction with Porous Structures. J. Waterw. Port. Coast. Ocean. Eng. 1999, 125, 322–330. [Google Scholar] [CrossRef]
- Colagrossi, A.; Antuono, M.; Le Touze, D. Theoretical Considerations on the Free Surface Role in the Smoothed-Particle-Hydrodynamics Model. Phys. Rev. E 2009, 79, 056701. [Google Scholar] [CrossRef]
- Chabalko, C.; Balachandran, B. GPU based simulation of physical system characterized by mobile discrete interactions. In Developments in Parallel, Distributed, Grid and Cloud Computing for Engineering; Topping, B.H.V., Ivanyi, P., Eds.; Saxe-Cobrug Publications: Stirlingshire, UK, 2013; pp. 95–124. [Google Scholar]
- Liu, M.B.; Liu, G.R.; Lam, K.Y. Constructing smoothing functions in smoothed particle hydrodynamics with applications. J. Comput. Appl. Math. 2003, 155, 263–284. [Google Scholar] [CrossRef]
- Yang, X.F.; Peng, S.L.; Liu, M.B. A new kernel function for SPH with applications to free surface flows. Appl. Math. Model. 2014, 38, 3822–3833. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Lattanzio, J.C. A refined particle method for astrophysical problems. Astron. Astrophys. 1985, 149, 135–143. [Google Scholar]
- Wendland, H. Piecewise Polynomial, Positive Definite and Compactly Supported Radial Functions of Minimal Degree. Adv. Comput. Math. 1995, 4, 389–396. [Google Scholar] [CrossRef]
- Dehnen, W.; Aly, H. Improving convergence in smoothed particle hydrodynamics simulations without pairing instability. Mon. Not. R. Astron. Soc. 2012, 425, 1068–1082. [Google Scholar] [CrossRef]
- Amicarelli, A.; Marongiu, J.-C.; Leboeuf, F.; Leduc, J.; Caro, J. SPH truncation error in estimating a 3D function. Comput. Fluids 2011, 44, 279–296. [Google Scholar] [CrossRef]
- Jiang, Y.; Fang, L.; Jing, X.; Sun, X.; Leboeuf, F. A second-order numerical method for elliptic equations with singular sources using local filter. Chin. J. Aeronaut. 2013, 26, 1398–1408. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics and its diverse applications. Annu. Rev. Fluid Mech. 2012, 44, 323–346. [Google Scholar] [CrossRef]
- Colagrossi, A.; Landrini, M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics. J. Comput. Phys. 2003, 191, 448–475. [Google Scholar] [CrossRef]
- Ferrari, A.; Dumbser, M.; Toro, E.F.; Armanini, A. A new 3D parallel SPH scheme for free surface flows. Comput. Fluids 2009, 38, 1203–1217. [Google Scholar] [CrossRef]
- Molteni, D.; Colagrossi, A. A simple procedure to improve the pressure evaluation in hydrodynamic context using the SPH. Comput. Phys. Commun. 2009, 180, 861–872. [Google Scholar] [CrossRef]
- Antuono, M.; Colagrossi, A.; Marrone, S.; Molteni, D. Free-surface flows solved by means of SPH schemes with numerical diffusive terms. Comput. Phys. Commun. 2010, 181, 532–549. [Google Scholar] [CrossRef]
- Morris, J.P.; Fox, P.J.; Zhu, Y. Modelling low Reynolds number incompressible flows using SPH. J. Comput. Phys. 1997, 136, 214–226. [Google Scholar] [CrossRef]
- Krimi, A.; Ramirez, L.; Khelladi, S.; Navarrina, F.; Deligant, M.; Nogueira, X. Improved δ-SPH Scheme with Automatic and Adaptive Numerical Dissipation. Water 2020, 12, 2858. [Google Scholar] [CrossRef]
- Biesel, F.; Suquet, F. Les Appareils Générateurs De Houle En Laboratoire-Laboratory Wave Generating Apparatus. La Houille Blanche 1951, 6, 147–165. [Google Scholar] [CrossRef]
- Ursell, Y.S.; Dean, F.; Yu, R.G. Forced small-amplitude water waves: A comparison of theory and experiment. J. Fluid Mech. 1960, 7, 3–52. [Google Scholar] [CrossRef]
- Schäffer, H.A. Second-order wavemaker theory for irregular waves. Ocean Eng. 1996, 23, 47–88. [Google Scholar] [CrossRef]
- Gōda, Y. Travelling Secondary Wave Crests in Wave Channels. Port Harb. Res. Inst. Minist. Transp. Jpn. 1967, 13, 32–38. [Google Scholar]
- Madsen, O.S. On the generation of long waves. J. Geophys. Res. 1971, 76, 8672–8683. [Google Scholar] [CrossRef]
- Altomare, C.; Domínguez, J.M.; Crespo, A.J.C.; González-Cao, J.; Suzuki, T.; Gómez-Gesteira, M.; Troch, P. Long-crested wave generation and absorption for SPH-based DualSPHysics model. Coast. Eng. 2017, 12, 37–54. [Google Scholar] [CrossRef]
- Trimulyono, A.; Hashimoto, H. Experimental Validation of Smoothed Particle Hydrodynamics on Generation and Propagation of Water Waves. J. Mar. Sci. Eng. 2019, 7, 17. [Google Scholar] [CrossRef]
- Crespo, A.J.C.; Domínguez, J.M.; Rogers, B.D.; Gómez-Gesteira, M.; Longshaw, S.; Canelas, R.; Vacondio, R.; Barreiro, A.; García-Feal, O. DualSPHysics: Open-source parallel CFD solver based on Smoothed Particle Hydrodynamics (SPH). Comput. Phys. Commun. 2015, 187, 204–216. [Google Scholar] [CrossRef]
- Hansom, J.D.; Switzer, A.D.; Pile, J. Extreme Waves: Causes, Characteristics, and Impact on Coastal Environments and Society In Coastal and Marine Hazards, Risks, and Disasters; Shroder, J.F., Ellis, J.T., Sherman, D.J., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 307–334. ISBN 9780123964830. [Google Scholar] [CrossRef]
- Manolidis, M.; Orzech, M.; Simeonov, J. Rogue Wave Formation in Adverse Ocean Current Gradients. J. Mar. Sci. Eng. 2019, 7, 26. [Google Scholar] [CrossRef]
- Slunyaev, A.; Kokorina, A. Numerical Simulation of the Sea Surface Rogue Waves within the Framework of the Potential Euler Equations. Izv. Atmos. Ocean. Phys. 2020, 56, 179–190. [Google Scholar] [CrossRef]
- Ducrozet, G.; Bonnefoy, F.; Ferrant, P. On the equivalence of unidirectional rogue waves detected in periodic simulations and reproduced in numerical wave tanks. Ocean Eng. 2016, 117, 346–358. [Google Scholar] [CrossRef]
- Moitra, A.; Chabalko, C.; Balachandran, B. Studies of Extreme Energy Localizations with Smoothed Particle Hydrodynamics. In Proceedings of the ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering, St. John’s, NL, Canada, 31 May–5 June 2015. [Google Scholar] [CrossRef]
- Chabalko, C.; Moitra, A.; Balachandran, B. Rogue Waves: New Forms Enabled by GPU Computing. Phys. Lett. A 2014, 378, 2377–2381. [Google Scholar]
- Moitra, A.; Chabalko, C.; Balachandran, B. Extreme Wave Solutions: Parametric Studies and Wavelet Analysis. Int. J. Non-Linear Mech. 2016, 83, 39–47. [Google Scholar]
- Wang, R.; Balachandran, B. Extreme Wave Formation in Unidirectional Sea Due to Stochastic Wave Phase Dynamics. Phys. Lett. A 2018, 382, 1864–1972. [Google Scholar]
- Shao, S.; Edmond, Y.M.L. Incompressible SPH method for simulating Newtonian and non-Newtonian flows with a free surface. Adv. Water Res. 2003, 26, 787–800. [Google Scholar] [CrossRef]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2000; ISBN 0521663962. [Google Scholar]
- Shephard, D. A Two- dimensional interpolation function for irregularly-spaced data. In Proceedings of the 23rd ACM National Conference, New York, NY, USA, 27–29 August 1968; pp. 517–524. [Google Scholar]
- Thomas, P.A.; Couchman, H.M.P. Simulating the formation of a cluster of galaxies. Mon. Not. R. Astron. Soc. 1992, 257, 11–31. [Google Scholar] [CrossRef]
- Crespo, A.J.C.; Gomez-Gesteira, M.; Dalrymple, R.A. Boundary conditions generated by dynamic particles in SPH methods. Comput. Mater. Contin. 2007, 5, 173–184. [Google Scholar] [CrossRef]
- Nvidia Corp. CUDA 10.1 Toolkit Documentation. Available online: https://docs.nvidia.com/cuda/archive/10.1/cuda-c-programming-guide/index.html (accessed on 26 November 2020).
- Maryland Advanced Research Computing Center (MARCC). Available online: https://www.marcc.jhu.edu/ (accessed on 26 November 2020).
- Delorme, L.; Colagrossi, A.; Souto-Iglesias, A.; Zamora-Rodríguez, R.; Botia-Vera, E. A set of canonical problems in sloshing. Part I: Pressure field in forced roll. Comparison between experimental results and SPH. Ocean Eng. 2009, 36, 168–178. [Google Scholar] [CrossRef]
- Souto-Iglesias, A.; Botia-Vera, E.; Martin, A.; Pérez-Arribas, E. A set of canonical problems in Sloshing. Part 0: Experimental setup and data processing. Ocean Eng. 2011, 38, 1823–1830. [Google Scholar] [CrossRef]
- Souto-Iglesias, A.; Botia-Vera, E.; Bulian, G. Repeatability and Two-Dimensionality of model scale sloshing impacts. In Proceedings of the 22nd International Offshore and Polar Engineering Conference, Rhodes, Greece, 17–22 June 2012. [Google Scholar]
- Botia-Vera, E.; Souto-Iglesias, A.; Bulian, G.; Lobovský, L. Three SPH Novel Benchmark Test Cases for free surface flows. In Proceedings of the 5th ERCOFTAC SPHERIC Workshop on SPH Applications, Manchester, UK, 23–25 June 2010. [Google Scholar]
- Adami, S.; Hu, X.Y.; Adams, N.A. A generalized wall boundary condition for smoothed particle hydrodynamics. J. Comput. Phys. 2012, 231, 7057–7075. [Google Scholar] [CrossRef]
- Buchner, B. Green Water on Ship-Type Offshore Structures. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2002. [Google Scholar]
- Green, M.D. Sloshing simulations with the smoothed particle hydrodynamics (SPH) method. Doctoral thesis. Imp. Coll. Lond. 2016. [Google Scholar] [CrossRef]
- Hughes, S.A. Laboratory wave reflection analysis using co-located gauges. Coast. Eng. 1993, 20, 223–247. [Google Scholar] [CrossRef]
- Byford, B. Non-Linear Wave Solver Function. MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcen-tral/fileexchange/67106-non-linear-wave-solver-function (accessed on 21 November 2020).
- Stokes, G.G. On the theory of oscillatory waves. Trans. Cambridge Philos. Soc. 1847, 8, 441. [Google Scholar]








| H/100 | |
|---|---|
| Boundary particle spacing | 0.6 |
| Smoothing length | 1.5 |
| 1000 | |
| Artificial viscosity coefficient | |
| used in momentum equation | |
| —SPH coefficient | |
| used in Morris viscosity factor | 8.97 × 10−7 |
| W/450 | |
|---|---|
| Boundary particle spacing | 0.6 |
| Smoothing length | 1.5 |
| 998 | |
| Artificial viscosity coefficient | |
| used in the momentum equation | |
| —SPH coefficient | |
| used in Morris viscosity factor | 8.97 × 10−7 |
| Height H | 0.12 m |
| Depth d | 0.66 m |
| Wavelength L | 4.52 m |
| Time Period T | 2 s |
| Initial phase δ | 0 |
| Steepness s | 0.026 |
| Relative depth | 0.146 |
| Boundary particle spacing | |
| Smoothing length | |
| 1000 | |
| Artificial viscosity coefficient | |
| used in momentum equation | |
| —SPH coefficient | |
| used in Morris viscosity factor | 8.97 × 10−7 |
| Time step (Fixed time integration) |
| Wendland C2 errors | {0.0176, 0.0162, 0.0156, 0.0155} |
| Wendland C4 errors | {0.0177, 0.0155, 0.0160, 0.0156} |
| Wendland C6 errors | {0.0195, 0.0165, 0.0164, 0.0159} |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chakraborty, S.; Balachandran, B. Wave Propagation Studies in Numerical Wave Tanks with Weakly Compressible Smoothed Particle Hydrodynamics. J. Mar. Sci. Eng. 2021, 9, 233. https://doi.org/10.3390/jmse9020233
Chakraborty S, Balachandran B. Wave Propagation Studies in Numerical Wave Tanks with Weakly Compressible Smoothed Particle Hydrodynamics. Journal of Marine Science and Engineering. 2021; 9(2):233. https://doi.org/10.3390/jmse9020233
Chicago/Turabian StyleChakraborty, Samarpan, and Balakumar Balachandran. 2021. "Wave Propagation Studies in Numerical Wave Tanks with Weakly Compressible Smoothed Particle Hydrodynamics" Journal of Marine Science and Engineering 9, no. 2: 233. https://doi.org/10.3390/jmse9020233
APA StyleChakraborty, S., & Balachandran, B. (2021). Wave Propagation Studies in Numerical Wave Tanks with Weakly Compressible Smoothed Particle Hydrodynamics. Journal of Marine Science and Engineering, 9(2), 233. https://doi.org/10.3390/jmse9020233






