1. Introduction
Oil spills may occur from regulated activities associated with offshore oil and gas exploration, production, decommissioning, and transportation. Prior to conducting an oil and gas lease sale, the Bureau of Ocean Energy Management (BOEM), the US Department of the Interior, conducts oil spill risk analysis (OSRA) to support National Environmental Policy Act (NEPA) analysis.
A large number of numerical models have been developed for simulating the processes associated with oil spills and analyzing oil spill risks. These models help decision makers answer many planning questions, such as which areas are more likely to be hit by spilled oil and how long it would take for spilled oil to reach a specific location. Several models have and are being used to estimate the trajectories of spilled oil. Smith et al. [
1] developed an oil spill risk analysis model to estimate the environmental hazards associated with oil resources. Reed et al. [
2] built the Oil Spill Contingency and Response (OSCAR) model for analyzing alternative spill response strategies. The National Oceanic and Atmospheric Administration (NOAA) developed tools to analyze statistics from potential spill trajectories [
3,
4]. Spill Impact MAPping model system (SIMAP) calculates the three-dimensional trajectory, fate, biological effects, and other impacts of spilled oil and fuels [
5,
6,
7]. The oil spill model code MEDSLIK-II is used to predict the transport and weathering of oil spills (e.g., [
8,
9,
10,
11]). Hole et al. [
12] studied the effect of river fronts on oil slick transport using high-resolution forcing models and an oil drift model. Their results compared well with satellite observations of the surface oil patches. A key component of these models is the use of a trajectory model to simulate oil spill trajectories under different environmental conditions and provide risk assessments in probabilistic terms. There have been several review papers summarizing the extensive literature on oil spill modeling, including [
13,
14,
15,
16,
17].
The US Department of the Interior has been developing and improving the OSRA model since the 1970s (e.g., [
18,
19]). The model is used to assess the potential spill risks associated with offshore oil and gas development. The OSRA model was designed for evaluating the likelihood of potential oil spill contact to the environmental resources based on different leasing and transportation scenarios before conducting lease sales [
1]. Compared with other oil spill models, the unique features of the OSRA model include the following: (1) its spatial scale is typically very large, up to thousands of kilometers (km), such as the entire Gulf of Mexico (GOM), and (2) its timescale is also very large, up to several decades. To provide external forcing and transport information for the OSRA model, BOEM (and its predecessors) has spent enormous efforts on physical oceanography and numerical modeling in the past decades (e.g., [
20,
21,
22,
23]), which are critical for the accuracy of the OSRA model results. There are no other oil spill models that are routinely applied on such large spatial and temporal scales with such detailed oceanographic information.
The occurrence of oil spills is fundamentally a matter of probability, which is affected by a variety of uncertain factors in the future. These factors include the oil volume that may be discovered and then produced, the chance that oil spills would occur from that volume, and the wind, ocean current, and sea ice that transport spilled oil. The OSRA model estimates the probability of spilled oil from hypothetical sources (such as wells, platforms, or tanker routes) contacting environmental resources (such as protected areas, tourist locations, or coastal ecosystems).
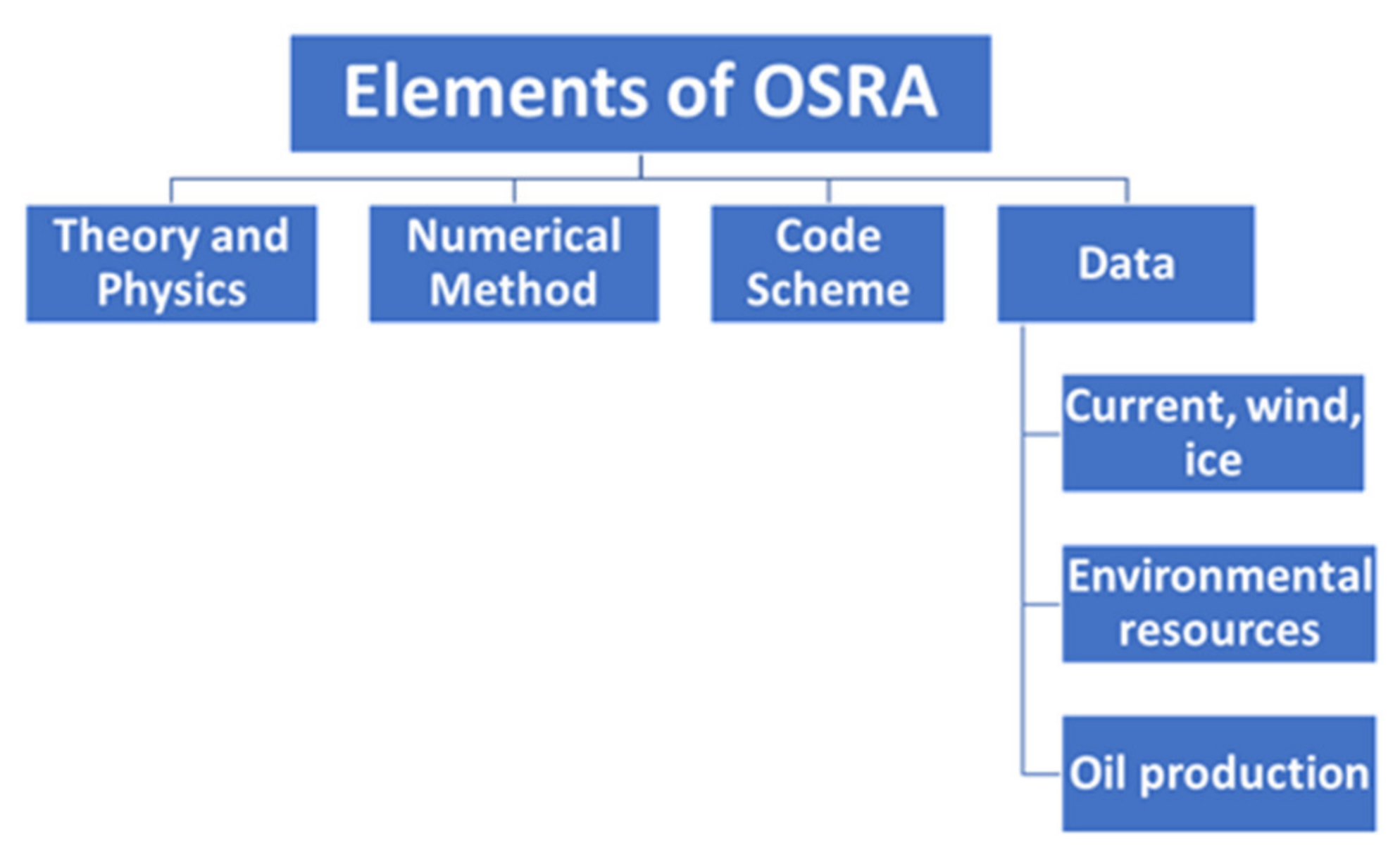
The OSRA model consists of four key elements (
Figure 1):
- (1)
Theory and physics associated with oil spill: This element has been constantly improved over the years.
Section 2,
Section 3 and
Section 4 of this paper present some of the recent improvements.
- (2)
Numerical methods employed in the model: Multiple numerical methods have been implemented to improve the model’s efficiency and accuracy.
- (3)
Code scheme that makes the numerical simulation fast and computationally efficient.
- (4)
Data: Include current, wind, and ice (usually from other models); environmental resources potentially affected by the hypothetical spills; and oil production associated with an individual lease sale or the entire national Outer Continental Shelf (OCS) oil and gas leasing program.
In past decades, BOEM and its predecessor agencies (Bureau of Ocean Energy Management, Regulation, and Enforcement and Minerals Management Service) have invested considerable resources to enhance these key elements (e.g., [
20,
21,
22,
23]). This paper presents some of the progress of the OSRA model and its applications in the past decade:
- (1)
- (2)
A more efficient way to estimate the probability of oil spill contact to environmental resources in the GOM (
Section 3) [
25]
- (3)
Oil weathering calculation in OSRA (
Section 4)
- (4)
Application to the Ixtoc I oil spill (
Section 5)
2. Risk of Catastrophic Oil Spills
2.1. Introduction
The Deepwater Horizon oil spill (DWH) in 2010 in the GOM is the largest accidental marine oil spill in the history of the petroleum industry. After the DWH, the question was, What is the probability that a catastrophic oil spill (with a volume over 1 million barrels (MMbbl)) will occur again? The answer to this question is required for safe and responsible offshore oil and gas development. This study focused on individual spills that occurred in a relatively short period of time (months or less), instead of chronically long-term spills.
Understanding the risks of extreme events is a demanding statistical problem. A common feature of extreme events is that they rarely occur, and few data are available to stochastically describe such events. Therefore, by definition, extreme events do not have sufficient historical data for traditional statistical methods. Extreme value theory (EVT) (e.g., [
26]) assesses the probability of events that are more extreme than any previously observed (or rarely observed in the past). EVT provides methods for the evaluation of rare events, even outside the range of previous observations. EVT is widely used in fields such as finance [
27,
28], earth sciences [
29,
30], traffic prediction [
31], economic damage [
32,
33], and large oil spills [
24,
34].
Catastrophic oil spills are defined in this study as oil spills of over 1 MMbbl in volume. These are very rare events, with high costs for society and the environment. Because catastrophic oil spills are rare, traditional statistical methods cannot be applied, due to the small amount of data. From 1996 to 2010, most of the OCS spills were less than 1 barrel (bbl) [
35]. The DWH volume was more than 8.5 times the volume that had been spilled in the previous 46 years from all OCS oil and gas activities.
This section (
Section 2) describes a study conducted by Ji et al. [
24] to estimate the risk of catastrophic oil spills in OCS areas. The study applied EVT to analyze oil spills in the OCS in the period 1964 through 2012 to determine the likelihood that a similar catastrophic spill could happen again.
2.2. Mathematical Method
An oil spill distribution, in practice, should be considered in two parts:
- (1)
The central part of the distribution includes spills that happen frequently, for which standard statistical models can be used (e.g., [
36,
37]).
- (2)
The extreme end of the oil spill distribution includes very large oil spills. In this case, models based on EVT are required.
Therefore, a combination of models is needed for OSRA. The Poisson distribution has been used in calculating the probability of OCS oil spills [
38]. The statistical distribution of catastrophic events can be analyzed by a generalized extreme value (GEV) distribution. The probabilities of extreme events can be estimated by fitting a model to a set of extreme event data, which consists of the tail of the complete data distribution. Here, a set of the largest annual oil spills (maxima) was used.
The blocks method based on EVT relies on deriving block maxima series as a preliminary step (e.g., [
29]). The GEV family of functions describes the distribution of the block maximum of a set of data, which are a series of independently and identically distributed observations. The cumulative distribution function,
F(
x;
µ,
σ,
γ), of the GEV is given by:
The GEV distribution employs three parameters: (1) the location parameter (
µ) specifying the center of the distribution, (2) the scale parameter (
σ) determining the size of deviations about the location parameter, and (3) the shape parameter (
γ) governing how rapidly the upper tail decays. The R statistical environment [
39,
40] was utilized to estimate these parameters.
2.3. Results
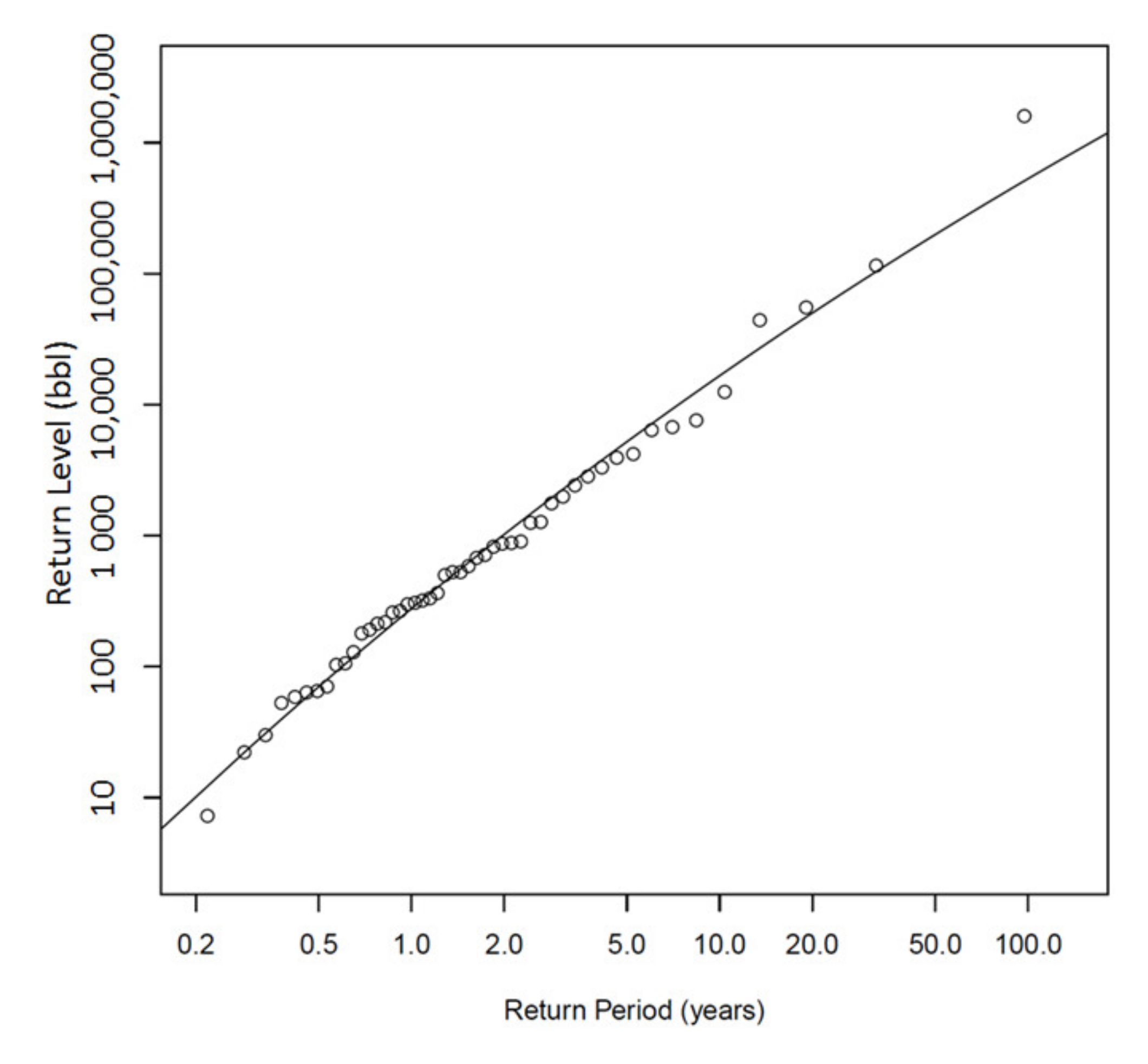
The results are as follows: (1) The location parameter (µ) is 2.442 (which is equivalent to 277 bbl), (2) the scale parameter (σ) is 0.839, and (3) the shape parameter (γ) is −0.073. The model data comparison is presented graphically using a probability–probability plot (PP plot) and a quantile–quantile plot (QQ plot).
The return level (spill volume) variable is the quantile value that is exceeded, on average, once in a period of time (return period in years).
Figure 2 gives return levels under different return periods. As examples, the return levels for the 10-year and 100-year return periods are 16 and 562 Mbbl (1 Mbbl = 1000 bbl), respectively. The return level of 1 MMbbl (i.e., the catastrophic oil spill) corresponds to a return period of 165 years, which means that a catastrophic spill is most likely to occur once in 165 years, and every year has a chance of occurring of 0.6% (=1/165). The 95% confidence level is between 41 years and more than 500 years. Because there are 49 years of observational data, it is not that meaningful to estimate periods longer than 500 years. Recent progress in technology and regulation should likely lower the oil spill risk.
2.4. Conclusions
In this study, GEV distributions were applied to analyze oil spills in the OCS in the 1964–2012 time frame. Major findings from this study include the following:
The blocks method from EVT was successfully applied to oil spill risk analysis. GEV distributions are capable of estimating the probabilities of oil spills in OCS areas using the 49 years of OCS oil spill data.
The return period of a catastrophic oil spill in OCS areas is estimated to be 165 years, with a 95% confidence interval between 41 years and more than 500 years.
The findings of this study are used for offshore oil and gas management at BOEM (e.g., [
41]) and other regulatory agencies (e.g., [
42]).
3. A More Efficient Way to Estimate the Probability of Oil Spill Contact to Environmental Resources in the GOM
Many improvements have been made over the past four decades on the OSRA model, e.g., [
43,
44,
45,
46,
47,
48]. As shown in
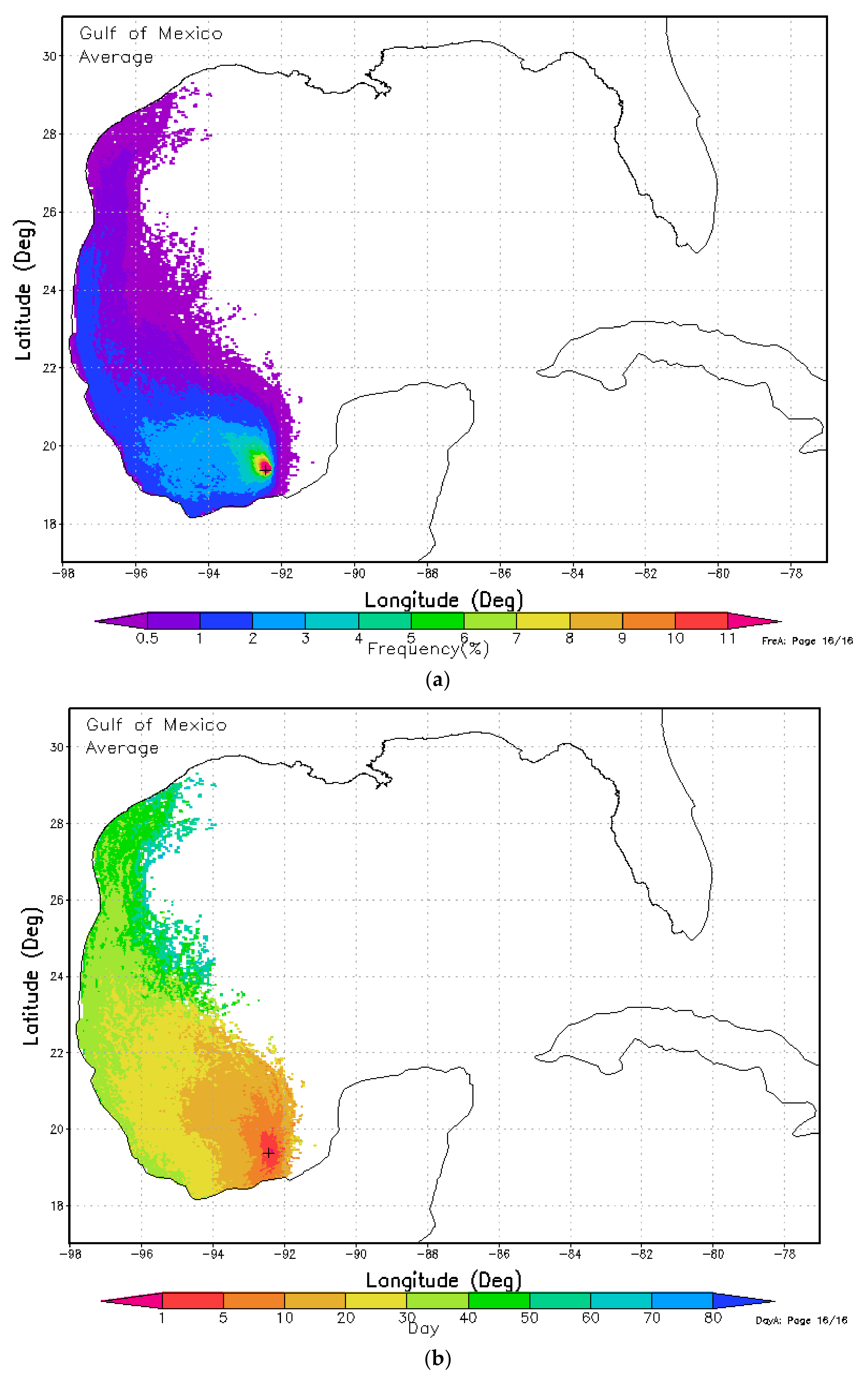
Figure 3, in the GOM, the OSRA model typically launches trajectories from over 6000 hypothetical oil spill locations (at 0.1° by 0.1° spatial resolution) in the offshore US waters within the planning areas for BOEM’s lease sales. These trajectories are initialized daily, and were simulated for up to 30 days, unless they touch the land boundary or flow out of the study domain. The surface ocean currents over several years or decades are used to calculate the trajectories on an hourly basis, along with a wind drift factor for the same durations. The probabilities of contact of these hypothetical spills to environmental resources are then calculated. This type of probability is a conditional probability, which assumes the condition of an accidental large oil spill (≥1000 bbl) occurs at these locations.
The conditional probability is derived by dividing the number of trajectories that touch a particular environmental resource by the millions of calculated trajectories. In the existing OSRA model, the spatially and temporally varying environmental resources are input to the OSRA model code and are in the OSRA model inputs. Thus, minor changes in the environmental resources will lead to a rerun of the OSRA model. Li and Johnson [
25] proposed a method to tabulate the contacts of trajectories to every non-land model grid and archive the original spill locations and the contact numbers in a database. Thus, the probability of the contact to a particular environmental resource can be inferred from the database instead of computing via the OSRA model, should any changes of environmental resources occur.
The oceanographic input to the OSRA model is a critical component for generating the trajectories from hypothetical spill locations. As such, BOEM has committed to improving and updating the ocean circulation model on a regular basis. The companion paper [
23] discusses BOEM-funded studies related to oil spill modeling in the past decade, including ocean circulation modeling and field observation projects for improving the understanding of circulation patterns, especially deep circulation patterns, in the GOM.
In Li and Johnson [
25], two sets of surface wind and ocean current, with one from 1993 to 1999 and the other from 2000 to 2007, were used to simulate the trajectories. (Wind data are in six-hourly intervals, while ocean current data are in three-hourly intervals). For 1993–1999, surface wind data are from the European Centre for Medium-Range Weather Forecasts [
20]. For 2000–2007, winds are from the National Centers for Environmental Prediction (NCEP) QuikSCAT blended (
https://rda.ucar.edu/datasets/ds744.4/ (accessed on 23 December 2020)). The ocean current data for both time frames were generated from the Princeton Regional Ocean Forecast System (PROFS) [
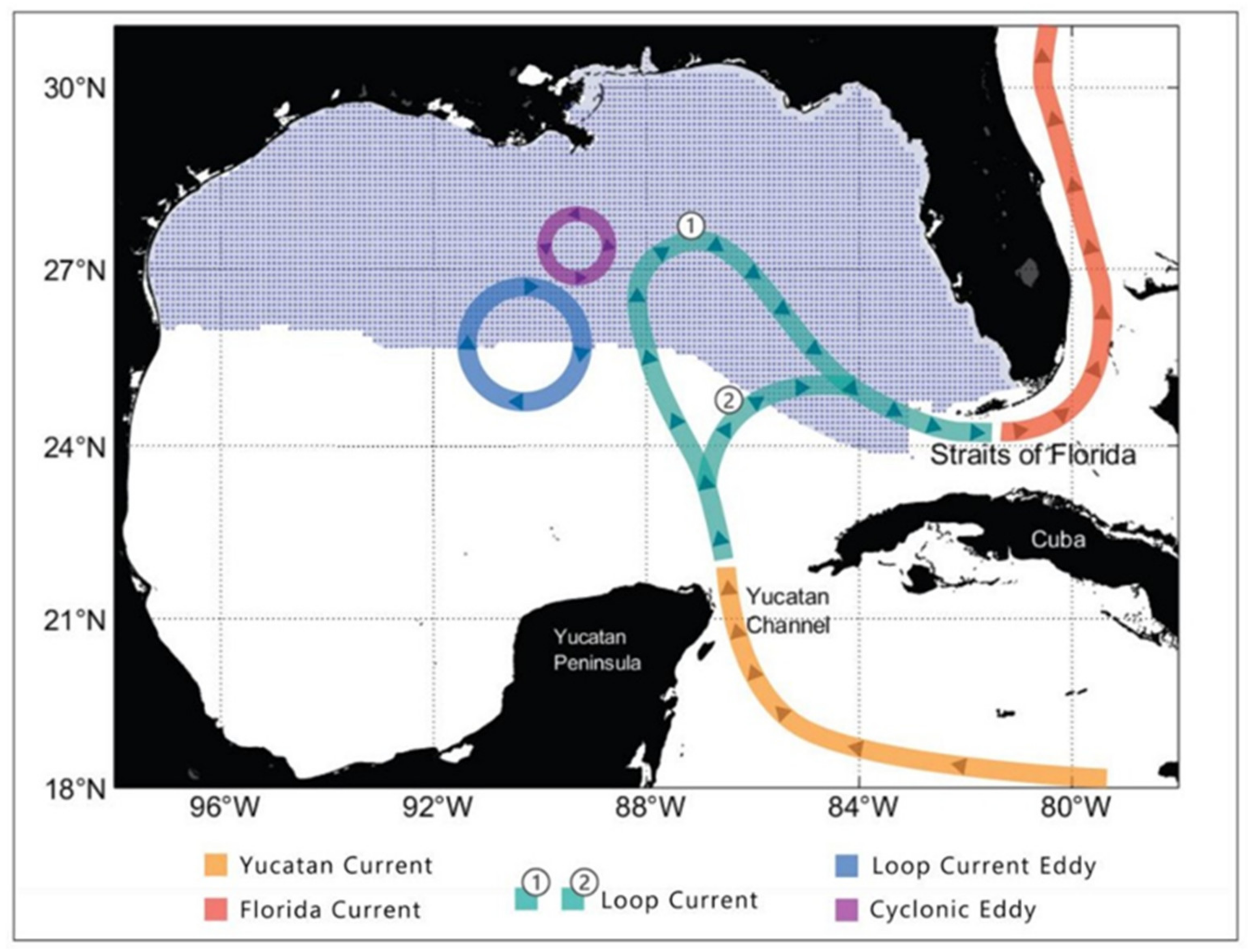
49,
50], but with different resolutions and data assimilation schemes. The model output was verified extensively with observations and was capable of reproducing the Loop Current and eddies spun off from the Loop Current, surface circulation pattern on and near the continental shelf, and ocean transport through the Yucatan Channel.
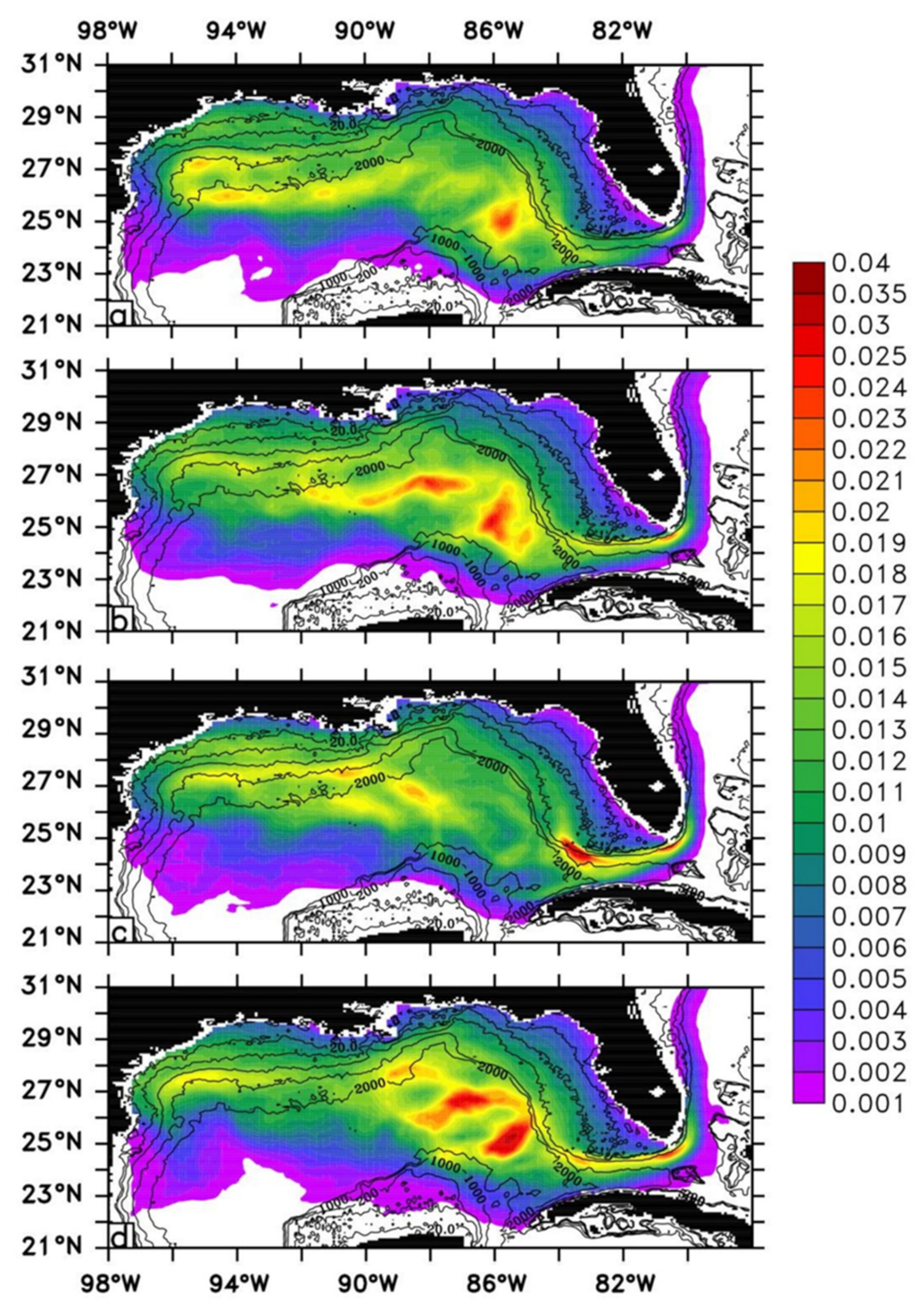
One advantage of this method is that it allows comparison of the annual conditional probabilities on a series of maps, as demonstrated in
Figure 4. The annual conditional probability represents the probability of contact initiated from the locations of hypothetical oil spills throughout a whole year for the environmental resources that are sensitive to oil spill impacts all year round. The annual conditional probability shows a strong variation for 2000–2006, and the distribution pattern reflects the convergence of the trajectory paths, essentially following the pattern of the Loop Current and Loop Current eddies. Similar patterns are observed for 1993–1999 (not shown).
A more efficient way to calculate the conditional probability is presented in this section that provides a solution to reduce the number of OSRA model simulations, as each lease sale often requires an updated OSRA run with slightly different hypothetical launch points and environmental resources. Additionally, this method provides a means to perform the sensitivity tests on the optimal number of launch points, spacing of launch points, and OSRA model resolution with respect to a particular wind and current data set. In regions dominated by mesoscale or sub-mesoscale eddies, a fine spacing of the launch points are likely needed, and the launch points may not need to be equally spaced in the planning area. The map distributions of the conditional probabilities show that areas of least contacted resources are in the west Florida shelf and east coast of Florida, while areas of most contacted resources are the Loop Current and eddies, assuming that the hypothetical spills are located throughout the GOM planning areas. Other OCS regions can benefit from this approach to improve their oil spill risk assessments.
4. Weathering Calculation in OSRA
There are factors not explicitly considered by the OSRA model that can affect the transport of spilled oil as well as the dimension, volume, and nature of the oil spills contacting environmental resources. For example, the physical and biological weathering of spilled oil was not included in the OSRA model in the past decades [
1]. The OSRA model used a more environmentally conservative approach by presuming persistence of spilled oil over the selected time duration of the trajectories. The spilled oil was considered as conservative, and oil weathering was neglected in the OSRA model. This assumption made the calculated probabilities higher than would have been obtained using weathering effects (e.g., [
51]).
This section discusses the implementation of weathering into the OSRA model and uses Cook Inlet, Alaska, as an example of this application.
4.1. Weathering and Its Representation in the OSRA Model
The physical and chemical characteristics of oil change almost immediately when oil is spilled in water due to evaporation, natural dispersion, emulsification, dissolution, oxidation, sedimentation, and biodegradation. All these processes interact with each other and are collectively referred to as oil weathering. Photochemical reactions and biodegradation can change the character and reduce the amount of oil over time. Major processes include the following [
52]:
Evaporation converts liquid oil to a gaseous phase. The lighter fractions of the oil are lost first. This is a major process that accounts for the loss of oil, particularly light oils. During the evaporation process, low-molecular-weight compounds with low boiling points are vaporized into the atmosphere. The process is dependent on the viscosity of the oil and atmospheric weather conditions. At 15 °C over a 2-day period, evaporation can remove almost 100% of gasoline, 80% of diesel fuel, 40% of light crude, 20% of heavy crude, and about 5–10% of Bunker C. The typical timescale of this process is less than 5 days.
Emulsification is the process by which very small water droplets are mixed into liquid oil. The oil is held in suspension in the water. The water content often reaches 50–80%. This process can increase the amount of recovered pollutant by two to four times and slows down other mixing processes. The onset of emulsification can be delayed for days, but once initiated, this process happens rapidly.
Natural dispersion mechanically breaks up an oil slick into small droplets that are mixed into the water column. Oil from the water surface is typically removed within days.
Dissolution is the mixing of the water-soluble components of oil into the water. The low-molecular-weight compounds often travel vertically and are lost to the water column. It is governed by many parameters, including the viscosity of the oil and weather conditions. Most water-soluble components of oil are toxic. The crude oil dissolution time period is less than 5 days.
Biodegradation is the breakdown of oil by microbes into smaller compounds and eventually into water and carbon dioxide. The biodegradation rate depends on oil type, temperature, nutrients, available oxygen, and amount of oil. This process can take weeks to months.
Formation of tarballs is the breakup of slicks of weathered heavy crudes and refined oils into small patches that persist for long distances. The timescale is days to weeks.
Sinking occurs when the density of the oil increases due to evaporation, dissolution, and interaction with particulates. The residual oil then sinks to the bottom and is incorporated in the sediment. Resurfacing occurs when the density of the residual oil reduces to such a degree that it can be refloated from the sediment bed.
Oil spill models simulate the transport and weathering of oil in waters. The primary purpose of the OSRA model is to calculate oil spill risk over very large spatial scales (up to thousands of kilometers) and very long timescales (up to a few decades). Simulating weathering processes in detail would be computationally prohibitive in the OSRA model. In addition, measured data are not adequate for justifying a detailed modeling approach and specifying the values of numerous parameters that might be involved. Therefore, the OSRA model utilizes the following formula for bulk oil mass weathering that is widely used in oil spill models, e.g., [
53]:
where Oil = oil volume at time
t, Oil
0 = initial oil volume,
k = rate of removal (or decay rate) in 1/day, and
t = time in days. The decay rate (
k) can also be expressed as the half-life time (
th), i.e., the time when the oil volume is reduced by half:
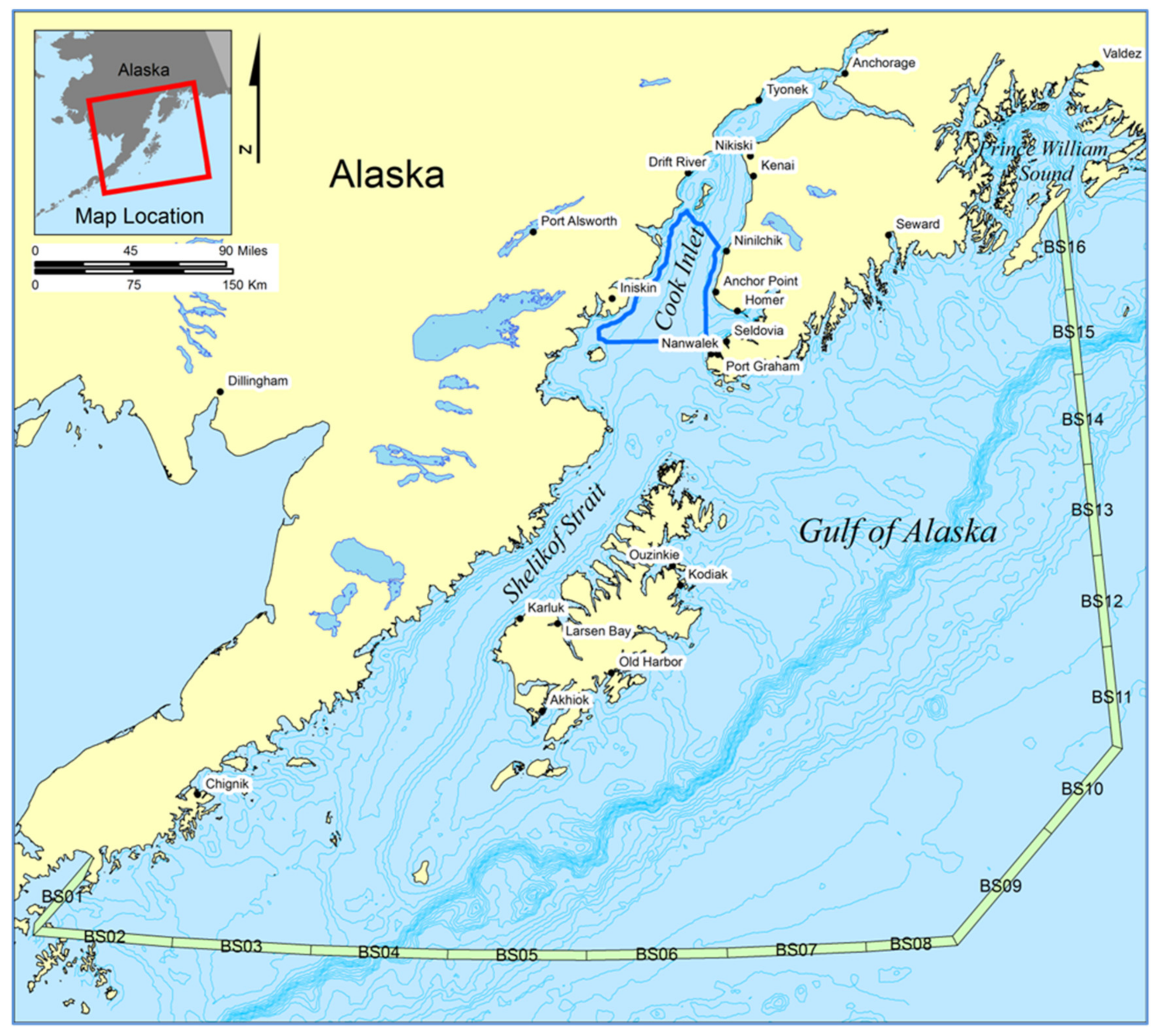
4.2. Application to Cook Inlet, Alaska
The US federal government offered a portion of the OCS lands in Cook Inlet, Alaska, for oil and gas leasing (Lease Sale 244) in 2017 [
51]. Because oil spills may occur from activities associated with offshore oil and gas production, BOEM conducts oil spill risk analysis to support NEPA analysis completed prior to conducting an oil and gas lease sale. Ji et al. [
51] documented the OSRA data and results used in the Cook Inlet OCS Lease Sale 244 Environmental Impact Statement.
The OSRA model estimated oil spill trajectories using model-simulated hindcast fields of winds, sea ice movement and concentration, and surface ocean currents in Cook Inlet and the Gulf of Alaska (
Figure 5). A state-of-the-art, three-dimensional coupled ice–ocean hydrodynamic model based on the Regional Ocean Modeling System (ROMS) simulated the wind-driven and density-induced ocean flow fields and the ice motion and concentration fields. [
54]. The OSRA calculation used the same wind fields used by Danielson et al. [
54]. The current and ice model has a resolution of 1.5 km. The wind fields have a resolution of 10 km.
The OSRA model domain (
Figure 5) had a resolution of 245 m by 256 m and a total of 8 million grid cells. The domain was chosen to be large enough to allow most hypothetical oil spill trajectories to develop without contacting the boundary segments through 110 days.
The OSRA model initiated a hypothetical oil spill trajectory from each potential lease block starting on day 1 in 1999 and then launched a new trajectory every day for 10 years (1999–2009). A total of 3600 trajectories were simulated from each launch point. The trajectories were driven by the hourly wind and ice or current data from the ocean model simulations from the years 1999 through 2009.
The model calculated conditional probabilities of contact to environmental resources within 1, 3, 10, 30, and 110 days of travel time for each of the hypothetical spill sites to serve as input into the final calculation of the conditional probabilities. Ji et al. [
51] provides detailed results, including about 70 tables and 20 figures.
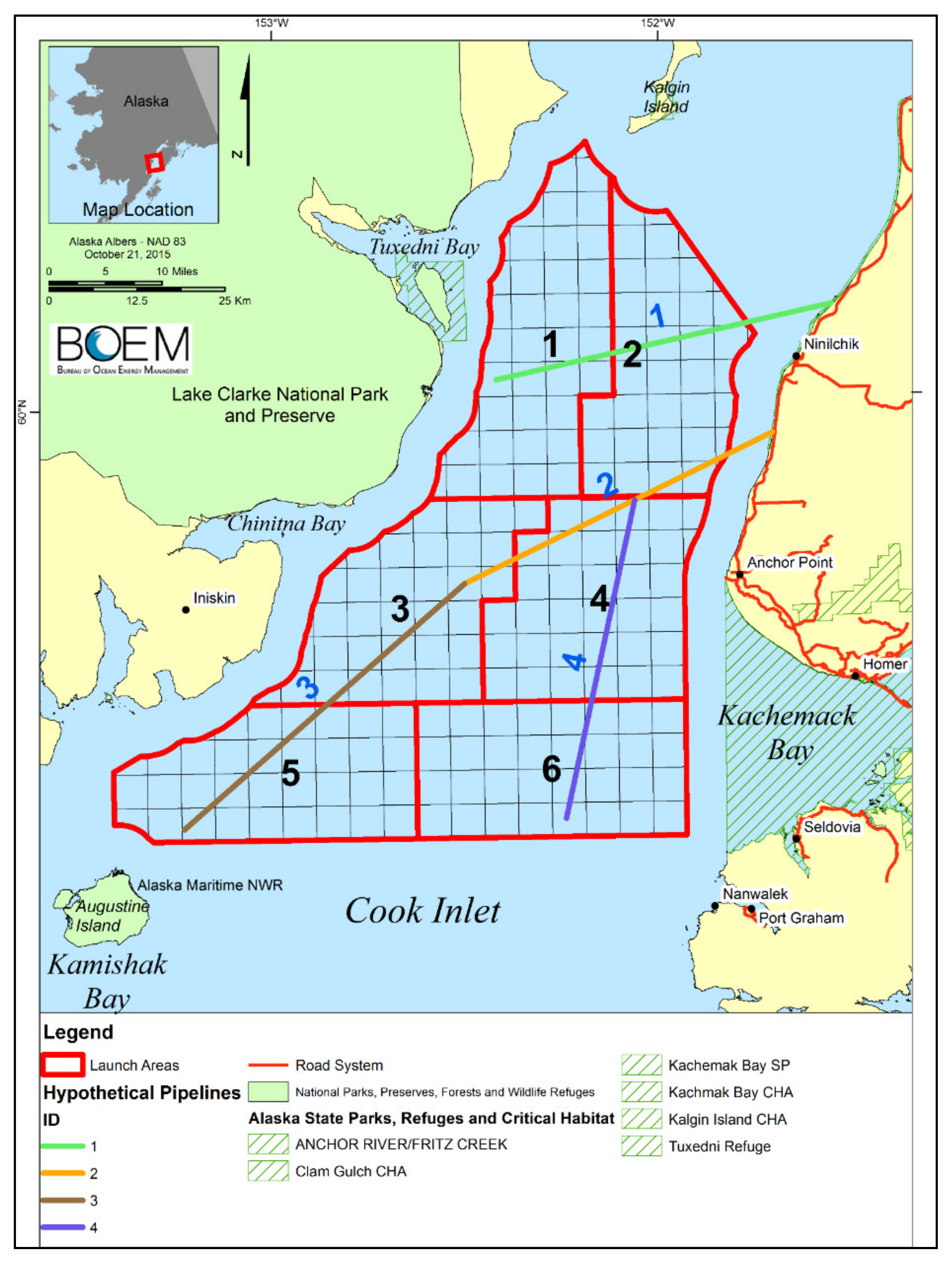
To show the possible impact that weathering can have on OSRA calculations,
Table 1 lists some environmental resource areas that might be affected by hypothetical spills from a launch area (LA6) (
Figure 6).
Table 1 gives the annual conditional probabilities (expressed as percentage chance) that a large oil spill starting from LA6 will contact environmental resource areas within 30 days, under the conditions of no weathering (
k = 0),
th = 15 days, and
th = 3 days. Ji et al. [
51] used the results of the no weathering case (
k = 0).
Table 1 shows that the including weathering in the OSRA model can significantly reduce the contact probabilities, even for a very slow decay rate of
th = 15 days. The weathering process reduces the amount of oil mass in the study area.
4.3. Conclusions
Since the inception of the OSRA model in the 1970s, the weathering effect has not been included in past OSRA analyses. This conservative approach led to overestimating the contact probabilities from hypothetical spills. The NEPA analysts considered the weathered oil results to describe various impacts on resources, thereby improving their use of the OSRA model results. This section describes the incorporation of the weathering effect into the OSRA model. The newly improved OSRA model was applied to Cook Inlet, Alaska. The preliminary results indicated that the incorporation of weathering into the OSRA model can reduce the contact probabilities significantly.
As discussed in
Section 4.1, the weathering of spilled oil depends on a variety of factors, including oil type, ocean condition, meteorological condition, and oil spill response. The calculation of oil characteristics through more complex weathering algorithms might provide more accurate information about the spilled oil at shorelines and environmental resources. It would be helpful to compare the updated OSRA model (with the simple weathering algorithm described in this paper) against other oil spill models (with more complex weathering algorithms). Further studies are needed before the weathering process can be fully employed in the OSRA model.
5. Application to the Ixtoc I Oil Spill
Knowledge of trajectories in the case of a potential oil spill is useful for preparedness and response. Understanding how the variability in oceanic and metrological conditions over multiple years influences oil trajectories is essential. The ocean circulation, local and regional, in tandem with prevailing meteorological conditions, determines the oil pathways [
55]. From the risk analysis point of view, this information can be helpful for contingency planning and response operations in the case of an actual oil spill (e.g., [
45]).
When a large oil spill happens, people often ask two key questions: Will it affect my environment (such as my beach, my shoreline, my park, etc.)? If so, when will it affect me (economically, physically, emotionally, etc.)? As an example, the OSRA model is applied to simulate the Ixtoc I oil spill using 15 years of Gulf of Mexico current and wind fields. The purpose is to understand the transport and distribution patterns of oil spilled at the Ixtoc I site. This study does not intend to hindcast the Ixtoc I spill event but to investigate the oil distribution patterns from the spill site under the conditions of historical currents and winds.
5.1. Background Information
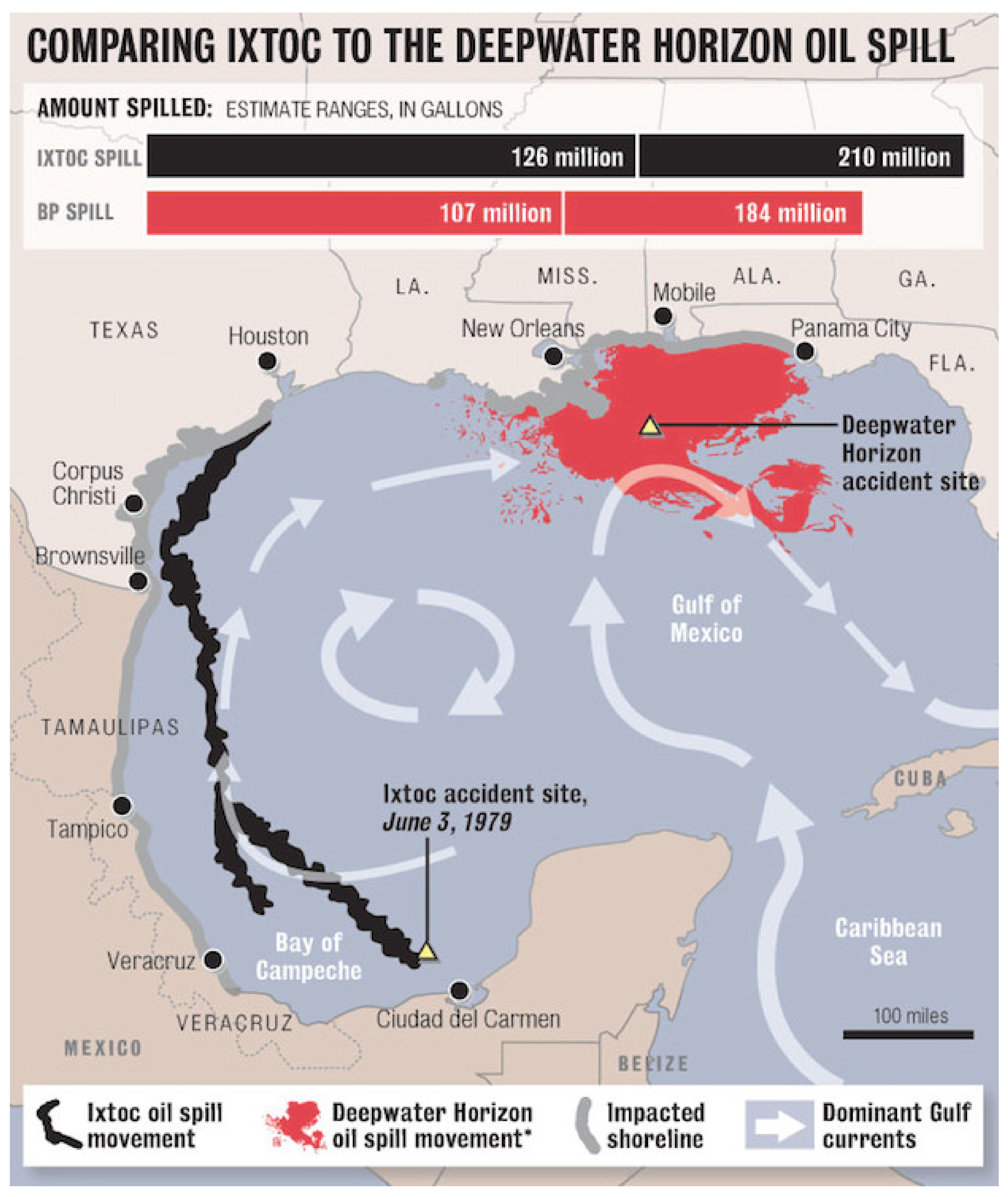
On 3 June 1979, the exploratory well of the Mexican state-owned oil company PEMEX (Petróleos Mexicanos), Ixtoc I (92°13′ W, 19°24′ N), blew out in the Bay of Campeche, about 80 km northwest of Ciudad del Carmen, Mexico (
Figure 7). The water depth at the site is about 50 m. About 10,000–15,000 bbl of oil were released daily for a period of 9.7 months (290 days). The spill, not brought under control until 23 March 1980, released at least 3.5 MMbbl (475,000 tons) of crude oil into the GOM [
56]. Ixtoc I was the largest offshore oil spill in history at that time, only surpassed 30 years later by the DWH in 2010 [
57].
The Ixtoc I oil spill was unique not only for its magnitude but also for the long interval between the release of oil and its impact on the environment. The accident was further aggravated by the absence of a rapid control response. The environmental impacts of the Ixtoc I oil spill were not extensively studied during and after the spill. The full extent of the damage is still unknown. Jernelöv and Lindén [
58] explained the general behavior of the spilled oil and gave a detailed account of the cleanup operations and the efforts implemented by PEMEX to stop the flow of oil. Jernelöv and Lindén [
58] estimated that 50% of the spilled oil evaporated into the atmosphere, 25% sank to the bottom, 12% degraded biologically and chemically, less than 1% landed on Texas beaches, and the remainder was mechanically removed or burned at the well site.
Even though 40 years have passed since the Ixtoc I oil spill, there are limited modeling studies on the transport and distribution of the spilled oil. During the Ixtoc I oil spill, Galt [
59] utilized trajectory models for the purposes of (1) providing daily forecasts of the expected movement and spreading of the oil, (2) describing the long-term prospects for Ixtoc I oil movement and defining the strategic threat under which the response should be planned, and (3) identifying threat areas associated with particular high-value regions. Anderson [
60] used three pairs of current and wind data sets to simulate the transport of the oil released from Ixtoc I. Both studies [
59,
60] used very limited wind and current fields, which hindered detailed simulation of this event.
5.2. Model Results
Conducting an oil spill risk analysis requires detailed information about ocean currents and wind fields [
61]. The ocean current inputs used in this study are numerically computed from an ocean circulation model of the GOM [
20,
49,
50].
Section 3 describes the ocean model and the OSRA model used in this study.
The OSRA model estimates and tracks spill particles released at the Ixtoc I site for 15 years (from 1 January 1993 to 31 December 2007). Trajectories of hypothetical spills were initiated every day from the Ixtoc I spill site over the simulation period. A total of 5400 trajectories (one spill per day for 15 years) were calculated. Jernelöv and Lindén [
58] reported that the microbial degradation of the Ixtoc I oil occurred at a relatively slow rate (microbes were nutrient starved). To estimate the oil spill risk conservatively, the OSRA model assumes that the weathering effect is minimal and is neglected. The weathering effect will be addressed later.
A wide variety of physical processes affect spilled oil. Analysis of the ocean currents and wind patterns in the vicinity of the Ixtoc I exploratory well shows that the oil would primarily move in a northeastward direction (
Figure 7). The essential transport mechanism of oil to Texas coastal waters was the Mexican Coastal Current. US waters were threatened when the Mexican Coastal Current was strong enough to move oil north along the Mexican coast before the winds could blow it onshore. Texas coastal surface currents also played a significant role in the movement of the oil [
58,
62].
Based on satellite data, Sun et al. [
62] reported that the patterns of the oil trajectory of the Ixtoc I oil spill were to the northwest and north, nearly parallel to the coastline, with possible oil landing on Mexican and Texas beaches. Field observations at selected beaches and islands along the coast of the western and southern GOM confirmed these satellite-based findings. Once the oil slicks arrived offshore along the Mexican coast, they were transported north with the northward Mexican Coastal Current. The main oil slick that entered the US waters might have come from 50 km offshore of Tampico [
58,
62].
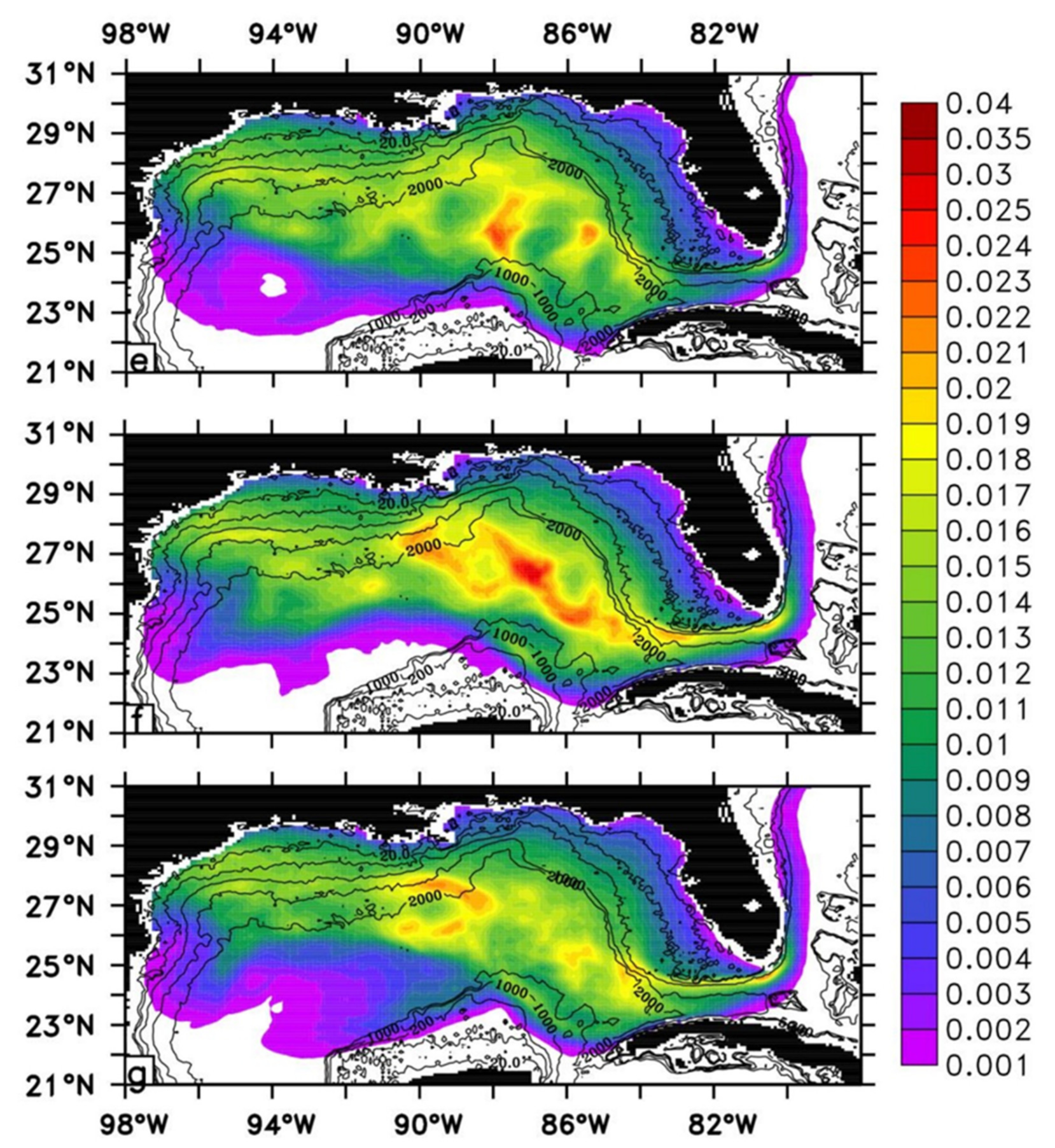
Figure 8a shows the probability of contact with oil spilled from the Ixtoc I location, averaged over 15 years (1993–2007).
Figure 8a reveals that the highest contact probabilities (more than 11%) are in the immediate area of the Ixtoc I well. The Texas coastal water and shoreline are likely affected by the spill, and the probability of contact is less than 1%. The distribution patterns of the spilled oil shown in
Figure 8a are generally consistent with the one of Ixtoc I shown in
Figure 7. Based on 15 years of simulations, the oil slicks driven by the surface current and wind fields are most likely to first drift west to west-northwest.
Figure 8a also indicates that the main slick is offshore in the Texas waters. The results shown in
Figure 8a are generally consistent with the statements of Galt [
59] and Figure 5b (satellite-based observations) of Sun et al. [
62]. Biggs et al. [
63] also reported similar patterns of transport in their discussions on eddies.
The impact of Ixtoc I oil in south Texas was first observed on 6 August 1979 (two months after the blowout), when a total of 26 to 28 km of shoreline was impacted with light to very light swashes of tar balls [
58]. Using remote sensing data, Sun et al. [
62] documented the surface footprint and trajectory of the released oil from Ixtoc I and also reported a shoreline contact time of about two months.
Figure 8b shows the time of contact with oil spilled from the Ixtoc I location, averaged over 15 years (1993–2007) of the OSRA model results. The typical time for the oil spilled at the Ixtoc I site to travel to the Texas shoreline is about 50 days. More detailed analysis indicates that for different years and different seasons, the travel time to the Texas shoreline varies from 40 days to more than 60 days. Therefore, the range of contact times obtained from the OSRA model is generally consistent with Galt [
59] and Sun et al. [
62].
Regional and local oceanographic and meteorological conditions control oil transport. There are distinctive differences between each year and each season with respect to oceanic circulation and wind fields (e.g., [
64]). Consequently, oil distribution patterns exhibit strong seasonal and annual variabilities.
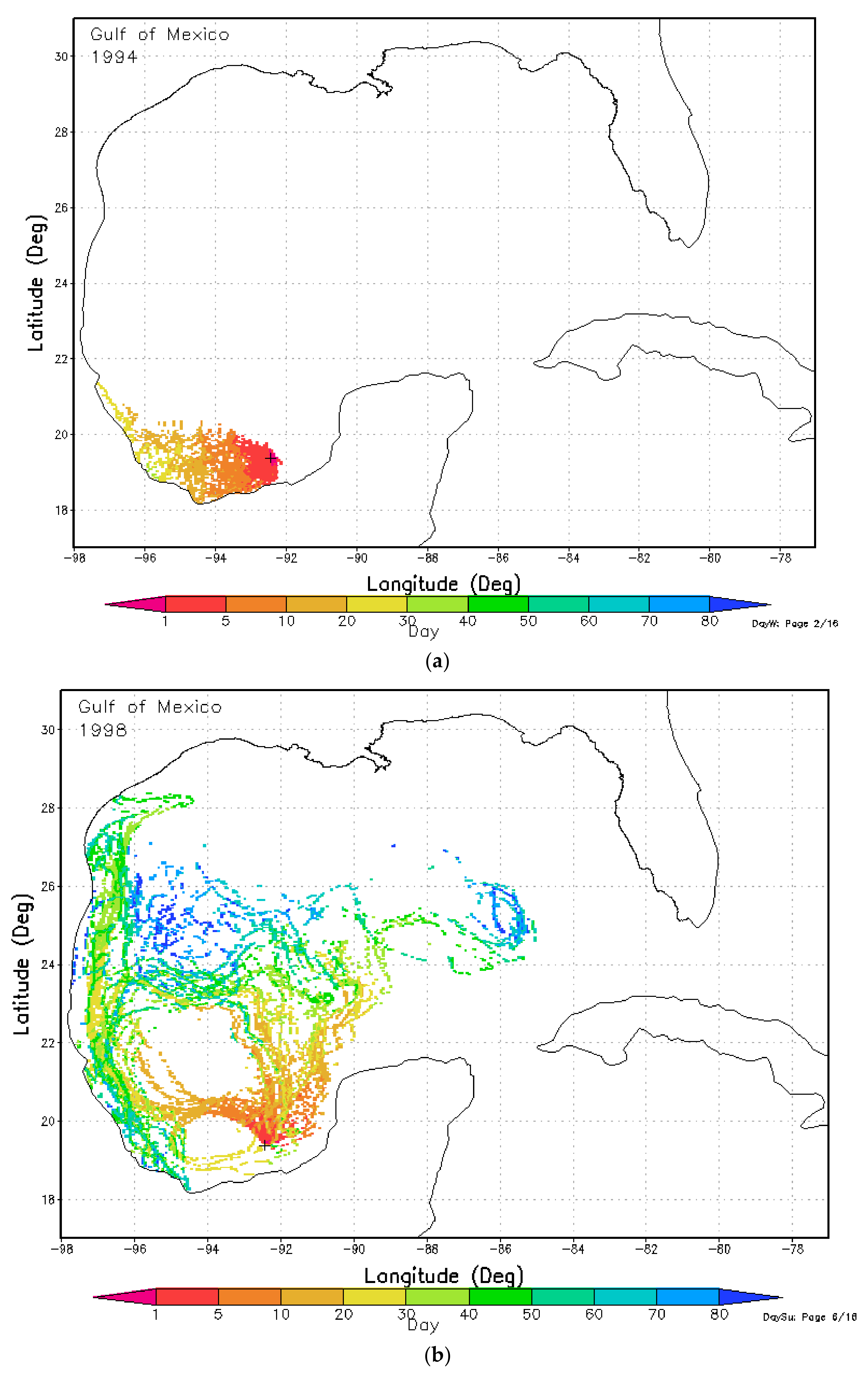
Figure 9a shows the time of contact for the oil spilled at the Ixtoc I site to reach a particular location in the winter (January–March) of 1994. The oil release in this period showed the highest risk of oil beaching in the Mexican shoreline. The spilled oil covered a relatively small area of the GOM in this case.
In contrast,
Figure 9b shows the time of contact with oil spilled from the Ixtoc I location in the summer (July–September) of 1998 and shows that a much larger area of the GOM is affected by the spilled oil. A significant portion of the oil is transported in the northeast direction. Sun et al. [
62] reported that oil slick appearance frequency and area of coverage increased in the east and northeast direction of the spill site after September 1979. The northward-flowing western GOM current reversed direction during September 1979, and major surface concentrations of oil were then found to the northeast, east, and southeast of the well [
65,
66].
Figure 9b exhibits some similarities with the observations reported by Sun et al. [
62], ERCO [
65], and Farrington [
66].
5.3. Discussion and Conclusions
The results shown in
Figure 8 and
Figure 9 were obtained under the assumption that the weathering effect is minimal and that the spilled oil is conservative. As what was discussed in
Section 4, neglecting weathering effects may lead to overestimating the probability of contact.
Numerical tests are conducted to analyze the sensitivity of the OSRA model results to parameters.
Figure 10a is the same as
Figure 8a, except the half-life time is set to 15 days. Comparing
Figure 10a with
Figure 8a, it is evident that the weathering process reduces the probability of contact, even though
Figure 10a still exhibits similar oil distribution patterns, and the spilled oil still reaches Texas coastal waters.
Figure 10b is the same as
Figure 8b, except the half-life time is set to 15 days. As expected, the patterns of contact time in
Figure 10b are very similar to the ones in
Figure 8b because the contact time is primarily determined by current and wind fields.
The study presented in this section is primarily for addressing these two questions: (1) When a large spill happens, will it affect certain areas? (2) If so, when will it affect those areas? Conclusions from this study are:
Using 15 years of current and wind fields, the OSRA model is applied to simulate the transport and distribution patterns of oil spilled at the Ixtoc I site. The model results are generally consistent with the observations reported by Galt [
59] and Sun et al. [
62].
The transport of the spill spilled from the Ixtoc I site is most likely westward and then northwestward. The spilled oil affects the Mexican coastal waters first and then travels northward, eventually reaching the Texas coastal regions.
The time needed for the oil from the Ixtoc I site to reach Texas waters varies from 40 days to more than 60 days.
The oil distribution patterns also vary seasonally and annually. In the months of January, February, and March, the spilled oil is more likely to move westward and then beach on the Mexican shoreline. In the months of July, August, and September, the spilled oil has a higher possibility of moving in the northeast direction and affecting a much larger area of the GOM.
6. Summary and Future Works
Because oil spills may occur from regulated activities associated with offshore oil and gas activities, BOEM carries out oil spill risk analyses to support NEPA analysis prior to conducting an oil and gas lease sale. This paper summarized some of the progress made in the past decade in the OSRA model and its applications.
A key element of the OSRA is the trajectory model that is driven by current and wind from other ocean models and atmospheric models. Therefore, the transport processes included in the OSRA model are largely determined by the characteristics of these models. To resolve and represent the Stokes shift and the Langmuir circulation, for example, not only the ocean model should be able to simulate these processes well, but also the output from the ocean model should be saved with sufficient spatial and temporal resolutions so that these processes can be represented in the trajectory model. The OSRA applications typically have spatial scales of thousands of kilometers and temporal scales of decades, which presents a challenge to realistically include these processes in the OSRA model. An interesting study would be to downscale the OSRA model to a smaller domain and then test the impacts of these oceanographic processes on the transport of spilled oil.
BOEM’s OSRA experts are studying different possibilities on how to further improve the OSRA model. These possibilities include different weathering effects, oil–beach interaction, three-dimensional modeling, and other improvements. Physical oceanographic processes, such as the Lagrangian coherent structures (e.g., [
67]), might also play a key role in affecting the oil transport. The goal is that by including additional effects and modeling the influence of physical, chemical, and biological processes not yet considered, BOEM will continue to improve the OSRA model and therefore better inform decisions. These efforts project BOEM’s OSRA modeling into the next decade and are aligned with BOEM’s Environmental Studies Program’s Decadal Vision document being prepared at the time of this writing. Therefore, BOEM modelers and managers are addressing internal and external alignments, priorities, and goals as the community adapts to the continuous changes.
Author Contributions
Conceptualization, Z.-G.J. and Z.L.; formal analysis, Z.-G.J. and Z.L.; writing and review, Z.-G.J., Z.L., W.J., and G.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank Bob LaBelle, Thomas Kilpatrick, and Rodney Cluck for reviewing the manuscript and Paulina Chen for editing the manuscript. C.J. Beegle-Krause also provided helpful comments for improving the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Smith, R.A.; Slack, J.R.; Wyant, T.; Lanfear, K.J. The Oil Spill Risk Analysis Model of the U.S. Geological Survey; Geological Survey Professional Paper 1227; United States Government Printing Office: Washington, DC, USA, 1982; p. 40.
- Reed, M.; Aamo, O.M.; Daling, P.S. Quantitative analysis of alternate oil spill response strategies using OSCAR. Spill Sci. Technol. Bull. 1995, 2, 67–74. [Google Scholar] [CrossRef]
- Galt, J.A.; Payton, D.L. Development of Quantitative Methods For Spill Response Planning: A Trajectory Analysis Planner. Spill Sci. Technol. Bull. 1999, 5, 17–28. [Google Scholar] [CrossRef]
- Barker, C.H.; Galt, J. Analysis of Methods Used in Spill Response Planning: Trajectory Analysis Planner TAP II. Spill Sci. Technol. Bull. 2000, 6, 145–152. [Google Scholar] [CrossRef]
- French, D.P.; Schuttenberg, H. Evaluation of net environmental benefit using fates and effects modeling. Paper ID #321. In Proceedings of the 1999 International Oil Spill Conference; American Petroleum Institute: Washington, DC, USA, 1999. [Google Scholar]
- McCay, D.F.; Whittier, N.; Dalton, C.; Rowe, J.; Sankaranarayanan, S.; Aurand, D. Modeling Fates and Impacts of Hypothetical Oil Spills in Delaware, Florida, Texas, California, and Alaska Waters, Varying Response Options Including Use of Dispersants. Int. Oil Spill Conf. Proc. 2005, 2005, 735–740. [Google Scholar] [CrossRef]
- McCay, D.F.; Crowley, D.; Rowe, J.J.; Bock, M.; Robinson, H.; Wenning, R.; Walker, A.H.; Joeckel, J.; Nedwed, T.J.; Parkerton, T.F. Comparative Risk Assessment of spill response options for a deepwater oil well blowout: Part 1. Oil spill modeling. Mar. Pollut. Bull. 2018, 133, 1001–1015. [Google Scholar] [CrossRef]
- De Dominicis, M.; Pinardi, N.; Zodiatis, G.; Lardner, R. MEDSLIK-II, a Lagrangian marine surface oil spill model for short-term forecasting—Part 1: Theory. Geosci. Model Dev. 2013, 6, 1851–1869. [Google Scholar] [CrossRef]
- Hoteit, I.; Abualnaja, Y.; Afzal, S.; Ait-El-Fquih, B.; Akylas, T.; Antony, C.; Dawson, C.; Asfahani, K.; Brewin, R.J.; Cavaleri, L.; et al. Towards an End-to-End Analysis and Prediction System for Weather, Climate, and Marine Applications in the Red Sea. Bull. Am. Meteorol. Soc. 2021, 102, E99–E122. [Google Scholar] [CrossRef]
- Goldman, R.; Biton, E.; Brokovich, E.; Kark, S.; Levin, N. Oil spill contamination probability in the southeastern Levantine basin. Mar. Pollut. Bull. 2015, 91, 347–356. [Google Scholar] [CrossRef]
- Neves, A.A.S.; Pinardi, N.; Martins, F. IT-OSRA: Applying ensemble simulations to estimate the oil spill risk associated to op-erational and accidental oil spills. Ocean Dyn. 2016, 66, 939–954. [Google Scholar] [CrossRef]
- Hole, L.R.; Dagestad, K.; Röhrs, J.; Wettre, C.; Kourafalou, V.; Androulidakis, Y.; Kang, H.; Le Hénaff, M.; Garcia-Pineda, O. The DeepWater Horizon Oil Slick: Simulations of River Front Effects and Oil Droplet Size Distribution. J. Mar. Sci. Eng. 2019, 7, 329. [Google Scholar] [CrossRef]
- Spaulding, M.L. A state-of-the-art review of oil spill trajectory and fate modeling. Oil Chem. Pollut. 1988, 4, 39–55. [Google Scholar] [CrossRef]
- ASCE Task Committee on Modeling of Oil Spills. State-of-the-art review of modeling transport and fate of oil spills. J. Hydraul. Eng. 1996, 122, 594–609. [Google Scholar] [CrossRef]
- Reed, M.; Johansen, Ø.; Brandvik, P.J.; Daling, P.; Lewis, A.; Fiocco, R.; Mackay, D.; Prentki, R. Oil Spill Modeling towards the Close of the 20th Century: Overview of the State of the Art. Spill Sci. Technol. Bull. 1999, 5, 3–16. [Google Scholar] [CrossRef]
- Drozdowski, A.; Nudds, S.; Hannah, C.G.; Niu, H.; Peterson, I.K.; Perrie, W.A. Review of Oil Spill Trajectory Modelling in the Presence of Ice; Canadian Technical Report of Hydrography and Ocean Sciences 274; Fisheries and Oceans Canada: Edmonton, AB, Canada, 2011. [Google Scholar]
- Spaulding, M.L. State of the art review and future directions in oil spill modeling. Mar. Pollut. Bull. 2017, 115, 7–19. [Google Scholar] [CrossRef] [PubMed]
- Smith, R.A.; Slack, J.R.; Davis, R.K. An Oil Spill Risk Analysis for the Mid-Atlantic Outer Continental Shelf Lease Area; Geo-logical Survey Open-File Report 76–451; U.S. Geological Survey: Reston, VA, USA, 1976; p. 24.
- Ji, Z.-G.; Smith, C. Oil Spill Risk Analysis: Cook Inlet Planning Area OCS Lease Sale 258; OCS Report 2021-001; Bureau of Ocean Energy Management: Sterling, VA, USA, 2021.
- Oey, L.-Y. Circulation Model of the Gulf of Mexico and the Caribbean Sea: Development of the Princeton Regional Ocean Forecast (& Hindcast) System–PROFS, and Hindcast Experiment for 1992–1999; OCS Study MMS 2005–049, Final Report; Department of the Interior, Minerals Management Service: Herndon, VA, USA, 2005; p. 174.
- Danielson, S.; Hill, D.F.; Hedstrom, K.S.; Beamer, J.P.; Curchitser, E.N. Demonstrating a High-Resolution Gulf of Alaska Ocean Circulation Model Forced Across the Coastal Interface by High-Resolution Terrestrial Hydrological Models. J. Geophys. Res. Oceans 2020, 125, e2019JC015724. [Google Scholar] [CrossRef]
- Johnson, M.A. Subtidal surface circulation in lower Cook Inlet and Kachemak Bay, Alaska. Reg. Stud. Mar. Sci. 2021, 41, 101609. [Google Scholar] [CrossRef]
- Li, Z.; Smith, C.; DuFore, C.; Zaleski, S.F.; Auad, G.; Johnson, W.; Ji, Z.-G.; O’Reilly, S.E. A multifaceted approach to advance oil spill modeling and physical oceanographic research at the United States Bureau of Ocean Energy Management. J. Mar. Sci. Eng. (submitted).
- Ji, Z.-G.; Johnson, W.R.; Wikel, G.L. Statistics of Extremes in Oil Spill Risk Analysis. Environ. Sci. Technol. 2014, 48, 10505–10510. [Google Scholar] [CrossRef]
- Li, Z.; Johnson, W. An Improved Method to Estimate the Probability of Oil Spill Contact to Environmental Resources in the Gulf of Mexico. J. Mar. Sci. Eng. 2019, 7, 41. [Google Scholar] [CrossRef]
- Reiss, R.-D.; Thomas, M. Statistical Analysis of Extreme Values with Applications to Insurance, Finance, Hydrology and Other Fields, 2nd ed.; Birkhauser: Basel, Switzerland, 2001. [Google Scholar]
- Sanders, D.E.A. The Modelling of Extreme Events. Br. Actuar. J. 2005, 11, 519–557. [Google Scholar] [CrossRef]
- Fasen, V.; Klüppelberg, C.; Menzel, A. Quantifying extreme risks. In Risk: A Multidisciplinary Introduction; Klüppelberg, C., Straub, D., Welpe, I., Eds.; Dordrecht: London, UK, 2014; pp. 151–181. [Google Scholar]
- Katz, R.W.; Parlange, M.B.; Naveau, P. Statistics of extremes in hydrology. Adv. Water Resour. 2002, 25, 1287–1304. [Google Scholar] [CrossRef]
- Fisher, R.A.; Tippett, L.H.C. Limiting forms of the frequency distribution of the largest or smallest member of a sample. In Proceedings of the Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press (CUP): Cambridge, UK, 1928; Volume 24, pp. 180–190. [Google Scholar]
- Zheng, L.; Ismail, K.; Meng, X. Freeway safety estimation using extreme value theory approaches: A comparative study. Accid. Anal. Prev. 2014, 62, 32–41. [Google Scholar] [CrossRef] [PubMed]
- Jagger, T.H.; Elsner, J.B.; Saunders, M.A. Forecasting US insured hurricane losses. In Climate Extremes and Society; Cambridge University Press (CUP): Cambridge, UK, 2009; pp. 189–208. [Google Scholar]
- McNeil, A.J. Estimating the Tails of Loss Severity Distributions Using Extreme Value Theory. ASTIN Bull. 1997, 27, 117–137. [Google Scholar] [CrossRef]
- Eckle, P.; Burgherr, P.; Michaux, E. Risk of Large Oil Spills: A Statistical Analysis in the Aftermath of Deepwater Horizon. Environ. Sci. Technol. 2012, 46, 13002–13008. [Google Scholar] [CrossRef]
- Anderson, C.M.; Mayes, M.; LaBelle, R.P. Oil Spill Occurrence Rates for Offshore Oil Spills; OCS Report BOEM 2012-0069; USDOI, BOEM: Herndon, VA, USA, 2012; p. 87.
- Ji, Z.-G.; Johnson, W.R.; Li, Z.; Liu, Y.; MacFadyen, A.; Weisberg, R.H. Oil Spill Risk Analysis Model and Its Application to the Deepwater Horizon Oil Spill Using Historical Current and Wind Data. Sea Ice 2011, 195, 227–236. [Google Scholar] [CrossRef]
- Ji, Z.-G.; Johnson, W.R.; DuFore, C.M. Oil-Spill Risk Analysis: Gulf of Mexico Outer Continental Shelf (OCS) Lease Sales, Eastern Planning Area, Central Planning Area, and Western Planning Area, 2017–2022, and Gulf-wide OCS Program, 2017–2086; OCS Report 2017-010; Bureau of Ocean Energy Management: Sterling, VA, USA, 2017.
- Ji, Z.-G.; Smith, C.; Johnson, W.R. Accessing Oil Spill Risk in Lower Cook Inlet, Alaska. In WIT Transactions on Engineering Sciences, Risk Analysis 2020; WIT Press: Southampton, UK, 2020; Volume 129, pp. 31–40. [Google Scholar]
- R Core Team R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013; ISBN 3-900051-07-01.
- Gilleland, E.; Ribatet, M.; Stephenson, A.G. A software review for extreme value analysis. Extremes 2012, 16, 103–119. [Google Scholar] [CrossRef]
- BOEM. Economic Analysis Methodology for the 2017–2022 Outer Continental Shelf Oil and Gas Leasing Program; U.S. Department of the Interior, Bureau of Ocean Energy Management: Sterling, VA, USA, 2016.
- NMFS. Biological Opinion on the Federally Regulated Oil and Gas Program Activities in the Gulf of Mexico; National Marine Fisheries Service, National Oceanic and Atmospheric Administration, U.S. Department of Commerce: Silver Spring, MA, USA, 2020; p. 695.
- Labelle, R.; Rainey, G.; Lanfear, K. An application of a vulnerability index to oil spill modeling in the Gulf of Mexico. Open-File Report 1982. [Google Scholar] [CrossRef]
- Labelle, R.; Anderson, C. Offshore oil-spill occurrence rates. In Proceedings of the OCEANS 96 MTS/IEEE Conference Proceedings. The Coastal Ocean—Prospects for the 21st Century, Fort Lauderdale, FL, USA, 23–26 September 2002; Volume 2, pp. 751–753. [Google Scholar]
- Ji, Z.-G.; Johnson, W.R.; Marshall, C.F.; Rainey, G.B.; Lear, E.M. Oil-Spill Risk Analysis: Gulf of Mexico Outer Continental Shelf (OCS) Lease Sales, Central Planning Area and Western Planning Area, 2003–2007, and Gulfwide OCS Program, 2003-2042; OCS Report 2002-032; U.S. Department of the Interior, Minerals Management Service: Herndon, VA, USA, 2002.
- Price, J.M.; Johnson, W.R.; Marshall, C.F.; Ji, Z.-G.; Rainey, G.B. Overview of the oil spill risk analysis (OSRA) model for en-vironmental impact assessment. Spill Sci. Technol. Bull. 2003, 8, 529–533. [Google Scholar] [CrossRef]
- Price, J.M.; Johnson, W.R.; Ji, Z.-G.; Marshall, C.F.; Rainey, G.B. Sensitivity testing for improved efficiency of a statistical oil-spill risk analysis model. Environ. Model. Softw. 2004, 19, 671–679. [Google Scholar] [CrossRef]
- Price, J.M.; Reed, M.; Howard, M.K.; Johnson, W.R.; Ji, Z.-G.; Marshall, C.F.; Guinasso, N.L.; Rainey, G.B. Preliminary assessment of an oil-spill trajectory model using satellite-tracked, oil-spill-simulating drifters. Environ. Model. Softw. 2006, 21, 258–270. [Google Scholar] [CrossRef]
- Oey, L.-Y.; Lee, H.; Schmitz, W.J., Jr. Effects of winds and Caribbean eddies on the frequency of Loop Current eddy shedding: A numerical model study. J. Geophys. Res. Space Phys. 2003, 108, 3324. [Google Scholar] [CrossRef]
- Chang, Y.-L.; Oey, L.; Xu, F.; Lu, H.-F.; Fujisaki, A. 2010 oil spill: Trajectory projections based on ensemble drifter analyses. Ocean Dyn. 2011, 61, 829–839. [Google Scholar] [CrossRef]
- Ji, Z.-G.; Smith, C.; Johnson, W.R. Oil-Spill Risk Analysis: Cook Inlet Planning Area; OCS Lease Sale 244, OCS Report 2016-032; U.S. Department of the Interior, Bureau of Ocean Energy Management: Sterling, VA, USA, 2016.
- NOAA. Trajectory Analysis Handbook. National Oceanic and Atmospheric Administration, NOAA Ocean Service: Seattle, WA, USA, 2002. [Google Scholar]
- Etkin, D.S.; French-McCay, D.; Michel, J. Review of the State-of-The-Art on Modeling Interactions between Spilled Oil and Shorelines for the Development of Algorithms for Oil Spill Risk Analysis Modeling; MMS OCS Study 2007-063; MMS Contract 0106PO39962; Environmental Research Consulting: Cortlandt Manor, NY, USA, 2007; p. 157. [Google Scholar]
- Danielson, S.; Hedstrom, K.; Curchitser, E. Cook Inlet Circulation Model Calculations, Final Report, BOEM OCS Study 2015-050; U.S. Department of the Interior, Bureau of Ocean Energy Management: Anchorage, AK, USA, 2016.
- Ji, Z.-G. Hydrodynamics and Water Quality: Modeling Rivers, Lakes, and Estuaries, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2017. [Google Scholar]
- Hooper, C.H. The IXTOC I Oil Spill: The Federal Scientific Response; US Department of Commerce, National Oceanic and Atmospheric Administration, Office of Marine Pollution Assessment: Silver Spring, MD, USA, 1982.
- On Scene Coordinator Report: Deepwater Horizon Oil Spill; Submitted to the National Response Team; United States Coast Guard: Washington, DC, USA, 2011. Available online: https://www.loc.gov/item/2012427375 (accessed on 10 February 2021).
- Jernelöv, A.; Lindén, O. Ixtoc I: A case study of the world’s largest oil spill. Ambio 1981, 10, 299–306. [Google Scholar]
- Galt, J.A. Transport, distribution, and physical characteristics of the oil: Part 1—offshore movement and distribution. In The Ixtoc I Oil Spill: The Federal Scientific Response; Hooper, C.H., Ed.; NOAA Hazardous Materials Response Project: Boulder, CO, USA, 1981; pp. 13–39. [Google Scholar]
- Anderson, E.L. Oilspill Hindcast Simulation of the IXTOC 1 Gulf of Mexico Spill. Master’s Thesis, University of Rhode Island, Kingston, RI, USA, 1983. Available online: https://digitalcommons.uri.edu/theses/1168/ (accessed on 10 February 2021).
- Ji, Z.-G. Use of Physical Sciences in Support of Environmental Management. Environ. Manag. 2004, 34, 159–169. [Google Scholar] [CrossRef]
- Sun, S.; Hu, C.; Tunnell, J.W., Jr. Surface oil footprint and trajectory of the Ixtoc-I oil spill determined from Landsat/MSS and CZCS observations. Mar. Pollut. Bull. 2015, 101, 632–641. [Google Scholar] [CrossRef] [PubMed]
- Biggs, D.C.; Fargion, G.S.; Leben, R.R.; Hamilton, P. Cleavage of a Gulf of Mexico loop current eddy by a deep water cyclone. J. Geophys. Res. Space Phys. 1996, 101, 20629–20641. [Google Scholar] [CrossRef]
- Zavala-Hidalgo, J.; Romero-Centeno, R.; Mateos-Jasso, A.; Morey, S.L.; Martínez-López, B. The response of the Gulf of Mexico to wind and heat flux forcing: What has been learned in recent years? Atmósfera 2014, 27, 317–334. [Google Scholar] [CrossRef]
- ERCO. Ixtoc Oil Spill Assessment. Final Report. Executive Summary. Report Prepared for the Bureau of Land Management; AA851-CTO-71; Energy Resources Co., Inc.: Cambridge, MA, USA, 1982; p. 37. [Google Scholar]
- Farrington, J.W. NOAA Ship Researcher/Contract Vessel Pierce Cruise to Ixtoc-1 Oil Spill: Overview and Integrative Data As-sessment and Interpretation; Report prepared for the Office of Marine Pollution Assessment, NOAA, NA80RAC0017; NOAA: Silver Spring, MD, USA, 1983. [Google Scholar]
- Allshouse, M.R.; Ivey, G.N.; Lowe, R.J.; Jones, N.L.; Beegle-Krause, C.J.; Xu, J.; Peacock, T. Impact of windage on ocean surface Lagrangian coherent structures. Environ. Fluid Mech. 2017, 17, 473–483. [Google Scholar] [CrossRef]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).