Hull Shape Design Optimization with Parameter Space and Model Reductions, and Self-Learning Mesh Morphing
Abstract
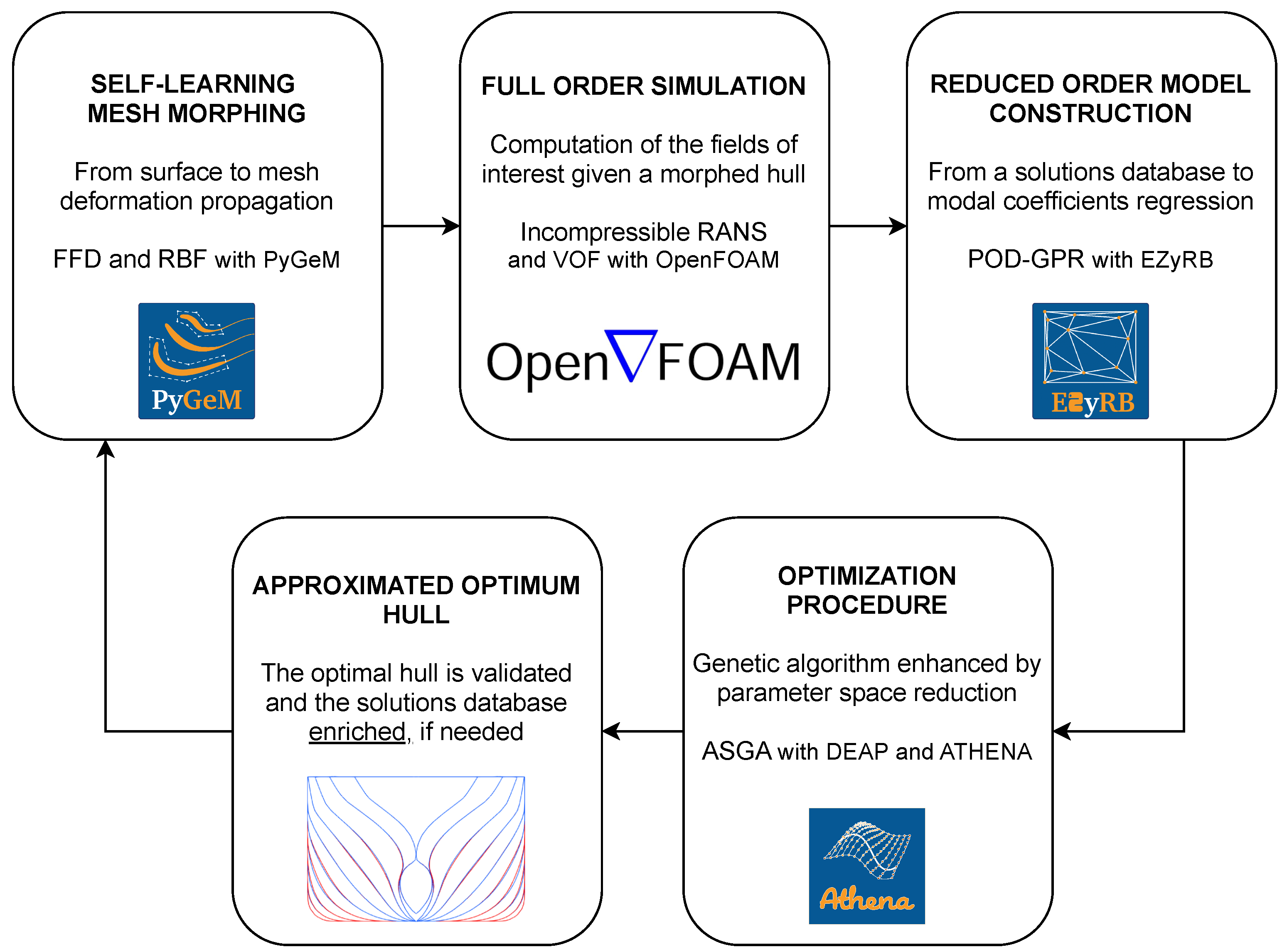
1. Introduction
2. Shape and Grid Parameterization
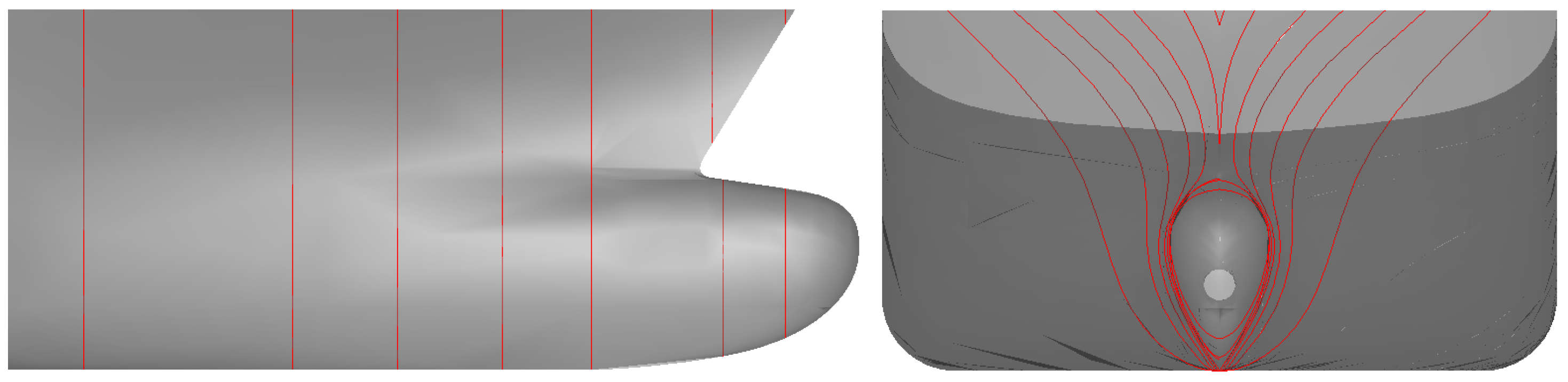
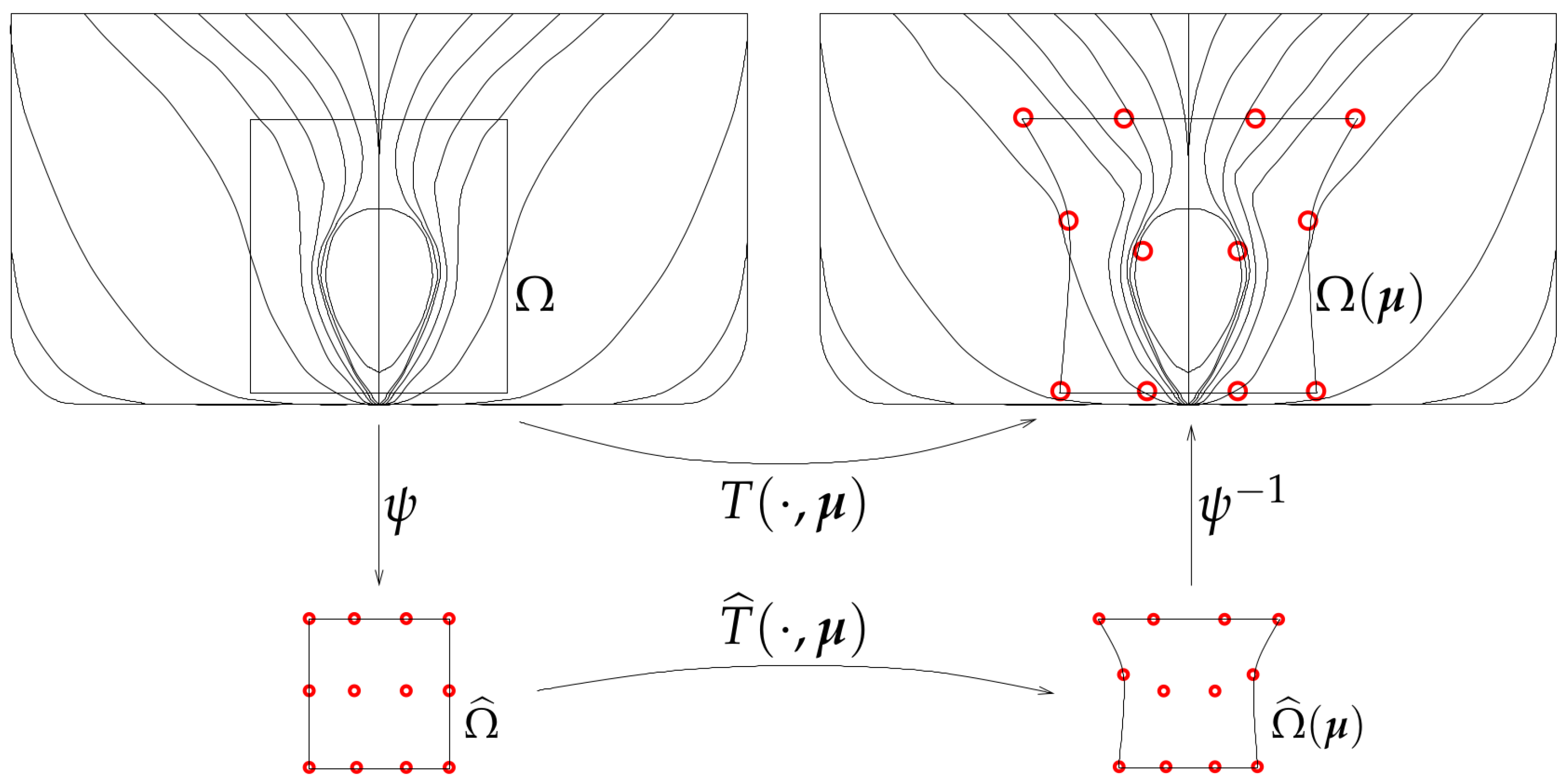
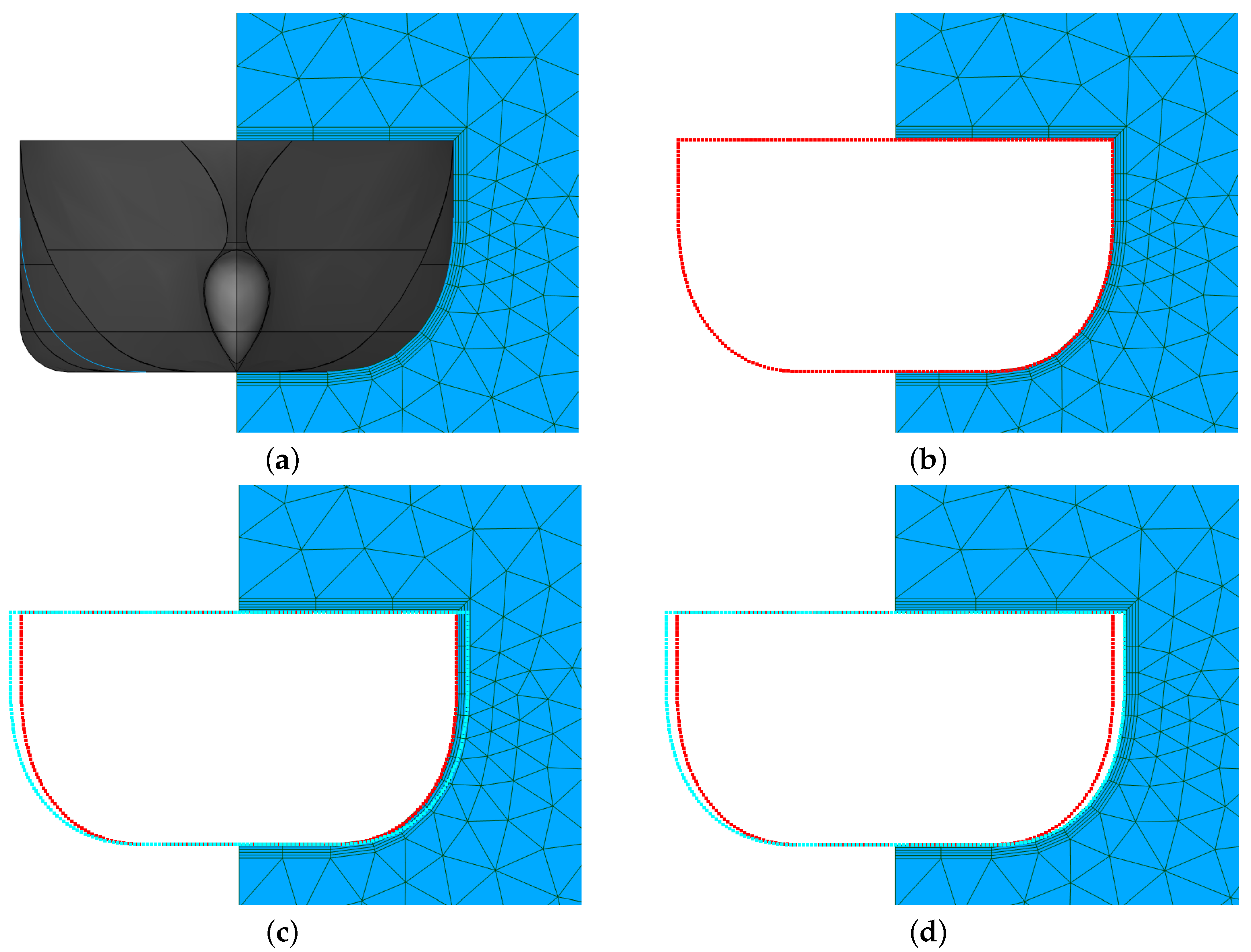
How to Combine Different Shape Parametrization Strategies
3. The Mathematical Model for Incompressible Fluids
3.1. The Full Order Model: Incompressible Rans
3.2. The Reduced Order Model: POD-GPR
4. Optimization Procedure with Built-In Parameters Reduction
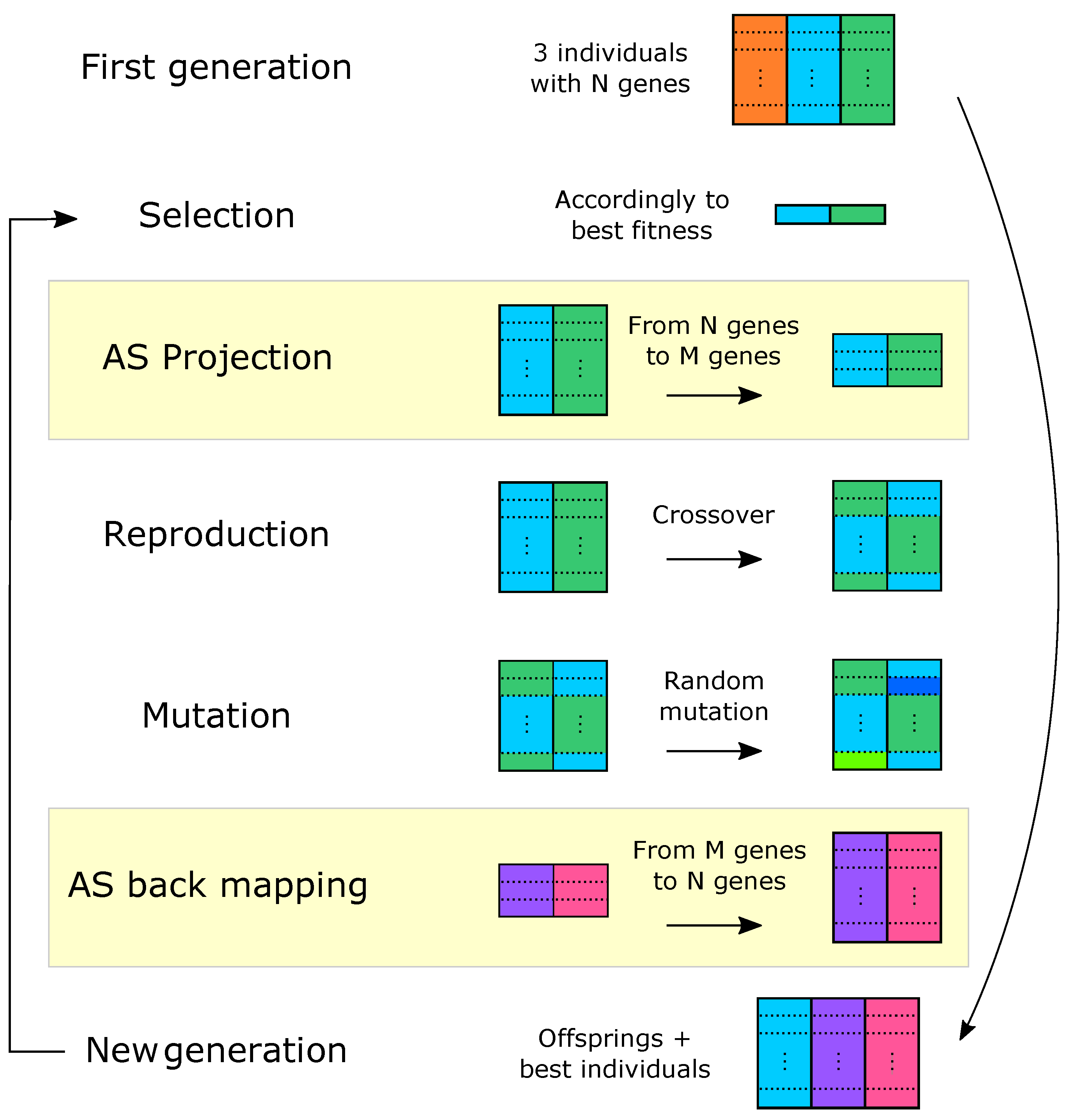
4.1. Genetic Algorithm
4.2. Active Subspaces
4.3. Active Subspaces-Based Genetic Algorithm
5. Numerical Results
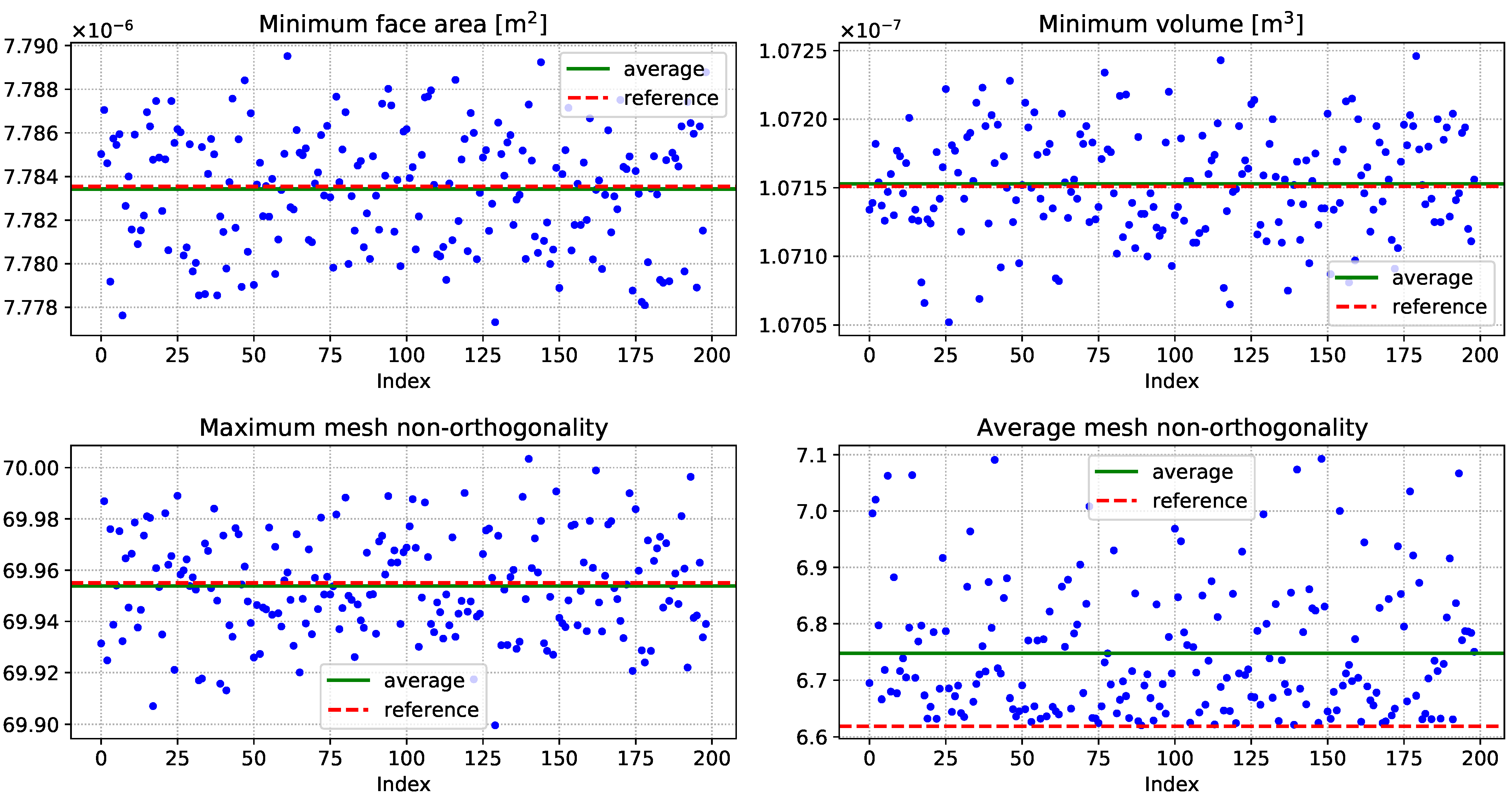
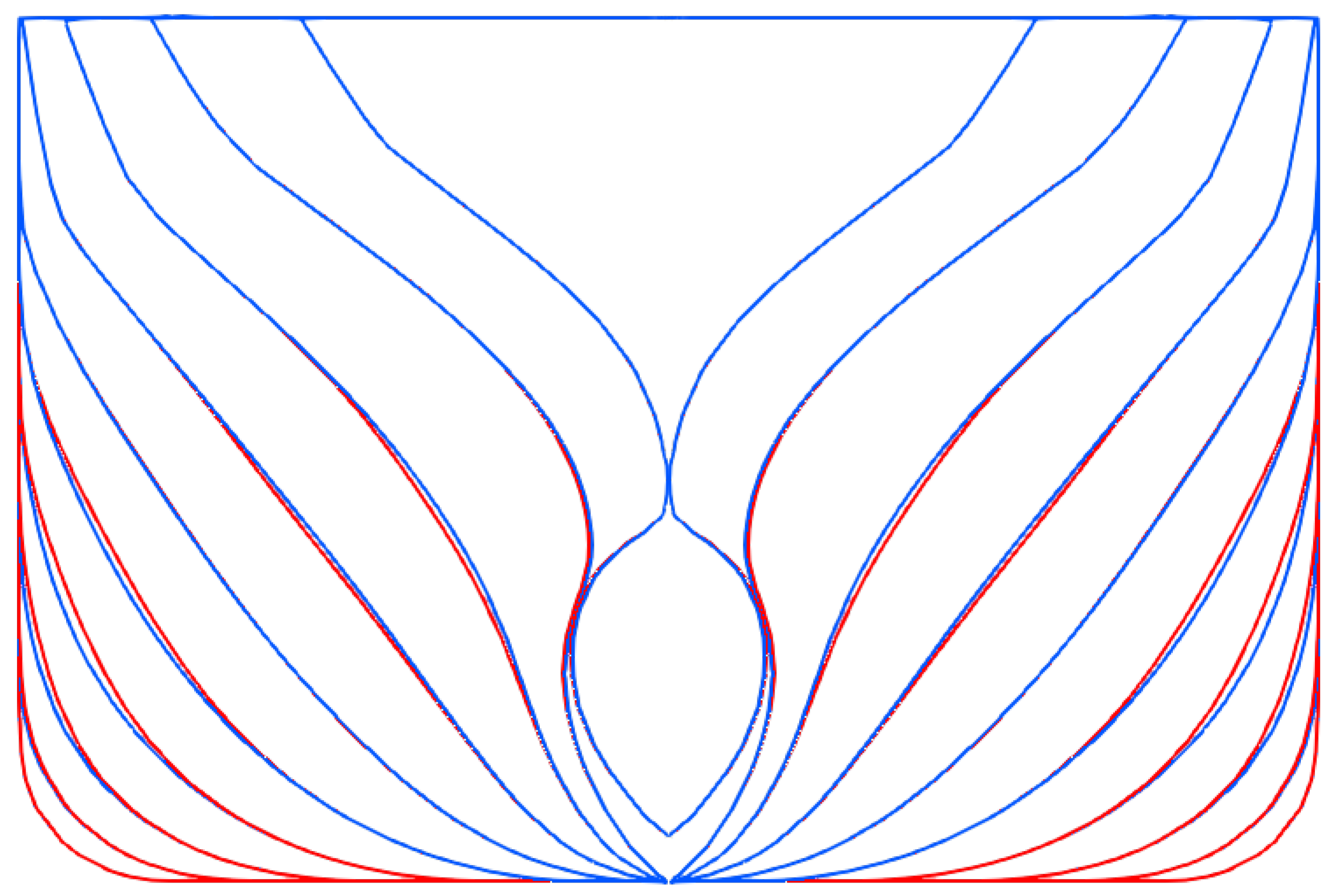
5.1. Self-Learning Mesh Morphing Parameters
- axis: 7 points layers located on sections 10, 12, 14, 16, 18, 20, 22;
- axis: 11 points layers that cover the whole hull beam, with the second and the second-to-last positioned on the lateral walls of the ship;
- axis: 7 points layers that cover the whole hull draft, aligning the 2nd and the 5th of them to the hull bottom and to the waterline, respectively.
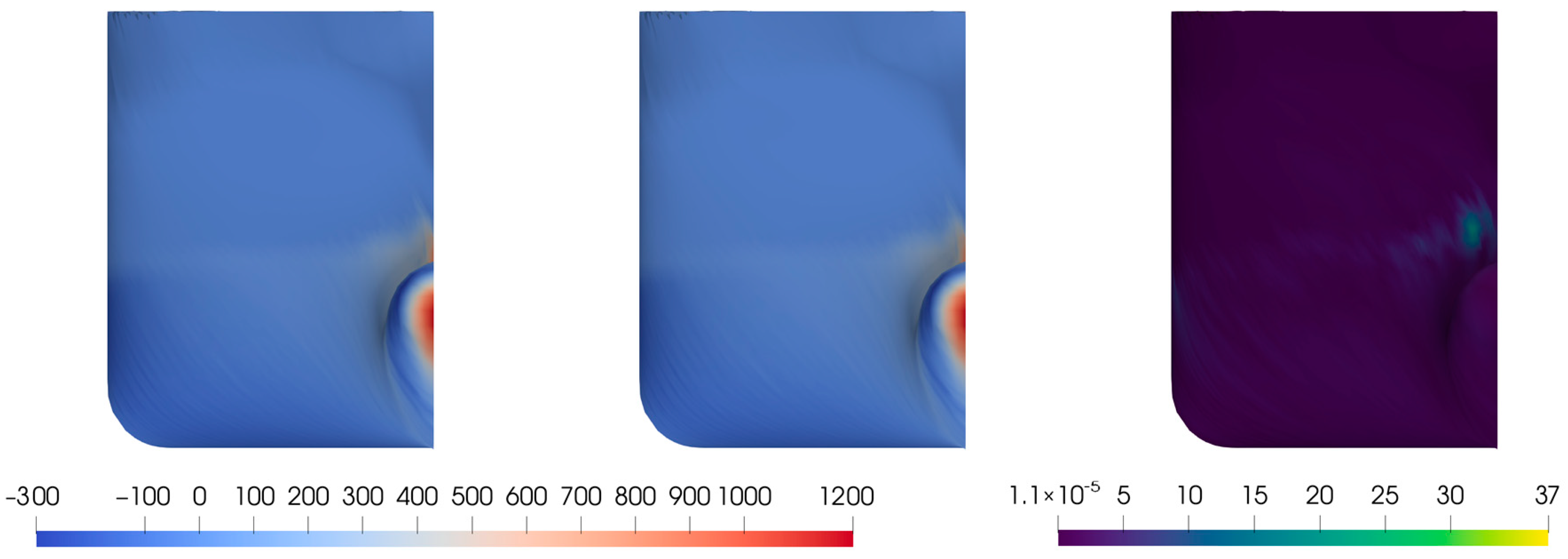
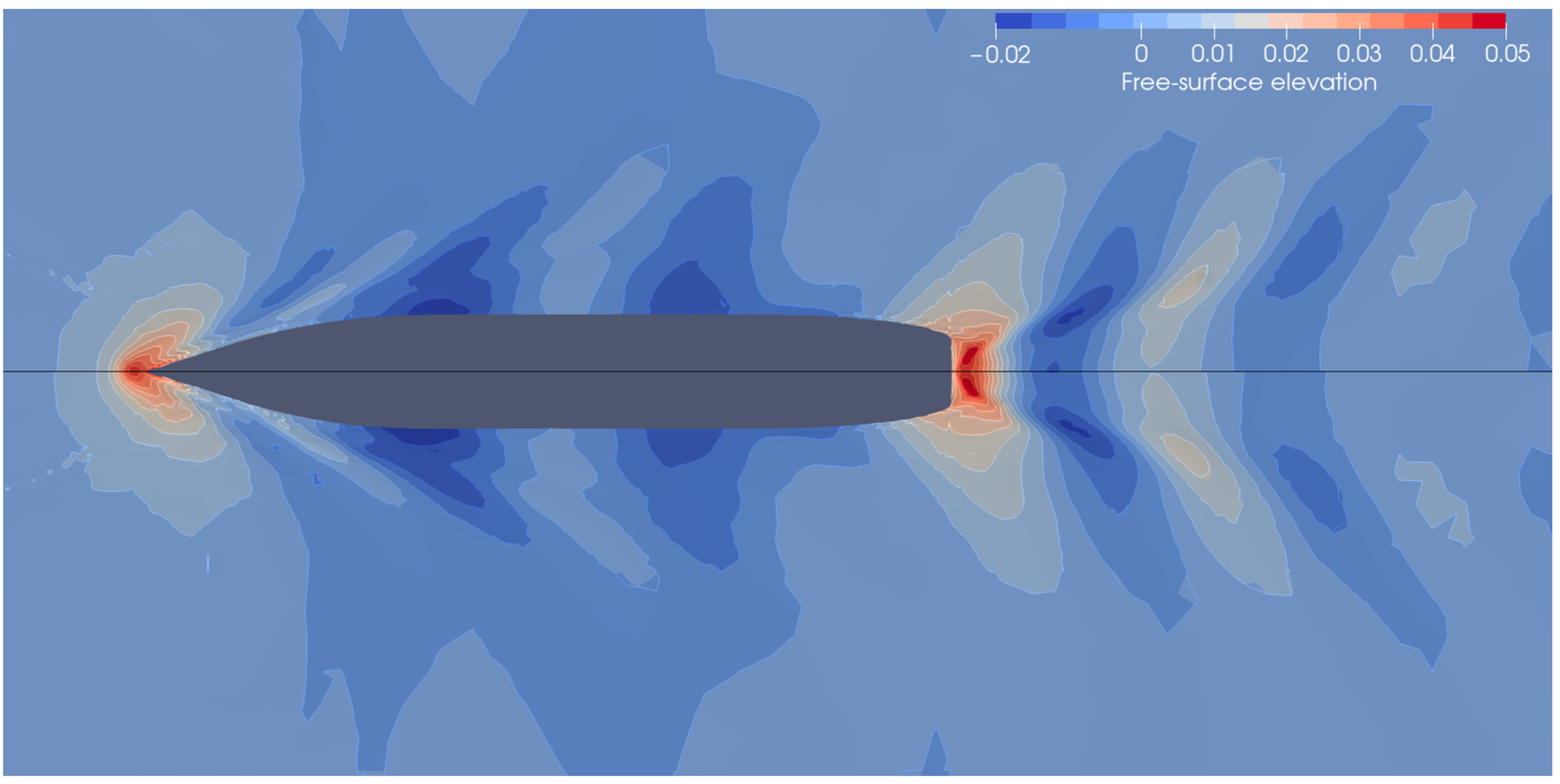
5.2. Reduced Order Model Construction
- at the inlet we set constant velocity, fixed flux condition for the pressure and a fixed profile for the VOF variable;
- at the outlet we set constant average velocity, zero-gradient condition for the pressure and variable height flow rate condition for VOF variable;
- at the bottom and lateral planes, we impose symmetric conditions for all the quantities;
- at the top plane, we set a pressure inlet outlet velocity condition for the velocity and nil pressure; VOF variable is fixed to 1 (air);
- at the hull surface, we impose no-slip condition for velocity, fixed flux condition for the pressure and zero-gradient condition for VOF variable.
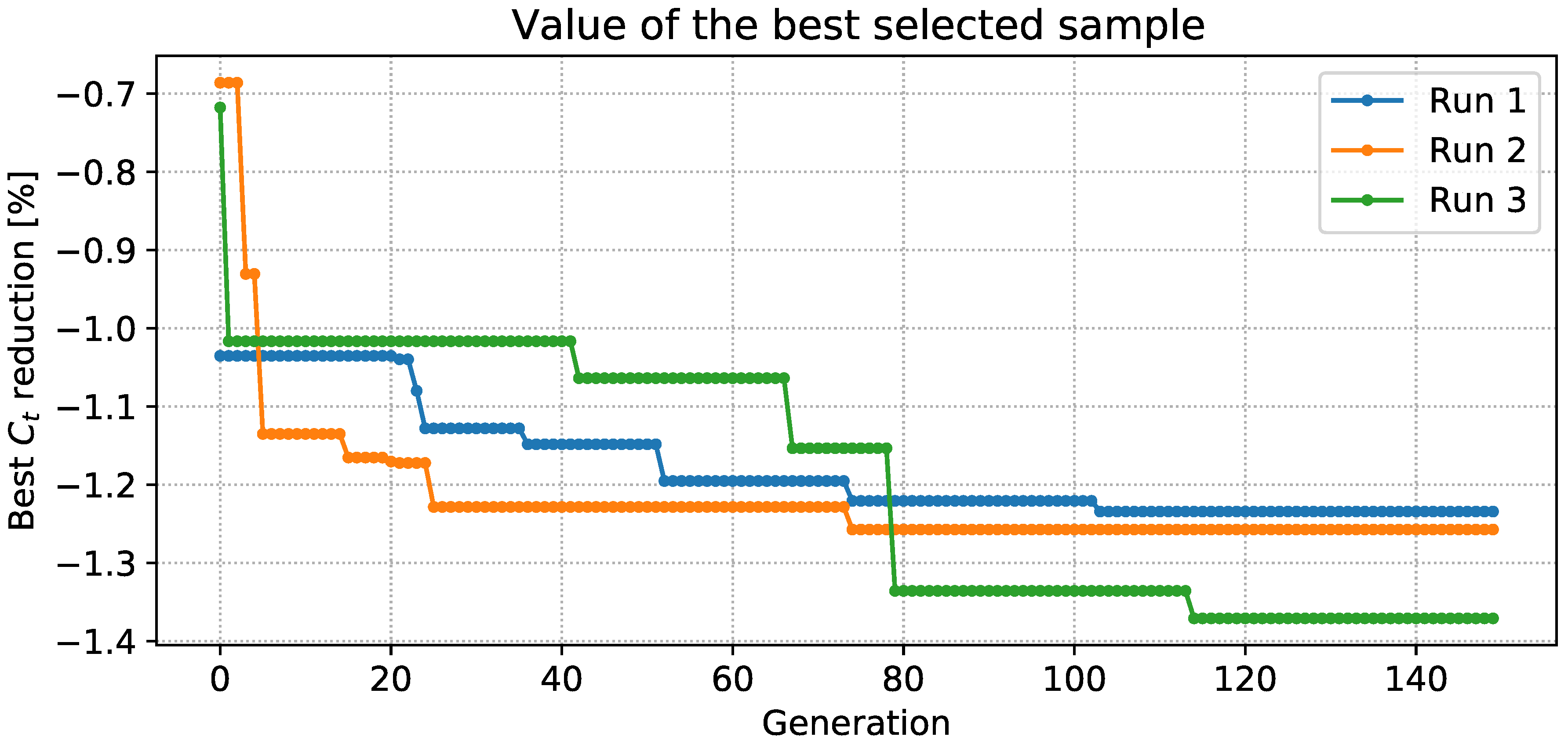
5.3. Optimization Procedure
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AS | Active subspaces |
| ASGA | Active subspaces genetic algorithm |
| CAD | Computer-aided design |
| CFD | Computational fluid dynamics |
| FFD | Free form deformation |
| FOM | Full order model |
| GA | Genetic algorithm |
| GPR | Gaussian process regression |
| HPC | High performance computing |
| PDE | Partial differential equation |
| POD | Proper orthogonal decomposition |
| POD-GPR | Proper orthogonal decomposition with Gaussian process regression |
| RBF | Radial basis functions |
| RANS | Reynolds averaged Navier–Stokes |
| ROM | Reduced order method |
| STL | Stereolithography tesselation language |
| VOF | Volume of fluid |
References
- Salmoiraghi, F.; Ballarin, F.; Corsi, G.; Mola, A.; Tezzele, M.; Rozza, G. Advances in geometrical parametrization and reduced order models and methods for computational fluid dynamics problems in applied sciences and engineering: Overview and perspectives. In Proceedings of the ECCOMAS Congress 2016—7th European Congress on Computational Methods in Applied Sciences and Engineering, Crete, Greece, 5–10 June 2016; pp. 1013–1031. [Google Scholar]
- Rozza, G.; Malik, M.H.; Demo, N.; Tezzele, M.; Girfoglio, M.; Stabile, G.; Mola, A. Advances in Reduced Order Methods for Parametric Industrial Problems in Computational Fluid Dynamics. In Proceedings of the ECCOMAS ECFD 7—6th European Conference on Computational Mechanics (ECCM 6) and 7th European Conference on Computational Fluid Dynamics (ECFD 7); Owen, R., de Borst, R., Reese, J., Chris, P., Eds.; ECCOMAS: Glasgow, UK, 2018; pp. 59–76. [Google Scholar]
- Demo, N.; Tezzele, M.; Gustin, G.; Lavini, G.; Rozza, G. Shape optimization by means of proper orthogonal decomposition and dynamic mode decomposition. In Proceedings of the Technology and Science for the Ships of the Future: Proceedings of NAV 2018: 19th International Conference on Ship & Maritime Research, 20–22 June 2018; IOS Press: Amsterdam, The Netherlands, 2018; pp. 212–219. [Google Scholar]
- Demo, N.; Ortali, G.; Gustin, G.; Rozza, G.; Lavini, G. An efficient computational framework for naval shape design and optimization problems by means of data-driven reduced order modeling techniques. Boll. Dell’Unione Mat. Ital. 2020, 1–20. [Google Scholar] [CrossRef]
- Tezzele, M.; Salmoiraghi, F.; Mola, A.; Rozza, G. Dimension reduction in heterogeneous parametric spaces with application to naval engineering shape design problems. Adv. Model. Simul. Eng. Sci. 2018, 5, 25. [Google Scholar] [CrossRef] [PubMed]
- Demo, N.; Tezzele, M.; Mola, A.; Rozza, G. An efficient shape parametrisation by free-form deformation enhanced by active subspace for hull hydrodynamic ship design problems in open source environment. In Proceedings of the ISOPE 2018: The 28th International Ocean and Polar Engineering Conference, Sapporo, Japan, 10–15 June 2018; Volume 3, pp. 565–572. [Google Scholar]
- Demo, N.; Tezzele, M.; Mola, A.; Rozza, G. A complete data-driven framework for the efficient solution of parametric shape design and optimisation in naval engineering problems. In Proceedings of the MARINE 2019: VIII International Conference on Computational Methods in Marine Engineering, Gothenburg, Sweden, 13–15 May 2019; Bensow, R., Ringsberg, J., Eds.; European Community on Computational Methods in Applied Sciences: Gothenburg, Sweden, 2019; pp. 111–121. [Google Scholar]
- Tezzele, M.; Demo, N.; Rozza, G. Shape optimization through proper orthogonal decomposition with interpolation and dynamic mode decomposition enhanced by active subspaces. In Proceedings of the MARINE 2019: VIII International Conference on Computational Methods in Marine Engineering, Gothenburg, Sweden, 13–15 May 2019; Bensow, R., Ringsberg, J., Eds.; European Community on Computational Methods in Applied Sciences: Gothenburg, Sweden, 2019; pp. 122–133. [Google Scholar]
- Villa, D.; Gaggero, S.; Coppede, A.; Vernengo, G. Parametric hull shape variations by Reduced Order Model based geometric transformation. Ocean. Eng. 2020, 216, 107826. [Google Scholar] [CrossRef]
- Diez, M.; Campana, E.F.; Stern, F. Design-space dimensionality reduction in shape optimization by Karhunen–Loève expansion. Comput. Methods Appl. Mech. Eng. 2015, 283, 1525–1544. [Google Scholar] [CrossRef]
- Serani, A.; Campana, E.F.; Diez, M.; Stern, F. Towards augmented design-space exploration via combined geometry and physics based Karhunen-Loève expansion. In Proceedings of the 18th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Denver, CO, USA, 5–9 June 2017; p. 3665. [Google Scholar]
- Mola, A.; Tezzele, M.; Gadalla, M.; Valdenazzi, F.; Grassi, D.; Padovan, R.; Rozza, G. Efficient reduction in shape parameter space dimension for ship propeller blade design. In Proceedings of the MARINE 2019: VIII International Conference on Computational Methods in Marine Engineering, Göteborg, Sweden, 13–15 May 2019; Bensow, R., Ringsberg, J., Eds.; pp. 201–212. [Google Scholar]
- Gaggero, S.; Vernengo, G.; Villa, D.; Bonfiglio, L. A reduced order approach for optimal design of efficient marine propellers. Ships Offshore Struct. 2020, 15, 200–214. [Google Scholar] [CrossRef]
- Gadalla, M.; Cianferra, M.; Tezzele, M.; Stabile, G.; Mola, A.; Rozza, G. On the comparison of LES data-driven reduced order approaches for hydroacoustic analysis. Comput. Fluids 2021, 216, 104819. [Google Scholar] [CrossRef]
- Jeong, K.L.; Jeong, S.M. A Mesh Deformation Method for CFD-Based Hull form Optimization. J. Mar. Sci. Eng. 2020, 8, 473. [Google Scholar] [CrossRef]
- Demo, N.; Tezzele, M.; Rozza, G. A supervised learning approach involving active subspaces for an efficient genetic algorithm in high-dimensional optimization problems. arXiv 2020, arXiv:2006.07282. [Google Scholar]
- Tezzele, M.; Demo, N.; Mola, A.; Rozza, G. PyGeM: Python Geometrical Morphing. In Software Impacts; Elsevier: Amsterdam, The Netherlands, 2020; Volume 7, p. 100047. [Google Scholar] [CrossRef]
- Romor, F.; Tezzele, M.; Rozza, G. ATHENA: Advanced Techniques for High dimensional parameter spaces to Enhance Numerical Analysis. 2020; Submitted. [Google Scholar]
- Demo, N.; Tezzele, M.; Rozza, G. EZyRB: Easy Reduced Basis method. J. Open Source Softw. 2018, 3, 661. [Google Scholar] [CrossRef]
- GPy. GPy: A Gaussian Process Framework in Python. 2012. Available online: http://github.com/SheffieldML/GPy (accessed on 1 January 2020).
- Moctar, O.E.; Shigunov, V.; Zorn, T. Duisburg Test Case: Post-panamax container ship for benchmarking. Ship Technol. Res. 2012, 59, 50–64. [Google Scholar] [CrossRef]
- Sederberg, T.; Parry, S. Free-Form Deformation of solid geometric models. In Proceedings of the SIGGRAPH—Special Interest Group on GRAPHics and Interactive Techniques; SIGGRAPH: Dallas, TX, USA, 1986; pp. 151–159. Available online: https://dblp.org/db/conf/siggraph/siggraph1986.html (accessed on 1 January 2020).
- Lassila, T.; Rozza, G. Parametric free-form shape design with PDE models and reduced basis method. Comput. Methods Appl. Mech. Eng. 2010, 199, 1583–1592. [Google Scholar] [CrossRef]
- Sieger, D.; Menzel, S.; Botsch, M. On shape deformation techniques for simulation-based design optimization. In New Challenges in Grid Generation and Adaptivity for Scientific Computing; Springer: Berlin/Heidelberg, Germany, 2015; pp. 281–303. [Google Scholar]
- OpenCFD. OpenFOAM—The Open Source CFD Toolbox—User’s Guide, 6th ed.; OpenCFD Ltd.: London, UK, 2018. [Google Scholar]
- Hirt, C.; Nichols, B. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Menter, F. Zonal two equation k-w turbulence models for aerodynamic flows. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, Orlando, FL, USA, 6–9 July 1993; p. 2906. [Google Scholar] [CrossRef]
- Volkwein, S. Proper Orthogonal Decomposition: Theory and Reduced-Order Modelling. In Lecture Notes; University of Konstanz: Konstanz, Germany, 2012. [Google Scholar]
- Strazzullo, M.; Ballarin, F.; Rozza, G. POD–Galerkin Model Order Reduction for Parametrized Time Dependent Linear Quadratic Optimal Control Problems in Saddle Point Formulation. J. Sci. Comput. 2020, 83, 55. [Google Scholar] [CrossRef]
- Girfoglio, M.; Quaini, A.; Rozza, G. A POD-Galerkin reduced order model for a LES filtering approach. arXiv 2020, arXiv:2009.13593. [Google Scholar]
- Hesthaven, J.S.; Rozza, G.; Stamm, B. Certified Reduced Basis Methods for Parametrized Partial Differential Equations, 1st ed.; Springer Briefs in Mathematics; Springer: Cham, Switzerland, 2015; p. 135. [Google Scholar] [CrossRef]
- Hijazi, S.; Stabile, G.; Mola, A.; Rozza, G. Data-Driven POD–Galerkin reduced order model for turbulent flows. J. Comput. Phys. 2020, 416, 109513. [Google Scholar] [CrossRef]
- Georgaka, S.; Stabile, G.; Star, K.; Rozza, G.; Bluck, M.J. A hybrid reduced order method for modelling turbulent heat transfer problems. Comput. Fluids 2020, 208, 104615. [Google Scholar] [CrossRef]
- Salmoiraghi, F.; Scardigli, A.; Telib, H.; Rozza, G. Free-form deformation, mesh morphing and reduced-order methods: Enablers for efficient aerodynamic shape optimisation. Int. J. Comput. Fluid Dyn. 2018, 32, 233–247. [Google Scholar] [CrossRef]
- Garotta, F.; Demo, N.; Tezzele, M.; Carraturo, M.; Reali, A.; Rozza, G. Reduced Order Isogeometric Analysis Approach for PDEs in Parametrized Domains. In Quantification of Uncertainty: Improving Efficiency and Technology: QUIET Selected Contributions; D’Elia, M., Gunzburger, M., Rozza, G., Eds.; Lecture Notes in Computational Science and Engineering; Springer: Cham, Switzerland, 2020; Volume 137, pp. 153–170. [Google Scholar] [CrossRef]
- Tezzele, M.; Demo, N.; Mola, A.; Rozza, G. An integrated data-driven computational pipeline with model order reduction for industrial and applied mathematics. Spec. Vol. ECMI 2020, in press. [Google Scholar]
- Wang, Q.; Hesthaven, J.S.; Ray, D. Non-intrusive reduced order modeling of unsteady flows using artificial neural networks with application to a combustion problem. J. Comput. Phys. 2019, 384, 289–307. [Google Scholar] [CrossRef]
- Ortali, G.; Demo, N.; Rozza, G. Gaussian process approach within a data-driven POD framework for fluid dynamics engineering problems. arXiv 2020, arXiv:2012.01989. [Google Scholar]
- Guo, M.; Hesthaven, J.S. Reduced order modeling for nonlinear structural analysis using Gaussian process regression. Comput. Methods Appl. Mech. Eng. 2018, 341, 807–826. [Google Scholar] [CrossRef]
- Williams, C.K.; Rasmussen, C.E. Gaussian Processes for Machine Learning; Adaptive Computation and Machine Learning Series; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Holland, J.H. Genetic algorithms and the optimal allocation of trials. SIAM J. Comput. 1973, 2, 88–105. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2020, 1–36. [Google Scholar] [CrossRef]
- El-Mihoub, T.A.; Hopgood, A.A.; Nolle, L.; Battersby, A. Hybrid Genetic Algorithms: A Review. Eng. Lett. 2006, 13, 124–137. [Google Scholar]
- Sivaraj, R.; Ravichandran, T. A review of selection methods in genetic algorithm. Int. J. Eng. Sci. Technol. 2011, 3, 3792–3797. [Google Scholar]
- Constantine, P.G. Active Subspaces: Emerging Ideas for Dimension Reduction in Parameter Studies; SIAM Spotlights: Philadelphia, PA, USA, 2015; Volume 2. [Google Scholar]
- Zahm, O.; Constantine, P.G.; Prieur, C.; Marzouk, Y.M. Gradient-based dimension reduction of multivariate vector-valued functions. SIAM J. Sci. Comput. 2020, 42, A534–A558. [Google Scholar] [CrossRef]
- Rozza, G.; Hess, M.; Stabile, G.; Tezzele, M.; Ballarin, F. Basic Ideas and Tools for Projection-Based Model Reduction of Parametric Partial Differential Equations. In Model Order Reduction; Benner, P., Grivet-Talocia, S., Quarteroni, A., Rozza, G., Schilders, W.H.A., Silveira, L.M., Eds.; De Gruyter: Berlin, Germany; Boston, MA, USA, 2020; Volume 2, Chapter 1; pp. 1–47. [Google Scholar] [CrossRef]
- Romor, F.; Tezzele, M.; Lario, A.; Rozza, G. Kernel-based Active Subspaces with application to CFD parametric problems using Discontinuous Galerkin method. arXiv 2020, arXiv:2008.12083. [Google Scholar]
- Tezzele, M.; Ballarin, F.; Rozza, G. Combined parameter and model reduction of cardiovascular problems by means of active subspaces and POD-Galerkin methods. In Mathematical and Numerical Modeling of the Cardiovascular System and Applications; Boffi, D., Pavarino, L.F., Rozza, G., Scacchi, S., Vergara, C., Eds.; SEMA-SIMAI Series; Springer: Berlin/Heidelberg, Germany, 2018; Volume 16, pp. 185–207. [Google Scholar] [CrossRef]
- Demo, N.; Tezzele, M.; Rozza, G. A non-intrusive approach for reconstruction of POD modal coefficients through active subspaces. C. R. MÉcanique L’AcadÉmie Des. Sci. 2019, 347, 873–881. [Google Scholar] [CrossRef]
- Tezzele, M.; Demo, N.; Stabile, G.; Mola, A.; Rozza, G. Enhancing CFD predictions in shape design problems by model and parameter space reduction. Adv. Model. Simul. Eng. Sci. 2020, 7. [Google Scholar] [CrossRef]
- Romor, F.; Tezzele, M.; Rozza, G. Multi-fidelity data fusion for the approximation of scalar functions with low intrinsic dimensionality through active subspaces. arXiv 2020, arXiv:2010.08349. [Google Scholar]
- Liu, B.; Lin, G. High-Dimensional Nonlinear Multi-Fidelity Model with Gradient-Free Active Subspace Method. Commun. Comput. Phys. 2020, 28, 1937–1969. [Google Scholar] [CrossRef]
- Fortin, F.A.; De Rainville, F.M.; Gardner, M.A.; Parizeau, M.; Gagné, C. DEAP: Evolutionary algorithms made easy. J. Mach. Learn. Res. 2012, 13, 2171–2175. [Google Scholar]
- Beckert, A.; Wendland, H. Multivariate interpolation for fluid-structure-interaction problems using radial basis functions. Aerosp. Sci. Technol. 2001, 5, 125–134. [Google Scholar] [CrossRef]
| 1. | Freely available at https://github.com/mathLab/ATHENA (accessed date 1 January 2020). |
| 2. | Imposed for y symmetry conservation. |





| Quantity | Value |
|---|---|
| Length between perpendiculars | |
| Waterline breadth | |
| Draught midships | |
| Volume displacement | |
| Block coefficient |
| Lattice Points | Parameter | Displacement Direction | ||
|---|---|---|---|---|
| Index x | Index y | Index z | ||
| 2 | 0 | 2–4 | x | |
| 2 | 10 | 2–4 | x | |
| 3 | 0 | 2–4 | x | |
| 3 | 10 | 2–4 | x | |
| 4 | 0 | 2–4 | x | |
| 4 | 10 | 2–4 | x | |
| 4 | 2–4 | 2 | y | |
| 4 | 6–8 | 2 | 2 | y |
| 4 | 2–4 | 3 | y | |
| 4 | 6–8 | 3 | 2 | y |
| 4 | 2–4 | 4 | y | |
| 4 | 6–8 | 4 | 2 | y |
| 3 | 2–4 | 2 | y | |
| 3 | 6–8 | 2 | 2 | y |
| 5 | 2–4 | 3 | y | |
| 5 | 6–8 | 3 | 2 | y |
| 4 | 0–1 | 2 | z | |
| 4 | 9–10 | 2 | z | |
| 5 | 0 | 3 | z | |
| 5 | 10 | 3 | z | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demo, N.; Tezzele, M.; Mola, A.; Rozza, G. Hull Shape Design Optimization with Parameter Space and Model Reductions, and Self-Learning Mesh Morphing. J. Mar. Sci. Eng. 2021, 9, 185. https://doi.org/10.3390/jmse9020185
Demo N, Tezzele M, Mola A, Rozza G. Hull Shape Design Optimization with Parameter Space and Model Reductions, and Self-Learning Mesh Morphing. Journal of Marine Science and Engineering. 2021; 9(2):185. https://doi.org/10.3390/jmse9020185
Chicago/Turabian StyleDemo, Nicola, Marco Tezzele, Andrea Mola, and Gianluigi Rozza. 2021. "Hull Shape Design Optimization with Parameter Space and Model Reductions, and Self-Learning Mesh Morphing" Journal of Marine Science and Engineering 9, no. 2: 185. https://doi.org/10.3390/jmse9020185
APA StyleDemo, N., Tezzele, M., Mola, A., & Rozza, G. (2021). Hull Shape Design Optimization with Parameter Space and Model Reductions, and Self-Learning Mesh Morphing. Journal of Marine Science and Engineering, 9(2), 185. https://doi.org/10.3390/jmse9020185







