Seakeeping Tests of a FOWT in Wind and Waves: An Analysis of Dynamic Coupling Effects and Their Impact on the Predictions of Pitch Motion Response
Abstract
1. Introduction
2. Materials and Methods
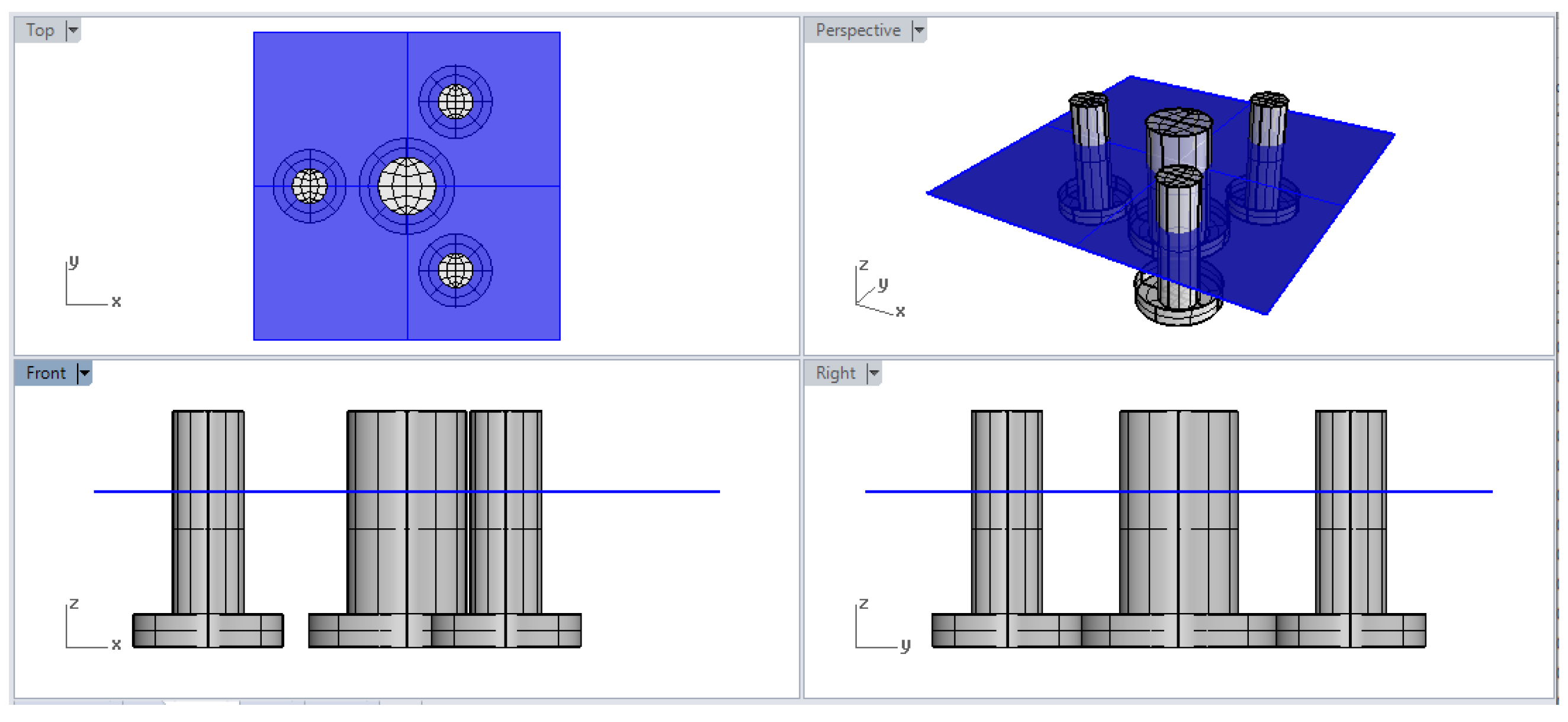
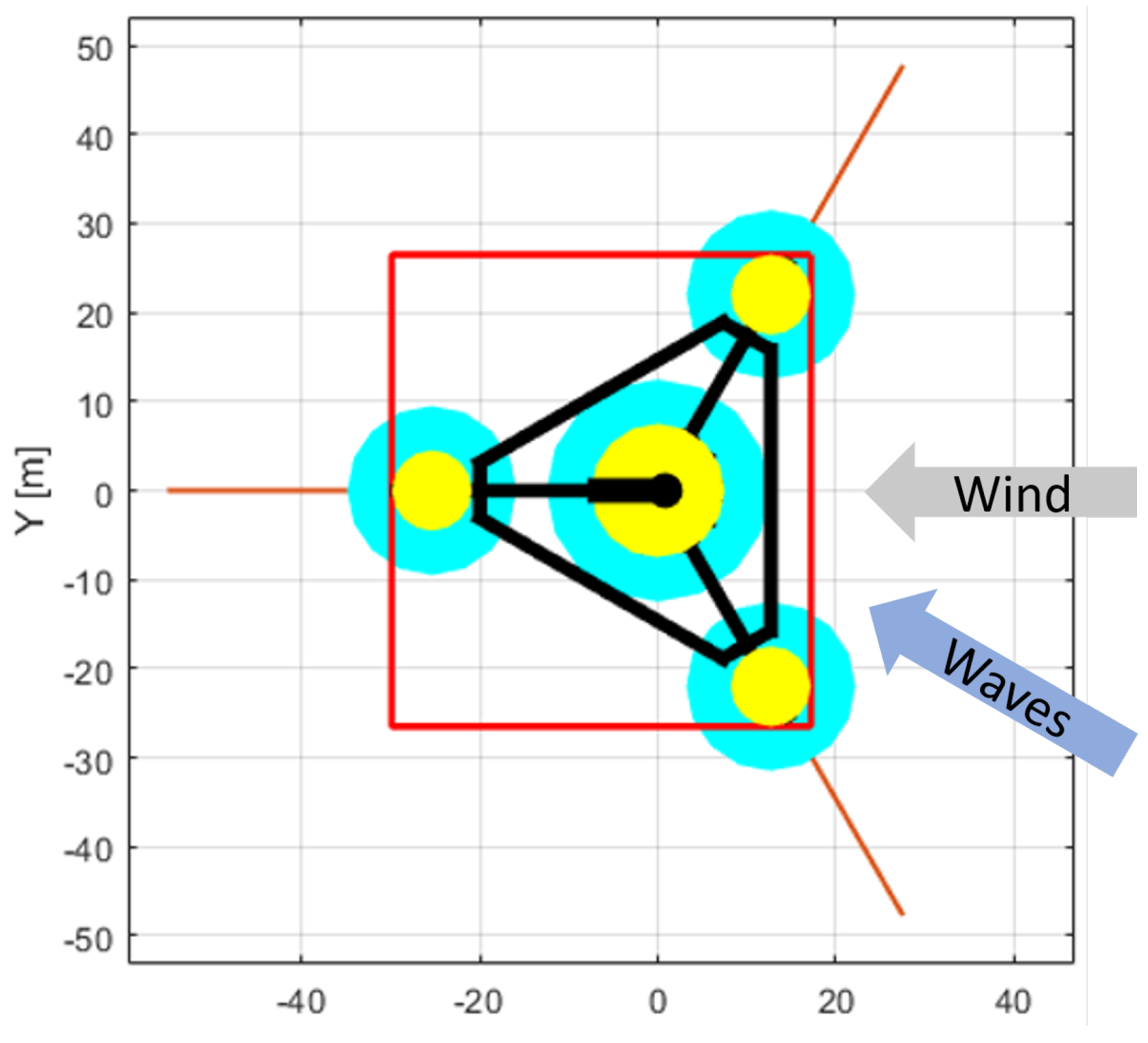
2.1. FOWT Geometry and Mooring System
2.2. Experimental Setup
2.3. Wind Force Emulation Using a Software-in-the-Loop (SIL) Scheme
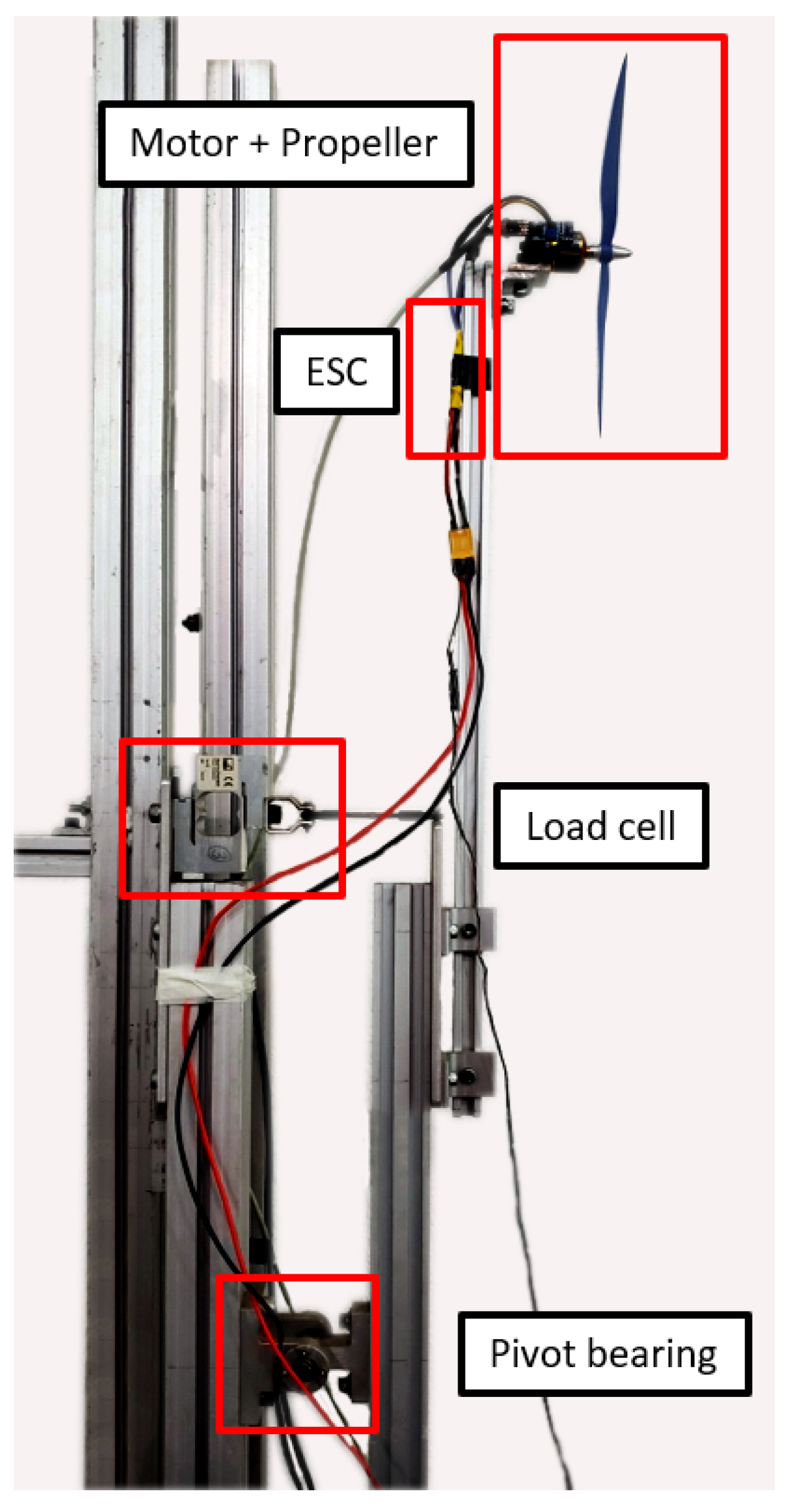
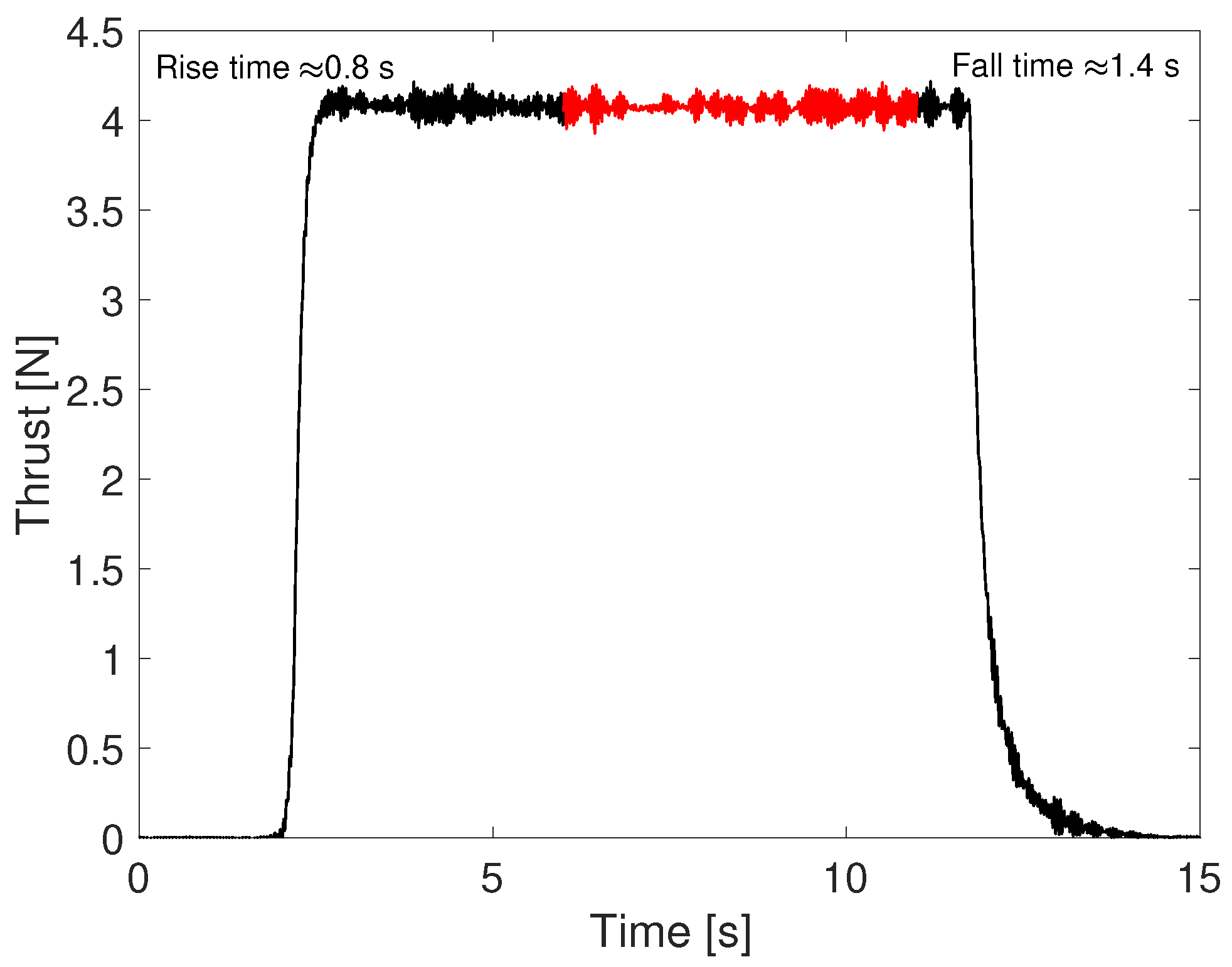
2.4. Wind Actuator
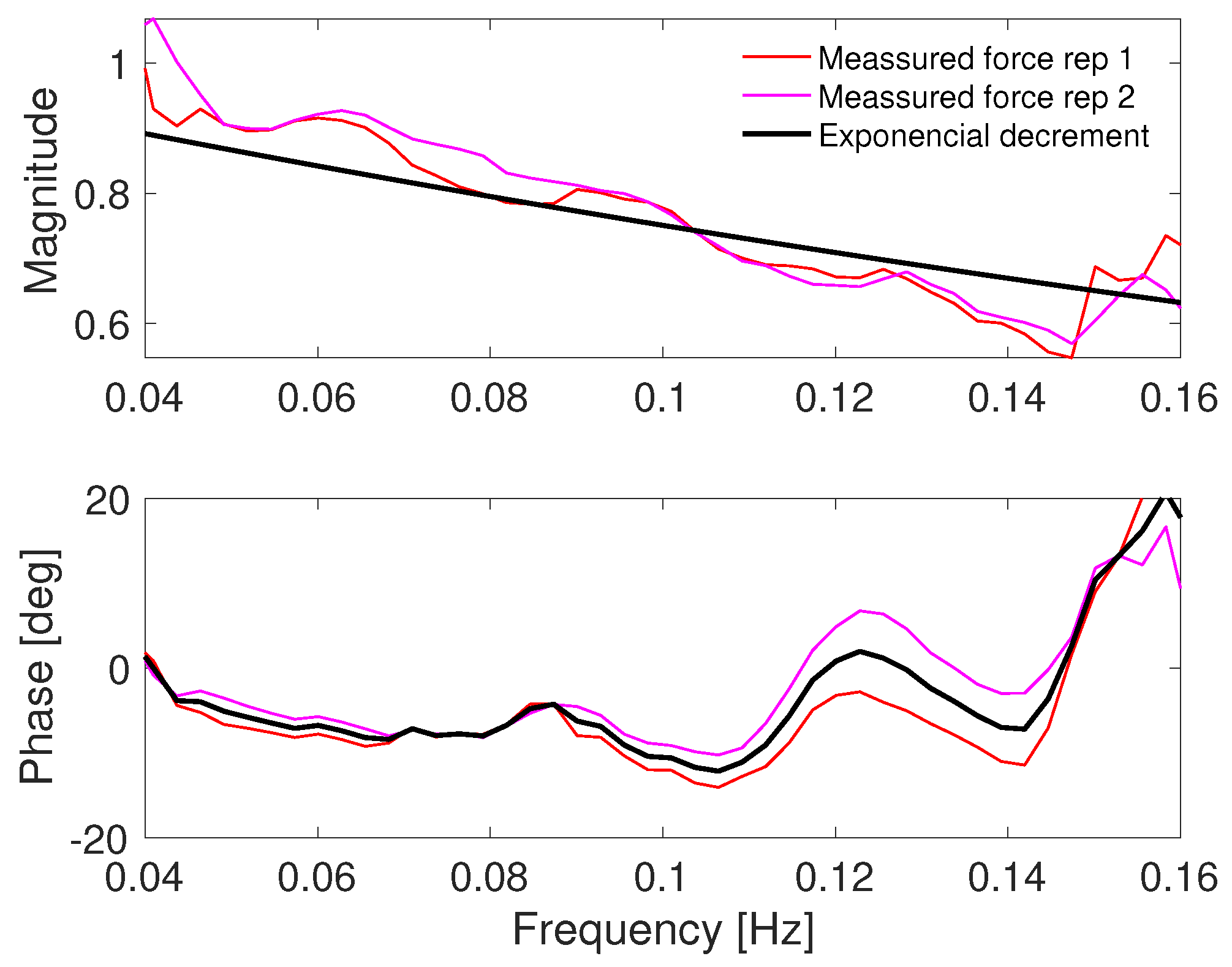
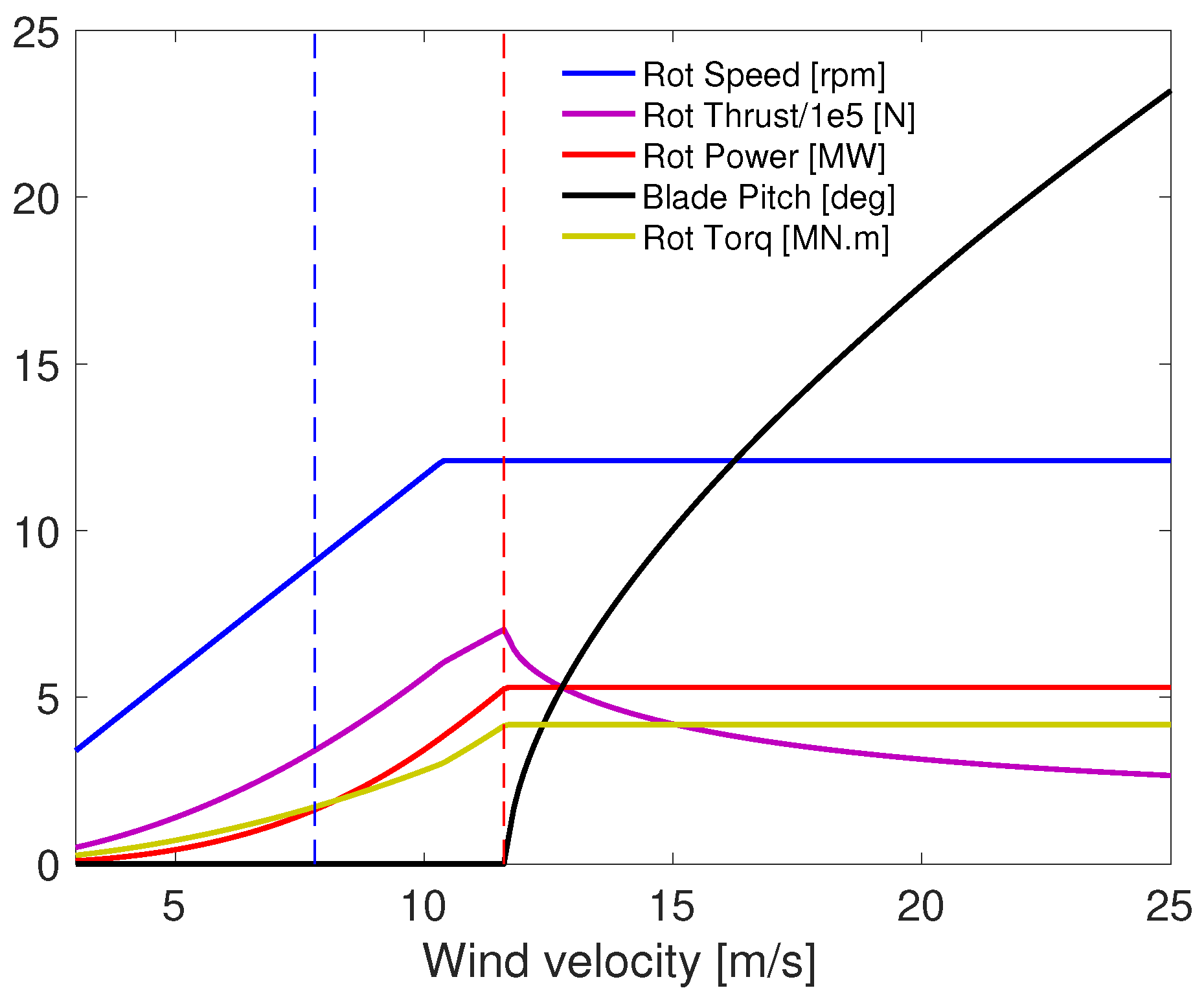
2.5. Wind Turbine Characterization
2.6. Numerical Model
3. Results and Discussion
3.1. Decay Tests
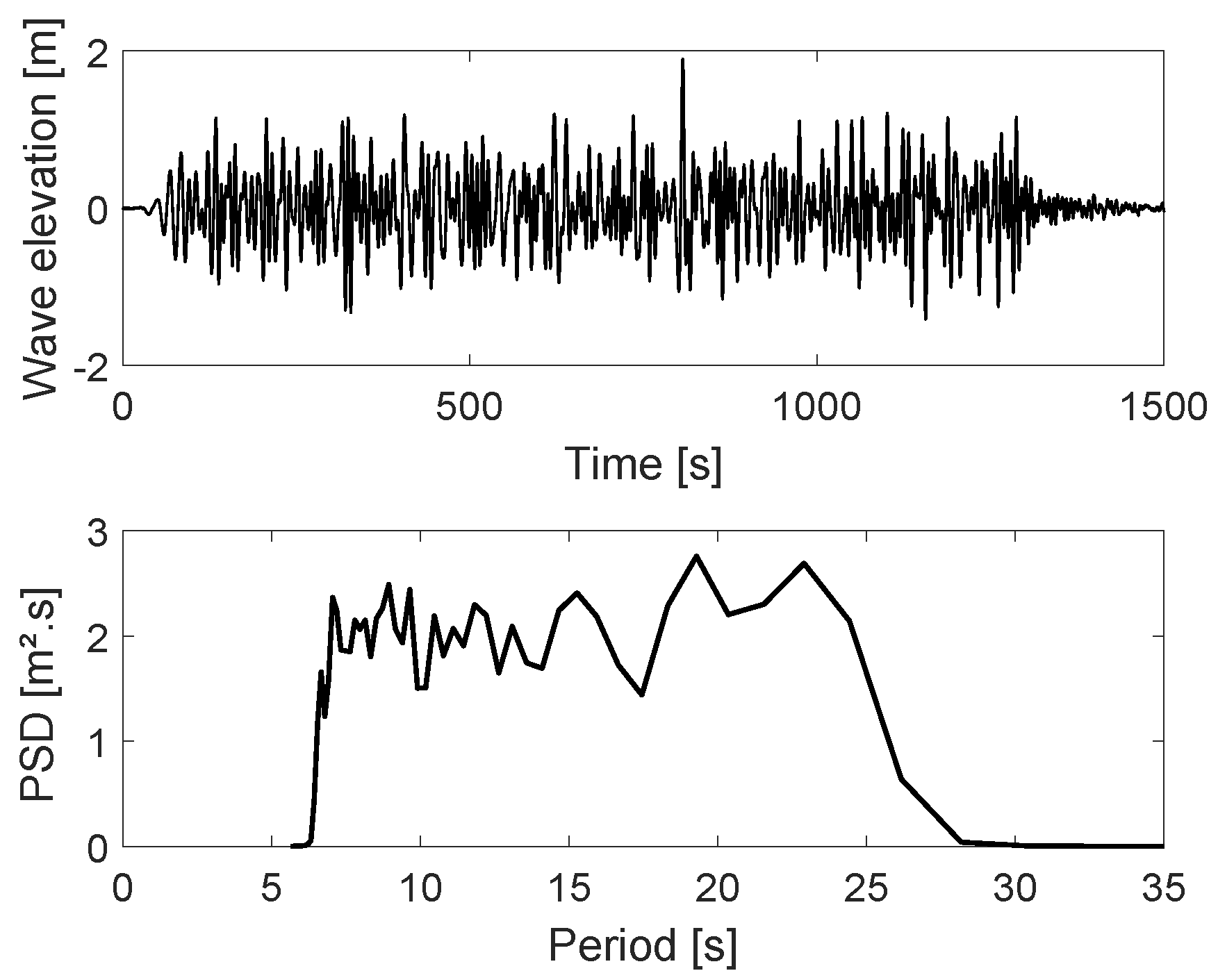
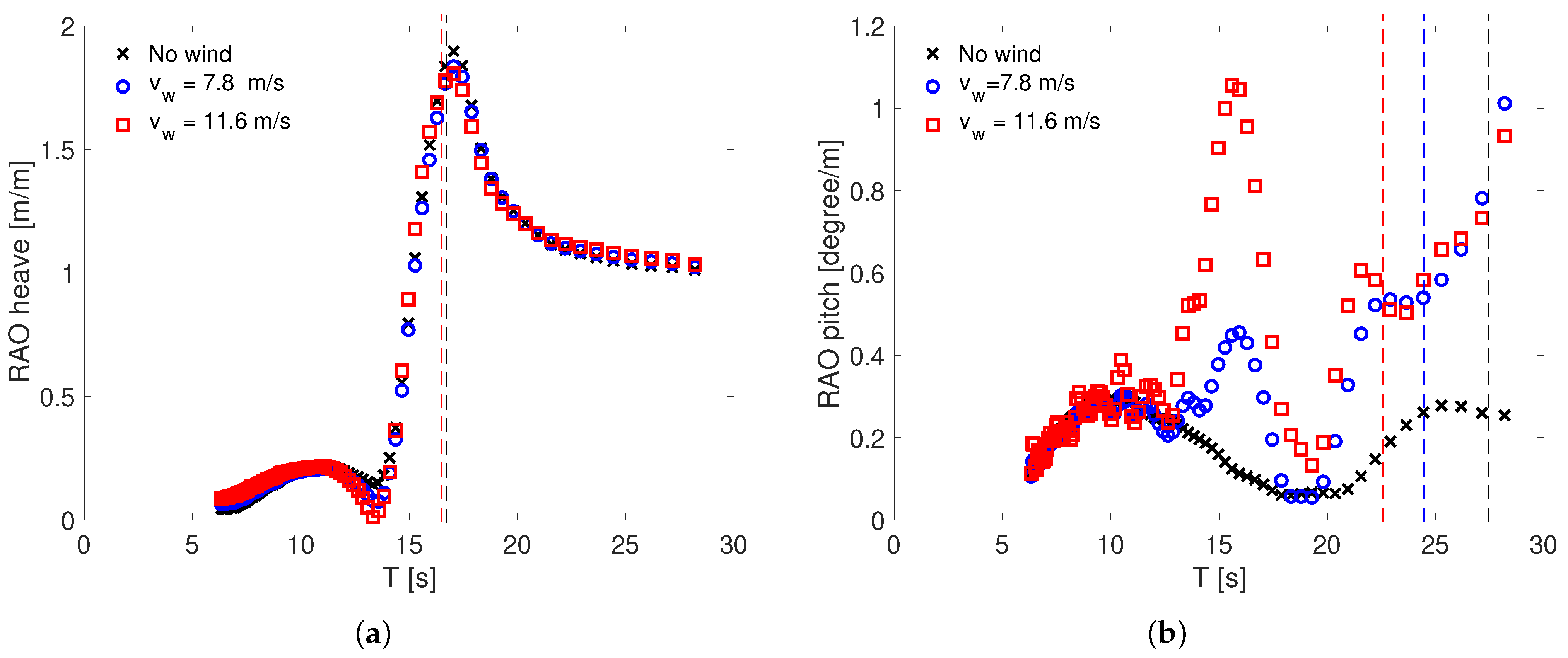
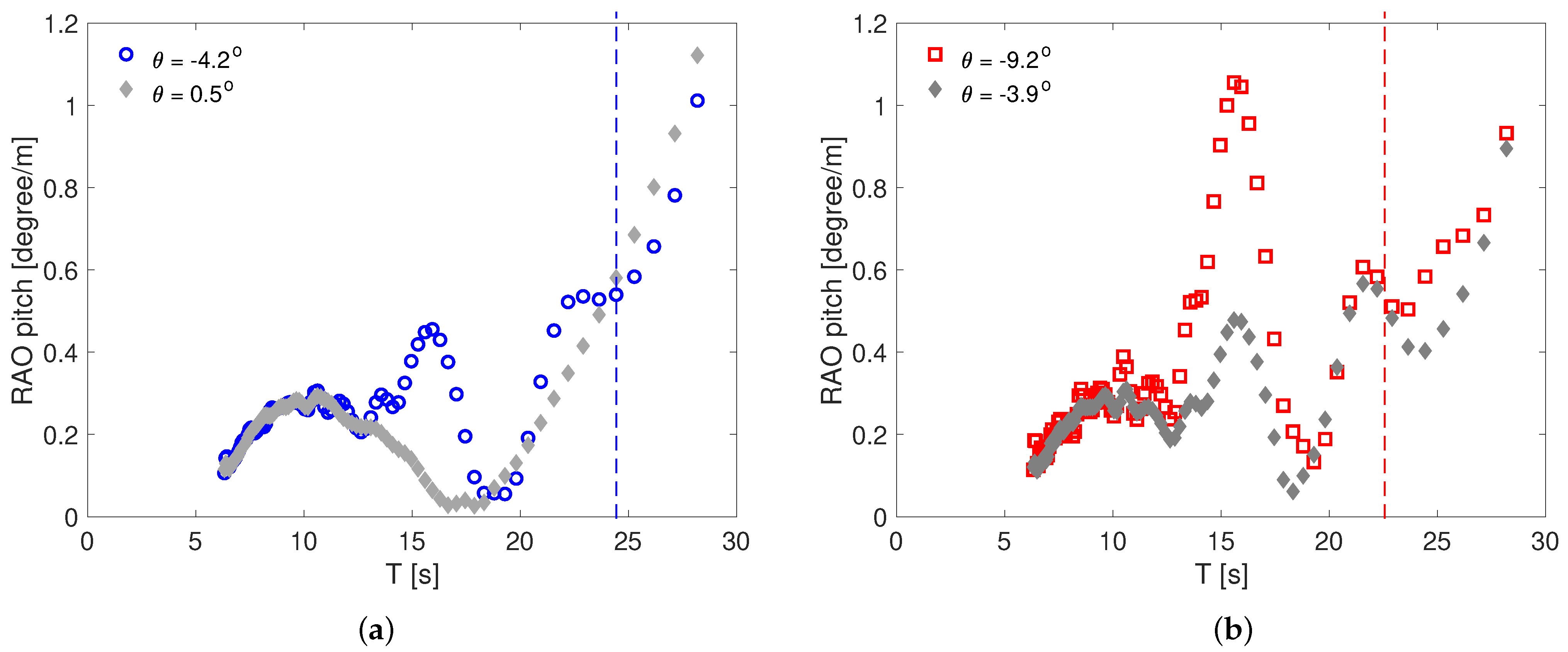
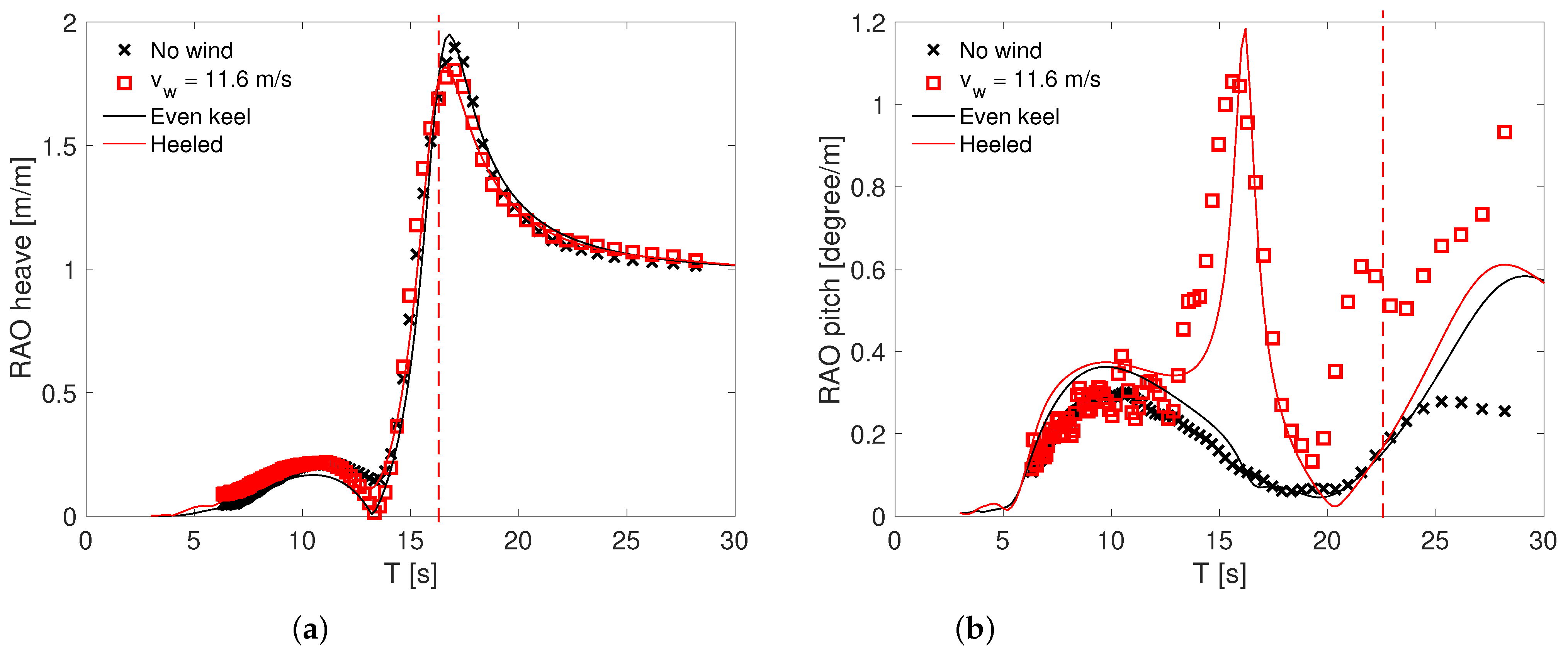
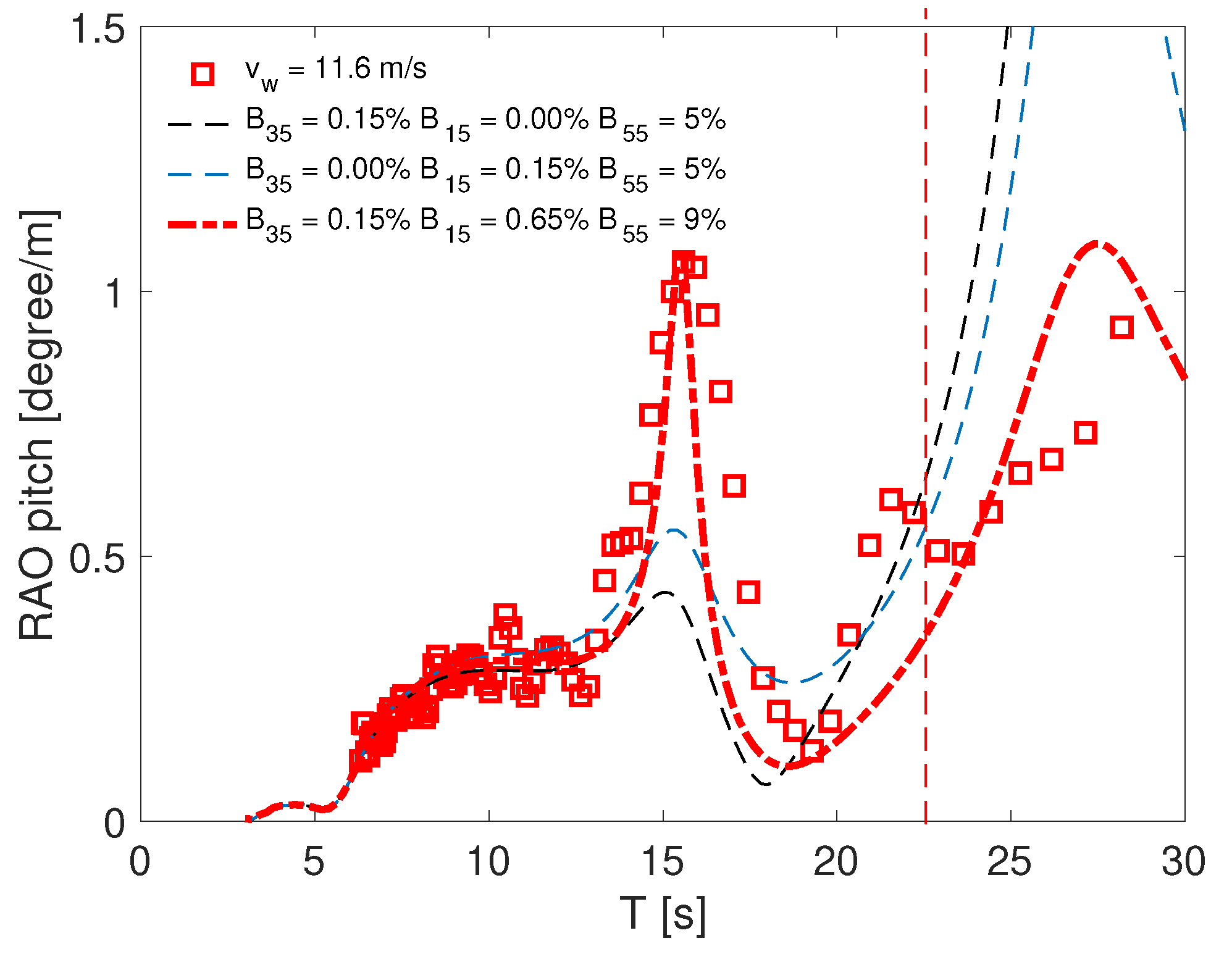
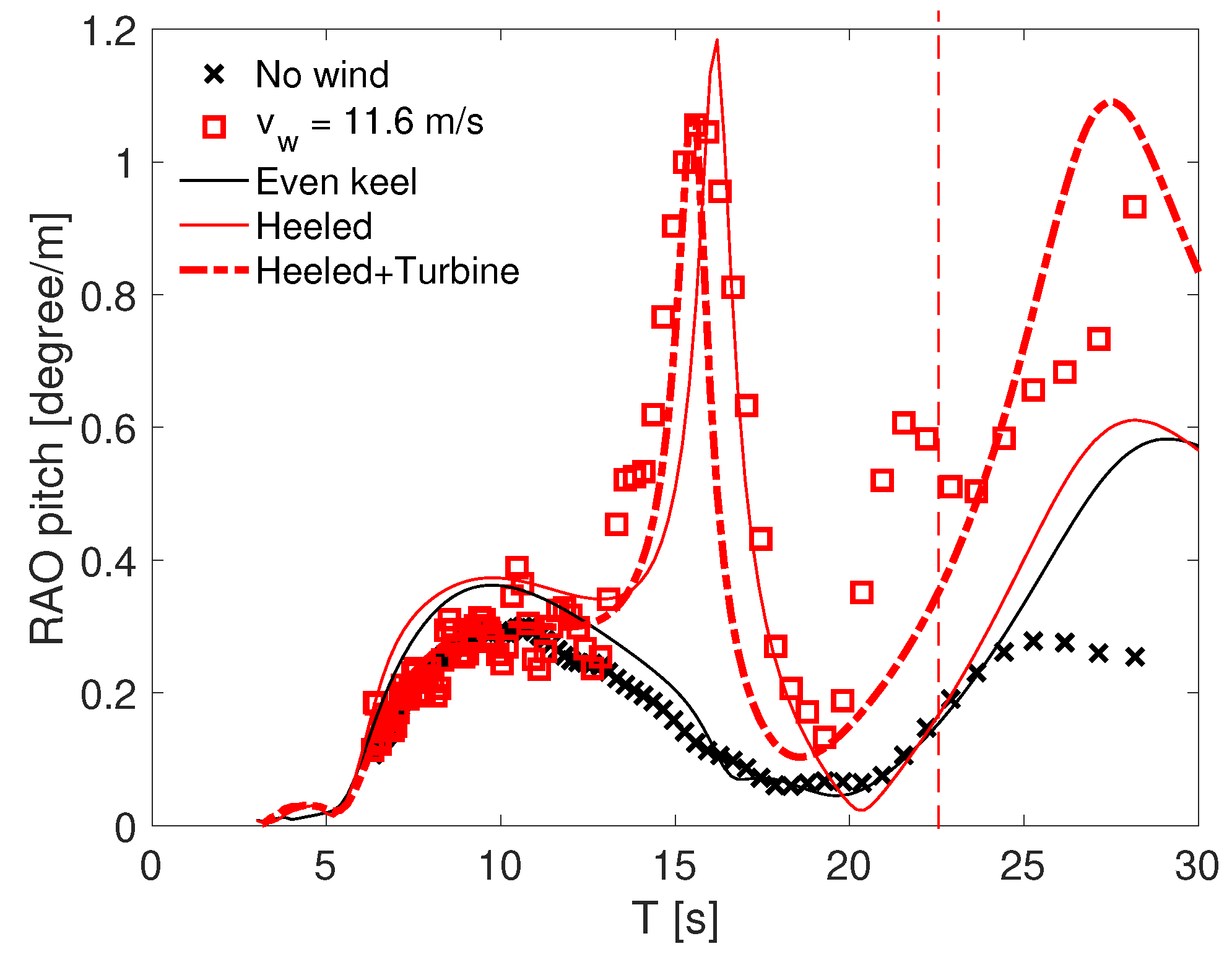
3.2. Responses in Waves
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sclavounos, P.; Tracy, C.; Lee, S. Floating Offshore Wind Turbines: Responses in a Seastate: Pareto Optimal Designs and Economic Assessment; Department of Mechanical Engineering – Massachusetts Institute of Technology: Cambridge, MA, USA, 2007. [Google Scholar]
- Hall, M.; Brad Buckham, B.; Curran Crawford, C. Evolving Offshore Wind: A Genetic Algorithm-Based Support Structure Optimization Framework for Floating Wind Turbines. In Proceedings of the OCEANS’13 MTS/IEEE, Bergen, Norway, 23–27 September 2013. [Google Scholar]
- Hall, M.; Brad Buckham, B.; Curran Crawford, C. Hydrodynamics-based floating wind turbine support platform optimization: A basis function approach. Renew. Energy 2014, 66, 559–569. [Google Scholar] [CrossRef]
- Roddier, D.; Cermelli, C.; Aubault, A.; Weinstein, A. Windfloat: A floating foundation for offshore wind turbines. J. Renew. Sustain. Energy 2010, 2, 033104. [Google Scholar] [CrossRef]
- Hall, M.; Moreno, J.; Thiagarajan, K. Performance Specifications for Real-Time Hybrid Testing of 1:50-Scale Floating Wind Turbine Models. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014. [Google Scholar]
- Saude, T.; Chabaud, V.; Thys, M. Real-Time Hybrid Model Testing of a Braceless Semi-Submersible Wind Turbine: Part I—The Hybrid Approach. In Proceedings of the ASME 2016 35th International Conference on Ocean, Offshore and Arctic Engineering, Busan, Korea, 19–24 June 2016. [Google Scholar]
- Azcona, J.; Bouchotrouch, F.; Gonzáles, M.; Garciadía, J.; Munduate, X.; Kelberlau, F.; Nygaard, T.A. Aerodynamic Thrust Modelling in Wave Tank Tests of Offshore Floating Wind Turbines Using a Ducted Fan. J. Phys. Conf. Ser. 2014, 524. [Google Scholar] [CrossRef]
- Battistella, T.; Paradinas, D.D.; Urbán, A.M.; Garcia, R.G. High Fidelity Simulation of Multi-MW Rotor Aerodynamics by Using a Multifan. In Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018. [Google Scholar]
- Azcona, J.; Bouchotrouch, F.; Vittori, F. Low-frequency dynamics of a floating wind turbine in wave tank–scaled experiments with SiL hybrid method. Wind Energy 2019, 22, 1402–1413. [Google Scholar] [CrossRef]
- Urbán, A.M.; Guanche, R. Wind turbine aerodynamics scale-modeling for floating offshore wind platform testing. J. Wind Eng. Ind. Aerodyn. 2019, 186, 49–57. [Google Scholar] [CrossRef]
- Stewart, G.; Muskulus, M. A Review and Comparison of Floating Offshore Wind Turbine Model Experiments. Energy Procedia 2016, 94, 227–231. [Google Scholar] [CrossRef]
- Chen, P.; Chen, J.; Hu, Z. Review of Experimental-Numerical Methodologies and Challenges for Floating Offshore Wind Turbines. J. Marine. Sci. Appl. 2020, 19, 339–361. [Google Scholar] [CrossRef]
- Gueydon, S.; Bayati, I.; de Ridder, E.J. Discussion of solutions for basin model tests of FOWTs in combined waves and wind. Ocean. Eng. 2020, 209, 107288. [Google Scholar] [CrossRef]
- Gonçalves, R.T.; Franzini, G.R.; Simos, A.N.; Neto, A.G.; Mello, P.C.; Carmo, B.S.; Nishimoto, K.; Malta, E.B.; Vieira, D.P.; Carmo, L.H.S.; et al. A Brazil-Japan Collaboration on a Conceptual Design of a Floating Offshore Wind Turbine for the São Paulo Coast. In Proceedings of the 27th International Congress on Waterborne Transportation, Shipbuilding and Offshore Constructions, Rio de Janeiro, RJ, Brazil, 23–25 October 2018. [Google Scholar]
- Mello, P.C.; Malta, E.B.; da Silva, R.O.P.; Candido, M.H.O.; do Carmo, L.H.S.; Alberto, I.F.; Franzini, G.R.; Simos, A.N.; Suzuki, H.; Gonçalves, R.T. Influence of heave plates on the dynamics of a floating offshore wind turbine in waves. J. Mar. Sci. Technol. 2020. [Google Scholar] [CrossRef]
- Carmo, L.H.S.; Mello, P.C.; Malta, E.B.; Franzini, G.R.; Simos, A.N.; Gonçalves, R.T.; Suzuki, H. ANALYSIS OF A FOWT model in bichromatic waves: An investigation on the effect of combined wave-frequency and slow motions on the calibration of drag and inertial force coefficients. In Proceedings of the ASME 2020 39th International Conference on Ocean, Offshore and Arctic Engineering, Virtual Conference, 3–7 August 2020. [Google Scholar]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development. Available online: https://www.nrel.gov/docs/fy09osti/38060.pdf (accessed on 9 February 2021).
- Jonkman, J.M. Influence of control on the pitch damping of a floating wind turbine. In Proceedings of the ASME Wind Energy Symposium, Reno, NV, USA, 7–10 January 2008. [Google Scholar]
- Souza, C.E.; Bachynski, E.E. Changes in surge and pitch decay periods of floating wind turbines for varying wind speed. Ocean. Eng. 2019, 180, 223–237. [Google Scholar] [CrossRef]
- Gueydon, S. OC6 semisubmersible unde waves and constant thrust. In Proceedings of the Oral presentation at DeepWind 2021 Conference, Digital Conference, 13–15 January 2021. [Google Scholar]
- Technomar. EdtoolsX Users’s Manual. 2020. Available online: https://www.technomar.com.br/ (accessed on 9 February 2021).
- Mello, P.C.; Carneiro, M.L.; Tannuri, E.A.; Kassab, F., Jr.; Marques, R.P.; Adamowski, J.C.; Nishimoto, K. A control and automation system for wave basins. J. Mechatron. (Oxf.) 2013, 23, 94–107. [Google Scholar] [CrossRef]
- Ning, A. A Simple Solution Method for the Blade Element Momentum Equations with Guaranteed Convergence. Wind Energy 2014, 1327–1345. [Google Scholar] [CrossRef]
- Pegoraro, B. Modelagem aerodinâmica de turbinas eólicas flutuantes (in Portuguese). Master of Science Thesis, Escola Politécnica da Universidade de São Paulo, São Paulo, Brazil, 2020. [Google Scholar]
- WAMIT, Inc. WAMIT Users’ Manual - Version 7; WAMIT, Inc.: Chestnut Hill, MA, USA, 2012. [Google Scholar]
- Suzuki, H.; Shiohara, H.; Schnepf, A.; Houtani, H.; Carmo, L.H.S.; Hirabayashi, S.; Haneda, K.; Chujo, T.; Nihei, Y.; Malta, E.B.; et al. Wave and wind responses of a very-light fowt with guy-wired-supported tower: Numerical and experimental studies. J. Mar. Sci. Eng. 2020, 8, 841. [Google Scholar] [CrossRef]
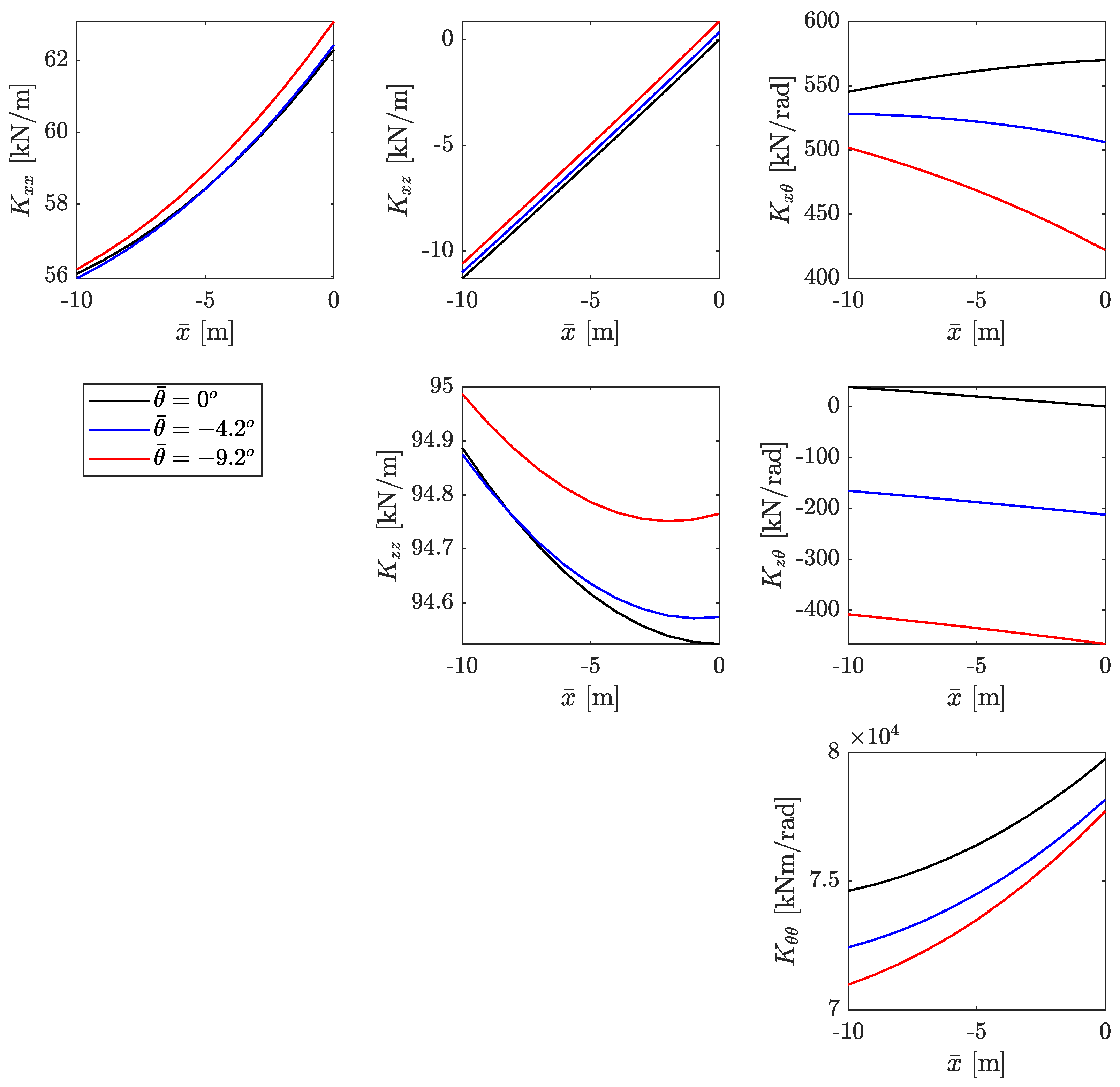
- Amaral, G.A. Analytical Assessment of the Mooring System Stiffness. Master’s Thesis, Escola Politécnica da Universidade de São Paulo, São Paulo, Brazil, 2020. [Google Scholar]
- Goupee, A.J.; Kimball, R.W.; Dagher, H.J. Experimental observations of active blade pitch and generator control influence on floating wind turbine response. Renew. Energy 2017, 104, 9–19. [Google Scholar] [CrossRef]
- Bachynski, E.E.; Thys, M.; Sauder, T.; Chabaud, V.; Saether, L.O. Real-time hybrid model testing of a braceless semi-submersible wind turbine. Part II: Experimental results. In Proceedings of the ASME 2016 35th International Conference on Ocean, Offshore and Arctic Engineering, Busan, Korea, 19–24 June 2016. [Google Scholar]
- Pesce, C.P.; Amaral, G.A.; Franzini, G.R. Mooring system stiffness: A general analytical formulation with an application to Floating Offshore Wind Turbines. In Proceedings of the ASME 2018 1st International Offshore Wind Technical Conference, San Francisco, CA, USA, 4–7 November 2018. [Google Scholar]
- Malta, E.B.; Gonçalves, R.T.; Matsumoto, F.T.; Pereira, F.R.; Fujarra, A.L.C.; Nishimoto, K. Damping Coefficient Analyses for Floating Offshore Structures. In Proceedings of the ASME 29th Internatiional Conference on Ocean, Offshore and Arctic Engineering, Shanghai, China, 6–11 June 2010. [Google Scholar]
- Silva, L.S.P.; Morishita, H.M.; Pesce, C.P.; Gonçalves, R.T. Nonlinear analysis of a heaving point absorber in frequency domain via statistical linearization. In Proceedings of the ASME 2019 38th International Conference on Ocean, Offshore and Arctic Engineering, Glasgow, UK, 9–14 June 2019. [Google Scholar]
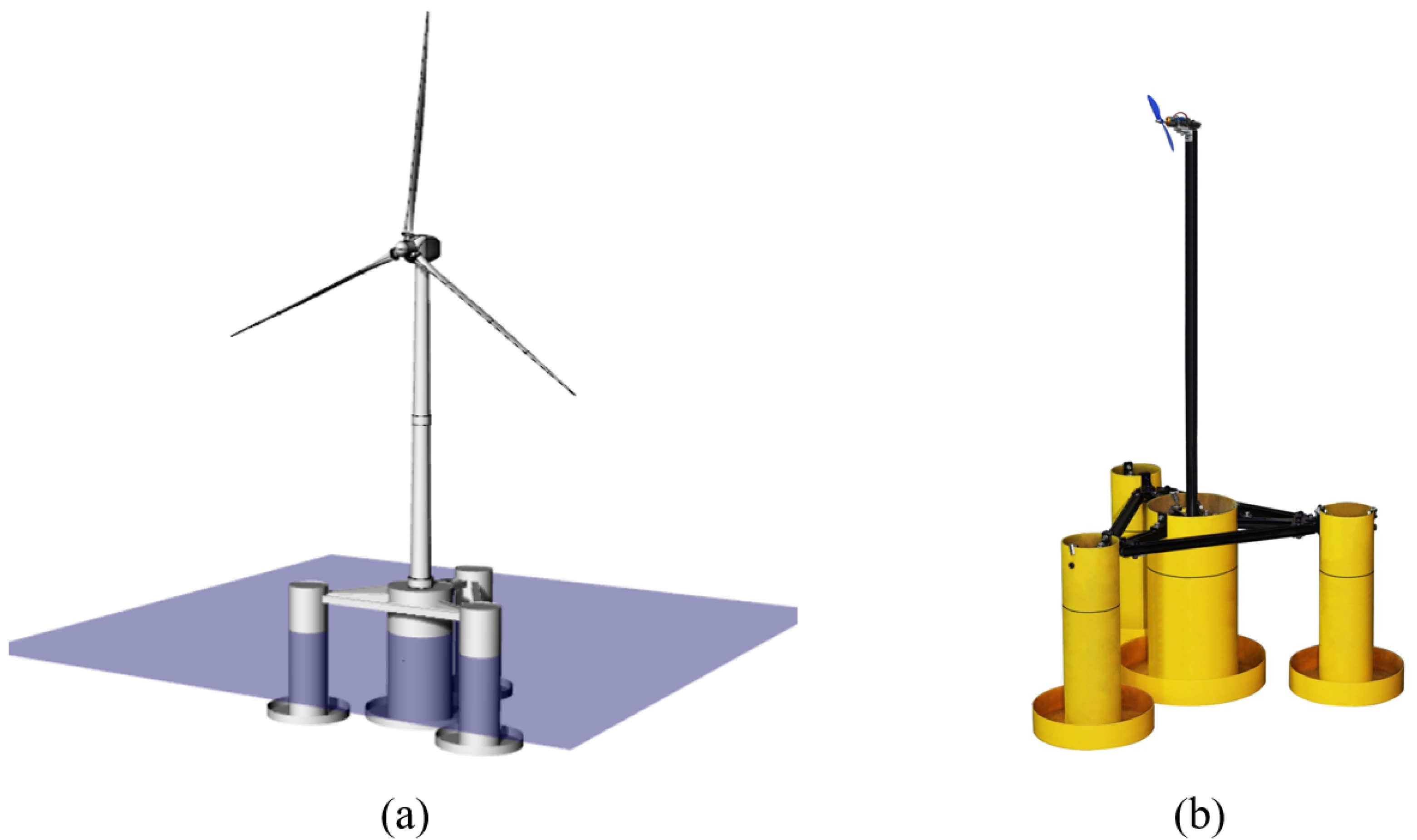
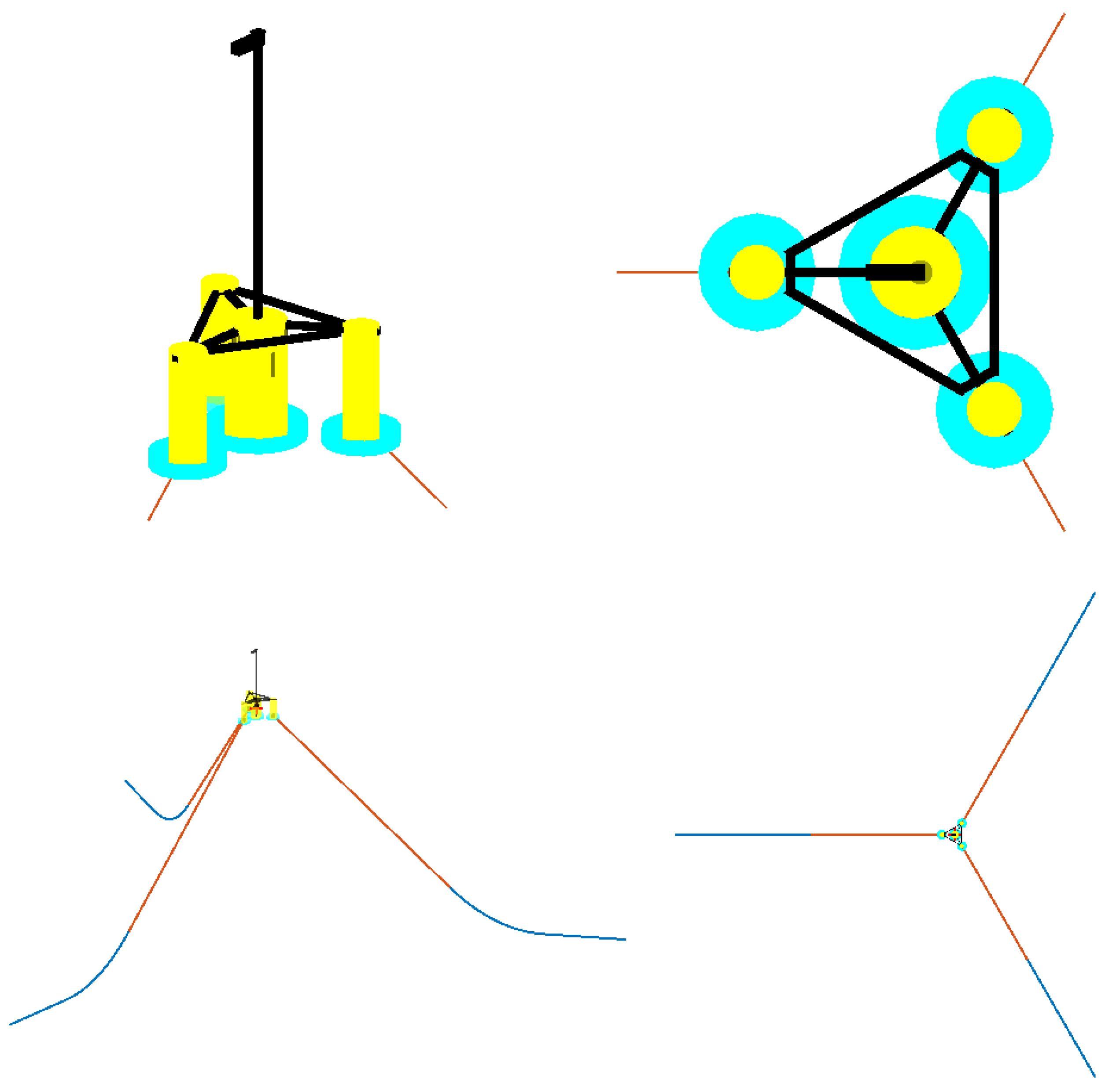


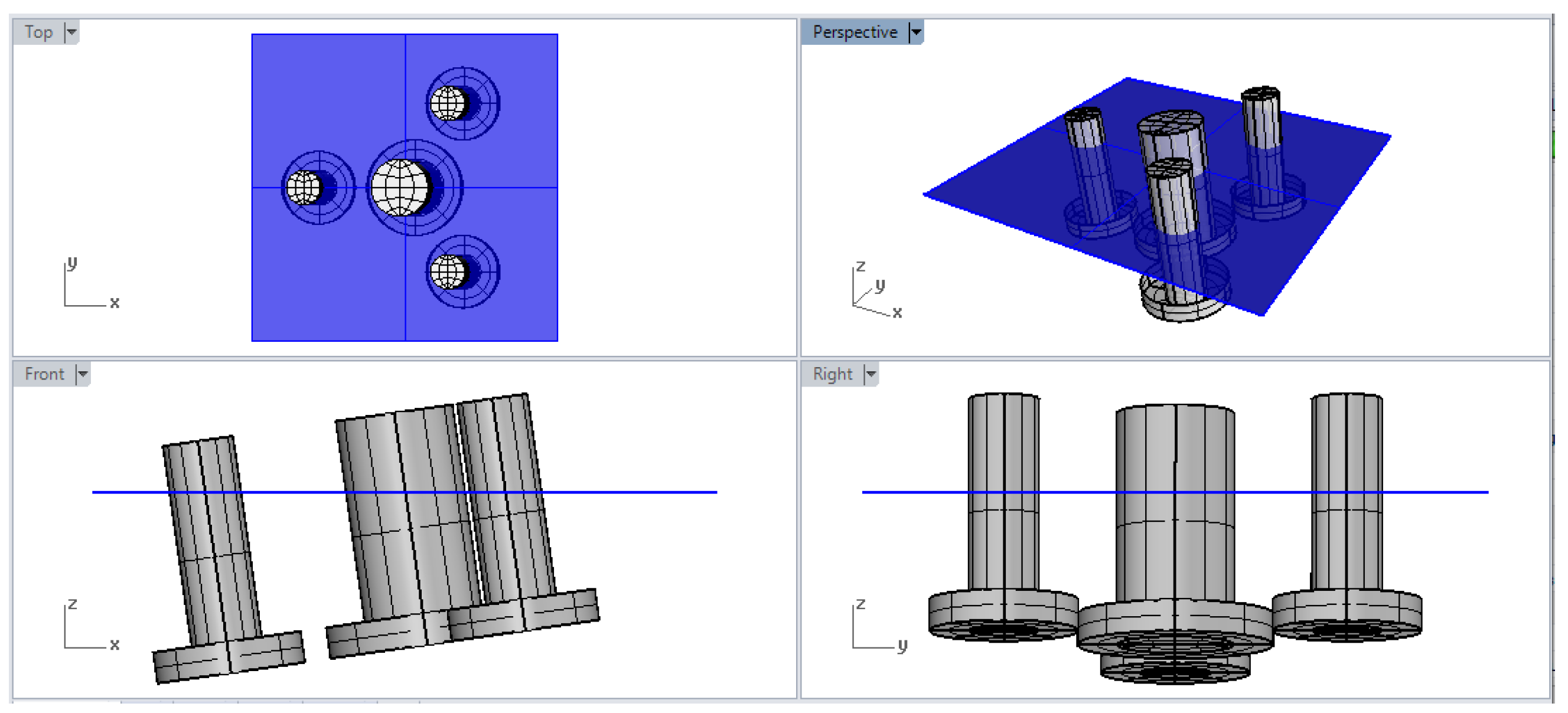
| Full Scale | Model Scale (1:80) | |
|---|---|---|
| Diameter of center column | 15 m | 187.5 mm |
| Diameter of side columns | 9 m | 112.5 mm |
| Draft | 20 m | 250 mm |
| Heave plate width | 4 m | 50 mm |
| Diameter of central column heave plate | 25 m | 312.5 mm |
| Diameter of side columns heave plate | 19 m | 237.5 mm |
| Mass | 6936 ton | 13.55 kg |
| Displacement | 7351 ton | 14.35 kg |
| CG (from bottom) | 14 m | 175 mm |
| Full Scale | Model Scale (1:80) | |
|---|---|---|
| Anchors’ depth | 302.8 m | 3785 mm |
| Anchors’ radius from center | 534.1 m | 6789 mm |
| Fairleads’ depth | 20 m | 250 mm |
| Fairleads’ radius | 30 m | 375 mm |
| Bottom segment material | Chain | Chain |
| Bottom segment length | 280 m | 3500 mm |
| Bottom segment equivalent submerged weight | 9.21 kN/m | 1.44 N/m |
| Upper segment material | Polyester | Polyester |
| Upper segment length | 347.6 m | 4345 mm |
| Upper segment equivalent submerged weight | 0.04 kN/m | 0.01 N/m |
| Wind Velocity | Periods (s) | |||
|---|---|---|---|---|
| (m/s) | T1 | T3 | T5 | T5 * |
| 0 | 97.0 | 16.2 | 27.6 | 27.9 |
| 7.8 | 99.6 | 16.2 | 24.5 | - |
| 11.6 | 102.8 | 16.0 | 22.6 | 24.6 |
| Wind Velocity | Mean Surge | Mean Trim Angle | ||
|---|---|---|---|---|
| (m/s) | Without TA | With TA | Without TA | With TA |
| 0 | 0.0 m | 0.0 m | 0.0° | 5.0° |
| 7.8 | −5.1 m | −5.8 m | −4.2° | 0.5° |
| 11.6 | −10.3 m | −11.1 m | −9.2° | −3.9° |
| Wind Velocity | T1 | T3 | T5 | |||
|---|---|---|---|---|---|---|
| (m/s) | Experimental | Numerical | Experimental | Numerical | Experimental | Numerical |
| 0 | 97.0 | 97.6 | 16.2 | 16.4 | 27.6 | 28.1 |
| 7.8 | 99.6 | 100.7 | 16.2 | 16.4 | 24.5 | 28.0 |
| 11.6 | 102.8 | 103.3 | 16.0 | 16.2 | 22.6 | 27.6 |
| T1 | T3 | T5 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Wind Velocity | Quadratic | Linear | Quadratic | Linear | Quadratic | Linear | |||
| (m/s) | |||||||||
| 0 | 2.0 | 6.7 | 5.6 | 0.3 | 18.1 | 2.9 | 0.6 | 3.7 | 2.9 |
| 7.8 | 4.0 | 7.8 | 8.8 | 0.3 | 16.6 | 2.7 | 6.5 | 4.1 | 7.5 |
| 11.6 | 5.5 | 7.3 | 9.4 | 0.8 | 13.3 | 2.6 | 6.9 | 15.4 | 13.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amaral, G.A.; Mello, P.C.; do Carmo, L.H.S.; Alberto, I.F.; Malta, E.B.; Simos, A.N.; Franzini, G.R.; Suzuki, H.; Gonçalves, R.T. Seakeeping Tests of a FOWT in Wind and Waves: An Analysis of Dynamic Coupling Effects and Their Impact on the Predictions of Pitch Motion Response. J. Mar. Sci. Eng. 2021, 9, 179. https://doi.org/10.3390/jmse9020179
Amaral GA, Mello PC, do Carmo LHS, Alberto IF, Malta EB, Simos AN, Franzini GR, Suzuki H, Gonçalves RT. Seakeeping Tests of a FOWT in Wind and Waves: An Analysis of Dynamic Coupling Effects and Their Impact on the Predictions of Pitch Motion Response. Journal of Marine Science and Engineering. 2021; 9(2):179. https://doi.org/10.3390/jmse9020179
Chicago/Turabian StyleAmaral, Giovanni A., Pedro C. Mello, Lucas H. S. do Carmo, Izabela F. Alberto, Edgard B. Malta, Alexandre N. Simos, Guilherme R. Franzini, Hideyuki Suzuki, and Rodolfo T. Gonçalves. 2021. "Seakeeping Tests of a FOWT in Wind and Waves: An Analysis of Dynamic Coupling Effects and Their Impact on the Predictions of Pitch Motion Response" Journal of Marine Science and Engineering 9, no. 2: 179. https://doi.org/10.3390/jmse9020179
APA StyleAmaral, G. A., Mello, P. C., do Carmo, L. H. S., Alberto, I. F., Malta, E. B., Simos, A. N., Franzini, G. R., Suzuki, H., & Gonçalves, R. T. (2021). Seakeeping Tests of a FOWT in Wind and Waves: An Analysis of Dynamic Coupling Effects and Their Impact on the Predictions of Pitch Motion Response. Journal of Marine Science and Engineering, 9(2), 179. https://doi.org/10.3390/jmse9020179







