3D Numerical Study of the Impact of Macro-Roughnesses on a Tidal Turbine, on Its Performance and Hydrodynamic Wake
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Setups
2.2. Governing Equations
- (i)
- Air and water are considered as viscous fluids.
- (ii)
- Both fluids are considered incompressible. This hypothesis can be questioned in the case of air, but the validation cases in air have a Mach number of 0.14. It is generally accepted that for a flow with a Mach number below 0.3, the fluid can be considered incompressible.
- (iii)
- Gravity is neglected.
- (iv)
- The study is carried out in the middle of the water column, so wave and bottom effects are neglected.
2.2.1. Reynolds-Averaged Navier-Stokes Turbulence Model
2.2.2. Large Eddy Simulation Turbulence Model
2.3. Boundary Conditions
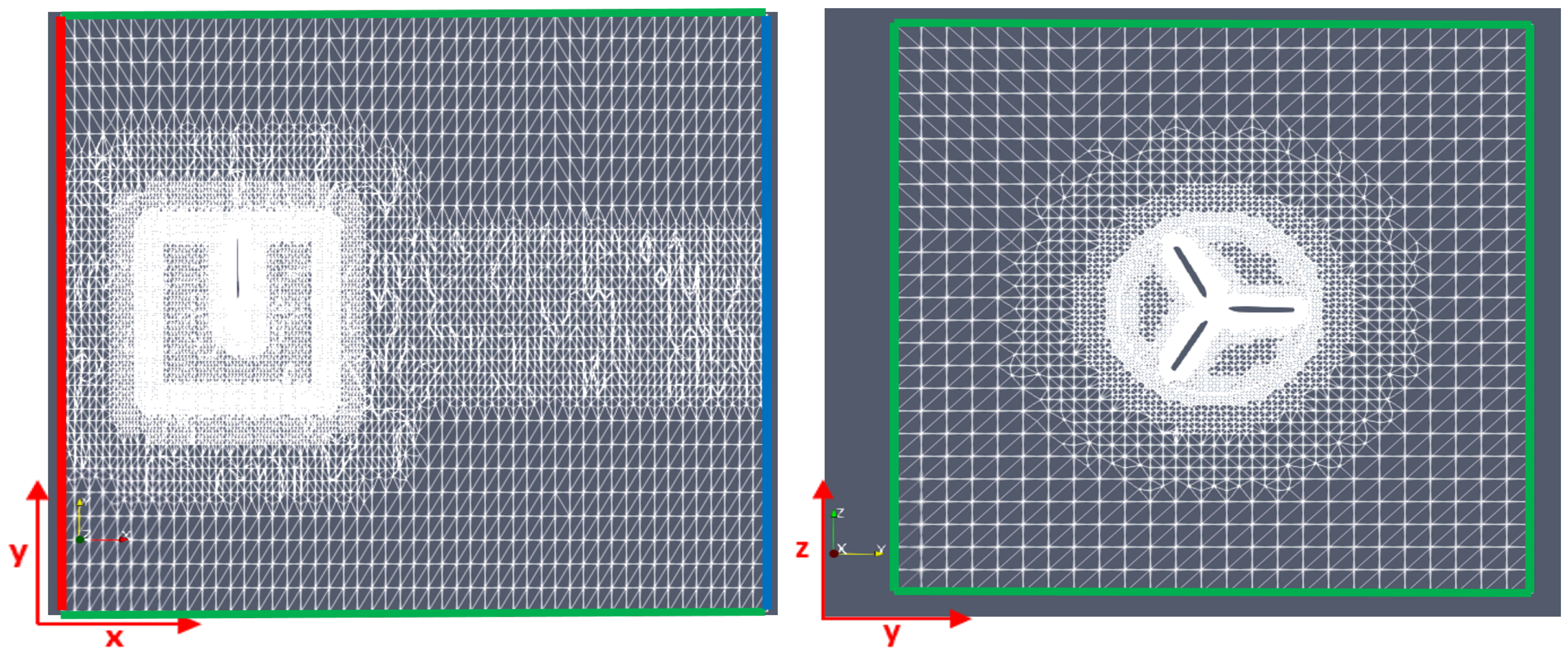
2.4. Geometries, Meshes and Numerical Setups
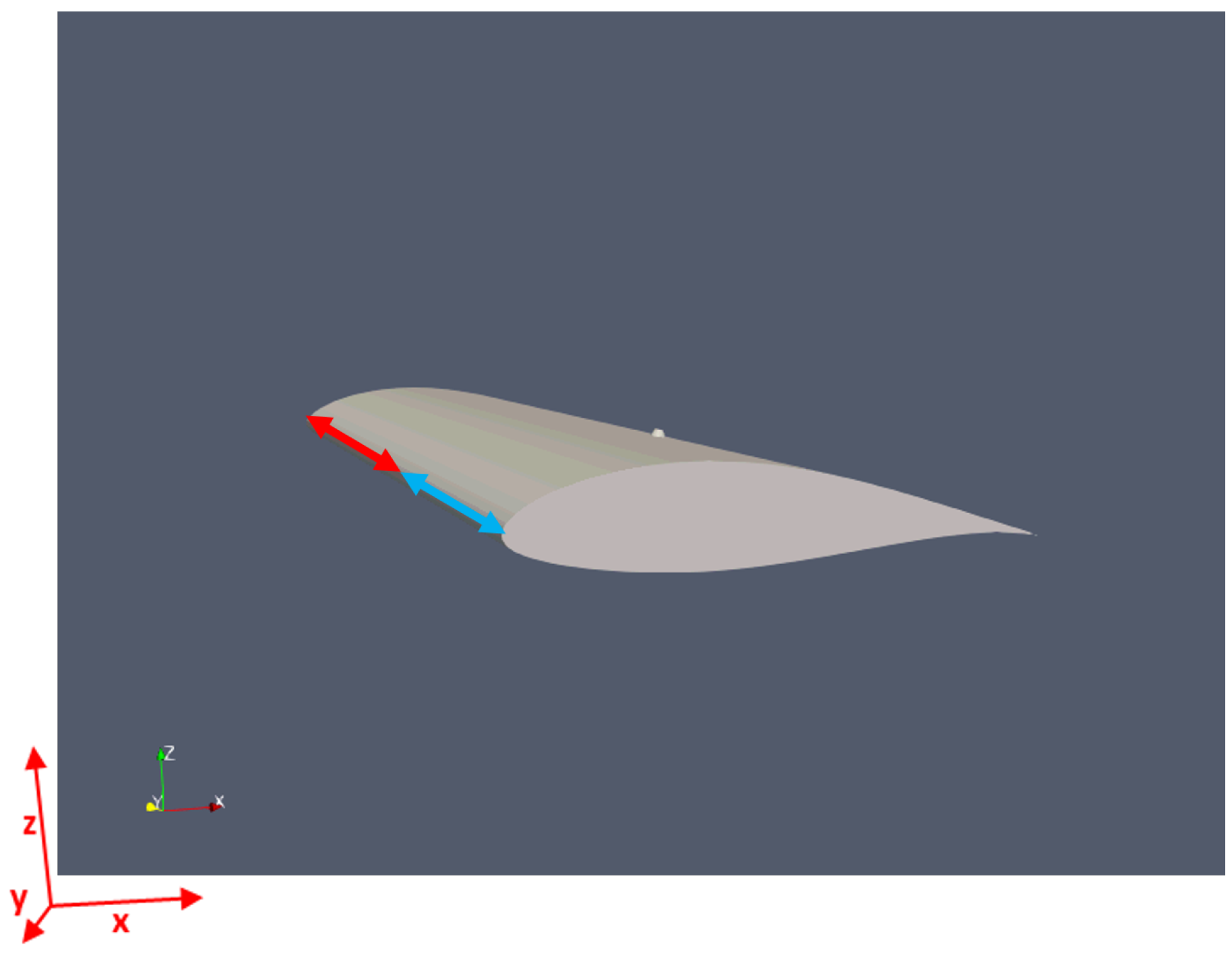
2.4.1. Motionless Blade Simulation with a Single Barnacle
2.4.2. Full Rotor Simulation with a Realistic Barnacle Colonisation
2.5. Test Case Summary
3. Results
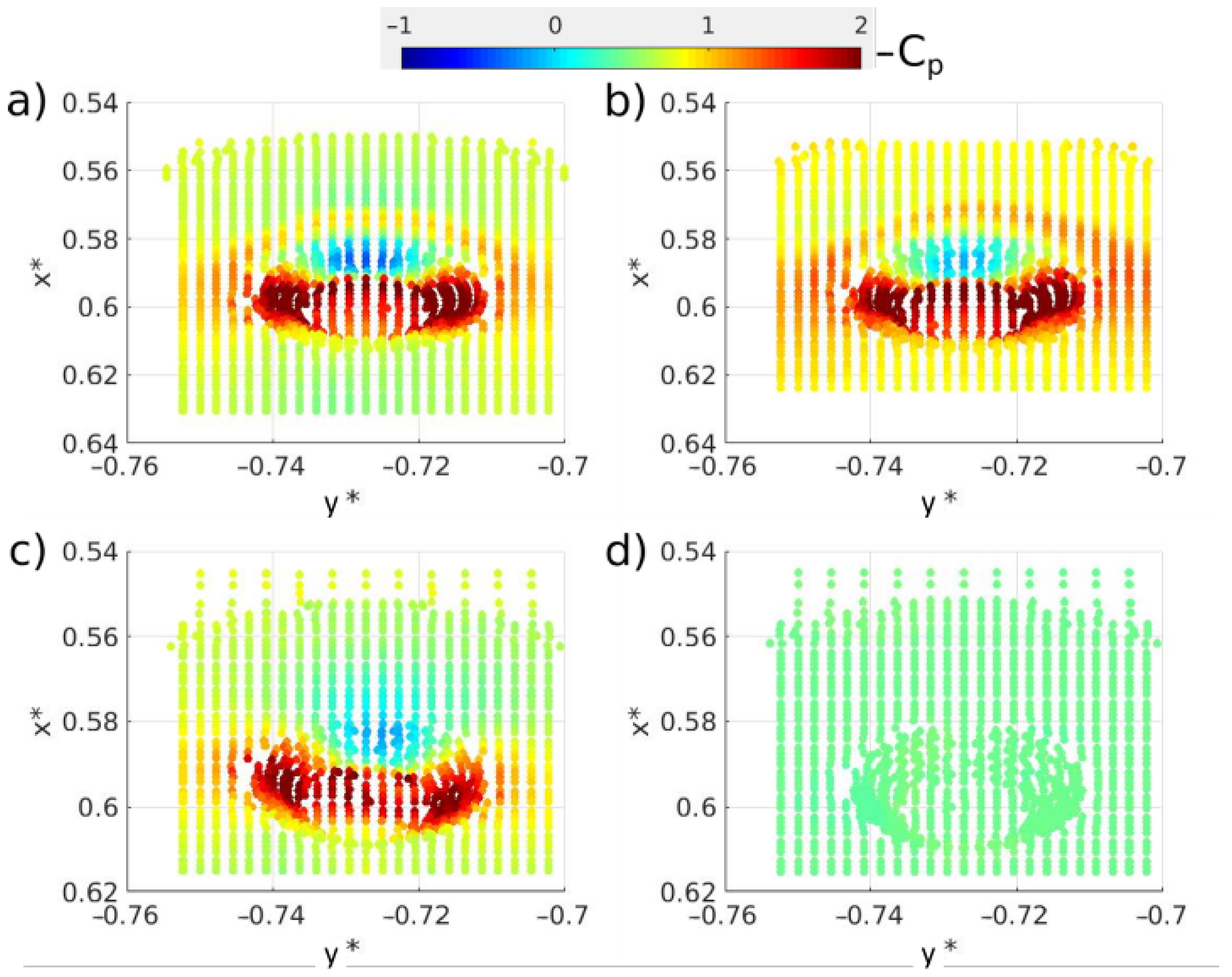
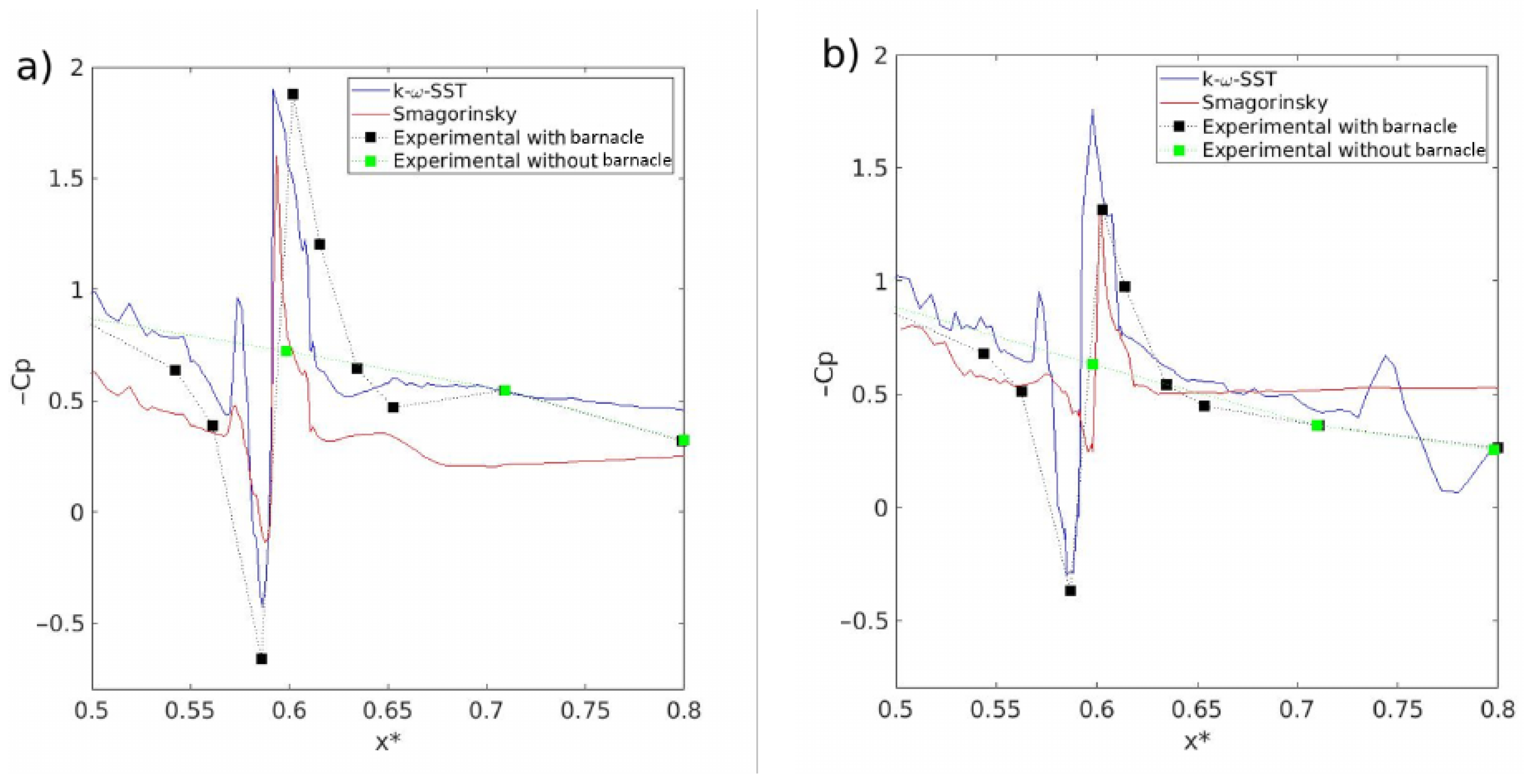
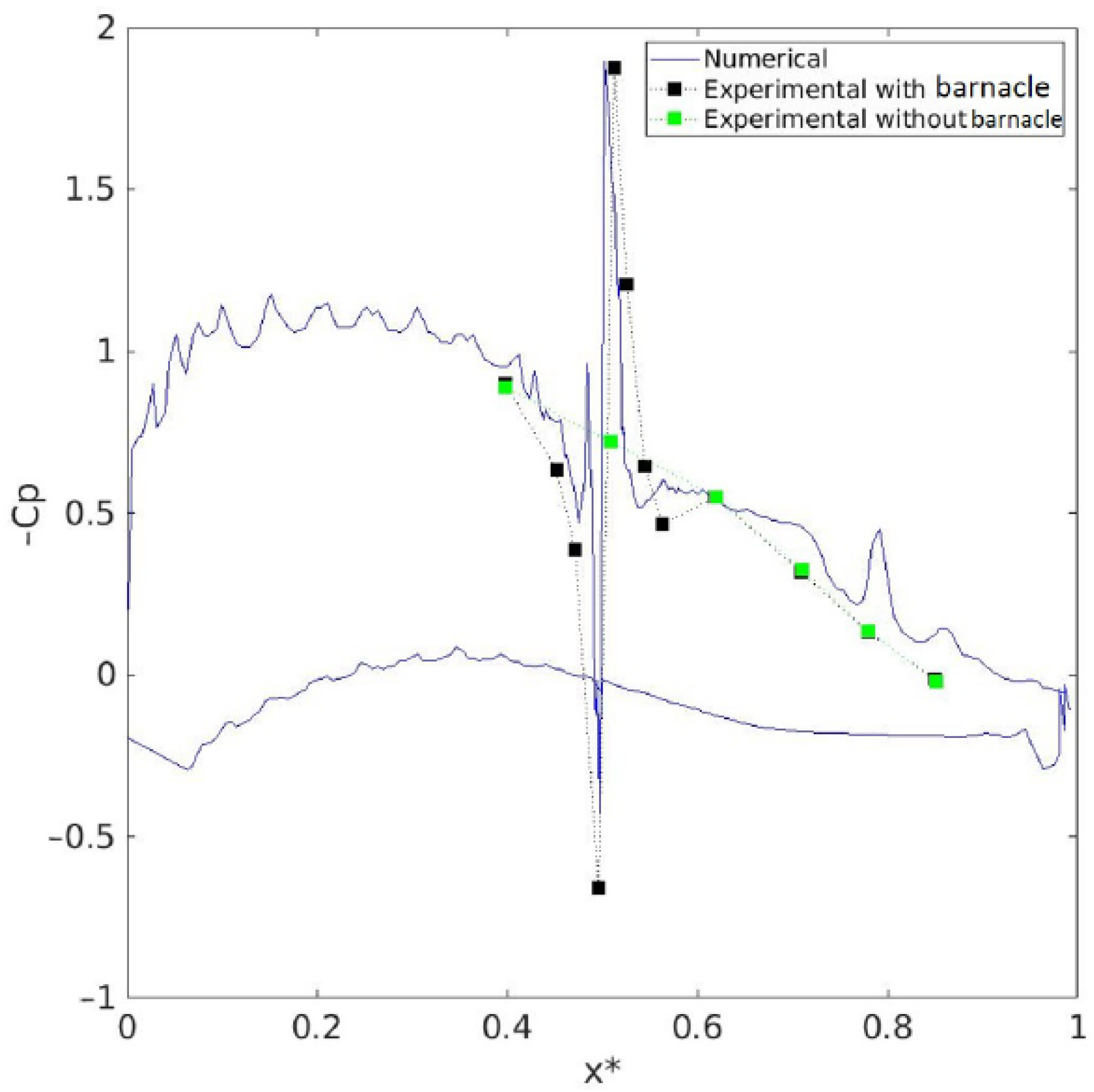
3.1. Motionless Blade Simulation with One Barnacle
3.2. Full Rotor Simulation Simulation
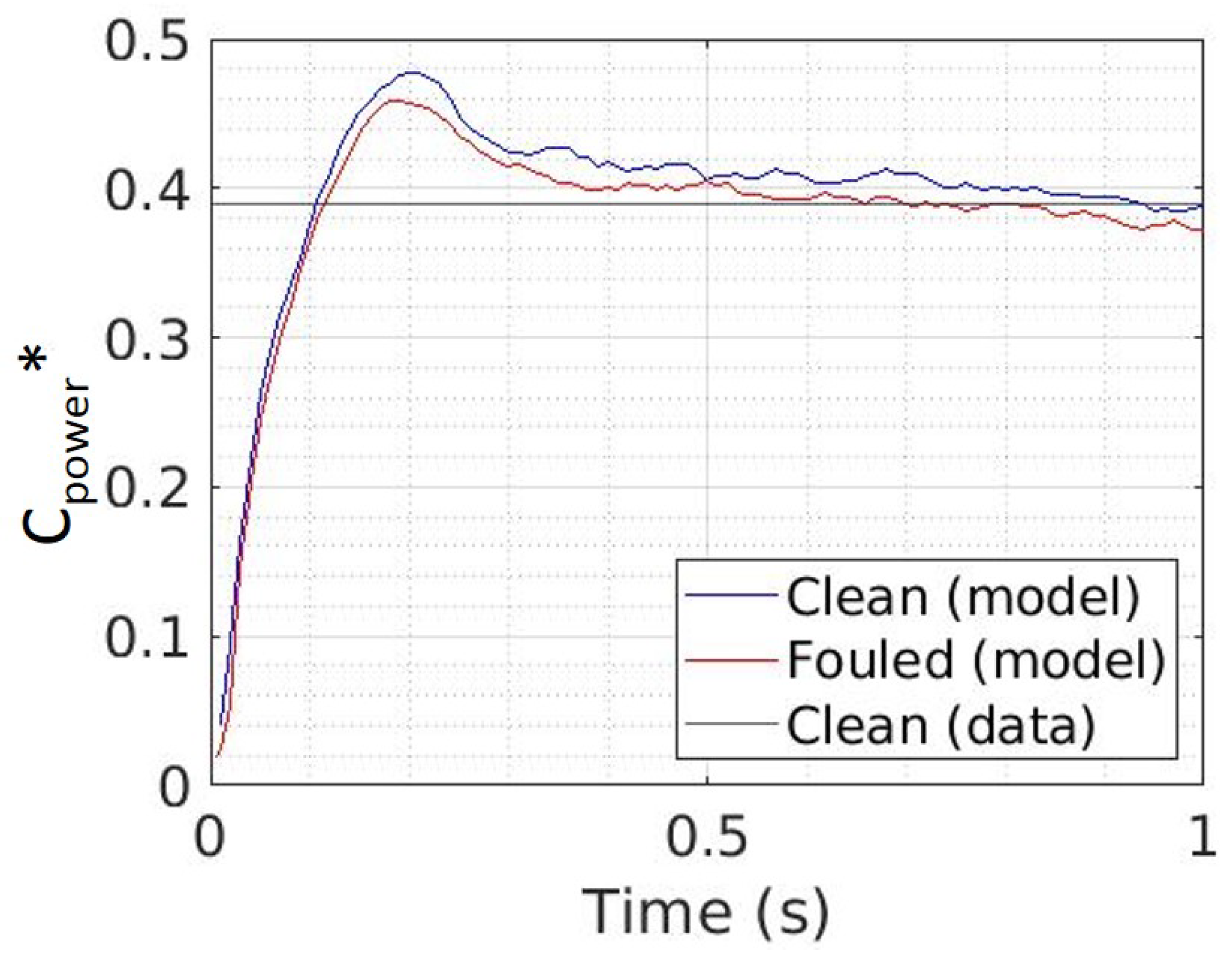
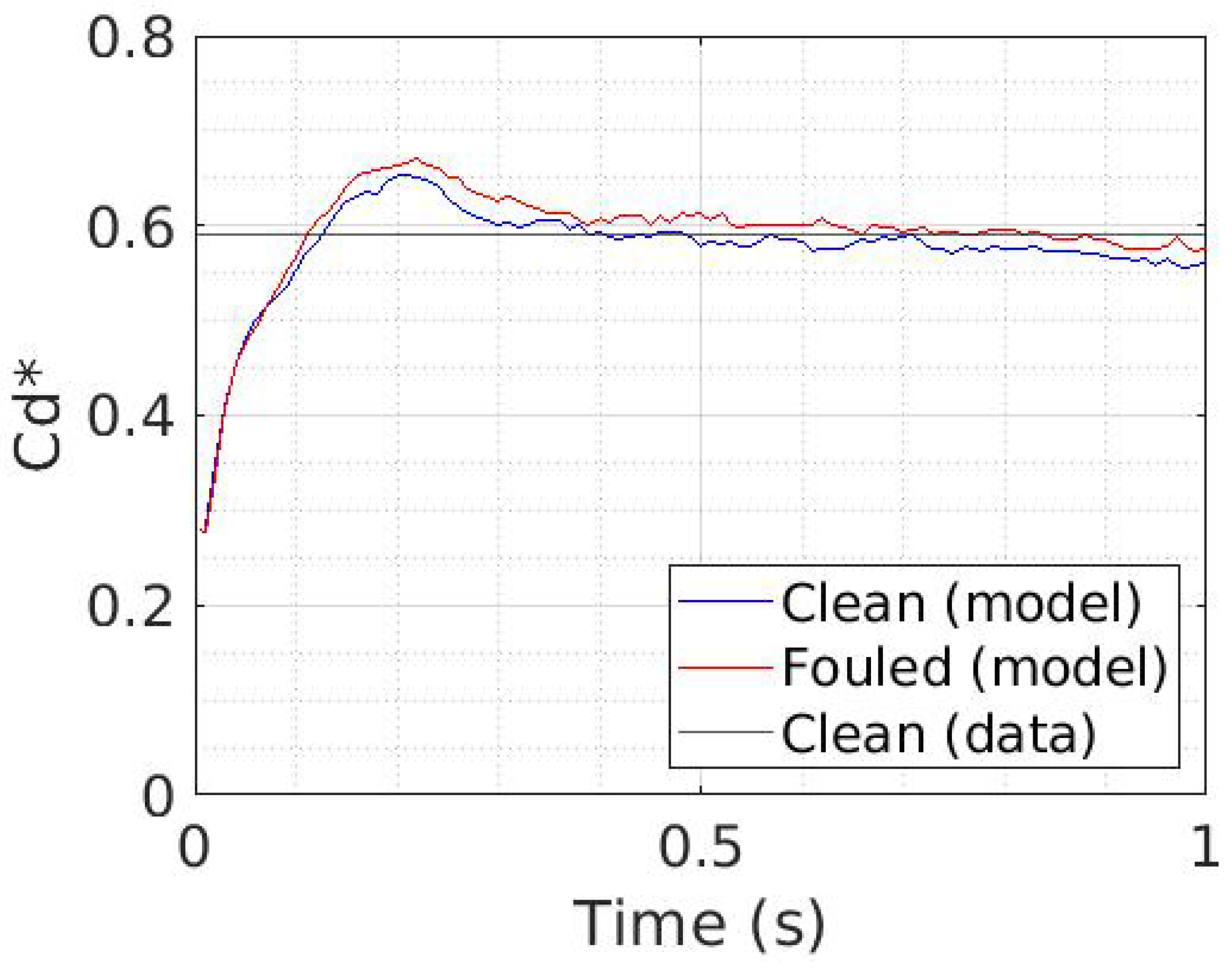
3.2.1. Impact of Biofouling on Tidal Turbine Performances
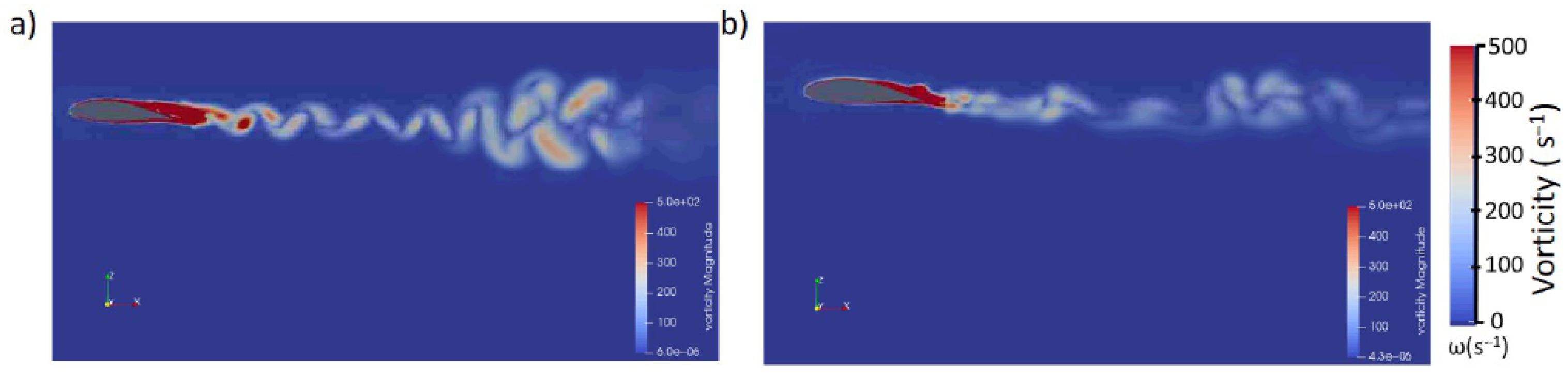
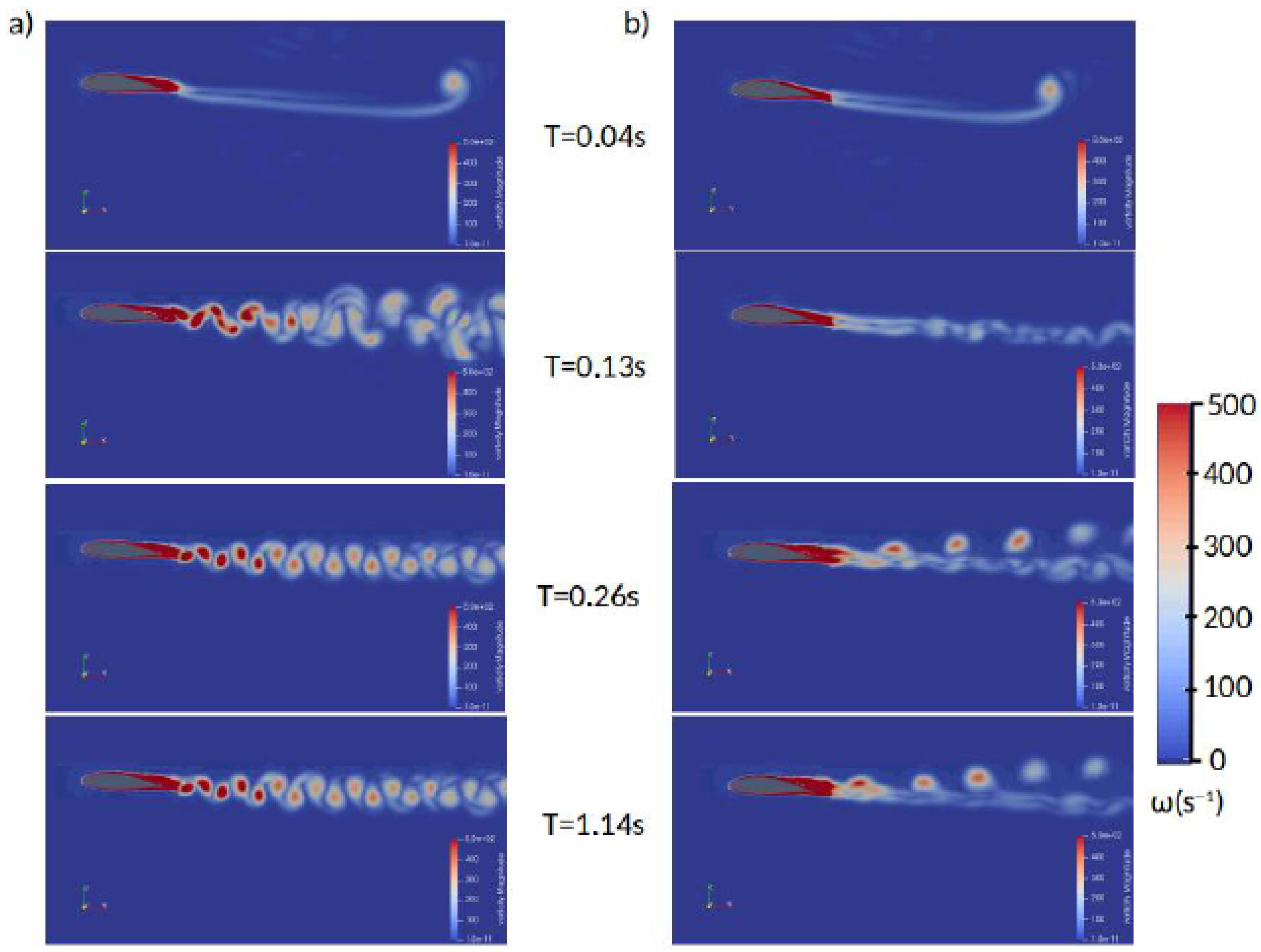
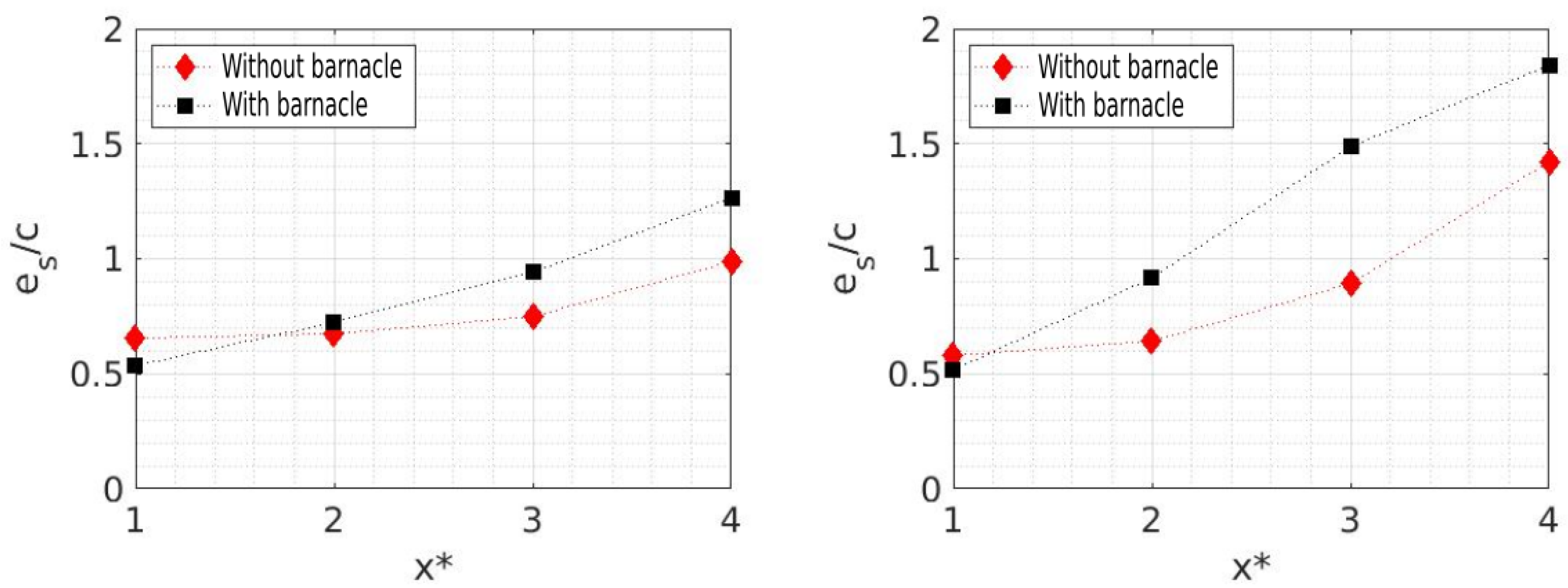
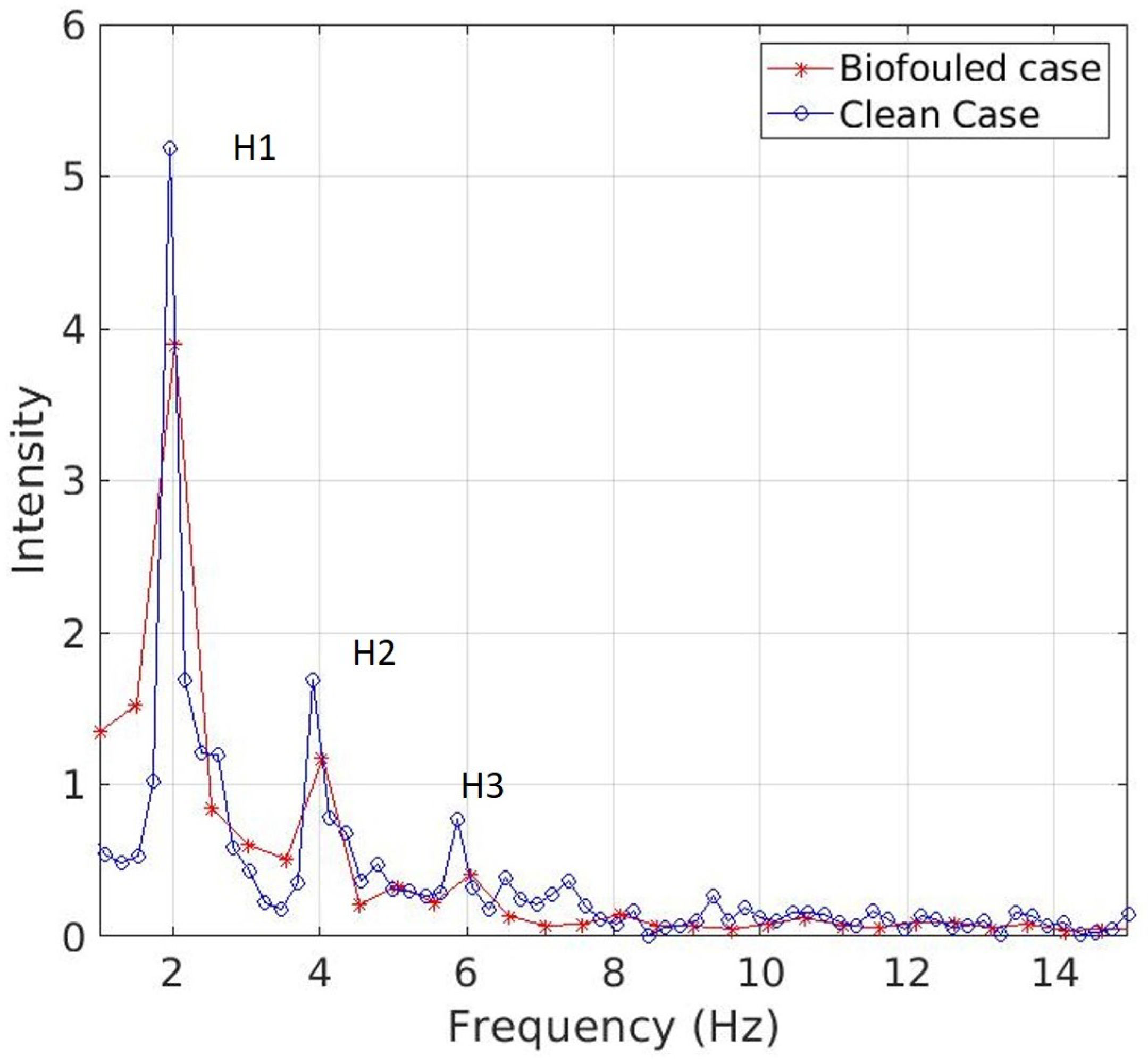
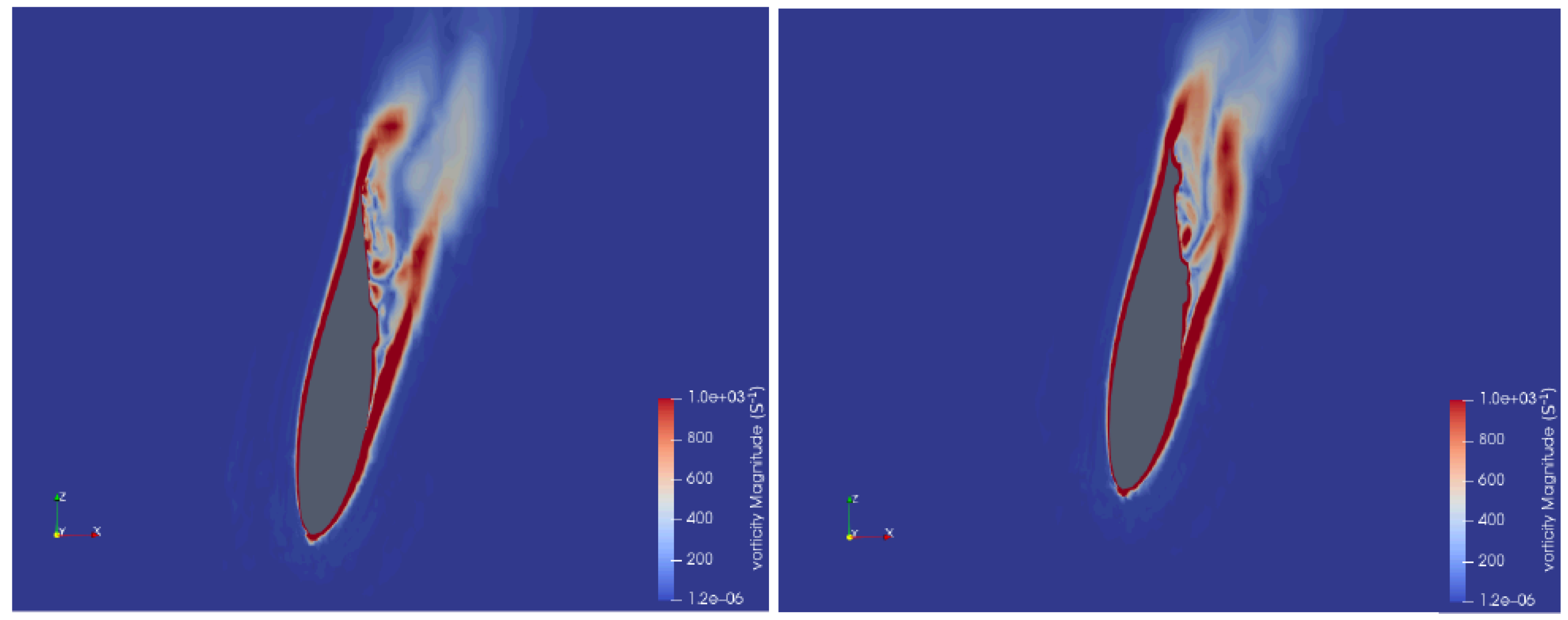
3.2.2. Impact of Biofouling on Tidal Turbine Wake
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Parameters | Definitions | Units |
| D | Rotor diameter | |
| R | Rotor radius | |
| c | Blade chord | |
| Computational domain inlet surface | - | |
| Computational domain outlet surface | - | |
| Computational domain side surfaces | - | |
| Kinematic viscosity | ||
| Rotor angular velocity | ||
| p | Fluid pressure | |
| u | Fluid velocity | |
| Fluid density | ||
| Inlet velocity magnitude | ||
| Undisturbed pressure | ||
| Tip speed ratio | ||
| Mean values | - | |
| Filtered values | - | |
| Dimensionless wall distance | - | |
| Rotor’s rotation speed | rad·s | |
| Turbulence intensity | - | |
| Dimensionless pressure coefficient | - | |
| Corrected dimensionless power coefficient | - | |
| Dimensionless drag coefficient | - |
| 1 | The French Research and Sea Exploitation Institute-Waves and Complex Environment Laboratory in Le Havre |
References
- Vinagre, P.A.; Simas, T.; Cruz, E.; Pinori, E.; Svenson, J. Marine Biofouling: A European Database for the Marine Renewable Energy Sector. J. Mar. Sci. Eng. 2020, 8, 495. [Google Scholar] [CrossRef]
- Titah-Benbouzid, H.; Benbouzid, M. Marine Renewable Energy Converters Biofouling: A Critical Review on Impacts and Prevention. In Proceedings of the EWTEC, Nantes, France, 6–11 September 2015; pp. 1–8. [Google Scholar]
- Kerr, A.; Beveridge, C.; Cowling, M.; Hodgkiess, T.; Parr, A.; Smith, M. Some physical factors affecting the accumulation of biofouling. J. Mar. Biol. Assoc. UK 1999, 79, 357–359. [Google Scholar] [CrossRef]
- Foveau, A.; Dauvin, J.C. Surprisingly diversified macrofauna in mobile gravels and pebbles from high-energy hydrodynamic environment of the ‘Raz Blanchard’ (English Channel). Reg. Stud. Mar. Sci. 2017, 16, 188–197. [Google Scholar] [CrossRef] [Green Version]
- Raoux, A.; Tecchio, S.; Pezy, J.; Lassalle, G.; Degraer, S.; Wilhelmsson, D.; Cachera, M.; Ernande, B.; Le Guen, C.; Haraldsson, M.; et al. Benthic and fish aggregation inside an offshore wind farm: Which effects on the trophic web functioning? Ecol. Indic. 2017, 72, 33–46. [Google Scholar] [CrossRef] [Green Version]
- Lindholdt, A.; Dam-Johansen, K.; Olsen, S.; Yebra, D.; Kiil, S. Effects of biofouling development on drag forces of hull coatings for ocean-going ships: A review. J. Coat. Technol. Res. 2015, 12, 415–444. [Google Scholar] [CrossRef]
- Song, S.; Ravenna, R.; Dai, S.; DeMarco Muscat-Fenech, C.; Tani, G.; Kemal Demirel, Y.; Atlar, M.; Day, S.; Incecik, A. Experimental investigation on the effect of heterogeneous hull roughness on ship resistance. Ocean Eng. 2021, 223, 108590. [Google Scholar] [CrossRef]
- Heechan, J.; Seung Woo, L.; Seung Jin, S. Measurement of Transitional Surface Roughness Effects on Flat-Plate Boundary Layer Transition. ASME J. Fluid Eng. 2019, 141, 074501. [Google Scholar]
- Balachandar, R.; Blakely, D. Surface roughness effects on turbulent boundary layers on a flat plate located in an open channel. J. Hydraul. Res. 2004, 42, 247–261. [Google Scholar] [CrossRef]
- Chakroun, W.; Al-Mesri, I.; Al-Fahad, S. Effect of Surface Roughness on the Aerodynamic Characteristics of a Symmetrical Airfoil. Wind Eng. 2004, 28, 547–564. [Google Scholar] [CrossRef]
- Gholamhosein, S.; Mirzaei, M.; Nazemi, M.M.; Fouladi, M.; Doostmahmoudi, A. Experimental study of ice accretion effects on aerodynamic performance of an NACA 23012 airfoil. Chin. J. Aeronaut. 2016, 29, 585–595. [Google Scholar]
- Orme, J.; Masters, I.; Griffiths, R. Investigation of the effects of the biofouling on the efficiency of marine current turbines. In Proceedings of the MAREC2001,International Conference of Marine Renewable Energies, London, UK, 27–28 March 2001; pp. 91–99. [Google Scholar]
- Walker, J.; Green, R.; Gillies, E.; Phillips, C. The effect of a barnacle-shaped excrescence on the hydrodynamic performance of a tidal turbine blade section. Ocean Eng. 2020, 217, 107849. [Google Scholar] [CrossRef]
- Rivier, A.; Bennis, A.C.; Jean, G.; Dauvin, J.C. Numerical simulations of biofouling effects on the tidal turbine hydrodynamic. Int. Mar. Energy J. 2018, 1, 101–109. [Google Scholar] [CrossRef]
- Picioreanu, C.; Vrouwenvelder, J.H.; van Loosdrecht, M. Three-dimensional modeling of biofouling and fluid dynamics in feed spacer channels of membrane devices. J. Membr. Sci. 2009, 345, 340–354. [Google Scholar] [CrossRef]
- Demirel, Y.K.; Turan, O.; Incecik, A. Predicting the effect of biofouling on ship resistance using CFD. Appl. Ocean Res. 2017, 62, 100–118. [Google Scholar] [CrossRef] [Green Version]
- Song, S.; Shi, W.; Demirel, Y.K.; Atlar, M. The effect of biofouling on the tidal turbine performance. In Applied Energy Symposium; MIT: Cambridge, MA, USA, 2019; pp. 1–10. [Google Scholar]
- Mycek, P. Numerical and Experimental Study of the Behaviour of Marine Current Turbines. Ph.D. Thesis, University of Le Havre, Le Havre, France, 2013. (In French). [Google Scholar]
- Greenshields, C. OpenFoam User Guide Version 6; OpenFOAM Foundation: London, UK, 2018. [Google Scholar]
- Ramirez-Pastran, J.; Duque-Daza, C. On the prediction capabilities of two SGS models for large-eddy simulations of turbulent incompressible wall-bounded flows in OpenFOAM. Cogent Eng. 2019, 6, 1679067. [Google Scholar] [CrossRef]
- Marten, D.; Peukert, J.; Pechlivanoglou, G.; Nayeri, C.; Paschereit, C. QBLADE: An Open Source Tool for Design and Simulation of Horizontal and Vertical Axis Wind Turbines. Int. J. Emerg. Technol. Adv. Eng. 2013, 3, 264–269. [Google Scholar]
- Community, B.O. Blender-a 3D Modelling and Rendering Package; Blender Foundation, Stichting Blender Foundation: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Robin, I.; Bennis, A.C.; Dauvin, J.C. 3D Simulation with Flow-Induced Rotation for Non-Deformable Tidal Turbines. J. Mar. Sci. Eng. 2021, 9, 250. [Google Scholar] [CrossRef]





| Turbine | IFREMER-LOMC | Unit |
|---|---|---|
| Profile | NACA 63418 | |
| Rotor Radius (R) | 350 | mm |
| Hub Radius | 46 | mm |
| Pitch | 0 | degrees |
| TSR | 4 | - |
| Parameter | Value | Unit |
|---|---|---|
| ρ | 1.177 | kg·m−3 |
| ν | 1.57 × 10−5 | m2·s−1 |
| U∞ | 45 | m·s−1 |
| p∞ | 1.013 × 106 | Pa |
| k | 1.898 | m2·s−2 |
| ω | 4.574 | s−1 |
| Parameter | Value | Unit |
|---|---|---|
| ρ | 1025 | kg·m−3 |
| ν | 1.3 × 10−6 | m2·s−1 |
| U∞ | 0.8 | m·s−1 |
| p∞ | 0 | Pa |
| ΩR | 9.143 | rad·s−1 |
| I∞ | 0.03 | - |
| Case Name | Fluid | Rotation | Barnacle | Angle of Attack |
|---|---|---|---|---|
| Blade 5° | Air | No | Only one | 5° |
| Blade 10° | Air | No | Only one | 10° |
| Blade 14° | Air | No | Only one | 14° |
| Blade 15° | Air | No | Only one | 15° |
| Rotor clean | Water | Yes | Realistic | 0° |
| Rotor colonised | Water | Yes | Realistic | 0° |
| Case Name | ΔTmin (s) | ΔTmin (s) | ΔXmin (m) | Total Running Time |
|---|---|---|---|---|
| Blade 5° | ∼10−7 | ∼10−4 | 1.26 | |
| Blade 10° | ∼10−7 | ∼10−4 | 1.21 | |
| Blade 14° | ∼10−7 | ∼10−4 | 1.16 | |
| Blade 15° | ∼10−7 | ∼10−4 | 1.15 | |
| Rotor clean | ∼10−9 | ∼10−4 | 2.41 | |
| Rotor colonised | ∼10−12 | ∼10−4 | 1.505 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robin, I.; Bennis, A.-C.; Dauvin, J.-C. 3D Numerical Study of the Impact of Macro-Roughnesses on a Tidal Turbine, on Its Performance and Hydrodynamic Wake. J. Mar. Sci. Eng. 2021, 9, 1288. https://doi.org/10.3390/jmse9111288
Robin I, Bennis A-C, Dauvin J-C. 3D Numerical Study of the Impact of Macro-Roughnesses on a Tidal Turbine, on Its Performance and Hydrodynamic Wake. Journal of Marine Science and Engineering. 2021; 9(11):1288. https://doi.org/10.3390/jmse9111288
Chicago/Turabian StyleRobin, Ilan, Anne-Claire Bennis, and Jean-Claude Dauvin. 2021. "3D Numerical Study of the Impact of Macro-Roughnesses on a Tidal Turbine, on Its Performance and Hydrodynamic Wake" Journal of Marine Science and Engineering 9, no. 11: 1288. https://doi.org/10.3390/jmse9111288
APA StyleRobin, I., Bennis, A.-C., & Dauvin, J.-C. (2021). 3D Numerical Study of the Impact of Macro-Roughnesses on a Tidal Turbine, on Its Performance and Hydrodynamic Wake. Journal of Marine Science and Engineering, 9(11), 1288. https://doi.org/10.3390/jmse9111288







