Three-Dimensional Surface Crack Growth of Maraging Steel Spherical Pressure Shell
Abstract
1. Introduction
2. Materials Test
2.1. Design and Manufacturing
2.2. Material Properties
2.3. Simplified Strip Model of Plastic Zone
3. Three-Dimensional Surface Crack Growth on Spherical Shell
3.1. The Finite Element Model of a Spherical Shell with Surface Crack
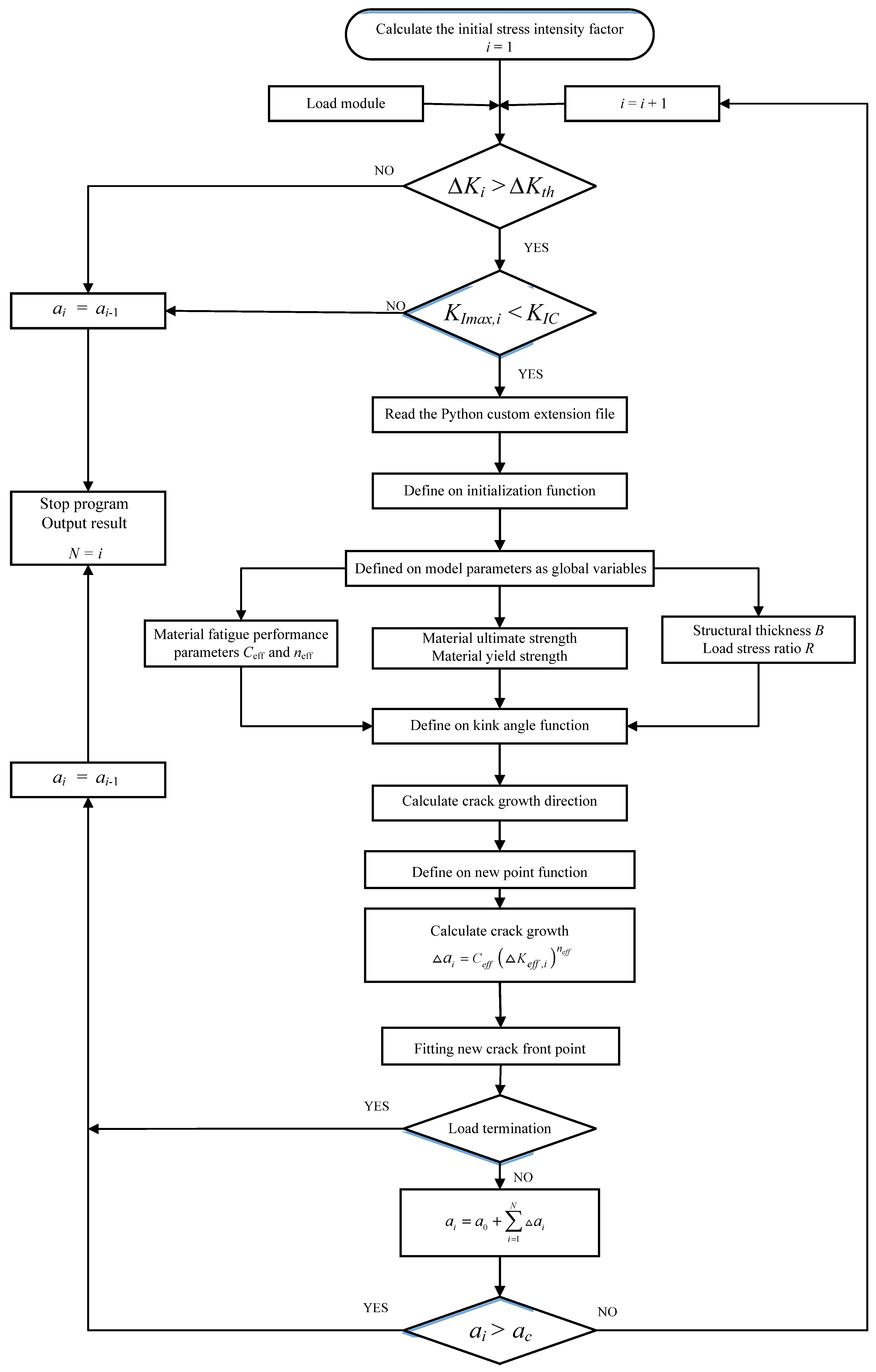
3.2. Three-Dimensional Surface Crack Growth Model of Spherical Shell
3.3. Simulation of Three-Dimensional Surface Crack Growth of Spherical Shell
4. Crack Growth Results and Analysis
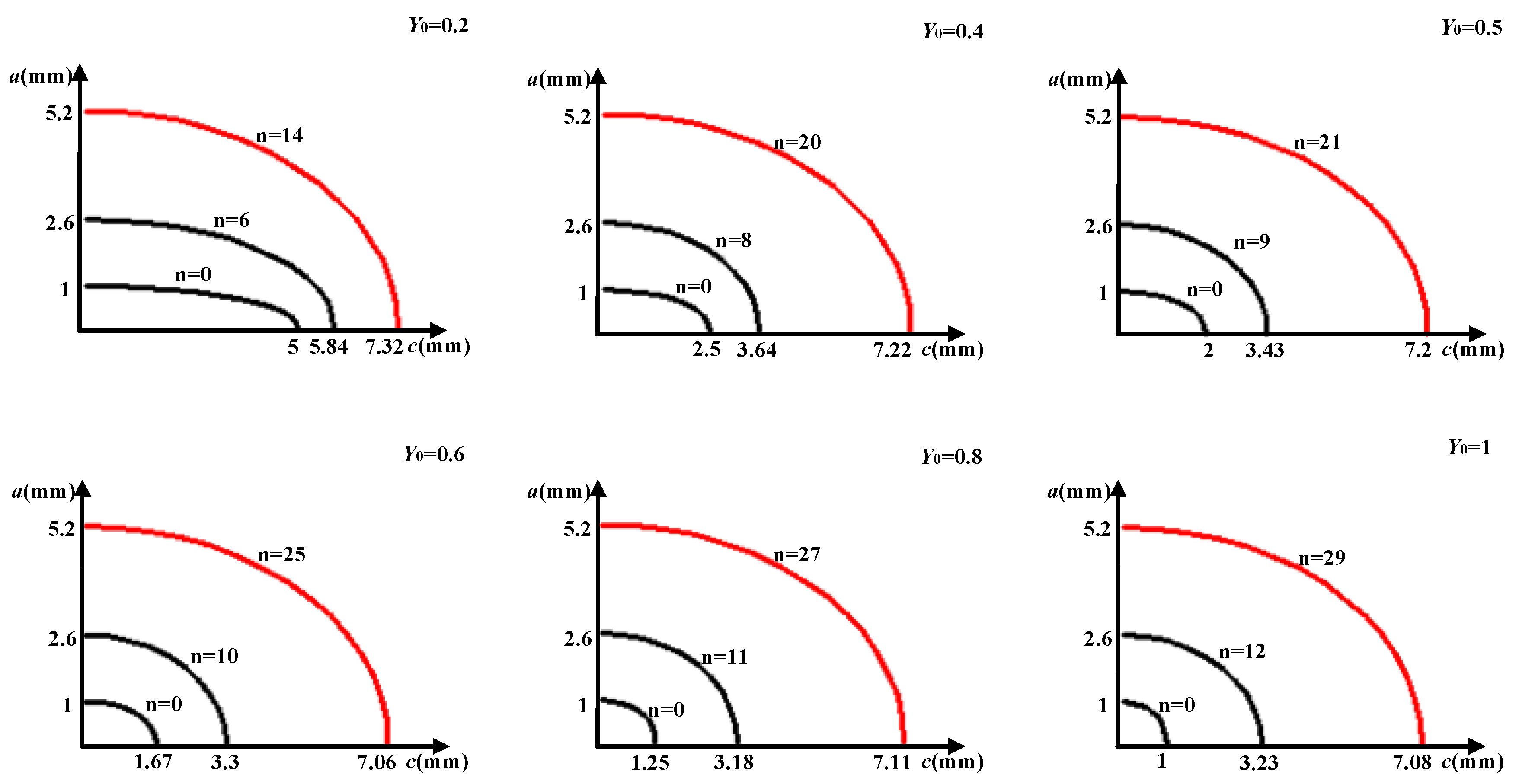
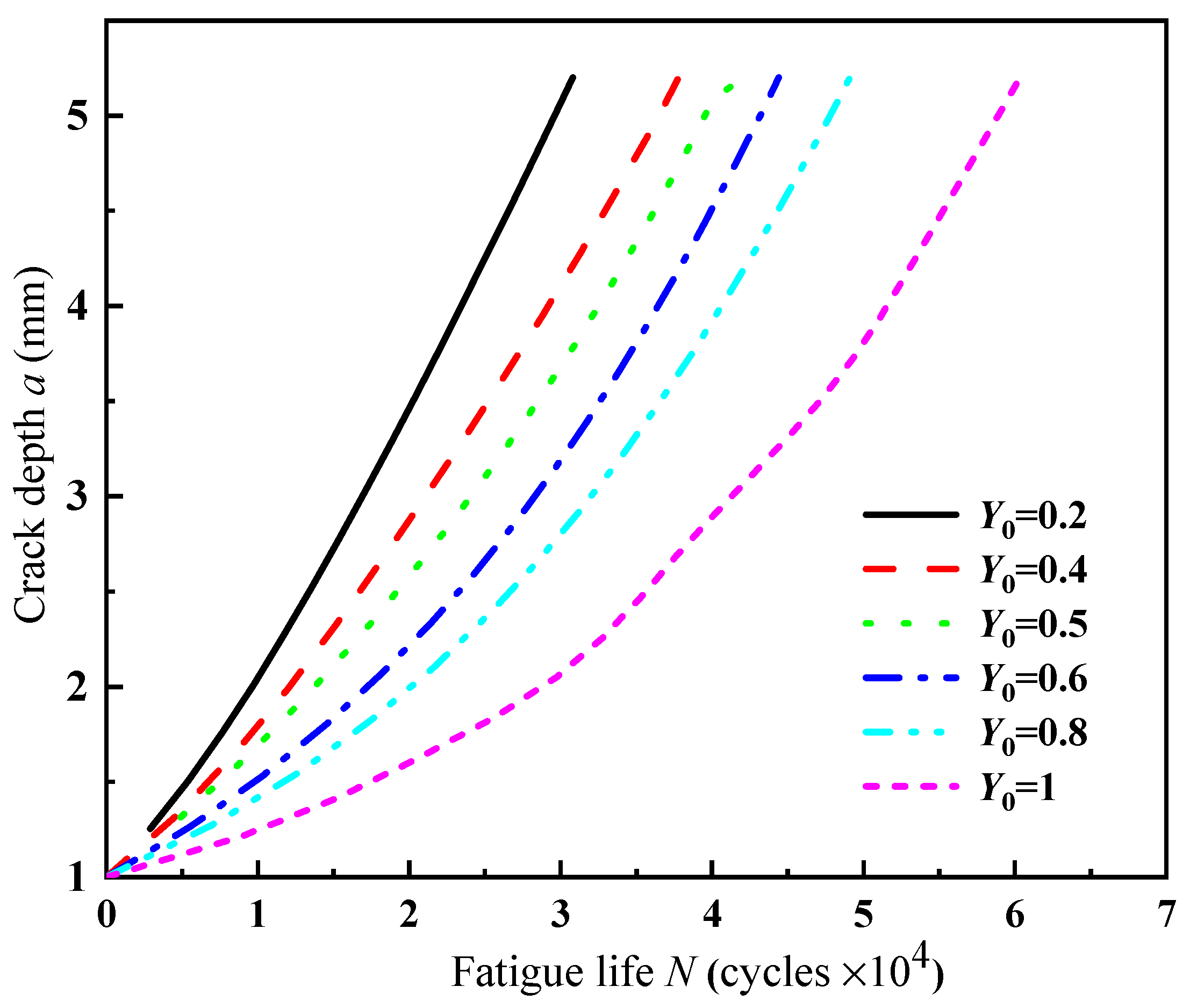
4.1. The Effect of Crack Initial Shape Ratio on Crack Growth
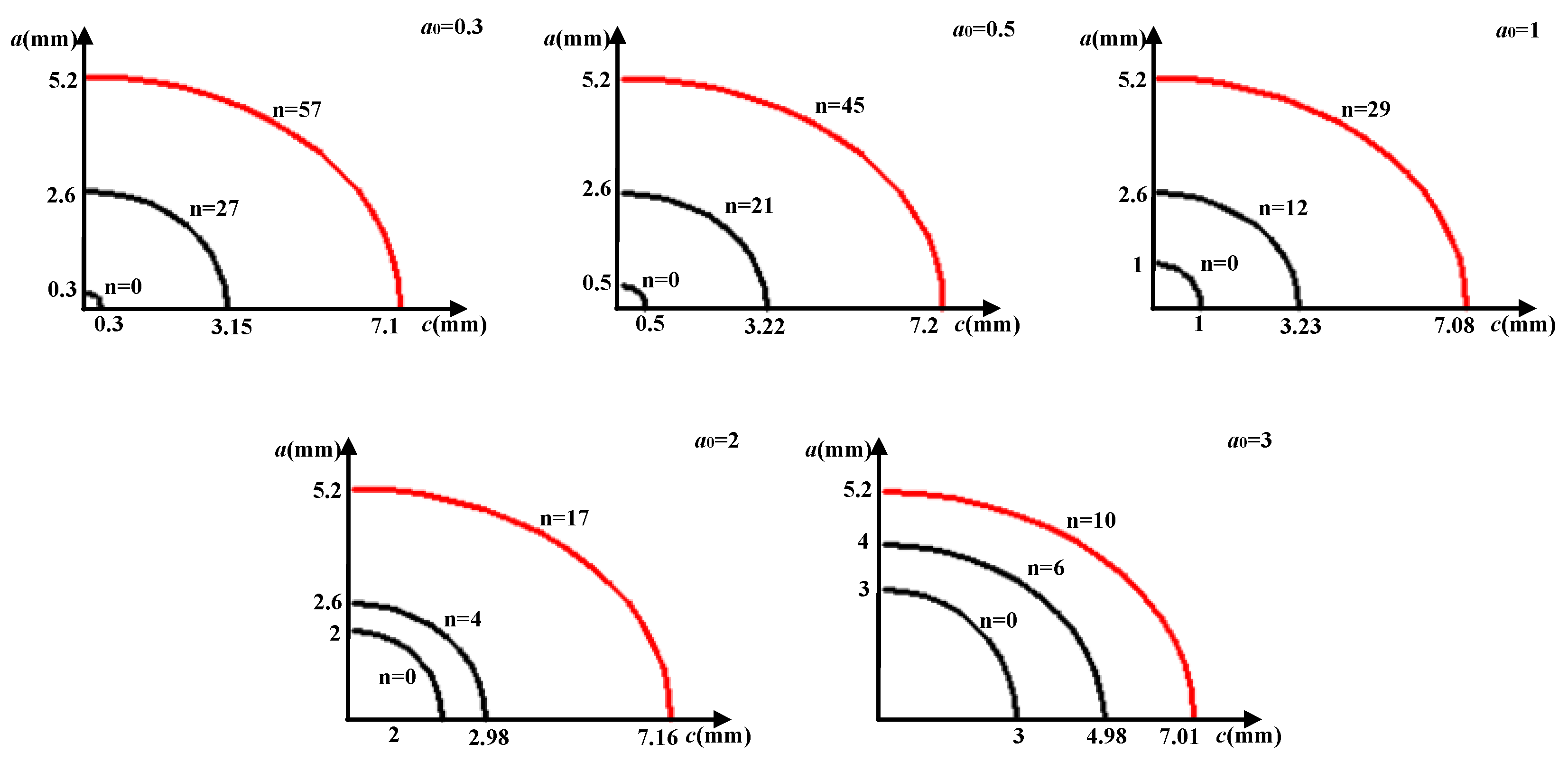
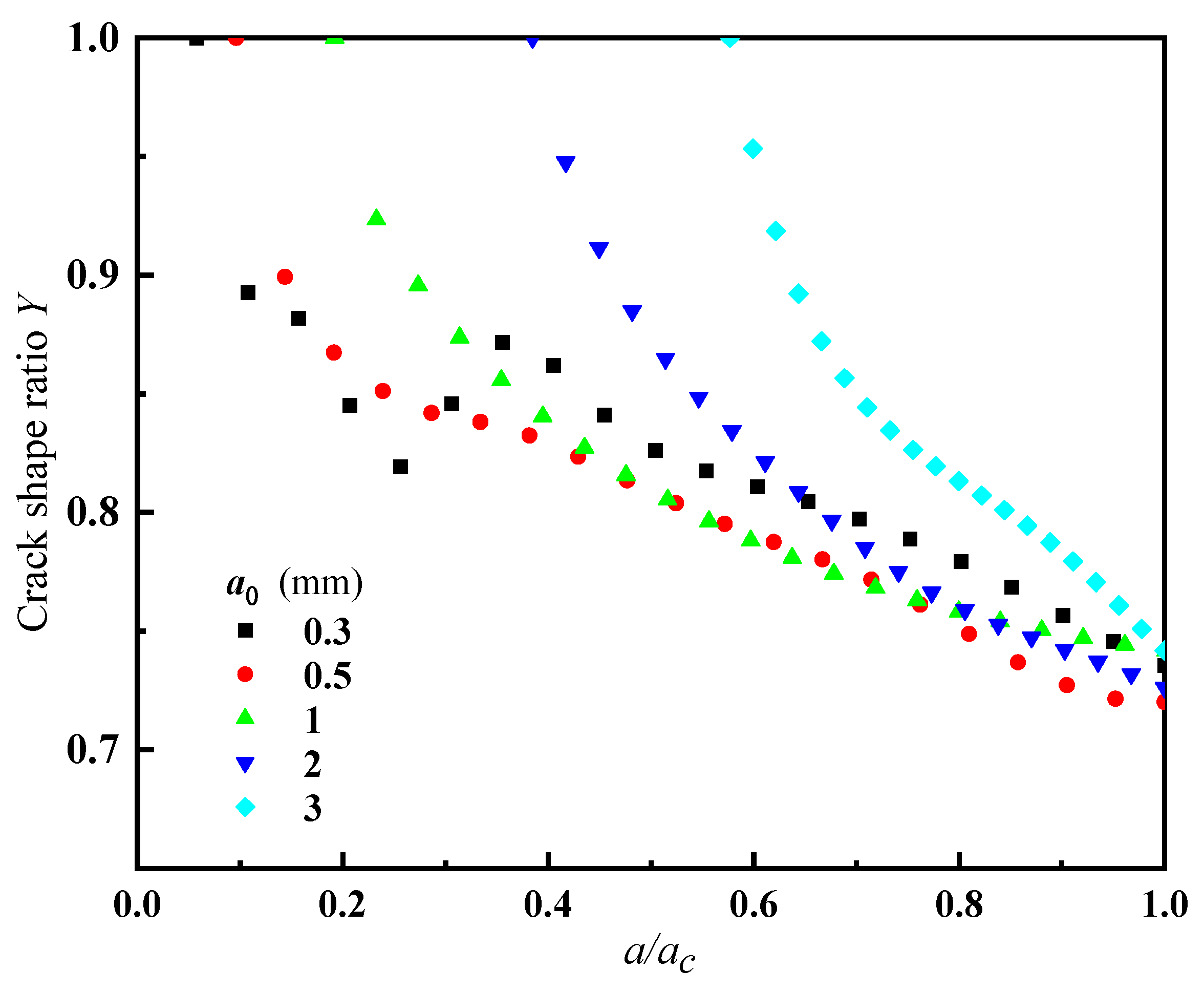
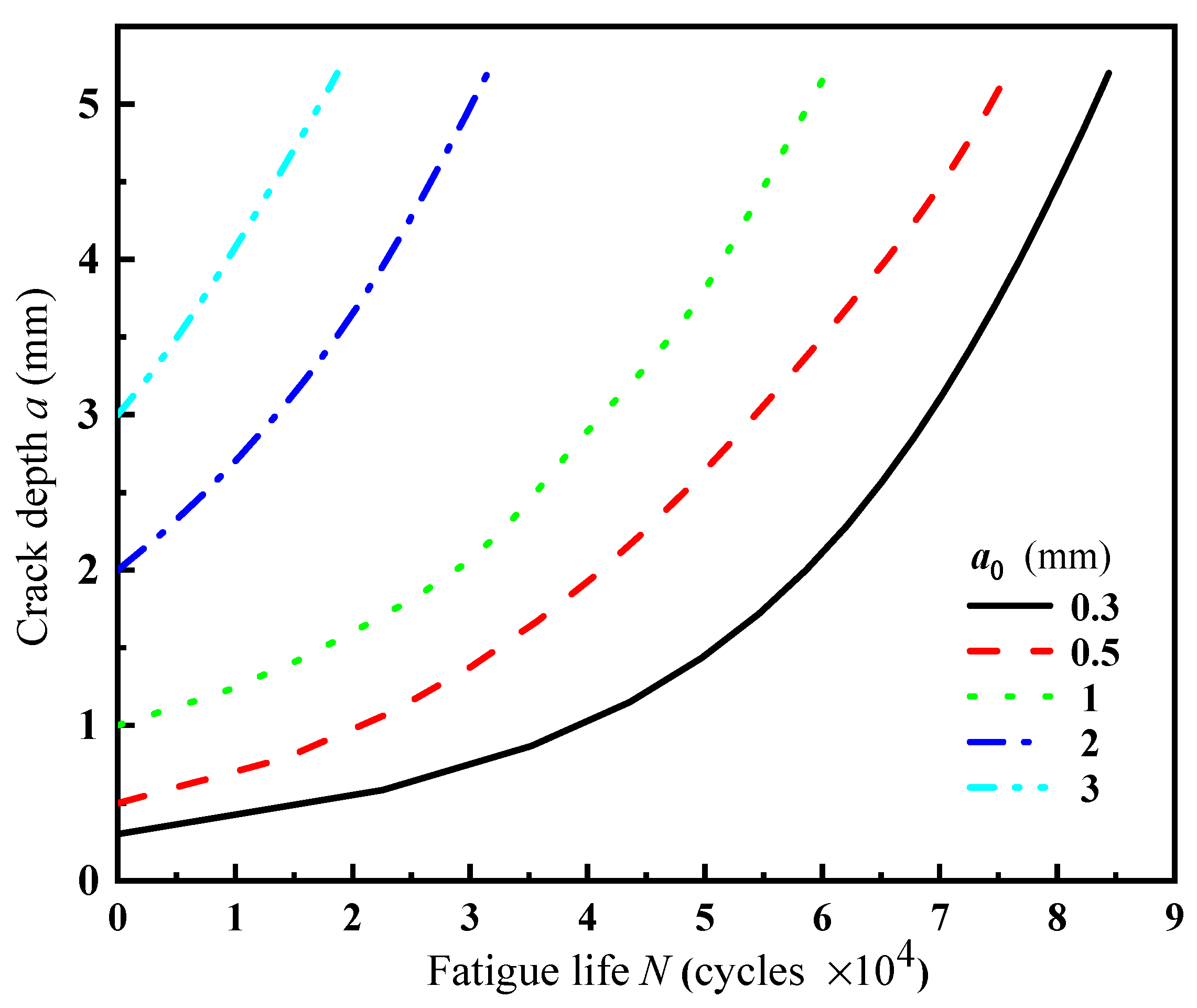
4.2. Effect of Initial Crack Depth on Crack Growth
5. Conclusions
- (1)
- When the initial semi-elliptical surface crack propagated on the spherical shell, the shape ratio of the crack was not constant. It is shown that the final shape of the crack tended to be stable when the crack propagated to the critical size of the spherical shell, and the final shape ratio of the crack was around 0.7.
- (2)
- For semi-elliptical surface cracks with the same initial depth and different shape ratios, the propagation rate of each point on the front edge was very different. The smaller the initial shape ratio (Y0 ≤ 0.2), that is, the narrower and longer the crack was, the rate of its development in depth was significantly higher than that in its transverse direction. The transverse crack growth rate was higher than that in depth when the initial shape ratio was between 0.4 and 0.8, and it developed very fast at first, and then tended to be gentle.
- (3)
- At the same initial crack depth, the smaller the crack shape ratio, the shorter the life of the spherical shell. The fatigue life of the spherical shell with a shape ratio of 0.2 was only 51.08% of that with a shape ratio of 1. That is, the narrower and longer the crack shape on the spherical shell surface, the greater the potential safety hazard of the spherical shell.
- (4)
- For semi-elliptical surface cracks with the same shape ratio (Y0 = 1), the fatigue life of the spherical shell caused by the crack with a larger initial size was lower. The fatigue life of the spherical shell with an initial crack depth of 3 mm was only 31.01% of that with an initial depth of 1 mm. There were some differences in the fatigue life of spherical shells with small initial size cracks, but the variation range was very small. When the initial depth of the crack was less than 1% of the wall thickness, it had little effect on the fatigue life.
- (5)
- The initial crack growth of different sizes changed from slow to fast. The growth rate of the small crack changed obviously, where the rate was gentle in the early stage of growth, and the speed was very fast when it reached the critical size.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Moorhouse, P. A modern history of the manned submersible. Mar. Technol. Soc. J. 2015, 49, 65–78. [Google Scholar] [CrossRef]
- Yongmei, Z. Opening reinforcement design and buckling of spherical shell subjected to external pressure. Int. J. Press. Vessel. Pip. 2017, 158, 29–36. [Google Scholar] [CrossRef]
- Luo, H.; Chen, C.; Liu, J. Prediction of Fatigue Crack Growth Life of 7050 Aluminum Alloy with Different Thicknesses under Various Load Ratios by Genetic Programming. J. Mater. Sci. Eng. 2017, 35, 26–31. [Google Scholar]
- Matvienko, Y.G.; Shlyannikov, V.; Boychenko, N. In-plane and out-of-plane constraint parameters along a three-dimensional crack-front stress field under creep loading. Fatigue Fract. Eng. Mater. Struct. 2013, 36, 14–24. [Google Scholar] [CrossRef]
- Shlyannikov, V.; Tumanov, A.; Zakharov, A. Surface flaws behavior under tension, bending and biaxial cyclic loading. Int. J. Fatigue 2016, 92, 557–576. [Google Scholar] [CrossRef]
- Wang, A.; Luan, C. Research on Crack Growth Characteristics Based on Crack Closure Effect. Coal Mine Mach. 2018, 39, 37–39. [Google Scholar]
- Yu, P.; She, C.; Guo, W. Equivalent thickness conception for corner cracks. Int. J. Solids Struct. 2010, 47, 2123–2130. [Google Scholar] [CrossRef][Green Version]
- Guo, W.; Xu, L.; Zhou, Z. Computational mechanics of three-dimensional fracture. Chin. J. Comput. Mech. 2016, 33, 431–440. [Google Scholar]
- Yu, P.; Guo, W. An equivalent thickness conception for prediction of surface fatigue crack growth life and shape evolution. Eng. Fract. Mech. 2012, 93, 65–74. [Google Scholar] [CrossRef]
- Wei, G.; Jiacai, Z.; Wanlin, G. Equivalent thickness-based three dimensional stress fields and fatigue growth of part-through cracks emanating from a circular hole. Eng. Fract. Mech. 2020, 228, 106927. [Google Scholar] [CrossRef]
- Ngoula, D.T.; Beier, H.T.; Vormwald, M. Fatigue crack growth in cruciform welded joints: Influence of residual stresses and of the weld toe geometry. Int. J. Fatigue 2016, 101 Pt 2, 253–262. [Google Scholar] [CrossRef]
- Chakherlou, T.N.; Mirzajanzadeh, M.; Vogwell, J. Investigation of the fatigue life and crack growth in torque tightened bolted joints. Aerosp. Sci. Technol. 2010, 15, 304–313. [Google Scholar] [CrossRef]
- Ai, S.; Yu, M.; Cheng, X. Analysis and application of three-dimensional crack growth based on FRANC3D. J. Mech. Strength 2018, 40, 251–254. [Google Scholar]
- Wang, Z.; Yue, Y.; Li, Y. Prediction of Dwell-Fatigue Crack Growth for Titanium Alloys Based on Zencrack. China Offshore Platf. 2018, 33, 22–28. [Google Scholar]
- GB/T 6398: Metallic Materials Fatigue Testing Fatigue Crack Growth; Chinese Standard Institute: Beijing, China, 2017.
- ASTM E647: Standard Test Method for Measurement of Fatigue Crack Growth Rates; American Society for Testing and Materials: West Conshohocken, PA, USA, 2013.
- GB/T 228.1: Metallic Materials—Tensile Testing-Part 1: Method of Test at Room Temperature; Chinese Standard Institute: Beijing, China, 2010.
- ISO 6892-1: Metallic Materials—Tensile Testing-Part 1: Method of Test at Room Temperature; International Organization for Standardization: Geneva, Switzerland, 2009.
- Bellett, D.; Taylor, D.; Marco, S.; Mazzeo, E.; Guillois, J.; Pircher, T. The fatigue behaviour of three-dimensional stress concentrations. Int. J. Fatigue 2005, 27, 207–221. [Google Scholar] [CrossRef]
- Chang, T.; Guo, W. A model for the through-thickness fatigue crack closure. Eng. Fract. Mech. 1999, 64, 59–65. [Google Scholar] [CrossRef]
- Paris, P.; Erdogan, F. A Critical Analysis of Crack Propagation Laws. J. Basic Eng. 1963, 85, 528–533. [Google Scholar] [CrossRef]
- Zhu, Y.; Yao, X.; Yang, L. Effect of stress intensity factor on surface crack of deep-sea spherical shell. J. Ship Mech. 2020, 5, 476–484. [Google Scholar]
- Zhang, J.; Gao, J.; Wang, W. Investigation on mechanical properties of deep sea spherical pressure hull. Shipbuild. China 2015, 4, 129–140. [Google Scholar]
- Germanischer Lloyd Group. Rules for Classification and Construction; Germanischer Lloyd: Hamburg, Germany, 2009. [Google Scholar]
- Zhang, S. Analysis on the Effects of Material and Structural Defects on the Property of Deep-Sea Manned Spherical Hull; Jiangsu University of Science and Technology: Zhenjiang, China, 2018. [Google Scholar]
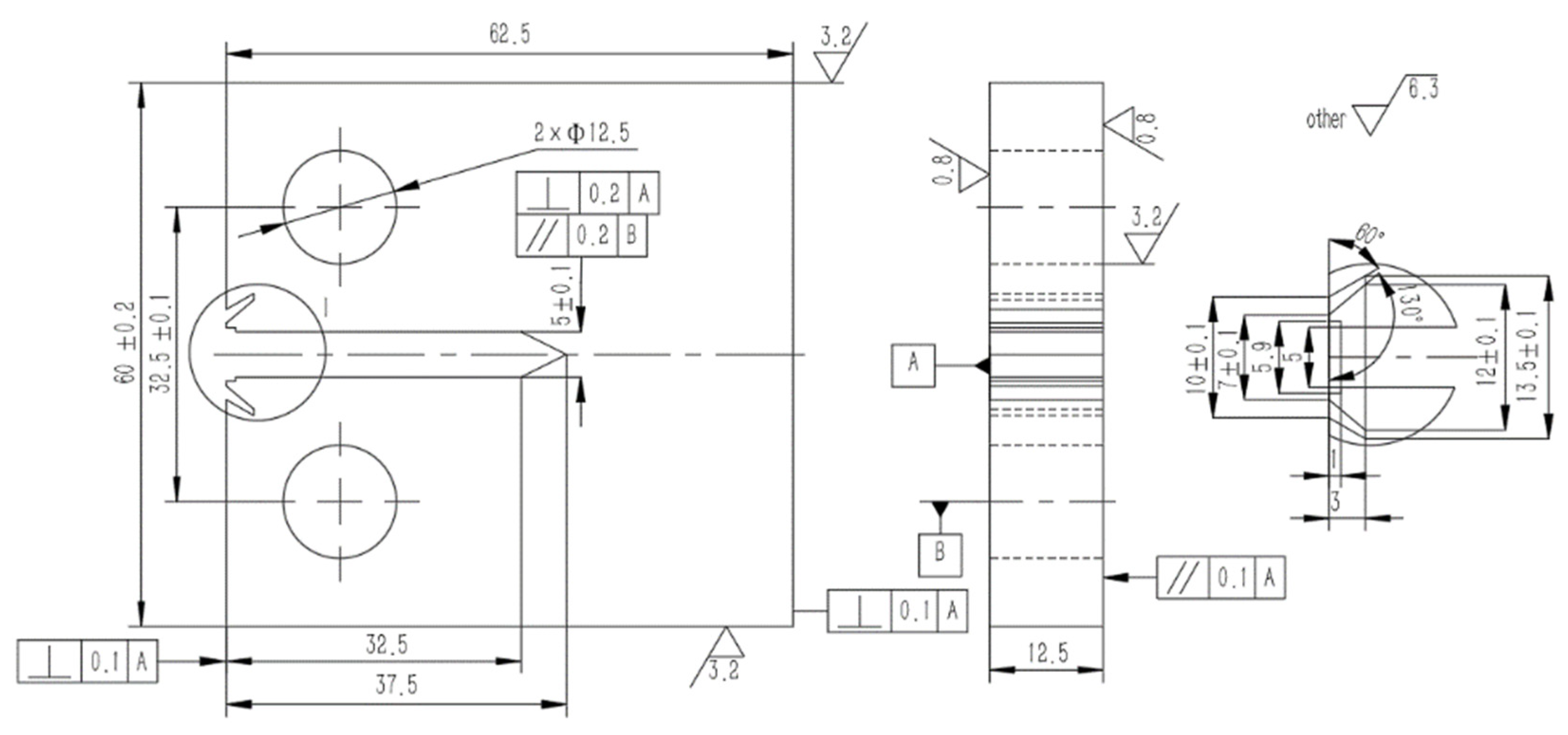
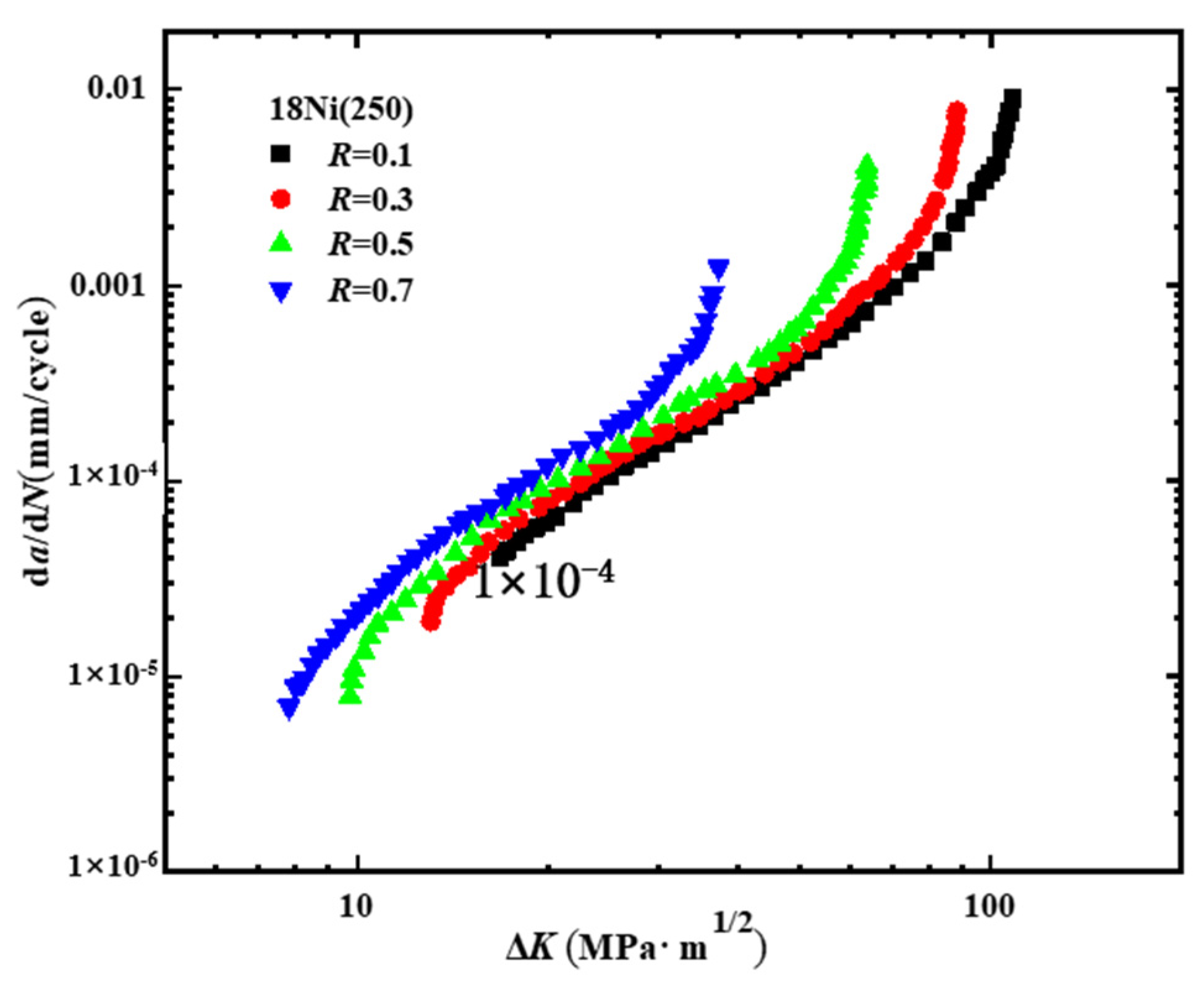
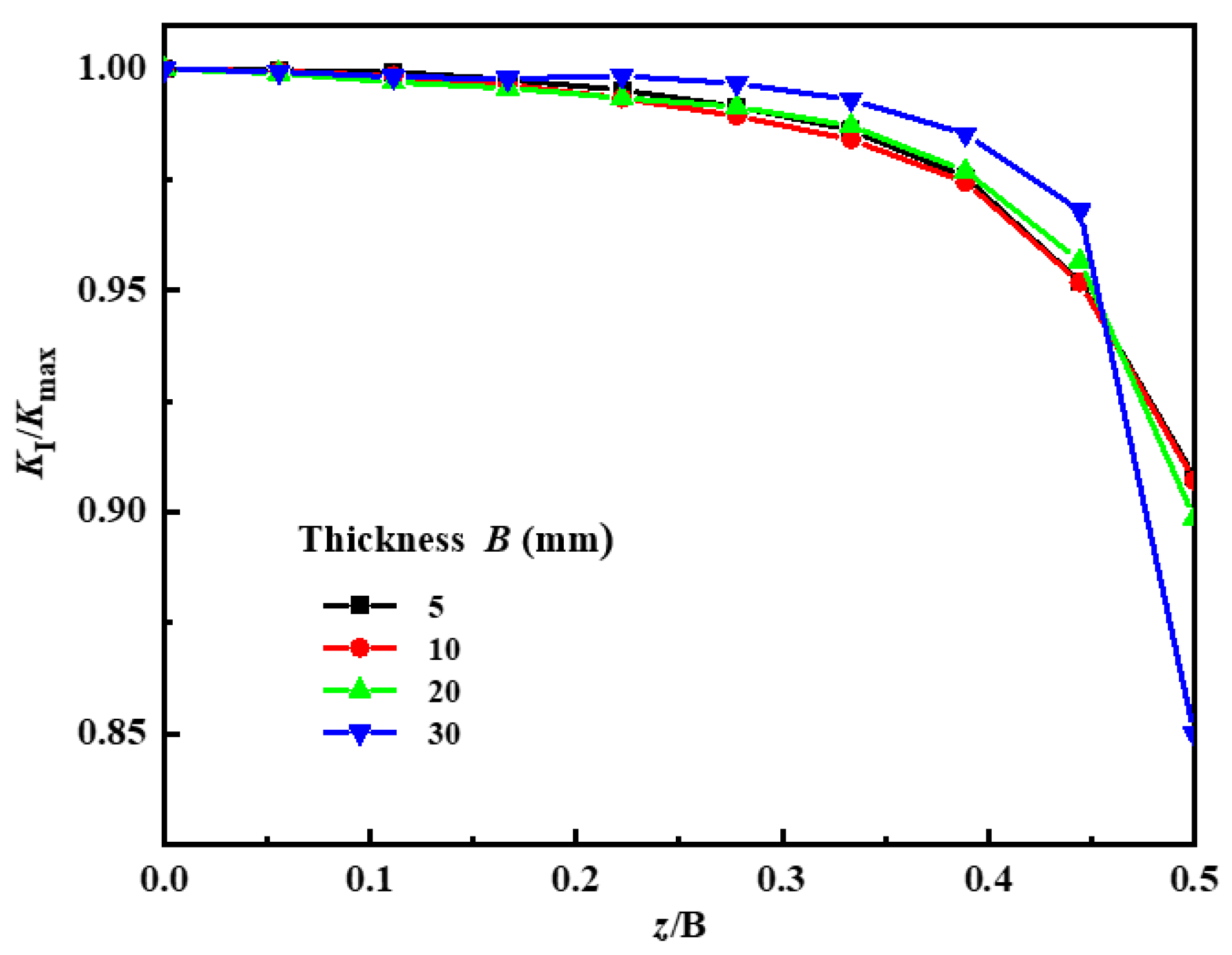
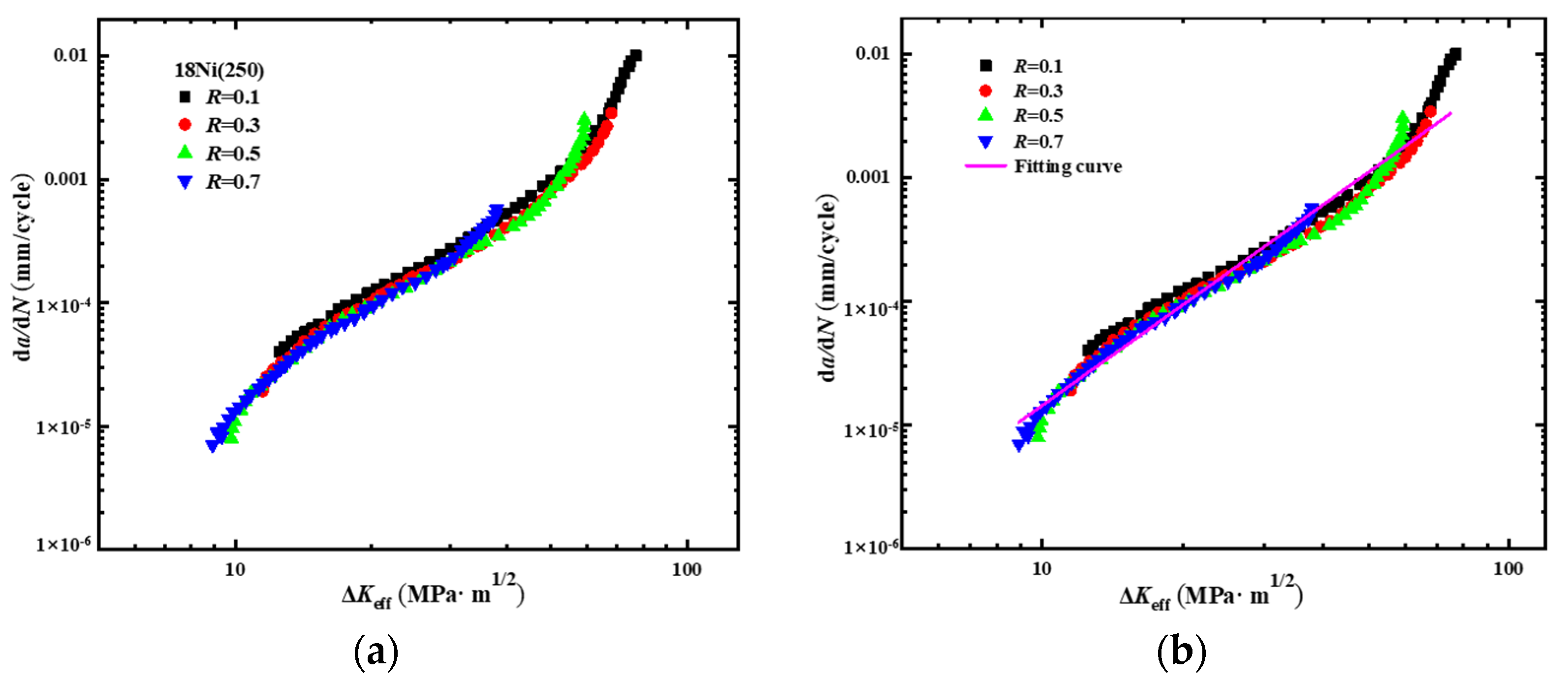


| Sample Number | Stress Ratio | Loading Frequency (Hz) | Load (KN) | |
|---|---|---|---|---|
| Maximum | Minimum | |||
| 1-1# | 0.1 | 5 | 5 | 0.5 |
| 1-2# | ||||
| 2-1# | 0.3 | 5 | 5 | 1.5 |
| 2-2# | ||||
| 3-1# | 0.5 | 5 | 5 | 2.5 |
| 3-2# | ||||
| 4-1# | 0.7 | 5 | 5 | 3.5 |
| 4-2# | ||||
| Chemical Specific Gravity (wt.%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| C | Si | Mn | S | P | Ni | Co | Mo | Al | Ti |
| 0.008 | 0.02 | 0.03 | 0.001 | 0.005 | 17.86 | 7.93 | 5.25 | 0.14 | 0.48 |
| Elastic Modulus E (GPa) | Poisson’s Ratio ν | Yield Strength σs (MPa) | Ultimate Strength σb (MPa) | Reduction of Area Z (%) | Elongation A (%) |
|---|---|---|---|---|---|
| 182 | 0.3 | 1833 | 1900 | 64.5 | 10.3 |
| Initial Crack Shape Ratio Y0 | ||||||
|---|---|---|---|---|---|---|
| 0.2 | 0.4 | 0.5 | 0.6 | 0.8 | 1 | |
| 2c (mm) | 14.64 | 14.44 | 14.4 | 14.12 | 14.22 | 14.16 |
| Y | 0.710 | 0.720 | 0.722 | 0.737 | 0.731 | 0.734 |
| N (cycle) | 30,800 | 37,800 | 40,800 | 44,400 | 49,100 | 60,300 |
| Initial Crack Depth a0 (mm) | |||||
|---|---|---|---|---|---|
| 0.3 | 0.5 | 1 | 2 | 3 | |
| 2c (mm) | 14.2 | 14.4 | 14.16 | 14.32 | 14.02 |
| Y | 0.732 | 0.720 | 0.734 | 0.726 | 0.741 |
| N (cycle) | 84,400 | 75,800 | 60,300 | 31,500 | 18,700 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Li, R.; Yang, J. Three-Dimensional Surface Crack Growth of Maraging Steel Spherical Pressure Shell. J. Mar. Sci. Eng. 2021, 9, 1280. https://doi.org/10.3390/jmse9111280
Zhu Y, Li R, Yang J. Three-Dimensional Surface Crack Growth of Maraging Steel Spherical Pressure Shell. Journal of Marine Science and Engineering. 2021; 9(11):1280. https://doi.org/10.3390/jmse9111280
Chicago/Turabian StyleZhu, Yongmei, Rujun Li, and Jiahao Yang. 2021. "Three-Dimensional Surface Crack Growth of Maraging Steel Spherical Pressure Shell" Journal of Marine Science and Engineering 9, no. 11: 1280. https://doi.org/10.3390/jmse9111280
APA StyleZhu, Y., Li, R., & Yang, J. (2021). Three-Dimensional Surface Crack Growth of Maraging Steel Spherical Pressure Shell. Journal of Marine Science and Engineering, 9(11), 1280. https://doi.org/10.3390/jmse9111280





