Geometry Optimization of Heaving Axisymmetric Point Absorbers under Parametrical Constraints in Irregular Waves
Abstract
:1. Introduction
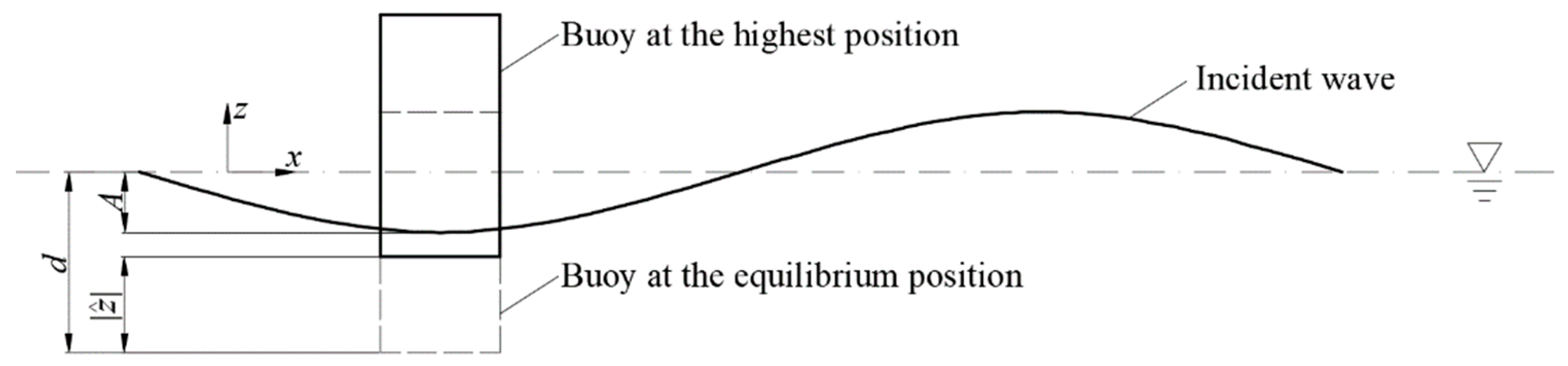
2. Configuration of the Point Absorber
3. Modelling
3.1. The Absorbed Power of a Point Absorber
3.2. Constraints
4. The Optimization Procedure and Results
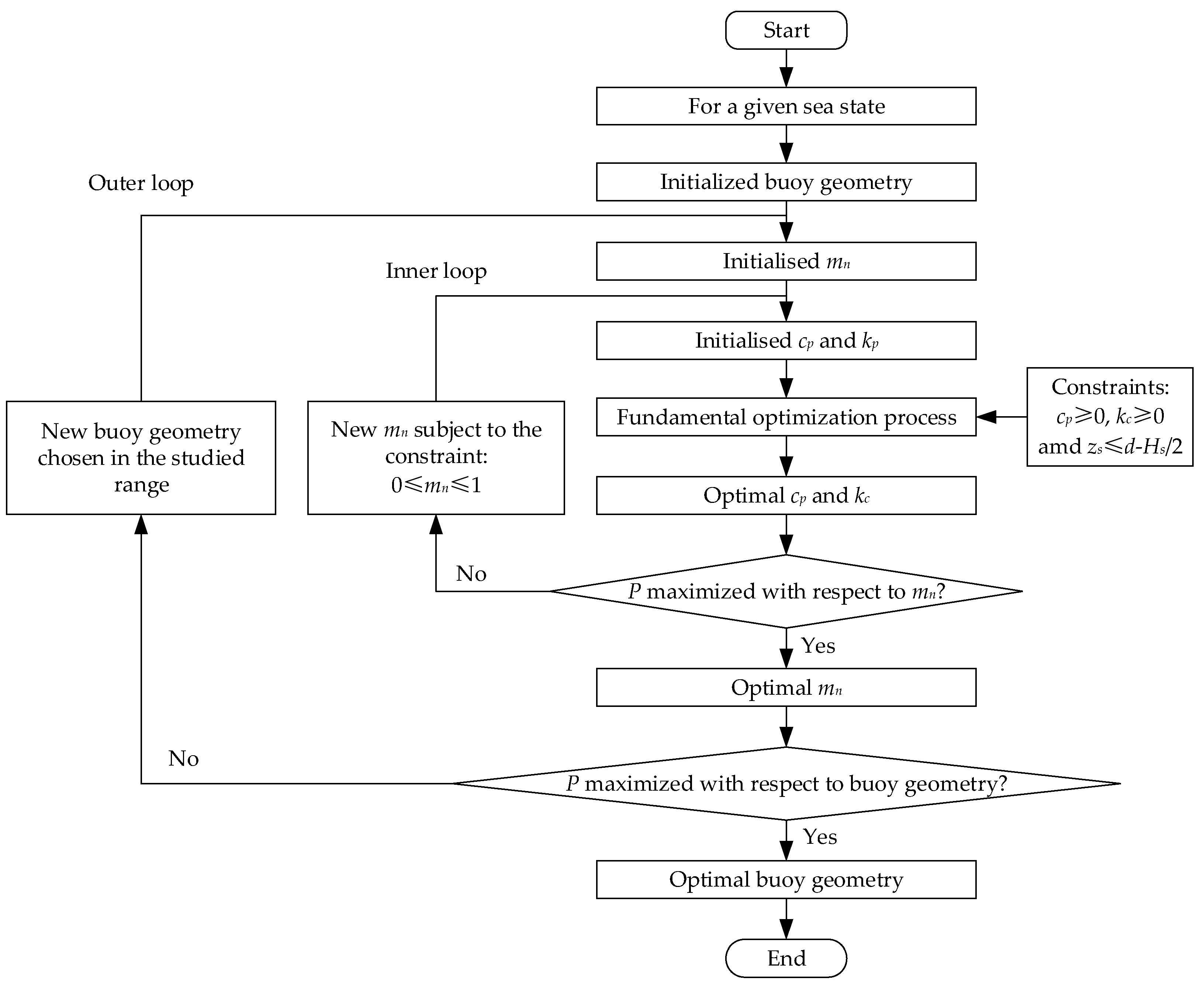
4.1. The Optimization Procedure
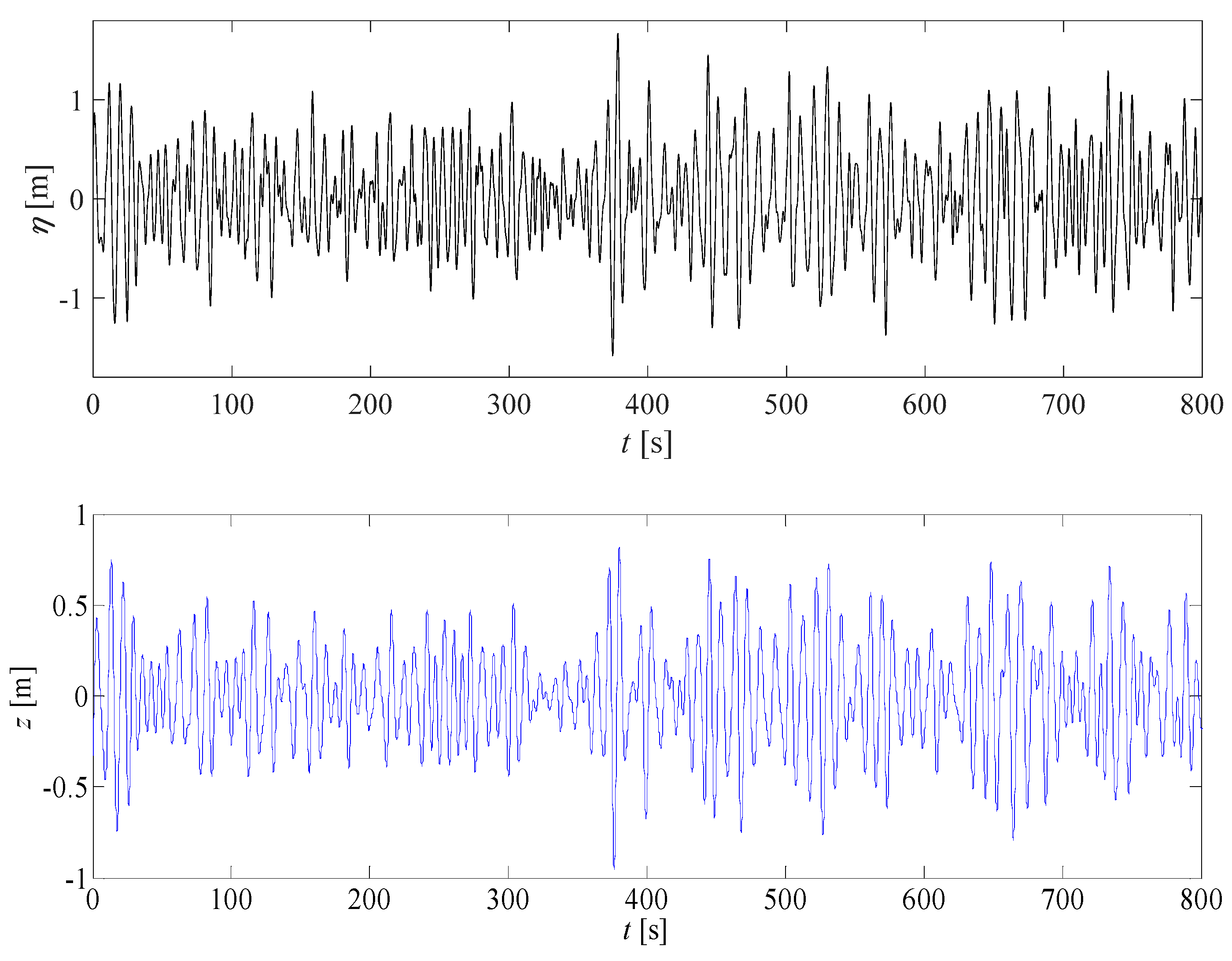
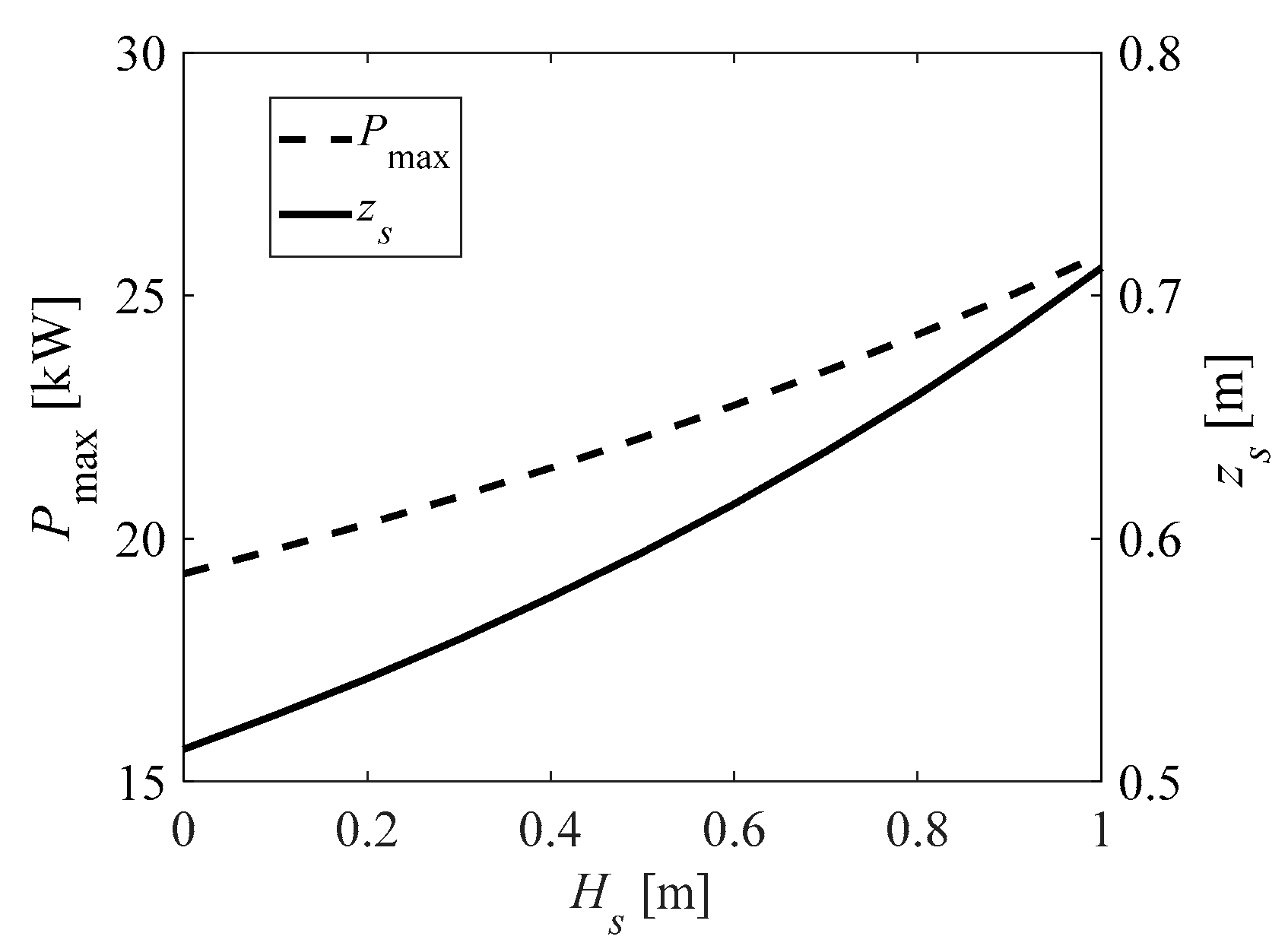
4.2. The Optimization Results
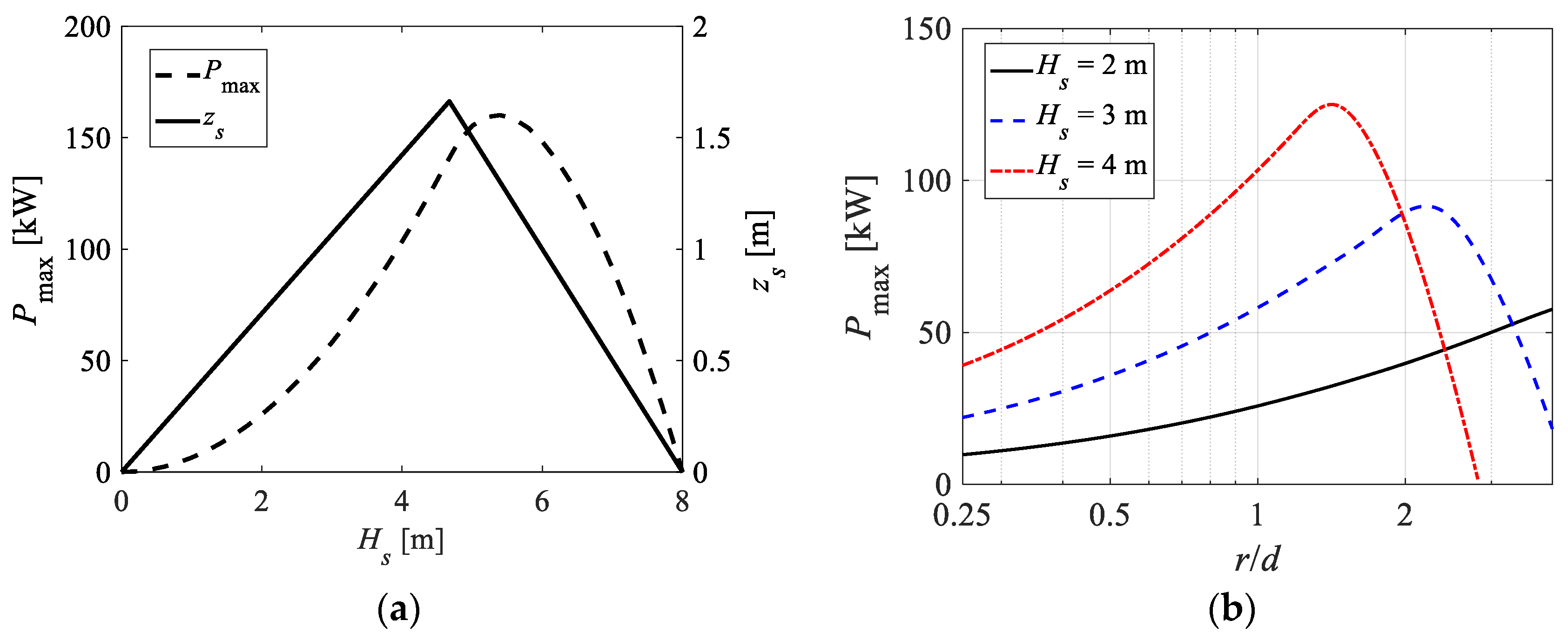
4.2.1. The Fundamental Optimization Process
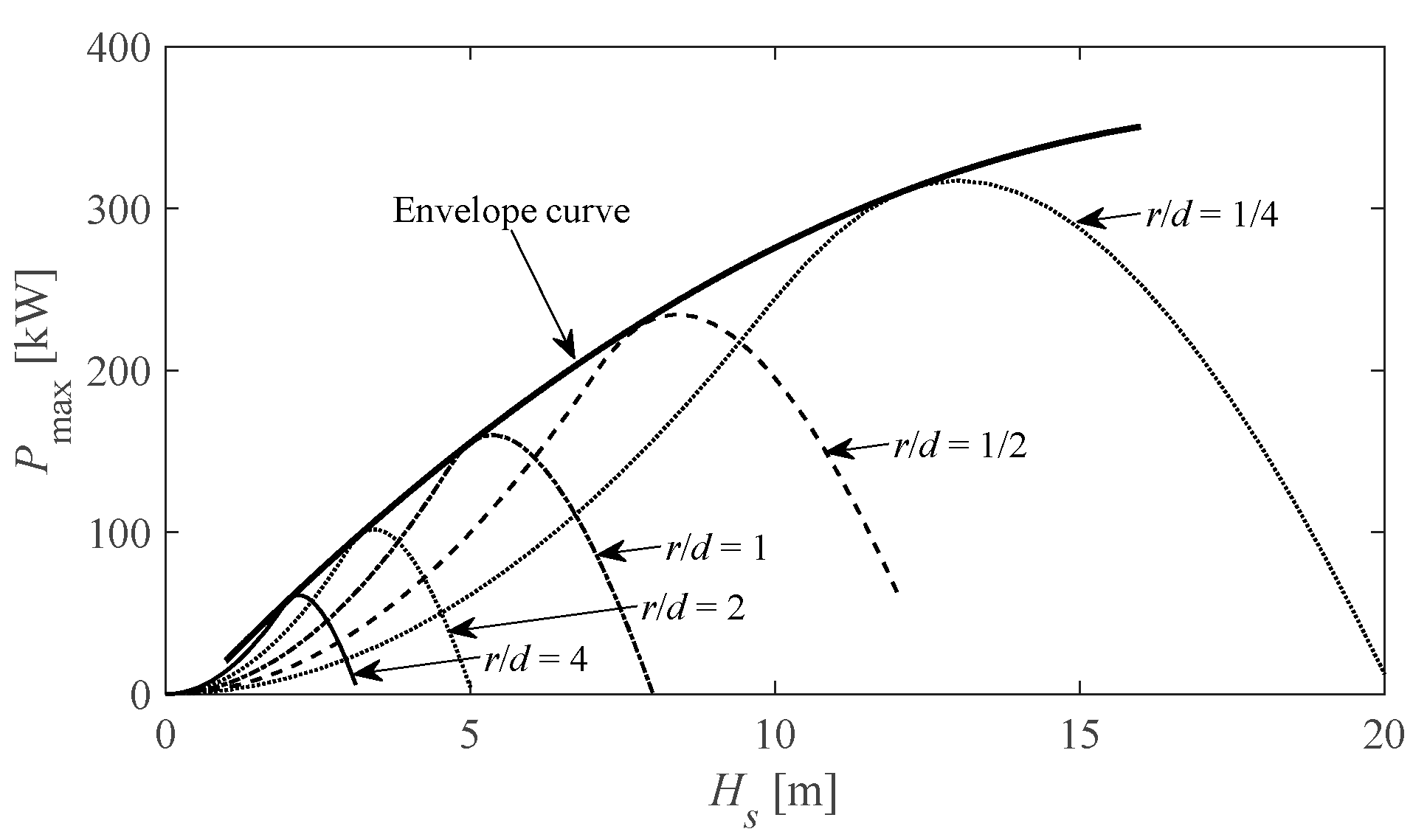
4.2.2. The Inner Loop
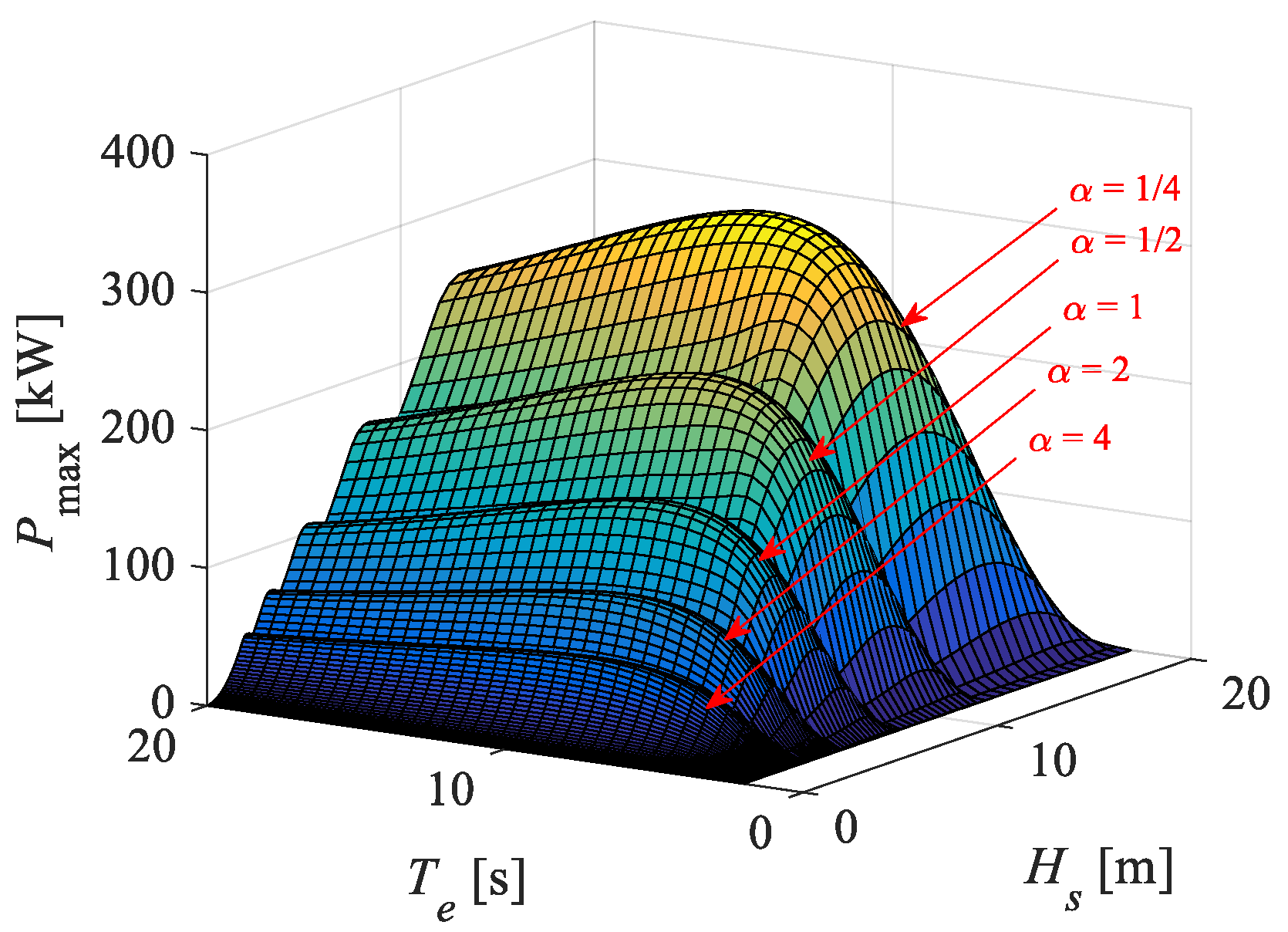
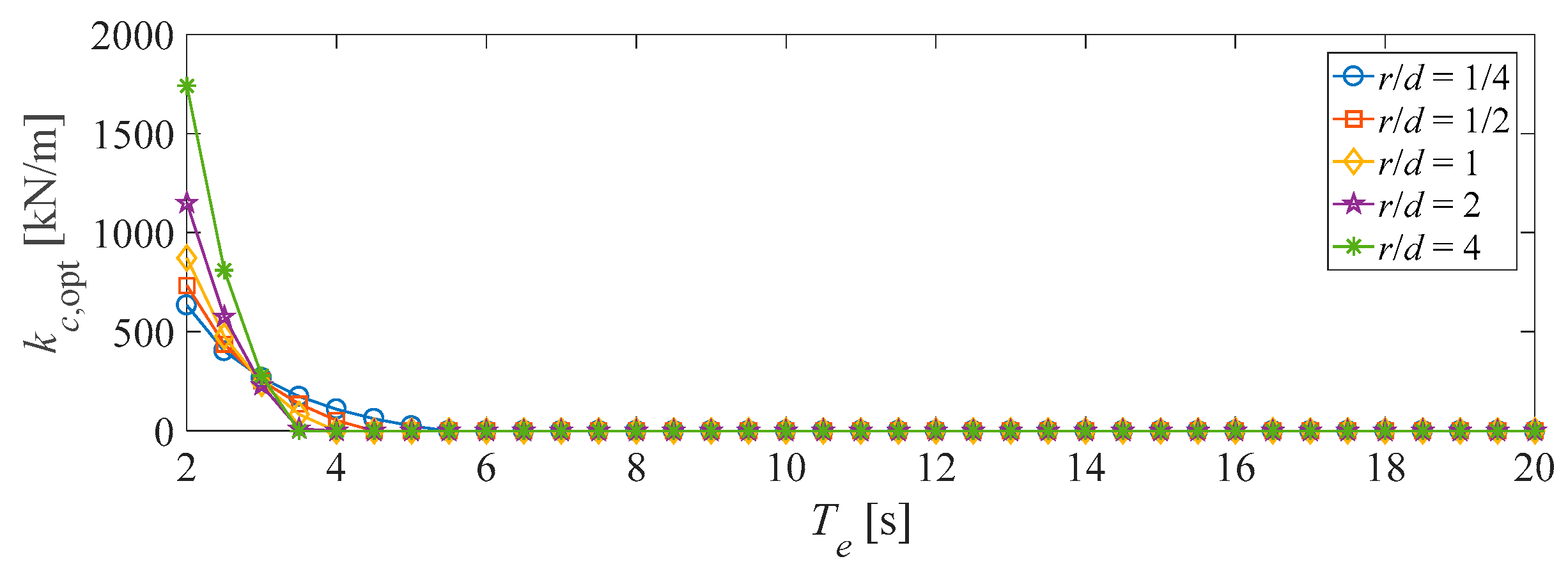
4.2.3. The Outer Loop
5. Discussion
6. Conclusions
Funding
Conflicts of Interest
References
- Wave Developers. Available online: http://www.emec.org.uk/marine-energy/wave-developers/ (accessed on 3 September 2021).
- Drew, B.; Plummer, A.R.; Sahinkaya, M.N. A review of wave energy converter technology. Proc. Inst. Mech. Eng. A-J. Pow. 2009, 223, 887–902. [Google Scholar] [CrossRef] [Green Version]
- Falcão, A.F.O. Wave energy utilization: A review of the technologies. Renew. Sust. Energy Rev. 2010, 14, 899–918. [Google Scholar] [CrossRef]
- Wu, J.; Yao, Y.; Zhou, L.; Chen, N.; Yu, H.; Li, W.; Göteman, M. Performance analysis of solo Duck wave energy converter arrays under motion constraints. Energy 2017, 139, 155–169. [Google Scholar] [CrossRef]
- Roh, C.; Ha, Y.J.; Shin, S.H.; Kim, K.H.; Park, J.Y. Advanced maximum power control algorithm based on a hydraulic system for floating wave energy converters. Processes 2021, 9, 1712. [Google Scholar] [CrossRef]
- Falnes, J.; Hals, J. Heaving buoys, point absorbers and arrays. Philos. Tran. R. Soc. A Math. Phy. Eng. Sci. 2012, 370, 246–277. [Google Scholar] [CrossRef] [Green Version]
- Antonio, F.D.O. Modelling and control of oscillating-body wave energy converters with hydraulic power take-off and gas accumulator. Ocean Eng. 2007, 34, 2021–2032. [Google Scholar]
- Greenhow, M.; White, S.P. Optimal heave motion of some axisymmetric wave energy devices in sinusoidal waves. Appl. Ocean Res. 1997, 19, 141–159. [Google Scholar] [CrossRef]
- Bharath, A.; Nader, J.R.; Penesis, I.; Macfarlane, G. Nonlinear hydrodynamic effects on a generic spherical wave energy converter. Renew. Energy 2018, 118, 56–70. [Google Scholar] [CrossRef]
- Sergiienko, N.Y.; Cazzolato, B.S.; Ding, B.; Hardy, P.; Arjomandi, M. Performance comparison of the floating and fully submerged quasi-point absorber wave energy converters. Renew. Energy 2017, 108, 425–437. [Google Scholar] [CrossRef] [Green Version]
- Demonte Gonzalez, T.; Parker, G.G.; Anderlini, E.; Weaver, W.W. Sliding mode control of a nonlinear wave energy converter model. J. Mar. Sci. Eng. 2021, 9, 951. [Google Scholar] [CrossRef]
- Evans, D.V. A theory for wave-power absorption by oscillating bodies. J. Fluid Mech. 1976, 77, 1–25. [Google Scholar] [CrossRef]
- Mei, C.C. Power extraction from water waves. J. Ship Res. 1976, 20, 63–66. [Google Scholar] [CrossRef]
- Budal, K.; Falnes, J. A resonant point absorber of ocean-wave energy. Nature 1975, 256, 478–479. [Google Scholar]
- Salter, S.H.; Jeffery, D.C.; Taylor, J.R.M. The architecture of nodding duck wave energy generators. Nav. Archit. 1976, 1, 21–24. [Google Scholar]
- Zhang, Z.; He, G.; Wang, Z. Real-coded genetic algorithm optimization in reduction of wave drift forces on an array of truncated cylinders. J. Mar. Sci. Tech. 2019, 24, 930–947. [Google Scholar] [CrossRef]
- Cochet, C.; Yeung, R.W. Dynamic analysis and configuration design of a two-component wave-energy absorber. In Proceedings of the ASME 31st International Conference on Ocean, Offshore and Arctic Engineering, Rio de Janeiro, Brazil, 1–6 July 2012; pp. 631–640. [Google Scholar]
- Babarit, A.; Hals, J.; Muliawan, M.J.; Kurniawan, A.; Moan, T.; Krokstad, J. Numerical benchmarking study of a selection of wave energy converters. Renew. Energy 2012, 41, 44–63. [Google Scholar] [CrossRef]
- McCabe, A.P.; Aggidis, G.A.; Widden, M.B. Optimizing the shape of a surge-and-pitch wave energy collector using a genetic algorithm. Renew. Energy 2010, 35, 2767–2775. [Google Scholar] [CrossRef]
- Garcia-Teruel, A.; Forehand, D. Optimal wave energy converter geometry for different modes of motion. In Proceedings of the 3rd International Conference on Renewable Energies Offshore (RENEW 2018), Lisbon, Portugal, 8–10 October 2018; Routledge Taylor & Francis Group: Abingdon, UK; pp. 299–305. [Google Scholar]
- Babarit, A.; Clement, A.H.; Gilloteaux, J.C. Optimization and time-domain simulation of the SEAREV wave energy converter. In Proceedings of the ASME 2005 24th International Conference on Offshore Mechanics and Arctic Engineering, Halkidiki, Grecee, 12–17 June 2005; pp. 703–712. [Google Scholar]
- Amini, E.; Asadi, R.; Golbaz, D.; Nasiri, M.; Naeeni, S.T.O.; Nezhad, M.M.; Piras, G.; Neshat, M. Comparative study of oscillating surge wave energy converter performance: A case study for southern coasts of the Caspian sea. Sustainability 2021, 13, 10932. [Google Scholar] [CrossRef]
- Azhari, B.; Wijaya, F.D.; Yazid, E. Performance of linear generator designs for direct drive wave energy converter under unidirectional long-crested random waves. Energies 2021, 14, 5098. [Google Scholar] [CrossRef]
- Wu, J.; Yao, Y.; Zhou, L.; Göteman, M. Real-time latching control strategies for the solo Duck wave energy converter in irregular waves. Appl. Energy 2018, 222, 717–728. [Google Scholar] [CrossRef]
- Goggins, J.; Finnegan, W. Shape optimisation of floating wave energy converters for a specified wave energy spectrum. Renew. Energy 2014, 71, 208–220. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, J. Power absorb performance of an oscillating-body WEC with nonlinear snap through PTO systems in irregular waves. Appl. Ocean Res. 2015, 52, 261–273. [Google Scholar] [CrossRef]
- Pols, A.; Gubesch, E.; Abdussamie, N.; Penesis, I.; Chin, C. Mooring analysis of a floating OWC wave energy converter. J. Mar. Sci. Eng. 2021, 9, 228. [Google Scholar] [CrossRef]
- Gilloteaux, J.-C.; Ringwood, J. Control-informed geometric optimisation of wave energy converters. IFAC Proc. Vol. 2010, 43, 366–371. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J. Geometry Optimization of Heaving Axisymmetric Point Absorbers under Parametrical Constraints in Irregular Waves. J. Mar. Sci. Eng. 2021, 9, 1136. https://doi.org/10.3390/jmse9101136
Wu J. Geometry Optimization of Heaving Axisymmetric Point Absorbers under Parametrical Constraints in Irregular Waves. Journal of Marine Science and Engineering. 2021; 9(10):1136. https://doi.org/10.3390/jmse9101136
Chicago/Turabian StyleWu, Jinming. 2021. "Geometry Optimization of Heaving Axisymmetric Point Absorbers under Parametrical Constraints in Irregular Waves" Journal of Marine Science and Engineering 9, no. 10: 1136. https://doi.org/10.3390/jmse9101136
APA StyleWu, J. (2021). Geometry Optimization of Heaving Axisymmetric Point Absorbers under Parametrical Constraints in Irregular Waves. Journal of Marine Science and Engineering, 9(10), 1136. https://doi.org/10.3390/jmse9101136




