Upper-Bound General Circulation of the Ocean: A Theoretical Exposition
Abstract
1. Introduction
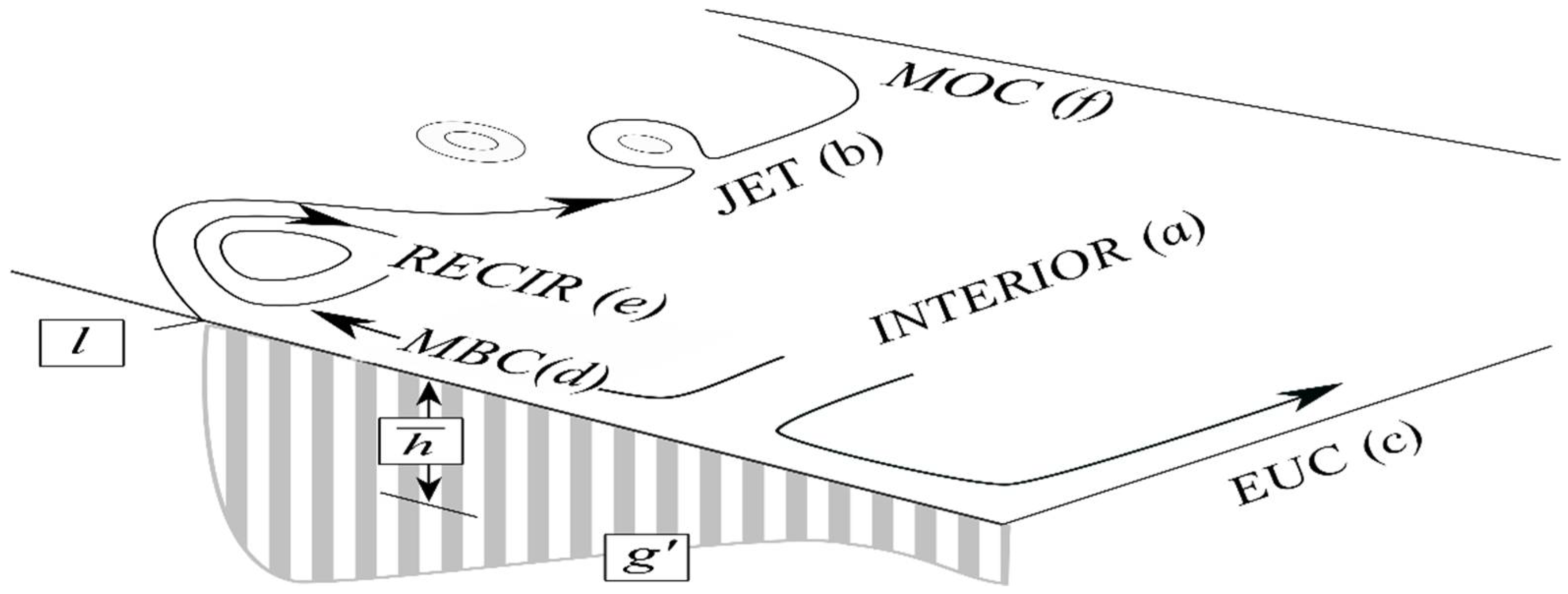
2. Model Configuration
3. Upper-Bound GOC
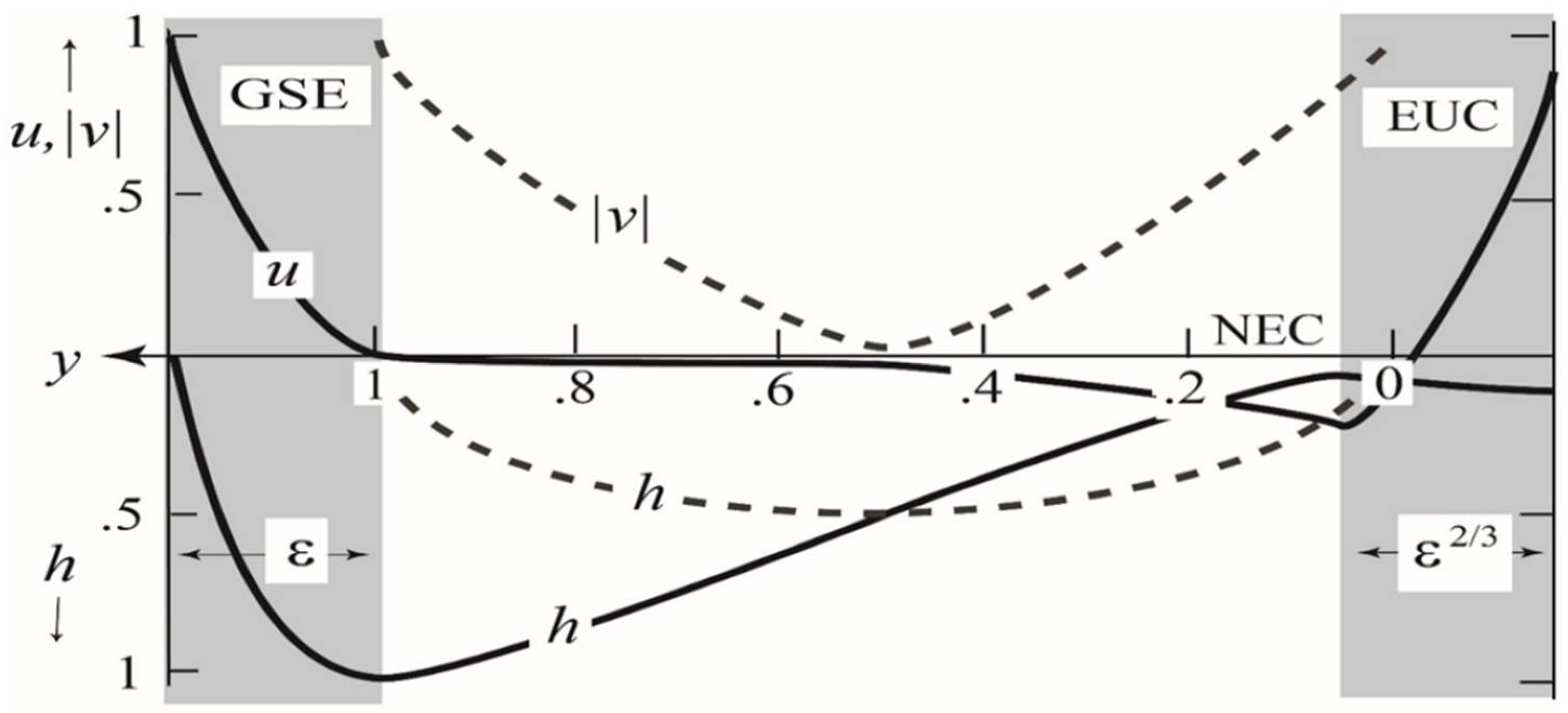
3.1. Interior
3.2. Frontal Jet
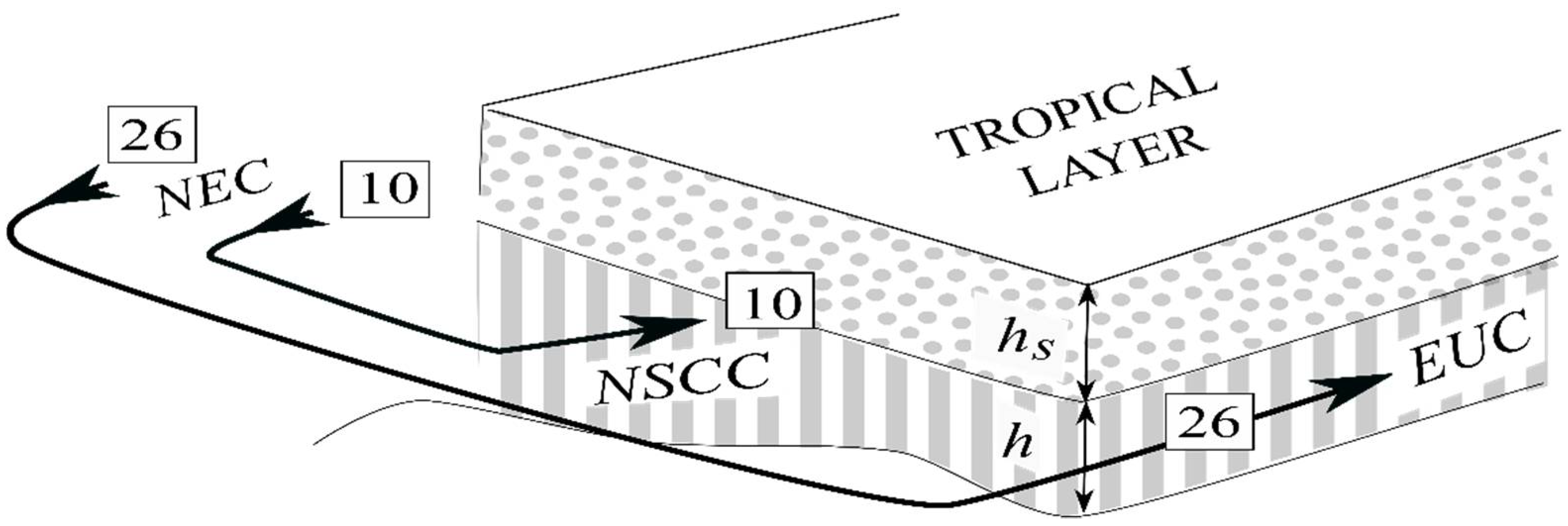
3.3. EUC
3.4. MBC
3.5. Recirculation
3.6. MOC
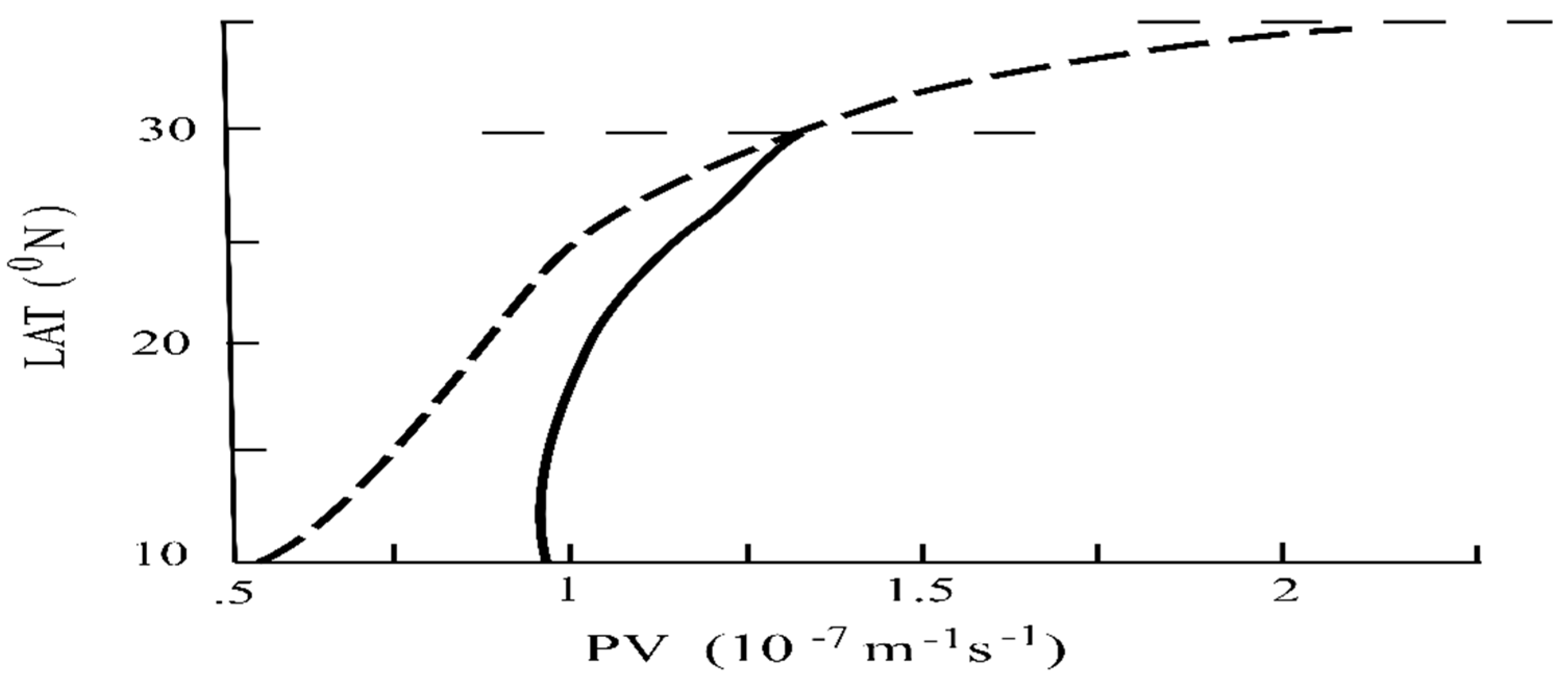
4. Sverdrup Perspective
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A
| EBC | Eastern boundary current |
| EUC | Equatorial undercurrent |
| GAC | General atmosphere circulation |
| GOC | General ocean circulation |
| GS | Gulf Stream |
| GSE | Gulf Stream extension |
| MBC | Meridional boundary current |
| MEP | Maximum entropy production |
| MOC | Meridional overturning circulation |
| NEC | North equatorial current |
| NSCC | Northern subsurface countercurrent |
| NT | Nonequilibrium thermodynamics |
| PV | Potential vorticity |
| B | Bernoulli function |
| Reduced gravity | |
| h | Thermocline depth |
| Mean thermocline depth (=.5 km) | |
| Thermocline depth scale (=2 =1 km) | |
| l | Warm-layer extent (=4000 km) |
| M | GS momentum flux at separation |
| P | Columnar PV |
| PV scale ( | |
| Q | GS mass transport at separation |
| Deformation radius = 40 km) | |
| u | Zonal current |
| Velocity scale (= | |
| v | Meridional current |
| y | Latitudinal distance |
| Distance scale ( | |
| Gradient of Coriolis parameter ( | |
| Transport scale () |
References
- Fu, L.-L.; Chelton, D.B.; Le Traon, P.-Y.; Morrow, R. Eddy dynamics from satellite altimetry. Oceanography 2010, 23, 14–25. [Google Scholar] [CrossRef]
- Colin de Verdière, A. Buoyancy driven planetary flows. J. Mar. Res. 1988, 46, 215–265. [Google Scholar] [CrossRef]
- Hogg, A.M.; Gayen, B. Ocean gyres driven by surface buoyancy forcing. Geophys. Res. Lett. 2020, 47, e2020GL088539. [Google Scholar] [CrossRef]
- Nakamura, M.; Kagimoto, T. Potential vorticity and eddy potential enstrophy in the North Atlantic Ocean simulated by a global eddy-resolving model. Dyn. Atm. Oceans 2006, 41, 28–59. [Google Scholar] [CrossRef]
- Liu, T.; Ou, H.-W.; Liu, X.; Chen, D. On the role of eddy mixing in the subtropical ocean circulation. Earth Space Sci. Open Arch. ESSOAr 2021. [Google Scholar] [CrossRef]
- Ou, H.-W. Possible bounds on the earth’s surface temperature: From the perspective of a conceptual global-mean model. J. Clim. 2001, 14, 2976–2988. [Google Scholar] [CrossRef]
- Ou, H.-W. Meridional thermal field of a coupled ocean-atmosphere system: A conceptual model. Tellus 2006, 58, 404–415. [Google Scholar] [CrossRef]
- Ou, H.-W. Hydrological cycle and ocean stratification in a coupled climate system: A theoretical study. Tellus 2007, 59, 683–694. [Google Scholar] [CrossRef]
- Ou, H.-W. Upper-bound general circulation of coupled ocean-atmosphere: Part 1. Atmosphere. Dyn. Atm. Oceans. 2013, 64, 10–26. [Google Scholar] [CrossRef][Green Version]
- Ozawa, H.; Ohmura, A.; Lorenz, R.D.; Pujol, T. The second law of thermodynamics and the global climate system: A review of the maximum entropy production principle. Rev. Geophys. 2003, 41. [Google Scholar] [CrossRef]
- Paltridge, G.W. Global dynamics and climate—A system of minimum entropy exchange. Q. J. R. Meteorol. Soc. 1975, 101, 475–484. [Google Scholar] [CrossRef]
- Kleidon, A. Non-equilibrium thermodynamics and maximum entropy production in the Earth system: Applications and implications. Naturwissenschaften 2009, 96, 653–677. [Google Scholar] [CrossRef] [PubMed]
- Ou, H.-W. Thermohaline circulation: A missing equation and its climate change implications. Clim. Dyn. 2018, 50, 641–653. [Google Scholar] [CrossRef]
- Evans, D.J.; Searle, D.J. The fluctuation theorem. Adv. Phys. 2002, 51, 1529. [Google Scholar] [CrossRef]
- Wang, G.M.; Sevick, E.M.; Mittag, E.; Searles, D.J.; Evans, D.J. Experimental demonstration of violations of the Second Law of Thermodynamics for small systems and short time scales. Phys. Rev. Lett. 2002, 89, 050601/1–050601/4. [Google Scholar] [CrossRef]
- Pierrehumbert, R.T. Chaotic mixing of tracer and vorticity by modulated travelling Rossby waves. Geophys. Astro. Fluid Dyn. 1991, 58, 285–319. [Google Scholar] [CrossRef]
- Brown, M.G.; Smith, K.B. Ocean stirring and chaotic low-order dynamics. Phys. Fluids 1991, A3, 1186–1192. [Google Scholar] [CrossRef]
- Turiel, A.; Nieves, V.; García-Ladona, E.; Font, J.; Rio, M.H.; Larnicol, G. The multifractal structure of satellite sea surface temperature maps can be used to obtain global maps of streamlines. Ocean Sci. 2009, 5. [Google Scholar] [CrossRef]
- Wiggins, S. Stirred but not mixed. Nature 1988, 333, 395–396. [Google Scholar] [CrossRef]
- Berloff, P.; McWilliams, J.; Bracco, A. Material transport in oceanic gyres. Part I: Phenomenology. J. Phys. Oceanogr. 2002, 32, 764–796. [Google Scholar] [CrossRef]
- Jenkins, W.J. The use of anthropogenic tritium and helium3 to study subtropical gyre ventilation and circulation. Phil. Trans. R. Soc. London 1988, 325, 43–61. [Google Scholar] [CrossRef]
- Rhines, P.B.; Young, W.R. Homogenization of potential vorticity in planetary gyres. J. Fluid Mech. 1982, 122, 347–367. [Google Scholar] [CrossRef]
- Böning, C.W.; Cox, M.D. Particle dispersion and mixing of conservative properties in an eddy-resolving model. J. Phys. Oceanogr. 1988, 18, 320–338. [Google Scholar] [CrossRef]
- Sarmiento, J.L. A tritium box model of the North Atlantic thermocline. J. Phys. Oceanogr. 1983, 13, 1269–1274. [Google Scholar] [CrossRef]
- Ierley, G.R.; Young, W.R. Can the western boundary layer affect the potential vorticity distribution in the Sverdrup interior of a wind-gyre? J. Phys. Oceanogr. 1983, 13, 1753–1763. [Google Scholar] [CrossRef][Green Version]
- Stommel, H. The Gulf Stream: A Physical and Dynamical Description; University of California Press: Berkeley, CA, USA, 1965; 248p. [Google Scholar]
- Toole, J.M.; Millare, R.C.; Wang, Z.; Pu, S. Observations of the Pacific North Equatorial Current Bifurcation at the Philippine Coast. J. Phys. Oceanogr. 1990, 20, 307–318. [Google Scholar] [CrossRef]
- McDowell, S.; Rhines, P.B.; Keffer, T. North Atlantic potential vorticity and its rela-tion to the general circulation. J. Phys. Oceanogr. 1982, 12, 1417–1436. [Google Scholar] [CrossRef]
- Holland, W.R.; Keffer, T.; Rhines, P.B. Dynamics of the oceanic general circulation: The potential vorticity field. Nature 1984, 308, 698–705. [Google Scholar] [CrossRef]
- Keffer, T. The ventilation of the world’s oceans: Maps of the potential vorticity field. J. Phys. Oceanogr. 1985, 15, 509–523. [Google Scholar] [CrossRef][Green Version]
- Lozier, M.S.; Owens, W.B.; Curry, R.G. The climatology of the North Atlantic. Prog. Oceanogr. 1995, 36, 1–44. [Google Scholar] [CrossRef]
- McCartney, M.S. The subtropical recirculation of mode waters. J. Mar. Res. 1982, 40, 427–464. [Google Scholar]
- Welander, P. Wind-driven circulation in one- and two-layer oceans of variable depth. Tellus 1968, 20, 1–15. [Google Scholar] [CrossRef]
- Johns, W.E.; Shay, T.J.; Bane, J.M.; Watts, D.R. Gulf Stream structure, transport, and recirculation near 68W. J. Geophys. Res. 1995, 100, 817–838. [Google Scholar] [CrossRef]
- Pedlosky, J. The link between western boundary current and equatorial undercurrent. J. Phys. Oceanogr. 1991, 21, 1553–1558. [Google Scholar] [CrossRef]
- Charney, J.G. Non-linear theory of a wind-driven homogeneous layer near the Equator. Deep-Sea Res. 1960, 6, 303–310. [Google Scholar] [CrossRef]
- Fine, R.A.; Peterson, W.H.; Ostund, H.G. The penetration of tritium into the tropical Pacific. J. Phys. Oceanogr. 1987, 17, 553–564. [Google Scholar] [CrossRef]
- Johnson, G.C.; McPhaden, M.J. Interior pycnocline flow from the subtropical to the equatorial Pacific Ocean. J. Phys. Oceanogr. 1999, 29, 3073–3089. [Google Scholar] [CrossRef]
- Goodman, P.J.; Hazeleger, W.; de Vries, P.; Cane, M. Pathways into the Pacific Equatorial Undercurrent: A trajectory analysis. J. Phys. Oceanogr. 2005, 35, 2134–2151. [Google Scholar] [CrossRef][Green Version]
- Wyrtki, K.; Kilonsky, B. Mean water and current structure during the Hawaii-to-Tahiti shuttle experiment. J. Phys. Oceanogr. 1984, 14, 242–254. [Google Scholar] [CrossRef]
- Talley, L.D.; Pickard, G.L.; Emery, W.J.; Swift, J.H. Introduction to Descriptive Physical Oceanography; Academic Press: New York, NY, USA, 2011; 560p. [Google Scholar]
- Ou, H.-W.; de Ruijter, W. Separation of an inertial boundary current from curved coastline. J. Phys. Oceanogr. 1986, 16, 280–289. [Google Scholar] [CrossRef][Green Version]
- Cessi, P. A stratified model of the inertial recirculation. J. Phys. Oceanogr. 1988, 18, 662–682. [Google Scholar] [CrossRef][Green Version]
- Worthington, L.V. On the North Atlantic Circulation; The Johns Hopkins Oceanographic Studies: Baltimore, MD, USA, 1976; Volume 6, pp. 1–110. [Google Scholar]
- Niiler, P.P. The observational basis for large scale circulation of the oceans. In The General Circulation of the Ocean; Abarbenel, H., Young, W.R., Eds.; Springer-Verlag: New York, NY, USA, 1986; pp. 1–54. [Google Scholar] [CrossRef]
- Auer, S.J. Five-year climatological survey of the Gulf Stream system and its associated rings. J. Geophys. Res. 1987, 92, 11709–11726. [Google Scholar] [CrossRef]
- Macdonald, A.M. The global ocean circulation: A hydrographic estimate and regional analysis. Progr. Oceanogr. 1998, 41, 281–382. [Google Scholar] [CrossRef]
- Wunsch, C. The decadal mean ocean circulation and Sverdrup balance. J. Mar. Res. 2011, 69, 417–434. [Google Scholar] [CrossRef]
- Gray, A.R.; Riser, S.C. A global analysis of Sverdrup balance using absolute geostrophic velocities from Argo. J. Phys. Oceanogr. 2014, 44, 1213–1229. [Google Scholar] [CrossRef]
- Schmitz, W.J.; Thompson, J.D.; Luyten, J.R. The Sverdrup circulation for the Atlantic along 24 N. J. Geophys. Res. Oceans 1992, 97, 7251–7256. [Google Scholar] [CrossRef]
- Hellerman, S.; Rosenstein, M. Normal monthly wind stress over the world ocean with error estimates. J. Phys. Oceanogr. 1983, 13, 1093–1104. [Google Scholar] [CrossRef]
- Hall, M.M. Velocity and transport structure of the Kuroshio extension at 35° N, 152° E. J. Geophys. Res. Oceans 1989, 94, 14445–14459. [Google Scholar] [CrossRef]
- Cox, M. An eddy resolving numerical model of the ventilated thermocline. J. Phys. Oceanogr. 1985, 15, 1312–1324. [Google Scholar] [CrossRef]
- Bryan, F.O.; Hecht, M.W.; Smith, R.D. Resolution convergence and sensitivity studies with North Atlantic circulation models. Part I: The western boundary current system. Ocean Model. 2007, 16, 141–159. [Google Scholar] [CrossRef]
- Holland, W.R.; Rhines, P.B. An example of eddy-induced ocean circulation. J. Phys. Oceanogr. 1980, 10, 1010–1031. [Google Scholar] [CrossRef]
- Luyten, J.R.; Pedlosky, J.; Stommel, H. The ventilated thermocline. J. Phys. Oceanogr. 1983, 13, 292–309. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, H.-W. Upper-Bound General Circulation of the Ocean: A Theoretical Exposition. J. Mar. Sci. Eng. 2021, 9, 1090. https://doi.org/10.3390/jmse9101090
Ou H-W. Upper-Bound General Circulation of the Ocean: A Theoretical Exposition. Journal of Marine Science and Engineering. 2021; 9(10):1090. https://doi.org/10.3390/jmse9101090
Chicago/Turabian StyleOu, Hsien-Wang. 2021. "Upper-Bound General Circulation of the Ocean: A Theoretical Exposition" Journal of Marine Science and Engineering 9, no. 10: 1090. https://doi.org/10.3390/jmse9101090
APA StyleOu, H.-W. (2021). Upper-Bound General Circulation of the Ocean: A Theoretical Exposition. Journal of Marine Science and Engineering, 9(10), 1090. https://doi.org/10.3390/jmse9101090





