Author Contributions
The four authors of the paper, A.S., A.P., L.L. and A.M. contributed as follows. Conceptualization, L.L. and A.P.; methodology, L.L., A.P. and A.S.; software, A.P. and A.S.; validation, A.S., L.L. and A.P.; formal analysis, A.S., A.P., L.L. and A.M.; investigation, A.S.; resources, L.L.; data curation, A.S.; writing—original draft preparation, A.S.; writing—review and editing, L.L., A.P. and A.M.; visualization, A.S.; supervision, L.L. and A.M.; project administration, A.S., L.L. and A.M.; funding acquisition, L.L. All authors have read and agreed to the published version of the manuscript.
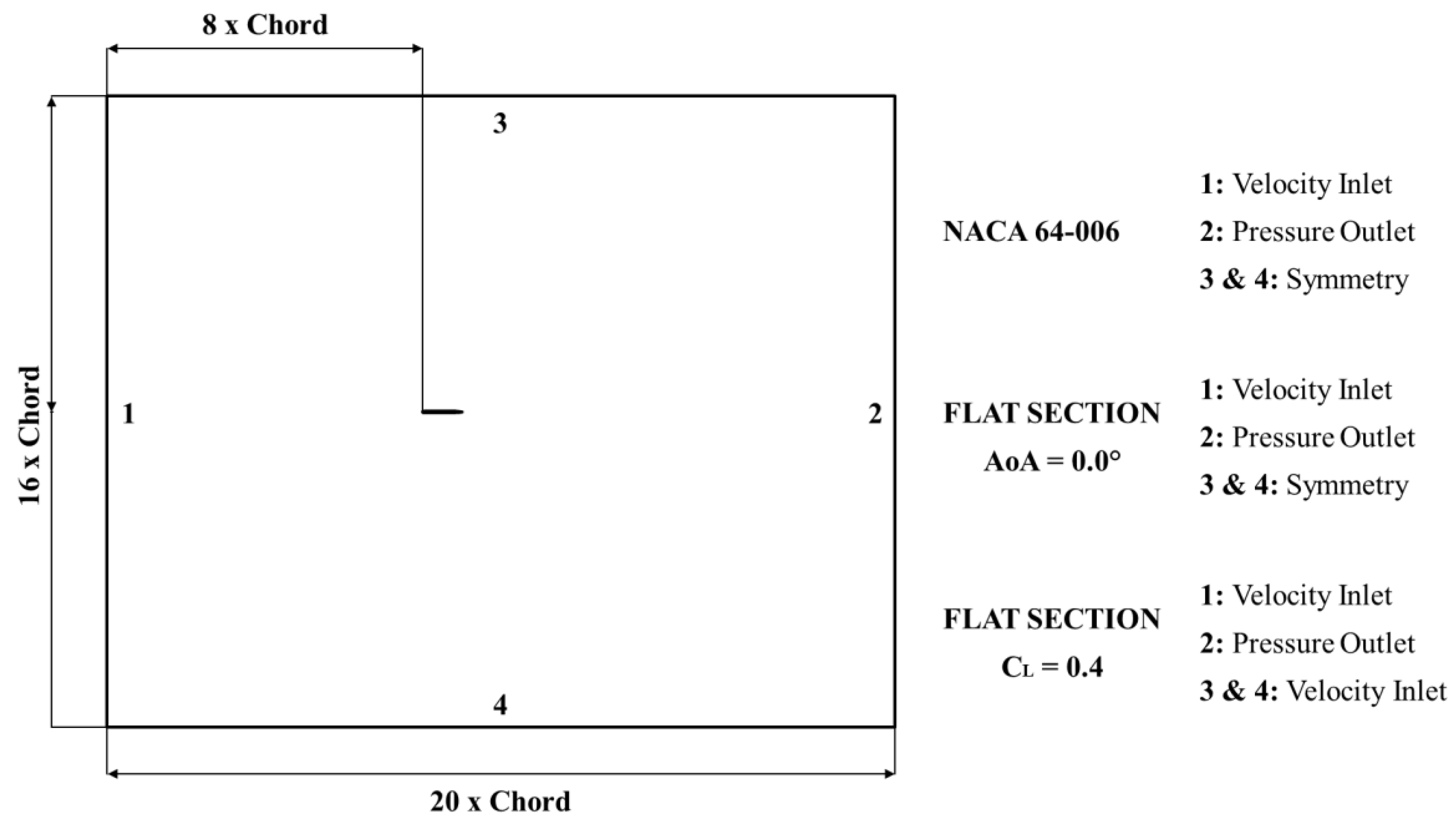
Figure 1.
Boundary definition.
Figure 1.
Boundary definition.
Figure 2.
View of the mesh surrounding the test case section, and close-ups of leading and trailing edges. For the test case, the angle of attack is achieved by rotation of the foil, while for the systematic computations the direction of the inflow is varied to obtain the requested lift coefficient (0.4).
Figure 2.
View of the mesh surrounding the test case section, and close-ups of leading and trailing edges. For the test case, the angle of attack is achieved by rotation of the foil, while for the systematic computations the direction of the inflow is varied to obtain the requested lift coefficient (0.4).
Figure 3.
Regression curve of lift coefficient (a) and drag coefficient (b).
Figure 3.
Regression curve of lift coefficient (a) and drag coefficient (b).
Figure 4.
Comparison of drag coefficients for the coarse grid and a finer one. The independent variable is the trailing edge angle (see below).
Figure 4.
Comparison of drag coefficients for the coarse grid and a finer one. The independent variable is the trailing edge angle (see below).
Figure 5.
Comparison between numerical and experimental results. Reynolds number 3,000,000.
Figure 5.
Comparison between numerical and experimental results. Reynolds number 3,000,000.
Figure 6.
Drag coefficient (CD × 103) for Reynolds number 300,000. Independent variable: trailing edge angle (a,b); nose radius (c,d).
Figure 6.
Drag coefficient (CD × 103) for Reynolds number 300,000. Independent variable: trailing edge angle (a,b); nose radius (c,d).
Figure 7.
Drag coefficient (CD × 103) for Reynolds number 900,000. Independent variable: trailing edge angle (a,b); nose radius (c,d).
Figure 7.
Drag coefficient (CD × 103) for Reynolds number 900,000. Independent variable: trailing edge angle (a,b); nose radius (c,d).
Figure 8.
Drag coefficient (CD × 103) for Reynolds number 1,500,000. Independent variable: trailing edge angle (a,b); nose radius (c,d).
Figure 8.
Drag coefficient (CD × 103) for Reynolds number 1,500,000. Independent variable: trailing edge angle (a,b); nose radius (c,d).
Figure 9.
Plots of axial velocity (upper) and pressure distribution (lower) for a thin and a thick section.
Figure 9.
Plots of axial velocity (upper) and pressure distribution (lower) for a thin and a thick section.
Figure 10.
Velocity plot and skin friction coefficient of short leading edge length (left) and long leading edge length (right).
Figure 10.
Velocity plot and skin friction coefficient of short leading edge length (left) and long leading edge length (right).
Figure 11.
Velocity plot and pressure plot of short trailing edge (left) and long trailing edge (right) sections.
Figure 11.
Velocity plot and pressure plot of short trailing edge (left) and long trailing edge (right) sections.
Figure 12.
Five different radii are compared. x-axis trailing edge angle, y-axis drag coefficient times 103.
Figure 12.
Five different radii are compared. x-axis trailing edge angle, y-axis drag coefficient times 103.
Figure 13.
Velocity plot and skin friction coefficient of large (left), medium (center) and small (right) trailing edge angle sections.
Figure 13.
Velocity plot and skin friction coefficient of large (left), medium (center) and small (right) trailing edge angle sections.
Figure 14.
Velocity plot and pressure plot of thin (left) and thick (right) sections.
Figure 14.
Velocity plot and pressure plot of thin (left) and thick (right) sections.
Figure 15.
Velocity plot and skin friction coefficient of short leading edge and long trailing edge (left) and long leading edge and short trailing edge (right) sections.
Figure 15.
Velocity plot and skin friction coefficient of short leading edge and long trailing edge (left) and long leading edge and short trailing edge (right) sections.
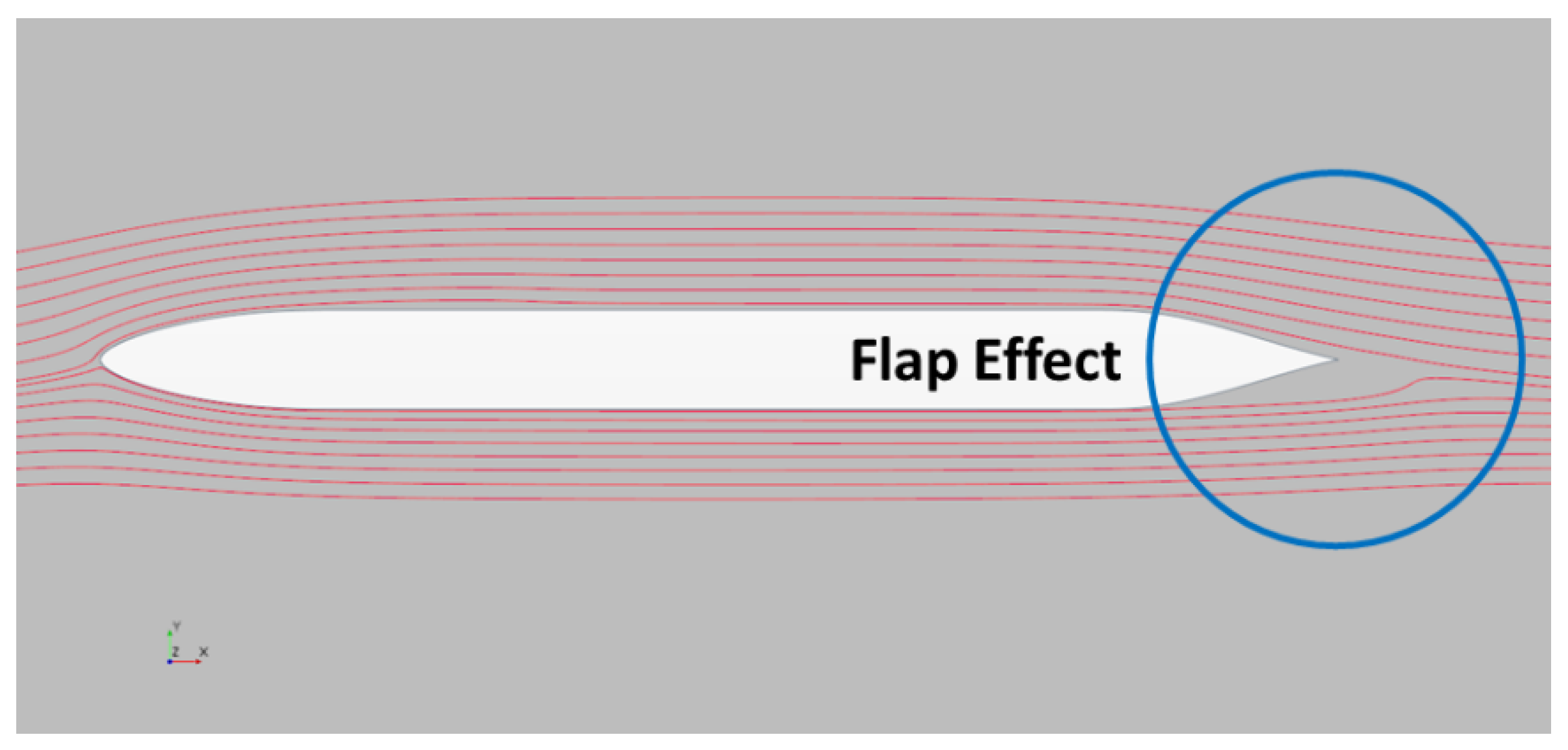
Figure 16.
Streamlines of long leading edge and short trailing edge section.
Figure 16.
Streamlines of long leading edge and short trailing edge section.
Figure 17.
Five different trailing edge angles are compared, x-axis nose radius, y-axis drag coefficient times 103.
Figure 17.
Five different trailing edge angles are compared, x-axis nose radius, y-axis drag coefficient times 103.
Figure 18.
Velocity plot and pressure plot of short leading edge (left) and long leading edge (right) sections.
Figure 18.
Velocity plot and pressure plot of short leading edge (left) and long leading edge (right) sections.
Table 1.
Numerical uncertainty of lift and drag coefficient for the test case at different grid densities.
Table 1.
Numerical uncertainty of lift and drag coefficient for the test case at different grid densities.
| Nr. Cells | Hi | CL | U (CL) | U (%CL) | CD | U | U (%CD) |
|---|
| 6.5 M | 1 | 0.4354 | 0.00187 | 0.5 | 0.00850 | 0.000102 | 1.2 |
| 3.6 M | 1.34 | 0.4337 | 0.00411 | 0.9 | 0.00849 | 0.000060 | 0.7 |
| 1.6 M | 2 | 0.4346 | 0.00237 | 0.5 | 0.00848 | 0.000106 | 1.3 |
| 0.4 M | 4.03 | 0.4342 | 0.00606 | 1.4 | 0.00862 | 0.000301 | 3.5 |
Table 2.
Numerical and experimental results for different angle of attack.
Table 2.
Numerical and experimental results for different angle of attack.
| Angle of Attack | Test Case | Abbott |
|---|
| α | CD | CD |
|---|
| 0.0 | 0.00344 | 0.0039 |
| 1.0 | 0.00348 | 0.0040 |
| 1.5 | 0.00352 | 0.0050 |
| 2.0 | 0.00362 | 0.0060 |
| 2.5 | 0.00640 | 0.0062 |
| 3.0 | 0.00670 | 0.0063 |
| 4.0 | 0.00770 | 0.0069 |
Table 3.
Ranges of Reynolds numbers, thicknesses, leading edge lengths, trailing edges lengths of 470, 420 and Optimist dinghies.
Table 3.
Ranges of Reynolds numbers, thicknesses, leading edge lengths, trailing edges lengths of 470, 420 and Optimist dinghies.
| Boat | Reynolds Number | Thickness (% Chord) | Leading Edge (% Chord) | Trailing Edge (% Chord) |
|---|
| Optimist | 280,000 | 5.52 | 21.43 | 21.43 |
| 290,000 | 7.14 | 20.69 | 20.69 |
| 420 | 830,000 | 3.76 | 25.30 | 25.30 |
| 850,000 | 4.82 | 24.71 | 24.71 |
| 470 | 910,000 | 4.26 | 18.08 | 35.49 |
| 1,500,000 | 7.89 | 11.70 | 22.97 |
Table 4.
Values and codes for the systematic investigation of Parallel-Sided sections.
Table 4.
Values and codes for the systematic investigation of Parallel-Sided sections.
| Reynolds Number | Sailing Condition | Thickness (% Chord) | Leading Edge (% Chord) | Trailing Edge (% Chord) | Nose Radius (% Thickn.) | Trailing Edge Angle [°] |
|---|
| 300,000 | AoA = 0.0° | T1 = 4% | LE1 = 10% | TE1 = 20% | R1 = 40% | A1 = AREF |
| 900,000 | CL = 0.4 | T2 = 8% | LE2 = 20% | TE2 = 40% | R2 = 20% | A2 = AREF |
| 1,500,000 | - | - | - | - | R3 = 10% | A3 = AREF |
| - | - | - | - | - | R4 = 5% | A4 = AREF |
| - | - | - | - | - | R5 = 2% | A5 = AREF |