A Geometric Calibration Method of Hydrophone Array Based on Maximum Likelihood Estimation with Sources in Near Field
Abstract
:1. Introduction
2. Error Model of Array Position with Near-Field Source
3. Methods
3.1. Near-Field Element Position Calibration Based on Maximum Likelihood Estimation
3.2. Multipath Compensation Method
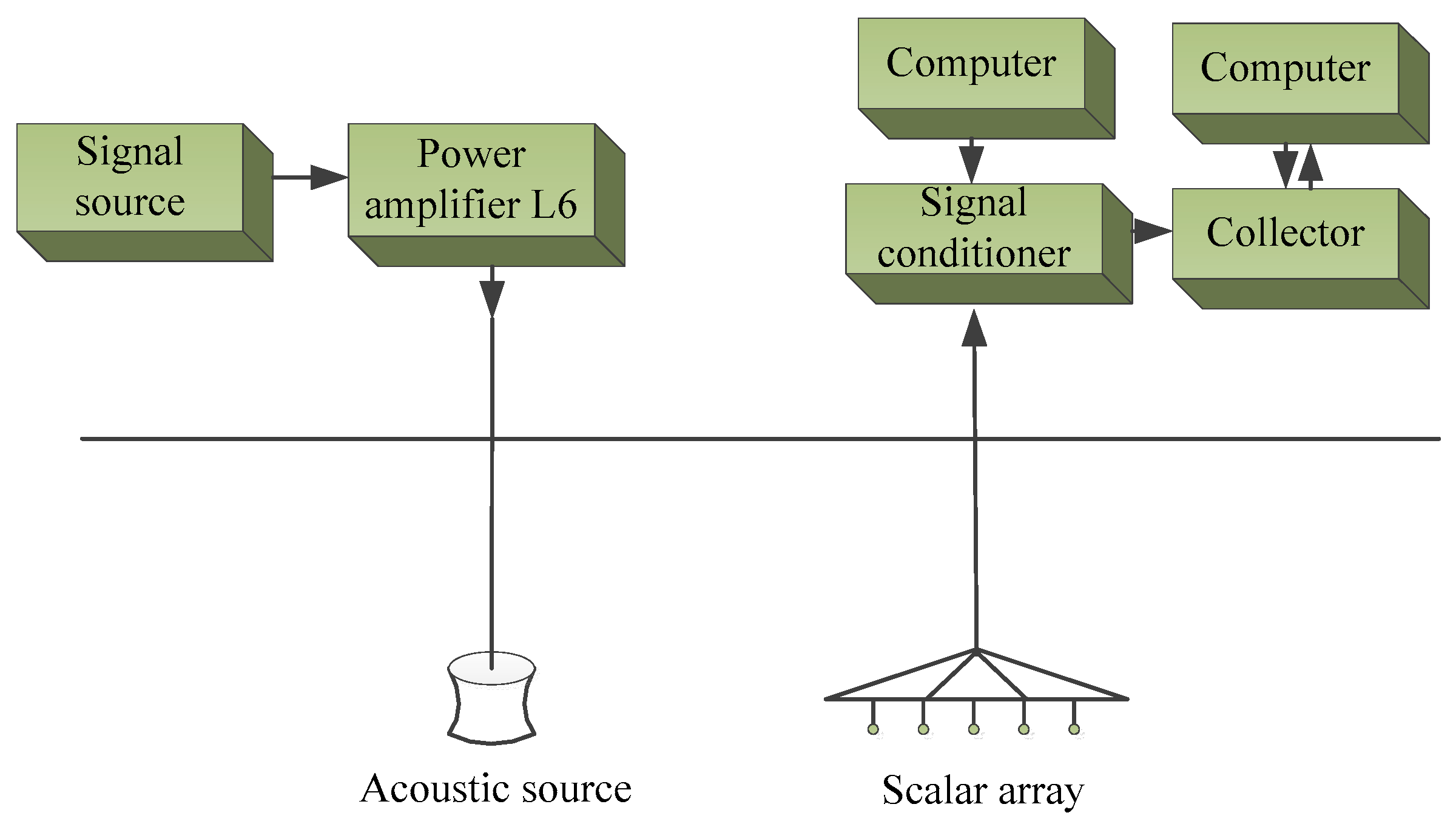
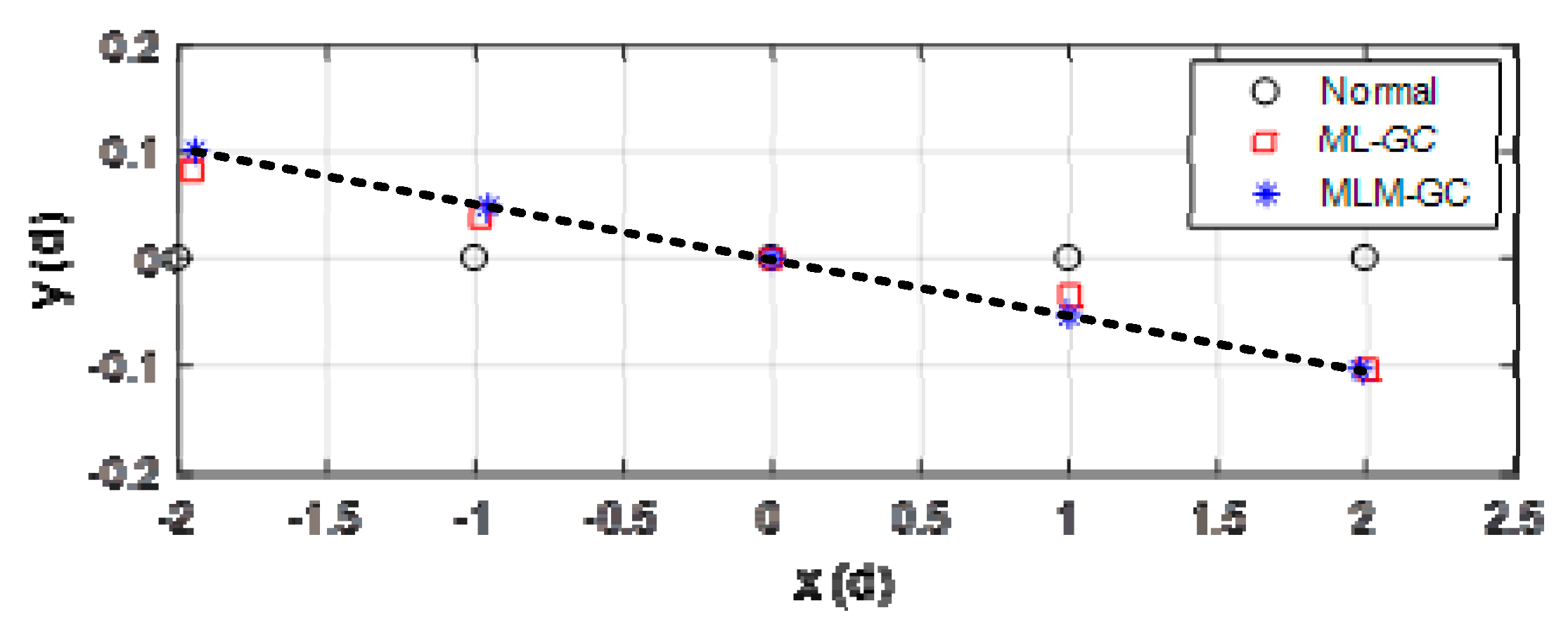
4. Simulation and Experiment
4.1. Simulation
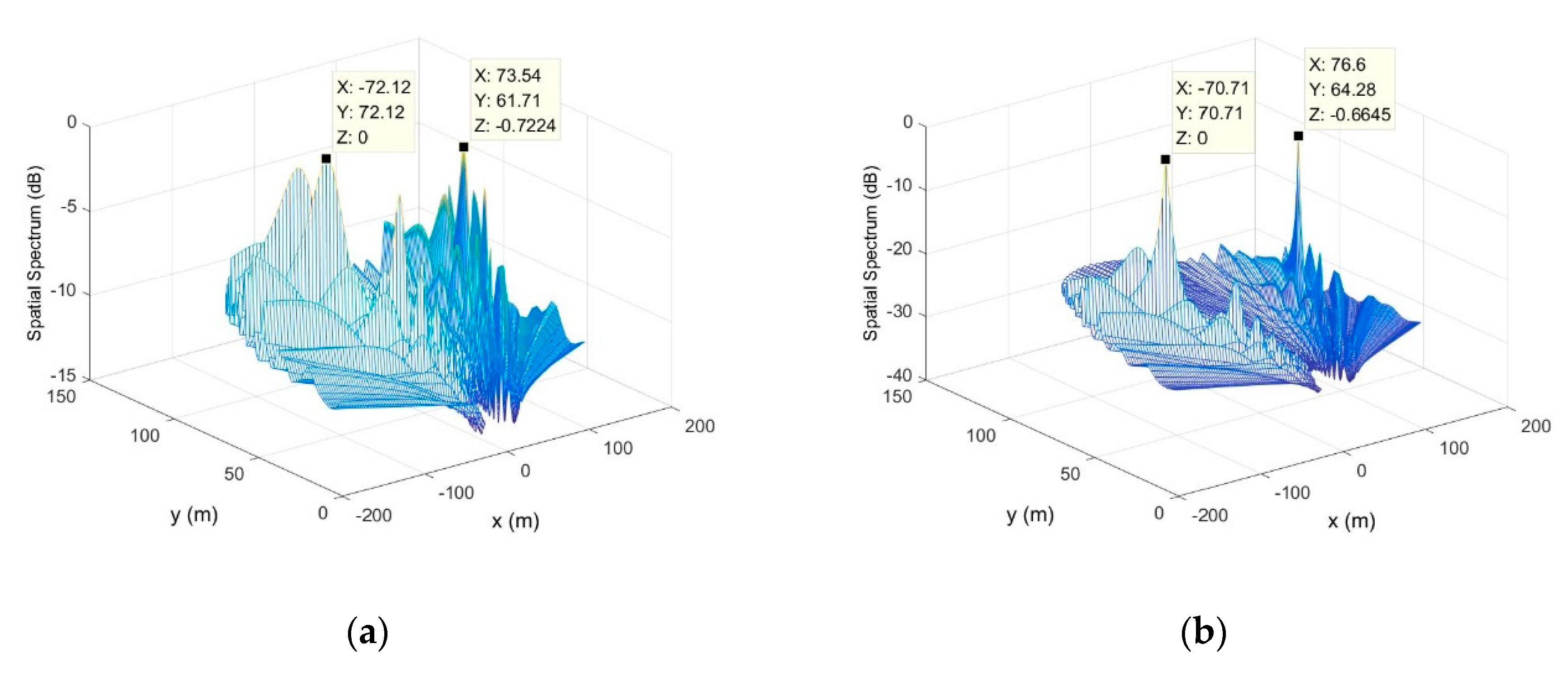
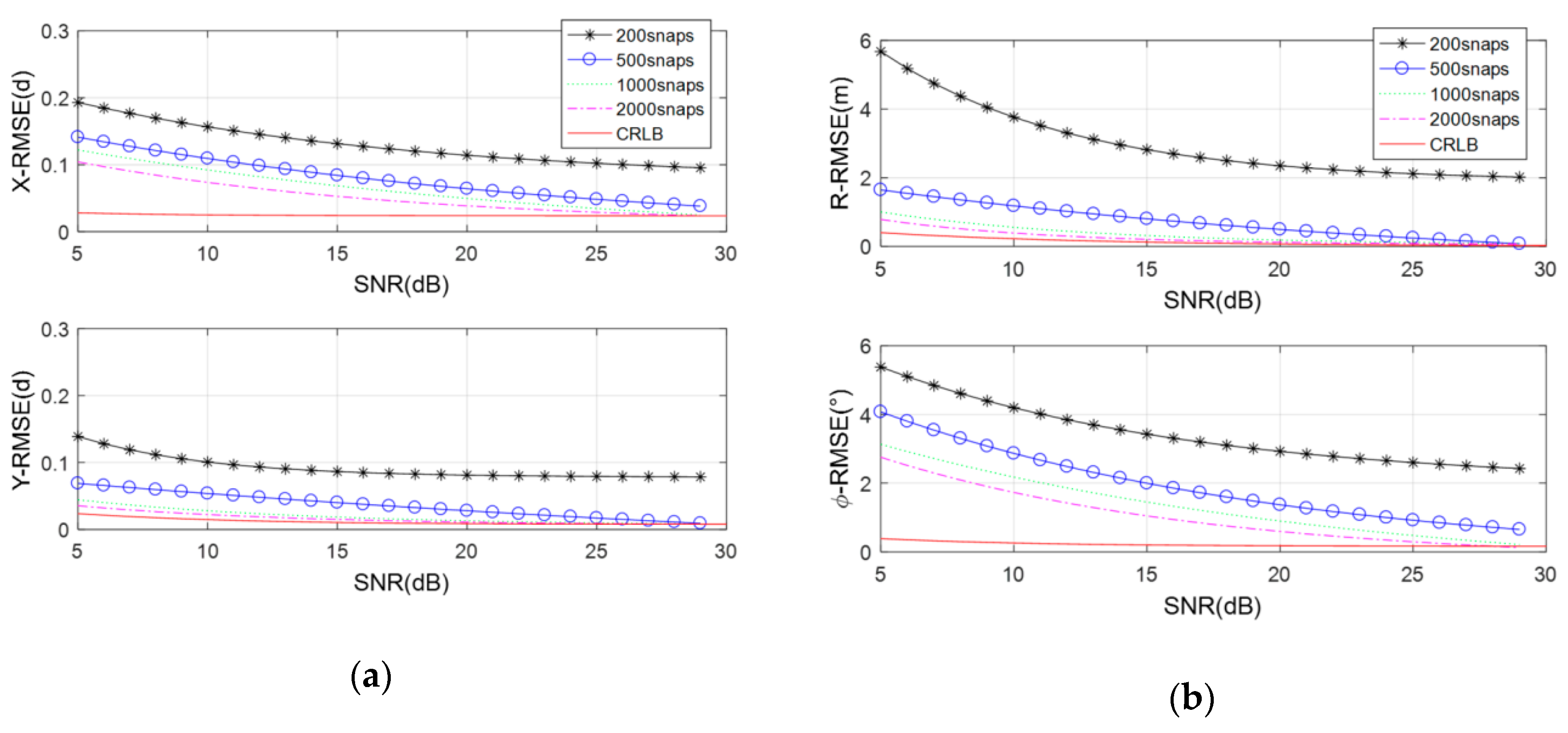
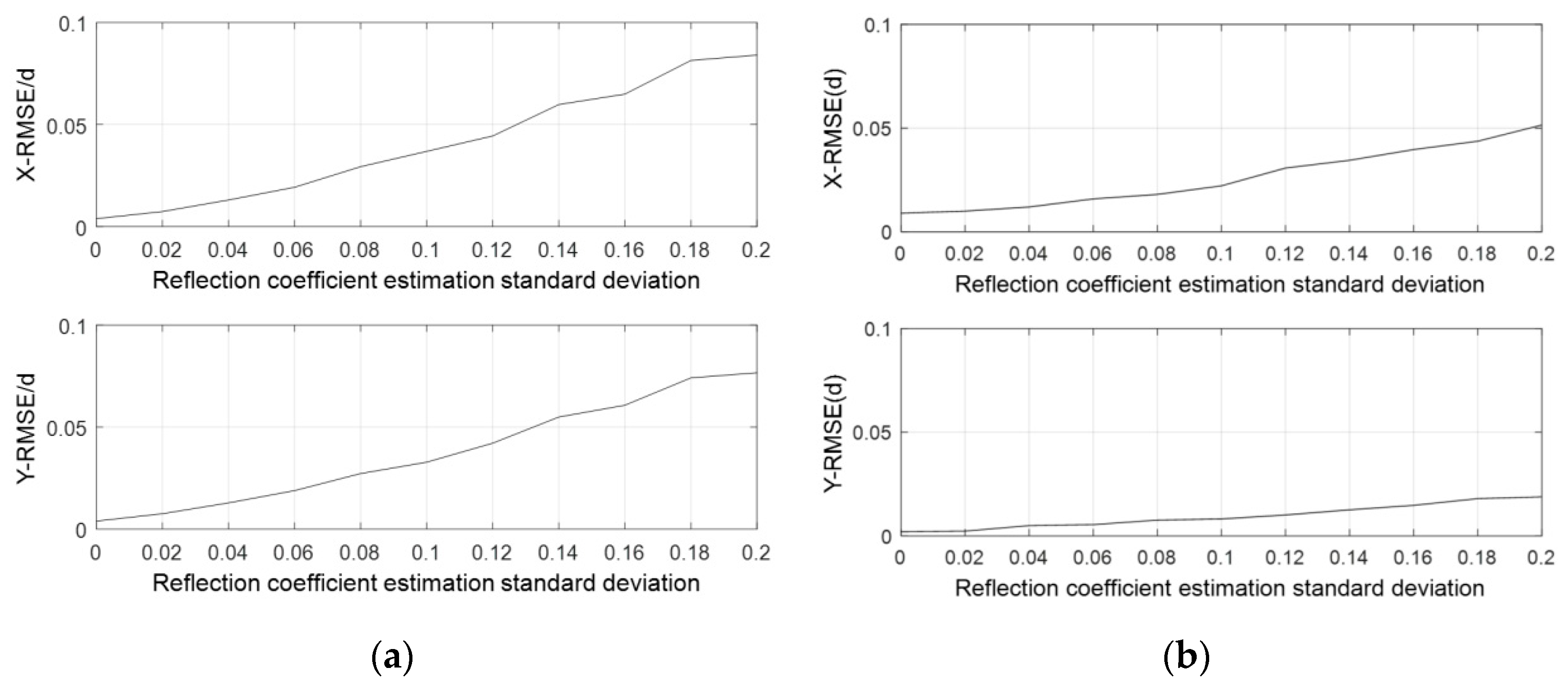
4.1.1. Near-field Auxiliary Calibration Method Base on Maximum Likelihood Estimation (ML-GC)
4.1.2. Near-Field Self-Calibration Method Based on Maximum Likelihood Estimation (ML-GAC)
4.1.3. Multipath Compensation Strategy for Auxiliary Calibration (MLM-GC)
4.2. Lake Experiment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, S.; Kainam, T.W.; Fangjiong, C. “Quasi-Blind” Calibration of an Array of Acoustic Vector-Sensors That Are Subject to GainErrors/Mis-Location/Mis-Orientation. IEEE Trans. Signal Process. 2014, 62, 2330–2344. [Google Scholar]
- Ping, K.T.; Kainam, T.W.; Yang, S. An Hybrid Cramer-Rao Bound in Closed Form for Direction-of-Arrival Estimation by an “Acoustic Vector Sensor” With Gain-Phase Uncertainties. IEEE Trans. Signal Process. 2014, 62, 2504–2516. [Google Scholar]
- Ye, T.; Yanru, W.; Xiaoliu, R. Mixed source localization and gain-phase perturbation calibration in partly calibrated symmetric uniform linear arrays. Signal Process. 2020, 166, 107267. [Google Scholar]
- Schmidt, R.O. Multilinear array manifold interpolation. IEEE Trans. Signal Process. 1992, 40, 857–866. [Google Scholar] [CrossRef]
- Boon, P.N.; Meng, H.E. A Gaid/Phase Calibration Technique for Adaptive Beamforming. In Proceedings of the ICCS, Singapore, 14–18 November 1994; Volume 3. [Google Scholar]
- Lev, M.; Messer, H. Sufficient condition for array calibration using source of mixed tapes. In Proceedings of the ICASSP, Albuquerque, NM, USA, 3–6 April 1990; Volume 5, pp. 2943–2946. [Google Scholar]
- Weiss, A.J.; Friedlander, B. Array Shape Calibration Using Sources in Unknown Locations-A Maximum Likelihood Approach. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 1958–1966. [Google Scholar] [CrossRef]
- Ng, B.P.; Lie, J.P.; Er, M.H.; Feng, A. A practical simple geometry and gain/phase calibration technique for antenna array processing. IEEE Trans. Antennas Propag. 2009, 57, 1963–1971. [Google Scholar]
- Kim, H.; Haimovich, A.M.; Eldar, Y.C. Non-coherent direction of arrival estimation from magnitude-only measurements. IEEE Signal Process. Lett. 2015, 22, 925–929. [Google Scholar] [CrossRef]
- Wang, Y.; Zou, N.; Liang, G. Auxiliary calibration method for near-field position of hydrophone array in strong multipath environment. Acta Phys. Sin. 2015, 64, 024304. [Google Scholar]
- Minqiu, C.; Xi, C.; Xingpeng, M. A subspace-based Manifold separation technique for array calibration. In Proceedings of the ISSPIT, St. Raphael Resort, Limassol, Cyprus, 12–14 December 2016; pp. 40–44. [Google Scholar]
- Nan, Z.; Yan, W.; Jin, F.; Guolong, L. A Geometry Calibration Technique for Hydrophone Array with Sources in Near Field. J. Comput. Acoust. 2016, 23, 1540008. [Google Scholar]
- Chen, Z.; Zhang, L.; Zhao, C.; Li, J. Calibration and Evaluation of a Circular Antenna Array for HF Radar Based on AIS Information. IEEE Geosci. Remote Sens. Lett. 2020, 17, 988–992. [Google Scholar] [CrossRef]
- Wang, D.; Wu, Y. A Novel Array Errors Auxiliary calibration Algorithm. Acta Electron. Sin. 2010, 38, 517–527. [Google Scholar] [CrossRef]
- Wu, Y.; Leshem, A.; Wijnholds, S.J. A computationally efficient calibration algorithm for the LOFAR radio astronomical array. In Proceedings of the ICASSP, Florence, Italy, 4–9 May 2014; pp. 5402–5406. [Google Scholar]
- Weiss, A.J.; Friedlander, B. Array shape calibration using eigenstructure methods. Signal Process. 1991, 22, 251–258. [Google Scholar] [CrossRef]
- Eric, K.L.; Hung, A. Critical Study of a Self-calibrating Direction-Finding Method for Arrays. IEEE Trans. Signal Process. 1994, 42, 471–474. [Google Scholar]
- Kim, K.S.; Yang, E.; Myung, N.H. Self-calibration of an active uniform linear array using phase gradient characteristics. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 497–501. [Google Scholar] [CrossRef]
- Jiajia, Z.; Hui, C.; Weiping, H.; Weijian, L. Self-Calibration of Mutual Coupling for Non-uniform Cross-Array. Circuits Syst. Signal Process. 2019, 38, 1137–1156. [Google Scholar]
- Ng, B.P.; Er, M.H.; Kot, C. Array gainlphase calibration techniques for adaptive beamforming and direction finding. IEEE Proc. Radar Sonar Navig. 1994, 141, 25–29. [Google Scholar] [CrossRef]
- Dajun, S.; Xiaoping, H.; Hongyu, C. Iterative multi-channel FH-MFSK reception in mobile shallow underwater acoustic channels. IET Commun. 2020, 14, 838–945. [Google Scholar]
- Van Trees, H.L. Optimum Array Processing; Wiley-Interscience: New York, NY, USA, 2002; pp. 746–762. [Google Scholar]
- Wan, S.; Chung, P.J.; Mulgrew, B. Maximum likelihood array calibration using particleswarm optimisation. IET Signal Process. 2012, 6, 456–465. [Google Scholar] [CrossRef]
- Tahere, Y. Parameter optimization of software reliability models using improved differential evolution algorithm. Math. Comput. Simul. 2020, 177, 46–62. [Google Scholar]
- Jaroslaw, B.; Bartosz, K.; Alina, M. Local Levenberg-Marquardt Algorithm for Learning Feedforward Neural Networks. J. Artif. Intell. Soft Comput. Res. 2020, 10, 299–316. [Google Scholar]
- Gang, Q.; Qingjun, S.; Lu, M. Channel prediction based temporal multiple sparse bayesian learning for channel estimation in fast time-varying underwater acoustic OFDM communications. Signal Process. 2020, 175, 107668. [Google Scholar]











| Element Num. | Nominal Position (d) | Actual Position (d) | ML−GC(d) | Absolute Error(d) | ||||
|---|---|---|---|---|---|---|---|---|
| X | Y | X | Y | X | Y | X | Y | |
| 1 | −42.000 | 0.000 | −41.952 | 0.040 | −41.954 | 0.048 | 0.002 | 0.008 |
| 2 | −41.000 | 0.000 | −40.975 | 0.046 | −40.970 | −0.047 | 0.005 | 0.001 |
| 3 | −40.000 | 0.000 | −39.967 | 0.094 | −39.967 | 0.095 | 0.000 | 0.001 |
| 4 | −39.000 | 0.000 | −39.112 | 0.127 | −39.114 | 0.130 | 0.002 | 0.003 |
| 5 | −38.000 | 0.000 | −38.061 | 0.120 | −38.063 | 0.123 | 0.002 | 0.003 |
| 6 | −2.000 | 0.000 | −2.078 | 0.071 | −2.078 | 0.072 | 0.000 | 0.001 |
| 7 | −1.000 | 0.000 | −1.005 | −0.038 | −1.006 | −0.035 | 0.001 | 0.003 |
| 8 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 9 | 1.000 | 0.000 | 1.079 | −0.004 | 1.079 | −0.003 | 0.000 | 0.001 |
| 10 | 2.000 | 0.000 | 1.943 | −0.129 | 1.941 | −0.127 | 0.002 | 0.002 |
| 11 | 38.000 | 0.000 | 37.977 | 0.067 | 37.970 | 0.065 | 0.007 | 0.002 |
| 12 | 39.000 | 0.000 | 39.257 | −0.154 | 39.257 | −0.153 | 0.000 | 0.001 |
| 13 | 40.000 | 0.000 | 39.861 | −0.087 | 39.863 | −0.085 | 0.002 | 0.002 |
| 14 | 41.000 | 0.000 | 41.052 | −0.104 | 41.046 | −0.107 | 0.006 | 0.003 |
| 15 | 42.000 | 0.000 | 42.139 | −0.044 | 42.135 | −0.046 | 0.004 | 0.002 |
| Element Num. | Nominal Position (d) | Actual Position (d) | ML−GAC (d) | Absolute Error (d) | ||||
|---|---|---|---|---|---|---|---|---|
| X | Y | X | Y | X | Y | X | Y | |
| 1 | 0 | 0 | 0.180 | −0.078 | 0.195 | −0.078 | 0.015 | 0.000 |
| 2 | 1 | 0 | 1.037 | −0.117 | 1.050 | −0.117 | 0.013 | 0.000 |
| 3 | 2 | 0 | 1.887 | 0.084 | 1.894 | 0.086 | 0.007 | 0.002 |
| 4 | 3 | 0 | 2.813 | 0.151 | 2.812 | 0.151 | 0.001 | 0.000 |
| 5 | 4 | 0 | 4.000 | 0.000 | 4.000 | 0.000 | 0.000 | 0.000 |
| 6 | 5 | 0 | 4.985 | 0.000 | 4.979 | 0.000 | 0.006 | 0.000 |
| 7 | 6 | 0 | 5.928 | 0.191 | 5.916 | 0.191 | 0.012 | 0.000 |
| 8 | 7 | 0 | 7.093 | −0.040 | 7.087 | −0.035 | 0.006 | 0.005 |
| 9 | 8 | 0 | 7.996 | −0.159 | 7.982 | −0.153 | 0.014 | 0.006 |
| Source Num. | Actual Distance (m) | Estimated Distance (m) | Absolute Error of Distance(m) | Actual DOA (Degree) | Estimated DOA (Degree) | Absolute Error of DOA (Degree) |
|---|---|---|---|---|---|---|
| 1 | 10 | 9.9912 | 0.0088 | −60 | −60.5811 | 0.5811 |
| 2 | 10 | 9.8115 | 0.1885 | 0 | 0.1484 | 0.1484 |
| 3 | 10 | 9.7834 | 0.2166 | 40 | 40.3403 | 0.3403 |
| DOA(Degree) | Distance(m) | |||
|---|---|---|---|---|
| Estimated Value | Absolute Deviation | Estimated Value | Absolute Deviation | |
| Before calibration | −14.9980 | 2.9980 | 2.8004 | 0.0996 |
| ML−GC | −12.0000 | 0.0000 | 3.1999 | 0.2999 |
| MLM−GC | −11.9976 | 0.0024 | 2.9004 | 0.0004 |
| Source Num. | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Estimated DOA (°) | −37.7077 | −18.6544 | 2.0127 | 31.4406 |
| DOA Deviation (°) | 2.4923 | 0.6456 | 1.8873 | 2.4594 |
| Estimated Distance (m) | 2.9546 | 2.5808 | 3.0798 | 2.9311 |
| Distance Deviation (m) | 0.0546 | 0.3192 | 0.1798 | 0.0311 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, N.; Jia, Z.; Fu, J.; Feng, J.; Liu, M. A Geometric Calibration Method of Hydrophone Array Based on Maximum Likelihood Estimation with Sources in Near Field. J. Mar. Sci. Eng. 2020, 8, 678. https://doi.org/10.3390/jmse8090678
Zou N, Jia Z, Fu J, Feng J, Liu M. A Geometric Calibration Method of Hydrophone Array Based on Maximum Likelihood Estimation with Sources in Near Field. Journal of Marine Science and Engineering. 2020; 8(9):678. https://doi.org/10.3390/jmse8090678
Chicago/Turabian StyleZou, Nan, Zhenqi Jia, Jin Fu, Jia Feng, and Mengqi Liu. 2020. "A Geometric Calibration Method of Hydrophone Array Based on Maximum Likelihood Estimation with Sources in Near Field" Journal of Marine Science and Engineering 8, no. 9: 678. https://doi.org/10.3390/jmse8090678
APA StyleZou, N., Jia, Z., Fu, J., Feng, J., & Liu, M. (2020). A Geometric Calibration Method of Hydrophone Array Based on Maximum Likelihood Estimation with Sources in Near Field. Journal of Marine Science and Engineering, 8(9), 678. https://doi.org/10.3390/jmse8090678




