The Relationship between Sea-Swell Bound Wave Height and Wave Shape
Abstract
1. Introduction
2. Background
2.1. The Spectrum
2.2. The Bispectrum
2.3. Wave Shape
3. Bound Variance
3.1. Predicted Bound Variance for Equilibrium Conditions
3.2. Observed Bound Variance from the Bispectrum
4. Data
4.1. CoastalGenesis2/SEAWAD Field Campaign
4.2. Data Processing
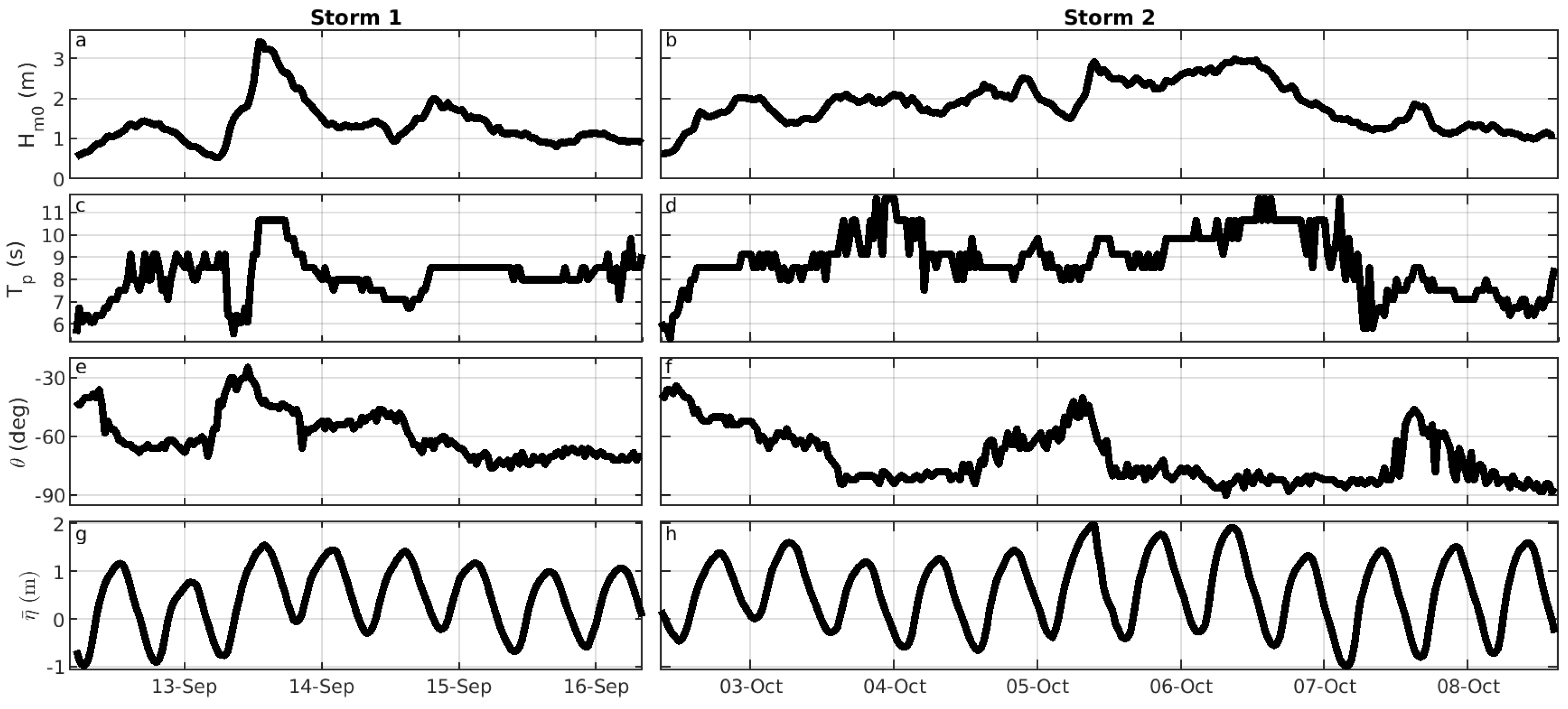
4.3. Data Selection and Overview
5. Results
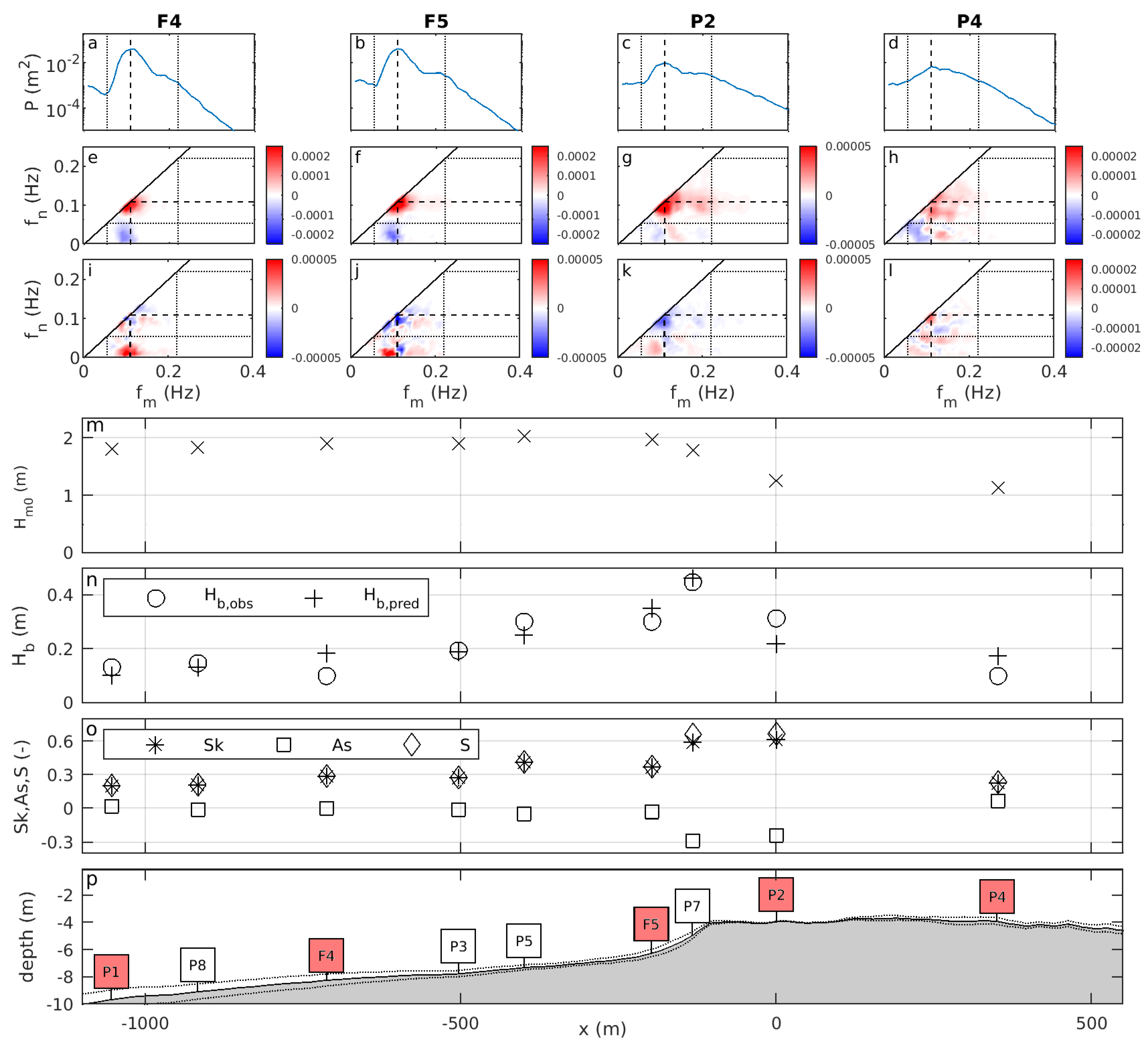
5.1. Spatial Evolution of the Spectrum and Bispectrum
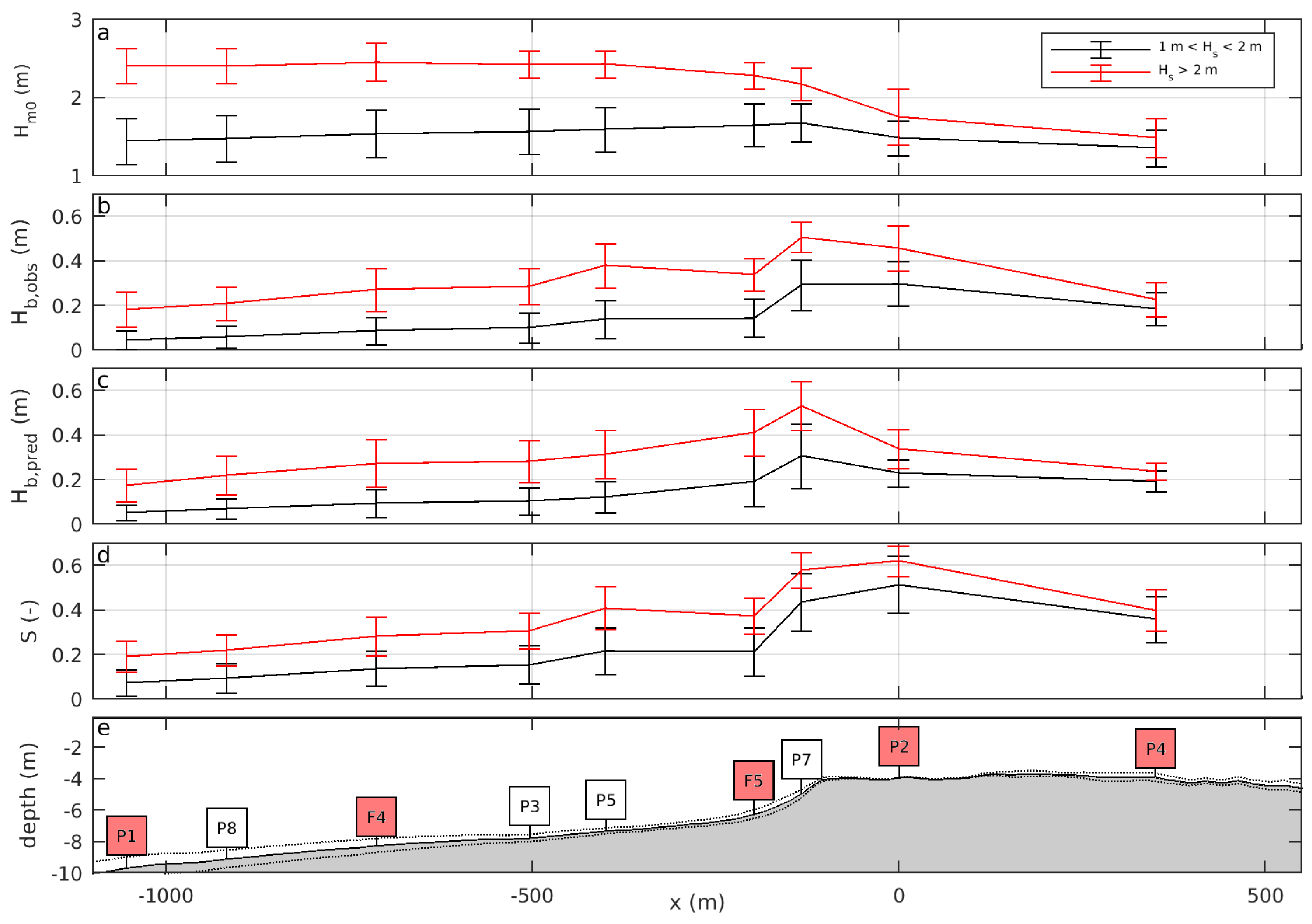
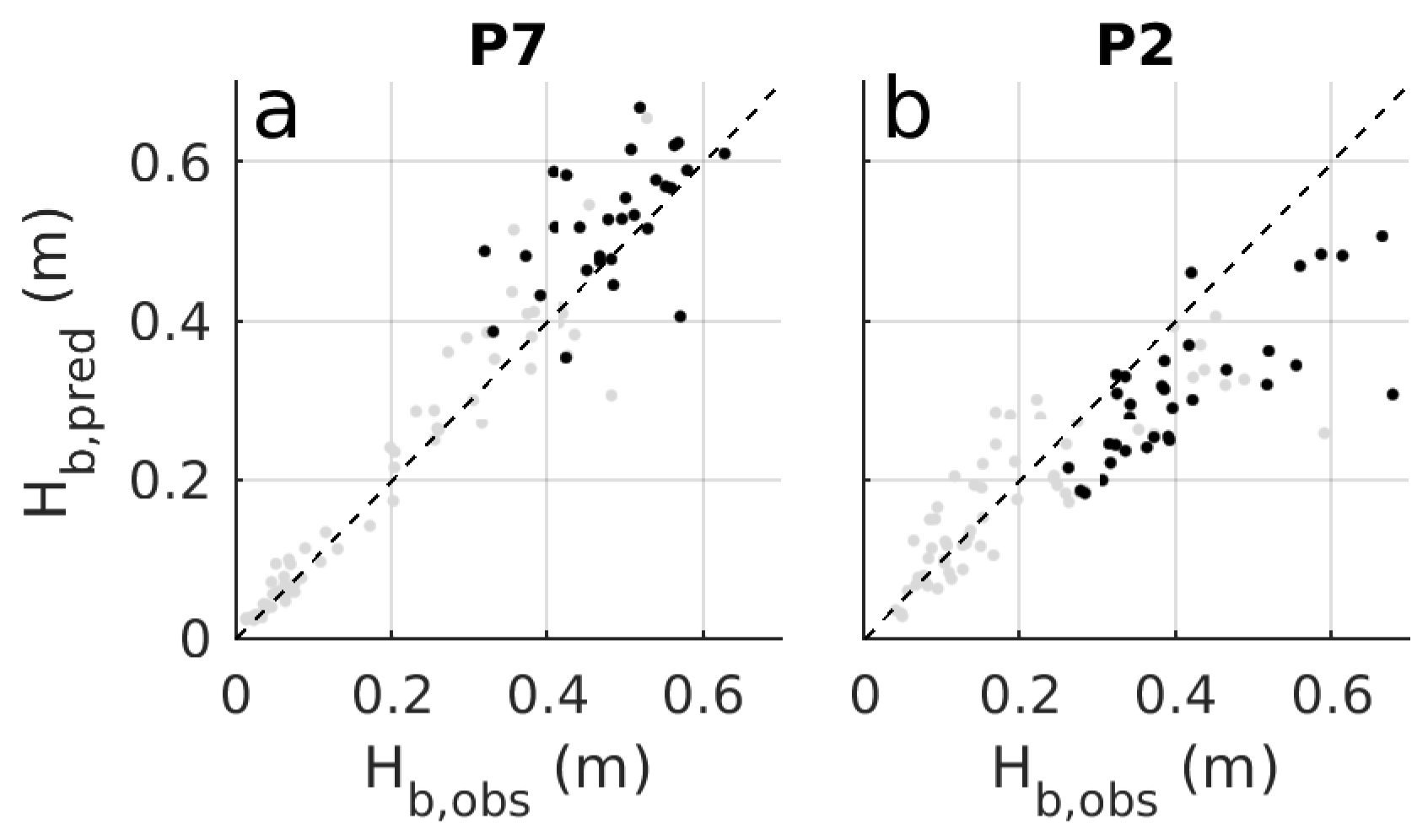
5.2. Predicted and Observed Bound Wave Height
5.3. Wave Shape as a Function of Observed Bound Wave Height
6. Discussion
6.1. Errors in Determining the Predicted Bound Wave Height
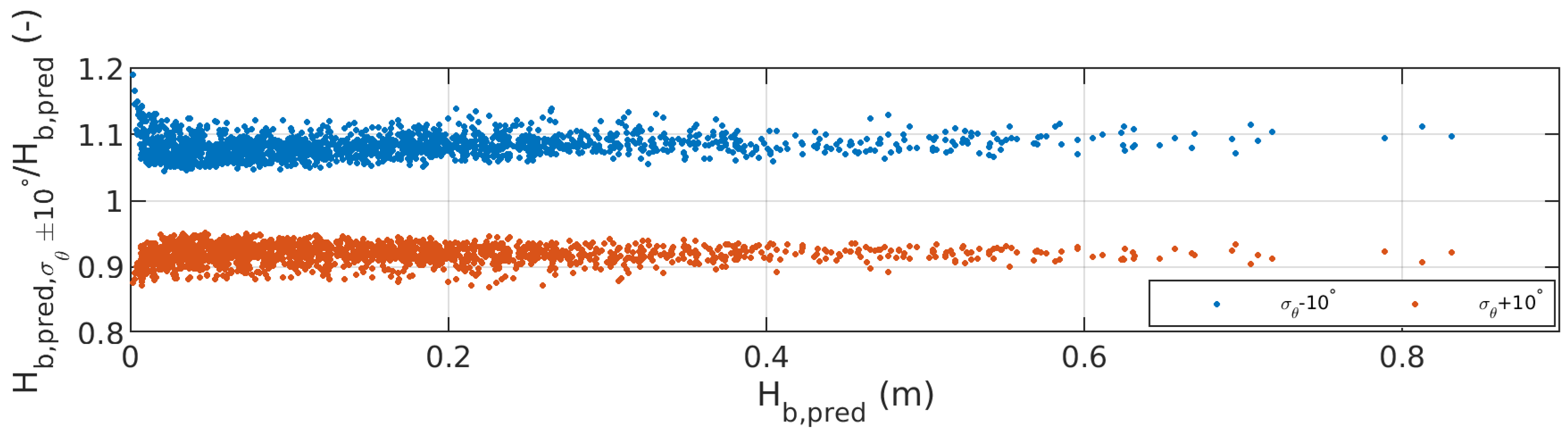
6.1.1. Directional Spreading
6.1.2. Current
6.1.3. Wave Breaking
6.1.4. Overall Validity of Equilibrium Bound Wave Height Theory
6.2. Applicability in Different Areas
6.3. Future Modeling Perspective
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
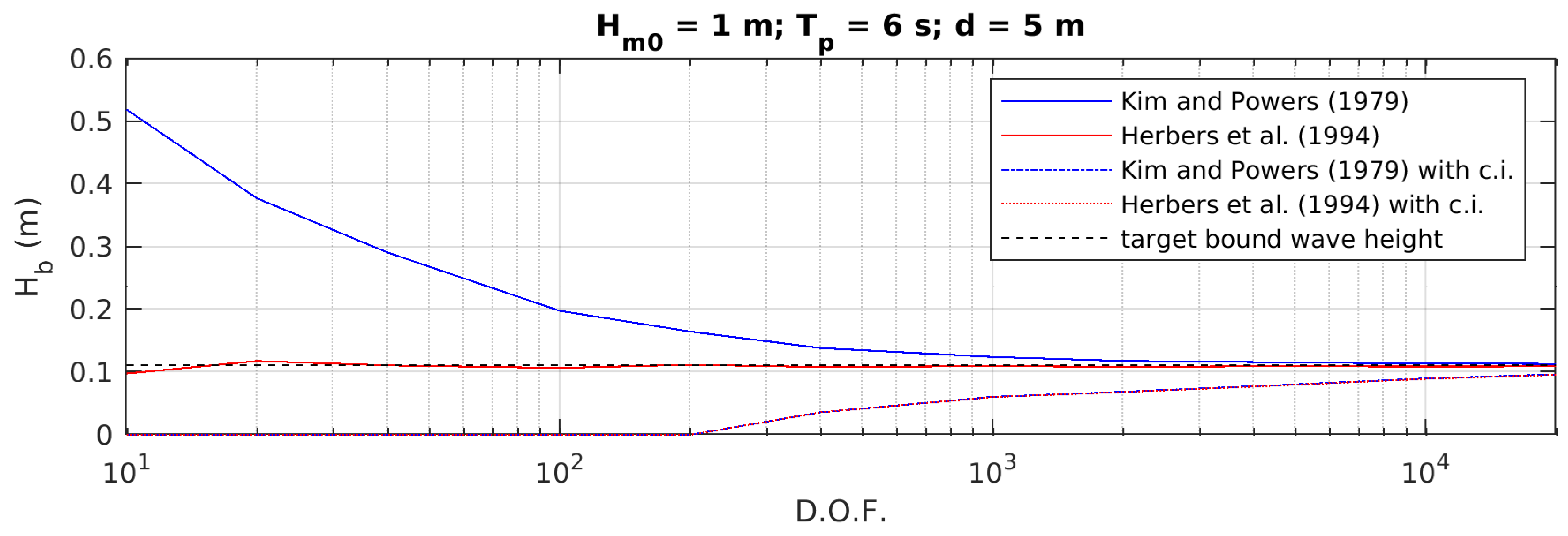
Appendix A. Accuracy of Bound Wave Height Formulations
Appendix A.1. Synthetic Timeseries
Appendix A.2. Formulations and Degrees of Freedom
References
- Hoefel, F.; Elgar, S. Wave-induced sediment transport and sandbar migration. Science 2003, 299, 1885–1887. [Google Scholar] [CrossRef] [PubMed]
- Hsu, T.J.; Elgar, S.; Guza, R. Wave-induced sediment transport and onshore sandbar migration. Coast. Eng. 2006, 53, 817–824. [Google Scholar] [CrossRef]
- Ruessink, B.G.; Michallet, H.; Abreu, T.; Sancho, F.; Van Der A, D.A.; Van Der Werf, J.J.; Silva, P.A. Observations of velocities, sand concentrations, and fluxes under velocity-asymmetric oscillatory flows. J. Geophys. Res. Ocean. 2011, 116. [Google Scholar] [CrossRef]
- Silva, P.A.; Abreu, T.; Van Der A, D.A.; Sancho, F.; Ruessink, B.; Van der Werf, J.; Ribberink, J.S. Sediment transport in nonlinear skewed oscillatory flows: Transkew experiments. J. Hydraul. Res. 2011, 49, 72–80. [Google Scholar] [CrossRef]
- Kranenburg, W.M.; Ribberink, J.S.; Schretlen, J.J.; Uittenbogaard, R.E. Sand transport beneath waves: The role of progressive wave streaming and other free surface effects. J. Geophys. Res. Earth Surface 2013, 118, 122–139. [Google Scholar] [CrossRef]
- Walstra, D.; Reniers, A.; Ranasinghe, R.; Roelvink, J.; Ruessink, B. On bar growth and decay during interannual net offshore migration. Coast. Eng. 2012, 60, 190–200. [Google Scholar] [CrossRef]
- Elgar, S.; Gallagher, E.L.; Guza, R. Nearshore sandbar migration. J. Geophys. Res. Ocean. 2001, 106, 11623–11627. [Google Scholar] [CrossRef]
- Masselink, G.; Austin, M.; O’Hare, T.; Russell, P. Geometry and dynamics of wave ripples in the nearshore zone of a coarse sandy beach. J. Geophys. Res. Ocean. 2007, 112. [Google Scholar] [CrossRef]
- Thornton, E.; Humiston, R.; Birkemeier, W. Bar/trough generation on a natural beach. J. Geophys. Res. Ocean. 1996, 101, 12097–12110. [Google Scholar] [CrossRef]
- Aagaard, T.; Hughes, M.; Møller-Sørensen, R.; Andersen, S. Hydrodynamics and sediment fluxes across an onshore migrating intertidal bar. J. Coast. Res. 2006, 2006, 247–259. [Google Scholar] [CrossRef]
- Ruessink, B.; Kuriyama, Y.; Reniers, A.; Roelvink, J.; Walstra, D. Modeling cross-shore sandbar behavior on the timescale of weeks. J. Geophys. Res. Earth Surface 2007, 112. [Google Scholar] [CrossRef]
- Chen, J.L.; Hsu, T.J.; Shi, F.; Raubenheimer, B.; Elgar, S. Hydrodynamic and sediment transport modeling of New River Inlet (NC) under the interaction of tides and waves. J. Geophys. Res. Ocean. 2015, 120, 4028–4047. [Google Scholar] [CrossRef]
- Reniers, A.J.H.M.; De Wit, F.P.; Tissier, M.F.S.; Pearson, S.G.; Brakenhoff, L.B.; Van Der Vegt, M.; Mol, J.; Van Prooijen, B.C. Wave-Skewness and Current-Related Ebb-Tidal Sediment Transport: Observations and Modeling. In The Proceedings of the Coastal Sediments 2019; World Scientific: Singapore, 2019. [Google Scholar]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions: 1. Model description and validation. J. Geophys. Res. Ocean. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Ris, R.; Holthuijsen, L.; Booij, N. A third-generation wave model for coastal regions: 2. Verification. J. Geophys. Res. Ocean. 1999, 104, 7667–7681. [Google Scholar] [CrossRef]
- Benoit, M.; Marcos, F.; Becq, F. Development of a third generation shallow-water wave model with unstructured spatial meshing. In Coastal Engineering 1996; American Society Of Civil Engineers: Reston, VA, USA, 1997; pp. 465–478. [Google Scholar]
- Tolman, H.L. A third-generation model for wind waves on slowly varying, unsteady, and inhomogeneous depths and currents. J. Phys. Oceanogr. 1991, 21, 782–797. [Google Scholar] [CrossRef]
- Janssen, T.; Herbers, T.; Battjes, J. Generalized evolution equations for nonlinear surface gravity waves over two-dimensional topography. J. Fluid Mech. 2006, 552, 393–418. [Google Scholar] [CrossRef]
- Lesser, G.R.; Roelvink, J.V.; Van Kester, J.; Stelling, G. Development and validation of a three-dimensional morphological model. Coast. Eng. 2004, 51, 883–915. [Google Scholar] [CrossRef]
- Walstra, D.; Roelvink, J.; Groeneweg, J. Calculation of wave-driven currents in a 3D mean flow model. In Coastal Engineering 2000; American Society Of Civil Engineers: Reston, VA, USA, 2001; pp. 1050–1063. [Google Scholar]
- Elias, E.; Walstra, D.; Roelvink, J.; Stive, M.; Klein, M. Hydrodynamic validation of Delft3D with field measurements at Egmond. In Coastal Engineering 2000; American Society Of Civil Engineers: Reston, VA, USA, 2001; pp. 2714–2727. [Google Scholar]
- Luettich, J.; Richard, A.; Westerink, J.J.; Scheffner, N.W. ADCIRC: An Advanced Three-Dimensional Circulation Model for Shelves, Coasts, and Estuaries. Report 1. Theory and Methodology of ADCIRC-2DDI and ADCIRC-3DL; Technical Report; Coastal Engineering Research Center: Vicksburg, MS, USA, 1992. [Google Scholar]
- Westerink, J.J.; Luettich, R., Jr.; Blain, C.; Scheffner, N.W. ADCIRC: An Advanced Three-Dimensional Circulation Model for Shelves, Coasts, and Estuaries. Report 2. User’s Manual for ADCIRC-2DDI; Technical Report; Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, 1994. [Google Scholar]
- Roelvink, J.; van Kessel, T.; Alfageme, S.; Canizares, R. Modelling of barrier island response to storms. Proc. Coast. Sediments 2003, 3, 1–11. [Google Scholar]
- Isobe, M.; Horikawa, K. Study on water particle velocities of shoaling and breaking waves. Coast. Eng. Jpn. 1982, 25, 109–123. [Google Scholar] [CrossRef]
- Doering, J.; Bowen, A. Parametrization of orbital velocity asymmetries of shoaling and breaking waves using bispectral analysis. Coast. Eng. 1995, 26, 15–33. [Google Scholar] [CrossRef]
- Abreu, T.; Silva, P.A.; Sancho, F.; Temperville, A. Analytical approximate wave form for asymmetric waves. Coast. Eng. 2010, 57, 656–667. [Google Scholar] [CrossRef]
- Ruessink, B.; Ramaekers, G.; Van Rijn, L. On the parameterization of the free-stream non-linear wave orbital motion in nearshore morphodynamic models. Coast. Eng. 2012, 65, 56–63. [Google Scholar] [CrossRef]
- Boechat Albernaz, M.; Ruessink, G.; Jagers, H.; Kleinhans, M.G. Effects of wave orbital velocity parameterization on nearshore sediment transport and decadal morphodynamics. J. Mar. Sci. Eng. 2019, 7, 188. [Google Scholar] [CrossRef]
- Rocha, M.; Silva, P.; Michallet, H.; Abreu, T.; Moura, D.; Fortes, J. Parameterizations of wave nonlinearity from local wave parameters: A comparison with field data. J. Coast. Res. 2013, 65, 374–379. [Google Scholar] [CrossRef]
- Rocha, M.V.L.; Michallet, H.; Silva, P.A. Improving the parameterization of wave nonlinearities—The importance of wave steepness, spectral bandwidth and beach slope. Coast. Eng. 2017, 121, 77–89. [Google Scholar] [CrossRef]
- De Wit, F.; Tissier, M.; Reniers, A. Characterizing Wave Shape Evolution on an Ebb Tidal Shoal. J. Mar. Sci. Eng. 2019, 7, 367. [Google Scholar] [CrossRef]
- Norheim, C.; Herbers, T.; Elgar, S. Nonlinear evolution of surface wave spectra on a beach. J. Phys. Oceanogr. 1998, 28, 1534–1551. [Google Scholar] [CrossRef]
- Eldrup, M.R.; Andersen, T.L. Numerical Study on Regular Wave Shoaling, DeShoaling and Decomposition of Free/Bound Waves on Gentle and Steep Foreshores. J. Mar. Sci. Eng. 2020, 8, 334. [Google Scholar] [CrossRef]
- Hasselmann, K.; Munk, W.; MacDonald, G. Bispectra of ocean waves. In Time Series Analysis; Rosenblatt, M., Ed.; John Wiley: Hoboken, NJ, USA, 1963; pp. 125–139. [Google Scholar]
- Elgar, S.; Guza, R. Observations of bispectra of shoaling surface gravity waves. J. Fluid Mech. 1985, 161, 425–448. [Google Scholar] [CrossRef]
- Eldeberky, Y.; Madsen, P.A. Deterministic and stochastic evolution equations for fully dispersive and weakly nonlinear waves. Coast. Eng. 1999, 38, 1–24. [Google Scholar] [CrossRef]
- Hasselmann, K. On the non-linear energy transfer in a gravity-wave spectrum Part 1. General theory. J. Fluid Mech. 1962, 12, 481–500. [Google Scholar] [CrossRef]
- Herbers, T.; Burton, M. Nonlinear shoaling of directionally spread waves on a beach. J. Geophys. Res. Ocean. 1997, 102, 21101–21114. [Google Scholar] [CrossRef]
- Salmon, J.; Smit, P.; Janssen, T.; Holthuijsen, L. A consistent collinear triad approximation for operational wave models. Ocean Model. 2016, 104, 203–212. [Google Scholar] [CrossRef]
- Becq-Girard, F.; Forget, P.; Benoit, M. Non-linear propagation of unidirectional wave fields over varying topography. Coast. Eng. 1999, 38, 91–113. [Google Scholar] [CrossRef]
- Madsen, P.A.; Eldeberky, Y. A new formulation of deterministic and stochastic evolution equations for three-wave interactions involving fully dispersive waves. In Coastal Engineering 1998; American Society of Civil Engineers: Reston, VA, USA, 1999; pp. 161–174. [Google Scholar]
- Phillips, O.M. On the dynamics of unsteady gravity waves of finite amplitude Part 1. The elementary interactions. J. Fluid Mech. 1960, 9, 193–217. [Google Scholar] [CrossRef]
- Leckler, F.; Ardhuin, F.; Peureux, C.; Benetazzo, A.; Bergamasco, F.; Dulov, V. Analysis and Interpretation of Frequency–Wavenumber Spectra of Young Wind Waves. J. Phys. Oceanogr. 2015, 45, 2484–2496. [Google Scholar] [CrossRef]
- Henderson, S.M.; Guza, R.; Elgar, S.; Herbers, T.; Bowen, A. Nonlinear generation and loss of infragravity wave energy. J. Geophys. Res. Ocean. 2006, 111. [Google Scholar] [CrossRef]
- Ruessink, B. Bound and free infragravity waves in the nearshore zone under breaking and nonbreaking conditions. J. Geophys. Res. Ocean. 1998, 103, 12795–12805. [Google Scholar] [CrossRef]
- Sheremet, A.; Guza, R.; Elgar, S.; Herbers, T. Observations of nearshore infragravity waves: Seaward and shoreward propagating components. J. Geophys. Res. Ocean. 2002, 107. [Google Scholar] [CrossRef]
- Van Dongeren, A.; Reniers, A.; Battjes, J.; Svendsen, I. Numerical modeling of infragravity wave response during DELILAH. J. Geophys. Res. Ocean. 2003, 108. [Google Scholar] [CrossRef]
- Roelvink, D.; Reniers, A.; Van Dongeren, A.; De Vries, J.V.T.; McCall, R.; Lescinski, J. Modelling storm impacts on beaches, dunes and barrier islands. Coast. Eng. 2009, 56, 1133–1152. [Google Scholar] [CrossRef]
- Guedes, R.M.; Bryan, K.R.; Coco, G. Observations of wave energy fluxes and swash motions on a low-sloping, dissipative beach. J. Geophys. Res. Ocean. 2013, 118, 3651–3669. [Google Scholar] [CrossRef]
- De Bakker, A.; Herbers, T.; Smit, P.; Tissier, M.; Ruessink, B. Nonlinear infragravity–wave interactions on a gently sloping laboratory beach. J. Phys. Oceanogr. 2015, 45, 589–605. [Google Scholar] [CrossRef]
- Herbers, T.; Elgar, S.; Guza, R. Infragravity-frequency (0.005–0.05 Hz) motions on the shelf. Part I: Forced waves. J. Phys. Oceanogr. 1994, 24, 917–927. [Google Scholar] [CrossRef]
- Herbers, T.; Guza, R. Wind-wave nonlinearity observed at the sea floor. Part II: Wavenumbers and third-order statistics. J. Phys. Oceanogr. 1992, 22, 489–504. [Google Scholar] [CrossRef]
- Herbers, T.; Guza, R. Nonlinear wave interactions and high-frequency seafloor pressure. J. Geophys. Res. Ocean. 1994, 99, 10035–10048. [Google Scholar] [CrossRef]
- Herbers, T.H.; Lowe, R.; Guza, R.T. Field observations of orbital velocities and pressure in weakly nonlinear surface gravity waves. J. Fluid Mech. 1992, 245, 413–435. [Google Scholar] [CrossRef]
- Young, I.; Eldeberky, Y. Observations of triad coupling of finite depth wind waves. Coast. Eng. 1998, 33, 137–154. [Google Scholar] [CrossRef]
- Sénéchal, N.; Bonneton, P.; Dupuis, H. Field experiment on secondary wave generation on a barred beach and the consequent evolution of energy dissipation on the beach face. Coast. Eng. 2002, 46, 233–247. [Google Scholar] [CrossRef]
- McComas, C.; Briscoe, M. Bispectra of internal waves. J. Fluid Mech. 1980, 97, 205–213. [Google Scholar] [CrossRef]
- Kim, Y.C.; Powers, E.J. Digital bispectral analysis and its applications to nonlinear wave interactions. IEEE Trans. Plasma Sci. 1979, 7, 120–131. [Google Scholar] [CrossRef]
- Haubrich, R.A. Earth noise, 5 to 500 millicycles per second: 1. Spectral stationarity, normality, and nonlinearity. J. Geophys. Res. 1965, 70, 1415–1427. [Google Scholar] [CrossRef]
- Elgar, S.; Guza, R.T. Statistics of bicoherence. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 1667–1668. [Google Scholar] [CrossRef]
- Agnon, Y.; Sheremet, A.; Gonsalves, J.; Stiassnie, M. Nonlinear evolution of a unidirectional shoaling wave field. Coast. Eng. 1993, 20, 29–58. [Google Scholar] [CrossRef]
- Van der Werf, J.J.; Alvarez Antolinez, J.A.; Brakenhoff, L.B.; Gawehn, M.; den Heijer, K.; de Looff, H.; van Maarseveen, M.C.G.; Meijer Holzhauer, H.; Mol, J.W.; Pearson, S.G.; et al. Datareport Kustgenese 2.0; Technical Report; Rijkswaterstaat: Utrecht, The Netherlands, 2019. [Google Scholar]
- Van Prooijen, B.C.; Tissier, M.F.S.; de Wit, F.P.; Pearson, S.G.; Brakenhoff, L.B.; van Maarseveen, M.C.G.; van der Vegt, M.; Mol, J.W.; Kok, F.; Holzhauer, H.; et al. Measurements of Hydrodynamics, Sediment, Morphology and Benthos on Ameland Ebb-Tidal Delta and Lower Shoreface. Earth Syst. Sci. Data 2020. in review. [Google Scholar]
- Lygre, A.; Krogstad, H.E. Maximum entropy estimation of the directional distribution in ocean wave spectra. J. Phys. Oceanogr. 1986, 16, 2052–2060. [Google Scholar] [CrossRef]
- Herbers, T.; Guza, R. Wind-wave nonlinearity observed at the sea floor. Part I: Forced-wave energy. J. Phys. Oceanogr. 1991, 21, 1740–1761. [Google Scholar] [CrossRef]
- Fenton, J. Nonlinear wave theories. Sea 1990, 9, 3–25. [Google Scholar]
- Hedges, T. Regions of validity of analytical wave theories. Proc. Inst. Civ. Eng.-Water Marit. Energy 1995, 112, 111–114. [Google Scholar] [CrossRef]
- Beji, S.; Battjes, J. Experimental investigation of wave propagation over a bar. Coast. Eng. 1993, 19, 151–162. [Google Scholar] [CrossRef]
- Herbers, T.; Elgar, S.; Guza, R. Directional spreading of waves in the nearshore. J. Geophys. Res. Ocean. 1999, 104, 7683–7693. [Google Scholar] [CrossRef]
- Stokes, G.G. On the theory of oscillatory waves. In Transactions of the Cambridge Philosophical Society; University Press: Cambridge, UK, 1880. [Google Scholar]
- Ursell, F. The long-wave paradox in the theory of gravity waves. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1953; Volume 49, pp. 685–694. [Google Scholar]
- Longuet-Higgins, M. The refraction of sea waves in shallow water. J. Fluid Mech. 1956, 1, 163–176. [Google Scholar] [CrossRef]
- Le Méhauté, B. An introduction to water waves. In An Introduction to Hydrodynamics and Water Waves; Springer: Berlin/Heidelberg, Germany, 1976; pp. 197–211. [Google Scholar]
- Madsen, O.S. On the generation of long waves. J. Geophys. Res. 1971, 76, 8672–8683. [Google Scholar] [CrossRef]
- Guza, R.; Thornton, E.B. Local and shoaled comparisons of sea surface elevations, pressures, and velocities. J. Geophys. Res. Ocean. 1980, 85, 1524–1530. [Google Scholar] [CrossRef]
- Soulsby, R. Coastal sediment transport: The COAST3D project. In Coastal Engineering 1998; American Society Of Civil Engineers: Reston, VA, USA, 1999; pp. 2548–2558. [Google Scholar]
- Ruessink, B.; Miles, J.; Feddersen, F.; Guza, R.; Elgar, S. Modeling the alongshore current on barred beaches. J. Geophys. Res. Ocean. 2001, 106, 22451–22463. [Google Scholar] [CrossRef]
- Van Rijn, L.; Ruessink, B.G.; Mulder, J. Coast3D-Egmond: The Behaviour of a Straight Sandy Coast on the Time Scale of Storms and Seasons: Process Knowledge and Guidelines for Coastal Management: End Document, March 2002; Aquapublications: Blokzijl, The Netherlands, 2002. [Google Scholar]
- Birkemeier, W.A.; Long, C.E.; Hathaway, K.K. DELILAH, DUCK94 & SandyDuck: Three nearshore field experiments. In Coastal Engineering 1996; American Society Of Civil Engineers: Reston, VA, USA, 1997; pp. 4052–4065. [Google Scholar]
- Reniers, A.; Thornton, E.; Stanton, T.; Roelvink, J. Vertical flow structure during Sandy Duck: Observations and modeling. Coast. Eng. 2004, 51, 237–260. [Google Scholar] [CrossRef]
- Roelvink, J.; Stive, M. Bar-generating cross-shore flow mechanisms on a beach. J. Geophys. Res. Ocean. 1989, 94, 4785–4800. [Google Scholar] [CrossRef]
- Drake, T.G.; Calantoni, J. Discrete particle model for sheet flow sediment transport in the nearshore. J. Geophys. Res. Ocean. 2001, 106, 19859–19868. [Google Scholar] [CrossRef]
- Eldeberky, Y. Nonlinear Transformation of Wave Spectra in the Nearshore Zone. Ph.D. Thesis, Department of Civil Engineering, Delft University of Technology, Delft, The Netherlands, 1996. [Google Scholar]
- Wei, G.; Kirby, J.T.; Grilli, S.T.; Subramanya, R. A fully nonlinear Boussinesq model for surface waves. Part 1. Highly nonlinear unsteady waves. J. Fluid Mech. 1995, 294, 71–92. [Google Scholar] [CrossRef]
- Madsen, P.A.; Sørensen, O.; Schäffer, H. Surf zone dynamics simulated by a Boussinesq type model. Part I. Model description and cross-shore motion of regular waves. Coast. Eng. 1997, 32, 255–287. [Google Scholar] [CrossRef]
- Bonneton, P.; Barthélemy, E.; Chazel, F.; Cienfuegos, R.; Lannes, D.; Marche, F.; Tissier, M. Recent advances in Serre–Green Naghdi modelling for wave transformation, breaking and runup processes. Eur. J. Mech.-B/Fluids 2011, 30, 589–597. [Google Scholar] [CrossRef]
- Zijlema, M.; Stelling, G.; Smit, P. SWASH: An operational public domain code for simulating wave fields and rapidly varied flows in coastal waters. Coast. Eng. 2011, 58, 992–1012. [Google Scholar] [CrossRef]
- Ma, G.; Shi, F.; Kirby, J.T. Shock-capturing non-hydrostatic model for fully dispersive surface wave processes. Ocean Model. 2012, 43, 22–35. [Google Scholar] [CrossRef]
- Elgar, S.; Sebert, G. Statistics of bicoherence and biphase. J. Geophys. Res. Ocean. 1989, 94, 10993–10998. [Google Scholar] [CrossRef]
- Mahmoudof, S.M.; Badiei, P.; Siadatmousavi, S.M.; Chegini, V. Observing and estimating of intensive triad interaction occurrence in very shallow water. Cont. Shelf Res. 2016, 122, 68–76. [Google Scholar] [CrossRef]
| 1 | Note that different conventions are found in literature. In this paper, the double-sided spectrum is presented, because the bispectrum (Equation (5)) is commonly also presented in a double-sided form and we want to prevent mixing up single- and double-sided spectra. Furthermore, for readability purposes, we present all equations as a function of the variance instead of the variance density. The variance density spectrum can be obtained by dividing the variance spectrum by . |
| 2 | KP79 refers to the methods and equations from Kim and Powers [59]. |
| 3 | HEG94 refers to the methods and equations from Herbers et al. [52]. |
| 4 | Different sign conventions can be found in the literature for the imaginary part of the bispectrum. In the present paper, we adopt the same representation as Norheim et al. [33], in which a negative value of is indicative of an energy transfer from and to . Note that the opposite convention is used in, e.g., Herbers and Burton [39] and De Bakker et al. [51]. |





| Location | Depth (m) | Sensor Height (m) | Measurement |
|---|---|---|---|
| P1 | 10.4 | 0.5 | p |
| P8 | 9.5 | 0.5 | p |
| F4 | 8.5 | 0.5 | |
| P3 | 8.2 | 0.5 | p |
| P5 | 7.9 | 0.5 | p |
| F5 | 6.6 | 0.5 | |
| P7 | 5.3 | 0.5 | p |
| P2 | 4.3 | 0.5 | p |
| P4 | 4.6 | 0.5 | p |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Wit, F.; Tissier, M.; Reniers, A. The Relationship between Sea-Swell Bound Wave Height and Wave Shape. J. Mar. Sci. Eng. 2020, 8, 643. https://doi.org/10.3390/jmse8090643
de Wit F, Tissier M, Reniers A. The Relationship between Sea-Swell Bound Wave Height and Wave Shape. Journal of Marine Science and Engineering. 2020; 8(9):643. https://doi.org/10.3390/jmse8090643
Chicago/Turabian Stylede Wit, Floris, Marion Tissier, and Ad Reniers. 2020. "The Relationship between Sea-Swell Bound Wave Height and Wave Shape" Journal of Marine Science and Engineering 8, no. 9: 643. https://doi.org/10.3390/jmse8090643
APA Stylede Wit, F., Tissier, M., & Reniers, A. (2020). The Relationship between Sea-Swell Bound Wave Height and Wave Shape. Journal of Marine Science and Engineering, 8(9), 643. https://doi.org/10.3390/jmse8090643






