SPH-FE-Based Numerical Simulation on Dynamic Characteristics of Structure under Water Waves
Abstract
1. Introduction
2. Governing Equations and Numerical Methods
2.1. SPH Model for Fluid
2.2. Equation of State
2.3. Finite Element Equation for Solid
2.4. Fluid–Solid Interface Treatment
3. Validation of Numerical Model
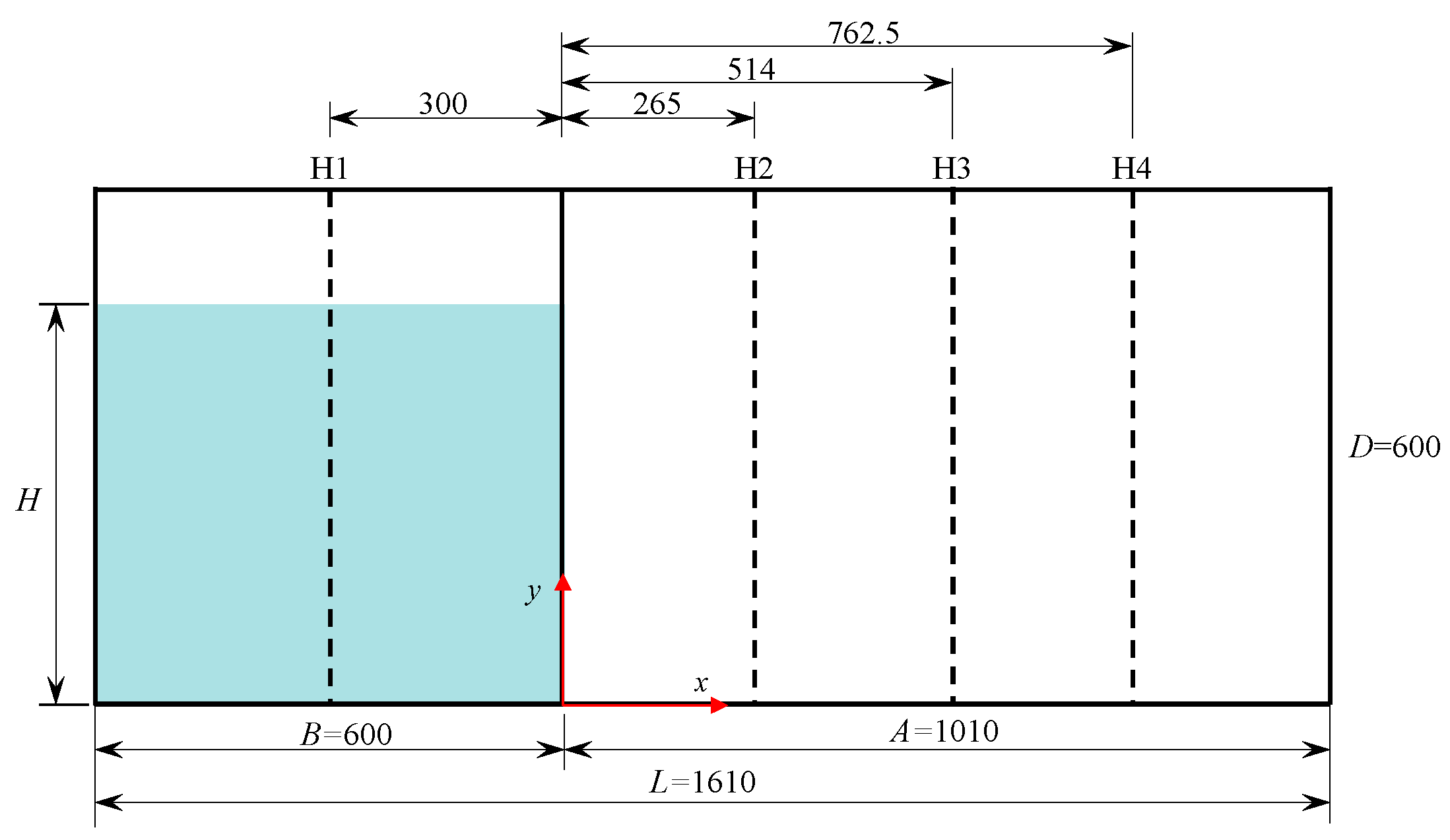
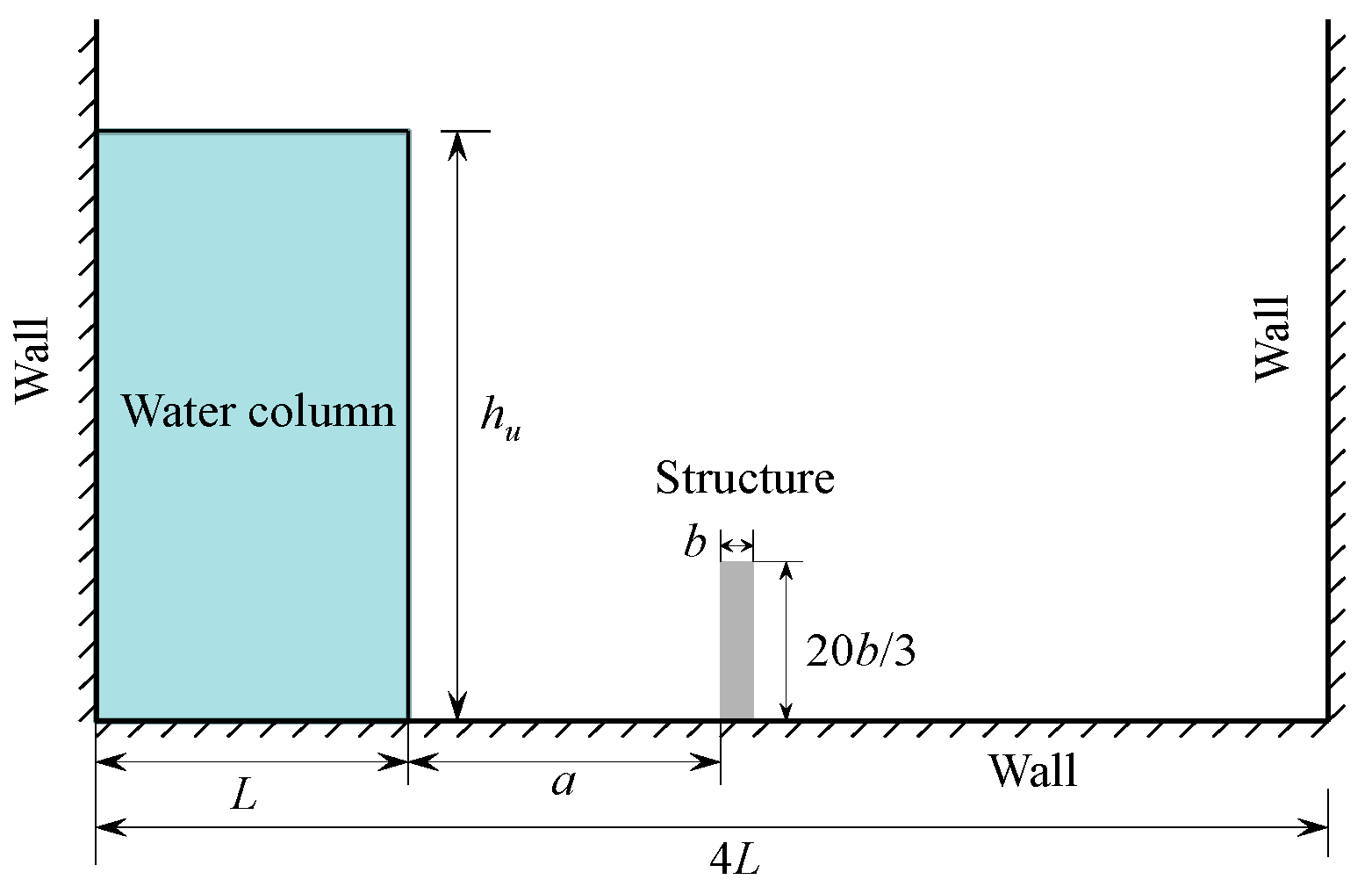
3.1. Computational Case Description
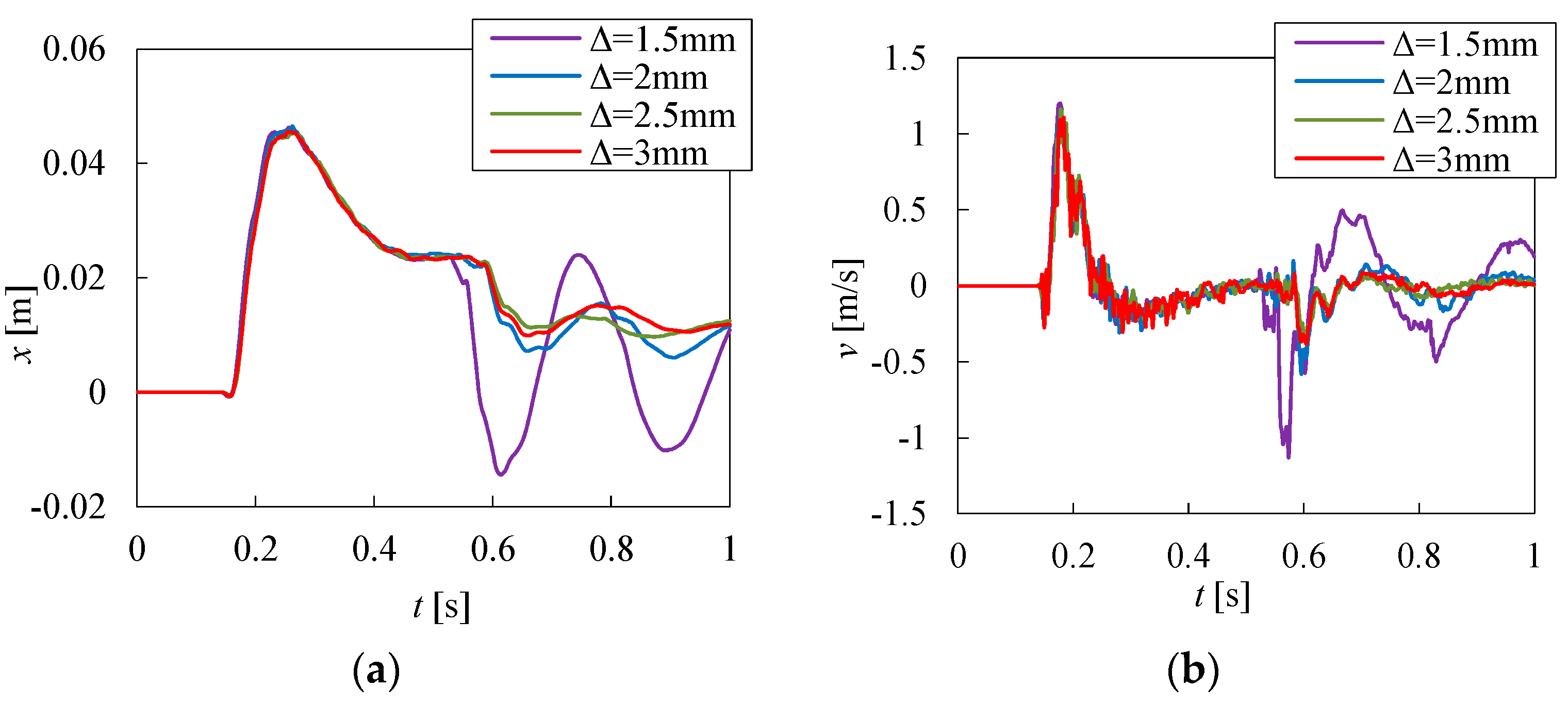
3.2. The Effect of SPH Particle Spacing
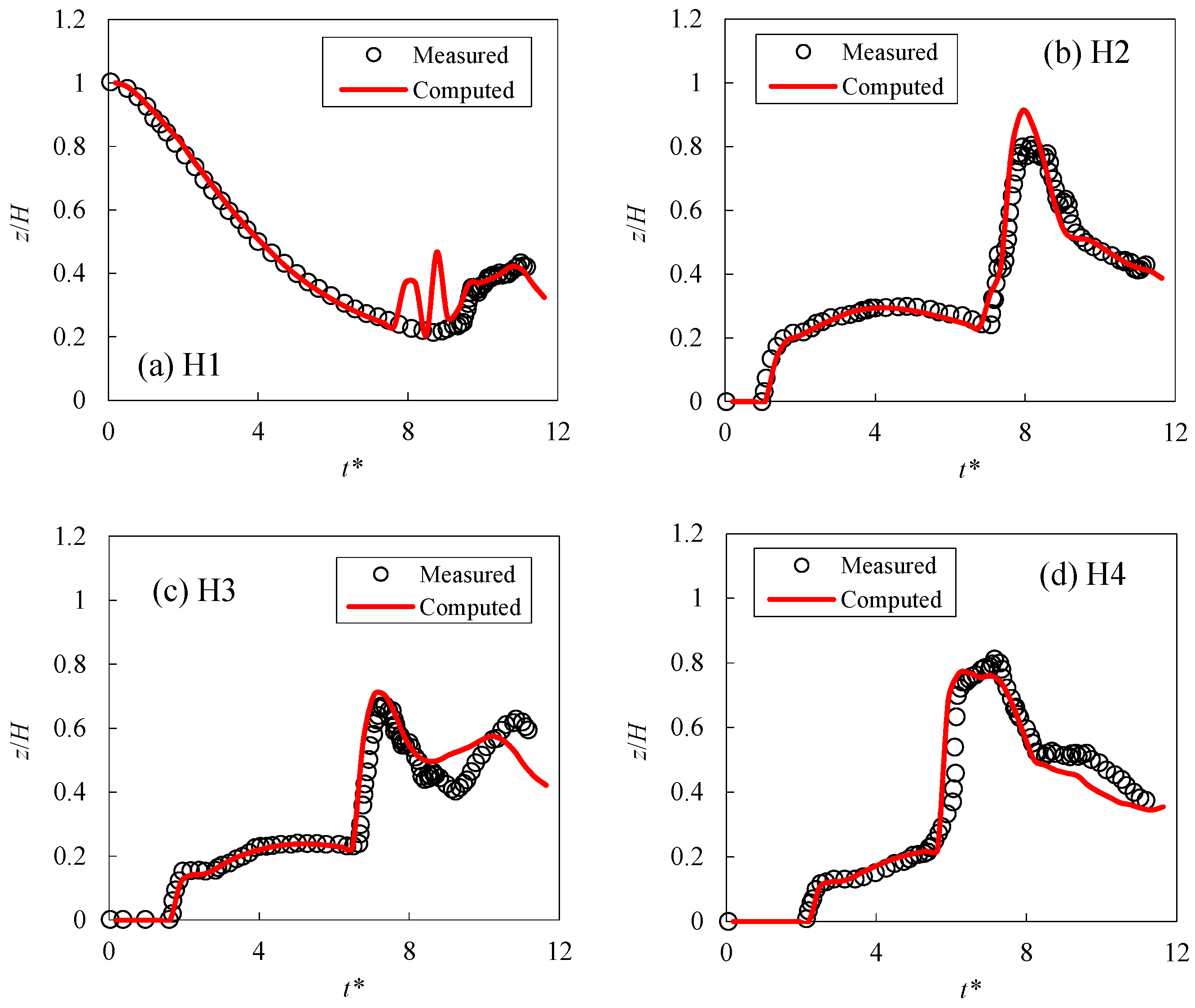
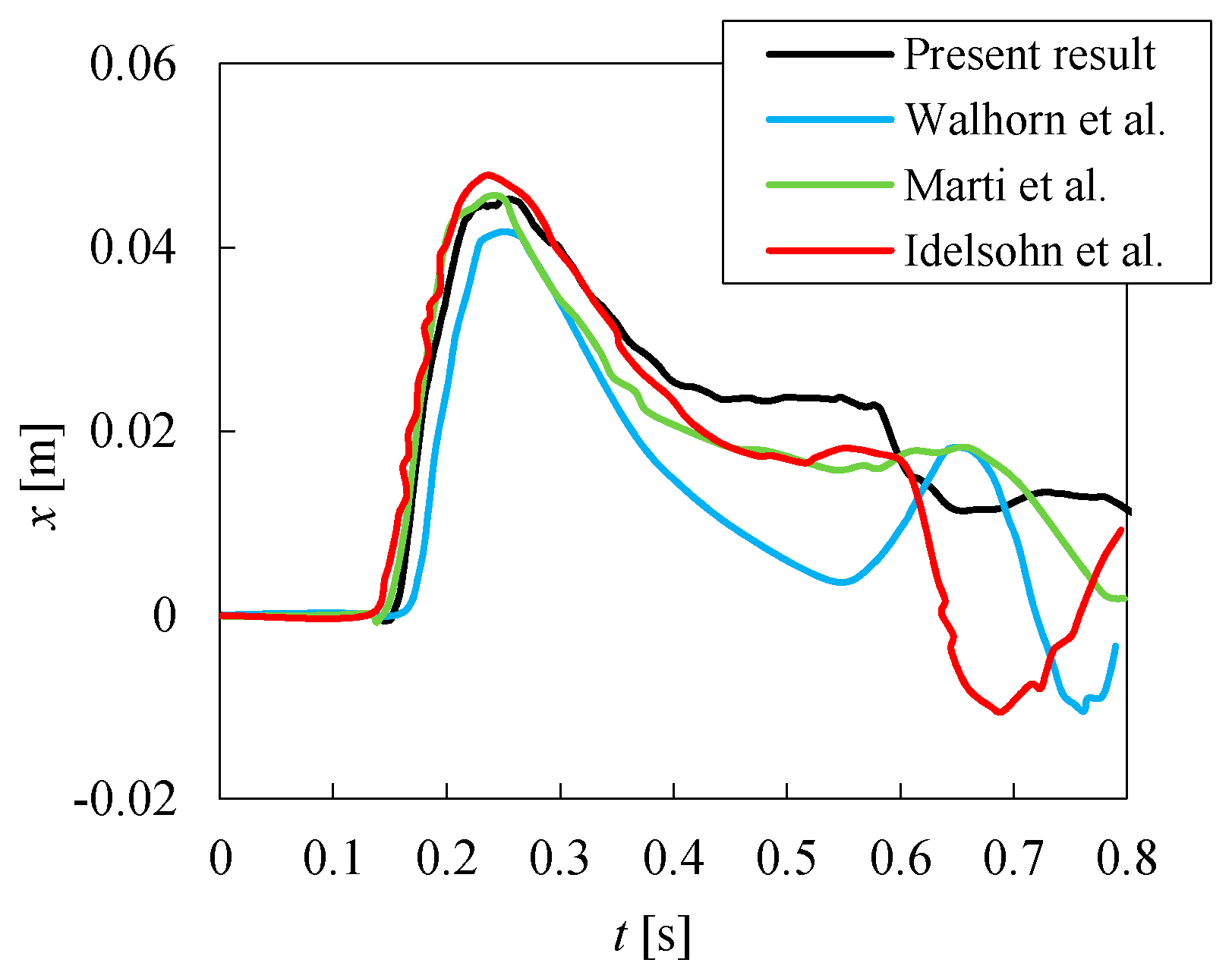
3.3. Model Verification
4. Analysis of Wave–Structure Interaction
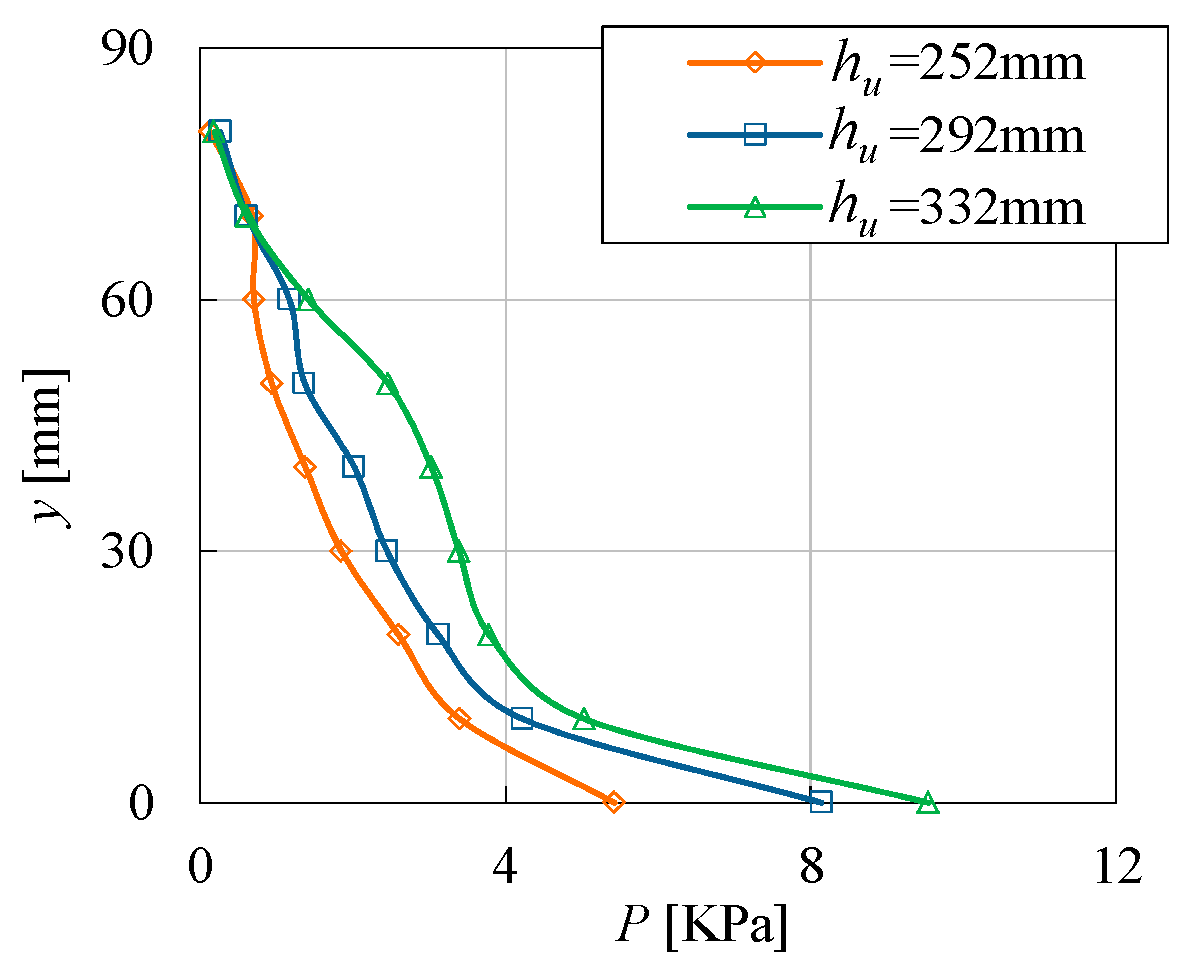
4.1. Effect of Water Column Height
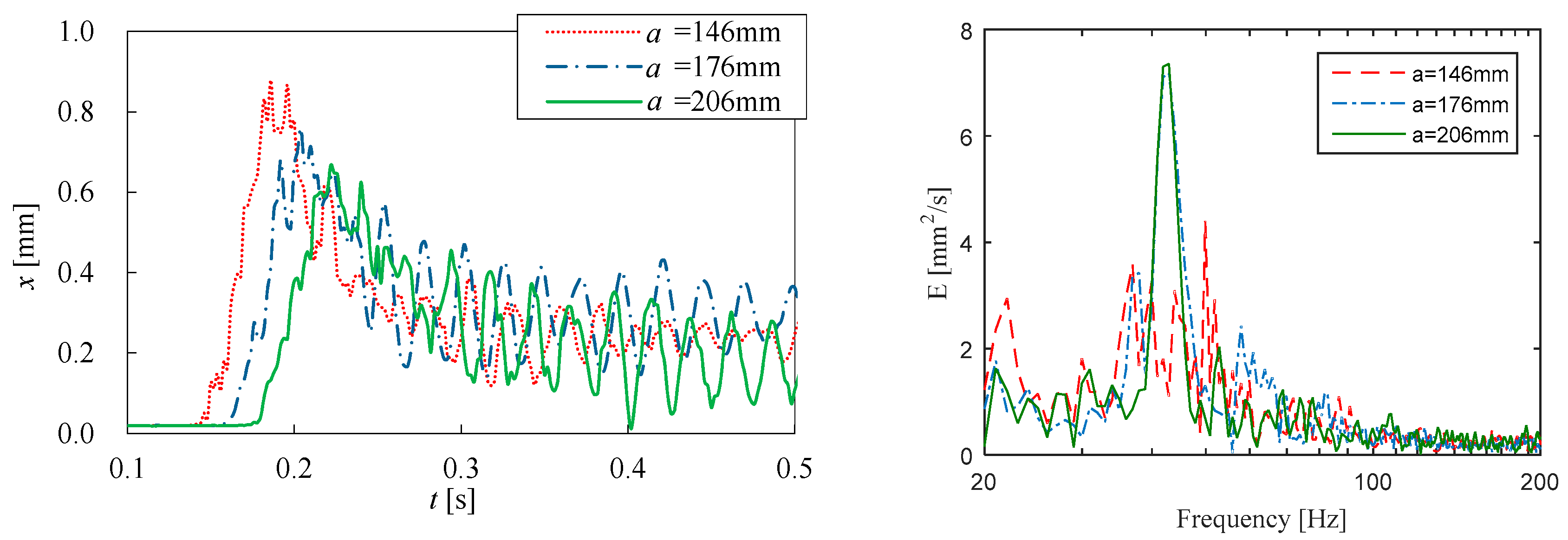
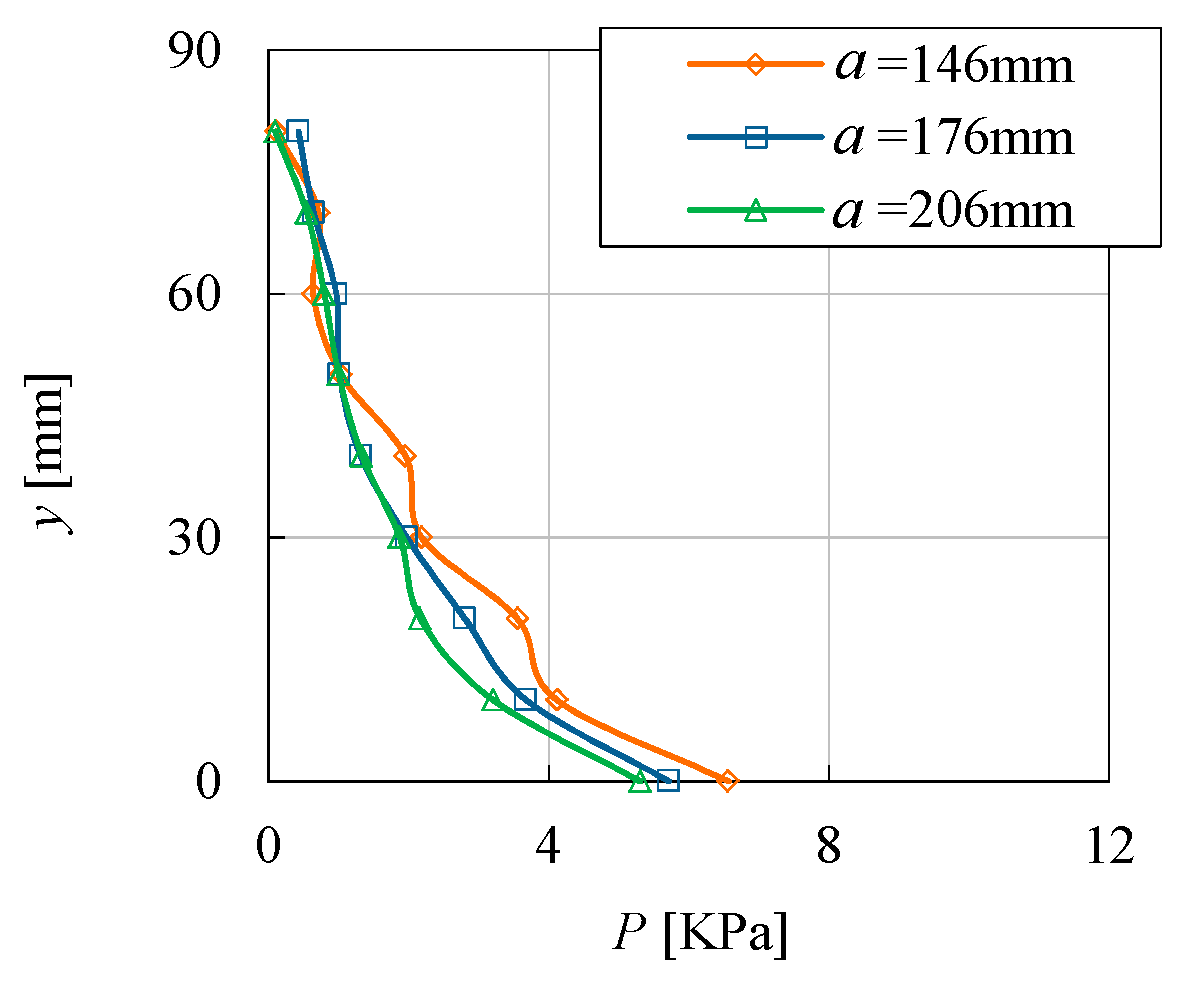
4.2. Effect of Distance between Water Column and Structure
4.3. Effect of the Structure Stiffness
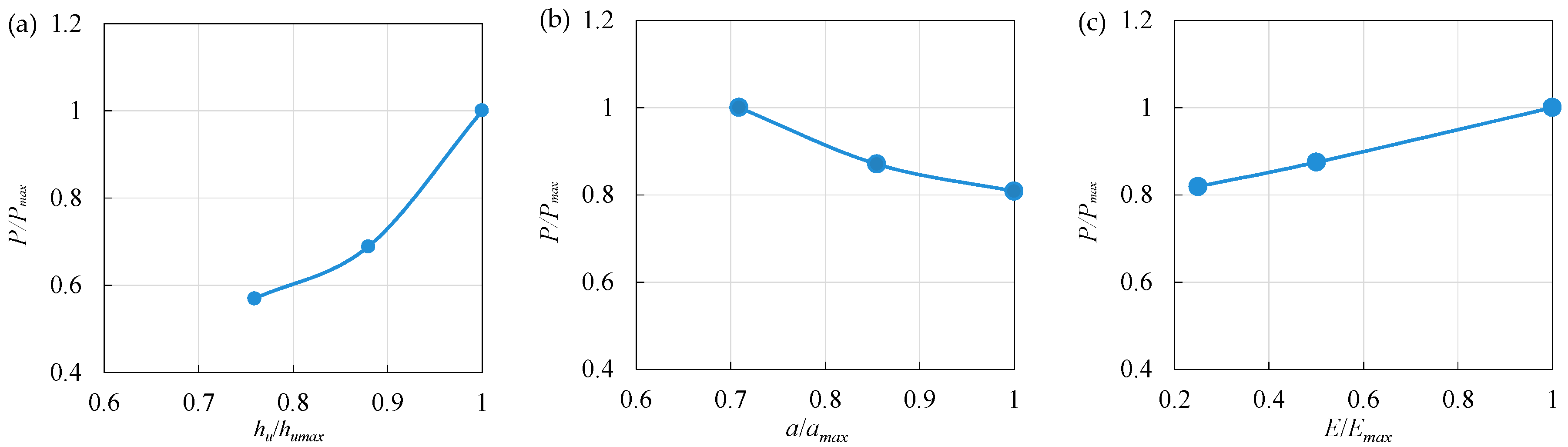
4.4. Comprehensive Analysis
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Validation of SPH Simulation
References
- Cuomo, G.; Allsop, W.; Bruce, T.; Pearson, J. Breaking wave loads at vertical seawalls and breakwaters. Coast. Eng. 2010, 57, 424–439. [Google Scholar] [CrossRef]
- Hsiao, S.C.; Lin, T.C. Tsunami-like solitary waves impinging and overtopping an impermeable seawall: Experiment and RANS modeling. Coast. Eng. 2010, 57, 1–18. [Google Scholar] [CrossRef]
- Liu, X.; Xu, H.H.; Shao, S.D.; Lin, P.Z. An improved incompressible SPH model for simulation of wave-structure interaction. Comput. Fluids 2013, 71, 113–123. [Google Scholar] [CrossRef]
- Ni, X.; Feng, W.B.; Wu, D. Numerical simulations of wave interactions with vertical wave barriers using the SPH method. Int. J. Numer. Methods Fluid. 2014, 76, 223–245. [Google Scholar] [CrossRef]
- Walhorn, E.; Kölke, A.; Hübner, B.; Dinkler, D. Fluid–structure coupling within a monolithic model involving free surface flows. Comput. Struct. 2005, 83, 2100–2111. [Google Scholar] [CrossRef]
- Marti, J.; Idelsohn, S.; Limache, A.; Calvo, N.; D’Elía, J. A fully coupled particle method for quasi incompressible fluid-hypoelastic structure interactions. Mecánica Comput. 2006, XXV, 809–827. [Google Scholar]
- Idelsohn, S.R.; Marti, J.; Limache, A.; Oñate, E. Unified Lagrangian formulation forelastic solids and incompressible fluids: Application to fluid structure interaction problems via the PFEM. Comput. Methods Appl. Mech. Eng. 2008, 197, 1762–1776. [Google Scholar] [CrossRef]
- Monaghan, J.J. Simulating free surface flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Lo, E.Y.M.; Shao, S.D. Simulation of near-shore solitary wave mechanics by an incompressible SPH method. Appl. Ocean Res. 2002, 24, 275–286. [Google Scholar]
- Sriram, V.; Ma, Q.W. Improved MLPG_R method for simulating 2D interaction between violent waves and elastic structures. J. Comput. Phys. 2012, 231, 7650–7670. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G.R. Smoothed Particle Hydrodynamics (SPH): An overview and recent developments. Arch. Comput. Methods Eng. 2010, 17, 25–76. [Google Scholar] [CrossRef]
- Liu, H.X.; Li, J.; Shao, S.D.; Tan, S.K. SPH modeling of tidal bore scenarios. Nat. Hazards 2015, 75, 1247–1270. [Google Scholar] [CrossRef][Green Version]
- St-Germain, P.; Nistor, L.; Townsend, R. Numerical Modeling of Tsunami-Induced Hydrodynamic Forces on Onshore Structures Using SPH. In Proceedings of the 33rd International Conference on Coastal Engineering (ICCE), Santander, Spain, 1–6 July 2012; pp. 1–15. [Google Scholar]
- Rafiee, A.; Thiagarajan, K.P. An SPH projection method for simulating fluid-hypoelastic structure interaction. Comput. Methods Appl. Mech. Engrg. 2009, 198, 2785–2795. [Google Scholar] [CrossRef]
- Dao, M.H.; Xu, H.; Chan, E.S.; Tkalich, P. Modelling of tsunami-like wave run-up, breaking and impact on a vertical wall by SPH method. Nat. Hazards Earth Syst. Sci. 2013, 13, 3457–3467. [Google Scholar] [CrossRef]
- St-Germain, P.; Nistor, L.; Townsend, R.; Shibayama, T. Smoothed-Particle hydrodynamics numerical modeling of structures impacted by tsunami bores. J. Waterw. Port Coast. Ocean Eng. 2014, 140, 66–81. [Google Scholar] [CrossRef]
- Vuyst, T.D.; Vignjevic, R.; Campbell, J.C. Coupling between meshless and finite element methods. Int. J. Impact Eng. 2005, 31, 1054–1064. [Google Scholar] [CrossRef]
- Groenenboom, P.H.L.; Cartwright, B.K. Hydrodynamics and fluid-structure interaction by coupled SPH-FE method. J. Hydraul. Res. 2010, 48, 61–73. [Google Scholar] [CrossRef]
- Hu, D.A.; Long, T.; Xiao, Y.H.; Han, X.; Gu, Y.T. Fluid-structure interaction analysis by coupled FE-SPH model based on a novel searching algorithm. Comput. Methods Appl. Mech. Eng. 2014, 276, 266–286. [Google Scholar] [CrossRef]
- Thiyahuddin, M.I.; Gu, Y.T.; Gover, R.B.; Thambiratnam, D.P. Fluid-structure interaction analysis of full scale vehicle-barrier impact using coupled SPH-FEA. Eng. Anal. Bound. Elem. 2013, 42, 26–36. [Google Scholar] [CrossRef][Green Version]
- Petsehek, A.C.; Libersky, L.D. Cylindrical smoothed particle hydrodynamies. J. Comput. Phys. 1993, 109, 76–80. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Xiao, Y.H.; Han, X.; Hu, D.A. FE-SPH coupling simulation of fluid structure interaction. Chin. J. Appl. Mech. 2011, 28, 13–18. (In Chinese) [Google Scholar]
- Johnson, G.R.; Stryk, R.A.; Beissel, S.R.; Holmquist, T.J. An algorithm to automatically convert distorted finite elements into meshless particles during dynamic deformation. Int. J. Impact Eng. 2002, 27, 997–1013. [Google Scholar] [CrossRef]
- Chanson, H. Tsunami surges on dry coastal plains: Application of dam break equations. Coast. Eng. J. 2006, 48, 355–370. [Google Scholar] [CrossRef]
- Bressan, L.; Guerrero, M.; Antonini, A.; Petruzzelli, V.; Archetti, R.; Lamberti, A.; Tinti, S. A laboratory experiment on the incipient motion of boulders by high-energy coastal flows. Earth Surf. Proc. Land. 2018, 43, 2935–2947. [Google Scholar] [CrossRef]
- Gómez-Gesteira, M.; Dalrymple, R.A. Using a three-dimensional smoothed particle hydrodynamic method for wave impact on a tall structure. J. Waterw. Port Coast. Ocean Eng. 2004, 130, 63–69. [Google Scholar] [CrossRef]
- Lobovský, L.; Botia-Vera, E.; Castellana, F.; Mas-Soler, J.; Souto-Iglesias, A. Experimental investigation of dynamic pressure loads during dam break. J. Fluid. Struct. 2014, 48, 407–434. [Google Scholar] [CrossRef]
- Zech, Y.; Soares-Frazão, S. Dam-break flow experiments and real-case data: A database from the European IMPACT research. J. Hydraul. Res. 2007, 45, 5–7. [Google Scholar] [CrossRef]
- Lauber, G.; Hager, W.H. Experiments to dambreak wave: Horizontal channel. J. Hydraul. Res. 1998, 36, 291–307. [Google Scholar] [CrossRef]
- Hu, C.; Sueyoshi, M. Numerical simulation and experiment on dam break problem. J. Mar. Sci. Appl. 2010, 9, 109–114. [Google Scholar] [CrossRef]
- Swegle, J.W.; Attaway, S.W.; Heinstein, M.W.; Mello, F.J.; Hicks, D.L. An Analysis of Smoothed Particle Hydrodynamics; Sandia Report: Washington, DC, USA, 1994. [Google Scholar]
- Liu, G.R.; Liu, M.B. Smoothed Particle Hydrodynamics: A Meshfree Particle Method; World Scientific: Singapore, 2003. [Google Scholar]
- Xu, J.Z.; Tang, W.H. Initial smoothing length and space between particles in SPH method for numerical simulation of high-speed impacts. Chin. J. Comput. Phys. 2009, 26, 548–552. (In Chinese) [Google Scholar]







| Test No. | Initial Particle Spacing Δ [mm] | Number of Particles |
|---|---|---|
| 1 | 3.0 | 4753 |
| 2 | 2.5 | 6786 |
| 3 | 2.0 | 10,658 |
| 4 | 1.5 | 18,915 |
| Test No. | hu [mm] | a [mm] | E [kPa] |
|---|---|---|---|
| 1 | 292 | 146 | 3.0 × 107 |
| 2 | 252 | 146 | 3.0 × 107 |
| 3 | 332 | 146 | 3.0 × 107 |
| 4 | 292 | 176 | 3.0 × 107 |
| 5 | 292 | 206 | 3.0 × 107 |
| 6 | 292 | 146 | 1.5 × 107 |
| 7 | 292 | 146 | 7.5 × 106 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Li, J. SPH-FE-Based Numerical Simulation on Dynamic Characteristics of Structure under Water Waves. J. Mar. Sci. Eng. 2020, 8, 630. https://doi.org/10.3390/jmse8090630
Yang Y, Li J. SPH-FE-Based Numerical Simulation on Dynamic Characteristics of Structure under Water Waves. Journal of Marine Science and Engineering. 2020; 8(9):630. https://doi.org/10.3390/jmse8090630
Chicago/Turabian StyleYang, Yilin, and Jinzhao Li. 2020. "SPH-FE-Based Numerical Simulation on Dynamic Characteristics of Structure under Water Waves" Journal of Marine Science and Engineering 8, no. 9: 630. https://doi.org/10.3390/jmse8090630
APA StyleYang, Y., & Li, J. (2020). SPH-FE-Based Numerical Simulation on Dynamic Characteristics of Structure under Water Waves. Journal of Marine Science and Engineering, 8(9), 630. https://doi.org/10.3390/jmse8090630





