A Coupled Artificial Compressibility Method for Free Surface Flows
Abstract
1. Introduction
2. Governing Equations
3. Numerical Framework
3.1. Spatial Discretization
3.2. Temporal Discretization
3.3. Turbulence Modeling
3.4. Wave Generation and Absorption
3.5. Volume Fraction Boundedness
4. Numerical Results
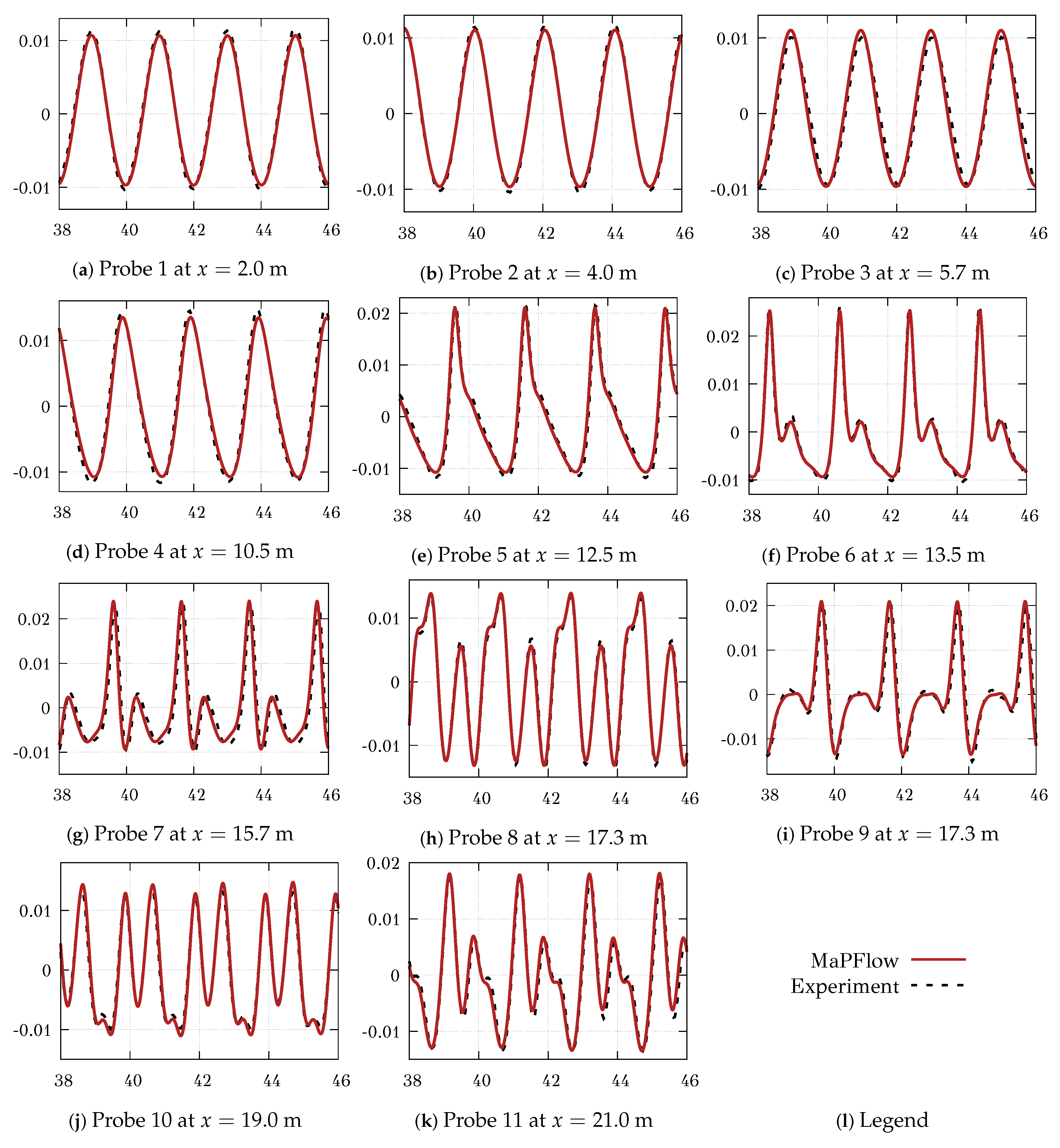
4.1. Numerical Wave Tank
4.1.1. Wave Generation and Absorption
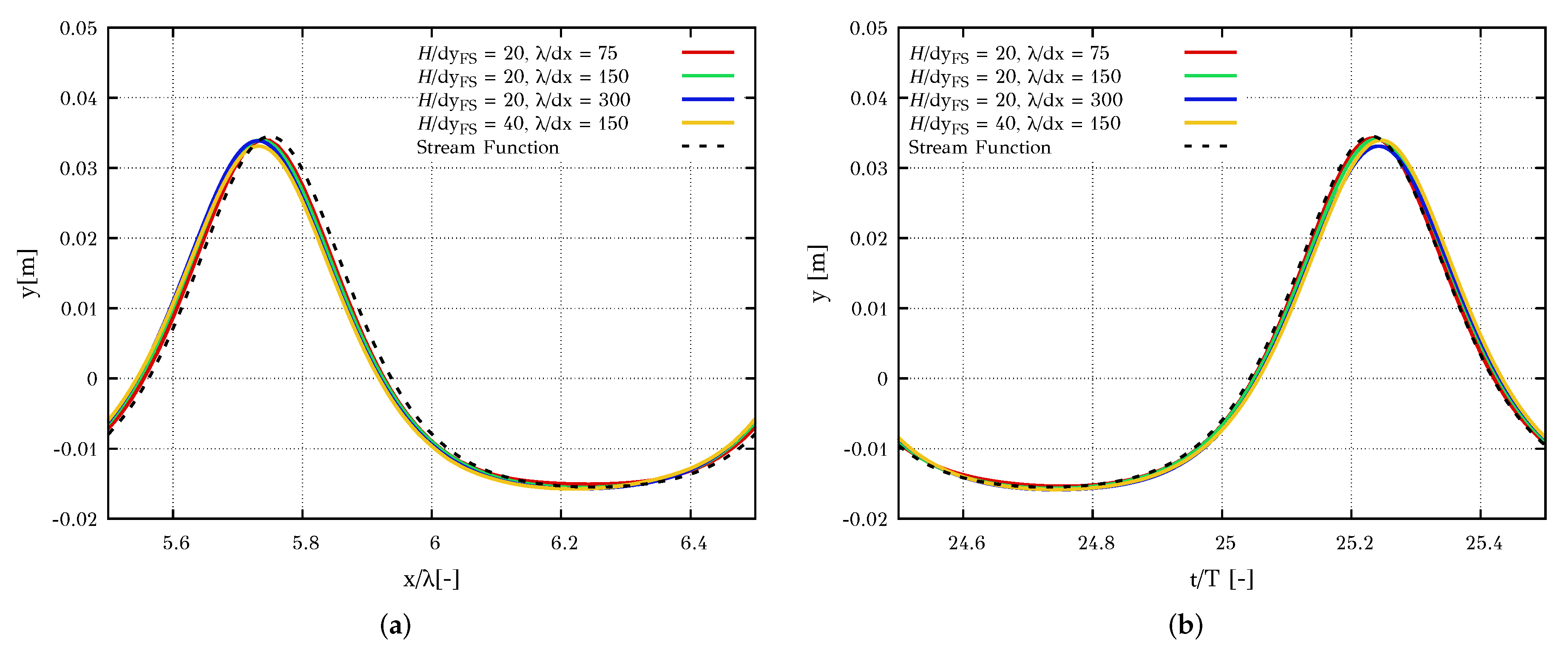
4.1.2. Grid and Timestep Independence
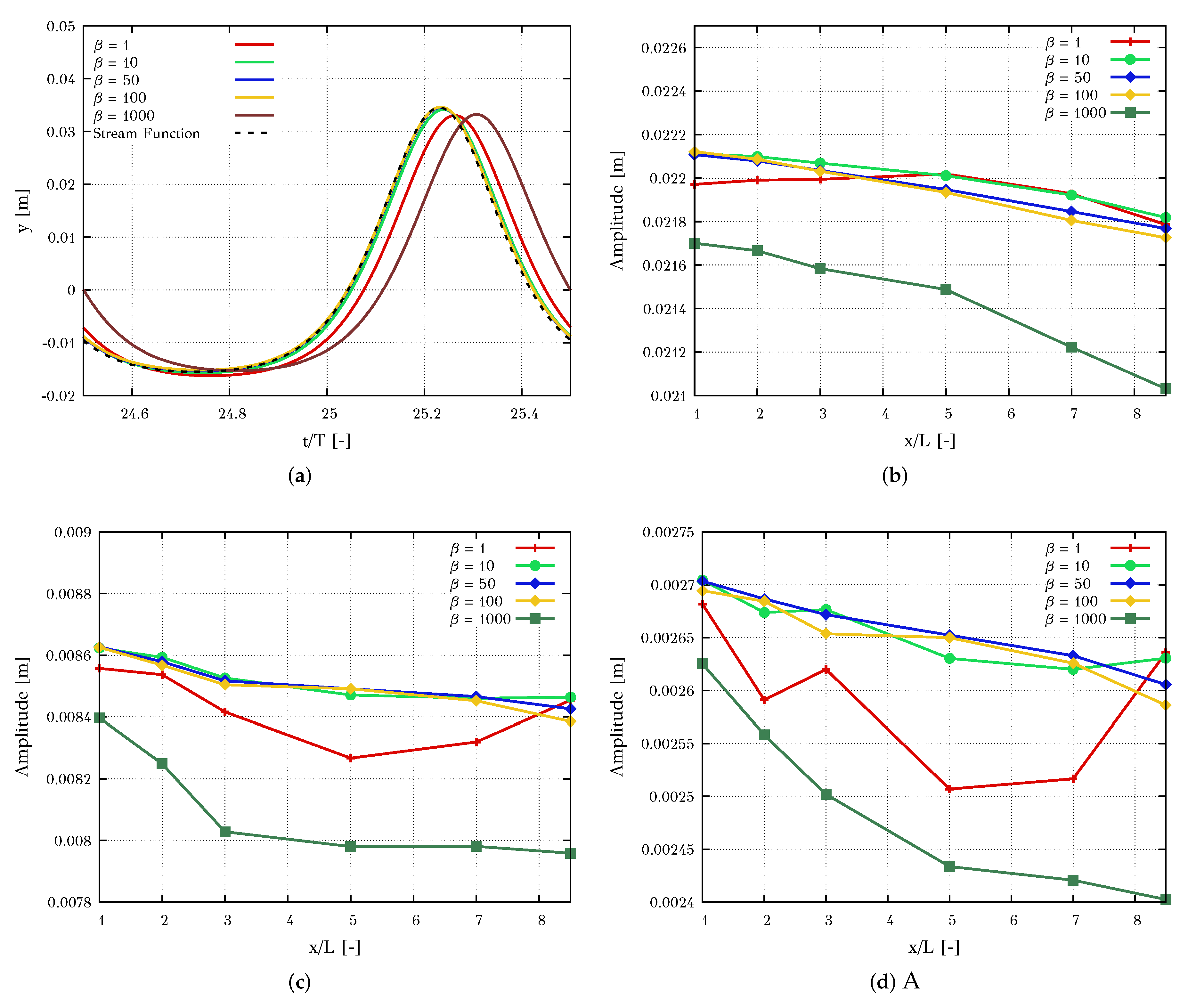
4.1.3. Influence of the Artificial Compressibility Parameter
4.2. Wave Interaction with Variable Bathymetry
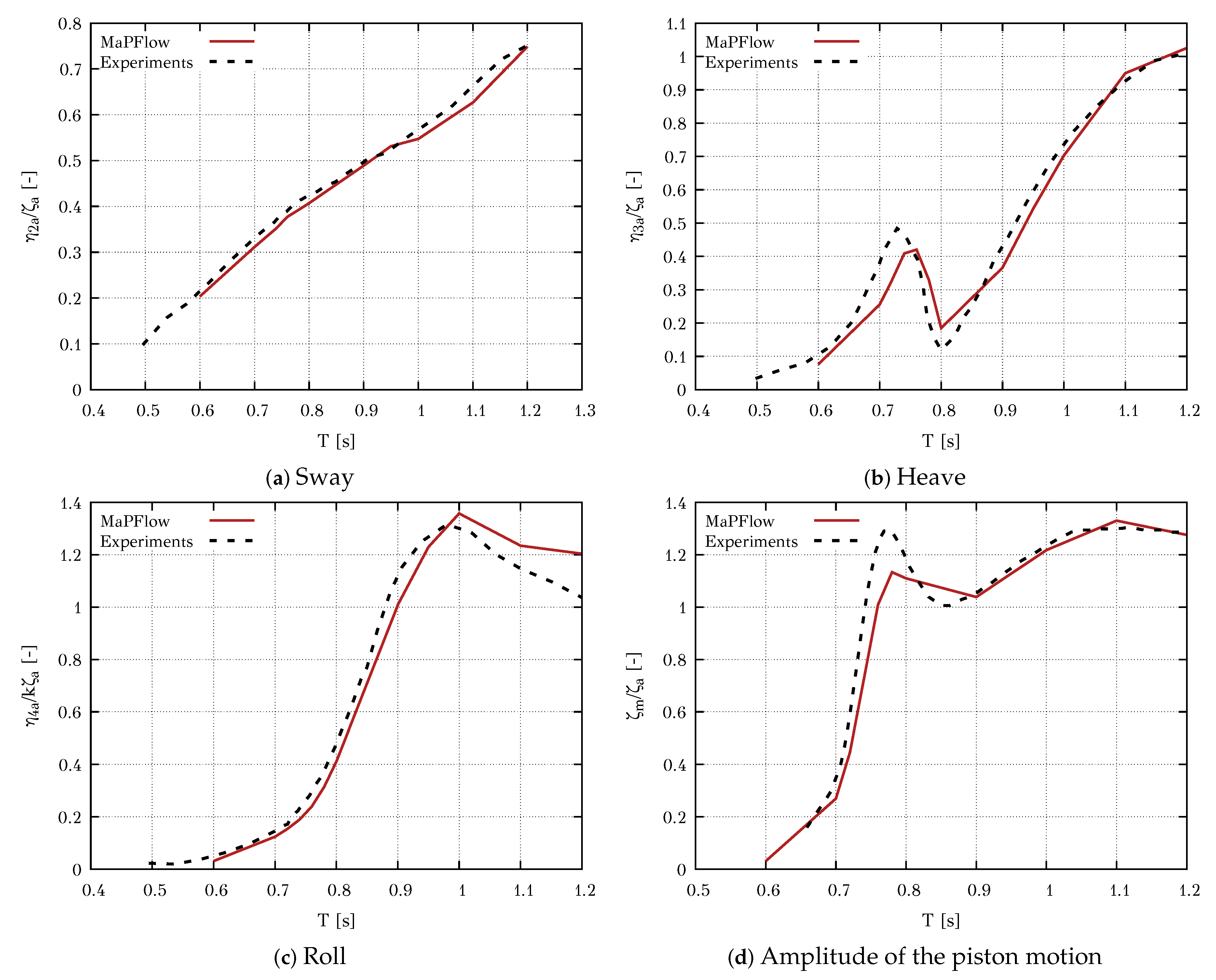
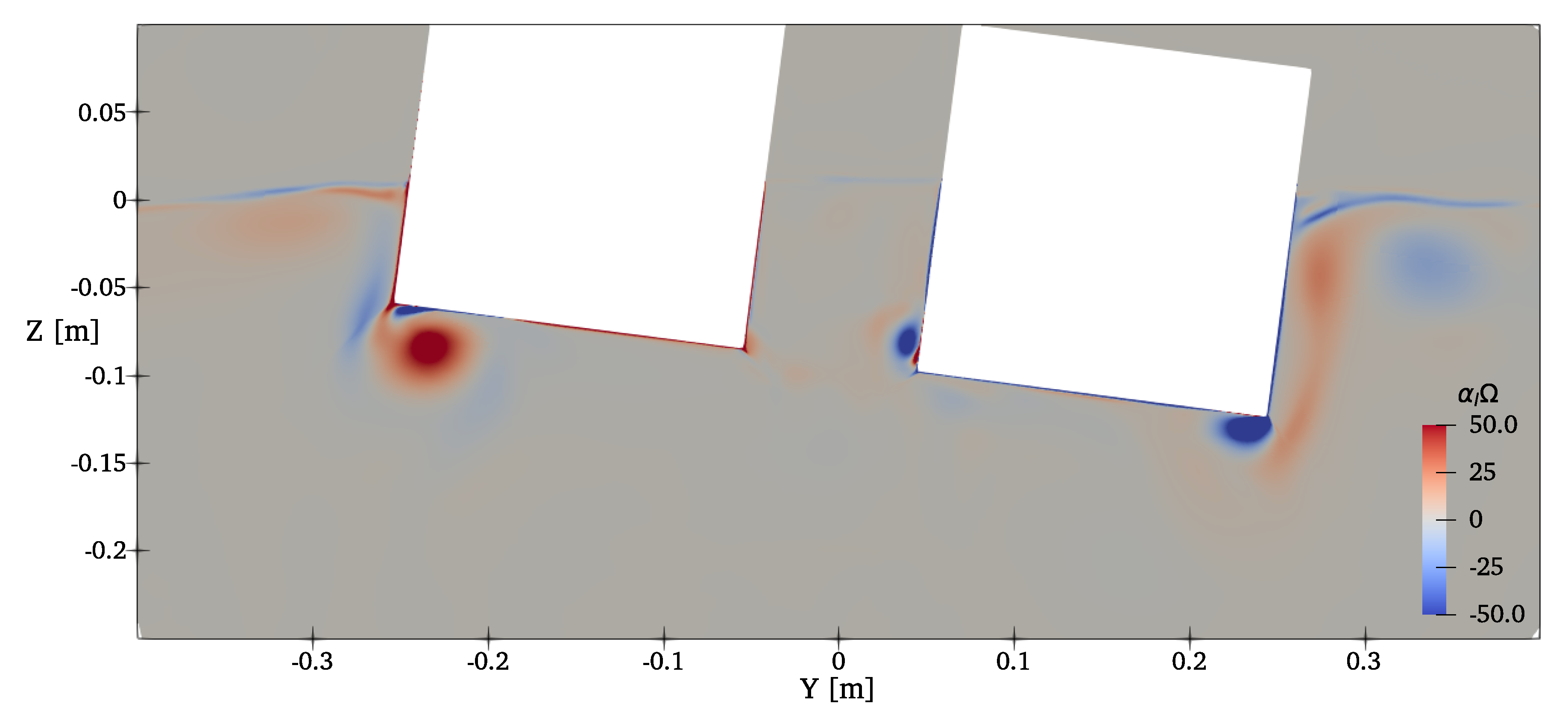
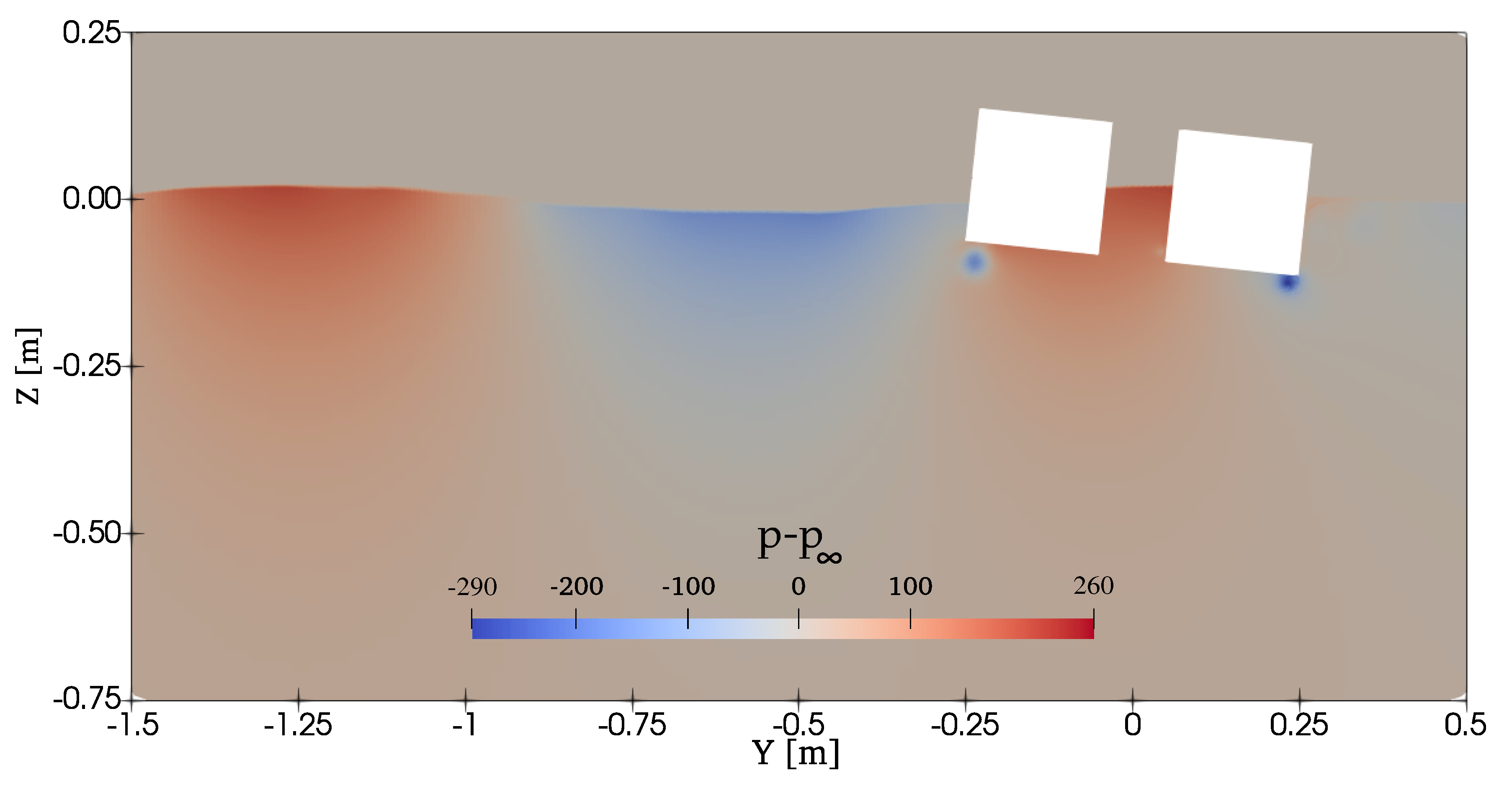
4.3. Moonpool-Type Floater
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
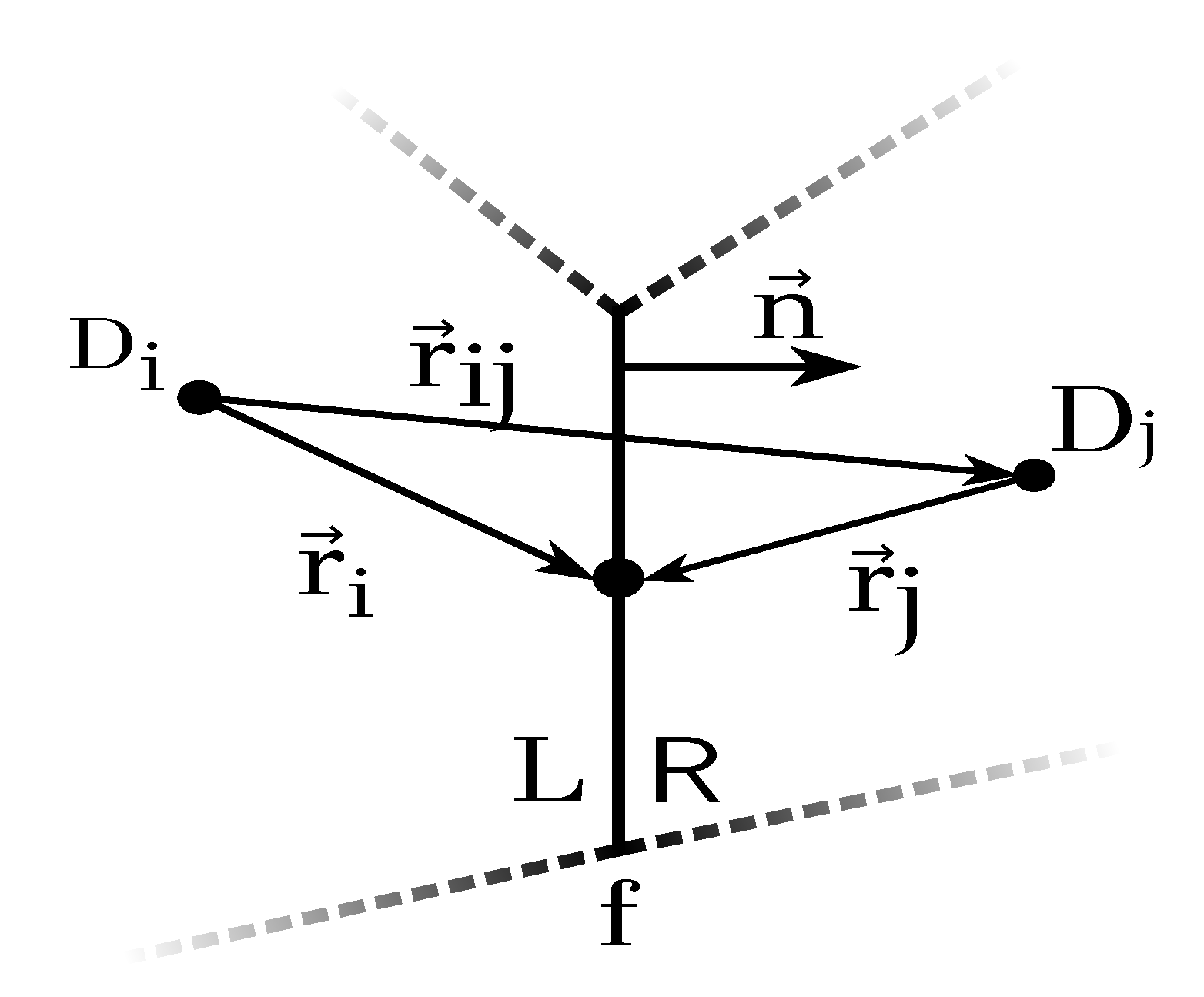
Appendix A. Discretization of the Hyperbolic System of Equations
References
- Grilli, S. Fully nonlinear potential flow models used for long wave runup prediction. In Chapter in Long-Wave Runup Models; Yeh, H., Liu, P., Synolakis, C., Eds.; World Scientific Pub Co Pte Lt.: Singapore, 1997; pp. 116–180. [Google Scholar]
- Filippas, E. Hydrodynamic Analysis of Ship and Marine Biomimetic Systems in Waves Using GPGPU Programming. Ph.D. Thesis, National Technical University of Athens, School of Naval Architecture and Marine Engineering, Zografou, Greece, 2019. [Google Scholar]
- Manolas, D. Hydro-aero-elastic Analysis of Offshore Wind Turbines. Ph.D. Thesis, National Technical University of Athens, School of Mechanical Engineering, Zografou, Greece, 2015. [Google Scholar]
- Papoutsellis, C.; Athanassoulis, G. A new efficient Hamiltonian approach to the nonlinear water-wave problem over arbitrary bathymetry. arXiv 2017, arXiv:1704.03276. [Google Scholar]
- Filippas, E.S.; Papadakis, G.P.; Belibassakis, K.A. Free-Surface Effects on the Performance of Flapping-Foil Thruster for Augmenting Ship Propulsion in Waves. J. Mar. Sci. Eng. 2020, 8, 357. [Google Scholar] [CrossRef]
- Takizawa, A.; Koshizuka, S.; Kondo, S. Generalization of physical component boundary fitted co-ordinate (PCBFC) method for the analysis of free-surface flow. Int. J. Numer. Methods Fluids 1992, 15, 1213–1237. [Google Scholar] [CrossRef]
- Tzabiras, G.D. Resistance and Self-Propulsion Simulations for a Series-60, CB = 0.6 Hull at Model and Full Scale. Ship Technol. Res. 2004, 51, 21–34. [Google Scholar] [CrossRef]
- Hirt, C.; Nichols, B. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Sussman, M.; Smereka, P.; Osher, S. A level set approach for computing solutions to incompressible two-phase flow. J. Comput. Phys. 1994, 114, 146–159. [Google Scholar] [CrossRef]
- Harlow, F.H.; Welch, J.E. Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface. Phys. Fluids 1965, 8, 2182–2189. [Google Scholar] [CrossRef]
- Vukcevic, V. Numerical Modelling of Coupled Potential and Viscous Flow for Marine Applications. Ph.D. Thesis, Fakultet Strojarstva i Brodogradnje, Zagreb, Croatia, 2017. [Google Scholar] [CrossRef]
- Plumerault, L.R.; Astruc, D.; Villedieu, P.; Maron, P. A numerical model for aerated-water wave breaking. Int. J. Numer. Methods Fluids 2012, 69, 1851–1871. [Google Scholar] [CrossRef]
- Liu, S.; Gatin, I.; Obhrai, C.; Ong, M.C.; Jasak, H. CFD simulations of violent breaking wave impacts on a vertical wall using a two-phase compressible solver. Coast. Eng. 2019, 154, 103564. [Google Scholar] [CrossRef]
- Kim, J.; Moin, P. Application of a Fractional-Step Method to Incompressible Navier-Stokes Equations. J. Comput. Phys. 1985, 59, 308–323. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the Implicitly Fluid Flow Equations by Operator-Splitting. J. Comput. Phys. 1985, 62, 40–65. [Google Scholar] [CrossRef]
- Rhie, C.M.; Chow, W.L. Numerical study of the turbulent flow past an airfoil with trailing edge separation. AIAA J. 1983, 21, 1525–1532. [Google Scholar] [CrossRef]
- Queutey, P.; Visonneau, M. An interface capturing method for free-surface hydrodynamic flows. Comput. Fluids 2007, 36, 1481–1510. [Google Scholar] [CrossRef]
- Higuera, P.; Lara, J.L.; Losada, I.J. Realistic wave generation and active wave absorption for Navier-Stokes models. Application to OpenFOAM®. Coast. Eng. 2013. [Google Scholar] [CrossRef]
- Angelidis, D.; Chawdhary, S.; Sotiropoulos, F. Unstructured Cartesian refinement with sharp interface immersed boundary method for 3D unsteady incompressible flows. J. Comput. Phys. 2016, 325, 272–300. [Google Scholar] [CrossRef]
- Chorin, A.J. A Numerical Method for Solving Incompressible Visous Flow Problems. J. Comput. Phys. 1967, 135, 118–125. [Google Scholar] [CrossRef]
- Merkle, C.; Tsai, P. Application of Runge-Kutta Schmes to Incompressible Flows. In Proceedings of the AIAA 24th Aerospace Sciences Meeting, Reno, NV, USA, 6–9 January 1986. [Google Scholar]
- Turkel, E. Preconditioned methods for solving the incompressible and low speed compressible equations. J. Comput. Phys. 1987, 72, 277–298. [Google Scholar] [CrossRef]
- Kelecy, F.J.; Pletcher, R.H. The development of a free surface capturing approach for multidimensional free surface flows in closed containers. J. Comput. Phys. 1997, 138, 939–980. [Google Scholar] [CrossRef]
- Kunz, R.F.; Boger, D.A.; Stinebring, D.R.; Chyczewski, T.S.; Lindau, J.W.; Gibeling, H.J.; Venkateswaran, S.; Govindan, T.R. A preconditioned Navier-Stokes method for two-phase flows with application to cavitation prediction. Comput. Fluids 2000, 29, 849–875. [Google Scholar] [CrossRef]
- Wackers, J.; Koren, B. Efficient computation of steady water flow with waves. Int. J. Numer. Methods Fluids 2008, 56, 1567–1574. [Google Scholar] [CrossRef]
- Papadakis, G.; Voutsinas, S.G. A strongly coupled Eulerian Lagrangian method verified in 2D external compressible flows. Comput. Fluids 2019, 195, 104325. [Google Scholar] [CrossRef]
- Papadakis, G.; Manolesos, M. The flow past a flatback airfoil with flow control devices: Benchmarking numerical simulations against wind tunnel data. Wind Energy Sci. 2020, 5, 911–927. [Google Scholar] [CrossRef]
- Karypis, G. METIS A Software Package for Partitioning Unstructured Graphs, Partitioning Meshes, and Computing Fill-Reducing Orderings of Sparse Matrices Version; Technical Report; Department of Computer Science & Engineering, University of Minnesota: Minneapolis, MN, USA, 2013. [Google Scholar]
- Dingemans, M. Comparison of Computations With Boussinesq-Like Models And Laboratory; Technical Report; Delft Hydralics: Delft, The Netherlands, 1994. [Google Scholar]
- Fredriksen, A.G.; Kristiansen, T.; Faltinsen, O.M. Wave-induced response of a floating two-dimensional body with a moonpool. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373. [Google Scholar] [CrossRef] [PubMed]
- Vukčević, V.; Roenby, J.; Gatin, I.; Jasak, H. A Sharp Free Surface Finite Volume Method Applied to Gravity Wave Flows. arXiv 2018, arXiv:1804.01130. [Google Scholar]
- Leonard, B.P. Simple high-accuracy resolution program for convective modelling of discontinuities. Int. J. Numer. Methods Fluids 1988, 8, 1291–1318. [Google Scholar] [CrossRef]
- Ubbink, O. Numerical Prediction of Two Fluid Systems With Sharp Interfaces. Ph.D. Thesis, Department of Mechanical Engineering Imperial College of Science, Technology & Medicine, London, UK, 1997. [Google Scholar]
- Muzaferija, S.; Perić, M. Computation of free-surface flows using interface-tracking and interface-capturing methods. In Nonlinear Water Waves Interaction; WIT Press: Southampton, UK, 1999; pp. 59–100. [Google Scholar]
- Wackers, J.; Koren, B.; Raven, H.C.; van der Ploeg, A.; Starke, A.R.; Deng, G.B.; Queutey, P.; Visonneau, M.; Hino, T.; Ohashi, K. Free-Surface Viscous Flow Solution Methods for Ship Hydrodynamics. Arch. Comput. Methods Eng. 2011, 18, 1–41. [Google Scholar] [CrossRef]
- Darwish, M.; Moulkaled, F. Convective Schemes for Capturing Interfaces of Free-Surface Flows on Unstructured Grids. Numer. Heat Transf. 2006, 49, 19–42. [Google Scholar] [CrossRef]
- Biedron, R.; Vatsa, V.; Atkins, H. Simulation of Unsteady Flows Using an Unstructured Navier-Stokes Solver on Moving and Stationary Grids. In Proceedings of the 23rd AIAA Applied Aerodynamics Conference, Toronto, ON, Canada, 6–9 June 2005; pp. 1–17. [Google Scholar] [CrossRef]
- Ahn, H.T.; Kallinderis, Y. Strongly coupled flow/structure interactions with a geometrically conservative ALE scheme on general hybrid meshes. J. Comput. Phys. 2006, 219, 671–696. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Devolder, B.; Rauwoens, P.; Troch, P. Application of a buoyancy-modified k-ω SST turbulence model to simulate wave run-up around a monopile subjected to regular waves using OpenFOAM®. Coast. Eng. 2017, 125, 81–94. [Google Scholar] [CrossRef]
- Larsen, B.E.; Fuhrman, D.R. On the over-production of turbulence beneath surface waves in Reynolds-averaged Navier–Stokes models. J. Fluid Mech. 2018, 853, 419–460. [Google Scholar] [CrossRef]
- Kato, M.; Launder, B. The modeling of turbulent flow around stationary and vibrating square cylinders. Turbul. Shear. Flows 1993, 10.4:1–10.4:6. [Google Scholar] [CrossRef]
- Jacobsen, N.G.; Fuhrman, D.R.; Fredsøe, J. A wave generation toolbox for the open-source CFD library: OpenFoam®. Int. J. Numer. Methods Fluids 2012, 70, 1073–1088. [Google Scholar] [CrossRef]
- Fenton, J.D. The numerical solution of steady water wave problems. Comput. Geosci. 1988, 14, 357–368. [Google Scholar] [CrossRef]
- Perić, R.; Abdel-Maksoud, M. Reliable damping of free-surface waves in numerical simulations. Ship Technol. Res. 2016, 63, 1–13. [Google Scholar] [CrossRef]
- Leonard, B. The ULTIMATE conservative difference scheme applied to unsteady one-dimensional advection. Comput. Methods Appl. Mech. Eng. 1991, 88, 17–74. [Google Scholar] [CrossRef]
- Van Leer, B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Jasak, H. ERror Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows. Ph.D. Thesis, Department of Mechanical Engineering Imperial College of Science, Technology and Medicine, London, UK, 1996. [Google Scholar]
- Beji, S.; Battjes, J.A. Experimental investigation of wave propagation over a bar. Coast. Eng. 1993, 19, 151–162. [Google Scholar] [CrossRef]
- Ntouras, D.; Manolas, D.; Papadakis, G.; Riziotis, V. Exploiting the limit of BEM solvers in moonpool type floaters. Sci. Mak. Torque Wind 2020. to be published. [Google Scholar]
- Tan, L.; Lu, L.; Tang, G.Q.; Cheng, L.; Chen, X.B. A viscous damping model for piston mode resonance. J. Fluid Mech. 2019, 510–533. [Google Scholar] [CrossRef]
- Zhao, Y.; Tai, J.; Ahmed, F. Simulation of micro flows with moving boundaries using high-order upwind FV method on unstructured grids. Comput. Mech. 2001, 28, 66–75. [Google Scholar] [CrossRef]
- Fredriksen, A.G. A Numerical and Experimental Study of a Two-Dimensional Body with Moonpool in Waves and Current. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2015. [Google Scholar]
- Roe, P.L. Approximate Riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 1981, 43, 357–372. [Google Scholar] [CrossRef]

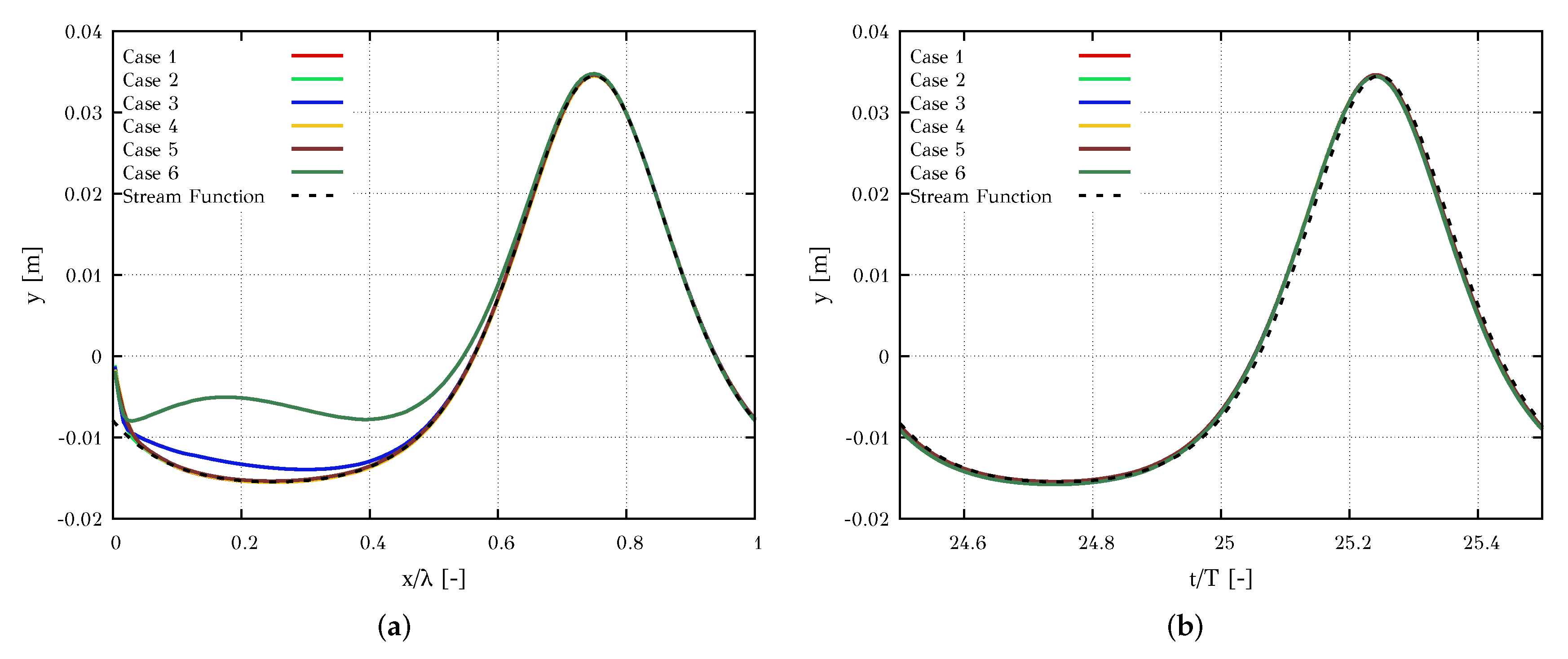
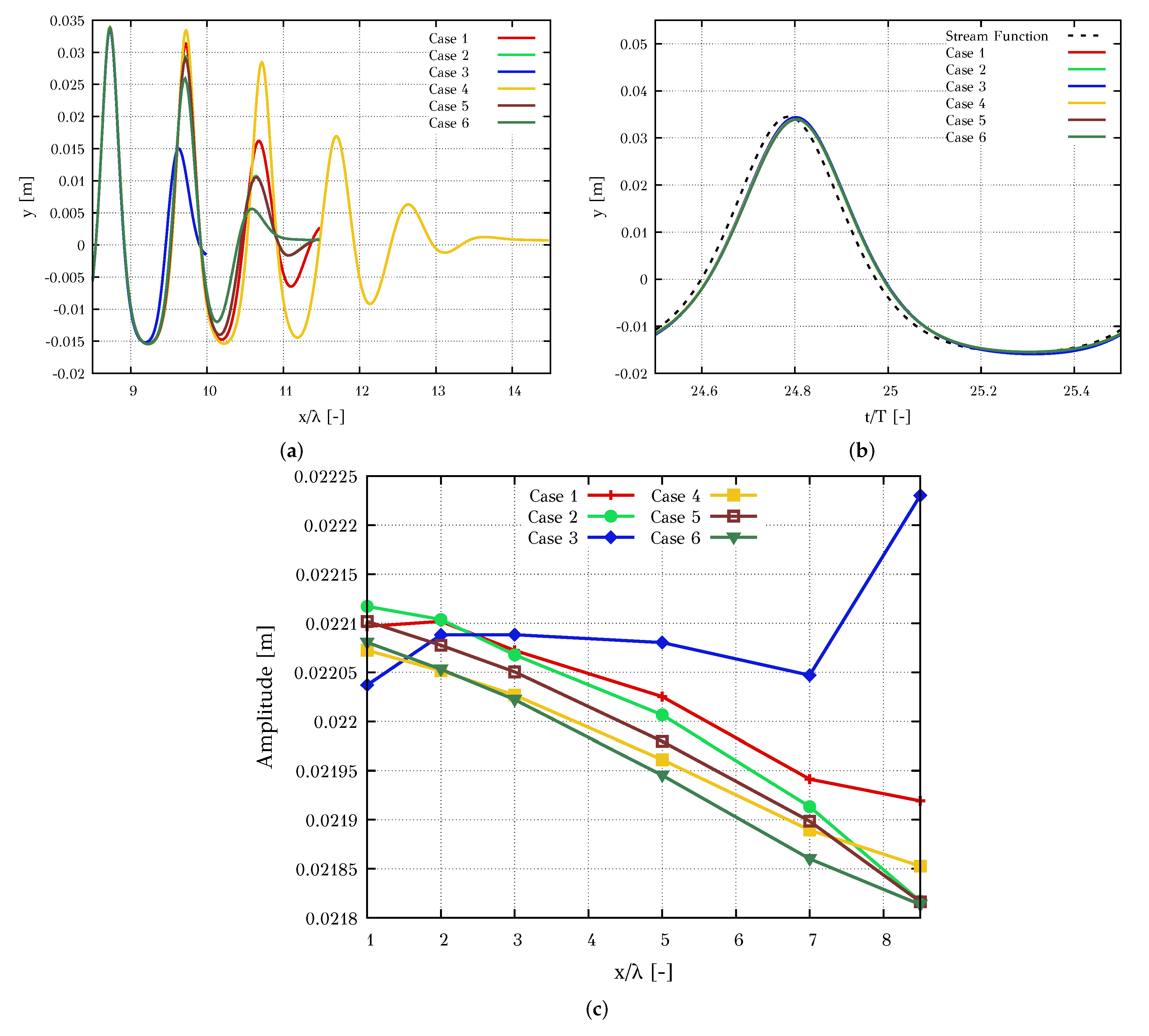



| # Case | Forcing | Exponent n |
|---|---|---|
| 1 | 60 | 3.5 |
| 2 | 120 | 3.5 |
| 3 | 300 | 3.5 |
| 4 | 60 | 2 |
| 5 | 60 | 5 |
| 6 | 600 | 2 |
| # Case | Harmonics | |||
|---|---|---|---|---|
| 1st | 2nd | 3rd | 4th | |
| 1 | 0.40 | 0.45 | 0.88 | 0.87 |
| 2 | 0.40 | 0.42 | 0.77 | 0.91 |
| 3 | 0.37 | 0.39 | 0.63 | 1.08 |
| 4 | 0.44 | 0.38 | 0.69 | 1.29 |
| 5 | 0.40 | 0.49 | 1.10 | 0.87 |
| 6 | 0.42 | 0.37 | 0.31 | 1.72 |
| # Case | Harmonics | |||
|---|---|---|---|---|
| 1st | 2nd | 3rd | 4th | |
| 1 | 0.12 | 0.06 | 0.78 | 1.60 |
| 2 | 0.20 | 0.09 | 0.58 | 1.41 |
| 3 | 0.30 | 0.27 | 0.33 | 1.15 |
| 4 | 0.31 | 0.33 | 0.21 | 1.04 |
| 5 | 0.03 | 0.32 | 1.11 | 1.90 |
| 6 | 0.42 | 0.71 | 0.32 | 0.35 |
| # Case | Forcing | Exponent n | Length [L] |
|---|---|---|---|
| 1 | 60 | 3.5 | 3 |
| 2 | 120 | 3.5 | 3 |
| 3 | 120 | 3.5 | 1.5 |
| 4 | 120 | 3.5 | 6 |
| 5 | 120 | 3.5 | 3 * |
| 6 | 250 | 3.5 | 3 * |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ntouras, D.; Papadakis, G. A Coupled Artificial Compressibility Method for Free Surface Flows. J. Mar. Sci. Eng. 2020, 8, 590. https://doi.org/10.3390/jmse8080590
Ntouras D, Papadakis G. A Coupled Artificial Compressibility Method for Free Surface Flows. Journal of Marine Science and Engineering. 2020; 8(8):590. https://doi.org/10.3390/jmse8080590
Chicago/Turabian StyleNtouras, Dimitris, and George Papadakis. 2020. "A Coupled Artificial Compressibility Method for Free Surface Flows" Journal of Marine Science and Engineering 8, no. 8: 590. https://doi.org/10.3390/jmse8080590
APA StyleNtouras, D., & Papadakis, G. (2020). A Coupled Artificial Compressibility Method for Free Surface Flows. Journal of Marine Science and Engineering, 8(8), 590. https://doi.org/10.3390/jmse8080590






