A Hybrid Wind Load Estimation Method for Container Ship Based on Computational Fluid Dynamics and Neural Networks
Abstract
1. Introduction
2. Wind Load Estimation with Neural Networks Hybrid Method
2.1. Theoretical Background
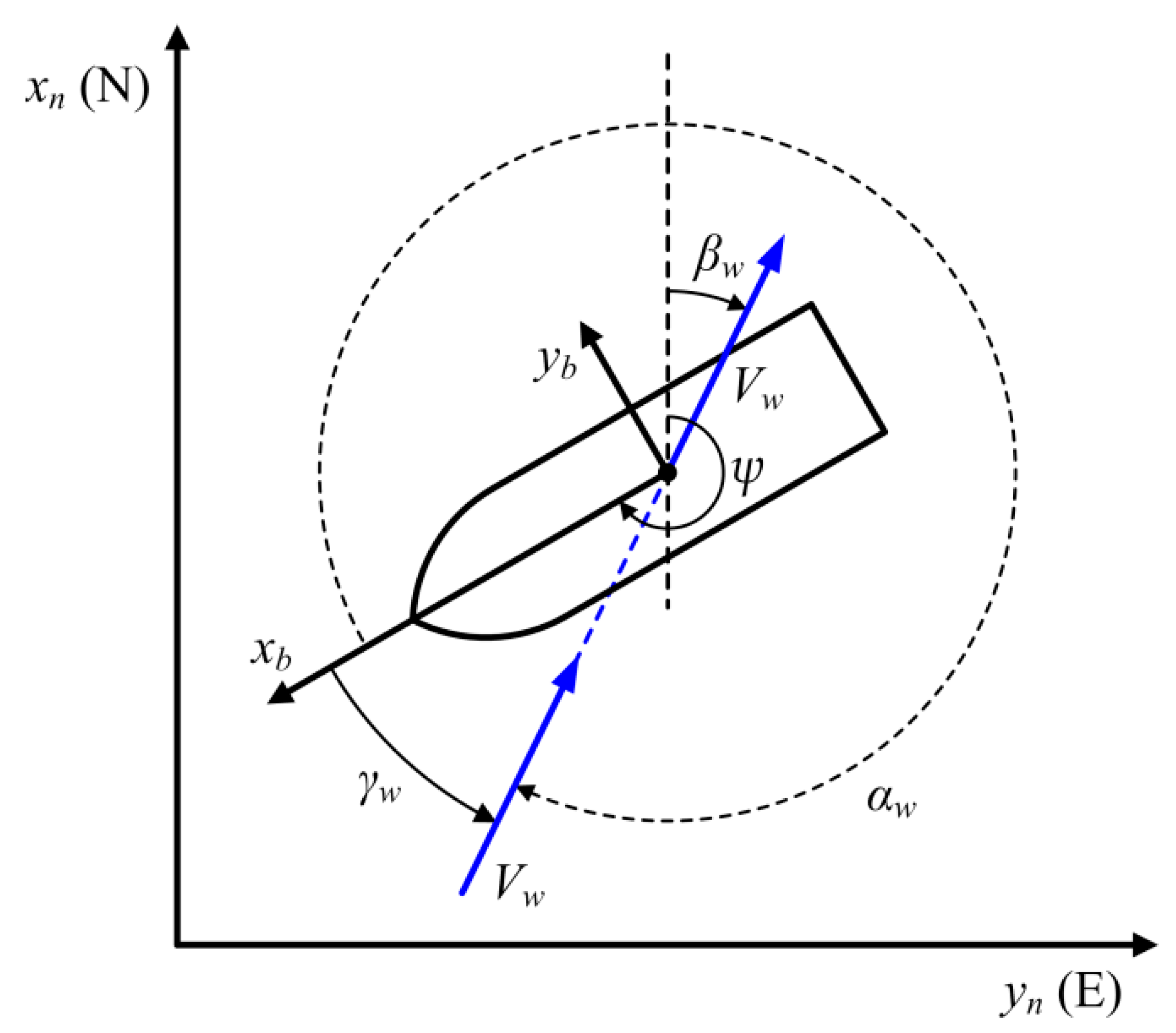
2.2. Notation and Reference Frames
2.3. Wind Loads on a Ship at Zero Forward Speed
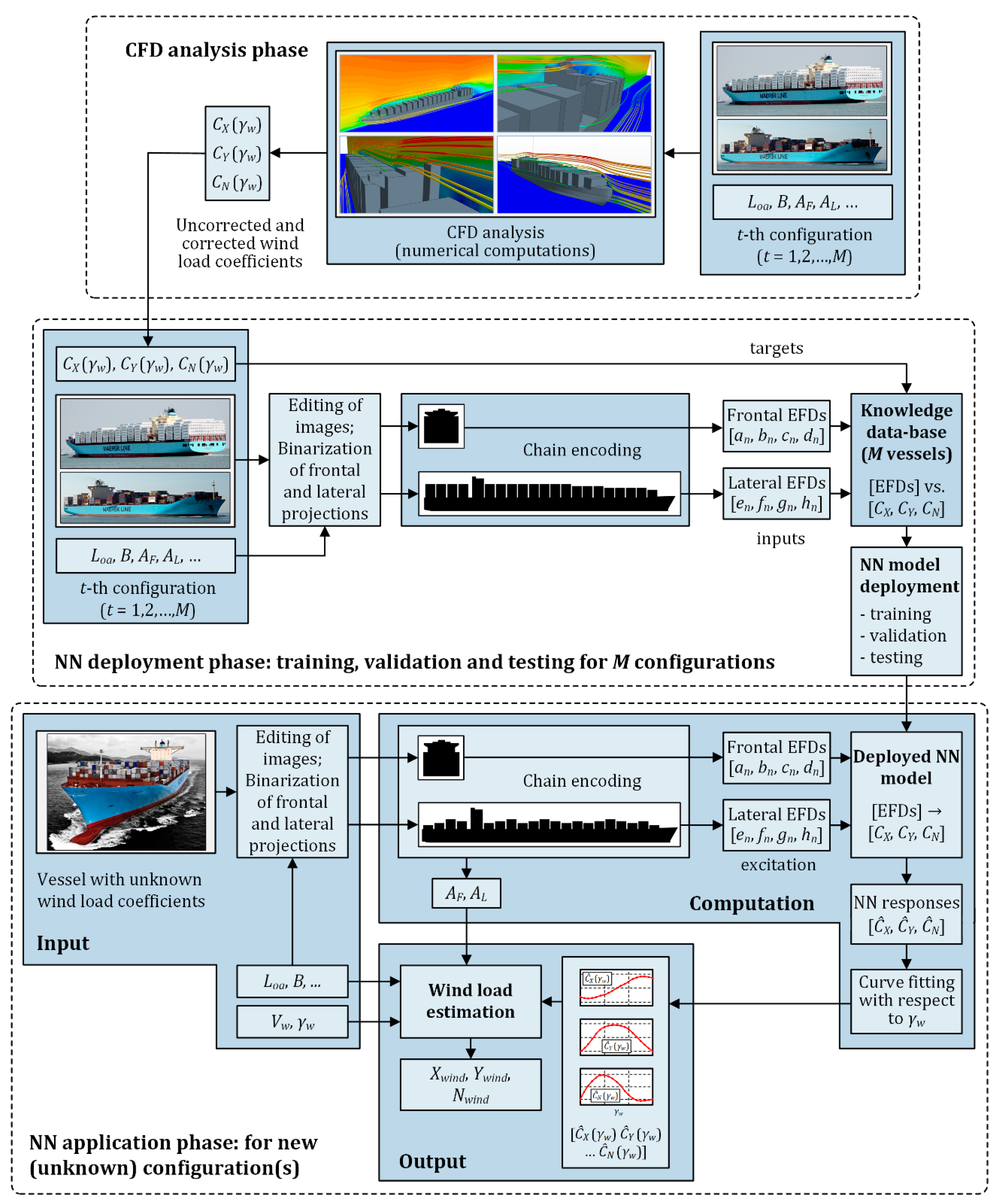
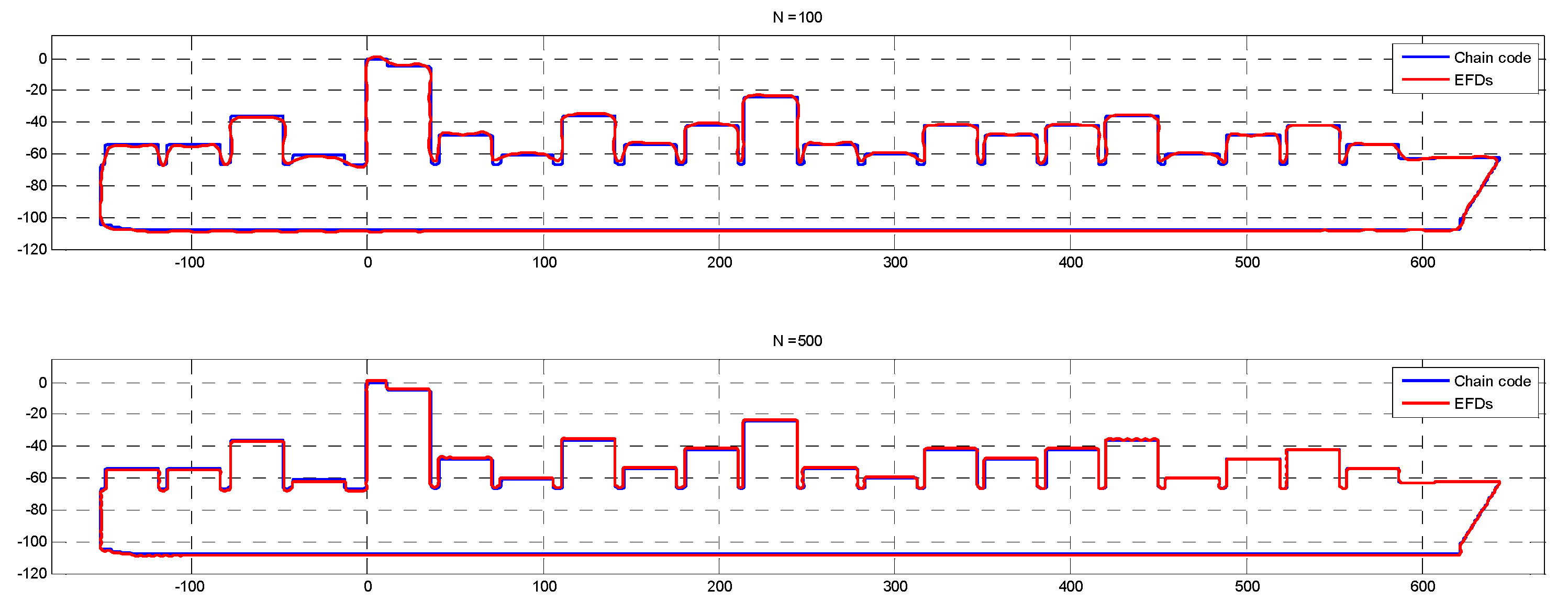
2.4. Methodological Framework for Wind Loads Estimation Based on CFD, EFDs and GRNN
- (i)
- Estimation of wind load coefficients by CFD simulations;
- (ii)
- Deployment of the model based on CFD results, EFDs and GRNN;
- (iii)
- Cross-validation of GRNN responses, GRNN testing and further application of developed neural network model.
3. Wind Loads Estimation Using CFD
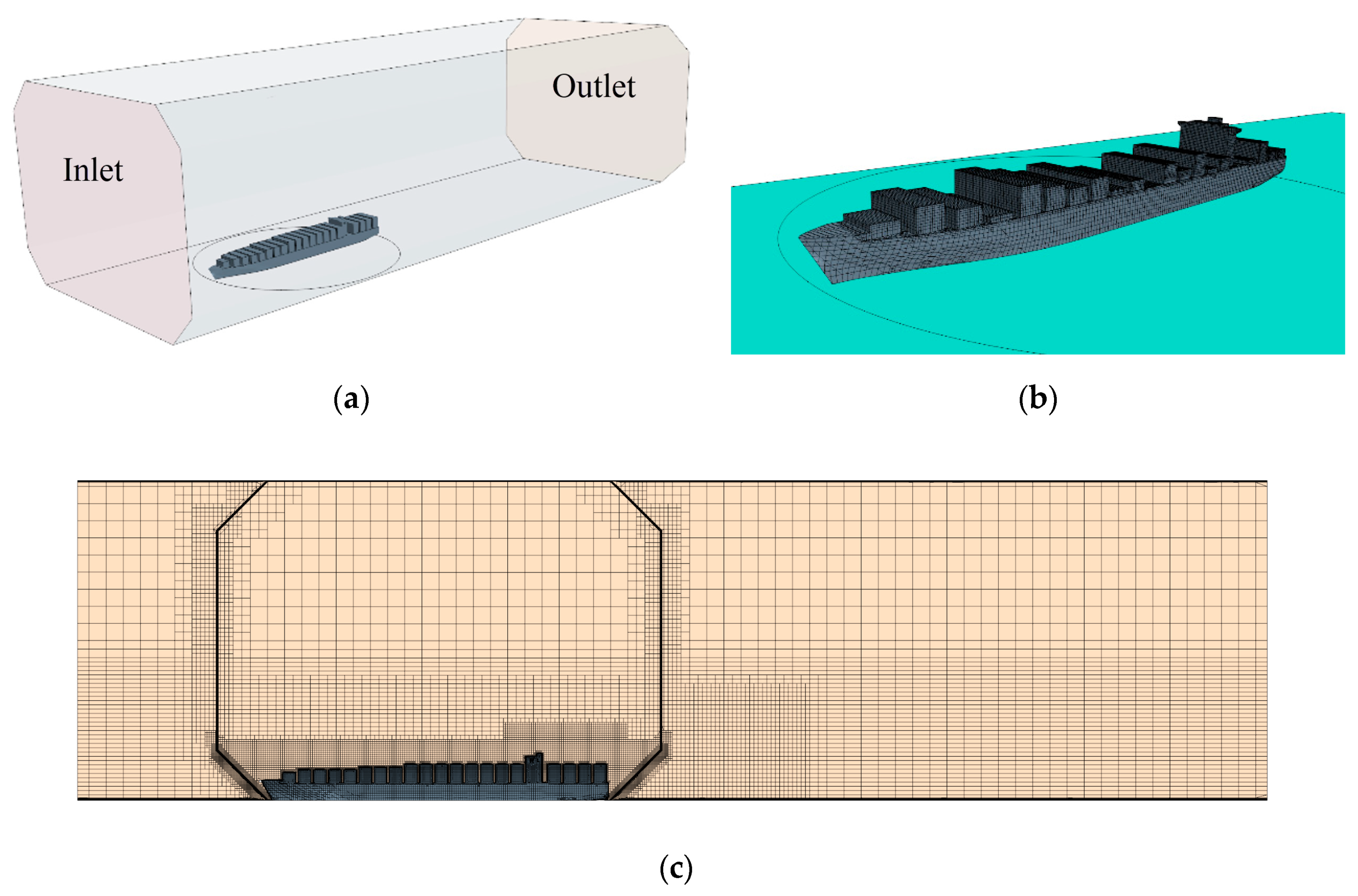
3.1. Computational Geometry and Grid
3.2. Boundary Conditions
3.3. Computational Settings
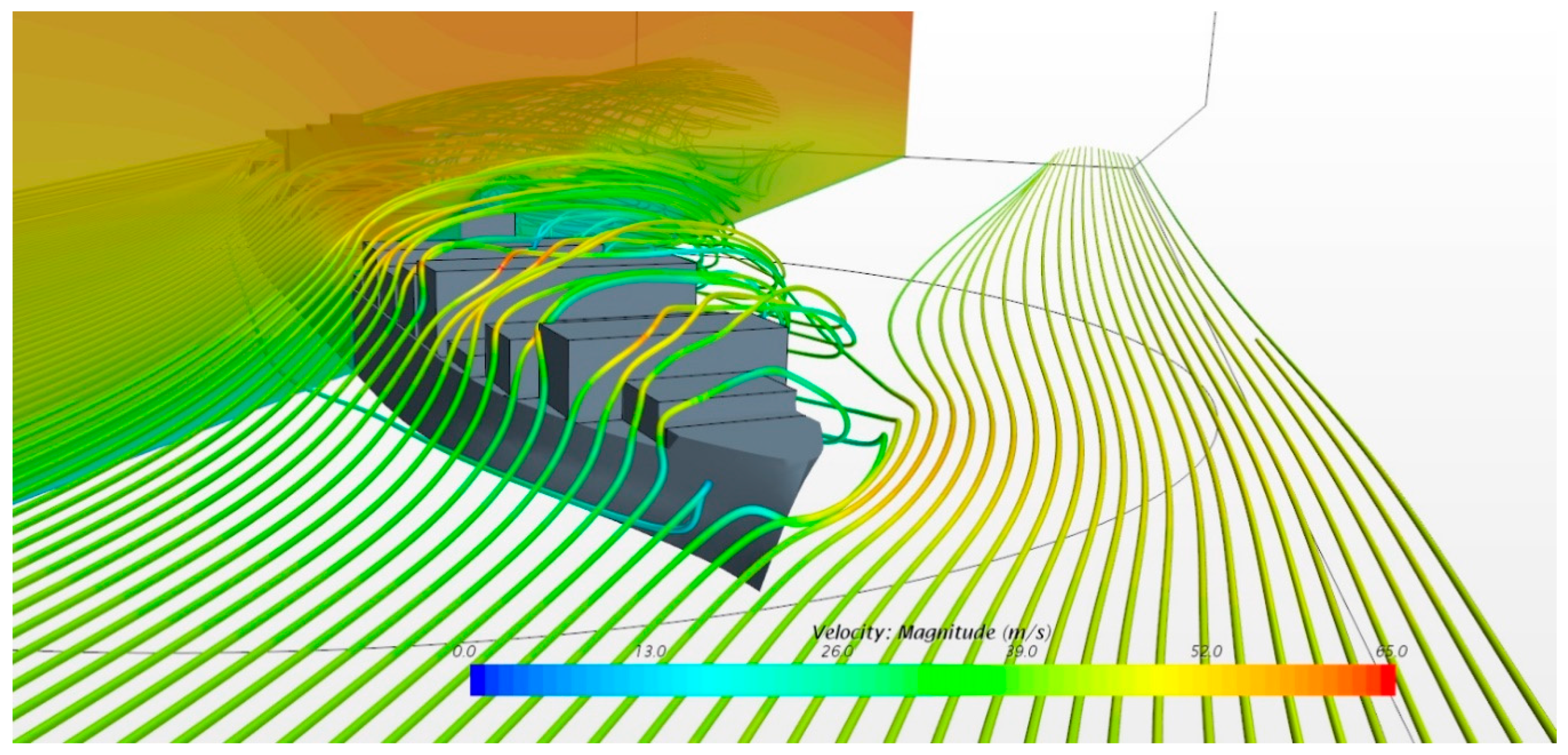
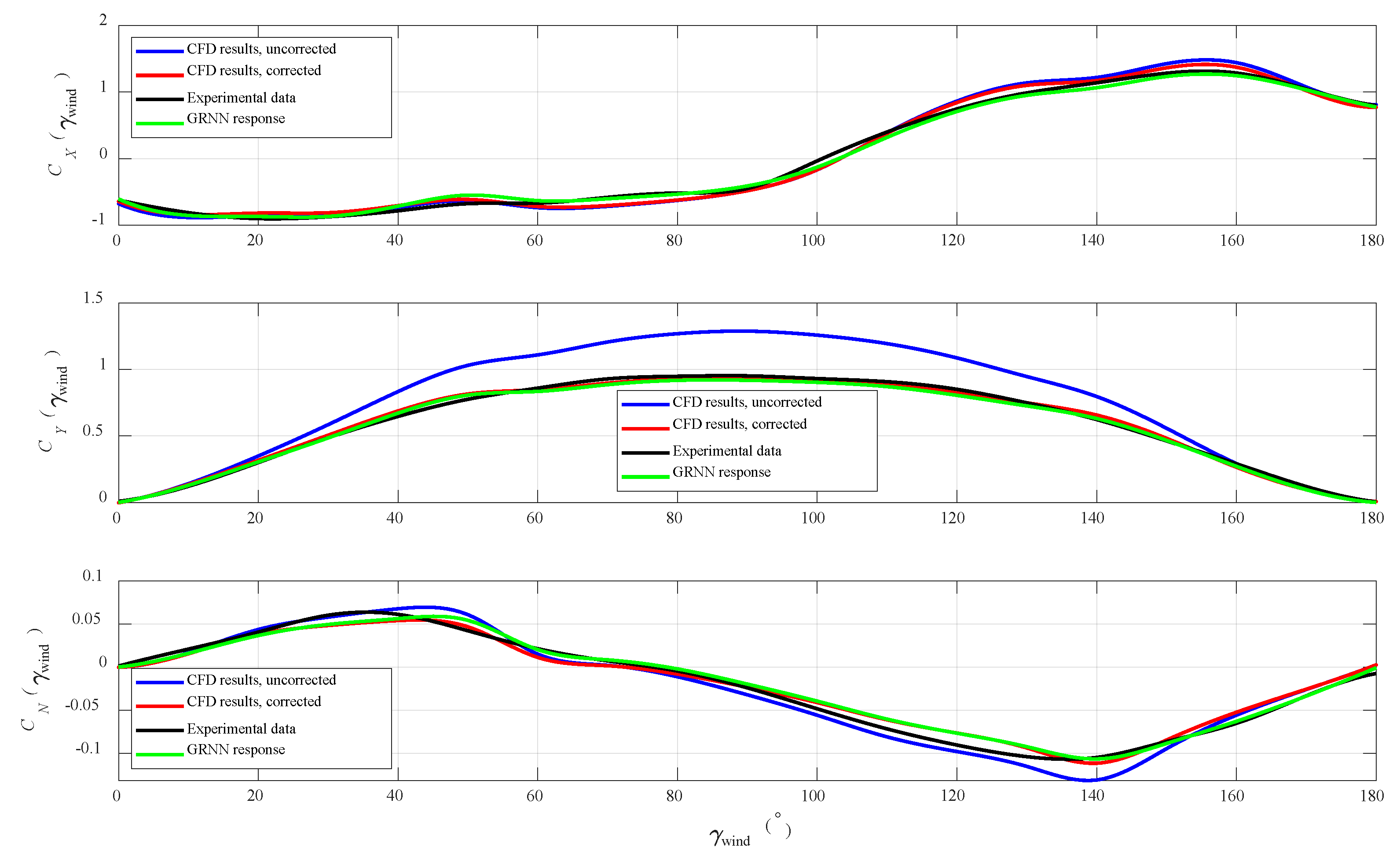
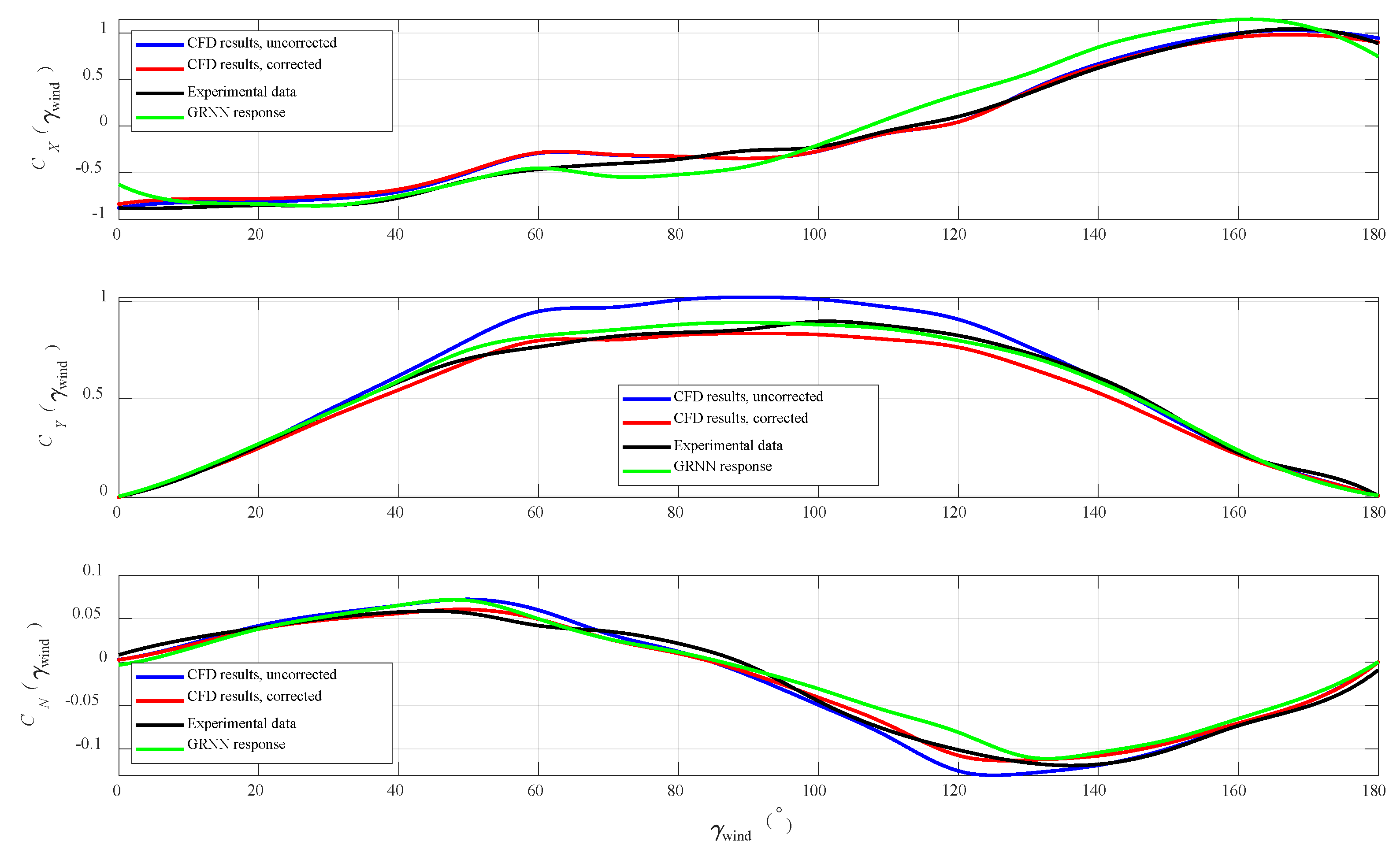
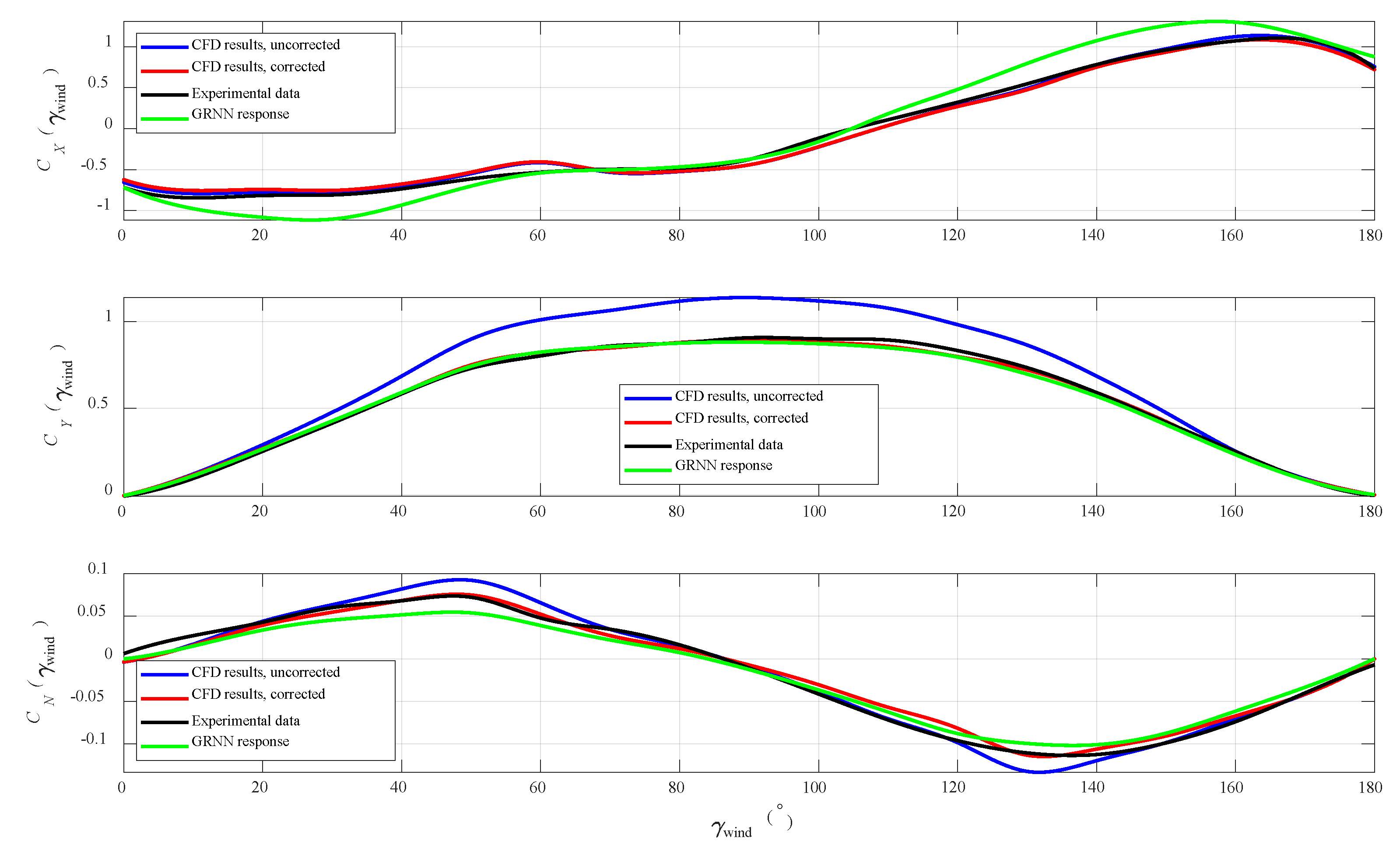
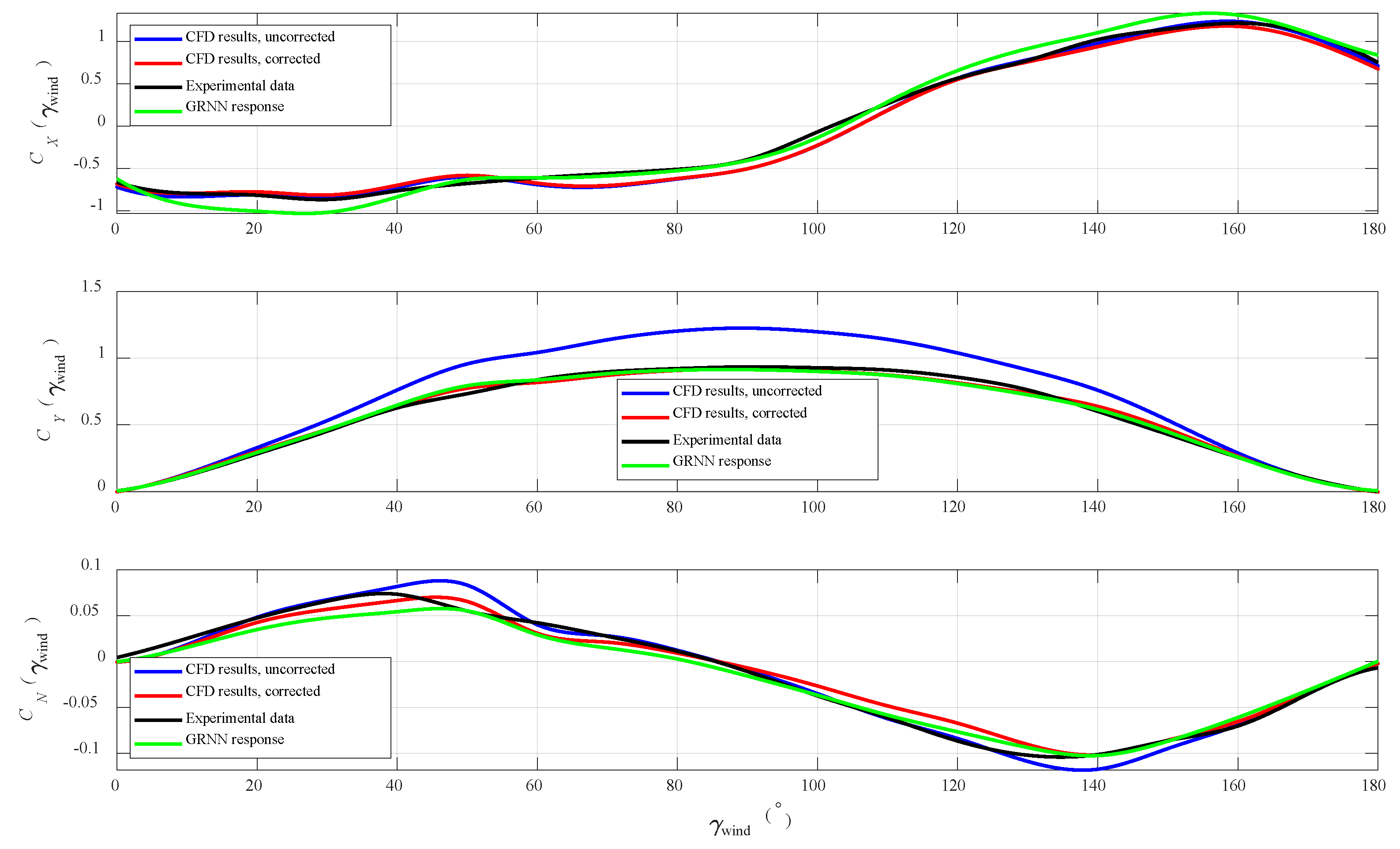
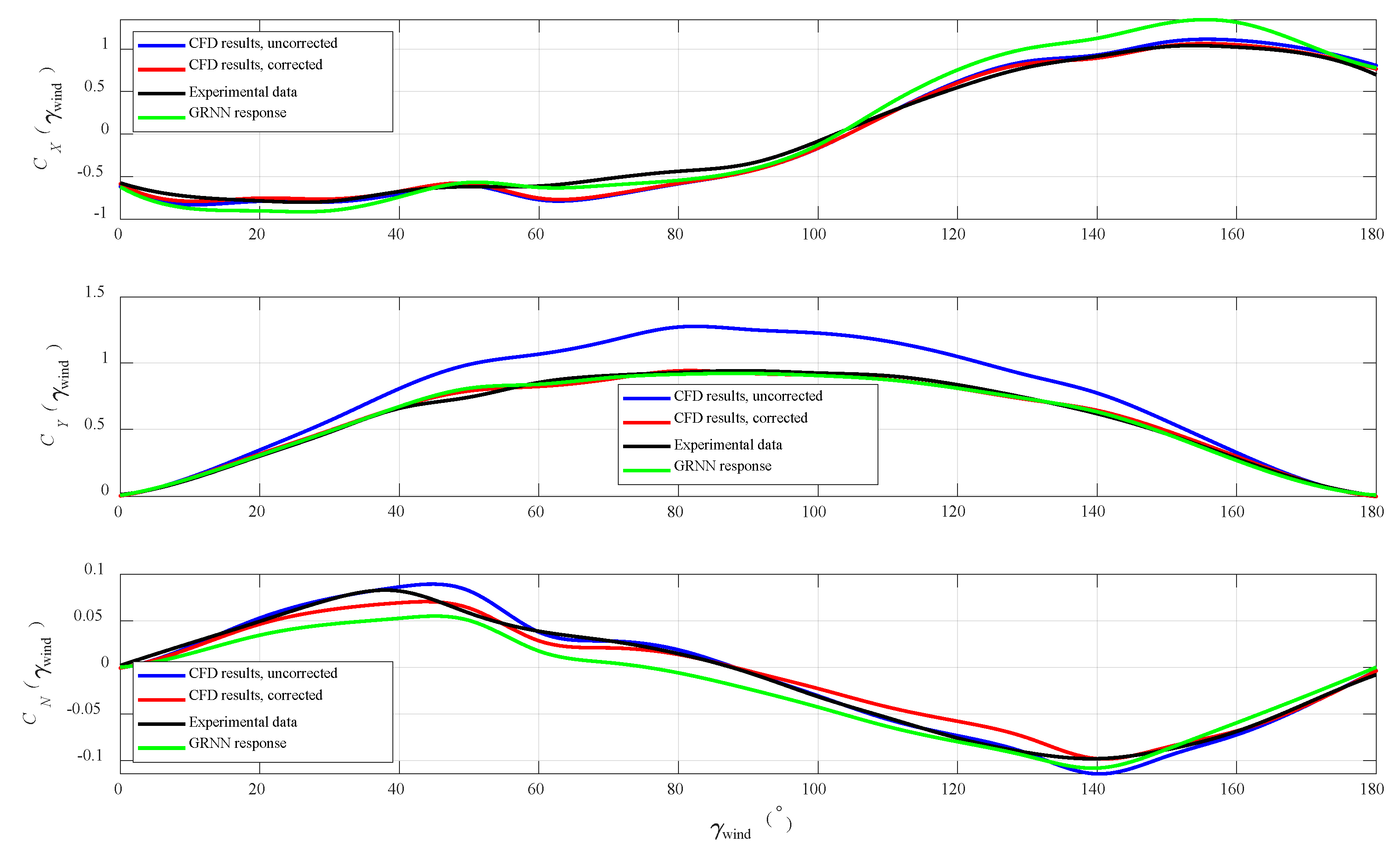
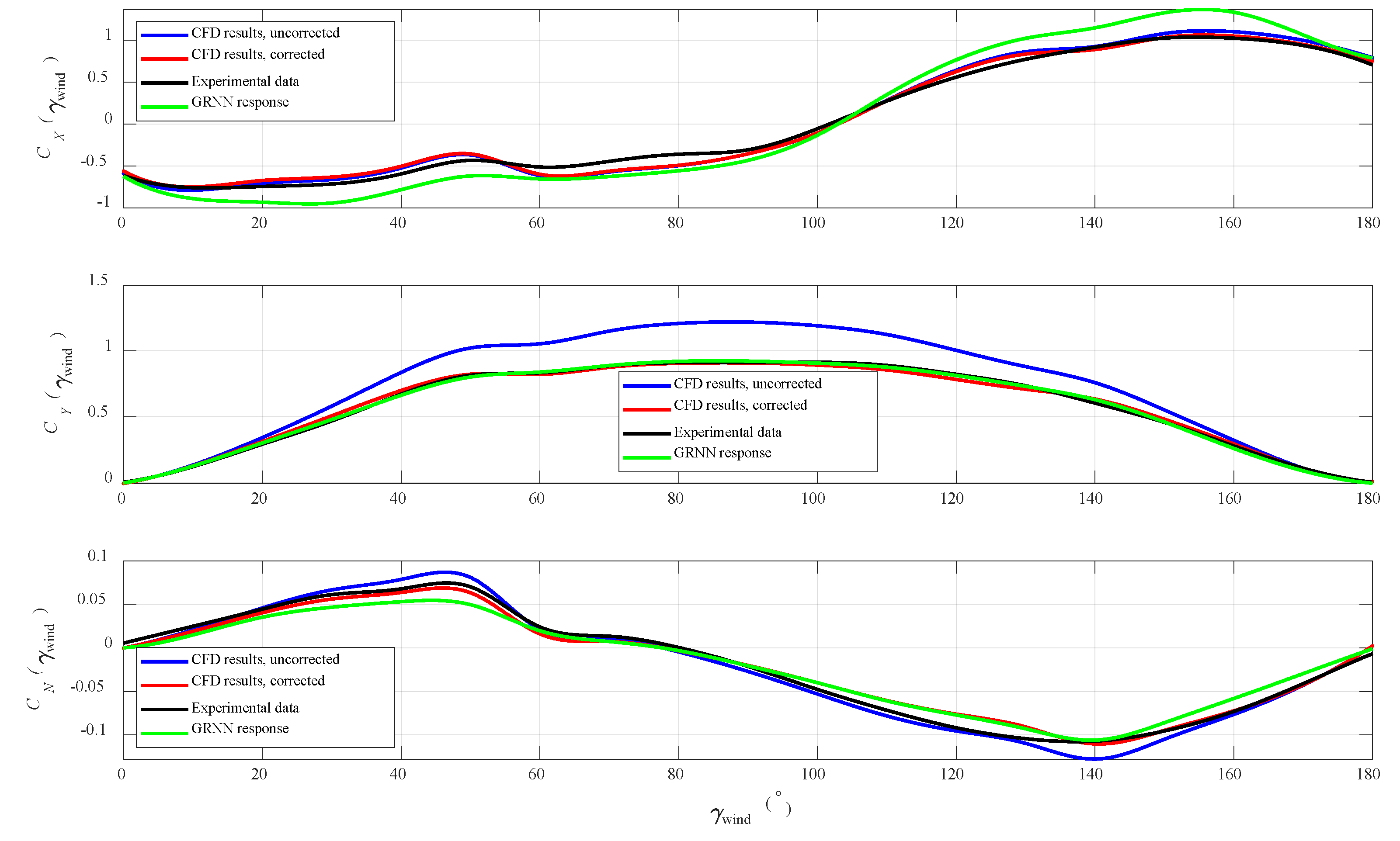
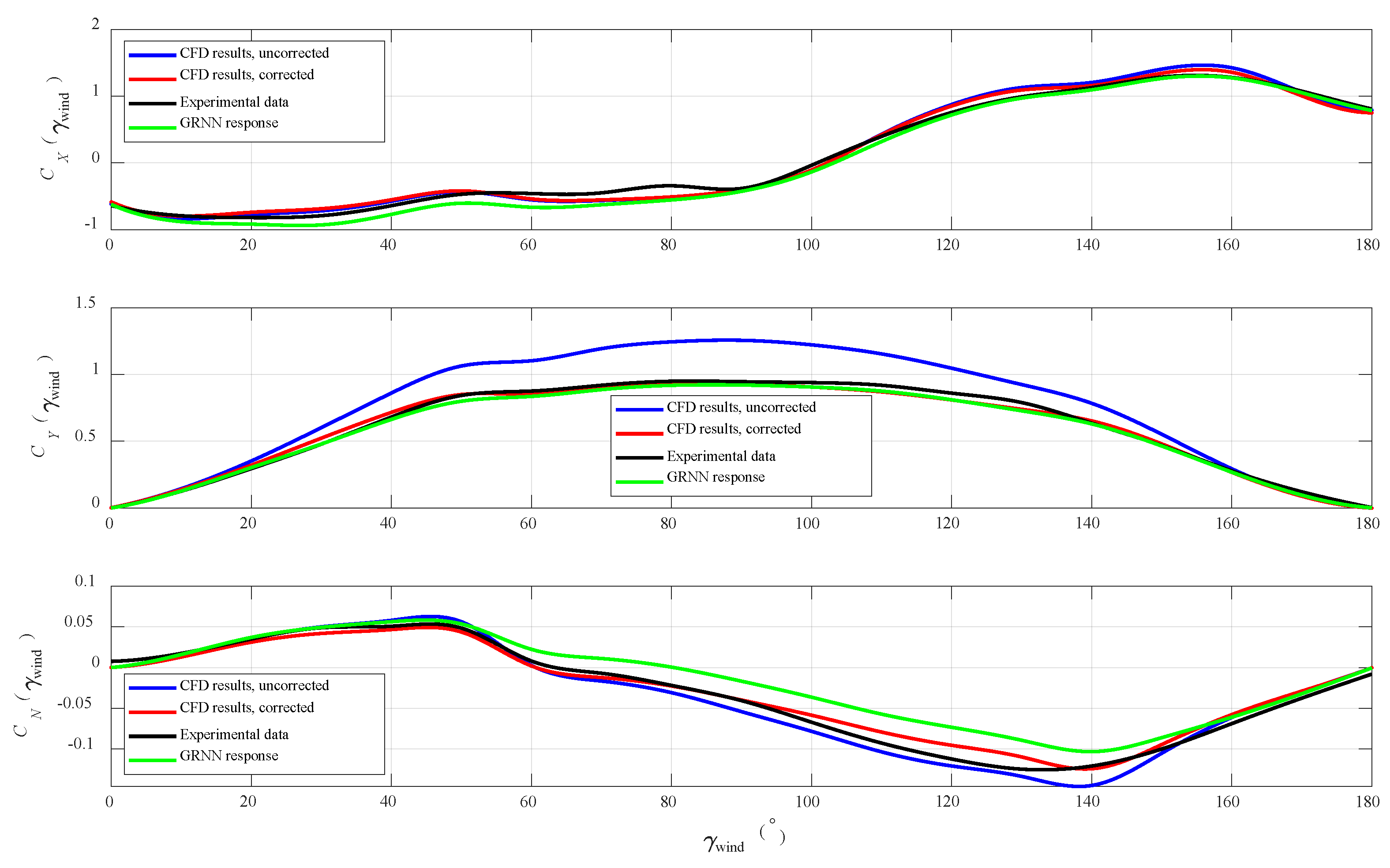
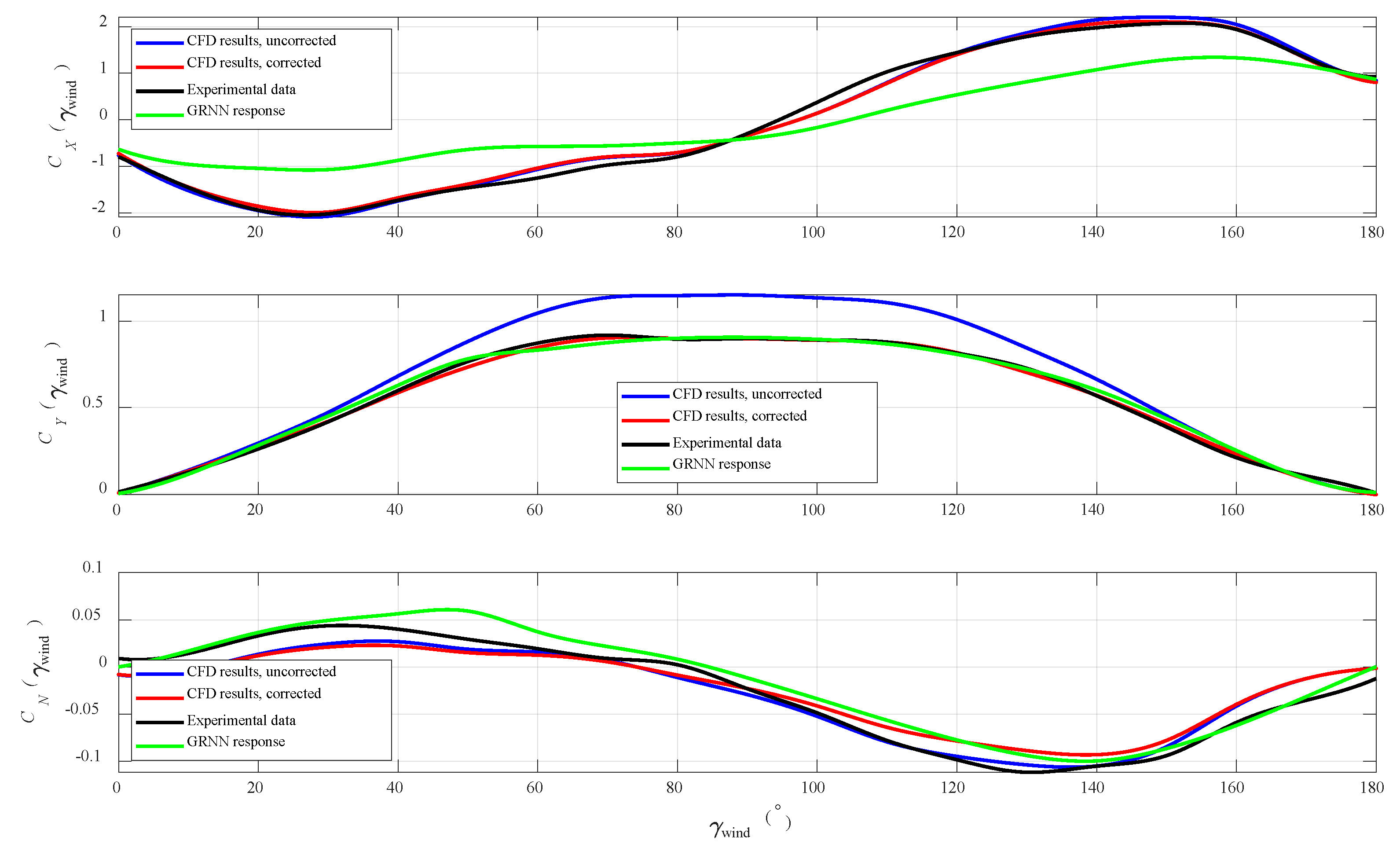
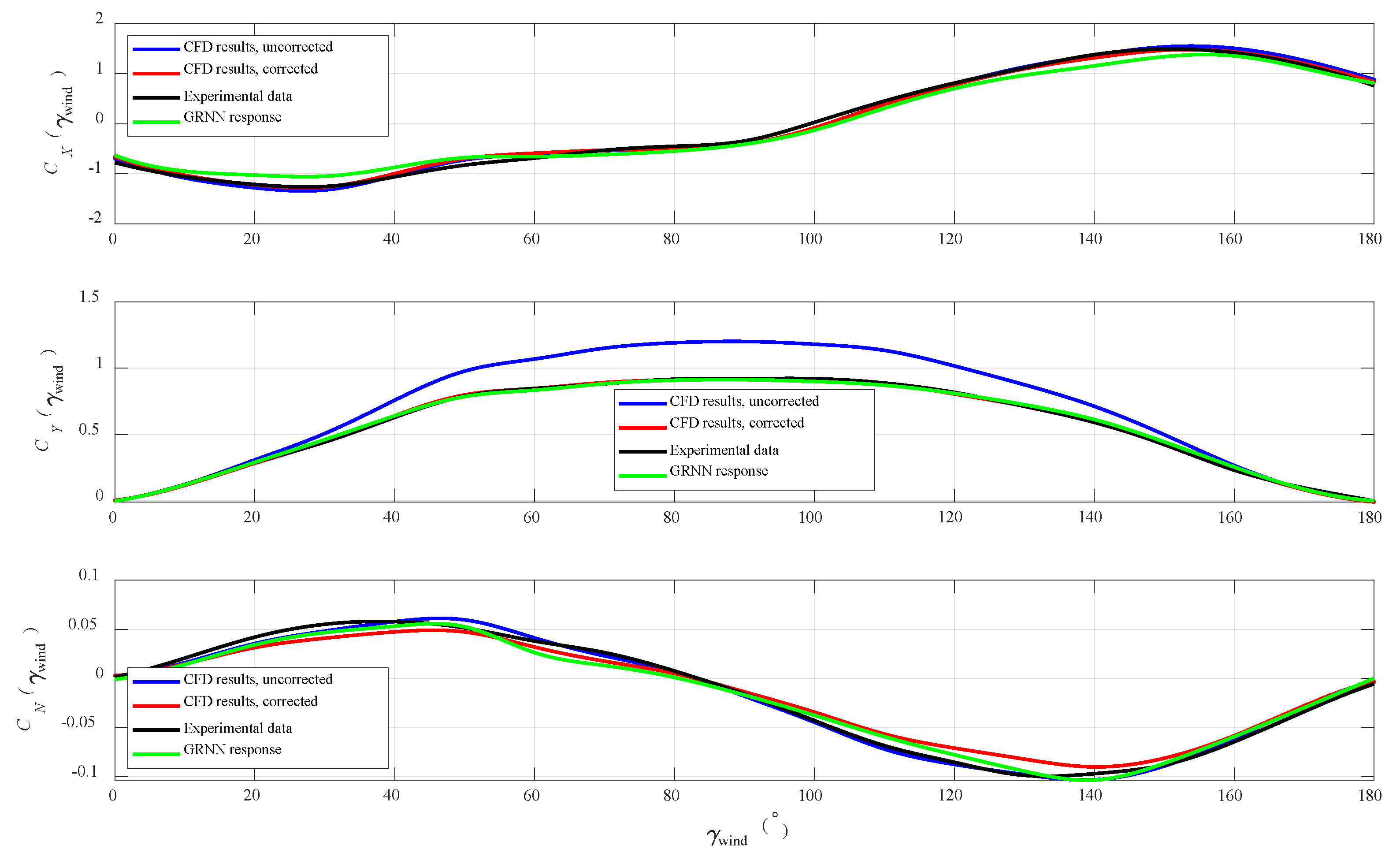
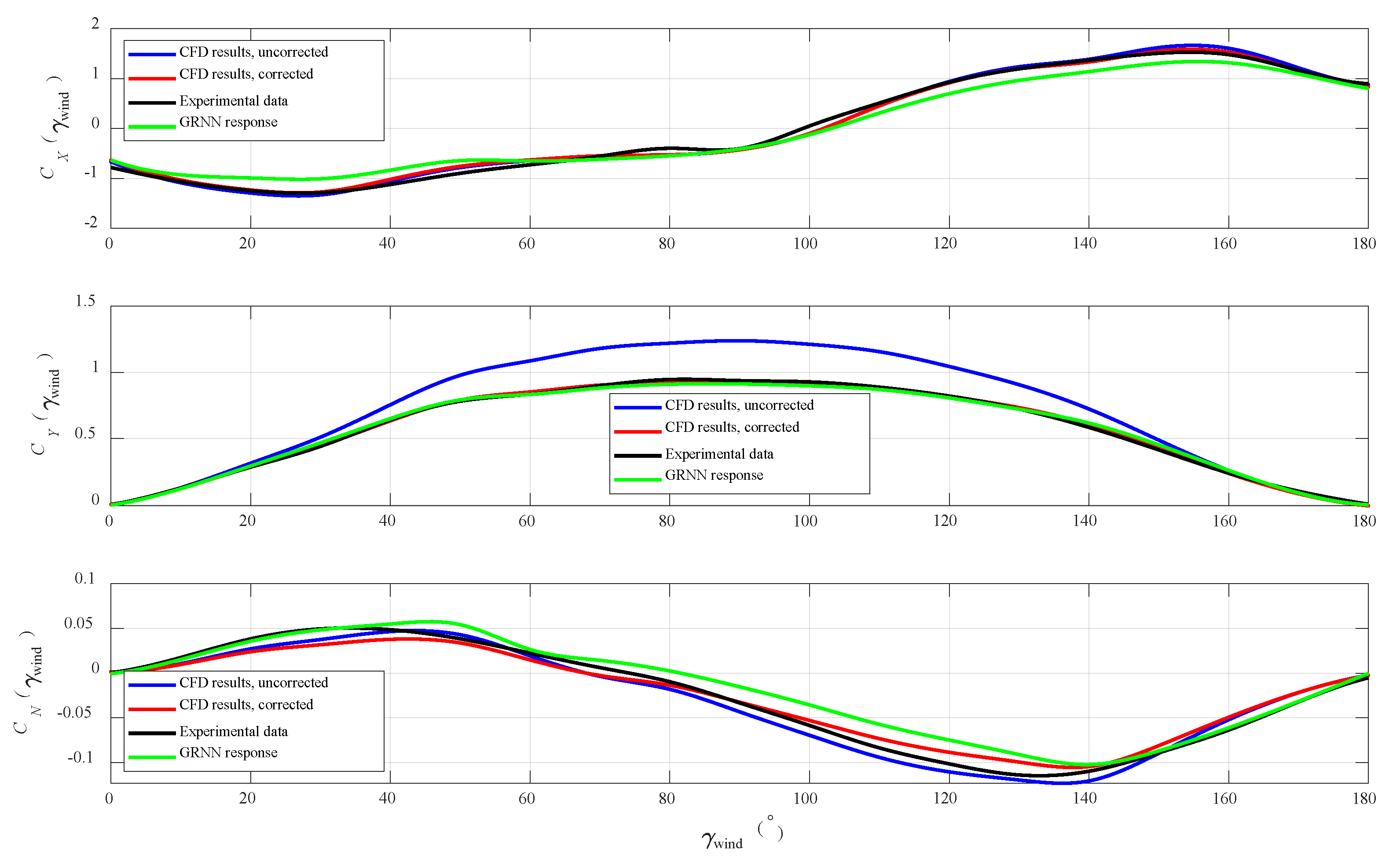
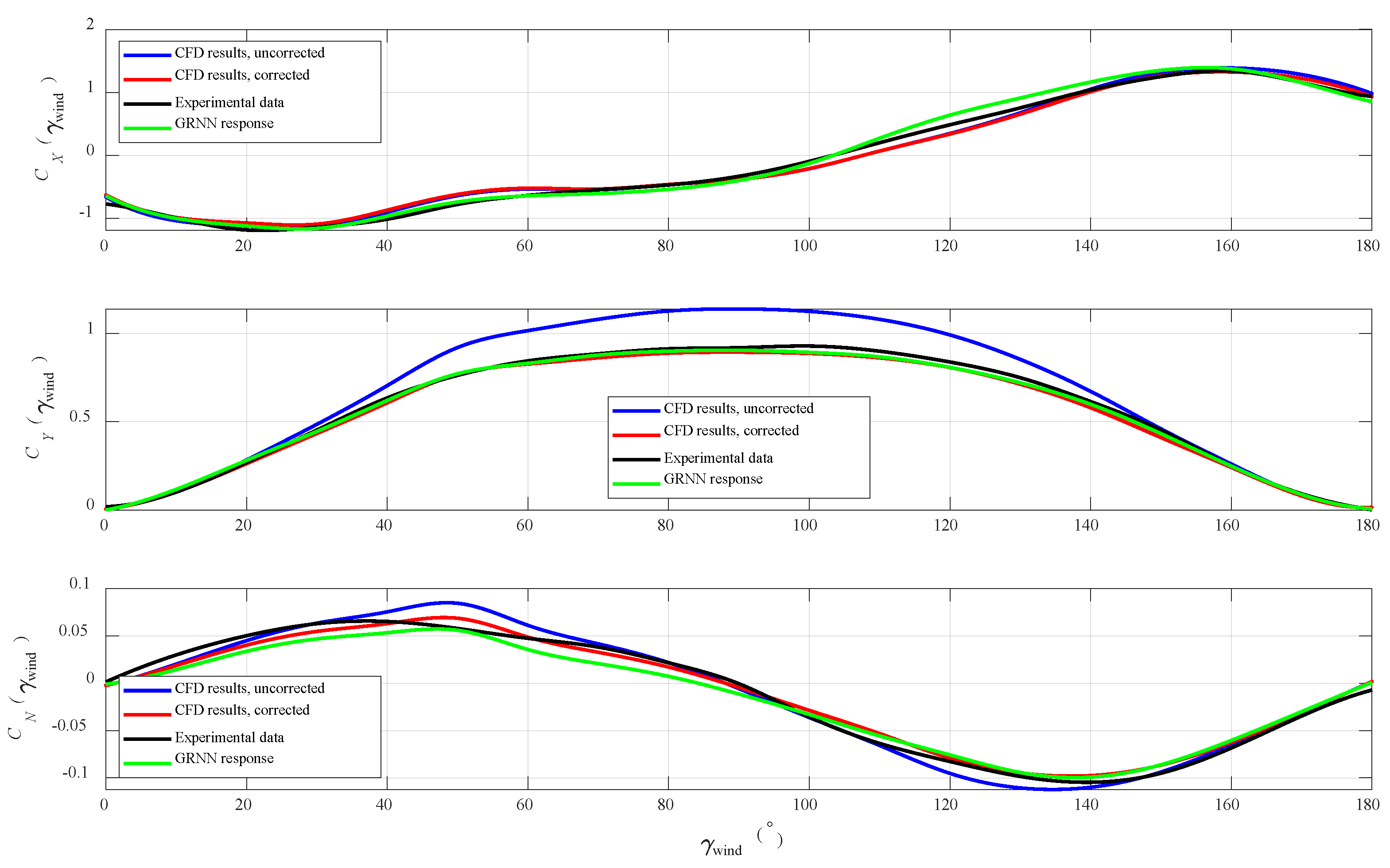
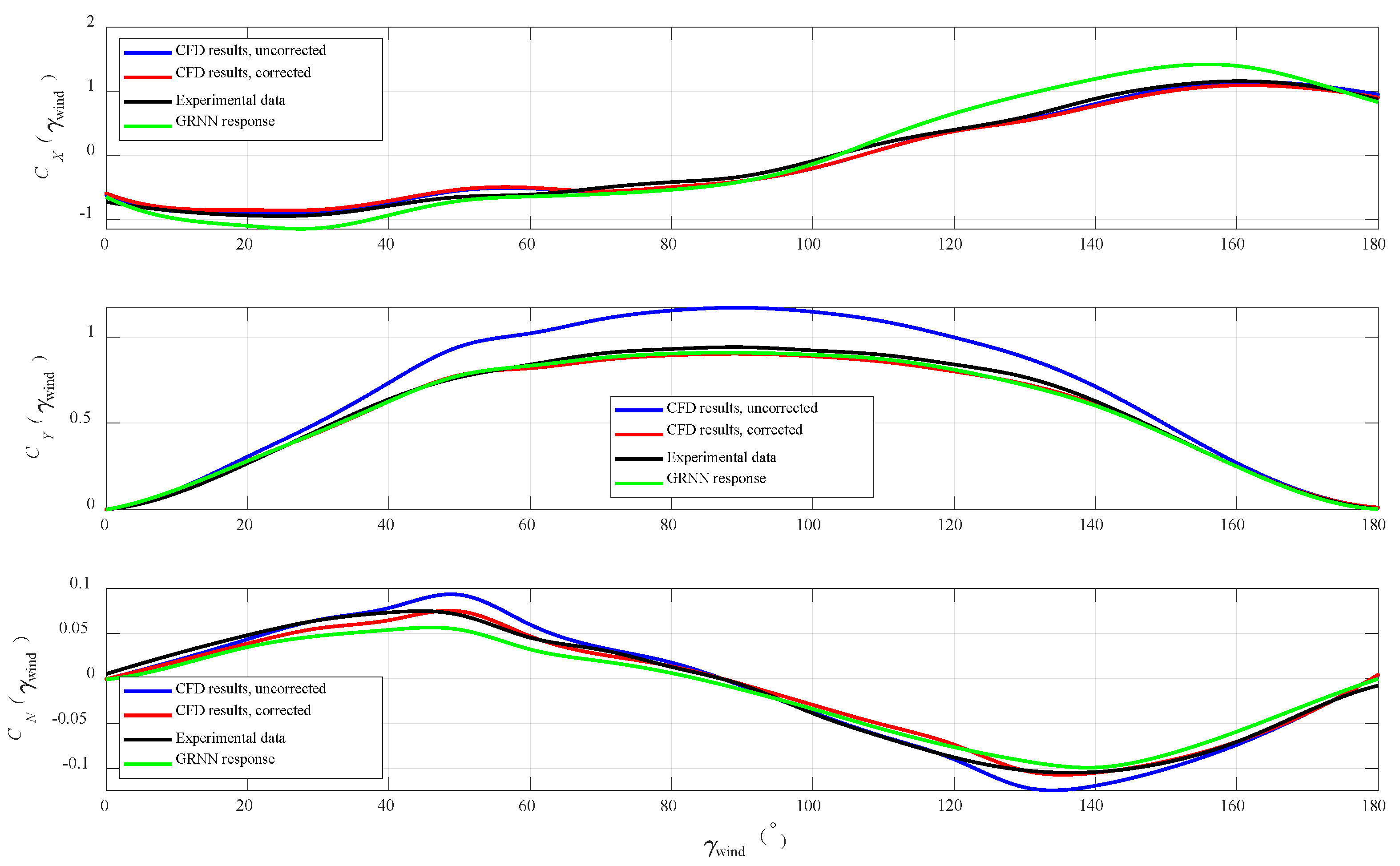
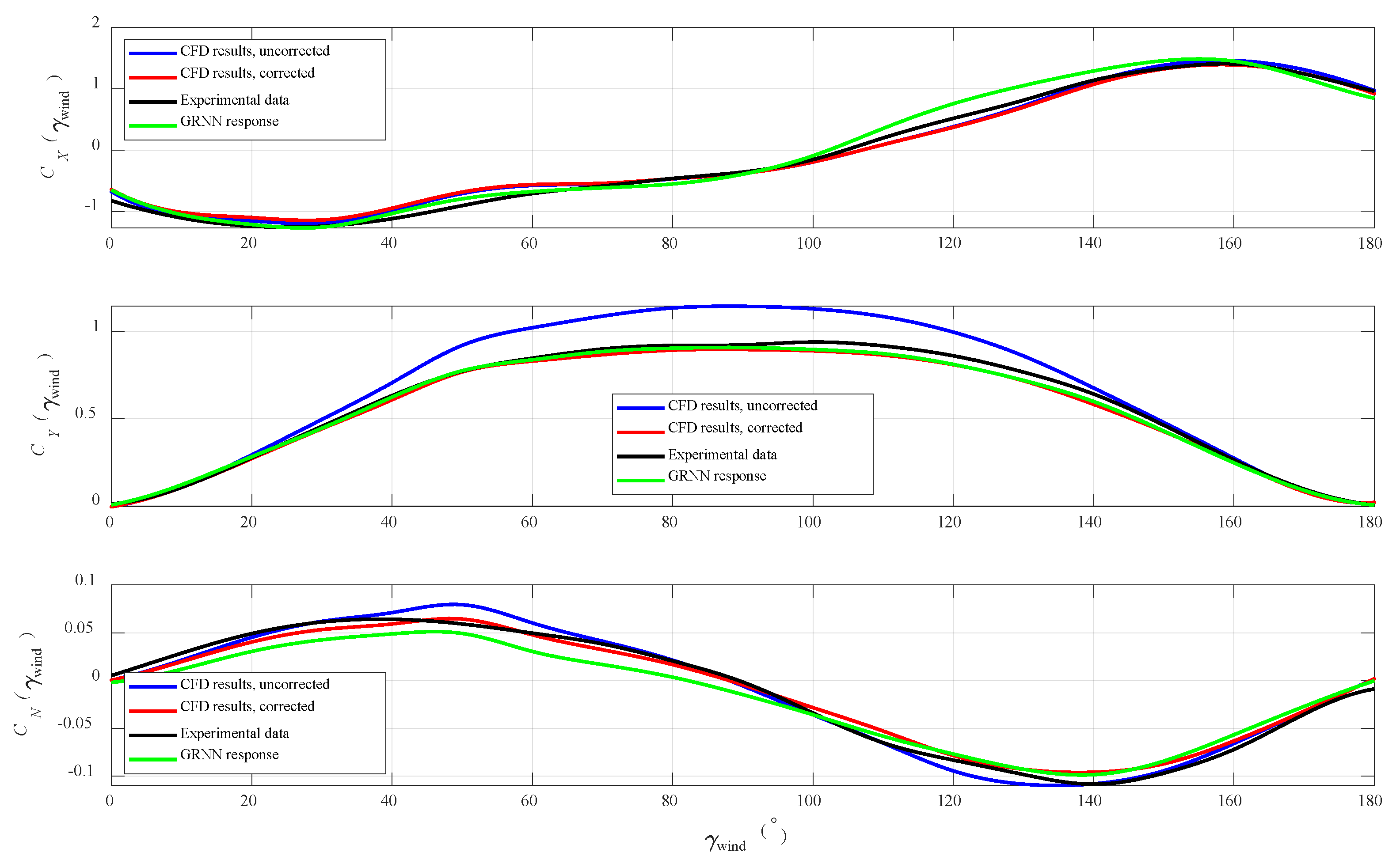
4. Numerical Results
5. Discussion
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CAD | Computer-Aided Design |
| CFD | Computational Fluid Dynamics |
| EFD | Elliptic Fourier Descriptors |
| GRNN | Generalized Regression Neural Network |
| LNG | Liquefied Natural Gas |
| NED | North-East-Down |
| NN | Neural Network |
| RANS | Reynolds-averaged Navier–Stokes |
References
- Isherwood, R.M. Wind resistance of merchant ships. R. Inst. Nav. Archit. 1972, 114, 327–338. [Google Scholar]
- Gould, R.W.F. The Estimation of Wind Loads on Ship Superstructures; Monograph, No. 8; The Royal Institution of Naval Architects: London, UK, 1982; p. 34. [Google Scholar]
- Blendermann, W. Schiffsform und Windlast-Korrelations-und Regressionanalyse von Windkanalmes-Sungen am Modell; Report No. 533; Institut fur Schiffbau der Universitat Hamburg: Hamburg, Germany, 1993; 132p. [Google Scholar]
- Blendermann, W. Parameter identification of wind loads on ships. J. Wind Eng. Ind. Aerodyn. 1994, 51, 339–351. [Google Scholar] [CrossRef]
- Blendermann, W. Estimation of wind loads on ships in wind with a strong gradient. In Proceedings of the 14th International Conference on Offshore Mechanics and Arctic Engineering (OMAE), New York, NY, USA, 18–22 June 1995; ASME: New York, NY, USA, 1995; Volume l-A, pp. 271–277. [Google Scholar]
- Blendermann, W. Floating docks: Prediction of wind loads in extreme winds. Schiff Hafen 1996, 48, 67–70. [Google Scholar]
- Haddara, M.R.; Guedes Soares, C. Wind loads on marine structures. Mar. Struct. 1999, 12, 199–209. [Google Scholar] [CrossRef]
- Brizzolara, S.; Rizzuto, E. Wind heeling moments on very large ships. Some insights through CFD results. In Proceedings of the 9th International Conference on Stability of Ships and Ocean Vehicles, Rio de Janeiro, Brazil, 25–29 September 2006; pp. 781–793. [Google Scholar]
- Wnek, A.D.; Guedes Soares, C. CFD assessment of the wind loads on an LNG carrier and floating platform models. Ocean. Eng. 2015, 97, 30–36. [Google Scholar] [CrossRef]
- Janssen, W.D.; Blocken, B.; van Wijhe, H.J. CFD simulations of wind loads on a container ship: Validation and impact of geometrical simplifications. J. Wind. Eng. Ind. Aerodyn. 2017, 166, 106–116. [Google Scholar] [CrossRef]
- Andersen, I.M.V. Wind loads on post-panamax containership. Ocean Eng. 2013, 58, 115–134. [Google Scholar] [CrossRef]
- Valčić, M.; Prpić-Oršić, J. Hybrid method for estimating wind loads on ships based on elliptic Fourier analysis and radial basis neural networks. Ocean Eng. 2016, 122, 227–240. [Google Scholar] [CrossRef]
- Prpić-Oršić, J.; Valčić, M.; Vučinić, D. Application of pattern recognition method for estimating wind loads on ships and marine objects. In Materialwissenschaft und Werkstofftechnik—Material Science and Engineering Technology; WILEY-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2017; Volume 48, pp. 387–400. [Google Scholar]
- Valčić, M.; Prpić-Oršić, J.; Vučinić, D. Application of pattern recognition method for estimating wind loads on ships and marine objects. In Visual Computing—Advancing Engineering Practice; Series Lecture Notes in Mechanical Engineering; Springer: Singapore, 2019; 38p. [Google Scholar]
- Prpić-Oršić, J.; Valčić, M. Sensitivity analysis of wind load estimation method based on elliptic Fourier descriptors. In Proceedings of the Maritime Technology and Engineering—MARTECH 2016, Lisabon, Portugal, 4–6 July 2016; pp. 151–160. [Google Scholar]
- Specht, D.F. A General Regression Neural Network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef] [PubMed]
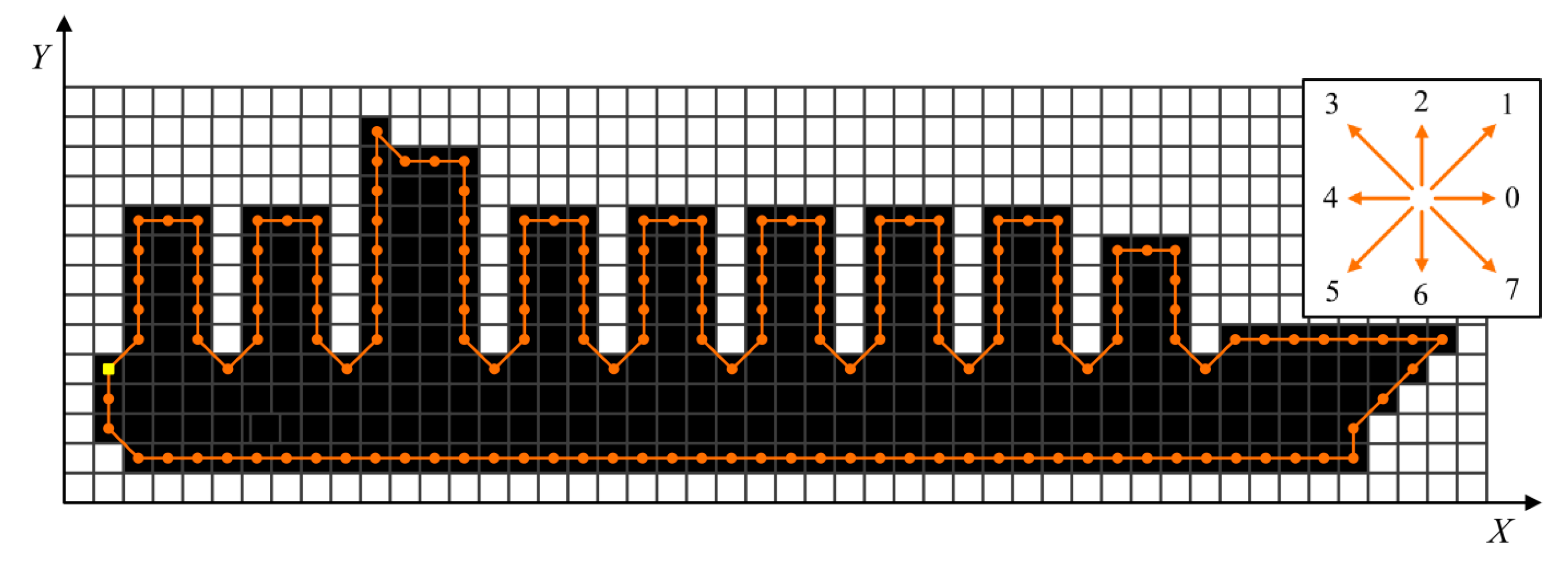
- Freeman, H. Computer Processing of Line-Drawing Images. Comput. Surv. 1974, 6, 57–97. [Google Scholar] [CrossRef]
- Granlund, G.H. Fourier Preprocessing for Hand Print Character Recognition. IEEE Trans. Comput. 1972, 21, 195–201. [Google Scholar] [CrossRef]
- Pavlidis, T. Algorithms for Graphics and Image Processing; Springer: Berlin/Heidelberg, Germany, 1982. [Google Scholar]
- Nixon, M.S.; Aguado, A.S. Feature Extraction and Image Processing, 2nd ed.; Academic Press (Elsevier): London, UK, 2008. [Google Scholar]
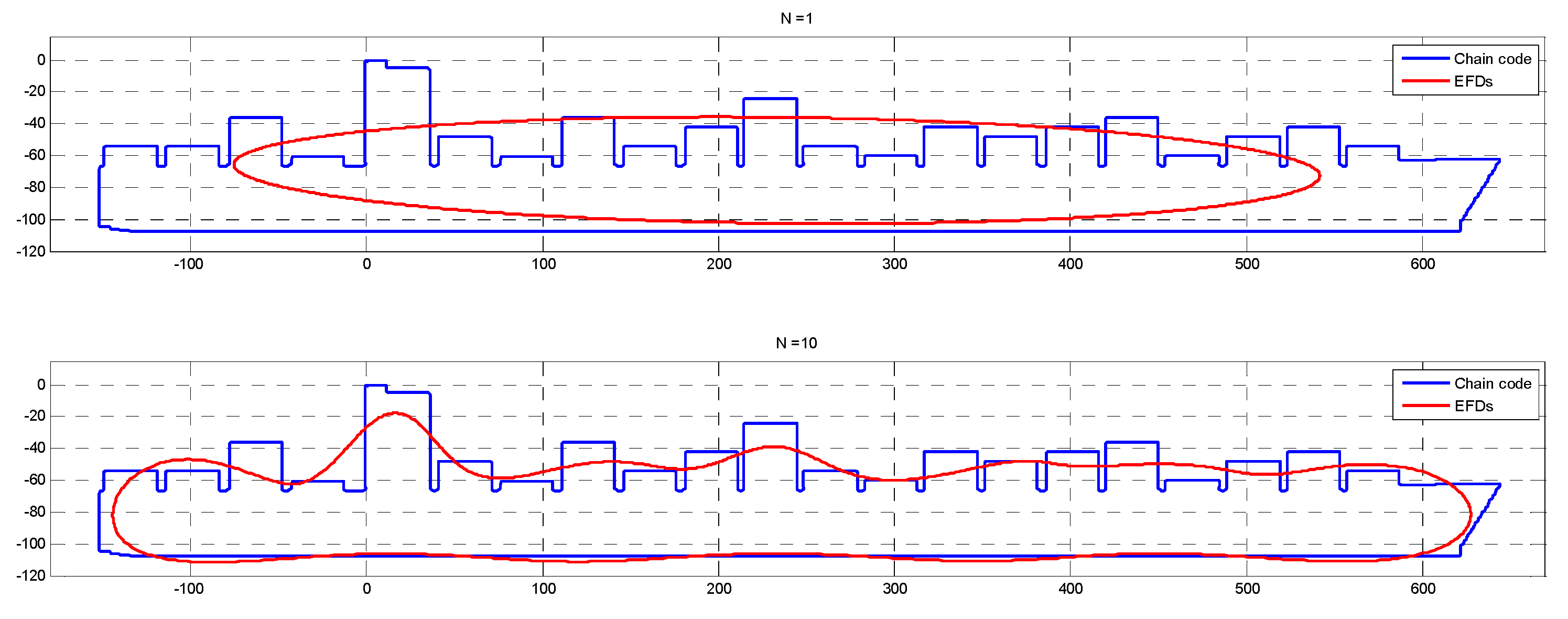
- Kuhl, F.P.; Giardina, C.R. Elliptic Fourier Features of a Closed Contour. Comput. Graph. Image Process. 1982, 18, 236–258. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Sons Ltd.: Chichester, UK, 2011. [Google Scholar]
- Norwegian Maritime Directory. Regulations for Mobile Offshore Units. 1997. Available online: http://www.sjofartsdir.no/en/Legislation_and_International_Relations/Translated_Norwegian_legislation/Regulations-for-Mobile-Offshore-Units (accessed on 20 June 2020).
- Wieringa, J. Updating the Davenport roughness classification. J. Wind Eng. Ind. Aerodyn. 1992, 41, 357–368. [Google Scholar] [CrossRef]
- Blocken, B.; Carmeliet, J.; Stathopoulos, T. CFD evaluation of the wind speed conditions in passages between buildings—Effect of wall-function roughness modifications on the atmospheric boundary layer flow. J. Wind Eng. Ind. Aerodyn. 2007, 95, 941–962. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
| # | Frontal Configu-Ration | Lateral Configuration | # | Frontal Configu-Ration | Lateral Configuration |
|---|---|---|---|---|---|
| 1 |  |  | 8 |  |  |
| 2 | 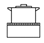 |  | 9 |  |  |
| 3 | 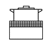 |  | 10 |  |  |
| 4 |  |  | 11 | 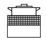 |  |
| 5 |  |  | 12 | 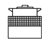 |  |
| 6 |  |  | 13 |  |  |
| 7 |  |  |
| A: CFD Results vs. Experimental Data | B: GRRN Responses vs. CFD Results | |||||
|---|---|---|---|---|---|---|
| t | ||||||
| 1 | 0.006830 0.077113 | 0.000001 0.022939 | 0.001013 0.007878 | −0.018669 0.083724 | −0.013219 0.008449 | 0.001119 0.004969 |
| 2 | 0.028897 0.070867 | −0.031025 0.029837 | 0.000250 0.006619 | 0.019692 0.156943 | 0.036904 0.021176 | 0.005489 0.006890 |
| 3 | −0.001519 0.067631 | −0.002002 0.016848 | 0.001721 0.007465 | 0.021038 0.217758 | −0.005834 0.007852 | −0.003374 0.008509 |
| 4 | −0.040542 0.069472 | −0.001895 0.024665 | 0.001351 0.008477 | 0.039521 0.126639 | −0.001958 0.011143 | −0.005018 0.004919 |
| 5 | −0.027537 0.071166 | 0.000302 0.021155 | 0.000559 0.008445 | 0.066050 0.124721 | −0.003438 0.013194 | −0.011163 0.009887 |
| 6 | 0.004378 0.066045 | 0.000507 0.021938 | 0.000101 0.007114 | −0.011767 0.190404 | −0.001516 0.020347 | −0.000170 0.007039 |
| 7 | 0.009061 0.079468 | −0.009399 0.028647 | 0.002226 0.007970 | −0.095680 0.076000 | −0.013755 0.017702 | 0.013060 0.009611 |
| 8 | 0.015437 0.112929 | −0.004332 0.014446 | 0.001051 0.016156 | −0.032795 0.642980 | 0.008992 0.020995 | 0.009923 0.017630 |
| 9 | −0.000038 0.061642 | −0.000605 0.010249 | 0.001022 0.008962 | −0.020133 0.106340 | 0.001654 0.008042 | −0.002510 0.005232 |
| 10 | 0.006541 0.072194 | −0.000360 0.012062 | 0.000443 0.009953 | −0.028850 0.157382 | −0.001015 0.014933 | 0.008996 0.009849 |
| 11 | 0.008620 0.090098 | −0.021369 0.014297 | 0.000902 0.006874 | 0.020806 0.128550 | 0.009962 0.006351 | −0.004635 0.005230 |
| 12 | −0.012284 0.079605 | −0.015912 0.020094 | 0.000107 0.007031 | 0.042008 0.231174 | 0.003056 0.007483 | −0.002915 0.008500 |
| 13 | 0.025503 0.103171 | −0.026480 0.019025 | 0.001303 0.007147 | 0.035129 0.163835 | 0.008007 0.006242 | −0.006211 0.007112 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prpić-Oršić, J.; Valčić, M.; Čarija, Z. A Hybrid Wind Load Estimation Method for Container Ship Based on Computational Fluid Dynamics and Neural Networks. J. Mar. Sci. Eng. 2020, 8, 539. https://doi.org/10.3390/jmse8070539
Prpić-Oršić J, Valčić M, Čarija Z. A Hybrid Wind Load Estimation Method for Container Ship Based on Computational Fluid Dynamics and Neural Networks. Journal of Marine Science and Engineering. 2020; 8(7):539. https://doi.org/10.3390/jmse8070539
Chicago/Turabian StylePrpić-Oršić, Jasna, Marko Valčić, and Zoran Čarija. 2020. "A Hybrid Wind Load Estimation Method for Container Ship Based on Computational Fluid Dynamics and Neural Networks" Journal of Marine Science and Engineering 8, no. 7: 539. https://doi.org/10.3390/jmse8070539
APA StylePrpić-Oršić, J., Valčić, M., & Čarija, Z. (2020). A Hybrid Wind Load Estimation Method for Container Ship Based on Computational Fluid Dynamics and Neural Networks. Journal of Marine Science and Engineering, 8(7), 539. https://doi.org/10.3390/jmse8070539






