MaRINET2 Tidal Energy Round Robin Tests—Performance Comparison of a Horizontal Axis Turbine Subjected to Combined Wave and Current Conditions
Abstract
1. Introduction
2. Experimental Set-Up
2.1. Turbine Prototype Specifications
2.2. Experimental Plan
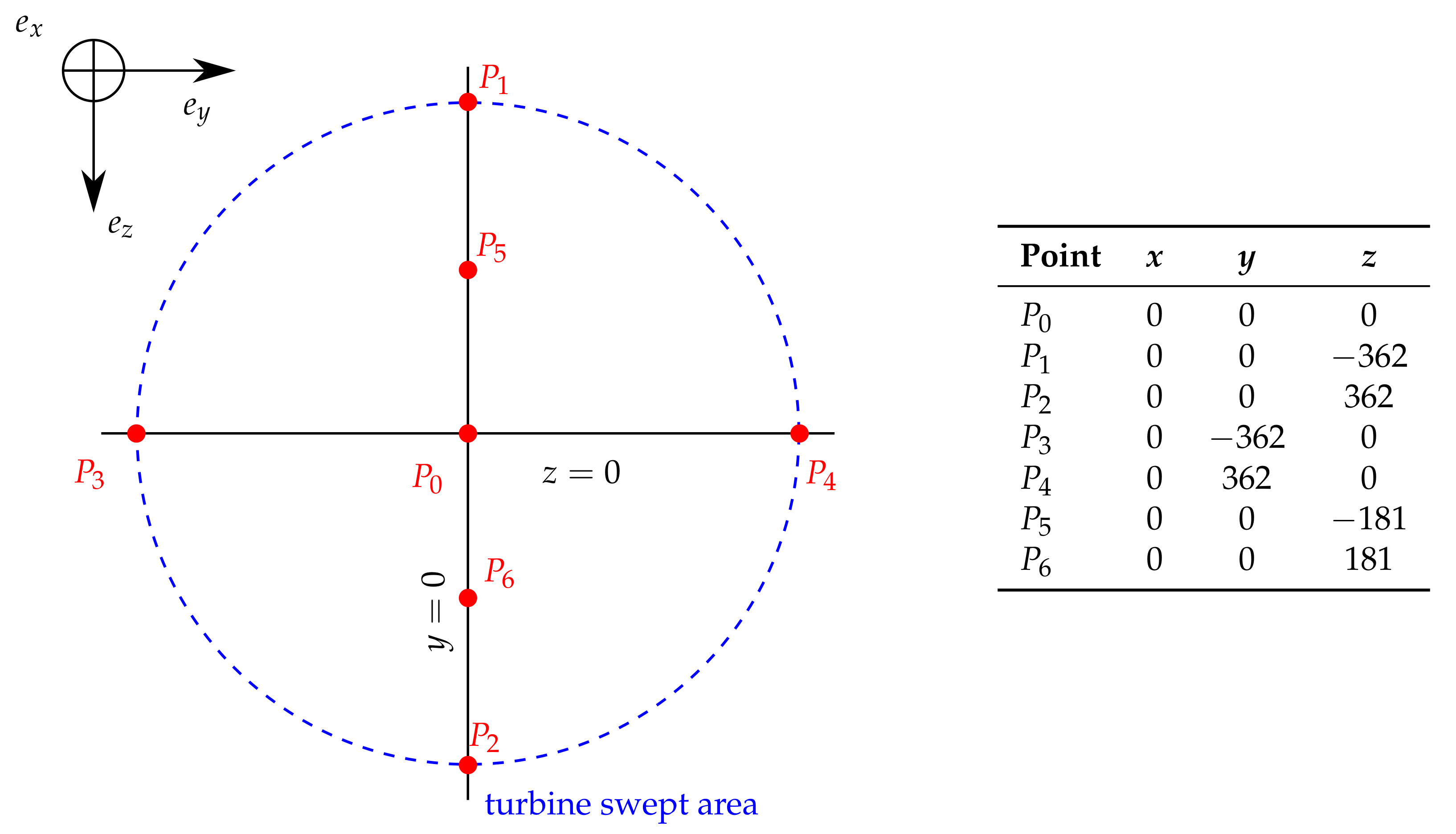
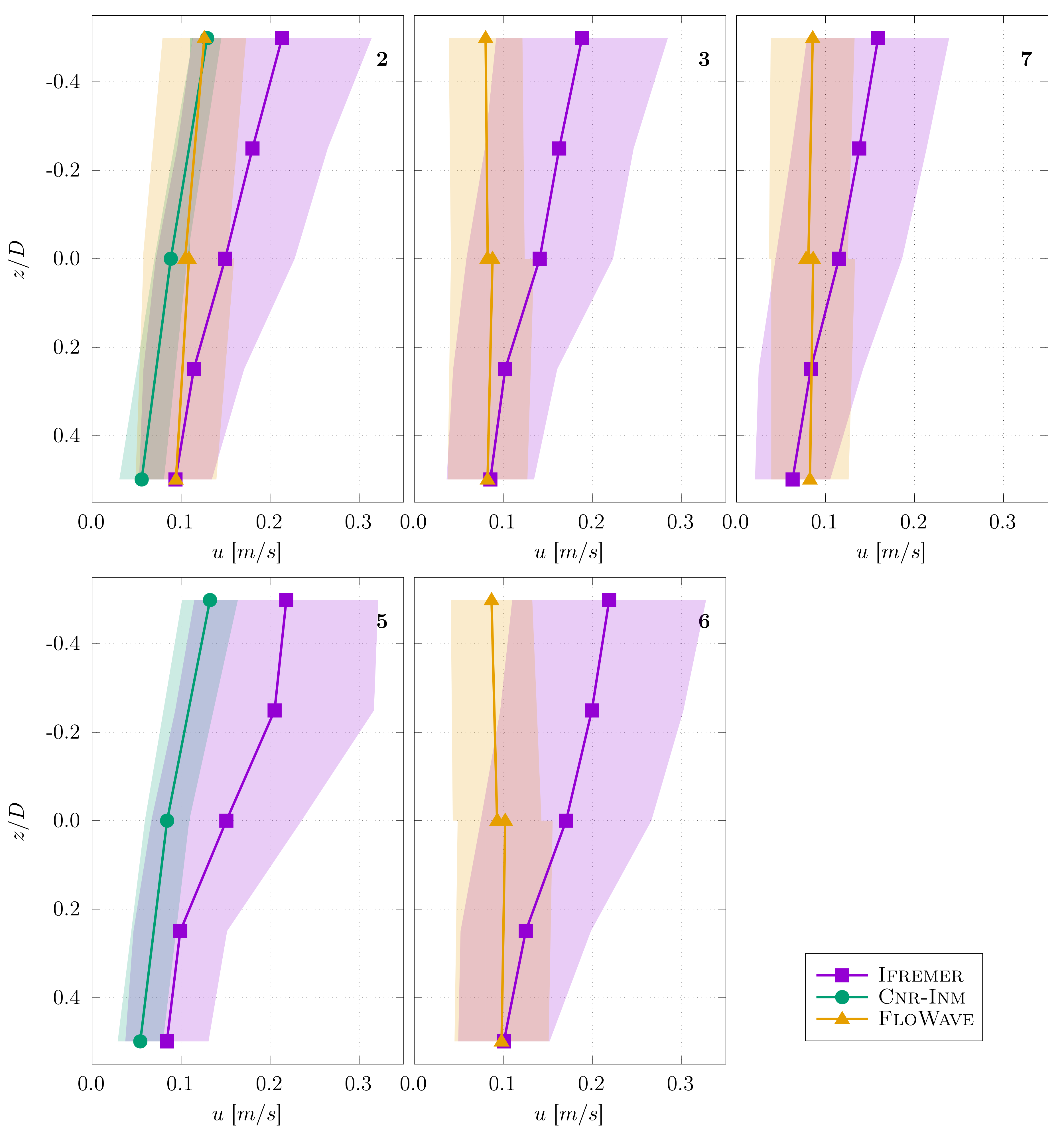
2.3. Flow Measurement and Characterisation
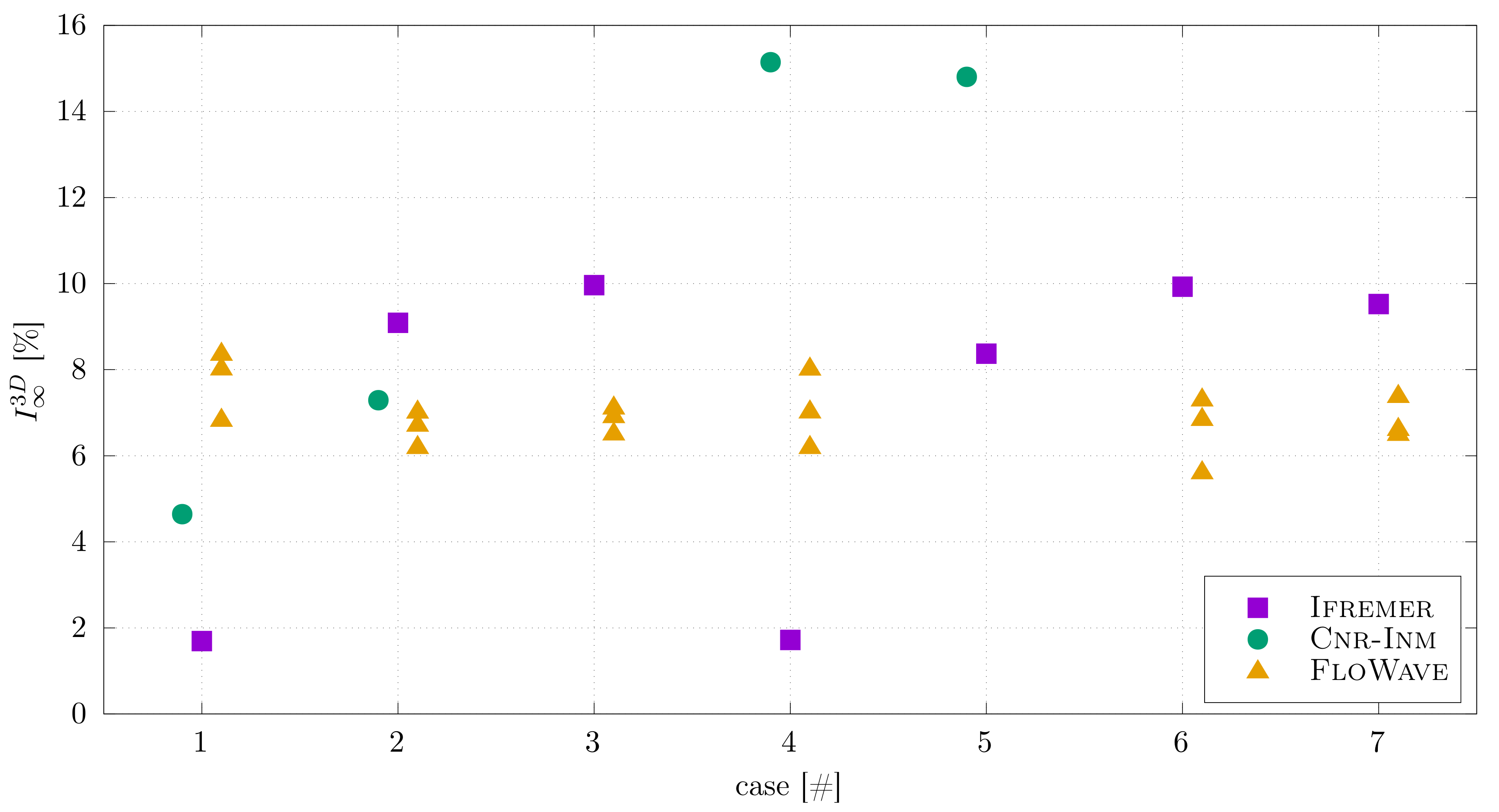
3. Input Flow Characteristics
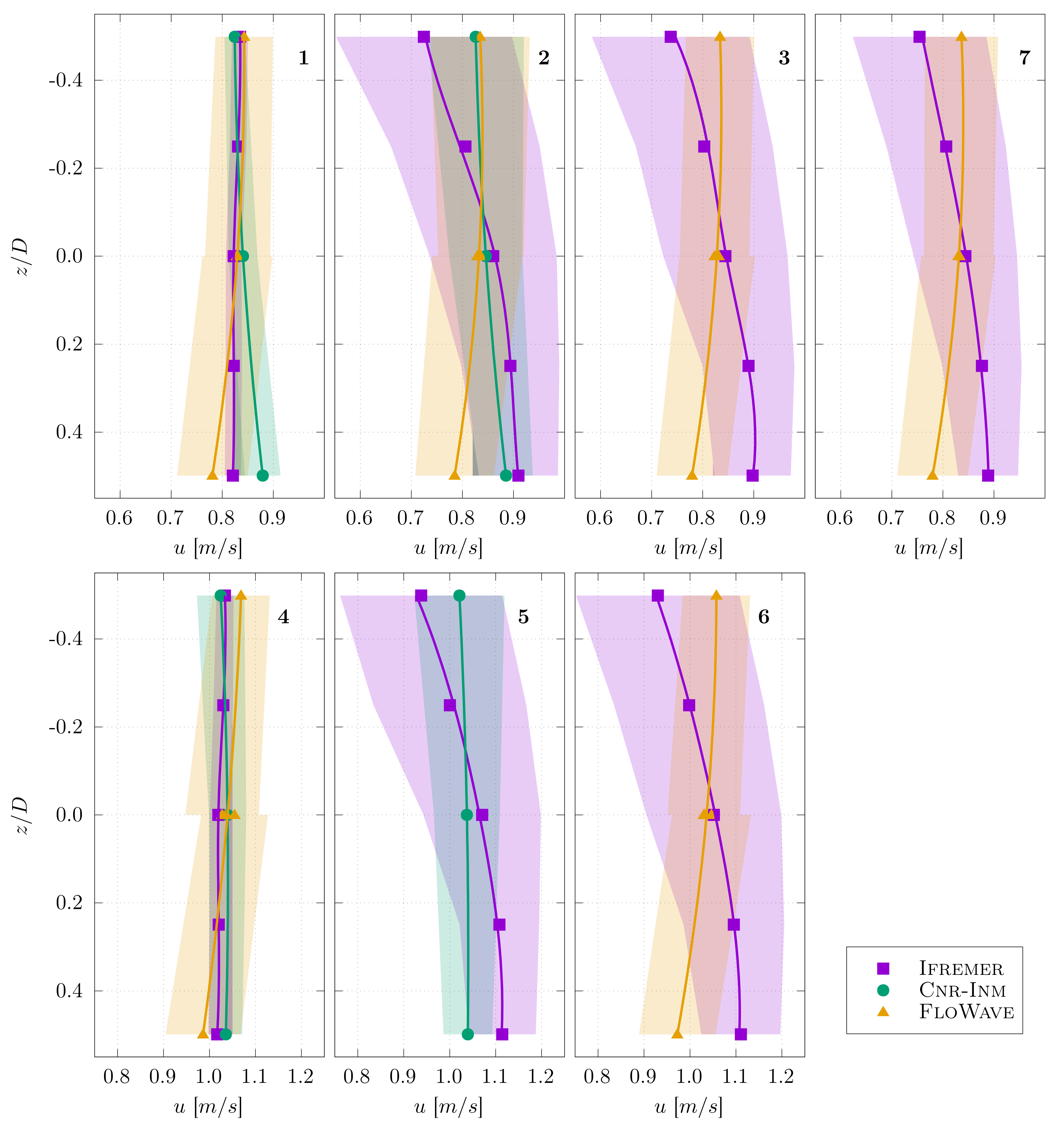
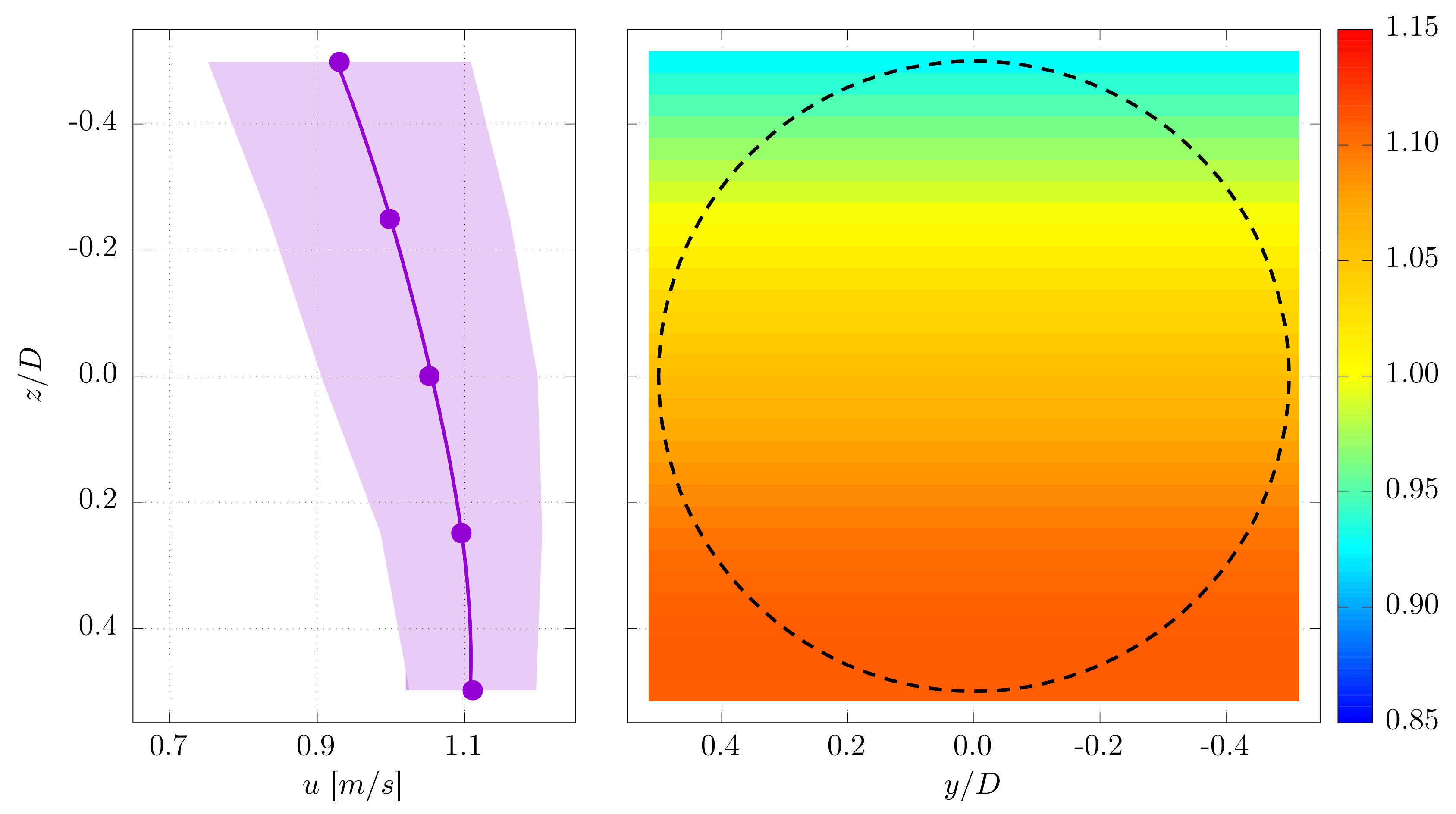
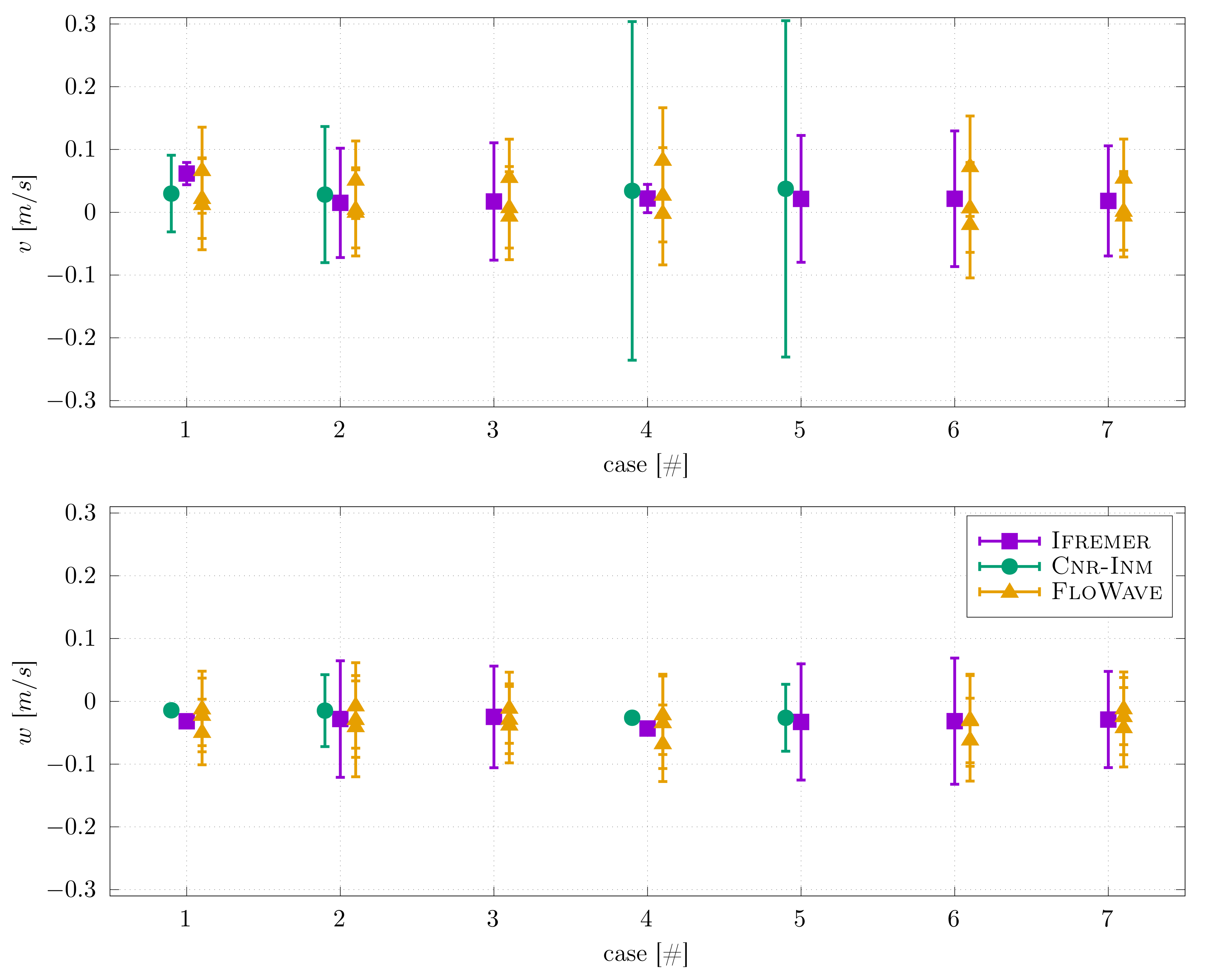
3.1. Flow Velocity Characterisation
- It accounts for the velocity gradient over the entire turbine disc. The hypothesis about a constant velocity along the transverse dimension y is at least confirmed by the measurements carried out at FLOWAVE, where the central point () is repeated for three different transverse positions: , and results show a similar average velocity. Identical measurements have been carried out at IFREMER for previous trials showing the same results. At the towing tank of CNR-INM, the transversal velocity variation is null and thus, this approach does not alter the final velocity distribution.
- There is no turbine effects linked to the momentum theory on the velocity measurement because the acquisition is carried out without the turbine, but at the same location.
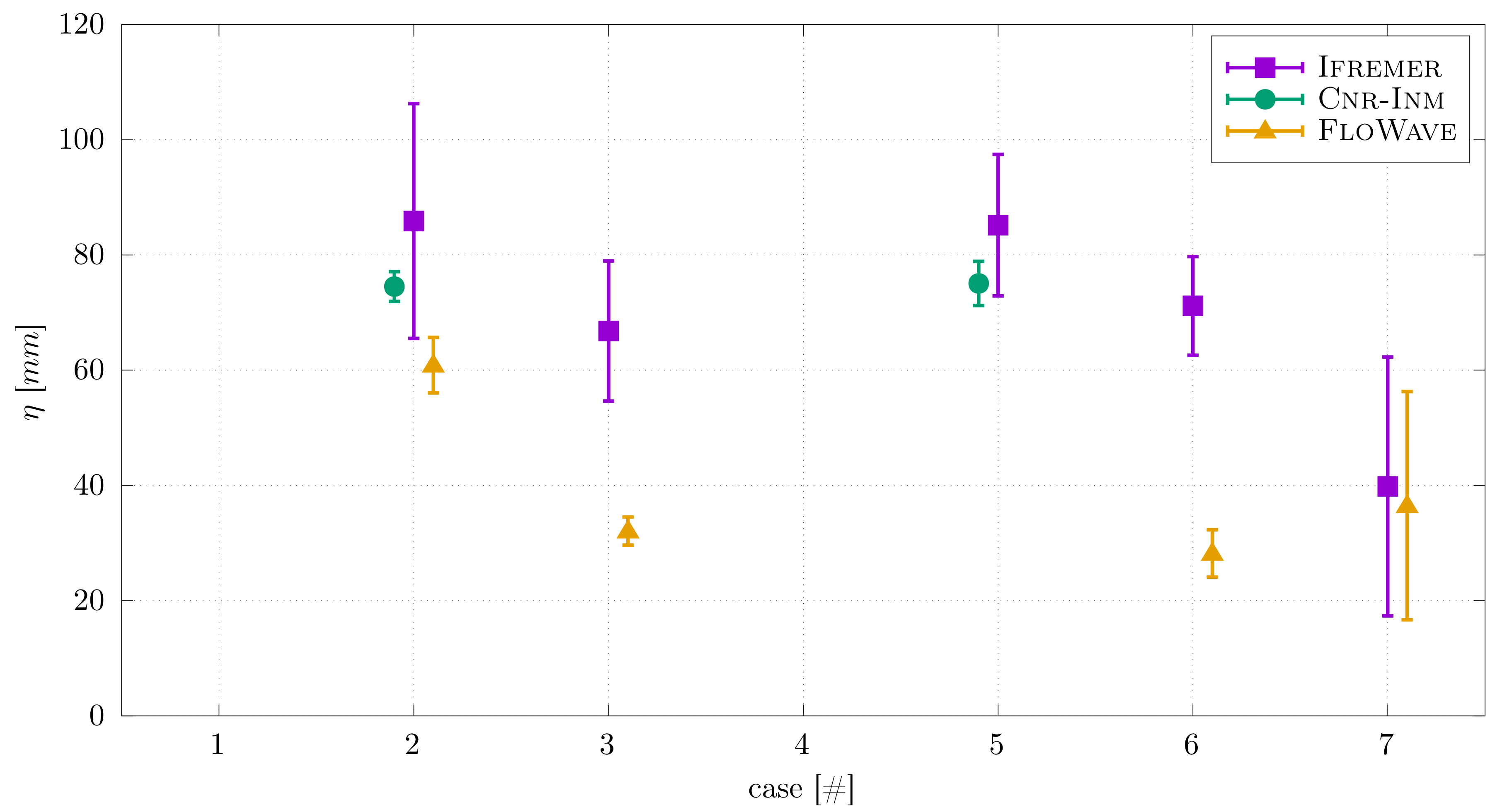
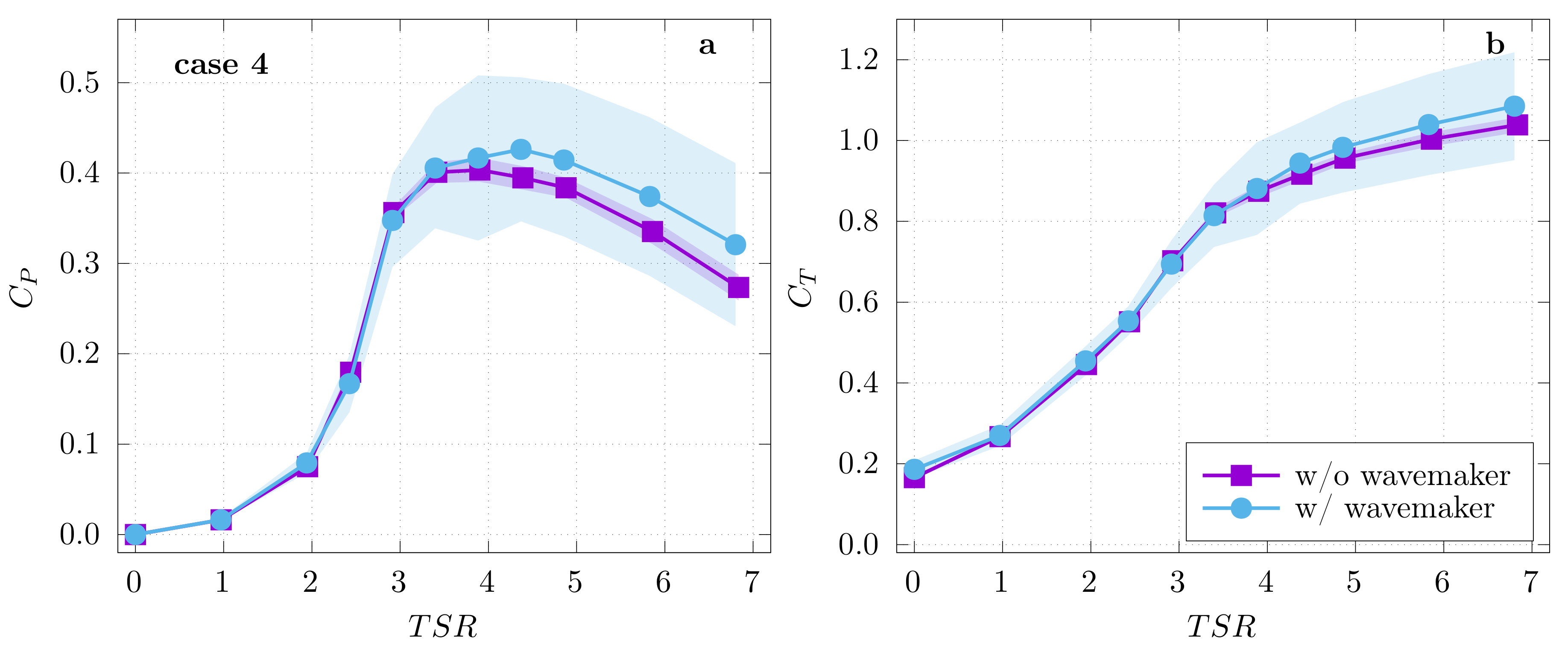
3.2. The Wave Effects
4. Performance Comparisons
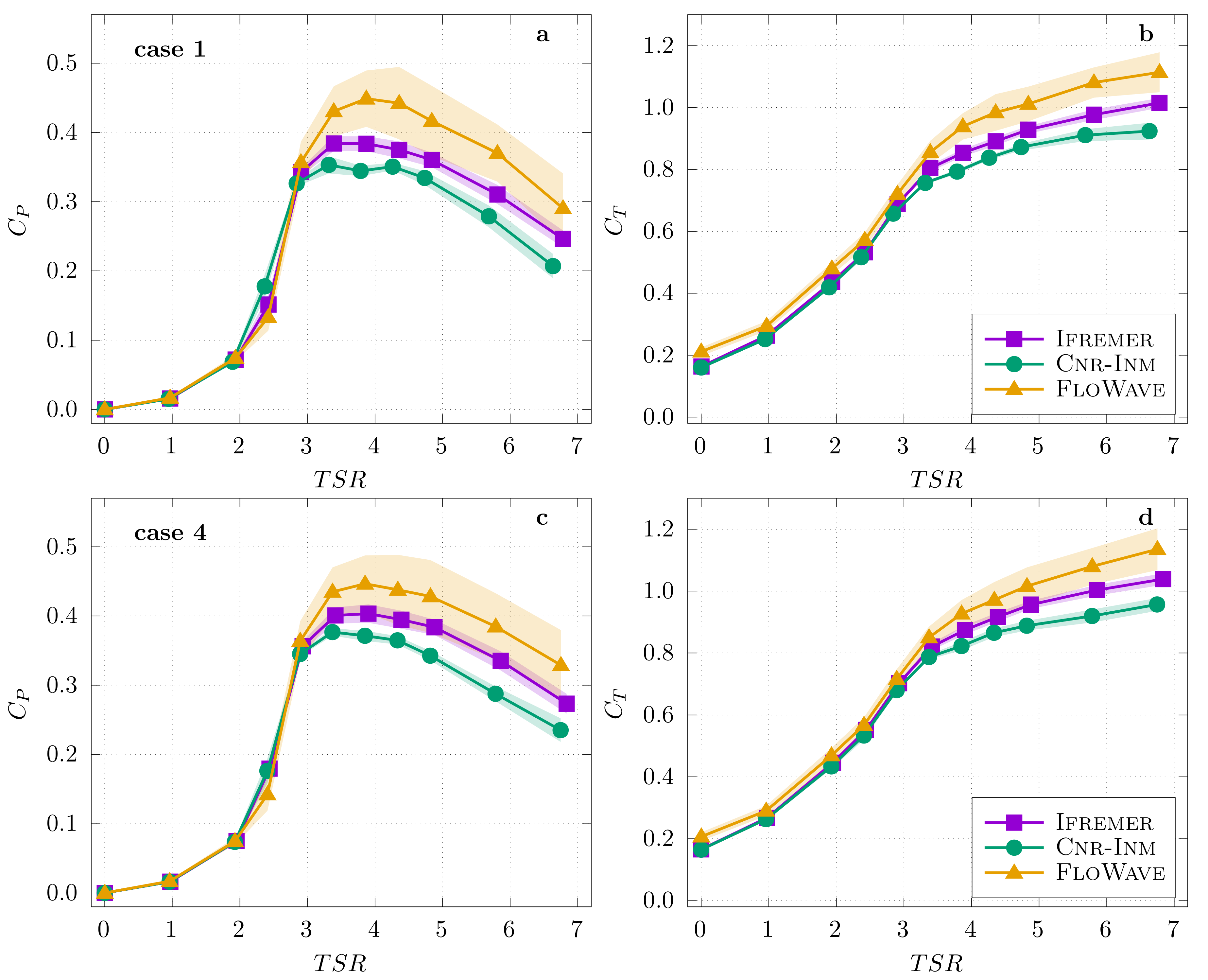
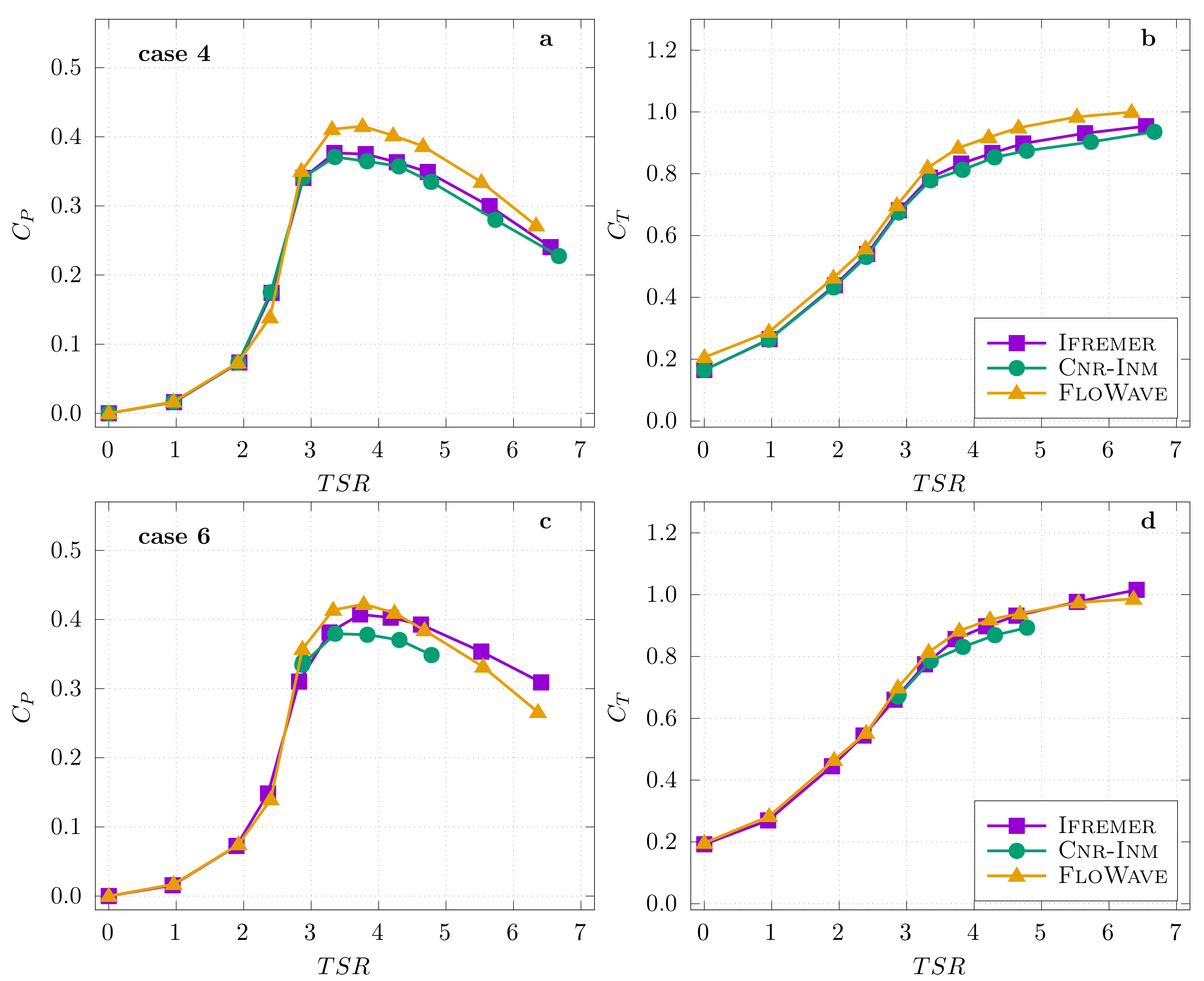
4.1. Turbine Performance Comparison with Current-Only
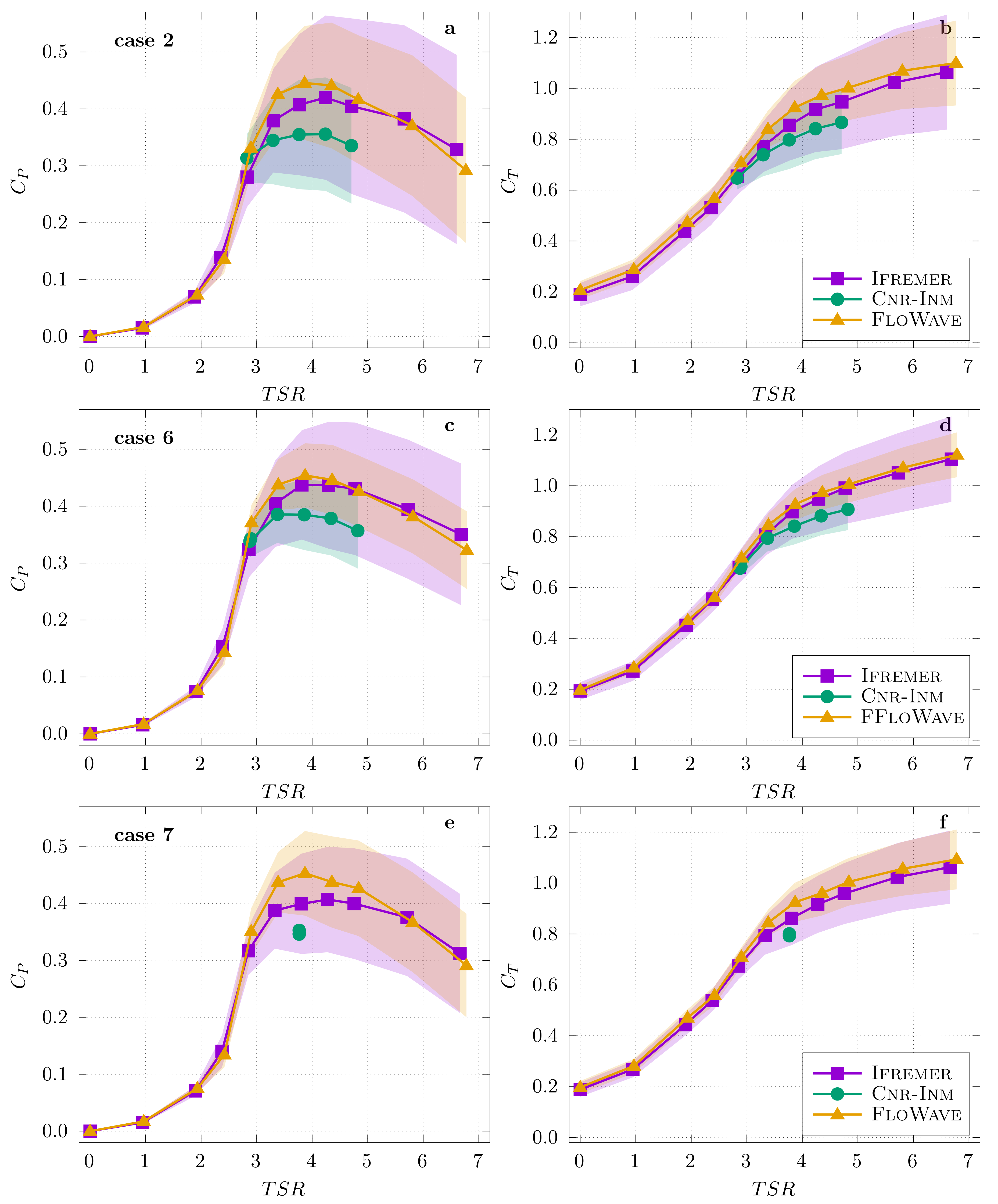
4.2. Turbine Performance Comparison with Current and Wave Conditions
5. Discussion
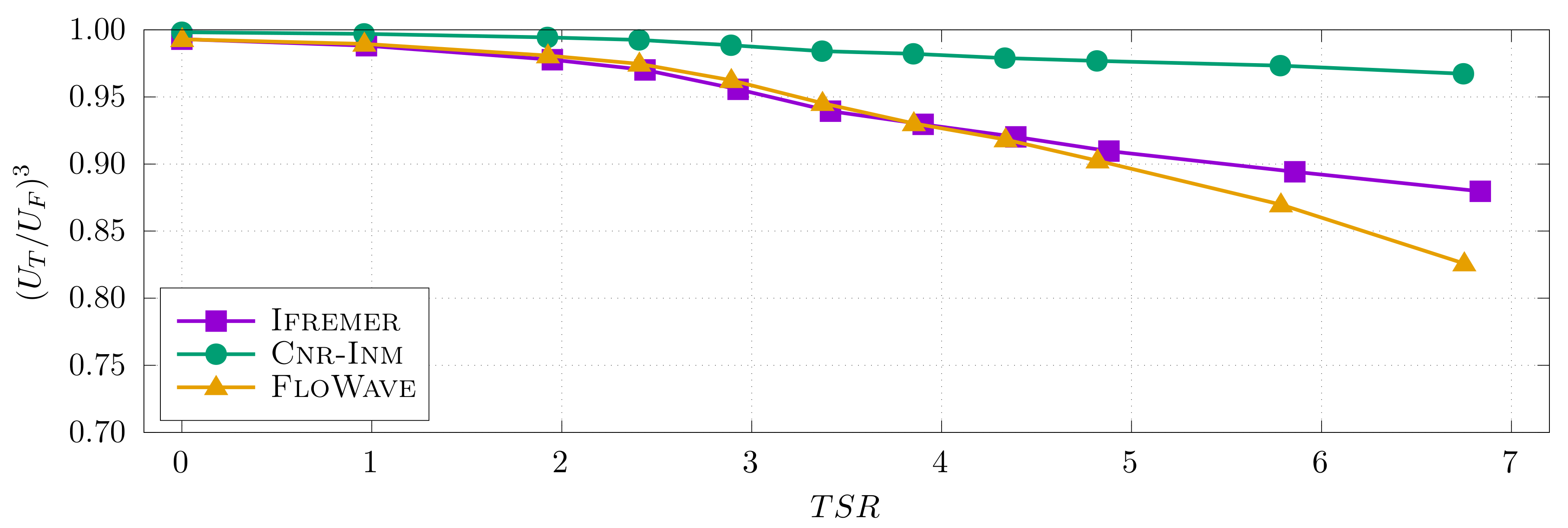
5.1. Blockage Effects
- The turbine cannot be located exactly in the mid-position of the tank due to the floor mounting design. Thus, it is likely that distances to the surrounding walls differ from either side.
- The depth of the tank (2 m) is relatively small compared to the tank diameter. Thus, the depth could be predominant in terms of blockage for the turbine.
5.2. Turbulence Effects
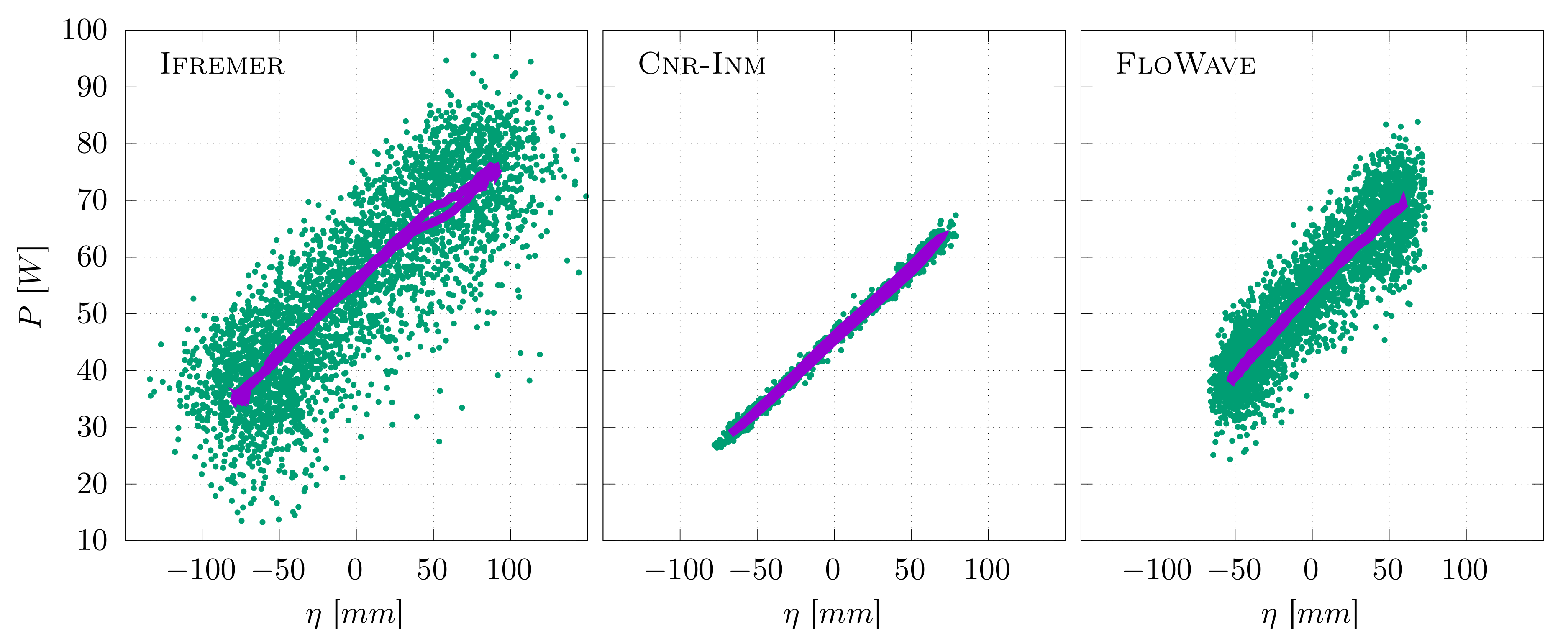
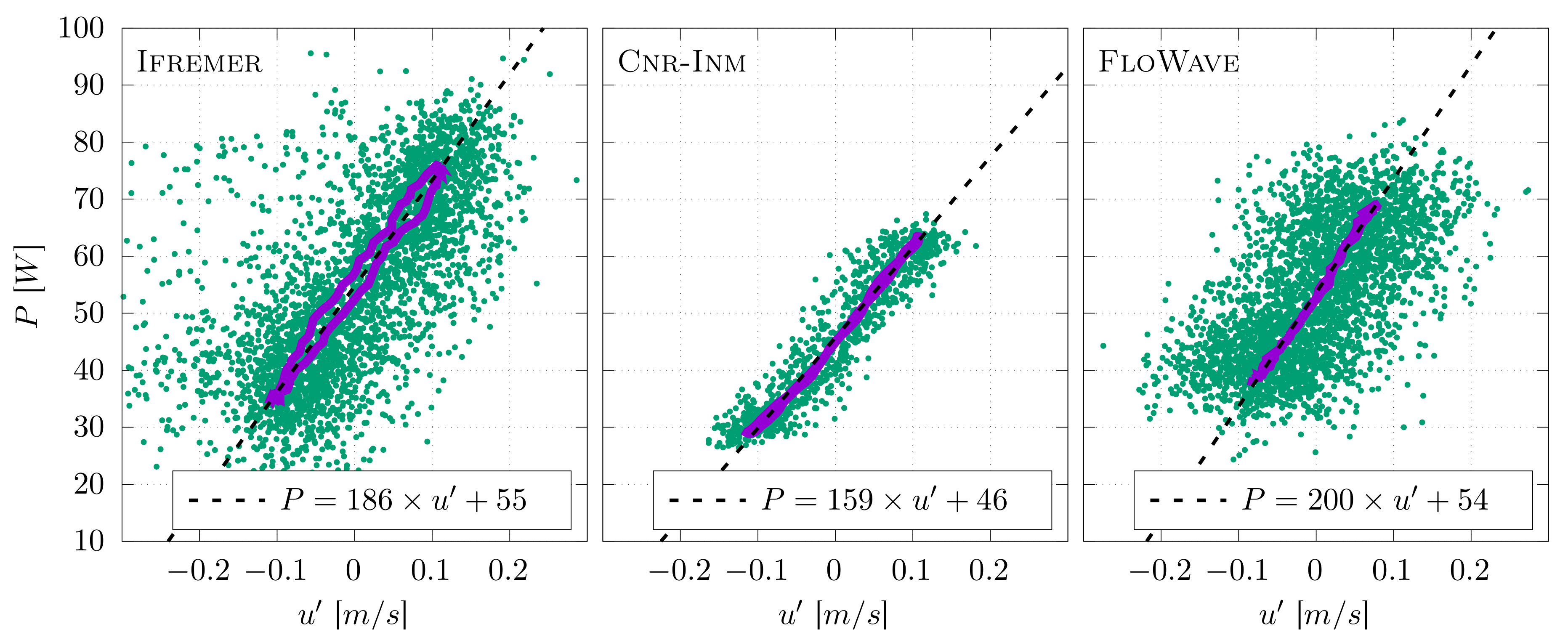
5.3. Wave and Current Interaction Effects
- the highest values are observed for FLOWAVE because of the low velocity (0.827 m/s) compared to the relatively high power (54 W)
- the lowest values are obtained for CNR-INM because of the high velocity (0.848 m/s) compared to the relatively low power (46 W)
5.4. Synthesis on the Tidal Turbine Performance Characteristics
6. Conclusions
7. Data Accessibility
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Turbine Performance Comparison within an Individual Test Site

References
- Aubrun, S.; Bastankhah, M.; Cal, R.B.; Conan, B.; Hearst, R.J.; Hoek, D.; Hölling, M.; Huang, M.; Hur, C.; Karlsen, B.; et al. Round-robin tests of porous disc models. J. Phys. Conf. Ser. 2019, 1256. [Google Scholar] [CrossRef]
- IEC. Marine Energy-Wave, Tidal and Other Water Current Converters-Part 200: Electricity Producing Tidal Energy Converters-Power Performance Assessment; Technical Report; International Electrotechnical Commission: Geneva, Switzerland, 2013. [Google Scholar]
- IEC. Marine Energy-Wave, Tidal and Other Water Current Converters-Part 201: Tidal Energy Resource Assessment and Characterization; Technical Report; International Electrotechnical Commission: Geneva, Switzerland, 2015. [Google Scholar]
- IEC. Marine Energy-Wave, Tidal and Other Water Current Converters-Part 202: Scale Testing of Tidal Stream Energy Systems; Technical Report; International Electrotechnical Commission: Geneva, Switzerland, 2021. [Google Scholar]
- Specialist Committee on Testing of Marine Renewable Devices. Recommended Procedures and Guidelines-Model Tests for Current Turbine. Technical Report. 2017. Available online: https://www.ittc.info/media/8127/75-02-07-038.pdf (accessed on 24 June 2020).
- Specialist Committee on Testing of Marine Renewable Devices. Recommended Procedures and Guidelines-Uncertainty Analysis-Example for Horizontal Axis Turbines. Technical Report. 2017. Available online: https://www.ittc.info/media/8141/75-02-07-0315.pdf (accessed on 24 June 2020).
- EquiMar. Protocols for the Equitable Assessment of Marine Energy Converters, 1st ed.; Number 213380; The Institute for Energy Systems, The University of Edinburgh: Edinburgh, UK, 2011. [Google Scholar]
- Germain, G.; Chapeleau, A.; Gaurier, B.; Macadré, L.M.; Scheijgrond, P. Testing of marine energy technologies against international standards. Where do we stand? In Proceedings of the 12th European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–1 September 2017. [Google Scholar]
- Germain, G.; Gaurier, B.; Harrold, M.J.; Ikhennicheu, M.; Scheijgrond, P.; Southall, A.; Trasch, M. Protocols for testing marine current energy converters in controlled conditions.Where are we in 2018? In Proceedings of the 4th Asian Wave and Tidal Energy Conference, Taipei, Taiwan, 9–13 September 2018. [Google Scholar]
- Gaurier, B.; Germain, G.; Facq, J.V.; Johnstone, C.; Grant, A.D.; Day, A.H.; Nixon, E.; Di Felice, F.; Costanzo, M. Tidal energy “round Robin” tests comparisons between towing tank and circulating tank results. Int. J. Mar. Energy 2015, 12, 87–109. [Google Scholar] [CrossRef]
- Bahaj, A.S.; Molland, A.F.; Chaplin, J.R.; Batten, W.M.J. Power and thrust measurements of marine current turbines under various hydrodynamic flow conditions in a cavitation tunnel and a towing tank. Renew. Energy 2007, 32, 407–426. [Google Scholar] [CrossRef]
- Murray, R.E.; Ordonez-Sanchez, S.; Porter, K.E.; Doman, D.A.; Pegg, M.J.; Johnstone, C. Towing Tank and Flume Testing of Passively Adaptive Composite Tidal Turbine Blades. In Proceedings of the 12th European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–1 September 2017. [Google Scholar]
- Gaurier, B.; Davies, P.; Deuff, A.; Germain, G. Flume tank characterization of marine current turbine blade behaviour under current and wave loading. Renew. Energy 2013, 59, 1–12. [Google Scholar] [CrossRef]
- Galloway, P.W.; Myers, L.E.; Bahaj, A.B.S. Quantifying wave and yaw effects on a scale tidal stream turbine. Renew. Energy 2014, 63, 297–307. [Google Scholar] [CrossRef]
- Martinez, R.; Payne, G.S.; Bruce, T. The effects of oblique waves and currents on the loadings and performance of tidal turbines. Ocean Eng. 2018, 164, 55–64. [Google Scholar] [CrossRef]
- Ordonez-Sanchez, S.; Allmark, M.; Porter, K.; Ellis, R.; Lloyd, C.; Santic, I.; O’Doherty, T.; Johnstone, C. Analysis of a Horizontal-Axis Tidal Turbine Performance in the Presence of Regular and Irregular Waves Using Two Control Strategies. Energies 2019, 12, 367. [Google Scholar] [CrossRef]
- Draycott, S.; Payne, G.; Steynor, J.; Nambiar, A.; Sellar, B.; Venugopal, V. An experimental investigation into non-linear wave loading on horizontal axis tidal turbines. J. Fluids Struct. 2019, 84, 199–217. [Google Scholar] [CrossRef]
- McNaughton, J.; Harper, S.; Sinclair, R.; Sellar, B. Measuring and Modelling the Power Curve of a Commercial-Scale Tidal Turbine. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015. [Google Scholar]
- Durán Medina, O.; Schmitt, F.G.; Calif, R.; Germain, G.; Gaurier, B. Turbulence analysis and multiscale correlations between synchronized flow velocity and marine turbine power production. Renew. Energy 2017, 112, 314–327. [Google Scholar] [CrossRef]
- Gaurier, B.; Ikhennicheu, M.; Druault, P.; Germain, G.; Facq, J.V.; Pinon, G. Etude Expérimentale des Effets de Sillage d’un Large Obstacle posé sur le Comportement D’Une Hydrolienne. 2018. Available online: https://archimer.ifremer.fr/doc/00482/59334/62112.pdf (accessed on 24 June 2020).
- Gaurier, B.; Germain, G.; Pinon, G. How to correctly measure turbulent upstream flow for marine current turbine performances evaluation? In Advances in Renewable Energies Offshore-Proceedings of the 3rd International Conference on Renewable Energies Offshore, RENEW 2018, Lisbon, Portugal, 8–10 October 2018; Taylor & Francis Group: London, UK, 2019; pp. 23–30. [Google Scholar]
- Davies, P.; Germain, G.; Gaurier, B.; Boisseau, A.; Perreux, D. Evaluation of the durability of composite tidal turbine blades. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20120187. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, T.; Mahfuz, H. Fatigue characterization of GFRP and composite sandwich panels under random ocean current loadings. Int. J. Fatigue 2018, 111, 124–133. [Google Scholar] [CrossRef]
- Filipot, J.F.; Prevosto, M.; Maisondieu, C.; Le Boulluec, M.; Thomson, J. Wave and turbulence measurements at a tidal energy site. In Proceedings of the 11th Current, Waves and Turbulence Measurement, St. Petersburg, FL, USA, 2–6 March 2015; pp. 1–9. [Google Scholar] [CrossRef]
- Draycott, S.; Sutherland, D.; Steynor, J.; Sellar, B.; Venugopal, V. Re-creating waves in large currents for tidal energy applications. Energies 2017, 10. [Google Scholar] [CrossRef]
- Gaurier, B.; Germain, G.; Facq, J.V.; Bacchetti, T. Wave and Current Flume Tank of IFREMER at Boulogne-sur-mer. Description of the Facility and Its Equipment; Technical Report; Ifremer: Brest, France, 2018. [Google Scholar] [CrossRef]
- Institute of Marine Engineering. Consiglio Nazionale delle Ricerche-Towing Tanks; Institute of Marine Engineering: London, UK, 2019. [Google Scholar]
- Sutherland, D.R.; Noble, D.R.; Steynor, J.; Davey, T.; Bruce, T. Characterisation of current and turbulence in the FloWave Ocean Energy Research Facility. Ocean Eng. 2017, 139, 103–115. [Google Scholar] [CrossRef]
- Payne, G.S.; Stallard, T.; Martinez, R. Design and manufacture of a bed supported tidal turbine model for blade and shaft load measurement in turbulent flow and waves. Renew. Energy 2017, 107, 312–326. [Google Scholar] [CrossRef]
- SixAxes. Société Française, Spécialisée Dans l’étude et la Fabrication de Chaîne de Mesure de Force Depuis plus de 22 Ans; SixAxes: Argenteuil, France, 2017. [Google Scholar]
- Goring, D.G.; Nikora, V.I. Despiking acoustic doppler velocimeter data. J. Hydraul. Eng. 2002, 128, 117–126. [Google Scholar] [CrossRef]
- Mycek, P.; Gaurier, B.; Germain, G.; Pinon, G.; Rivoalen, E. Experimental study of the turbulence intensity effects on marine current turbines behaviour. Part I: One single turbine. Renew. Energy 2014, 66, 729–746. [Google Scholar] [CrossRef]
- Blackmore, T.; Myers, L.E.; Bahaj, A.S. Effects of turbulence on tidal turbines: Implications to performance, blade loads, and condition monitoring. Int. J. Mar. Energy 2016, 14, 1–26. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Brevik, I.; Bjørn, A. Flume experiment on waves and currents. I. Rippled bed. Coast. Eng. 1979, 3, 149–177. [Google Scholar] [CrossRef]
- Klopman, G. Vertical structure of the flow due to wave and currents-Laser-Doppler flow measurements for waves following or opposing a current. In WL Report H840-30, Part II, for Rijkswaterstaat; Technical Report; Deltares (WL): Delft, The Netherlands, 1994. [Google Scholar]
- Guo, X.; Yang, J.; Gao, Z.; Moan, T.; Lu, H. The surface wave effects on the performance and the loading of a tidal turbine. Ocean Eng. 2018, 156, 120–134. [Google Scholar] [CrossRef]
- Draycott, S.; Steynor, J.; Davey, T.; Ingram, D.M. Isolating incident and reflected wave spectra in the presence of current. Coast. Eng. J. 2018, 60, 39–50. [Google Scholar] [CrossRef]
- Gaurier, B.; Ordonez-Sanchez, S.; Germain, G.; Facq, J.V.; Johnstone, C.; Salvatore, F.; Santic, I. MaRINET2 Tidal “Round Robin” Dataset: Comparisons Between Towing and Circulating Tanks Test Results for a Tidal Energy Converter Submitted to Wave and Current Interactions. SEANOE: Brest, France, 2018. [Google Scholar] [CrossRef]
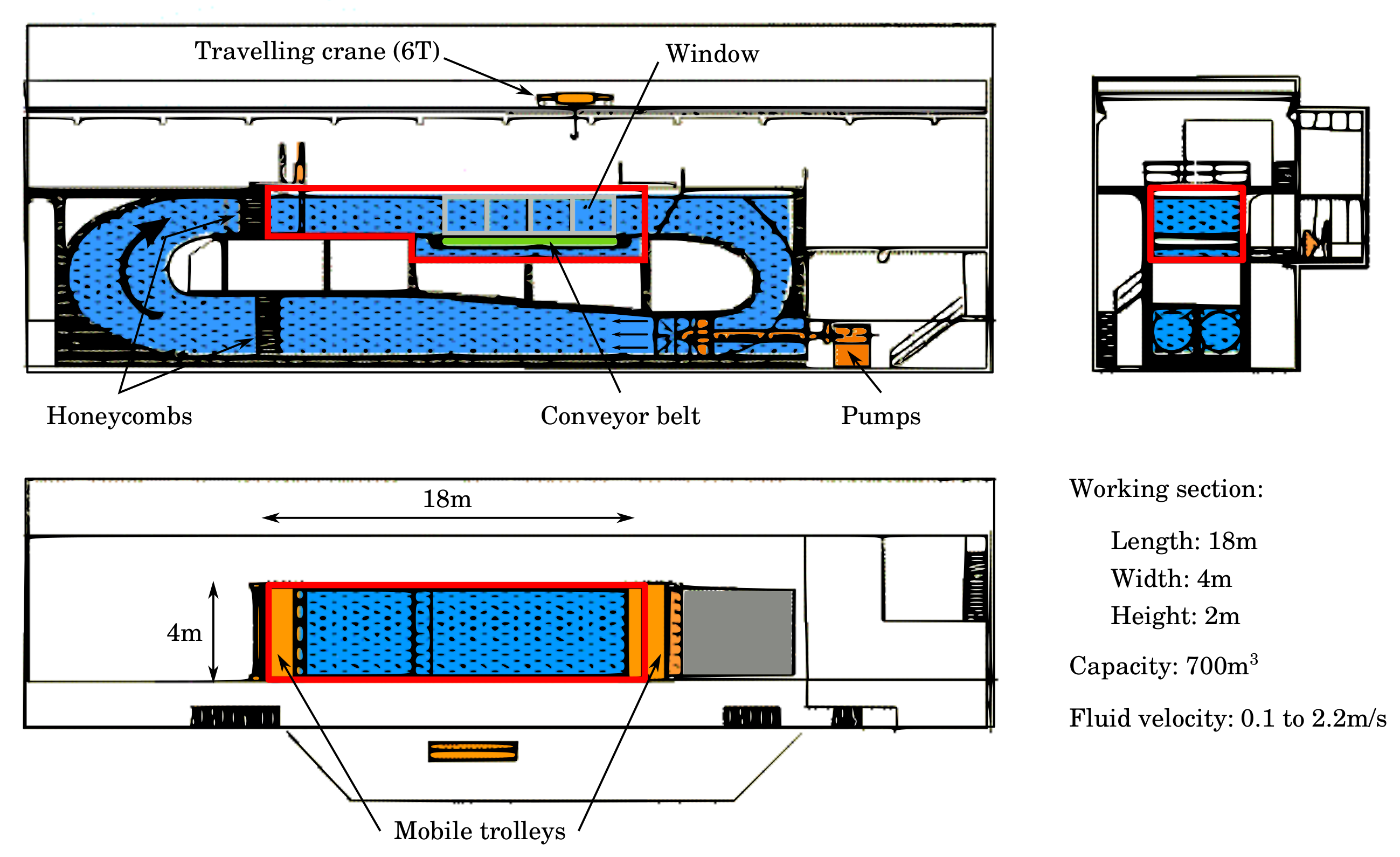

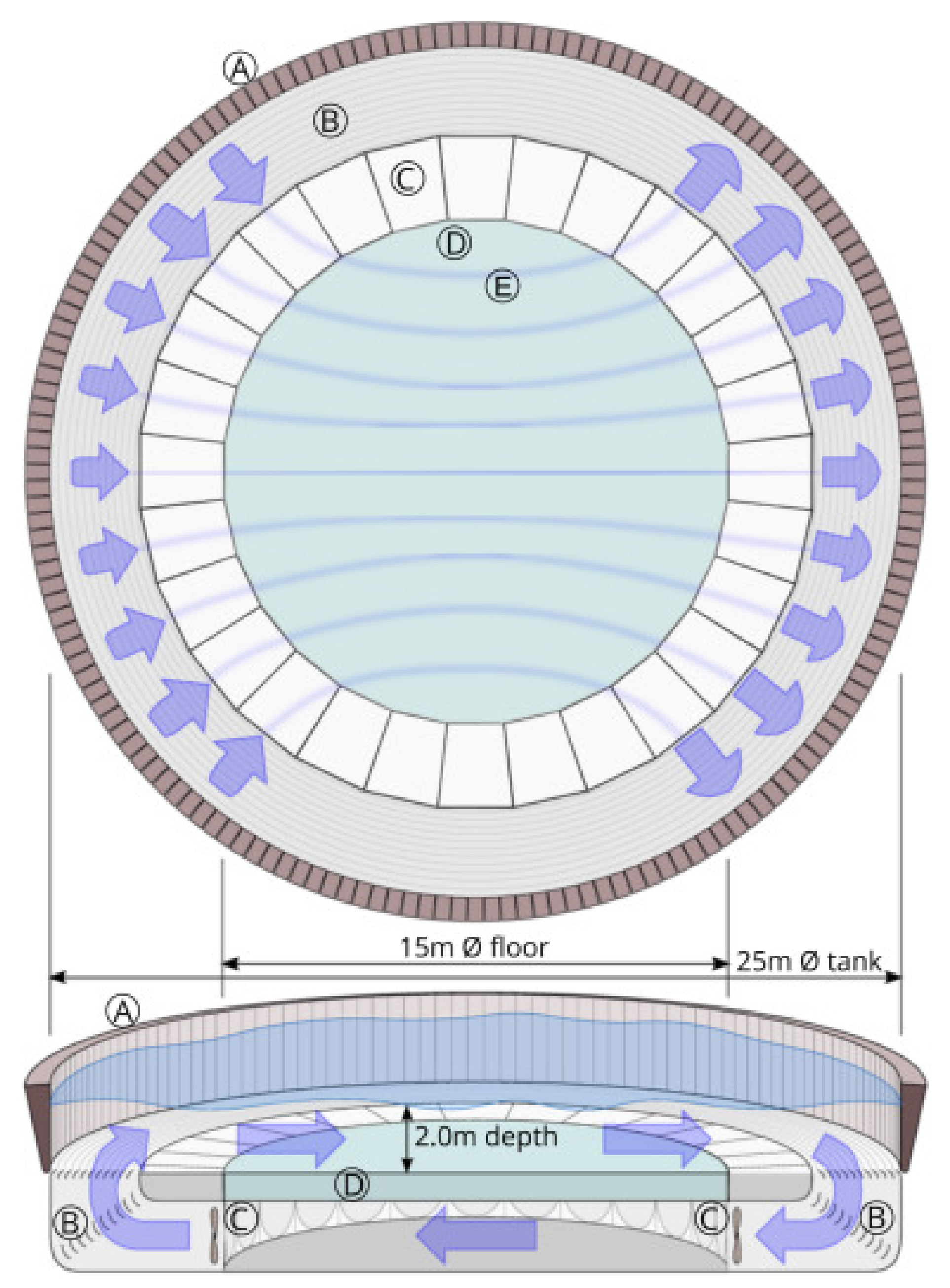

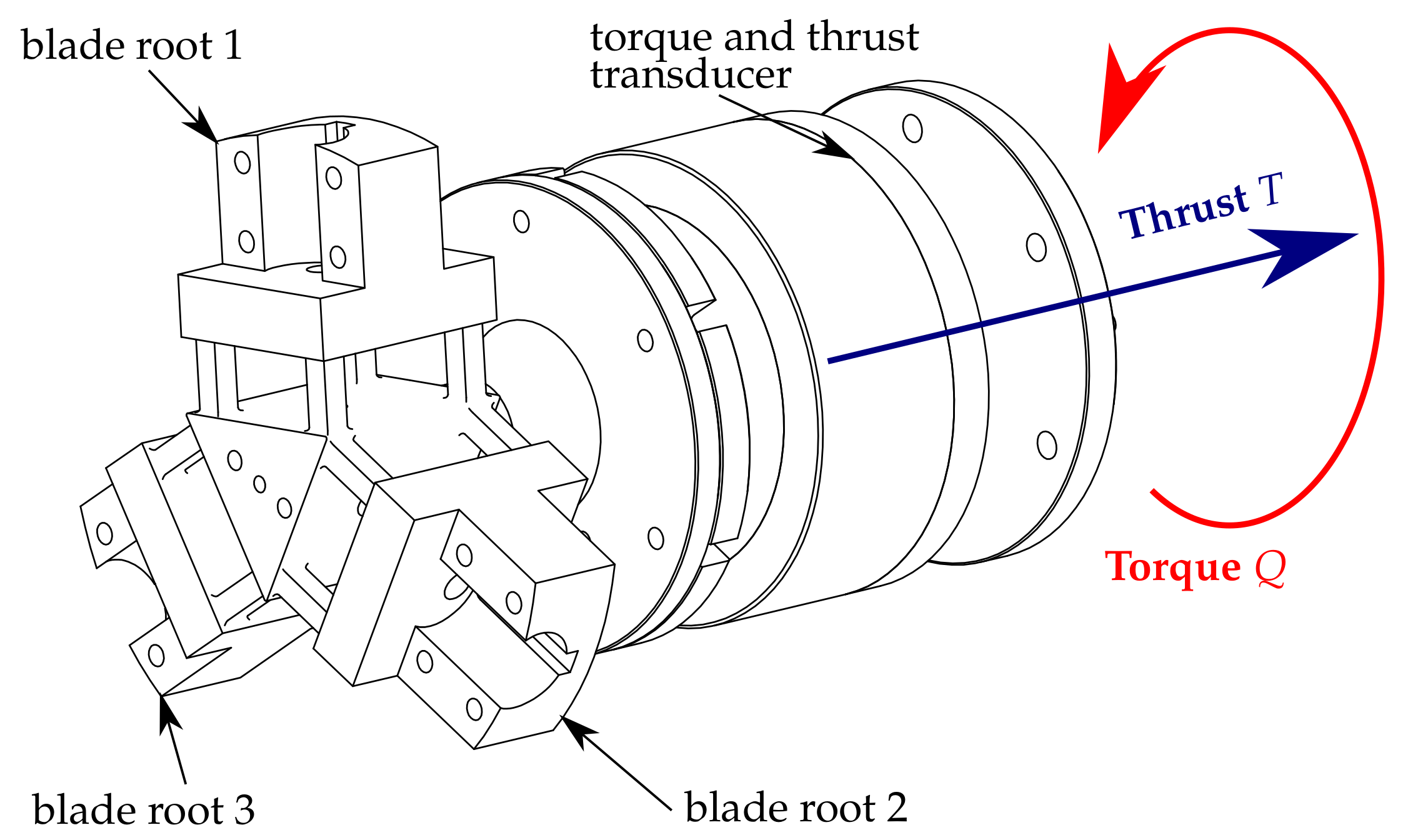
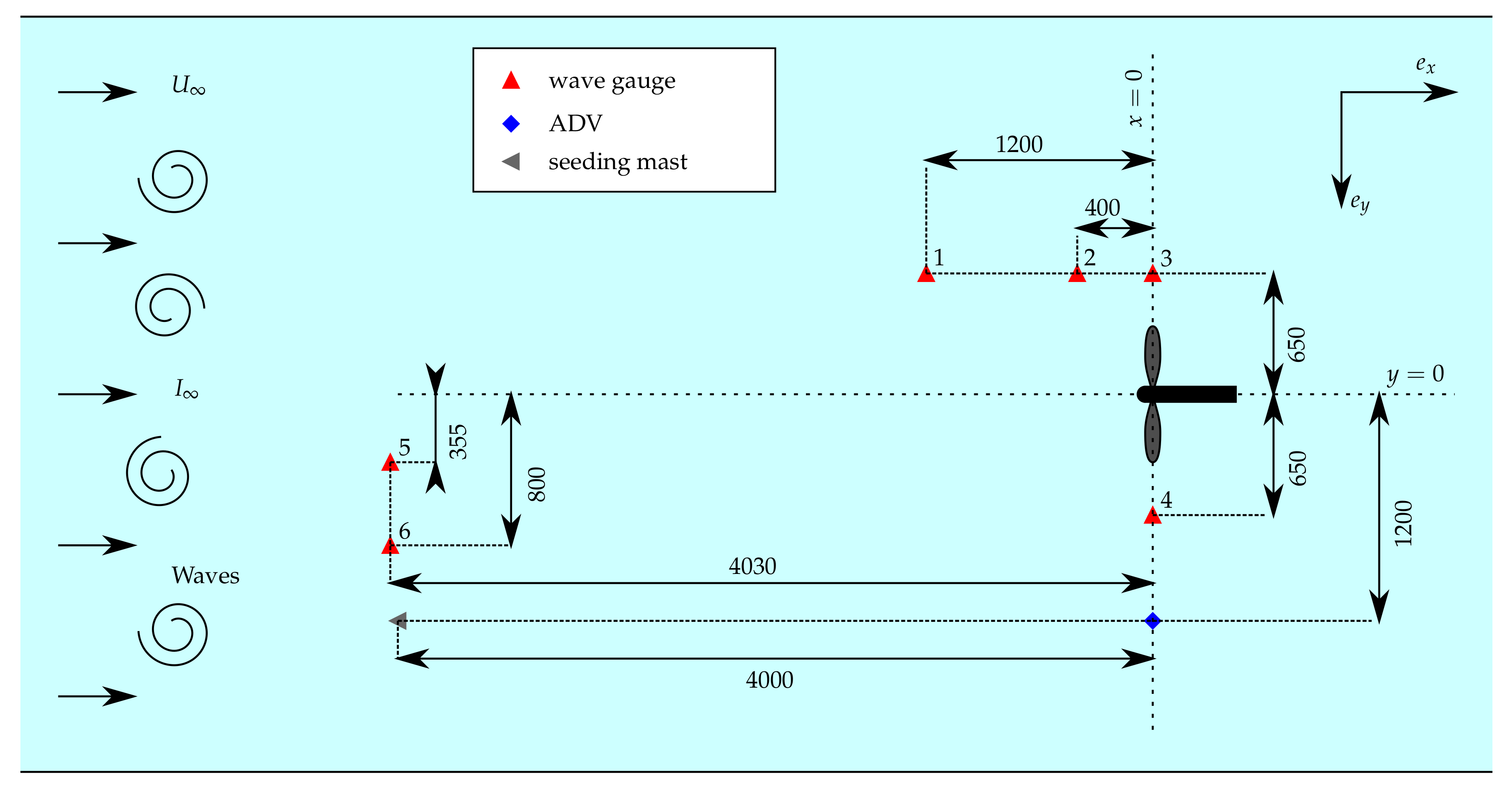
| Laboratory Name | IFREMER | CNR-INM | FLOWAVE |
|---|---|---|---|
| Type of tank | flume | towing | flume |
| Length [m] | 18 | 220 | 15 |
| Width × Depth [m] | 4 × 2 | 9 × 3.5 | 15 × 2 |
| Blockage ratio [%] | 5.1 | 1.3 | 1.4 |
| Speed range [m/s] | 0.1 to 2.2 | 0.1 to 10 | 0.1 to 1.6 |
| Turbulence int. [%] | 1.5 to 15 | NA | 5 to 11 |
| Wave freq. [Hz] | 0.5 to 2 | 0.4 to 1.25 | 0.2 to 1.2 |
| Wave max. amp. [mm] | 150 | 450 | 450 |
| Torque and Thrust Transducer | |
|---|---|
| Thrust | 500 N |
| Torque | 50 N·m |
| Case | Type | Flow Speed | Wave | Wave |
|---|---|---|---|---|
| [m/s] | freq. [Hz] | ampl. [mm] | ||
| 1 | current | 0.8 | - | - |
| 2 | regular | 0.8 | 0.6 | 75 |
| 3 | regular | 0.8 | 0.5 | 35 |
| 4 | current | 1.0 | - | - |
| 5 | regular | 1.0 | 0.7 | 75 |
| 6 | regular | 1.0 | 0.6 | 55 |
| 7 | irregular | 0.8 | s | mm |
| Case # | IFREMER | CNR-INM | FLOWAVE |
|---|---|---|---|
| 1 | 0.826 | 0.843 | 0.825 |
| 2 | 0.848 | 0.848 | 0.827 |
| 3 | 0.846 | NA | 0.822 |
| 4 | 1.024 | 1.037 | 1.036 |
| 5 | 1.056 | 1.036 | NA |
| 6 | 1.047 | NA | 1.031 |
| 7 | 0.840 | NA | 0.826 |
| Case # | 1 | 4 | 2 | 6 | 7 | |
|---|---|---|---|---|---|---|
| [W] | IFREMER | 44.5 | 89.2 | 56.4 | 109.2 | 52.0 |
| CNR-INM | 43.8 | 86.9 | 45.7 | 89.5 | 45.4 | |
| FLOWAVE | 52.9 | 104.0 | 53.5 | 104.5 | 53.7 | |
| [W] | IFREMER | 1.2 | 2.9 | 19.4 | 24.0 | 11.8 |
| CNR-INM | 1.5 | 1.2 | 12.8 | 11.6 | 5.5 | |
| FLOWAVE | 4.8 | 9.6 | 12.0 | 13.0 | 8.8 | |
| [N] | IFREMER | 112.9 | 188.7 | 139.0 | 206.6 | 135.3 |
| CNR-INM | 111.0 | 174.5 | 125.6 | 176.2 | 119.5 | |
| FLOWAVE | 132.5 | 206.1 | 131.5 | 204.2 | 130.8 | |
| [N] | IFREMER | 1.5 | 3.2 | 25.3 | 24.4 | 16.6 |
| CNR-INM | 0.8 | 1.8 | 17.9 | 11.5 | 7.7 | |
| FLOWAVE | 6.0 | 9.8 | 15.0 | 13.3 | 10.9 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaurier, B.; Ordonez-Sanchez, S.; Facq, J.-V.; Germain, G.; Johnstone, C.; Martinez, R.; Salvatore, F.; Santic, I.; Davey, T.; Old, C.; et al. MaRINET2 Tidal Energy Round Robin Tests—Performance Comparison of a Horizontal Axis Turbine Subjected to Combined Wave and Current Conditions. J. Mar. Sci. Eng. 2020, 8, 463. https://doi.org/10.3390/jmse8060463
Gaurier B, Ordonez-Sanchez S, Facq J-V, Germain G, Johnstone C, Martinez R, Salvatore F, Santic I, Davey T, Old C, et al. MaRINET2 Tidal Energy Round Robin Tests—Performance Comparison of a Horizontal Axis Turbine Subjected to Combined Wave and Current Conditions. Journal of Marine Science and Engineering. 2020; 8(6):463. https://doi.org/10.3390/jmse8060463
Chicago/Turabian StyleGaurier, Benoît, Stephanie Ordonez-Sanchez, Jean-Valéry Facq, Grégory Germain, Cameron Johnstone, Rodrigo Martinez, Francesco Salvatore, Ivan Santic, Thomas Davey, Chris Old, and et al. 2020. "MaRINET2 Tidal Energy Round Robin Tests—Performance Comparison of a Horizontal Axis Turbine Subjected to Combined Wave and Current Conditions" Journal of Marine Science and Engineering 8, no. 6: 463. https://doi.org/10.3390/jmse8060463
APA StyleGaurier, B., Ordonez-Sanchez, S., Facq, J.-V., Germain, G., Johnstone, C., Martinez, R., Salvatore, F., Santic, I., Davey, T., Old, C., & Sellar, B. (2020). MaRINET2 Tidal Energy Round Robin Tests—Performance Comparison of a Horizontal Axis Turbine Subjected to Combined Wave and Current Conditions. Journal of Marine Science and Engineering, 8(6), 463. https://doi.org/10.3390/jmse8060463








