Abstract
Numerical models have been widely used for the resource characterization and assessment of tidal instream energy. The accurate assessment of tidal stream energy resources at a feasibility or project-design scale requires detailed hydrodynamic model simulations or high-quality field measurements. This study applied a three-dimensional finite-volume community ocean model (FVCOM) to simulate the tidal hydrodynamics in the Passamaquoddy–Cobscook Bay archipelago, with a focus on the Western Passage, to assist tidal energy resource assessment. IEC Technical specifications were considered in the model configurations and simulations. The model was calibrated and validated with field measurements. Energy fluxes and power densities along selected cross sections were calculated to evaluate the feasibility of the tidal energy development at several hotspots that feature strong currents. When taking both the high current speed and water depth into account, the model results showed that the Western Passage has great potential for the deployment of tidal energy farms. The maximum extractable power in the Western Passage was estimated using the Garrett and Cummins method. Different criteria and methods recommended by the IEC for resource characterization were evaluated and discussed using a sensitivity analysis of energy extraction for a hypothetical tidal turbine farm in the Western Passage.
1. Introduction
Instream tidal energy is one of the most popular marine renewable energy sources because it is highly predictable and the associated technology is relatively mature [1,2,3,4]. One of the important steps toward harvesting instream tidal energy is resource characterization and assessment, at either the project-design or regional scales. Although significant efforts have been made to assess the maximum potential of tidal stream energy at a system-wide scale using theoretical methods or numerical models [5,6,7,8,9,10,11,12], the accurate assessment of tidal energy resources at the project-design scale requires detailed tidal hydrodynamic information obtained from intense field measurements [13,14,15] and high-resolution simulations using three-dimensional (3-D) numerical models [16,17,18,19,20,21]. Field measurements can not only provide direct and accurate resource assessment at a specific site but also support model validation and build confidence in the models. On the other hand, numerical models can be used to generate rich data sets at larger spatial–temporal scales to support resource assessment and guide further field measurements. For example, numerical models can be used to evaluate the efficiency of multiple tidal farms [22,23], the effects of tidal energy extraction on vertical mixing [24], and flushing time [25,26], and provide better coverage in both the temporal and spatial domains than measurements. Extended model validation using high-quality measured data is essential to minimize the uncertainties of resource assessment. The International Electrotechnical Commission (IEC) Technical Specification (TS) recommends that tidal resource characterization be conducted based on detailed and accurate hydrodynamic information, which can be obtained from either direct field measurements or hydrodynamic modeling [27]. Specifically, IEC recommends that for small projects whose total extracted power is less than 10 MW or 2% of the theoretical tidal resource, extractable energy at the project site should be estimated based on the modeled undisturbed flow or direct velocity measurements at the turbine locations. However, for large projects whose total expected power output is greater than 10 MW or 2% of the total theoretical undisturbed resource, high-resolution modeling should be used, along with adequate model validation using measurement data and energy extraction simulations [27].
Clearly, to follow the IEC recommendations for tidal resource characterization and assessment, the tidal hydrodynamic model should be developed with a high resolution and be validated using field measurements, which could be challenging at times because of the need for high-performance computing resources and the lack of field measurements. A previous modeling study was carried out to evaluate the efficiency of energy extraction in the Western Passage in the U.S. state of Maine [28]. However, this model was validated with limited measured data, and the theoretical resources in the Western Passage were not assessed. Over the last decade, a number of numerical models have been developed to assess the amount of energy extraction by adding a momentum sink term in the governing equations based on the actuator-disc theory [7,17,28,29,30,31]. Numerical models that have energy extraction capabilities enable accurate and realistic resource characterization and assessment, as well as environmental interactions, at any desired project scale [32,33]. This study presents a modeling effort conducted to assess the tidal energy resources at a highly energetic site—the Western Passage [12,34]—using a high-resolution hydrodynamic model. This study followed the IEC recommendations for model configurations and model validation. The theoretical resources in the Western Passage were estimated based on the theory developed by Garrett and Cummins [5] and the model results. Finally, a sensitivity analysis with energy extraction from a tidal turbine farm was conducted to demonstrate the advantage of using numerical modeling to support tidal energy resource assessment by providing essential information.
2. Methods
2.1. Study Site
The Western Passage is an energetic tidal channel between New Brunswick, Canada, and the state of Maine in the United States (Figure 1). It is part of a large and complex coastal system, the Passamaquoddy–Cobscook Bay archipelago, which consists of many tidal channels and coastal bays, including Passamaquoddy Bay, Head Harbor Passage, Cobscook Bay, and South Bay. The Passamaquoddy–Cobscook Bay archipelago is connected to the mouth of the Bay of Fundy, which has one of the largest tidal ranges in the world [29]. Because of the large tidal range in the coastal bay system, many of the tidal channels show strong tidal currents and, therefore, hold great promise for tidal energy development [28,35]. The Western Passage has been identified as one of the top-ranked sites for tidal stream energy development in U.S. coastal waters, based on the initial nation-wide tidal resource assessment [12] and a number of criteria, including tidal power density, market value, energy price, shipping cost, and transmission distance [34]. Moreover, its relatively deep channel makes the Western Passage a favorable site for tidal power development.
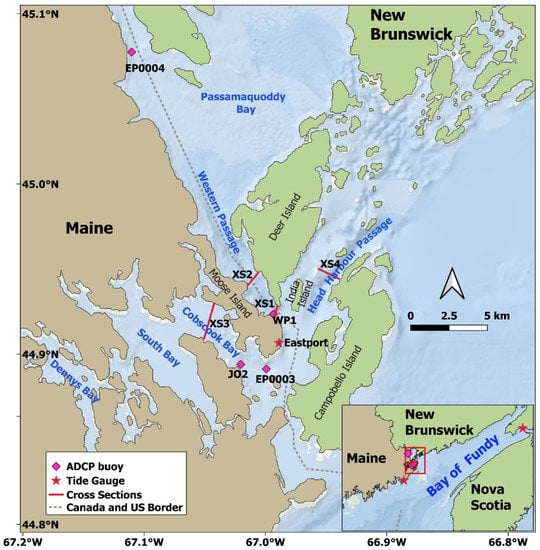
Figure 1.
Map of the study site and locations of the observation stations.
Although the focus of this study was on the tidal hydrodynamics in the Passamaquoddy–Cobscook Bay archipelago, to minimize the open-boundary effect on the area of interest, i.e., the Western Passage and other tidal channels, and to better understand the tidal wave propagation from the Gulf of Maine into the Bay of Fundy and the archipelago, the model domain was extended farther out to cover the entire Bay of Fundy and the northern part of the Gulf of Maine. Figure 2. shows the model domain and bathymetry distribution. Bathymetric data were obtained from various data resources. Bathymetry in the large area of the Bay of Fundy and Gulf of Maine was interpolated from the National Oceanic and Atmospheric Administration’s (NOAA’s) ETOPO1 1-arc-minute Global Relief Model [36]. Inside the Passamaquoddy–Cobscook Bay archipelago, bathymetric data were digitized from NOAA and Canadian Hydrographic Service navigation charts and supplemented with multi-beam data for the Western Passage and Cobscook Bay [28]. Water depths in most of the coastal areas are generally shallow and less than 100 m. The deepest area in the model domain is near the open boundary and the southeast side of Grand Manan Island.
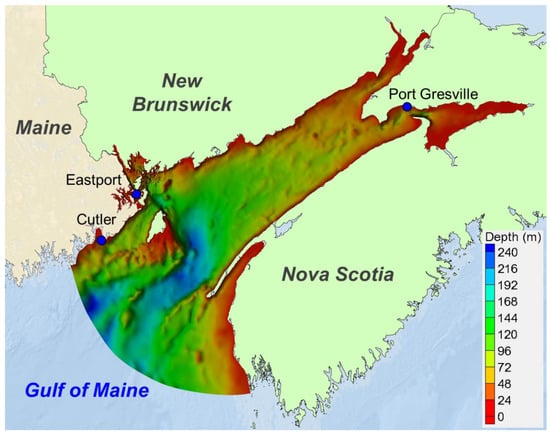
Figure 2.
Model domain and bathymetry. The three blue circles represent the tide stations used for model calibration of the water level.
2.2. Tidal Hydrodynamic Model
The unstructured-grid, finite-volume, community ocean model (FVCOM) [37,38] was used in this study to simulate the tidal hydrodynamics in the Western Passage and its adjacent coastal waters, including the Bay of Fundy. FVCOM solves the 3-D primitive Navier–Stokes equations to simulate water surface elevation, velocity, salinity, temperature, and other transport constituents. FVCOM employs a number of ocean turbulence closure models for the parameterization of the vertical eddy viscosity and thermal diffusion coefficient. In the present study, the Mellor–Yamada level 2.5 (MY-2.5) turbulent closure model was used [39]. The unstructured-grid modeling framework in FVCOM is particularly suitable for resolving complex coastlines and providing accurate simulations with great computational efficiency. FVCOM has been widely used around the world to simulate a wide range of coastal problems, including coastal hydrodynamics [40,41,42,43], water quality and sediment transport [44,45,46,47], storm surge and coastal flooding [48,49,50,51,52], and tidal energy [7,18,20,21,28].
To enable the assessment of future scenarios of proposed tidal turbine array development, a numerical model that has energy extraction capabilities is required. To simulate tidal energy extraction, a marine hydrokinetic (MHK) module was implemented in the FVCOM model based on the momentum sink approach [7,28]. The FVCOM-MHK model was validated in an idealized tidal channel and bay system against an analytical solution [7] and applied to simulate tidal energy extraction and the associated environmental impacts [53,54,55]. The total extracted tidal power by a tidal turbine farm at any location with a velocity can be calculated using the following formula [7]:
where N is the number of turbines in each grid element, M is the total number of elements containing turbines, is sea water density, CT is the turbine thrust coefficient, As is the flow-facing area swept by turbines, and is the velocity vector at the turbine hub height.
2.3. Model Configurations and Boundary Conditions
The Passamaquoddy–Cobscook Bay archipelago is strongly dominated by tidal forcing, with little influence of river discharge and wind-induced wave action [28]. There are two major rivers in the Passamaquoddy–Cobscook Bay archipelago system. The St. Croix River, which forms part of the United States–Canada border between Maine and New Brunswick, discharges into the Passamaquoddy Bay. The Dennys River discharges into the Dennis Bay in Maine. The long-term annual means of the streamflow are 21.24 m3/s and 5.6 m3/s for the St. Croix River and Dennys River, respectively, which are relatively small compared to the model domain [28]. Wind-driven circulation in the archipelago system is also small compared to the strong tidal current. Therefore, similar to [28], the sea surface wind, salinity, and temperature effects are not considered in this study.
The model grid for the Western Passage was initially developed by Rao et al. [28], and the model domain was further extended out to cover the entire Bay of Fundy and northern Gulf of Maine (Figure 2). According to IEC standards, a minimum 50 m grid resolution is required for a Stage 2 design layout study. To meet the IEC recommendations, the model grid resolution in this study varies from 20 m in the Western Passage to approximately 1000 m near the mouth of the Bay of Fundy and 2000 m along the open boundary in the northern Gulf of Maine. The model mesh consists of about 231,000 elements and 120,000 grid nodes. The model grid for the entire model domain is presented in Figure 3a, and Figure 3b shows a zoom-in grid for the Passamaquoddy–Cobscook Bay archipelago, where the Western Passage, Cobscook Bay, and Head Harbor Passage have the highest grid resolution of 20 m. Although stratification in the Passamaquoddy–Cobscook Bay archipelago is weak because the influence of river discharge is small, a depth-averaged modeling analysis is not accurate enough because tidal energy extraction is designed to occur at a specific water depth (hub height) of the water column. Therefore, all simulations in this study were run in 3-D mode. The model vertical resolution was specified to have 15 uniform sigma layers. Open-boundary conditions were specified with tidal elevation time histories generated using 13 tidal constituents obtained from the TPXO7.2 global ocean tide database [53]. The 13 tidal constituents were M2, S2, N2, K2, K1, O1, P1, Q1, M4, MS4, MN4, Mm, and Mf.
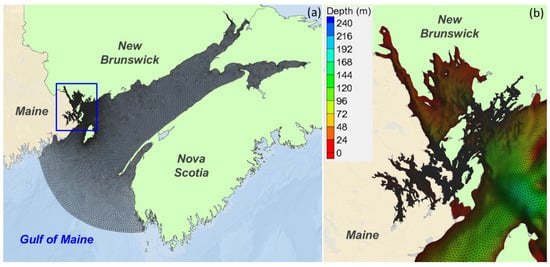
Figure 3.
(a) Model grid of the finite-volume community ocean model (FVCOM) for the model domain that consists of the Passamaquoddy–Cobscook Bay archipelago (blue box), Bay of Fundy, and northern Gulf of Maine; (b) zoomed-in model grid with bathymetry for the Passamaquoddy–Cobscook Bay archipelago.
The wetting and drying process was simulated in the model domain with a wetting–drying criterion of 0.05 m. The model was run with an external-mode time step of 0.05 s, and a multiplier of 5 was used for the internal mode simulation. The initial hydrodynamic conditions were a null velocity and water level throughout the model domain. A one-week spin-up period was used such that the model reached dynamic equilibrium. Model simulations were conducted for three separate periods: July 2000 and September 2001 for model calibration and from April to June 2017 (three months) for model validation.
2.4. Observation Data for Model Calibration and Validation
Field measurements are important not only for site-specific tidal energy resource characterization but also for numerical model validation. Two types of data were used in this study to support model calibration and validation: water surface elevation and tidal current. Field data in the study area are very limited. There is only one NOAA real-time tidal gauge (8410140) in the model domain, located at Eastport, Maine. Therefore, additional water-level data were obtained from XTide predictions to support model calibration. Two XTide stations were selected from outside of the archipelago—at Cutler, Maine, and Port Greville, Nova Scotia (Figure 2). Measurements of historical currents in the Passamaquoddy–Cobscook Bay archipelago are also very limited.
Historical current data collected by NOAA were available through the Currents Measurement Interface for the Study of Tides, a web-based data management system maintained by NOAA to analyze and disseminate current data from coastal and estuarine collections. Current measurements were conducted by NOAA during the period of June to September 2000 at Estes Head (EP0003) and St. Croix River (EP0004), both in Maine (Figure 1). Two bottom-mounted acoustic Doppler current profilers (ADCPs) were deployed at depths of 34.1 m and 32 m at EP0003 and EP0004, respectively. Current speed and direction data were obtained at 6 min intervals and a vertical bin resolution of 2 m. A historical current buoy J02 was deployed by the Northeastern Regional Association of Coastal Ocean Observation Systems (NERACOOS) in Cobscook Bay for the period of September 2001 to June 2007 (Figure 1). Current data from EP0003, EP0004, and J02 were used for model calibration.
To better characterize the tidal hydrodynamics and turbulence characteristics, a more recent survey was conducted by the National Renewable Energy Laboratory (NREL) at station WP1 in the Western Passage (Figure 1). Two bottom-mounted ADCPs (a 600 kHz Workhorse Sentinel and a 500 kHz Nortek Signature) were deployed for a period of three months from April to June 2017. The ADCP was deployed at a water depth of 45 m and configured at a sampling interval of 6 min and vertical bin size of 1 m. The water level was also measured at the site during the ADCP deployment period. The observed water-level and velocity data at the WP1 station were used for model validation.
In this study, the water-level data at Eastport, Cutler, and Port Greville, as well as the current data from NOAA and NERACOOS, were used for model calibration. The most recent data, for both the water-level and velocity measurements collected by NREL at station WP1, were used for model validation. Station information for all the measurements used for model calibration and validation is listed in Table 1.

Table 1.
List of observed data stations for model calibration and validation.
3. Results and Discussion
3.1. Model Calibration
To accurately assess the tidal energy resources at any specific site or the maximum tidal energy potential (i.e., a theoretical undisturbed resource) using a modeling approach, it is important to calibrate and validate the numerical model using field observations. In this study, model calibration was performed by comparing modeled tidal elevations and velocities with field measurements at various locations during different time periods. Three representative error statistical parameters, the root-mean-square-error (RMSE), the scattered index (SI), and the coefficient of determination (R2), were calculated to assess the model’s ability to reproduce the characteristics in the study domain. Model parameters, such as the bottom roughness, vertical layers, and open-boundary sponge layer (radius, and friction coefficient), were also adjusted iteratively during the calibration runs to achieve an overall satisfactory agreement between the model predictions and field observations. The final calibrated bottom roughness height was 0.005 m. The calibrated radius and friction coefficient of the open-boundary sponge layer were 1500 m and 0.001, respectively. Two model runs with 15 and 30 uniform sigma layers were conducted to evaluate the effect of the total number of vertical layers on model accuracy. The model results with 30 vertical layers showed little improvement in model performance error statistics over 15 vertical layers. Therefore, 15 vertical layers were selected in all the model runs to achieve better runtime efficiency while maintaining the same level of model accuracy.
The simulated water levels at Cutler, Eastport, and Port Greville were compared with the data for a 14-day period in October 2001 (Figure 4). Overall, the model reproduced the tide-level variations precisely in both the tidal range and phase in the Passamaquoddy–Cobscook Bay archipelago and Bay of Fundy. The water-level time history at all three stations indicated that the tide in the model domain is dominated by semi-diurnal tide (M2) with a strong signal of spring-neap tidal cycle. The tidal wave is amplified as it propagates from the Gulf of Maine (near the open boundary) (Figure 4a) into the Passamaquoddy–Cobscook Bay archipelago (Figure 4b) and toward the Bay of Fundy (Figure 4c). The root-mean-square errors (RMSEs) at the three tidal stations ranged between 0.15 m at Cutler station and 0.41 m at Port Greville station, where the tidal range is greater than 10 m during spring tide (Table 2). The correlation coefficients (R2) were persistently higher than 99% at all three stations (Table 2). The scatter indexes (SIs) were relatively small, indicating that the model was able to reproduce the water level accurately and consistently (Table 2).
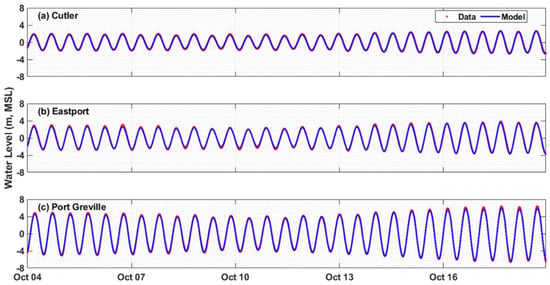

Table 2.
Error statistics of water-level predictions for model calibration.
The modeled depth-averaged principal velocities were compared with the measured data at stations EP0003 and EP0004 for July 2000 and at station J02 for October 2001 (Figure 5). Overall, the model results matched the measurements well, especially during flood tides. However, the model overpredicted the ebb currents at EP0003, where the measurements showed tidal current asymmetry with flood currents larger than ebb currents (Figure 5a). The error statistics for current predictions at EP0003, EP0004, and J02 are presented in Table 3. The largest RMSE is 0.38 m/s at station EP0003, which is consistent with the time–series plot shown in Figure 5a. The RMSEs at EP0004 and J02 are 0.14 m/s and 0.27 m/s, respectively, which are satisfactory for the current predictions. The correlation coefficients (R2) for the current predictions are all above 0.94, indicating that the model predictions are highly correlated to the measurements at all three stations.
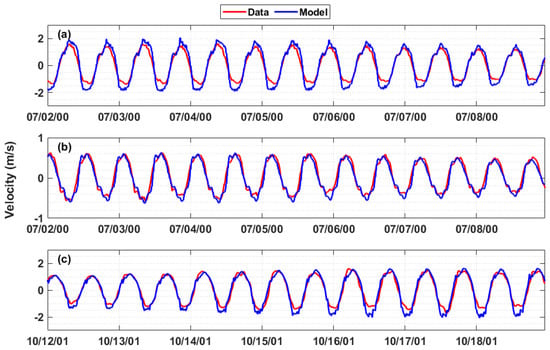
Figure 5.
Comparison of the modeled and observed depth-averaged tidal currents (principal component) at (a) EP0003, (b) EP0004, and (c) J02. A positive value denotes the flood current. Station locations are shown in Figure 1.

Table 3.
Error statistics of the current predictions at stations EP0003, EP0004, and J02.
3.2. Model Validation
Once the model was calibrated, model validation was conducted for a different simulation period using the calibrated model parameters. The recent observed data, including water level and velocity collected at station WP1 in the Western Passage, were used for model validation. The model was run for three months, corresponding to the measurement period of April to June 2017.
The long (three-month) record of field measurements at WP1 allowed for accurate harmonic analysis. Therefore, the model skills for predicting water level and currents at WP1 were evaluated by comparing the tidal level harmonic constituents derived from the measurements and model results. Water levels were decomposed into 10 tidal components (M2, N2, S2, K1, O1, P1, Q1, M4, M6, and MK3) using harmonic analysis. Comparisons of the constituents of each observed and predicted tidal level are provided in Table 4. The maximum difference between modeled and measured tidal constituents is −0.11 m for the principal lunar semi-diurnal tide M2, which is about 3.9% underpredicted relative to the observed M2 constitute (2.62 m). Differences between the model predictions and measurements for other tidal constituents are all small; even the percentage error is high because of the small magnitudes of the constituents. Therefore, the model performed very well in simulating the tidal elevation as part of the model validation.

Table 4.
Comparison of the observed and modeled water level at WP1 in the Western Passage.
To better visualize a comparison between the modeled and observed velocity through the water column, velocity contours were generated with respect to water depth and time (Figure 6). The distribution pattern of the modeled velocity contours for the u (east) and v (north) components (Figure 6c,d) is very similar to the observations (Figure 6a,b). Both model results and observations show consistently strong currents through the entire water column, with distinct flood and ebb tidal signals. In general, both the model results and the observed data showed a stronger flood current (negative u and positive v) than an ebb current (positive u and negative v). The velocity magnitudes were mostly uniformly distributed through the water column, except for the modeled v-velocity, which showed a slightly weaker current near the surface during the flood tide (positive value) (Figure 6d).
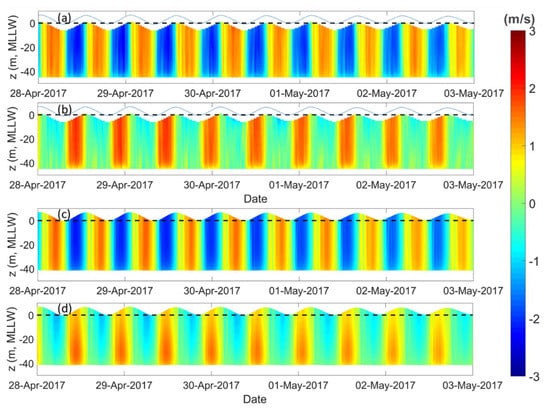
Figure 6.
Comparison of the observed and modeled velocity time series through the water column at station WP1 in the Western Passage. (a,b) The observed east (u) and north (v) velocity components; (c,d) the modeled east (u) and north (v) velocity components.
Figure 7 shows a comparison of the vertical profiles of the velocity percentiles based on the three-month model results and observed data. Velocity percentiles were calculated as 10%, 25%, 50%, 75%, and 90%. Overall, the model results are similar to the observations in terms of the range of the velocity percentiles. Strong tidal asymmetry in the velocity profiles is seen in both the modeled results and the observations, where currents are stronger during flood tides (negative value) and weaker during ebb tides (positive value) (Figure 7c,f). The mean error of the predicted mean velocity-magnitude profile is −0.134 m/s, where the negative sign indicates model underprediction, and the percentage error is 11%. Although the model showed good overall skill in predicting the velocity vertical profiles in the Western Passage, it overpredicted the v-velocity component during flood tides (negative value) and underpredicted it during ebb tides (positive value) (Figure 7b,e). In particular, the model predicted a strong ebb current near the bottom (Figure 7e), which was not shown in the observed data (Figure 7b). The cause of such a discrepancy between the model results and observed data is likely due to the accuracy of model bathymetry, which was mainly interpolated from bathymetric datasets digitized from old NOAA navigation charts [28] that may not accurately represent the real bathymetry in the Western Passage when the ADCP data were collected in 2017.
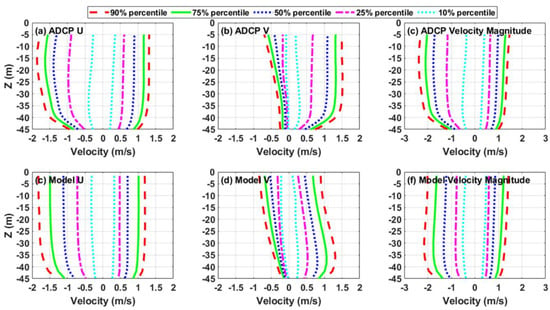
Figure 7.
Comparison of the observed and modeled vertical profiles of velocity percentiles at station WP1 in the Western Passage based on three months of records: (a,b) the observed east (u) and north (v) velocity components; (d,e) the modeled east (u) and north (v) velocity components; (c,f) the observed and modeled velocity magnitudes, with positive as the ebb current and negative as the flood current. Velocity percentiles were calculated as 10%, 25%, 50%, 75%, and 90%.
The error statistics calculated at WP1 show the model’s excellent ability to simulate a tidal current (Table 5). Similar to the water-level results, the model underpredicted the M2 tidal current by 0.21 m/s, which is 12.4% of the M2 current speed. All other predicted tidal constituents are no more than 0.07 m/s smaller than the observed tidal current constituents. The model validation results in this study are comparable to those presented in [28]. Because the tide is the dominant force in the system, the model is considered fully capable of reproducing tidal hydrodynamics and characterizing the tidal energy resources in the Western Passage.

Table 5.
Comparison of the observed and modeled tidal current constituents at WP1 in the Western Passage.
3.3. Characteristics of Tidal Hydrodynamics
Once the model was calibrated and validated, the model results could be used to characterize the resource and identify hotspots for tidal energy development in the region. Figure 8 shows the horizontal distribution of the depth-averaged velocities during peak flood and ebb tides. Clearly, strong currents exist along the main channel of the Western Passage, Cobscook Bay, and Head Harbor Passage. In general, these areas with strong currents during both the flood and ebb tides represent potential hotspots for future tidal energy development. However, tidal asymmetry also exists in some areas between the flood and ebb tides. For example, in the tidal channel between Deer Island and Indian Island, the tidal currents are much stronger during the flood tide (Figure 8b) than those during the ebb tide (Figure 8a). On the other hand, the ebb currents (Figure 8b) are significantly stronger than the flood currents in the Head Harbor Passage (Figure 8a).
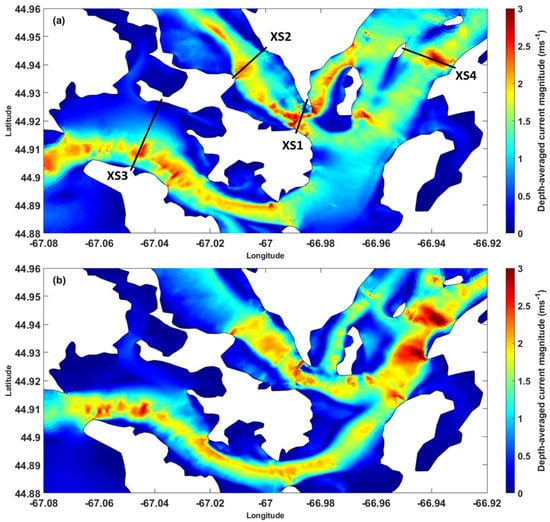
Figure 8.
Depth-averaged velocity magnitudes in the Western Passage, Cobscook Bay, and Head Harbor Passage during (a) peak flood and (b) peak ebb tides in spring tide on April 28, 2017.
Because tidal turbines are installed in the water column to assess the feasibility of a project site for tidal energy extraction, the vertical structure of the current magnitude and the water depth distribution should be considered. Based on the results of the depth-averaged velocity distribution (Figure 8), the current magnitudes along the four cross sections with strong tidal currents were generated. Cross sections XS1 and XS2 are located in the Western Passage, cross section XS3 is in the Cobscook Bay, and cross section XS4 is in the Head Harbor Passage. Areas where strong currents occur only during flood or ebb tides, such as the south part of the Head Harbor Passage and the channel between Deer Island and Indian Island, were not selected for cross-sectional velocity analysis.
Figure 9 shows the normal velocity magnitudes along XS1 in the south end of the Western Passage. The water depth in the deep channel is about 120 m. A positive value indicates the flood current flowing away from the reader (Figure 9a). Strong flood and ebb currents occupy most of the deep channel and the U.S. side of the passage (left side) through the entire water column; the maximum current magnitude is greater than 2.5 m/s during the flood tide. The current distribution on the north end of the cross section is complicated; consistent ebb currents (negative value) occur during both the flood and ebb tides, and reverse flow (positive value) occurs at the bottom layer of the water column during the ebb tide. The consistently strong tidal currents in the deep channel and the U.S. side of the passage indicate that the area is a good candidate for tidal turbine farm deployment.
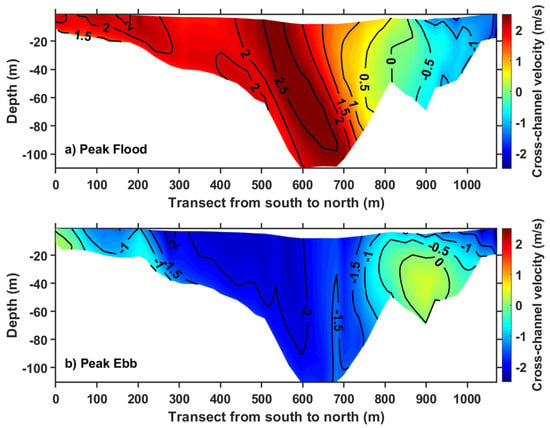
Figure 9.
Normal velocity magnitudes at (a) peak flood and (b) peak ebb tides along cross section XS1 in the Western Passage. Positive velocity is away from the reader. The cross-section location is shown in Figure 1.
Strong currents were observed in XS2 (Figure 10), especially on the U.S. side (the left side of the plot). The current speed in the main channel is approximately 1.75 m/s during both the flood and ebb tidal phases. The maximum current speed (>2 m/s) occurs in the U.S. side of the passage where the water depth is relatively shallow—about 30 m. Again, the current structure on the Canadian side is small and complicated, showing strong vertical shear during the flood tide (Figure 10a).
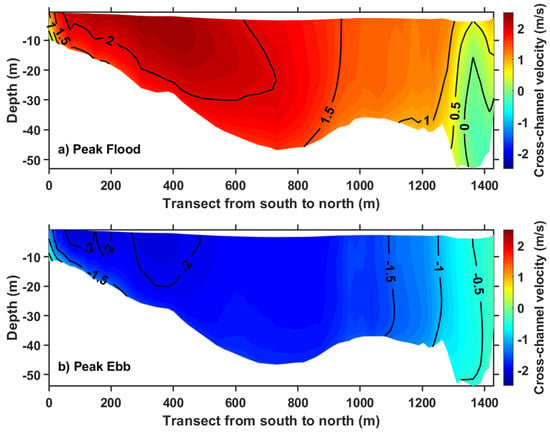
Figure 10.
Normal velocity magnitudes at (a) peak flood and (b) peak ebb tides along cross section XS2 in the Western Passage. Positive velocity is away from the reader. The cross-section location is shown in Figure 1.
Figure 11 shows the current distribution along XS3 in Cobscook Bay. Although strong currents (over 2.5 m/s) are present during both the flood and ebb tides in the main channel, the water depth is very shallow. Most of the cross section is less than 10 m deep, and the deepest water depth is 25 m, which makes the area challenging for the deployment of tidal turbine farms.
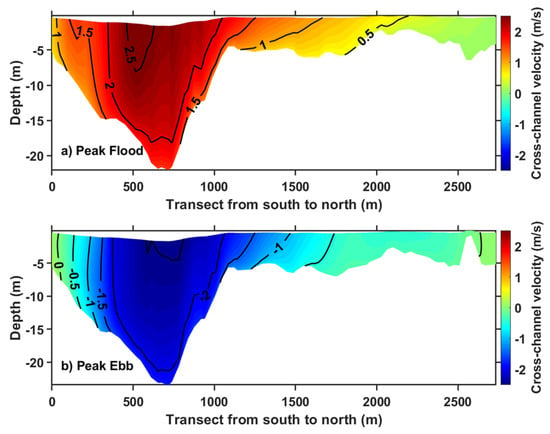
Figure 11.
Normal velocity magnitudes at (a) peak flood and (b) peak ebb tides along cross section XS3 in Cobscook Bay. Positive velocity is away from the reader. The cross-section location is shown in Figure 1.
XS4 in the Head Harbor Passage (Canada) shows the strongest current magnitude and the largest area of high velocity among the four cross sections. The current speeds in most parts of this cross section are greater than 1.5 m/s during the flood tide (Figure 12a) and greater than 2 m/s during the ebb tide (Figure 12b). The seabed in the cross section is relatively flat, but the water depth is shallow (approximately 30 m deep for most of the cross section). Again, this shallow water depth may pose a challenge for the installation of tidal turbine farms, unless small tidal turbines (e.g., rotor diameters less than 15 m) are considered.
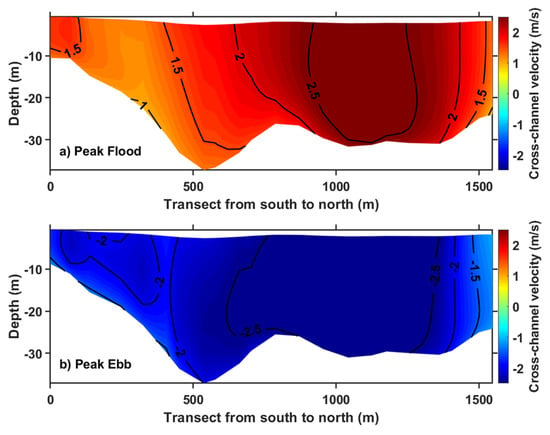
Figure 12.
Normal velocity magnitudes at (a) the peak flood and (b) peak ebb tides along cross section XS4 in Head Harbor Passage. Positive velocity is toward the reader. The cross-section location is shown in Figure 1.
3.4. Along-Channel Kinetic Energy Flux
The predicted tidal currents within the potential deployment area can be used to estimate the tidal kinetic-energy flux through a channel cross section. First, the temporal-averaged power density at any location can be calculated using the predicted tidal currents as follows:
where is the temporal-averaged power density (kW/m2) at any location or grid cell in the model, N is the total number of velocity output timesteps over the simulation period, is the seawater density (1025 kg/m3), and U is the current magnitude normal to the cross section (m/s).
Figure 13 shows the distribution of the mean power density at each of the four cross sections (XS1–XS4). XS1 maintains around 1.0 kW/m2, which is evenly distributed in the middle–bottom layers of the channel that are deep enough for device deployment (Figure 13a). XS2 and XS3 show a range of 1–2 kW/m2 power density available near the surface (Figure 13b,c). The highest power density value, up to 3.0 kW/m2, was identified at XS4, which presented the strongest current at a magnitude of 2.5 m/s (Figure 13d).
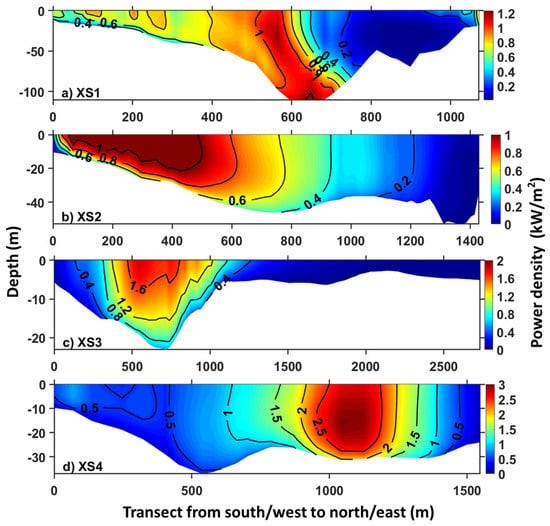
Figure 13.
Predicted tidal power density along cross sections (a) XS1 and (b) XS2 in the Western Passage, (c) XS3 in Cobscook Bay, and (d) XS4 in Head Harbor Passage. The locations of the cross sections are shown in Figure 1.
The mean tidal kinetic-energy flux Pxs across a cross section can be estimated by multiplying the mean power density with the grid cell area and integrating it over the entire cross section using the following formula:
where Ncell is the total number of model grid cells projected along the cross section, and Acell is the projected area for each grid cell. Based on Equation (3), the tidal kinetic energy flux Pxs for each of the four cross sections was estimated to be 45.8 × 103 (kW) for XS1, 22.3 × 103 (kW) for XS2, 9.03 × 103 (kW) for XS2, and 48.6 × 103 (kW) for XS4, respectively.
3.5. Energy Extraction in the Western Passage
As described in Section 3.4, the tidal energy fluxes in the Western Passage (XS1) and the Head Harbor Passage (XS4) are much greater than those in XS2 and XS3. However, compared to XS4 in the Head Harbor Passage, the Western Passage (XS1) is more favorable for tidal energy deployment because of its greater water depth. In this section, the tidal energy extraction capacity in the Western Passage was evaluated through a theoretical analysis and the use of a hypothetical tidal turbine farm. The maximum theoretical extractable tidal power can be estimated based on the formula developed by Garrett and Cummins [5] for a tidal channel connected to two basins:
where γ is a dimensionless constant in the range of 0.21 to 0.24, is the largest tidal constituent amplitude (M2) in the channel, and are the additional Mt tidal constituent amplitudes. Specifying γ = 0.22, = 1025 kg/m3, g = 9.81 m/s2, Qmax = 74,388 m3/s, and from Table 4 into Equation (4) yields Pmax = 447,825 (kW). The Pmax value can be used as a reference (upper limit) for the development of tidal energy projects in the Western Passage. It should be noted that Equation (4) likely overestimates the Pmax value due to the simplification and assumptions made in the derivation of the equation [5].
A hypothetical tidal turbine farm was considered to simulate the energy extraction at a realistic scale in the Western Passage. The tidal farm is located at the south end and U.S. side of the Western Passage, where strong tidal currents occur. The tidal farm consists of a total of 19 tidal turbines, with along-channel spacing of 160 m and cross-channel spacing of 80 m (Figure 14). The tidal turbine hub height and diameter are 15 m and 20 m, respectively. The configuration of the tidal turbine farm is listed in Table 6.
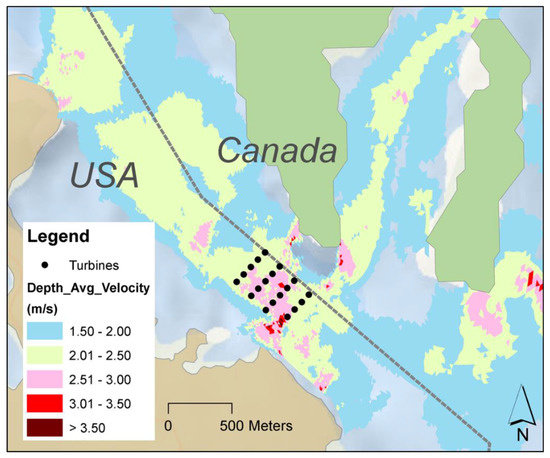
Figure 14.
Layout of the hypothetical tidal turbine farm in the Western Passage.

Table 6.
Tidal turbine configuration and simulated extractable power in the Western Passage.
The tidal energy extraction was simulated using the FVCOM-MHK model [7] based on Equation (1). The extractable energy at any specific site depends on not only the current speed but also the thrust coefficient, which is a function of the turbine design and flow speed for characterizing power extraction efficiency. Many far-field modeling studies showed that a turbine can potentially reach peak efficiency for extracting the maximum power, i.e., 59% of the available power in a system (called the Betz Limit) when the thrust coefficient is specified to be in the range of 0.8–1 [30,33,54,55,56]. Based on the values reported in the previous studies, a thrust coefficient of 0.9 was chosen in this study. For simplicity, the cut-in and cut-out velocities were not considered. The simulated temporally averaged extracted energy was 4810 (kW) for the tidal farm or 253 (kW) per turbine. Because the theoretical resources in the Western Passage are estimated to be 447,825 (kW), the extracted energy by the hypothetical tidal turbine farm is 1.07% of the theoretical resources, which is below the 2% threshold specified in the IEC standards [27].
Another method recommended in the IEC TS for tidal energy resource assessment is to estimate the extractable power of a tidal farm using measured or modeled undisturbed flow when the expected extractable power is smaller than 10 MW or 2% of the theoretical resource in the system. For the purpose of comparison, the extractable power was also estimated using Equation (1) and the modeled undisturbed velocity. All parameters in the calculation were kept the same as those specified in the FVCOM-MHK simulations, including the thrust coefficient (0.9), turbine blade diameter (20 m) in Equation (1), and undisturbed velocity at the turbine hub height (15 m from the seabed) at the 19 turbine locations. The estimated mean power extracted by the tidal farm based on the modeled undisturbed flow field was 5198 (kW), which is 1.2% of the theoretical resources. The extractable power estimated based on the FVCOM-MHK model run with energy extraction is slightly smaller than that directly calculated using undisturbed flow, which is expected because of the flow reduction caused by the turbines and the interactions among the turbines in the tidal farm in the FVCOM-MHK simulations.
Clearly, by doubling the number of tidal turbines in the existing tidal farm, i.e., increasing the turbine distribution density twofold, the estimated extractable power using modeled undisturbed flow will likely exceed the 10 MW and the 2% thresholds. However, the extractable power for the same tidal farm calculated using the FVCOM-MHK model with energy extraction may not exceed both thresholds because the efficiency of energy extraction decreases as the number of turbines increases in the tidal farm [7,22]. Therefore, it is better to use the numerical model with energy extraction to accurately estimate the extractable energy, especially when the energy extraction by the tidal farm is expected to exceed 10 MW or 2% of the theoretical resources.
4. Summary
A high-resolution tidal hydrodynamic model using the unstructured-grid FVCOM was developed to simulate the tidal hydrodynamics and characterize the tidal energy resource in the Passamaquoddy–Cobscook Bay archipelago. The model was calibrated and validated with observation data. The model performance error statistics show good model skills in reproducing the tidal hydrodynamics in the study domain. The mean power densities along selected cross sections were calculated and analyzed. The model results show multiple hotspots that have strong tidal currents where potential tidal instream energy projects could be developed. However, the shallow water depths in some strong current areas, such as Cobscook Bay and Head Harbor Passage, may limit the potential deployment of tidal turbines unless small turbines are considered. The Western Passage on the U.S. side shows great potential for tidal energy extraction because of its strong tidal currents and greater water depth.
The theoretical resources, i.e., the upper limit of extractable energy, in the Western Passage, were estimated to be 447,825 (kW) based on the model results validated using the Garrett and Cummins method [5]. The extractable power for the hypothetical tidal farm was calculated using two different methods recommended by IEC TS, one with undisturbed flow and the other with the FVCOM-MHK model that simulates energy extraction directly. While these two methods provide similar results when the extracted energy is small, the extractable energy estimated using the undisturbed flow method is generally greater because the flow field interaction with the tidal turbine farm is not considered. It should be noted that although IEC recommends two criteria (the extraction of 10 MW or 2% of the theoretical resources) for determining the need to model energy extraction for resource characterization, the 2% criterion could be exceeded before the 10 MW threshold when the system’s theoretical resources are smaller than 500 MW. Therefore, the best practice for tidal resource characterization is to use the method of hydrodynamic modeling with energy extraction.
In this study, the turbine cut-in and cut-out velocities were not considered in the energy extraction simulations, which could overestimate the extractable energy by the tidal turbine farm. In addition, the energy loss due to the effect of friction by the turbine supporting structure was also not considered in the simulations. These factors should be incorporated in future studies to improve the accuracy of the extractable power estimates. As a best practice, tidal resource assessments using model simulations should be conducted with the support of field measurements to ensure quality control because the model results always contain errors and uncertainties. Finally, the Garrett and Cummins’ method (Equation (4)) was developed based on a 1-dimensional governing equation for the tidal flow. Further, the water levels at both ends of the channel are independent, and the head difference can be represented by a sinusoidal function with a tidal amplitude [5]. However, in reality, tidal currents typically vary across the channel, and the tides at both ends of the channel may not be fully independent. Therefore, future studies are needed to modify the Garrett and Cummins method to improve the accuracy of the Pmax estimate using theoretical analysis and numerical modeling approaches.
Author Contributions
Conceptualization, Z.Y., K.H. and L.K.; methodology, Z.Y., T.W., K.H., L.K. and H.X.; validation, Z.Y., T.W., Z.X. and X.F.; formal analysis, Z.Y., T.W. and Z.X.; investigation, Z.Y. and T.W.; resources, Z.Y., L.K. and H.X.; data curation, Z.Y., T.W., H.X. and L.K.; writing—original draft preparation, Z.Y.; writing—review and editing, Z.Y., T.W., K.H. and L.K.; visualization, T.W. and Z.X.; supervision, Z.Y.; project administration, Z.Y.; funding acquisition, Z.Y. and L.K. All authors have read and agreed to the published version of the manuscript.
Funding
The U.S. Department of Energy, Office of Energy Efficiency and Renewable Energy, Water Power Technologies Office funded the research performed by Pacific Northwest National Laboratory, operated by Battelle Memorial Institute under Contract DE-AC05-76RL01830, and by the National Renewable Energy Laboratory, operated by Alliance for Sustainable Energy, LLC under Contract DE-AC36-08GO28308. The views expressed in this article do not necessarily represent the views of the DOE or the U.S. Government. The publisher, by accepting the article for publication, acknowledges that the U.S. Government retains a non-exclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this work, or allow others to do so, for U.S. Government purposes.
Acknowledgments
All model simulations were performed using the Institutional Computing Facility at Pacific Northwest National Laboratory. The authors thank the technical steering committee, chaired by Tuba Ozkan-Haller at the Oregon State University, for their oversight and input during this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Uihlein, A.; Magagna, D. Wave and tidal current energy—A review of the current state of research beyond technology. Renew. Sustain. Energy Rev. 2016, 58, 1070–1081. [Google Scholar] [CrossRef]
- Bahaj, A.S. New research in tidal current energy. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20120501. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Bryden, I.G.; Couch, S.I.; Owen, A.; Melville, G. Tidal current resource assessment. Proc. Inst. Mech. Eng. Part A J. Power Energy 2007, 221, 125–135. [Google Scholar] [CrossRef]
- Hussain, A.; Arif, S.M.; Aslam, M. Emerging renewable and sustainable energy technologies: State of the art. Renew. Sustain. Energy Rev. 2017, 71, 12–28. [Google Scholar] [CrossRef]
- Garrett, C.; Cummins, P. The power potential of tidal currents in channels. Proc. R. Soc. A Math. Phys. Eng. Sci. 2005, 461, 2563–2572. [Google Scholar] [CrossRef]
- Garrett, C.; Cummins, P. Maximum power from a turbine farm in shallow water. J. Fluid Mech. 2013, 714, 634–643. [Google Scholar] [CrossRef]
- Yang, Z.Q.; Wang, T.P.; Copping, A.E. Modeling tidal stream energy extraction and its effects on transport processes in a tidal channel and bay system using a three-dimensional coastal ocean model. Renew. Energy 2013, 50, 605–613. [Google Scholar] [CrossRef]
- Blanchfield, J.; Garrett, C.; Wild, P.; Rowe, A. The extractable power from a channel linking a bay to the open ocean. Proc. Inst. Mech. Eng. Part A J. Power Energy 2008, 222, 289–297. [Google Scholar] [CrossRef]
- Bahaj, A.S.; Myers, L. Analytical estimates of the energy yield potential from the Alderney Race (Channel Islands) using marine current energy converters. Renew. Energy 2004, 29, 1931–1945. [Google Scholar] [CrossRef]
- Vennell, R.; Funke, S.W.; Draper, S.; Stevens, C.; Divett, T. Designing large arrays of tidal turbines: A synthesis and review. Renew. Sustain. Energy Rev. 2015, 41, 454–472. [Google Scholar] [CrossRef]
- Adcock, T.A.A.; Draper, S. Power extraction from tidal channels—Multiple tidal constituents, compound tides and overtides. Renew. Energy 2014, 63, 797–806. [Google Scholar] [CrossRef]
- Defne, Z.; Haas, K.A.; Fritz, H.M.; Jiang, L.D.; French, S.P.; Shi, X.; Smith, B.T.; Neary, V.S.; Stewart, K.M. National geodatabase of tidal stream power resource in USA. Renew. Sustain. Energy Rev. 2012, 16, 3326–3338. [Google Scholar] [CrossRef]
- Thiebaut, M.; Filipot, J.F.; Maisondieu, C.; Damblans, G.; Duarte, R.; Droniou, E.; Chaplain, N.; Guillou, S. A comprehensive assessment of turbulence at a tidal-stream energy site influenced by wind-generated ocean waves. Energy 2020, 191, 116550. [Google Scholar] [CrossRef]
- Thiebaut, M.; Sentchev, A.; du Bois, P.B. Merging velocity measurements and modeling to improve understanding of tidal stream resource in Alderney Race. Energy 2019, 178, 460–470. [Google Scholar] [CrossRef]
- Lewis, M.; McNaughton, J.; Marquez-Dominguez, C.; Todeschini, G.; Togneri, M.; Masters, I.; Allmark, M.; Stallard, T.; Neill, S.; Goward-Brown, A.; et al. Power variability of tidal-stream energy and implications for electricity supply. Energy 2019, 183, 1061–1074. [Google Scholar] [CrossRef]
- Wilcox, K.W.; Zhang, J.T.; McLeod, I.M.; Gerber, A.G.; Jeans, T.L.; McMillan, J.; Hay, A.; Karsten, R.; Culina, J. Simulation of device-scale unsteady turbulent flow in the Fundy Tidal Region. Ocean Eng. 2017, 145, 59–76. [Google Scholar] [CrossRef]
- Work, P.A.; Haas, K.A.; Defne, Z.; Gay, T. Tidal stream energy site assessment via three-dimensional model and measurements. Appl. Energy 2013, 102, 510–519. [Google Scholar] [CrossRef]
- Cowles, G.W.; Hakim, A.R.; Churchill, J.H. A comparison of numerical and analytical predictions of the tidal stream power resource of Massachusetts, USA. Renew. Energy 2017, 114, 215–228. [Google Scholar] [CrossRef]
- Marta-Almeida, M.; Cirano, M.; Soares, C.G.; Lessa, G.C. A numerical tidal stream energy assessment study for Baia de Todos os Santos, Brazil. Renew. Energy 2017, 107, 271–287. [Google Scholar] [CrossRef]
- Li, X.R.; Li, M.; McLelland, S.J.; Jordan, L.B.; Simmons, S.M.; Amoudry, L.O.; Ramirez-Mendoza, R.; Thorne, P.D. Modelling tidal stream turbines in a three-dimensional wave-current fully coupled oceanographic model. Renew. Energy 2017, 114, 297–307. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, T.; Copping, A.; Geerlofs, S. Modeling of in-stream tidal energy development and its potential effects in Tacoma Narrows, Washington, USA. Ocean Coast. Manag. 2014, 99, 52–62. [Google Scholar] [CrossRef]
- Sutherland, G.; Foreman, M.; Garrett, C. Tidal current energy assessment for Johnstone Strait, Vancouver Island. Proc. Inst. Mech. Eng. Part A J. Power Energy 2007, 221, 147–157. [Google Scholar] [CrossRef]
- Wang, T.P.; Yang, Z.Q. A modeling study of tidal energy extraction and the associated impact on tidal circulation in a multi-inlet bay system of Puget Sound. Renew. Energy 2017, 114, 204–214. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, T. Modeling the effects of tidal energy extraction on estuarine hydrodynamics in a stratified estuary. Estuaries Coasts 2013, 38, 187–202. [Google Scholar] [CrossRef]
- Wang, T.; Yang, Z.; Copping, A. A modeling study of the potential water quality impacts from in-stream tidal energy extraction. Estuaries Coasts 2013, 38, 173–186. [Google Scholar] [CrossRef]
- Kadiri, M.; Ahmadian, R.; Bockelmann-Evans, B.; Rauen, W.; Falconer, R. A review of the potential water quality impacts of tidal renewable energy systems. Renew. Sustain. Energy Rev. 2012, 16, 329–341. [Google Scholar] [CrossRef]
- IEC. Marine Energy—Wave, Tidal and Other Water Current Converters—Part 201: Tidal Energy Resource Assessment and Characterization; IEC TS 62600-201; International Electrotechnical Commission: Geneva, Switzerland, 2015. [Google Scholar]
- Rao, S.; Xue, H.J.; Bao, M.; Funke, S. Determining tidal turbine farm efficiency in the Western Passage using the disc actuator theory. Ocean Dyn. 2016, 66, 41–57. [Google Scholar] [CrossRef]
- Karsten, R.; Swan, A.; Culina, J. Assessment of arrays of in-stream tidal turbines in the Bay of Fundy. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20120189. [Google Scholar] [CrossRef]
- Phoenix, A.; Nash, S. Specification of the thrust coefficient when using the momentum sink approach for modelling of tidal turbines. J. Renew. Sustain. Energy 2018, 10, 044502. [Google Scholar] [CrossRef]
- Roc, T.; Conley, D.C.; Greaves, D. Methodology for tidal turbine representation in ocean circulation model. Renew. Energy 2013, 51, 448–464. [Google Scholar] [CrossRef]
- Yang, Z.; Copping, A. Marine Renewable Energy—Resource Characterization and Physical Effects; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Ahmadian, R.; Falconer, R.; Bockelmann-Evans, B. Far-field modelling of the hydro-environmental impact of tidal stream turbines. Renew. Energy 2012, 38, 107–116. [Google Scholar] [CrossRef]
- Kilcher, K.; Thresher, R.; Tinnesand, H. Marine Hydrokinetic Energy Site Identification and Ranking Methodology Part II: Tidal Energy; National Renewable Energy Laboratory: Golden, CO, USA, 2016; p. 30.
- Brooks, D.A. The tidal-stream energy resource in Passamaquoddy-Cobscook Bays: A fresh look at an old story. Renew. Energy 2006, 31, 2284–2295. [Google Scholar] [CrossRef]
- Amante, C.; Eakins, B.W. ETOPO1 1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis; NOAA Technical Memorandum NESDIS NGDC-24 2009; National Geophysical Data Center, NOAA: Boulder, CO, USA, 2009.
- Chen, C.; Liu, H.; Beardsley, R.C. An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: Application to coastal ocean and estuaries. J. Atmos. Ocean. Technol. 2003, 20, 159–186. [Google Scholar] [CrossRef]
- Chen, C.B.; Robert, C.; Cowles, G. An unstructured grid, finite-volume coastal ocean model (FVCOM) system. Oceanography 2006, 19, 78–89. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a turbulence closure-model for geophysical fluid problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
- Xuan, J.; Yang, Z.; Huang, D.; Wang, T.; Zhou, F. Tidal residual current and its role in the mean flow on the Changjiang Bank. J. Mar. Syst. 2016, 154, 66–81. [Google Scholar] [CrossRef]
- Lai, Z.; Ma, R.; Gao, G.; Chen, C.; Beardsley, R.C. Impact of multichannel river network on the plume dynamics in the Pearl River estuary. J. Geophys. Res. Ocean. 2015, 120, 5766–5789. [Google Scholar] [CrossRef]
- Chen, T.Q.; Zhang, Q.H.; Wu, Y.S.; Ji, C.; Yang, J.S.; Liu, G.W. Development of a wave-current model through coupling of FVCOM and SWAN. Ocean Eng. 2018, 164, 443–454. [Google Scholar] [CrossRef]
- Xiao, Z.Y.; Wang, X.H.; Roughan, M.; Harrison, D. Numerical modelling of the Sydney Harbour Estuary, New South Wales: Lateral circulation and asymmetric vertical mixing. Estuar. Coast. Shelf Sci. 2019, 217, 132–147. [Google Scholar] [CrossRef]
- Khangaonkar, T.; Sackmann, B.; Long, W.; Mohamedali, T.; Roberts, M. Simulation of annual biogeochemical cycles of nutrient balance, phytoplankton bloom(s), and DO in Puget Sound using an unstructured grid model. Ocean Dyn. 2012, 62, 1353–1379. [Google Scholar] [CrossRef]
- Khangaonkar, T.; Nugraha, A.; Hinton, S.; Michalsen, D.; Brown, S. Sediment transport into the Swinomish Navigation Channel, Puget Sound—Habitat restoration versus navigation maintenance needs. J. Mar. Sci. Eng. 2017, 5, 19. [Google Scholar] [CrossRef]
- Luo, L.; Wang, J.; Schwab, D.J.; Vanderploeg, H.; Leshkevich, G.; Bai, X.Z.; Hu, H.G.; Wang, D.X. Simulating the 1998 spring bloom in Lake Michigan using a coupled physical-biological model. J. Geophys. Res. Ocean. 2012, 117. [Google Scholar] [CrossRef]
- Hakim, A.R.; Cowles, G.W.; Churchill, J.H. The impact of tidal stream turbines on circulation and sediment transport in Muskeget Channel, MA. Mar. Technol. Soc. J. 2013, 47, 122–136. [Google Scholar] [CrossRef]
- Yang, Z.Q.; Wang, T.P.; Leung, R.; Hibbard, K.; Janetos, T.; Kraucunas, I.; Rice, J.; Preston, B.; Wilbanks, T. A modeling study of coastal inundation induced by storm surge, sea-level rise, and subsidence in the Gulf of Mexico. Nat. Hazards 2014, 71, 1771–1794. [Google Scholar] [CrossRef]
- Wang, T.P.; Yang, Z.Q. The nonlinear response of storm surge to sea-level rise: A modeling approach. J. Coast. Res. 2019, 35, 287–294. [Google Scholar] [CrossRef]
- Yoon, J.J.; Shim, J.S. Estimation of storm surge inundation and hazard mapping for the southern coast of Korea. J. Coast. Res. 2013, 65 (Suppl. 1), 856–861. [Google Scholar] [CrossRef]
- Ge, J.; Much, D.; Kappenberg, J.; Nino, O.; Ding, P.; Chen, Z. Simulating storm flooding maps over HafenCity under present and sea level rise scenarios. J. Flood Risk Manag. 2014, 7, 319–331. [Google Scholar] [CrossRef]
- Chen, C.S.; Beardsley, R.C.; Luettich, R.A.; Westerink, J.J.; Wang, H.; Perrie, W.; Xu, Q.C.; Donahue, A.S.; Qi, J.H.; Lin, H.C.; et al. Extratropical storm inundation testbed: Intermodel comparisons in Scituate, Massachusetts. J. Geophys. Res. Ocean. 2013, 118, 5054–5073. [Google Scholar] [CrossRef]
- Egbert, G.D.; Erofeeva, S.Y. Efficient inverse modeling of barotropic ocean tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- Murray, R.O.; Gallego, A. A modelling study of the tidal stream resource of the Pentland Firth, Scotland. Renew. Energy 2017, 102, 326–340. [Google Scholar] [CrossRef]
- Haverson, D.; Bacon, J.; Smith, H.C.M.; Venugopal, V.; Xiao, Q. Modelling the hydrodynamic and morphological impacts of a tidal stream development in Ramsey Sound. Renew. Energy 2018, 126, 876–887. [Google Scholar] [CrossRef]
- Plew, D.R.; Stevens, C.L. Numerical modelling of the effect of turbines on currents in a tidal channel—Tory Channel, New Zealand. Renew. Energy 2013, 57, 269–282. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).