Challenges in Description of Nonlinear Waves Due to Sampling Variability
Abstract
1. Introduction
2. Set-Up of Numerical Simulations
3. Results
3.1. Analyzed Wave Parameters
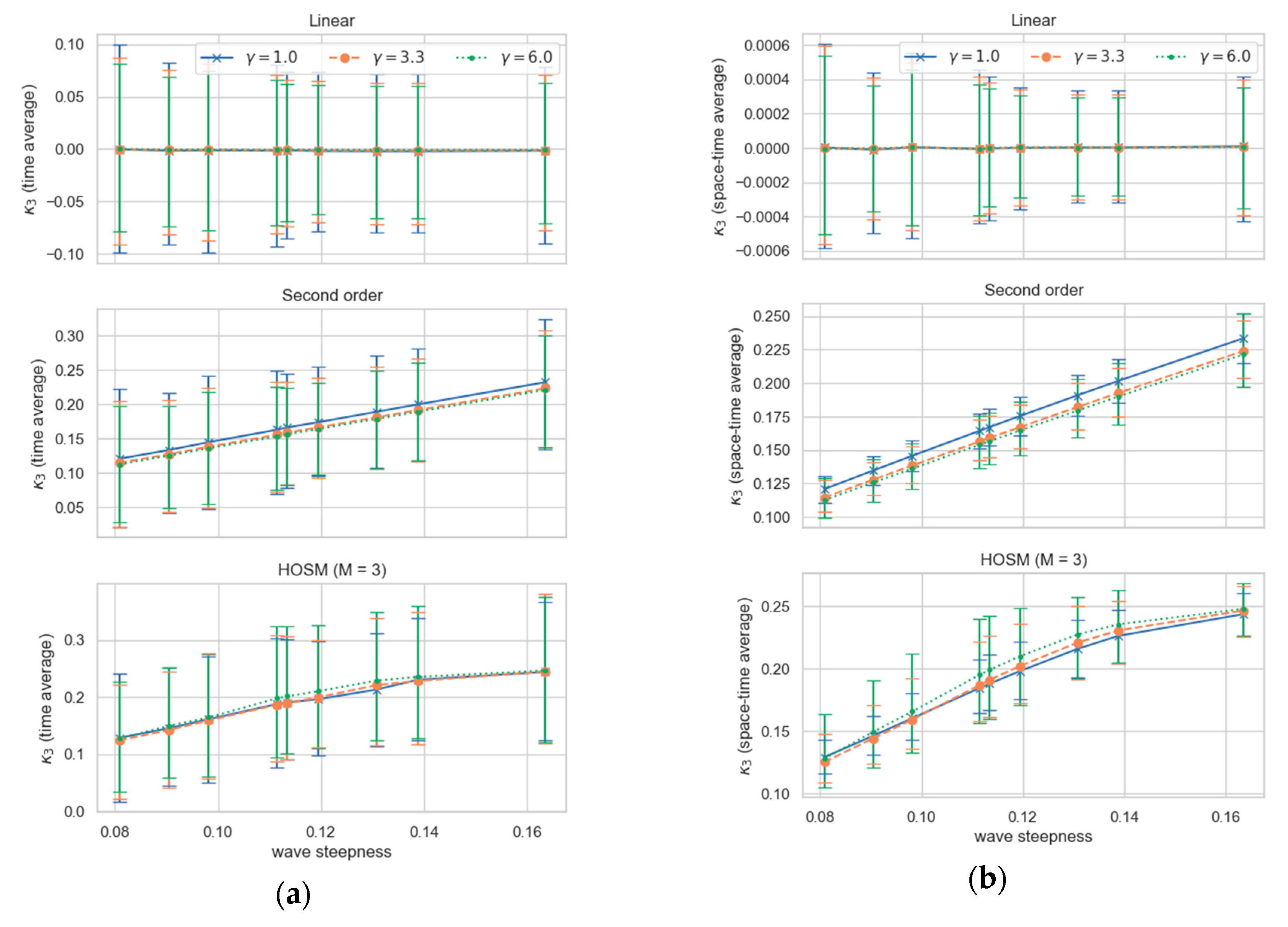
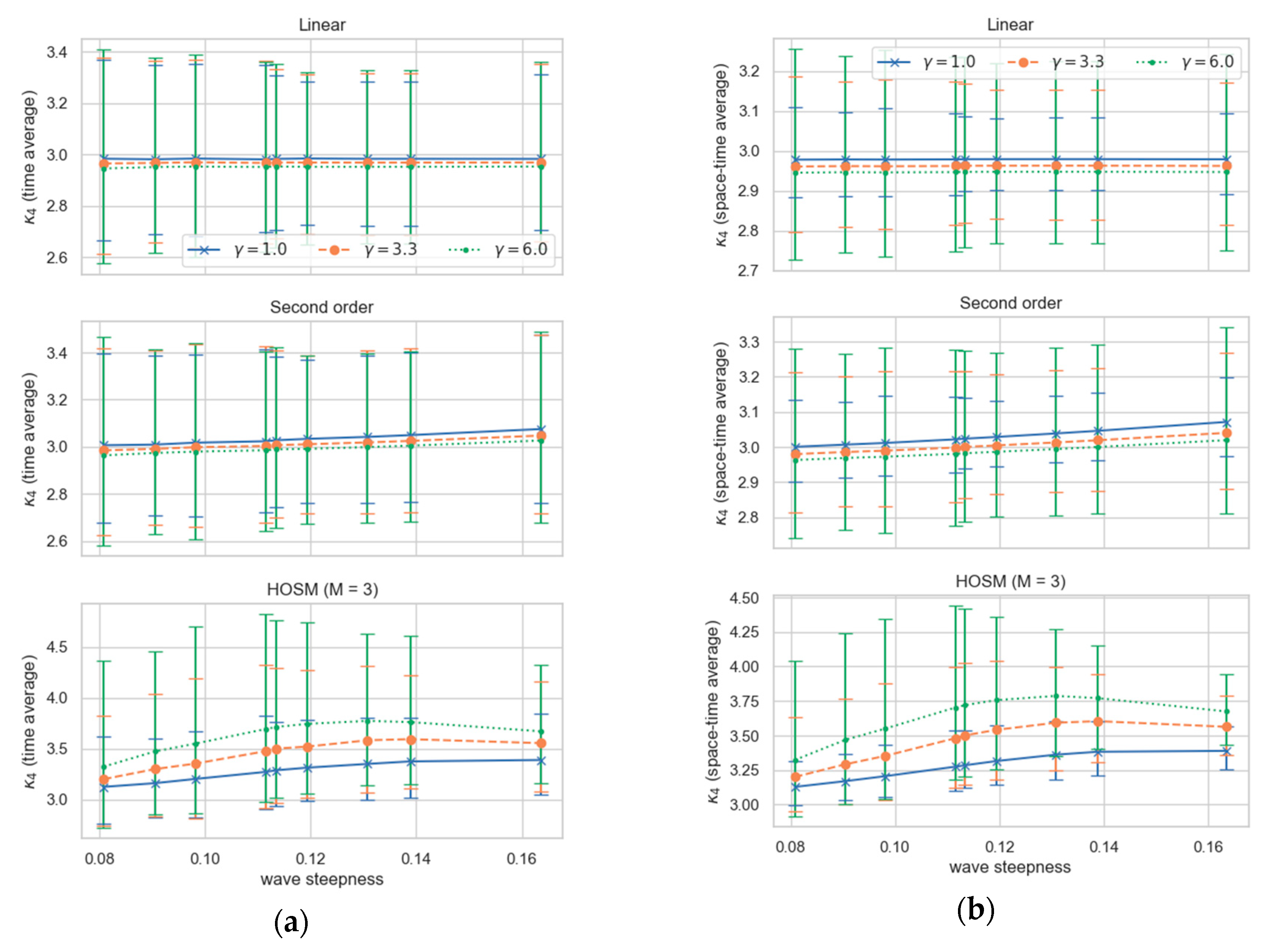
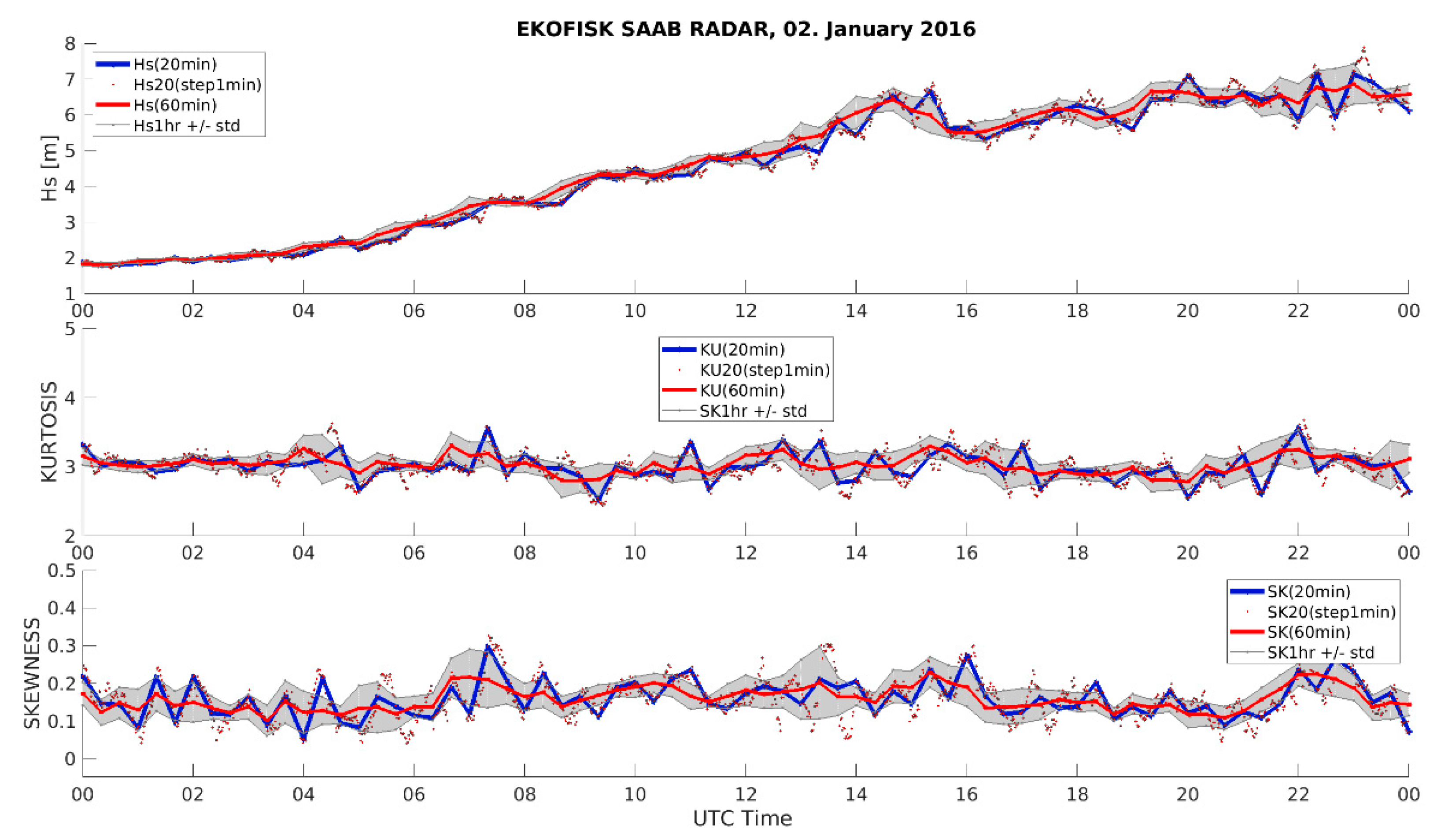
3.2. Comparison of Temporal and Spatial Statistics of Selected Wave Parameters
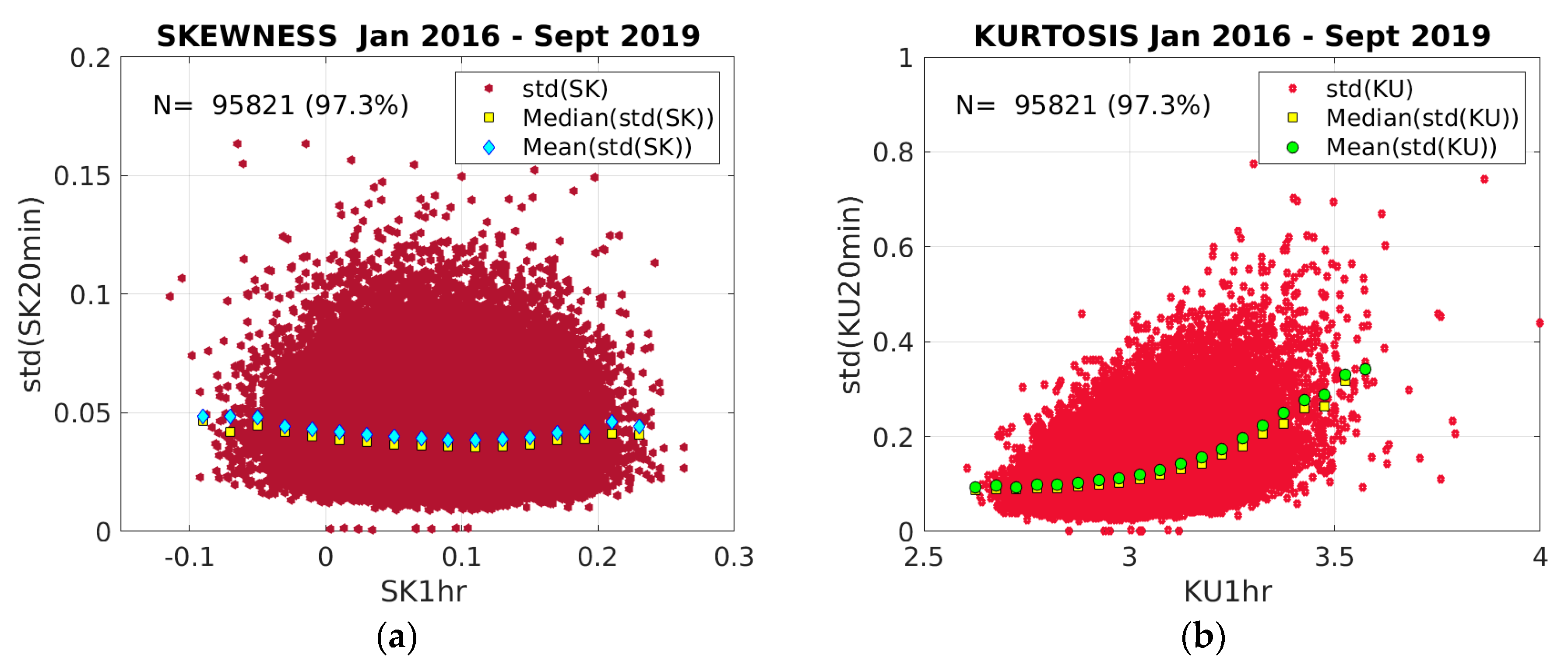
3.3. Correlation between Wave Characteristics and Sampling Variability
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bitner-Gregersen, E.M.; Hagen, Ø. Uncertainties in Data for the Offshore Environment. Struct. Saf. 1990, 7, 11–34. [Google Scholar] [CrossRef]
- Bitner-Gregersen, E.M. Sea state duration and probability of occurrence of a freak wave. In Proceedings of the OMAE 2003, Cancun, Mexico, 8–13 June 2003. [Google Scholar]
- Bitner-Gregersen, E.M.; Magnusson, A.K. Effect of intrinsic and sampling variability on wave parameters and wave statistics. Ocean Dyn. 2014, 64, 1643–1655. [Google Scholar] [CrossRef]
- Gramstad, O.; Bitner-Gregersen, E.M.; Trulsen, K.; Nieto Borge, J.C. Modulational instability and rogue waves in crossing sea states. J. Phys. Oceanogr. 2018, 48, 1317–1331. [Google Scholar] [CrossRef]
- Gemmrich, J.; Thomson, J.; Erick Rogers, W.; Pleskachevsky, A.; Lehner, S. Spatial characteristics of ocean surface waves. Ocean Dyn. 2016, 66, 1025–1035. [Google Scholar] [CrossRef]
- Bitner-Gregersen, E.M.; Gramstad, O. Impact of sampling variability on sea surface characteristics of nonlinear waves. In Proceedings of the OMAE 2018 Conference, Madrid, Spain, 17–22 June 2018. [Google Scholar]
- Benetazzo, A.; Barrariol, F.; Bergamasco, F.; Torsello, A.; Carniel, S.; Sclavo, M. Observation of Extreme Sea Waves in a Space–Time Ensemble. Am. Meteorol. Soc. 2015, 45, 2261–2275. [Google Scholar] [CrossRef]
- Benetazzo, A.; Barrariol, F.; Bergamasco, F.; Torsello, A.; Carniel, S.; Sclavo, M. On the shape and likelihood of oceanic rogue waves. Sci. Rep. 2017, 7, 8276. [Google Scholar] [CrossRef]
- Bitner-Gregersen, E.M.; Gramstad, O. Comparison of temporal and spatial statistics of nonlinear waves. In Proceedings of the OMAE 2018 Conference, Glasgow, UK, 9–14 June 2019. [Google Scholar]
- Longuet-Higgins, M.S. On the statistical distribution of the heights of sea waves. J. Mar. Res. 1952, 11, 245–266. [Google Scholar]
- Donelan, M.A.; Pierson, W.J. The sampling variability of estimates of spectra of wind generated gravity waves. J. Geophys. Res. 1983, 88, 4381–4392. [Google Scholar] [CrossRef]
- Young, I.R. Probability distribution of spectral integrals. J. Waterw. Ports Coast. Ocean Eng. 1986, 112, 338–341. [Google Scholar] [CrossRef]
- Forristall, G.Z.; Heideman, J.C.; Leggett, I.M.; Roskam, B.; Vanderschuren, L. Effect of sampling variability on hindcast and measured wave heights. J. Waterw. Port Coast. Ocean Eng. 1996, 122, 216–225. [Google Scholar] [CrossRef]
- Tucker, M.J. Recommended Standard for Wave Data Sampling and Real Time Processing; Tech. Rep.3, 14/186; E&P Forum: London, UK, 1992; pp. 25–28. [Google Scholar]
- Piterbarg, V.I. Asymptotic methods in the theory of Gaussian processes and fields. AMS Transl. Math. Monogr. 1996, 148. [Google Scholar]
- Krogstad, H.E.; Liu, J.; Socquet-Juglard, H.; Dysthe, K.B.; Trulsen, K. Spatial extreme value analysis of nonlinear simulations of random surface waves. In Proceedings of the OMAE 2004, OMAE 51336, Vancouver, BC, Canada, 20–25 June 2004. [Google Scholar]
- Forristall, G. Maximum Crest Heights under a Model TLP Deck. In Proceedings of the 30th International Conference on Offshore Mechanics and Arctic Engineering, OMAE2011-49837, Rotterdam, The Netherlands, 19–24 June 2011. [Google Scholar]
- Forristall, G. Maximum Crest Heights over an Area: Laboratory Measurements Compared to Theory. In Proceedings of the 34th International Conference on Ocean, Offshore and Artic Engineering, OMAE2015-41061, St. John’s, NL, Canada, 31 May–5 June 2015. [Google Scholar]
- Socquet-Juglard, H.; Dysthe, K.; Trulsen, K.; Krogstad, H.E.; Liu, J. Probability distributions of surface gravity waves during spectral changes. J. Fluid Mech. 2005, 542, 195–216. [Google Scholar] [CrossRef]
- Trulsen, K.; Nieto Borge, J.C.; Gramstad, O.; Aouf, L.; Lefèvre, J.M. Crossing sea state and rogue wave probability during the Prestige accident. J. Geophys. Res. Oceans 2015, 120, 7113–7136. [Google Scholar] [CrossRef]
- Hagen, Ø.; Birknes-Berg, J.; Grue, I.H.; Lian, G.; Bruserud, K.; Vestbøstad, T. Long-term area statistics for maximum crest height under fixed platform deck. In Proceedings of the OMAE 2018 Conference, OMAE2019-77263, Madrid, Spain, 17–22 June 2018. [Google Scholar]
- NORSOK. The Norwegian Standard N-003, Edition 3, Action and Action Effects; NORSOK: Oslo, Norway, January 2017. [Google Scholar]
- Dommermuth, D.G.; Yue, D.K. A high–order spectral method for the study of nonlinear gravity waves. J. Fluid Mech. 1989, 184, 267–288. [Google Scholar] [CrossRef]
- West, B.J.; Brueckner, K.A.; Jand, R.S.; Milder, D.M.; Milton, R.L. A new method for surface hydrodynamics. J. Geophys. Res. 1987, 92, 11803–11824. [Google Scholar] [CrossRef]
- Xiao, W.; Liu, Y.; Wu, G.; Yue, D.K.P. Rogue wave occurrence and dynamics by direct simulations of nonlinear wave-field evolution. J. Fluid Mech. 2013, 720, 357–392. [Google Scholar] [CrossRef]
- Bitner-Gregersen, E.M.; Magnusson, A.K. Extreme Wave Events in Field Data and in a Second Order Wave Model. In Proceedings of the ROGUE’2004 Conference, Brest, France, 20–22 October 2004. [Google Scholar]
- Haver, S. Evidences of the Existence of Freak Waves. In Proceedings of the ROGUE Waves 2000, Brest, France, 29–30 November 2000; pp. 129–140. [Google Scholar]
- Longuet-Higgins, M. The effect of non-linearities on statistical distributions in the theory of sea waves. J. Fluid Mech. 1963, 17, 459–480. [Google Scholar] [CrossRef]
- Bai, J.; Ng, S. Tests for Skewness, Kurtosis, and Normality for Time Series Data. J. Bus. Econ. Stat. 2005, 23, 49–60. [Google Scholar] [CrossRef]
- Bao, Y. On sample skewness and kurtosis. Econom. Rev. 2013, 32, 415–448. [Google Scholar] [CrossRef]
- Onorato, M.; Osborne, A.; Serio, M.; Cavaleri, L.; Brandini, C.; Stansberg, C. Extreme waves, modulational instability and second order theory: Wave flume experiments on irregular waves. Eur. J. Mech. B Fluids 2006, 25, 586–601. [Google Scholar] [CrossRef]
- Toffoli, A.; Gramstad, O.; Trulsen, K.; Monbaliu, J.; Bitner-Gregersen, E.M.; Onorato, M. Evolution of weakly nonlinear random directional waves: Laboratory experiments and numerical simulations. J Fluid Mech. 2010, 664, 313–336. [Google Scholar] [CrossRef]
- Olagnon, M.; Magnusson, A.K. Sensitivity study of sea state parameters in correlation to extreme wave occurrences. In Proceedings of the 14th International Offshore and Polar Engineering Conference, ISOPE 3, Toulon, France, 23–28 May 2004. [Google Scholar]
- Olagnon, M.; Magnusson, A.K. Spectral parameters to characterize the risk of rogue wave occurrence in a sea state. In Proceedings of the ROGUES’2004 Conference, Brest, France, 20–22 October 2004. [Google Scholar]
- Vinje, T.; Haver, S. On the non-Gaussian structure of ocean waves. In Proceedings of the BOSS’94 Conference, Cambridge, MA, USA, 12–15 July 1994; Volume 2, pp. 453–480. [Google Scholar]
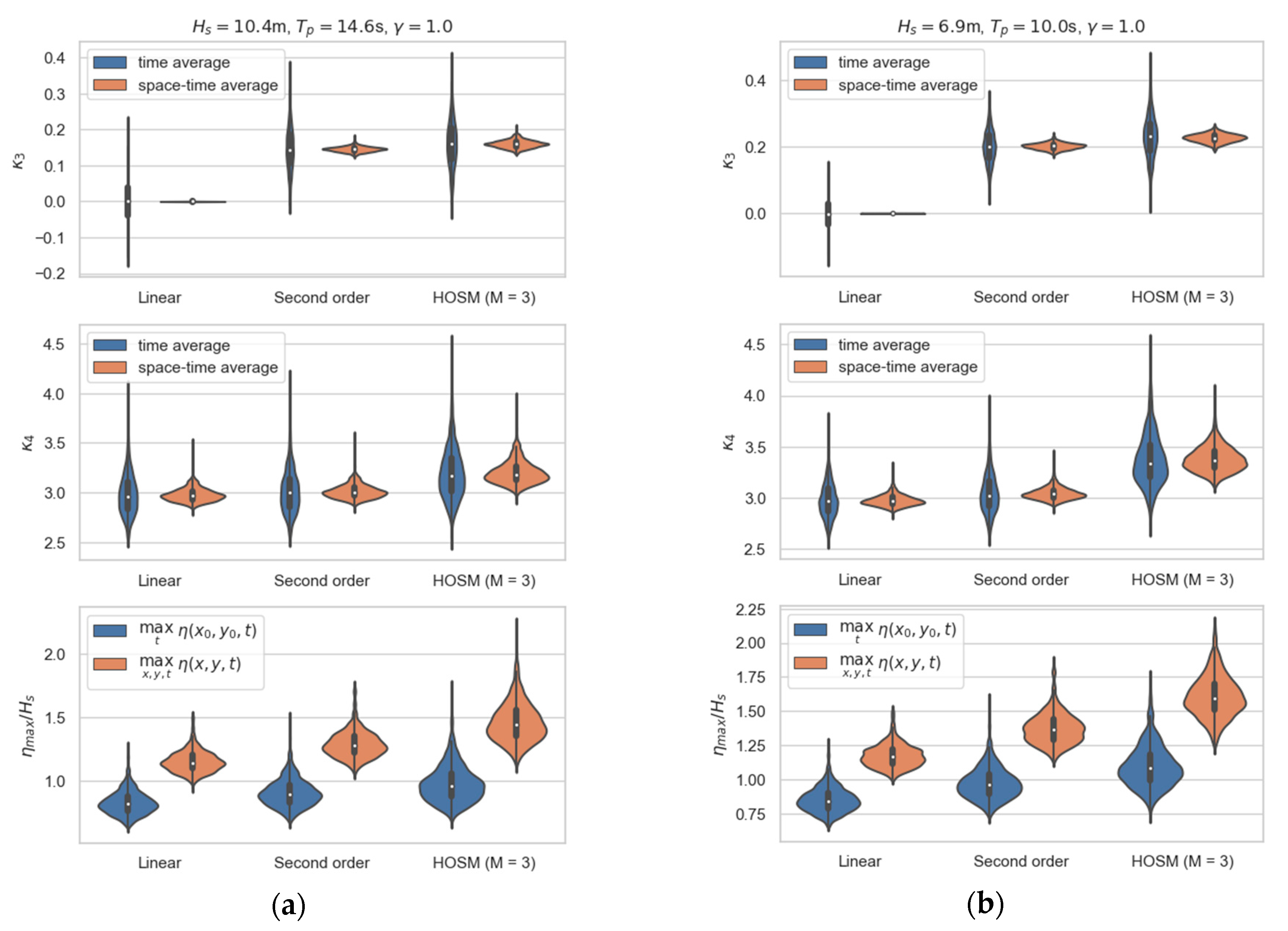
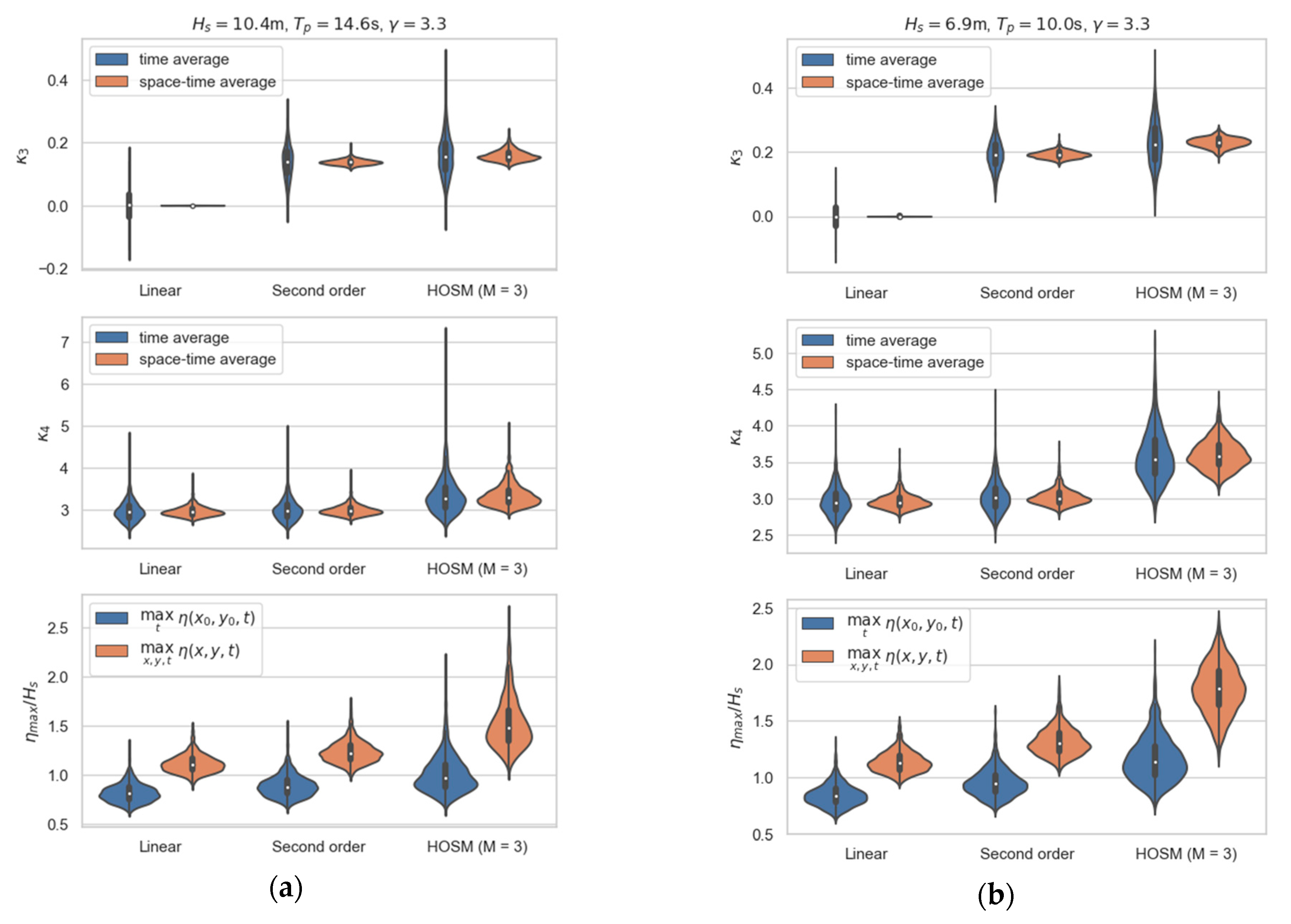
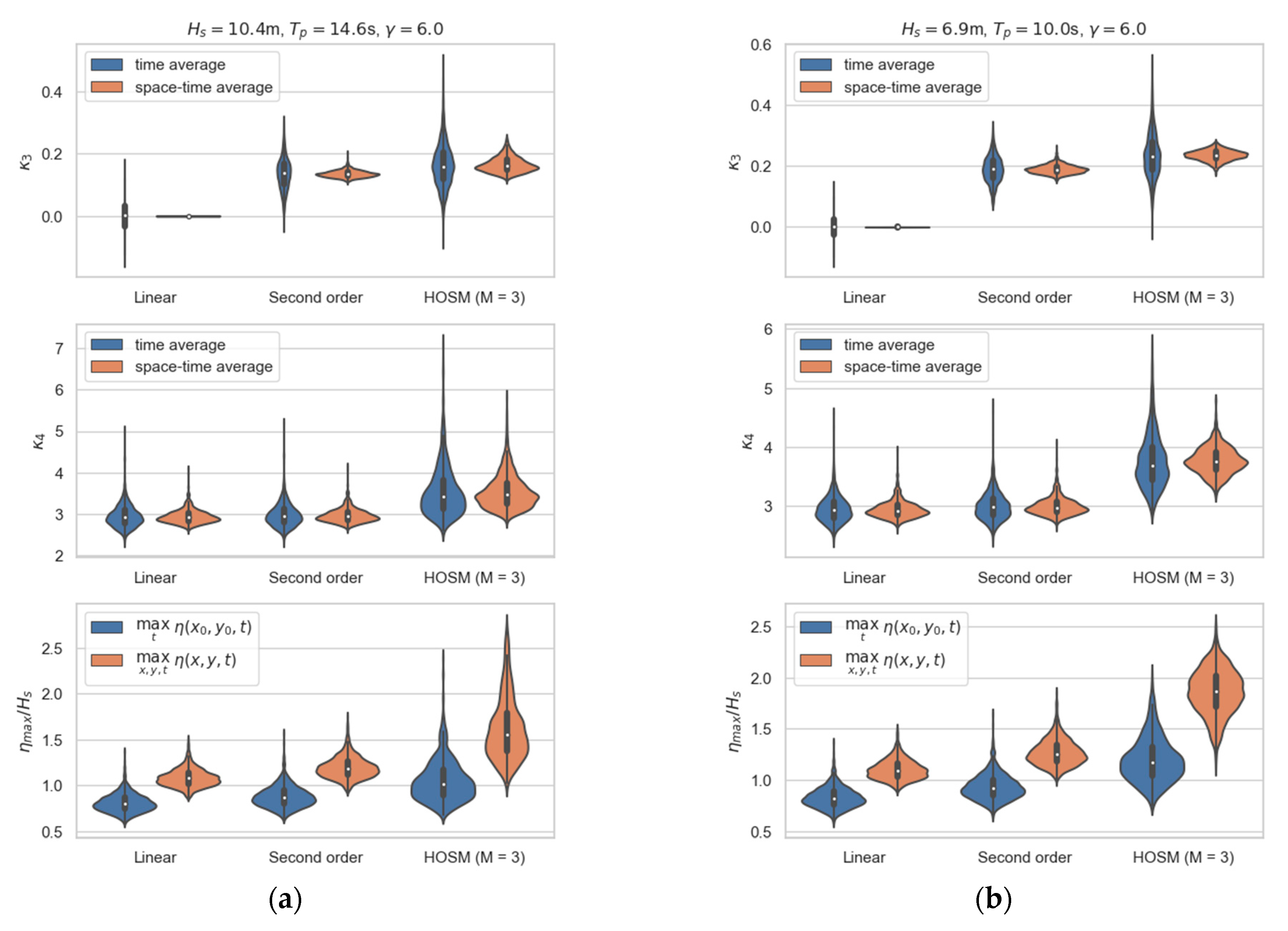
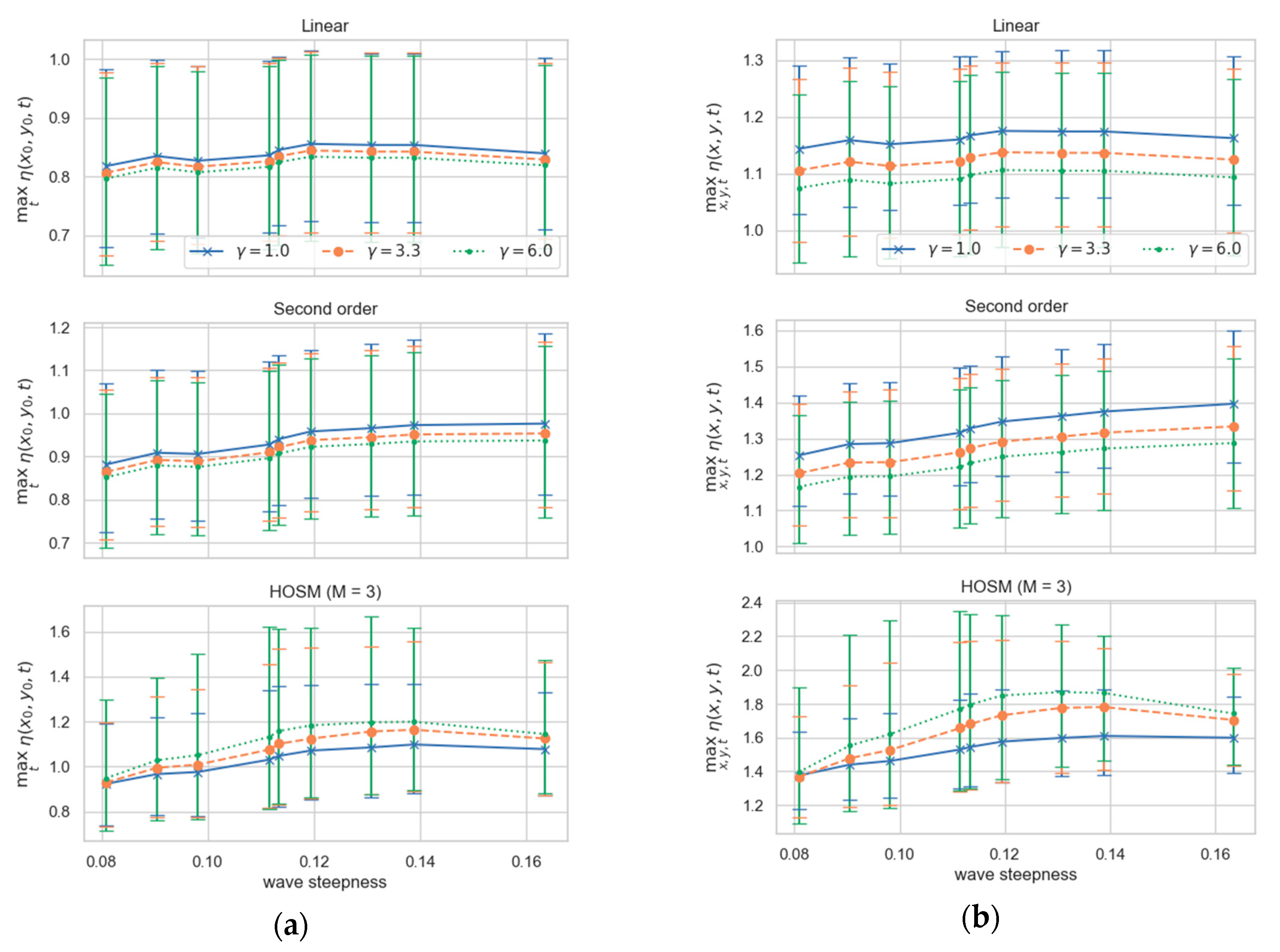
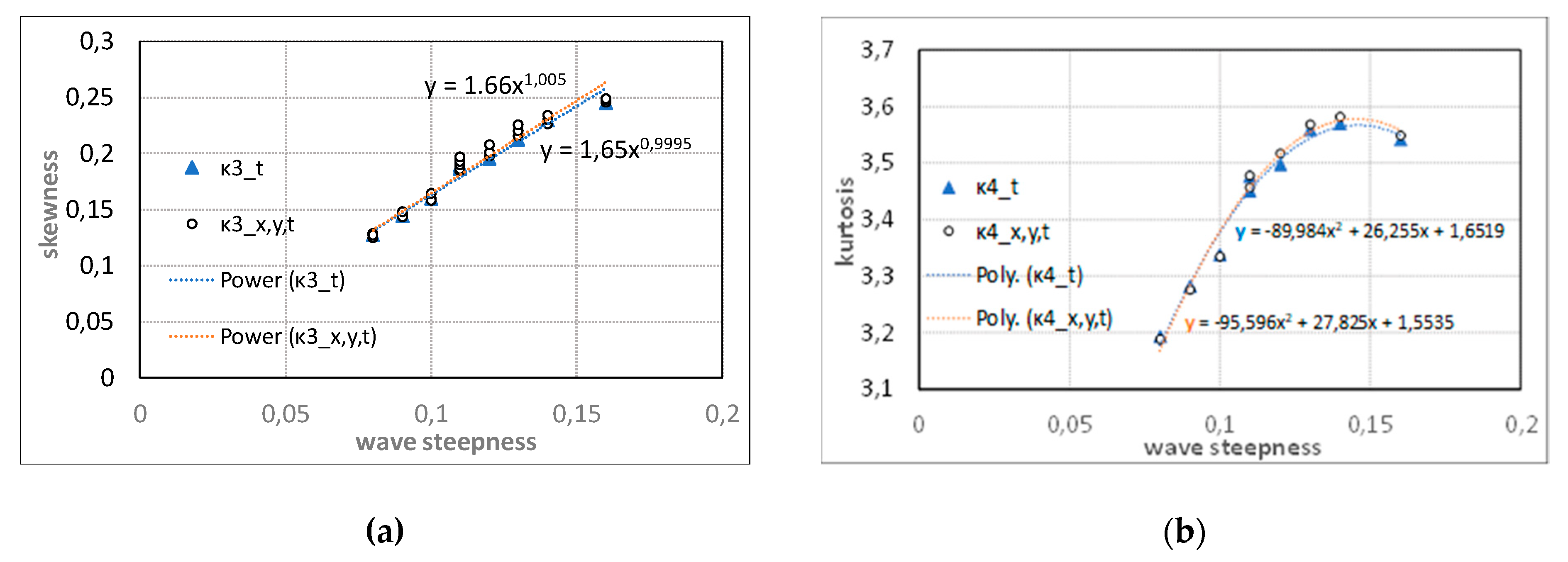
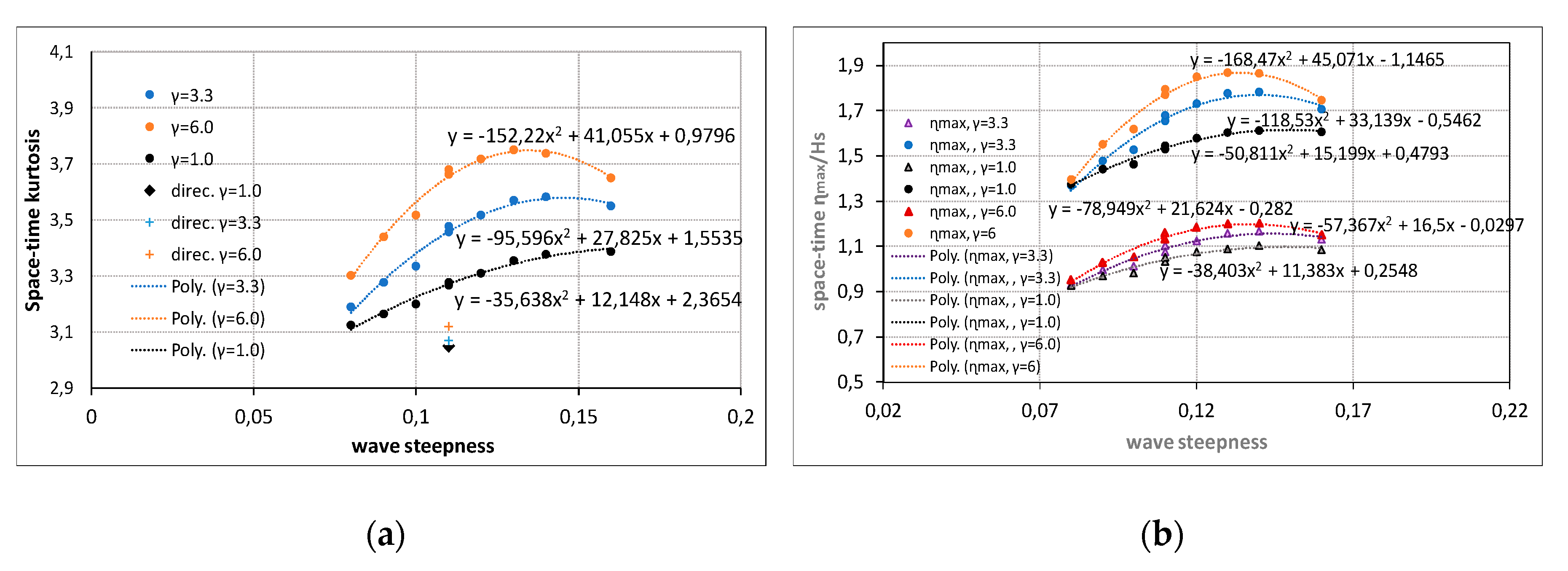
| Case | Date and Time | Hmo (m) | Tp (s) | Wave Steepness |
|---|---|---|---|---|
| 1 | 1 January 1995, 3:20 p.m. UTC | 11.2 | 16.7 | 0.08 |
| 2 | 5 February 1999, 4:40 a.m. UTC | 7.6 | 13.0 | 0.09 |
| 3 | 27 December 1998, 6:40 a.m. UTC | 10.4 | 14.6 | 0.10 |
| 4 | 25 October 1998, 4:00 p.m. UTC | 8.8 | 12.6 | 0.11 |
| 5 | 1 December 1999, 2:20 a.m. UTC | 7.2 | 11.3 | 0.11 |
| 6 | 1 January 1995, 11:00 p.m. UTC | 5.7 | 9.8 | 0.12 |
| 7 | Numerical simulations | 6.5 | 10.0 | 0.13 |
| 8 | Numerical simulations | 6.9 | 10.0 | 0.14 |
| 9 | 29 January 2000, 6:40 p.m. UTC | 12.1 | 12.2 | 0.16 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bitner-Gregersen, E.M.; Gramstad, O.; Magnusson, A.K.; Malila, M. Challenges in Description of Nonlinear Waves Due to Sampling Variability. J. Mar. Sci. Eng. 2020, 8, 279. https://doi.org/10.3390/jmse8040279
Bitner-Gregersen EM, Gramstad O, Magnusson AK, Malila M. Challenges in Description of Nonlinear Waves Due to Sampling Variability. Journal of Marine Science and Engineering. 2020; 8(4):279. https://doi.org/10.3390/jmse8040279
Chicago/Turabian StyleBitner-Gregersen, Elzbieta M., Odin Gramstad, Anne Karin Magnusson, and Mika Malila. 2020. "Challenges in Description of Nonlinear Waves Due to Sampling Variability" Journal of Marine Science and Engineering 8, no. 4: 279. https://doi.org/10.3390/jmse8040279
APA StyleBitner-Gregersen, E. M., Gramstad, O., Magnusson, A. K., & Malila, M. (2020). Challenges in Description of Nonlinear Waves Due to Sampling Variability. Journal of Marine Science and Engineering, 8(4), 279. https://doi.org/10.3390/jmse8040279





