Oil Droplet Dispersion under a Deep-Water Plunging Breaker: Experimental Measurement and Numerical Modeling
Abstract
1. Introduction
2. Methodology
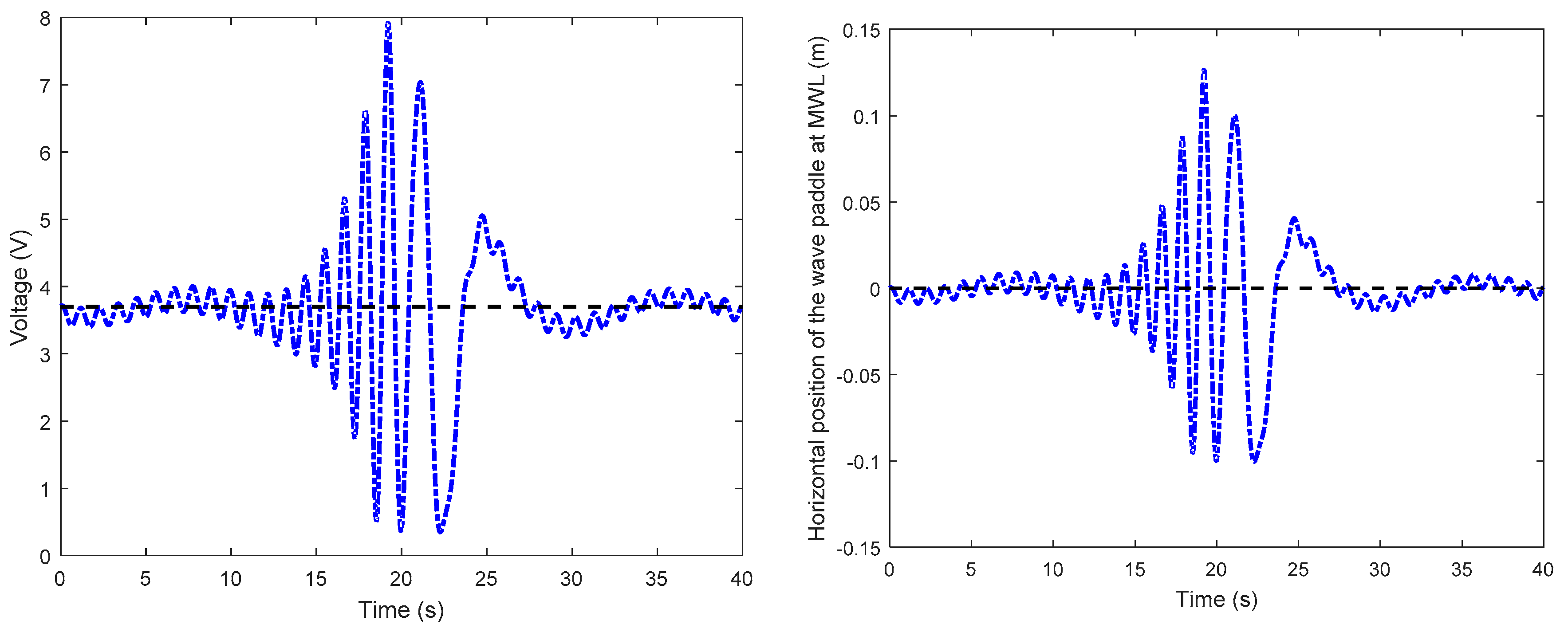
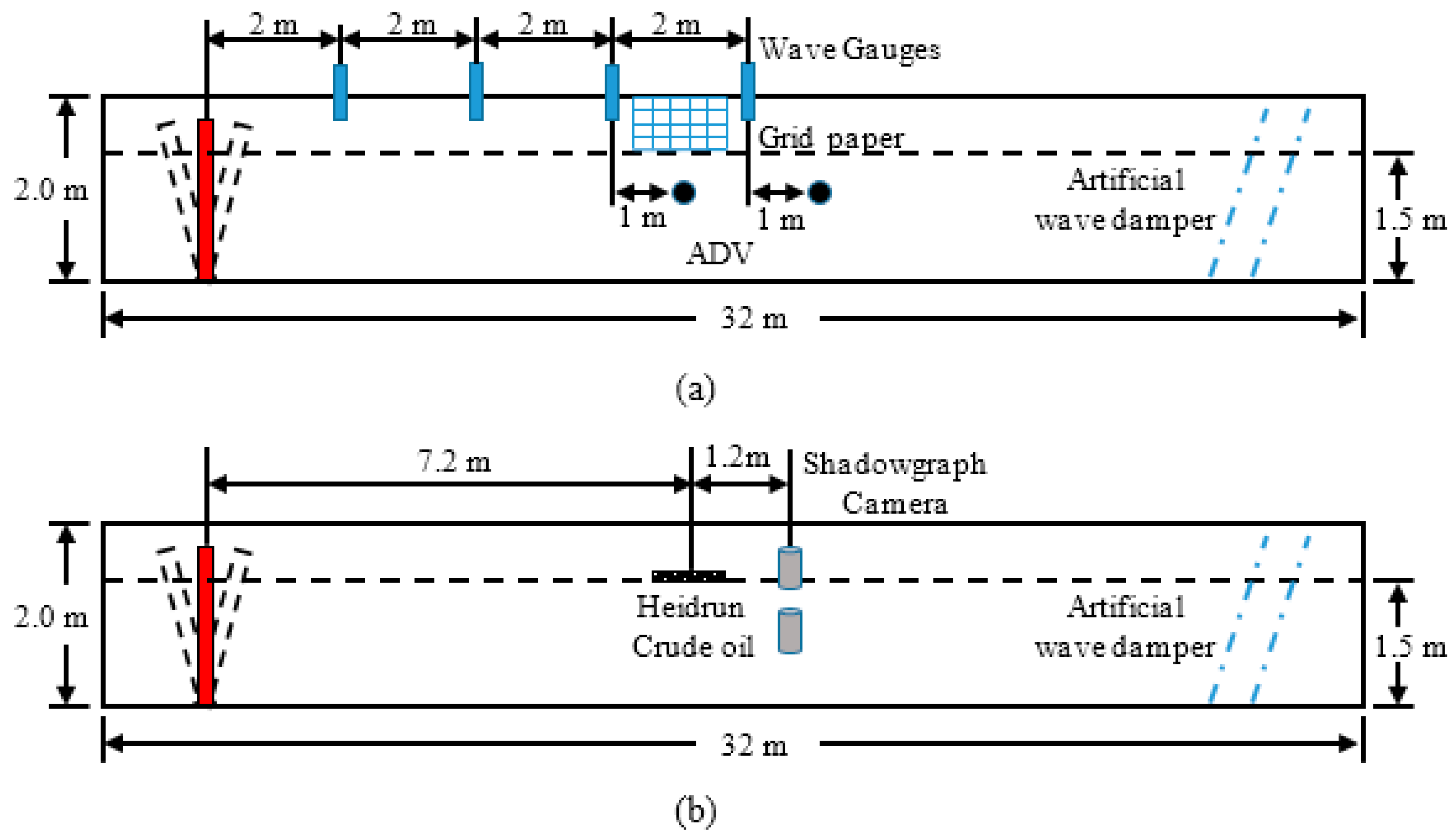
2.1. Experimental Approach
2.2. Numerical Approach
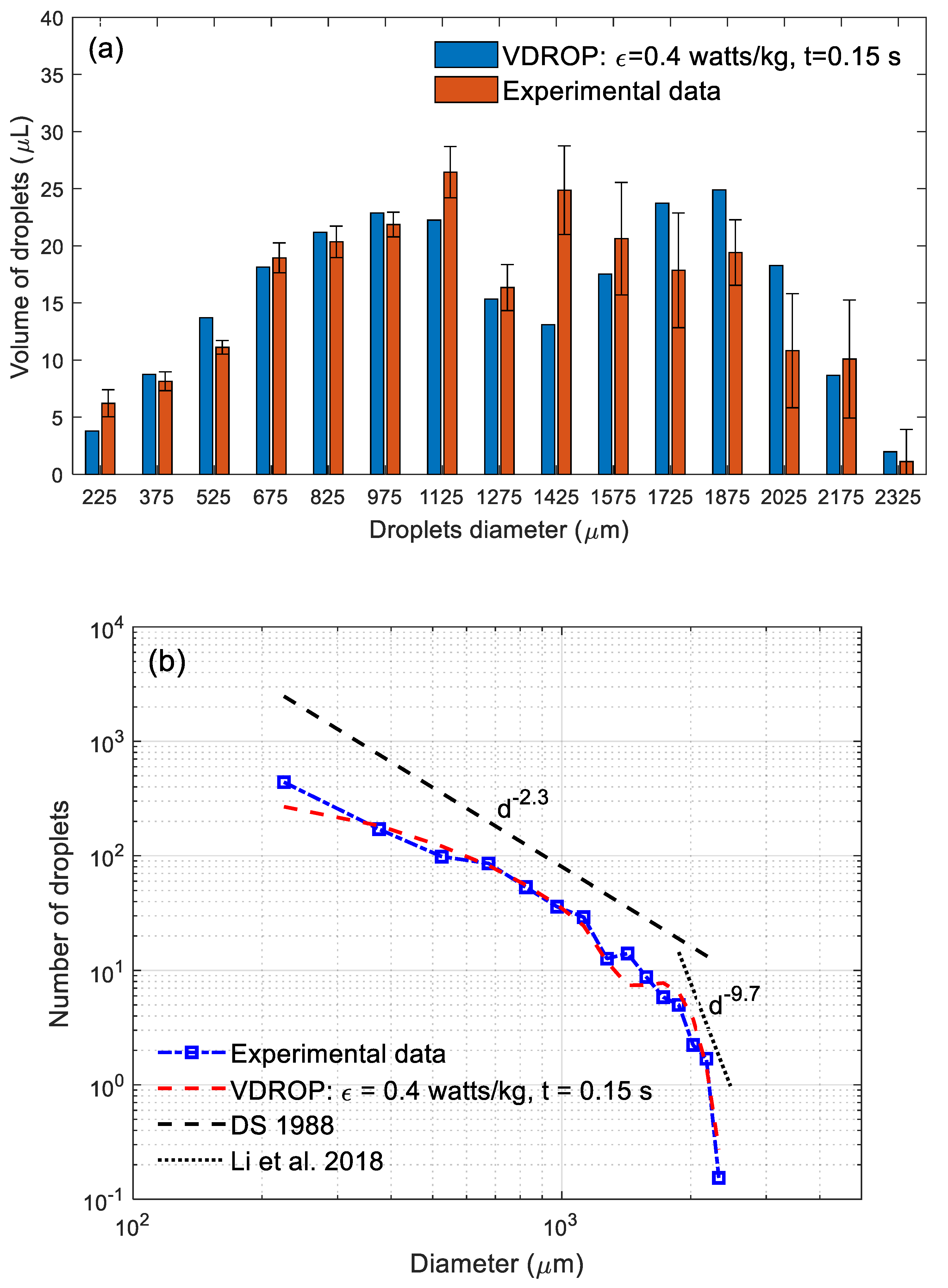
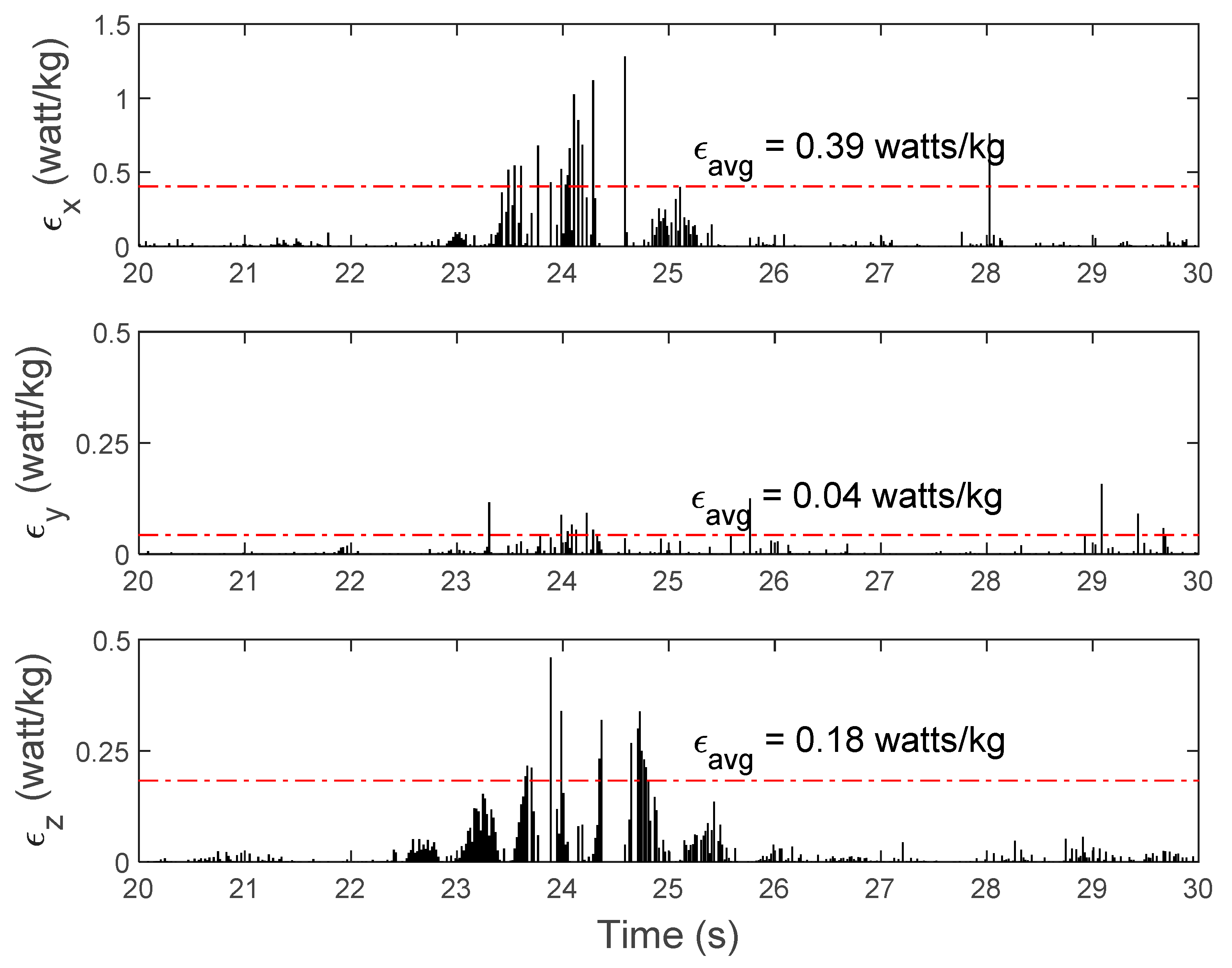
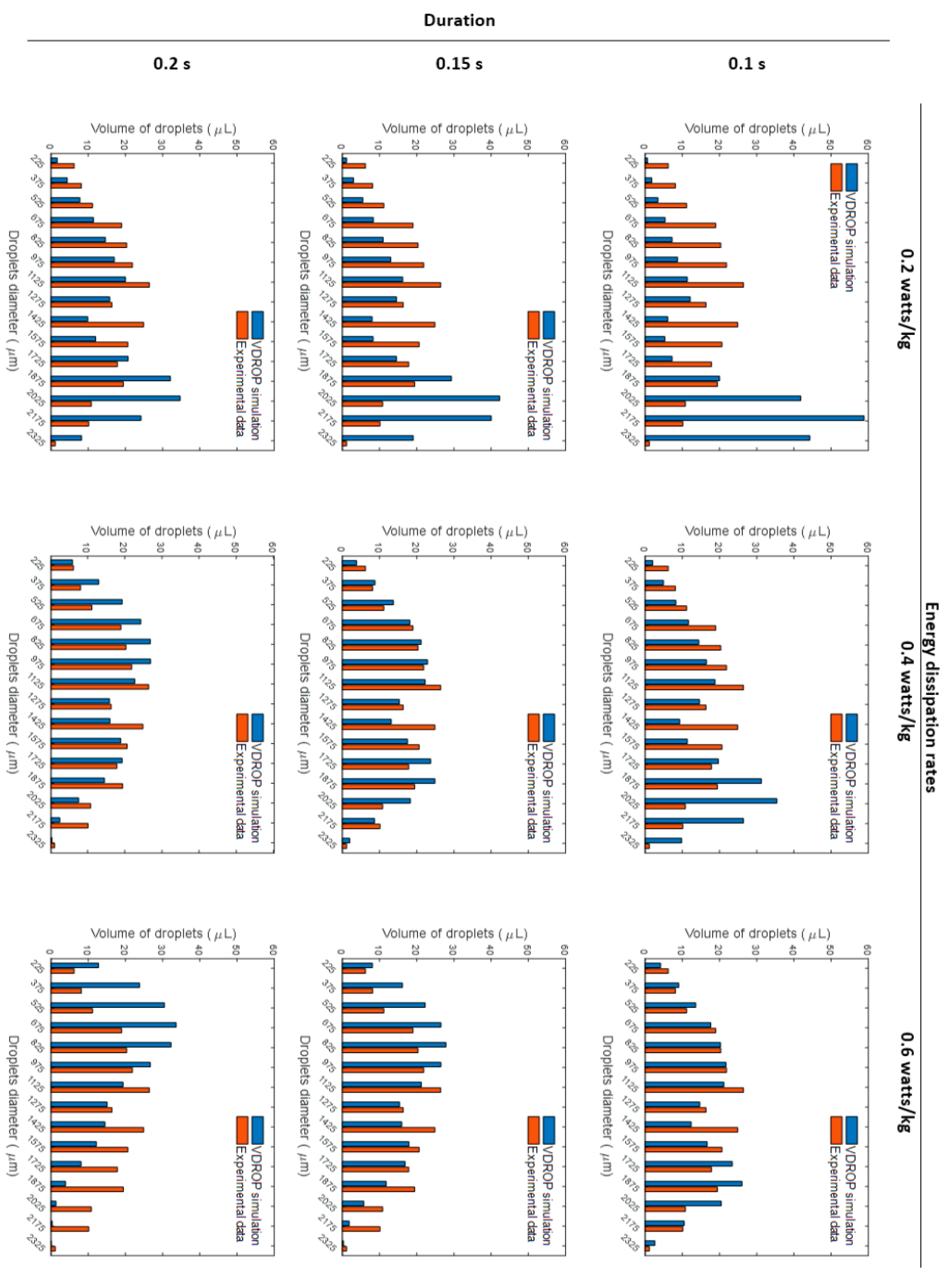
3. Results
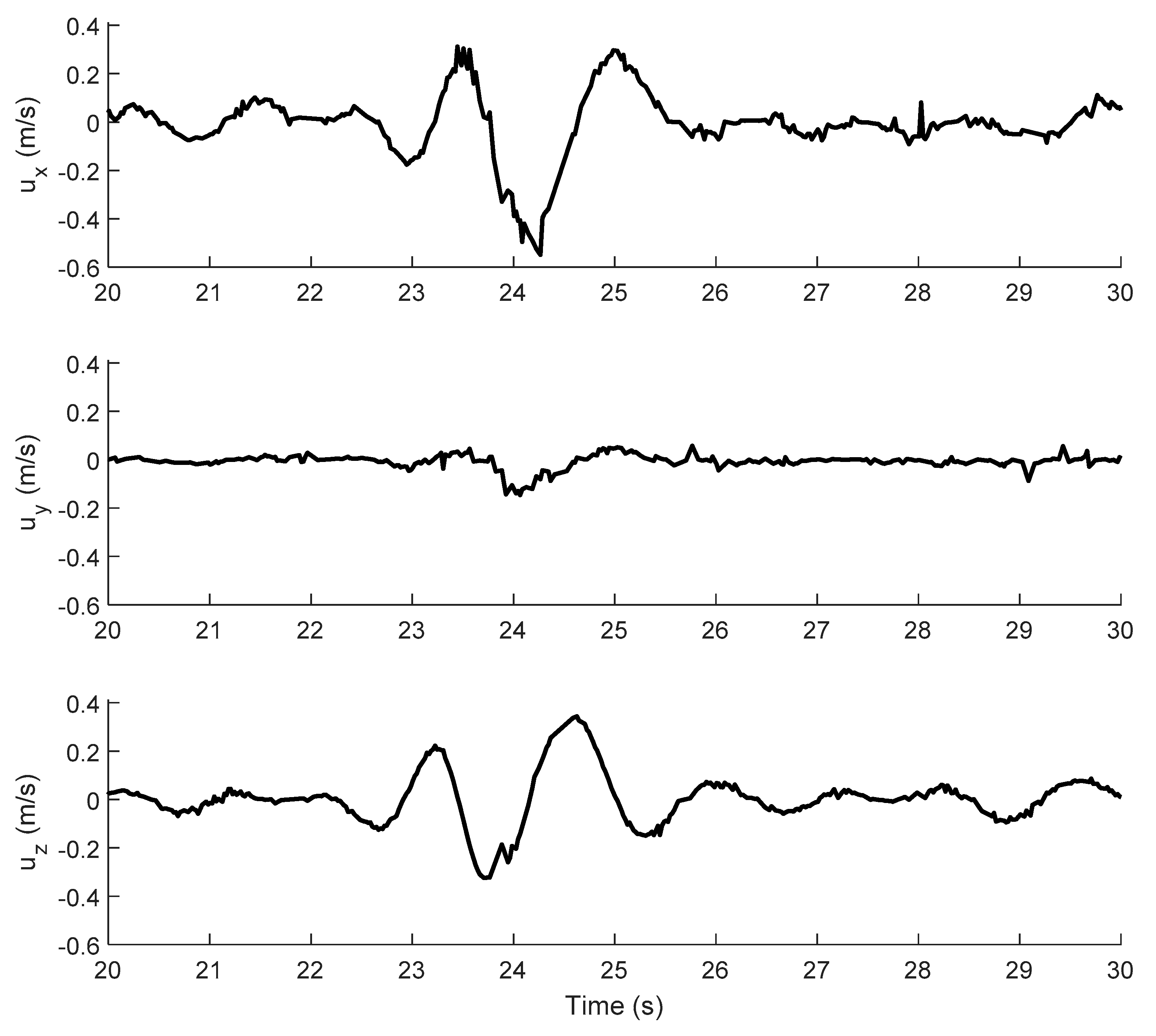
3.1. Characterization of the Plunging Breaker
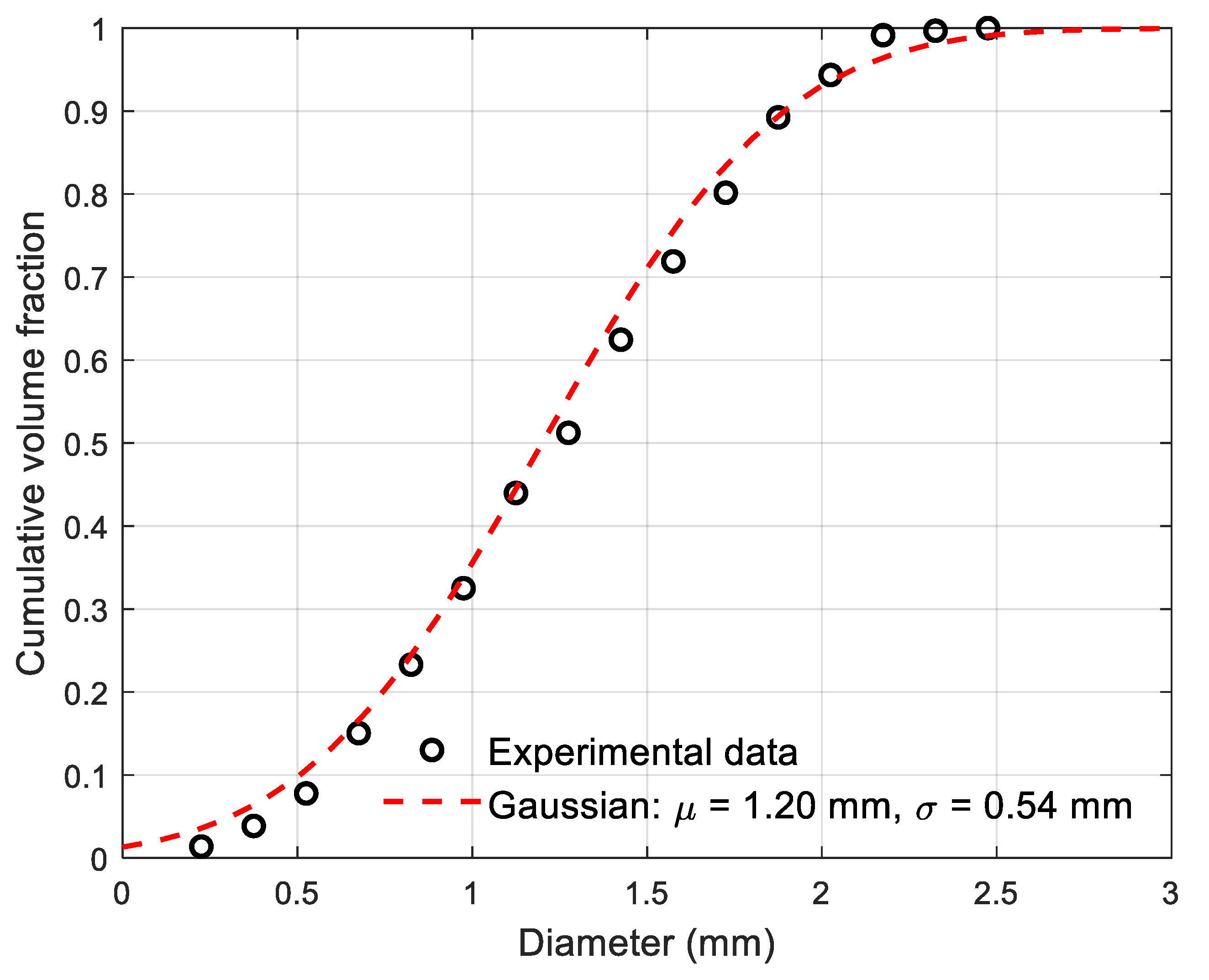
3.2. Oil Dispersion under the Plunging Breaker
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| n | n | ||||
|---|---|---|---|---|---|
| 1 | 0.9000 | 3.2597 | 17 | 0.4871 | 0.9548 |
| 2 | 0.8742 | 3.0754 | 18 | 0.4613 | 0.8563 |
| 3 | 0.8484 | 2,8965 | 19 | 0.4355 | 0.7632 |
| 4 | 0.8226 | 2.7230 | 20 | 0.4097 | 0.6754 |
| 5 | 0.7968 | 2.5548 | 21 | 0.3839 | 0.5930 |
| 6 | 0.7710 | 2.3920 | 22 | 0.3581 | 0.5160 |
| 7 | 0.7452 | 2.2346 | 23 | 0.3323 | 0.4443 |
| 8 | 0.7194 | 2.0825 | 24 | 0.3065 | 0.3779 |
| 9 | 0.6935 | 1.9357 | 25 | 0.2806 | 0.3170 |
| 10 | 0.6677 | 1.7944 | 26 | 0.2548 | 0.2613 |
| 11 | 0.6419 | 1.6583 | 27 | 0.2290 | 0.2111 |
| 12 | 0.6161 | 1.5277 | 28 | 0.2032 | 0.1662 |
| 13 | 0.5903 | 1.4024 | 29 | 0.1774 | 0.1267 |
| 14 | 0.5645 | 1.2825 | 30 | 0.1516 | 0.0925 |
| 15 | 0.5387 | 1.1679 | 31 | 0.1258 | 0.0637 |
| 16 | 0.5129 | 1.0587 | 32 | 0.1000 | 0.0402 |

References
- NRC. An Ecosystem Services Approach to Assessing the Impacts of the Deepwater Horizon Oil Spill in the Gulf of Mexico; NRC: Rockville, MD, USA, 2013.
- Li, M.; Garrett, C. The relationship between oil droplet size and upper ocean turbulence. Mar. Pollut. Bull. 1998, 36, 961–970. [Google Scholar] [CrossRef]
- Tkalich, P.; Chan, E.S. Vertical mixing of oil droplets by breaking waves. Mar. Pollut. Bull. 2002, 44, 1219–1229. [Google Scholar] [CrossRef]
- Delvigne, G.A.L.; Sweeney, C.E. Natural dispersion of oil. Oil Chem. Pollut. 1988, 4, 281–310. [Google Scholar] [CrossRef]
- Li, Z.; Kepkay, P.; Lee, K.; King, T.; Boufadel, M.C.; Venosa, A.D. Effects of chemical dispersants and mineral fines on crude oil dispersion in a wave tank under breaking waves. Mar. Pollut. Bull. 2007, 54, 983–993. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Lee, K.; King, T.; Boufadel, M.C.; Venosa, A.D. Oil droplet size distribution as a function of energy dissipation rate in an experimental wave tank. In Proceedings of the International Oil Spill Conference, Savannah, GA, USA, 4–8 May 2008. [Google Scholar]
- Li, Z.; Lee, K.; King, T.; Boufadel, M.C.; Venosa, A.D. Evaluating chemical dispersant efficacy in an experimental wave tank: 2-significant factors determining in situ oil droplet size distribution. Environ. Eng. Sci. 2009, 26, 1407–1418. [Google Scholar] [CrossRef]
- Li, Z.; Lee, K.; King, T.; Boufadel, M.C.; Venosa, A.D. Effects of temperature and wave conditions on chemical dispersion efficacy of heavy fuel oil in an experimental flow-through wave tank. Mar. Pollut. Bull. 2010, 60, 1550–1559. [Google Scholar] [CrossRef]
- Boufadel, M.C.; Wickley-Olsen, E.; King, T.; Li, Z.; Lee, K.; Venosa, A.D. Theoretical foundation for predicting dispersion effectiveness due to waves. In Proceedings of the International Oil Spill Conference, Savannah, GA, USA, 4–8 May 2008. [Google Scholar]
- Chen, Z.; Zhan, C.-S.; Lee, K.; Li, Z.-K.; Boufadel, M. Modeling oil droplet formation and evolution under breaking waves. Energy Sources Part A 2009, 31, 438–448. [Google Scholar] [CrossRef]
- Li, C.; Miller, J.; Wang, J.; Koley, S.S.; Katz, J. Size distribution and dispersion of droplets generated by impingement of breaking waves on oil slicks. J. Geophys. Res. Oceans 2017, 122, 7938–7957. [Google Scholar] [CrossRef]
- NRC. The Use of Dispersants in Marine Oil Spill Response; National Academies of Sciences and Engineering: Washington, DC, USA, 2019. [Google Scholar]
- Johansen, Ø.; Reed, M.; Bodsberg, N.R. Natural dispersion revisited. Mar. Pollut. Bull. 2015, 93, 20–26. [Google Scholar] [CrossRef]
- Wang, C.Y.; Calabrese, R.V. Drop breakup in turbulent stirred-tank contactors. Part II: Relative influence of viscosity and interfacial tension. AIChE J. 1986, 32, 667–676. [Google Scholar] [CrossRef]
- Johansen, Ø.; Brandvik, P.J.; Farooq, U. Droplet breakup in subsea oil releases—Part 2: Predictions of droplet size distributions with and without injection of chemical dispersants. Mar. Pollut. Bull. 2013, 73, 327–335. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Spaulding, M.; McCay, D.F.; Crowley, D.; Payne, J.R. Development of a unified oil droplet size distribution model with application to surface breaking waves and subsea blowout releases considering dispersant effects. Mar. Pollut. Bull. 2017, 114, 247–257. [Google Scholar] [CrossRef] [PubMed]
- Colella, D.; Vinci, D.; Bagatin, R.; Masi, M.; Bakr, E.A. A study on coalescence and breakage mechanisms in three different bubble columns. Chem. Eng. Sci. 1999, 54, 4767–4777. [Google Scholar] [CrossRef]
- Pohorecki, R.; Moniuk, W.; Bielski, P.; Zdrójkowski, A. Modelling of the coalescence/redispersion processes in bubble columns. Chem. Eng. Sci. 2001, 56, 6157–6164. [Google Scholar] [CrossRef]
- Zhao, L.; Torlapati, J.; Boufadel, M.C.; King, T.; Robinson, B.; Lee, K. VDROP: A comprehensive model for droplet formation of oils and gases in liquids-Incorporation of the interfacial tension and droplet viscosity. Chem. Eng. J. 2014, 253, 93–106. [Google Scholar] [CrossRef]
- Zhao, L.; Boufadel, M.C.; Socolofsky, S.A.; Adams, E.; King, T.; Lee, K. Evolution of droplets in subsea oil and gas blowouts: Development and validation of the numerical model VDROP-J. Mar. Pollut. Bull. 2014, 83, 58–69. [Google Scholar] [CrossRef]
- Zhao, L.; Boufadel, M.C.; Adams, E.; Socolofsky, S.A.; King, T.; Lee, K.; Nedwed, T. Simulation of scenarios of oil droplet formation from the Deepwater Horizon blowout. Mar. Pollut. Bull. 2015, 101, 304–319. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S. Mechanisms of Wave Breaking in Deep Water, in Sea Surface Sound: Natural Mechanisms of Surface Generated Noise in the Ocean; Kerman, B.R., Ed.; Springer: Dordrecht, The Netherlands, 1988; pp. 1–30. [Google Scholar]
- Wickley-Olsen, E.; Boufadel, M.C.; King, T.; Li, Z.; Lee, K.; Venosa, A.D. Regular and Breaking Waves in Wave Tank for Dispersion Effectiveness Testing. In Proceedings of the Arctic and Marine Oil Spill, Edmonton, AB, Canada, 5–7 June 2007. [Google Scholar]
- Wickley-Olsen, E.; Boufadel, M.C.; King, T.; Li, Z.; Lee, K.; Venosa, A.D. Regular and breaking waves in wave tank for dispersion effectiveness testing. In Proceedings of the 2008 International Oil Spill Program, Savannah, GA, USA, 4–8 May 2008. [Google Scholar]
- Botrus, D.; Boufadel, M.C.; Wickley-Olsen, E.; Weaver, J.; Weggel, R.; Lee, K.; Venosa, A.D. Wave tank to simulate the movement of oil under breaking waves. In Proceedings of the 31st AMOP Technical Seminar on Environmental Contamination and Response, Edmonton, AB, Canada, 2–5 June 2008. [Google Scholar]
- Rapp, R.J.; Melville, W.K. Laboratory measurements of deep-water breaking waves. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1990, 331, 735–800. [Google Scholar]
- Drazen, D.A.; Melville, W.K.; Lenain, L.U.C. Inertial scaling of dissipation in unsteady breaking waves. J. Fluid Mech. 2008, 611, 307–332. [Google Scholar] [CrossRef]
- Derakhti, M.; Banner, M.L.; Kirby, J.T. Predicting the breaking strength of gravity water waves in deep and intermediate depth. J. Fluid Mech. 2018, 848, R2. [Google Scholar] [CrossRef]
- King, T.L.; Robinson, B.; Cui, F.; Boufadel, M.; Lee, K.; Clyburne, J.A.C. An oil spill decision matrix in response to surface spills of various bitumen blends. Environ. Sci. Process. Impacts 2017, 19, 928–938. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Boufadel, M.C.; Katz, J.; Haspel, G.; Lee, K.; King, T.; Robinson, B. A New Mechanism of Sediment Attachment to Oil in Turbulent Flows: Projectile Particles. Environ. Sci. Technol. 2017, 51, 11020–11028. [Google Scholar] [CrossRef]
- Kaku, V.; Boufadel, M.; Venosa, A. Evaluation of mixing energy in laboratory flasks used for dispersant effectiveness testing. J. Environ. Eng. 2006, 132, 93–101. [Google Scholar] [CrossRef]
- Kaku, V.; Boufadel, M.; Venosa, A.; Weaver, J. Flow dynamics in eccentrically rotating flasks used for dispersant effectiveness testing. Environ. Fluid Mech. 2006, 6, 385–406. [Google Scholar] [CrossRef]
- Tsouris, C.; Tavlarides, L. Breakage and coalescence models for drops in turbulent dispersions. AIChE J. 1994, 40, 395–406. [Google Scholar] [CrossRef]
- Simard, R.; Ecuyer, P. Computing the Two-sided kolmogorov-smirnov distribution. J. Stat. Softw. 2011, 39, 18. [Google Scholar] [CrossRef]
- Narsimhan, G.; Ramkrishna, D.; Gupta, J.P. Analysis of drop size distributions in lean liquid-liquid dispersions. AIChE J. 1980, 26, 991–1000. [Google Scholar] [CrossRef]
- Tobin, T.; Muralidhar, R.; Wright, H.; Ramkrishna, D. Determination of coalescence frequencies in liquid—Liquid dispersions: Effect of drop size dependence. Chem. Eng. Sci. 1990, 45, 3491–3504. [Google Scholar] [CrossRef]
- Frisch, U.; Parisi, G. Fully developed turbulence and intermittency. In Turbulence and Predictability in Geophysical Fluid Dynamics and Climate Dynamics; North-Holland: New York, NY, USA, 1985; Volume 88, pp. 71–88. [Google Scholar]
- Frisch, U.; Sulem, P.-L.; Nelkin, M. A simple dynamical model of intermittent fully developed turbulence. J. Fluid Mech. 1978, 87, 719–736. [Google Scholar] [CrossRef]
- Meneveau, C.; Sreenivasan, K.R. Simple multifractal cascade model for fully developed turbulence. Phys. Rev. Lett. 1987, 59, 1424–1427. [Google Scholar] [CrossRef]
- Daskiran, C.; Ji, W.; Zhao, L.; Lee, K.; Coelho, G.; Nedwed, T.; Boufadel, M.C. Hydrodynamics and Mixing Characteristics in Different Size Aspirator Bottles for the Water Accommodated Fraction (WAF) Tests. ASCE. J. Environ. Eng. 2019, 146, 04019119. [Google Scholar] [CrossRef]
- Thompson, E.F.; Vincent, C. Significant wave height for shallow water design. J. Waterw. Port. Coast. Ocean. Eng. 1985, 111, 828–842. [Google Scholar] [CrossRef]
- De Waal, J.; van der Meer, J. Wave runup and overtopping on coastal structures. Coast. Eng. 1992, 1993, 1758–1771. [Google Scholar]
- Baldyga, J.; Podgórska, W. Drop break-up in intermittent turbulence: Maximum stable and transient sizes of drops. Can. J. Chem. Eng. 1998, 76, 456–470. [Google Scholar] [CrossRef]
- Zhao, L.; Boufadel, M.C.; King, T.; Robinson, B.; Conmy, R.; Lee, K. Impact of particle concentration and out-of-range sizes on the measurements of the LISST. Meas. Sci. Technol. 2018, 29, 055302. [Google Scholar] [CrossRef]
- Geng, X.; Boufadel, M.C.; Ozgokmen, T.; King, T.; Lee, K.; Lu, Y.; Zhao, L. Oil droplets transport due to irregular waves: Development of large-scale spreading coefficients. Mar. Pollut. Bull. 2016, 104, 279–289. [Google Scholar] [CrossRef]
- Boufadel, M.C.; Bechtel, R.D.; Weaver, J. The movement of oil under non-breaking waves. Mar. Pollut. Bull. 2006, 52, 1056–1065. [Google Scholar] [CrossRef]
- Boufadel, M.C.; Du, K.; Kaku, V.; Weaver, J. Lagrangian simulation of oil droplets transport due to regular waves. Environ. Model. Softw. 2007, 22, 978–986. [Google Scholar] [CrossRef]
- Elliott, A.J.; Wallace, D.C. Dispersion of surface plumes in the Southern North Sea. Deutsch. Hydrogr. Z. 1989, 42, 1–16. [Google Scholar] [CrossRef]
- Cui, F.; Boufadel, M.C.; Geng, X.; Gao, F.; Zhao, L.; King, T.; Lee, K. Oil droplets transport under a deep-water plunging breaker: Impact of droplet inertia. J. Geophys. Res. Oceans 2018, 123, 9082–9100. [Google Scholar] [CrossRef]
- Spaulding, M.L. A state-of-the-art review of oil spill trajectory and fate modeling. Oil Chem. Pollut. 1988, 4, 39–55. [Google Scholar] [CrossRef]
- Reed, M.; Johansen, Ø.; Brandvik, P.J.; Daling, P.; Lewis, A.; Fiocco, R.; Mackay, D.; Prentki, R. Oil spill modeling towards the close of the 20th century: Overview of the state of the art. Spill Sci. Technol. Bull. 1999, 5, 3–16. [Google Scholar] [CrossRef]
- Drennan, W.M.; Donelan, M.A.; Terray, E.A.; Katsaros, K.B. Oceanic turbulence dissipation measurements in SWADE. J. Phys. Oceanogr. 1996, 26, 808–815. [Google Scholar] [CrossRef]
- Pizzo, N.E.; Deike, L.; Melville, W.K. Current generation by deep-water breaking waves. J. Fluid Mech. 2016, 803, 275–291. [Google Scholar] [CrossRef]
- Deike, L.; Pizzo, N.; Melville, W.K. Lagrangian transport by breaking surface waves. J. Fluid Mech. 2017, 829, 364–391. [Google Scholar] [CrossRef]
- Boufadel, M.C.; Cui, F.; Katz, J.; Nedwed, T.; Lee, K. On the transport and modeling of dispersed oil under ice. Mar. Pollut. Bull. 2018, 135, 569–580. [Google Scholar] [CrossRef]
- Aiyer, A.; Yang, D.; Chamecki, M.; Meneveau, C. A population balance model for large eddy simulation of polydisperse droplet evolution. J. Fluid Mech. 2019, 878, 700–739. [Google Scholar] [CrossRef]







© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, F.; Geng, X.; Robinson, B.; King, T.; Lee, K.; Boufadel, M.C. Oil Droplet Dispersion under a Deep-Water Plunging Breaker: Experimental Measurement and Numerical Modeling. J. Mar. Sci. Eng. 2020, 8, 230. https://doi.org/10.3390/jmse8040230
Cui F, Geng X, Robinson B, King T, Lee K, Boufadel MC. Oil Droplet Dispersion under a Deep-Water Plunging Breaker: Experimental Measurement and Numerical Modeling. Journal of Marine Science and Engineering. 2020; 8(4):230. https://doi.org/10.3390/jmse8040230
Chicago/Turabian StyleCui, Fangda, Xiaolong Geng, Brian Robinson, Thomas King, Kenneth Lee, and Michel C. Boufadel. 2020. "Oil Droplet Dispersion under a Deep-Water Plunging Breaker: Experimental Measurement and Numerical Modeling" Journal of Marine Science and Engineering 8, no. 4: 230. https://doi.org/10.3390/jmse8040230
APA StyleCui, F., Geng, X., Robinson, B., King, T., Lee, K., & Boufadel, M. C. (2020). Oil Droplet Dispersion under a Deep-Water Plunging Breaker: Experimental Measurement and Numerical Modeling. Journal of Marine Science and Engineering, 8(4), 230. https://doi.org/10.3390/jmse8040230






