Use of Artificial Intelligence as a Problem Solution for Maritime Transport

Abstract

The purpose of this article is to propose a solution for the transport problem in sea freight using machine learning algorithms. An important aspect of sea transport is the organization of freight. In particular, the maritime freight network is a large complex system whose complexity of route maps and the variety of ship traffic render it difficult to model. When investigating the characteristics of the sea freight system, it is generally advisable to use rough models in which only significant approximations are introduced and a number of details are not taken into account. At the same time, an exact model is used in a detailed study of isolated areas of the network wherein it is the area which is explored in detail and not the connections between the said areas. By so doing, one should be careful not to overlook the deviations of the model from the real network in the first case and the connections between areas in the second.Building a model that accurately takes into account and describes all the details results in excessive complications in the design process, so, in practice, a number of assumptions are always used in the simulation which are basically approximations of the real characteristics related to ship movement, depending on the specific task. Four models are used in order to build an optimal cargo transportation system: Transnational cargo model; model of cargo transportation with a dedicated initial port of cargo departure; model of cargo transportation with dedicated initial ports of departure and final port of cargo distribution; model of cargo transportation on a circular chain of ports. The route conditions are given by the traveling wave equation and on the basis of these calculations the optimal route of cargo ship movement is put forth whereby conditions affecting freight traffic include: Number of ports, fuel quantity, port of cargo destination, as well as distances between ports and intermediate ports of call. The scientific contribution lies in the fact that the human role is reduced only to that of the system observer, which, in turn, simplifies the freight calculations, as well as helps reduce the cost of fuel and human resources.

1. Introduction

One of the main problems in transport organization lies in freight transportation. The first studies devoted to the development of an optimal transportation plan were carried out in the 1930s. In 1939, L.V. Kanto-Sidorovich mathematically described the transport problem related to linear programming [1]. In his research a class of tasks are defined which are in close relation to transport, one of which is the algorithm proposed as a transport problem solution called the method allows the multipliers. In 1949, L.V. Kantorovich and M.K. Gavurin published their work in which they proposed a solution to the problem of transport with constraints on bandwidth. Using the aspects of the general method, L.V. Kantorovich developed a method of potentials as the solution of linear programming problems [2]. A year later, a similar method was proposed by J. Danzig and F. Wolf [3].

Scientist A.L. Lourie proposed a method for solving the transport problem by approximating plans which were found to be conditionally optimal [3]. In 1985, O.I. Aven, S.E. Lovetsky, and G.E. Moiseenko published a paper on the problems of optimal planning and traffic flow management in transport networks [2]. In this paper, mathematical models of transport networks and transport flows were taken into consideration.

Another important task connected to transport is the organization of cargo transportation. In particular, the network of sea freight is a large complex system, the modeling of which is laden with additional difficulties due to the complexity of route maps and the diversity of ships. In studies on maritime cargo transport it is generally advisable to use rough models in which only significant approximations are introduced and a number of details are not taken into account. At the same time, an exact model is used in a detailed study of isolated areas of the network wherein it is the area which is studied in detail and not the connections between the said areas.

In doing so, one should not remain ignorant of the discrepancies between the model and the real network in the first case, or of the consequences of not taking into account the connections between areas in the second. Construction of a model that accurately takes into account and describes all the details includes unjustified complications in its design process, therefore, in practice, during the simulation, a number of assumptions and approximations of the real characteristics of the ship’s motions are always used, depending on the particular task. This work is devoted to the study on the process of cargo transport organization in sea freight. We will consider the task of constructing a dynamic model of cargo transport organization on an elongated section of the road with a large number of intermediate stop points along which the traffic will flow. It is assumed that an inter-port overpass between the initial points and the endpoints exists, where part of the cargo can be stored temporarily. 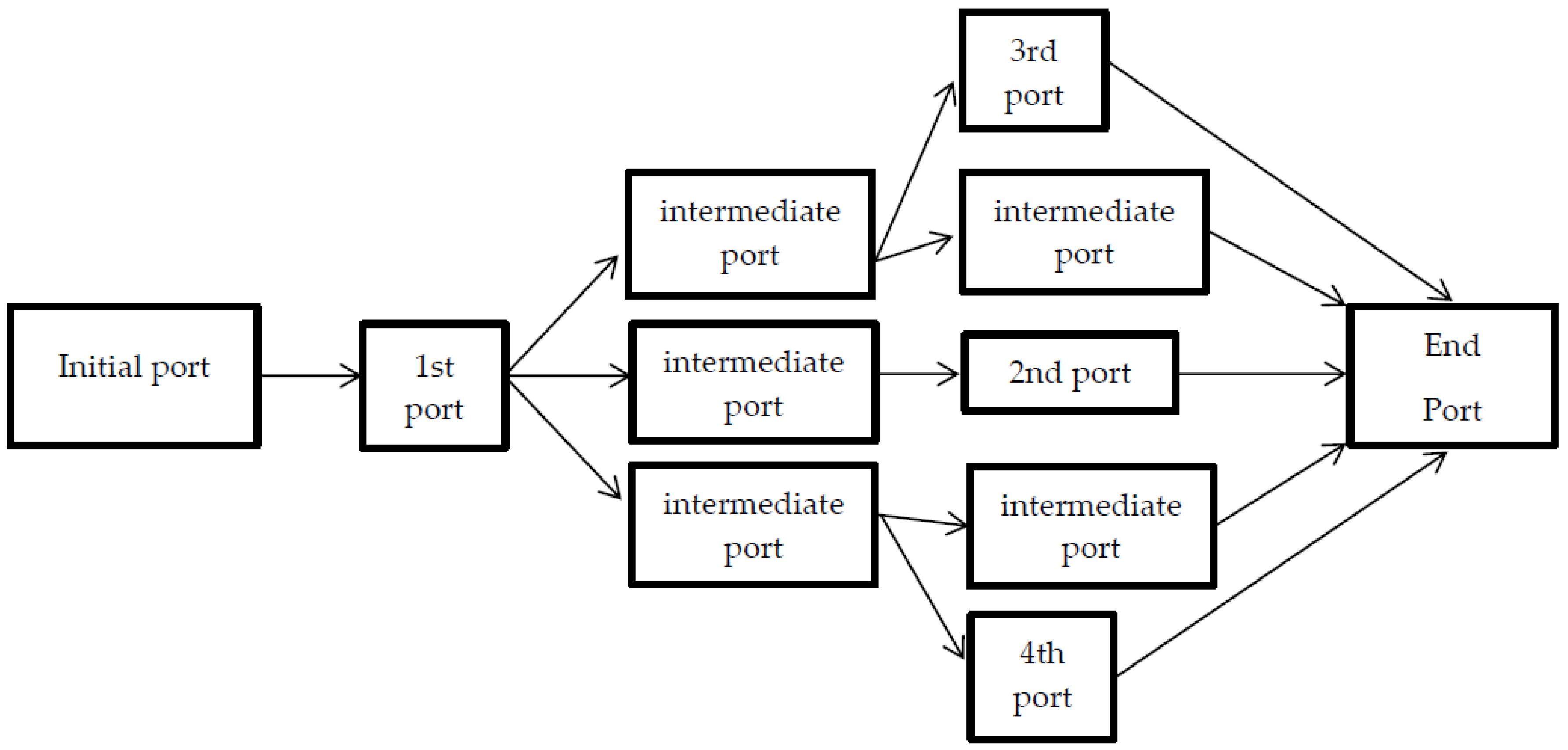Figure 1 shows the cargo transportation diagram for the transport problem.

In general, there are four main models of cargo transportation:

(1)

Model of transnational cargo transportation;

(2)

Model of cargo transportation with a dedicated initial delivery port;

(3)

Model of freight transport with dedicated initial delivery ports and terminal port of cargo distribution;

(4)

The model of cargo transportation on a circular chain of ports.

Which type of model will be employed depends on a set of particular conditions—the number of ports and their geographic location, the time of transportation, etc. The optimization accuracy differs only in the case of the first model since it is very difficult to optimize the traffic flow under unknown conditions. Next, we shall discuss the above models of freight transportation in more detail [1].

2. A Model of Transnational Cargo Transportation

This model describes the flow of traffic without the assigned initial ports of departure and the terminal port of cargo distribution, which is why we take the number of intermediate ports to be infinite in either direction. The port activities include receiving, processing, and discharging the goods, whereas the ports themselves have a given bandwidth [2].

Cargo handling takes place within port facilities where, in each node, the unit volume of goods is processed per unit time. The number of nodes is indicated in the n the port at the time t_k through z_n (t_k). This is to say that the number of processed cargo handling units in an uninterrupted operation within the entire chain of transportation is limited.

Under the port capacity Δ, we will consider the maximum number of nodes in which, respectively, the maximum cargo volume per unit time interval is processed.

The organization of such cargo manipulation depends on the technologies of cargo acceptance, processing, and delivery. The first technology is based on established regulatory rules for the interaction of neighboring ports. For each port number i there are rules for interaction with the previous (i − 1) port, as well as the following (i + 1) port. According to the rule of interaction with the previous port [4], the number of nodes are increased by port number i with intensity α (z_i−1 − z_i) if the number of nodes in the said port is smaller in comparison to the previous port.

In the said situation, the traffic flow is taken from the previous port. In the opposite scenario, the port number i would reduce the number of nodes with the same intensity, and the traffic flow would be sent on a redundant path.

According to the rule of interaction with the next port [5], the port number i reduces the number of nodes with intensity α (z_i−1 − z_i+1) if the number of nodes in the said port number is larger than in the next port. In this case, the traffic flow is sent to the next port. In the opposite case, the port number i would increase the number of nodes with the same intensity, and the traffic flow would be taken from a reverse path.

The first technology does not take into account the constraints on port capacity, moreover, it does not allow the port to be used to its full potential.

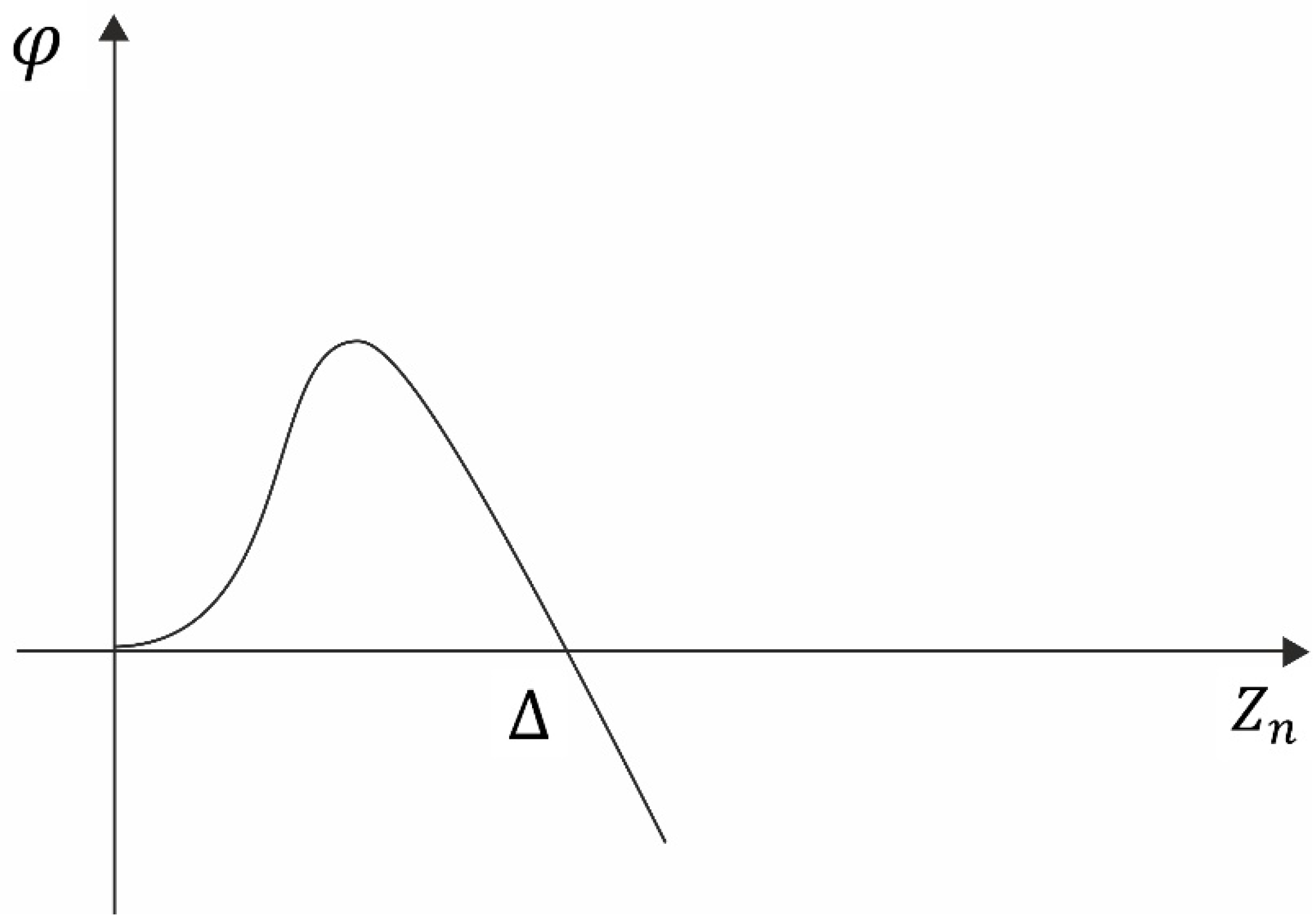
The second technology allows for both the increase in the number of nodes involved (if it is less than Δ), and its reduction (if it exceeds Δ). At the same time, cargo is either taken from or sent to the overpass. The form of the function φ, which specifies the rate of change in the number of nodes involved in the second technology, is shown in Figure 2.

Thus, taking into account the aspects of the first and second technologies, the rate of change of the number of involved nodes for the i-th port is described by the following differential equation:

$$\dot{z_i}\left(t\right)=\alpha \left(z_{i-1}-z_i\right)-\alpha \left(z_i-z_{i+1}\right)+\phi \left(z_i\right), i\in Z, t\in \left[0,+\infty \right).$$

(1)

Efficient transportation of goods requires an equally efficient and simple control system. It is derived from the fact that the volumes of processed goods for the scheduled time interval should coincide with the workload in all the ports. The said condition can be described as follows: There exists a number τ > 0, which depends on t and i, such that for all i ∈ Z and t ∈ [0, +∞), the equality is satisfied:

$$z_t\left(t\right)=z_{i+1}\left(t+\tau \right)$$

(2)

Solutions for the system of differential Equation (1) satisfying condition (2) are called solutions of the running wave type [6]. The constant τ, which is a shift between the moments of measurement and the comparison of volumes of goods, will be labeled as the characteristic of the control system. Thus, this model, describing the process of freight transport and their control system, is derived from a system of differential equations and a condition that defines a running wave:

$$\dot{z_i}\left(t\right)=\alpha z_{i-1}-2\alpha z_i+\alpha z_{i+1}+\phi \left(z_i\right), i\in Z, t\in \left[0,+\infty \right)$$

(3)

$$z_i\left(t\right)=z_{i+1}\left(t+\tau \right), i\in Z, t\in \left[0,+\infty \right)$$

(4)

The category of continuous functions {z_i} i ∈ Z defined on [0, +∞) is a solution for the system of differential Equation (3) if for all t ∈ [0, +∞) the functions z_i satisfy this system [5].

For μ ∈ (0, 1), we define the functions space with weights:

$$\begin{array}{c}{\vartheta }_{\mu }^1{C}^{\left(k\right)}\left(R\right)=\left\{x(·):x(·)\in C^{\left(k\right)}\left(R,R\right), \begin{array}{c}\max sup\\ 0\le r\le k,t\in R\end{array}\left|\right|x^{\left(r\right)}\left(t\right)e^{-\delta \left|t\right|}\left|\right|{}_R<+\infty \right\},\\ k=0,1,\dots , \mu =e^{-\delta }\end{array}$$

and the norm:

$$||x{\left|\right|}_{\mu }^{\left(k\right)}=\max su{p}_{0\le r\le k,t\in R}\left|\right|x^{\left(r\right)}\left(t\right)e^{-\delta \left|t\right|}\left|\right|{}_R$$

as well as the vector space ${К}^{-1}={П}_{-\infty }^{+\infty }{R}_i, R_i=R, i\in Z$ with elements $X={\left\{x_i\right\}}_{-\infty }^{+\infty }, x_i\in R, i\in Z$, and with the standard topology of the complete direct product.

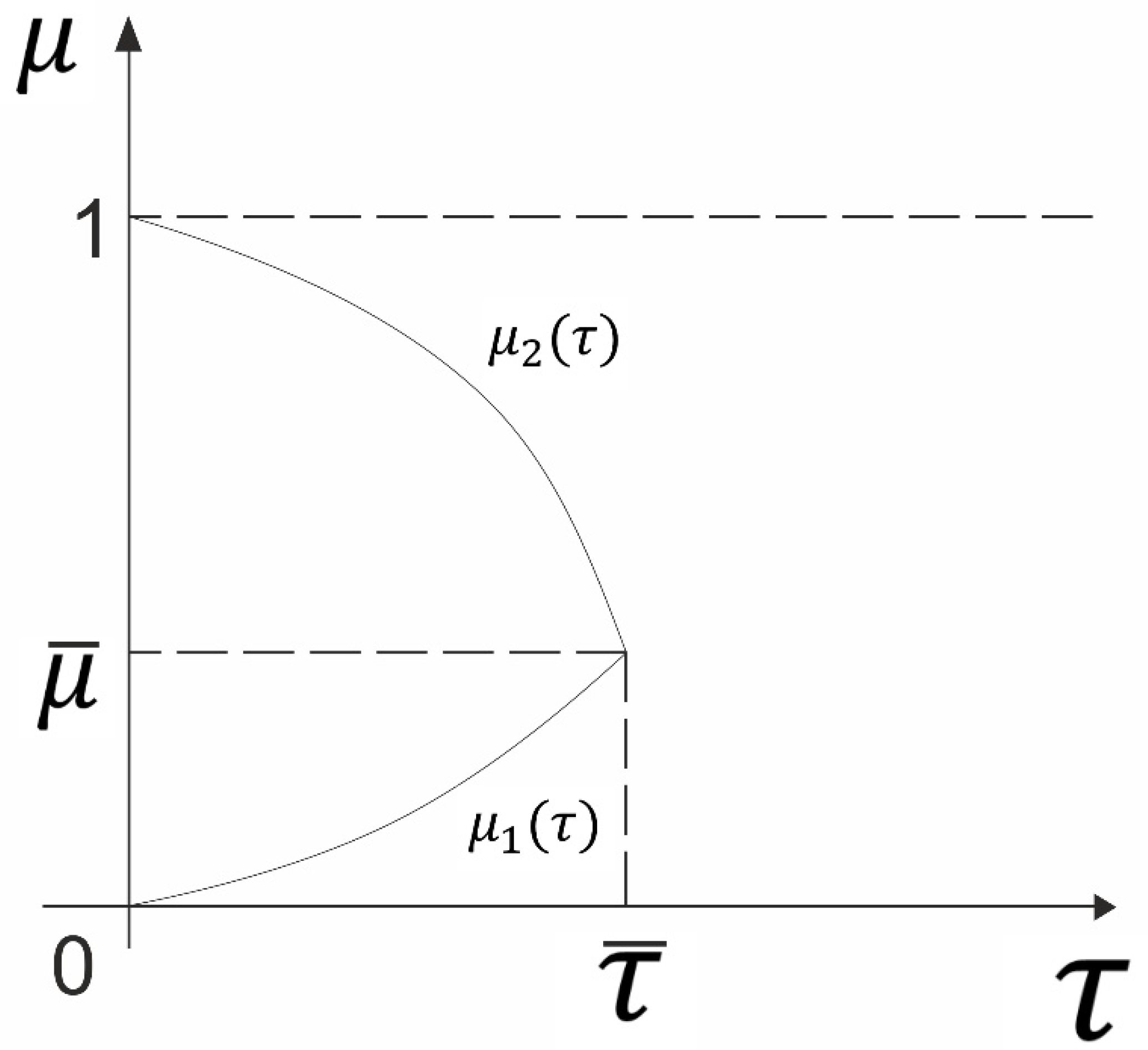
Figure 3 shows the functions ${\mu }_1\left(\tau \right)та{\mu }_2\left(\tau \right)$.

In the ${К}_{2\mu }^1$ space we define a category of Hilbert subspaces:

$${К}_{2\mu }^1=\left\{X:X\in K^{-1}; {\displaystyle \sum }_{i=-\infty }^{+\infty }{\left|x_i\right|}_R^2{\mu }^{2\left|i\right|}<+\infty \right\}, \mu \in \left(0,1\right),$$

with the norm

$$||X{\left|\right|}_{2\mu }={\left[{\displaystyle \sum }_{i=-\infty }^{+\infty }{\left|x_i\right|}_R^2{\mu }^{2\left|i\right|}<+\infty \right]}^{1/2}$$

Let’s denote

$$M\left(\tau \right)=\tau max\left[2\alpha ,L_0\right]$$

and consider the inequality between the two variables $\tau \in \left(0,+\infty \right)та\mu \in \left(0,1\right)$

$$M\left(\tau \right)\left[1+2{\mu }^{-1}\right]<ln {\mu }^{-1}, \mu \in \left(0,1\right)$$

(5)

The set of solutions for inequality (5) is described by functions ${\mu }_1\left(\tau \right)$ and ${\mu }_2\left(\tau \right)$, represented in Figure 3.

That is, for the initial data a > 0, $\overline{i}\in Z$ the initial time $\overline{t}\in \left[0,+\infty \right)$ and the characteristics τ satisfying the condition $0<\tau <\overline{\tau }$, there exists a solution $\{Z_i(·){\}}_{i\in Z}$, Equation (3) of the running wave type (condition (4)) with the characteristic τ satisfying the initial condition $Z_{\overline{i}}\left(\overline{t}\right)=a$. In such a solution for any $i\in Z$ the function $Z_i(·)$ belongs to the space $L_{\sqrt[\tau ]{\mu }}^1{C}^{\left(0\right)}\left(\left[0,+\infty \right)\right)$ for $\mu \in \left({\mu }_1\left(\tau \right),{\mu }_2\left(\tau \right)\right)$. Such a solution is unique and continuously depends on the initial condition a, where each coordinate $Z_i(·)$, $i\in Z$ continuously depends on the initial condition a as an element of space $L_{\sqrt[\tau ]{\mu }}^1{C}^{\left(0\right)}\left(\left[0,+\infty \right)\right)$.

System (3)–(4) has two stationary solutions of the running wave type:

$\overline{Z_1}\equiv \left\{\dots ,0,0,0,\dots \right\},\overline{Z_2}\equiv \left\{\dots ,\Delta ,\Delta ,\Delta ,\dots \right\}$. It states to reason that such solutions belong to the space $K_{2\mu }^1$ for $\mu \in \left(0,1\right)$.

The stationary solution $\overline{Z}={\left\{\overline{Z_i}\right\}}_{i\in Z}$ of equation system (3) in the phase space $K_{2\mu }^1$, $\mu \in \left(0,1\right)$ is Lyapunov stable if there exists $\gamma >0$ and $\overline{t}\ge 0$ such that for $d\in K_{2\mu }^1$ satisfies the condition $||d-\overline{z}{\left|\right|}_{2\mu }<\gamma$, solution Z(t) of Equation (3) exists with the initial condition $Z\left(\overline{t}\right)=d$; for ε > 0 there exists $0<{\sigma }_1<\gamma$ such that $||d-\overline{z}{\left|\right|}_{2\mu }<{\sigma }_1$, solution Z(t) of Equation (3) with the initial condition $Z\left(\overline{t}\right)=d$ satisfies the condition $||d-\overline{z}{\left|\right|}_{2\mu }<\epsilon$ for all $t>\overline{t}.$

Then, the stationary solution $\overline{Z}={\left\{\overline{Z_i}\right\}}_{i\in Z}$ of Equation (3) in the phase space $K_{2\mu }^1, \mu \in \left(0,1\right)$ is Lyapunov asymptotically stable if $\underset{t\to +\infty }{\lim }||Z\left(t\right)-\overline{Z}{\left|\right|}_{2\mu }=0$.

Determine:

$${\tau }_{max}=\sup \left\{\tau :\tau \le \tau , {\mu }_2\left(\tau \right)\ge \overline{\partial }\right\}$$

(6)

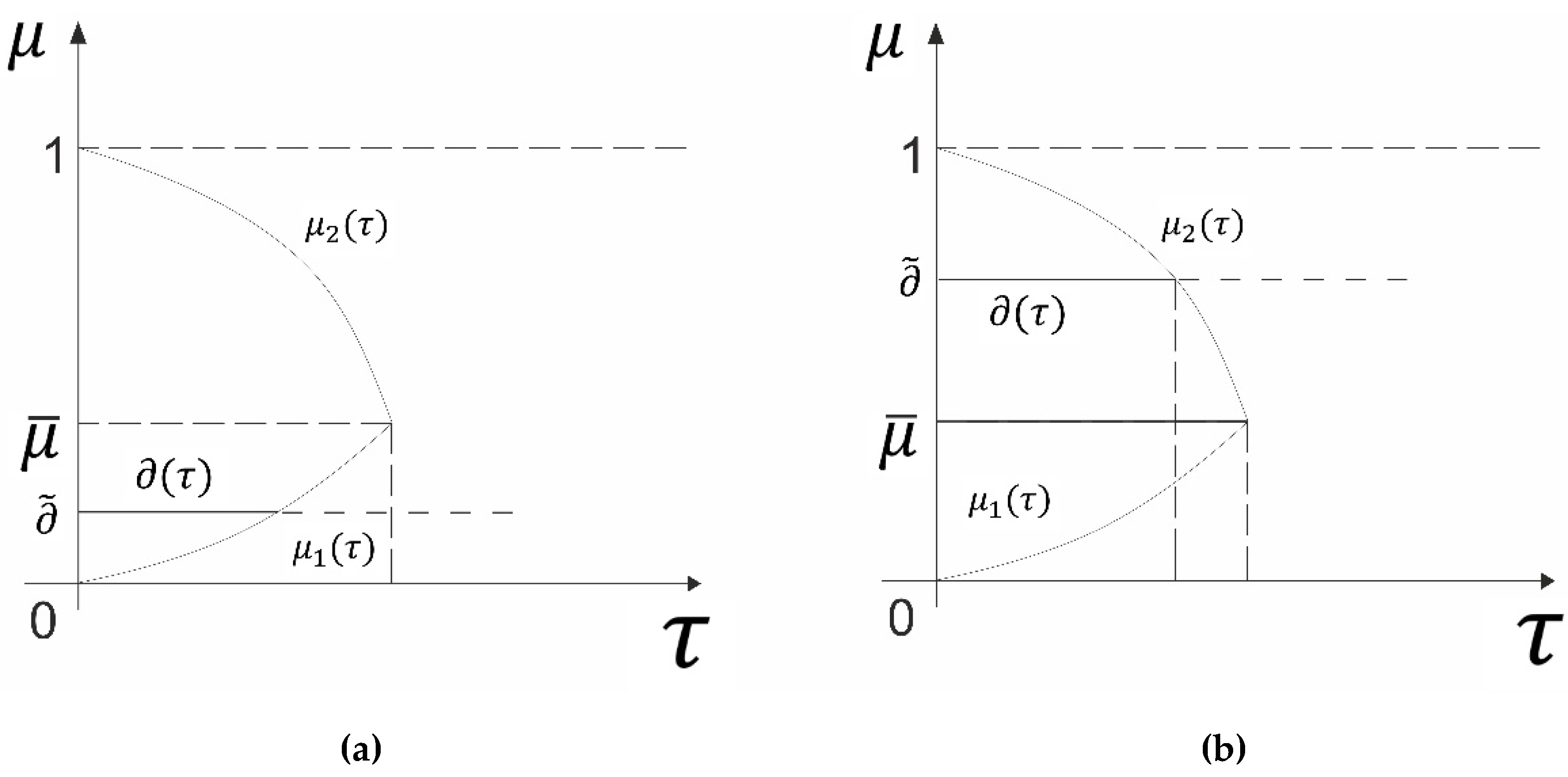
The function $\partial \left(\tau \right)=\max \left(\overline{\partial },{\mu }_1\left(\tau \right)\right)$ on the interval (0, ${\tau }_{max}$] is represented graphically in Figure 4 ($\tilde{\partial }<\overline{\mu }$ and $\tilde{\partial }>\overline{\mu }$ are also represented in Figure 4a,b respectively).

From this it follows that in order to make a stationary solution $\overline{z}={\left\{\overline{z_i}\right\}}_{i\in Z}$, $\overline{z_i}=\overline{z_{i+1}}$, $i\in Z$, the system of Equation (3) in the phase space $K_{2\mu }^1$, $\mu \in \left(0,1\right)$ is the solution to the transport problem of the transnational model, and the following conditions are met:

(1)

It is stable under Lyapunov;

(2)

There exists $\gamma >0$ and $t\ge 0$ such that for the number d₀ satisfying the condition $\left|d_0-{\overline{z}}_0\right|<\gamma$, solution $z\left(t\right)={\left\{z_n\left(t\right)\right\}}_{n\in Z}$ of system (3)–(4) with the initial condition $z_0\left(\overline{t}\right)=d_0$;

(3)

For ε > 0, there exists $0<{\sigma }_2<\gamma$ such that from the condition $\left|d_0-{\overline{z}}_0\right|<{\sigma }_2$ it follows that solution z(t) of system (3)–(4) with the initial condition $z_0\left(\overline{t}\right)=d_0$ satisfies the condition $||z\left(t\right)-\overline{z}{\left|\right|}_{2\mu }<\epsilon$ for all $t>\overline{t}$ [6].

3. Model of Freight Transportation with an Assigned Initial Port

This model is primarily characterized by an assigned starting point for shipping goods whereby the model will contain a stationary port i = 0 and several intermediate ports i = 1, 2, … Similar to the first model, the traffic flow organization is carried out using two technologies.

The first technology. The first technology which has been described in the first model operates in ports with i = 1, 2, … In the initial port i = 0, the first technology is determined by the rule of interaction with the next port and is described by function ψ(t), depending on time t ≥ 0. It is assumed that function ψ is continuously piecewise-differentiated. Since the starting point is nodal, it can be assumed that it is sufficiently large in power, so that, if necessary, it could attract more of the nodes involved, which cannot be conducted at intermediate points [7].

The second technology. The second technology from the first model repeats itself exactly for ports with numbers i = 1, 2, … For the initial port i = 0, the second technology from the previous model is used for unloading, so the rate of change in the number of involved processing nodes in the initial port in the second technology is described by the function ${\phi }_0\left(t\right)$, which depends on the number of nodes in the source port and meets the following conditions:

Equal to zero on the half-direct (−∞, Δ), and a decreasing function on the half-direct [Δ, +∞).

We shall assume that functions ${\phi }_0(·)i\phi (·)$ (defined in the first model) are infinitely differentiated. Obviously, if the volume of cargo in the 0th port does not exceed Δ, only the first technology is used.

Thus, taking into account the aspects of the first and second technology, the process of cargo transportation is described by a system of differential equations below:

$$\{\begin{array}{c}{\dot{z}}_0\left(t\right)=\psi \left(t\right)-\alpha z_0+\alpha z_1+{\phi }_0\left(z_0\right), t\in \left[0,+\infty \right);\\ {\dot{z}}_i\left(t\right)=\alpha z_{i-1}-2\alpha z_i+\alpha z_{i+1}+\phi \left(z_i\right), i=1,2,\dots , t\in \left[0,+\infty \right);\\ z_i\left(t\right)=z_{i+1}\left(t+\tau \right), i=0,1,2,\dots t\in \left[0,+\infty \right).\end{array}$$

(7)

The class of system solution (7) is extremely narrow; therefore, a broader class of solutions, called quasi-solutions of the running wave type, is used to describe the realizable modes of cargo transportation. These solutions are piecewise-absolutely-continuous, and the gaps, which are the multiple characteristics of the control system (parameter τ), are located at the points (ports).

For initial data a > 0, i ∈ {0, 1, …} and the initial time $\overline{t}\in \left[0,+\infty \right)$, all τ parameters that satisfy the condition 0 < τ < $\overline{\tau }$ (Figure 2) and functions $\psi \in C^{\infty }\left(\left[0,\tau \right],R\right)$ in the half-direct (τ, +∞) there exists a single piecewise continuous extension of the function ψ and the corresponding quasi-solution ${\left\{z_i(·)\right\}}_0^{+\infty }$ type of a traveling wave with characteristic τ of system (7) in the phase space $K_{2\mu }^1$, $\mu \in \left({\mu }_1\left(\tau \right),{\mu }_2\left(\tau \right)\right)$ satisfying the initial condition $z_{\overline{i}}\left(\overline{t}\right)=a$. Such a quasi-solution is unique, continuously depending on the initial condition a and the function ψ.

This means that in all ports and at specific points in time, multiple characteristics of control are present so it is necessary to change the number of nodes involved. This procedure requires additional capacities to be connected, which can only be found in the node’s initial port. In order to perform said action, a swift change is required in the number of nodes involved at the initial time at the initial port (change function ψ in the normal L₁ ([0, τ], R) so as to arrange controlled traffic with the help of certain technologies (obtain the so-called ε-quasi-solution, i.e., a quasi-solution for which the gaps are less than ε). A quasi-type runway wave with the characteristic τ is called the ε-quasi-solution of a waving wave type with the characteristic τ or (ε, τ)—quality solution if the inequalities are satisfied:

| z_0 (kτ − 0) − z_0 (kτ + 0) | < ε, k = 1, 2

(8)

For initial data a > 0, $\overline{i}\in \left\{0,1,\dots \right\},$ the initial moments of time $\overline{t}\in \left[0,+\infty \right)$, the characteristics τ satisfying the condition 0 < τ < $\overline{\tau }$, the arbitrary function $\psi \in C^{\infty }\left(\left[0,\tau \right],R\right)$ and an arbitrary ε > 0, there exists a function ψ_ε ∈ C ^ ∞ ([0, τ], R) different from ψ in the vicinity of the point 0 such that its continuation on (τ, +∞) and its corresponding quasi-solution $z_{i\epsilon }{\}}_0^{+\infty }$ of a traveling wave type with the characteristic τ of system (7) satisfies the initial condition z_ ($\overline{i}$ ε) ($\overline{t}$) = a, and belongs to the phase space $K_{2\mu }^1$ for $\mu \in \left({\mu }_1\left(\tau \right),{\mu }_2\left(\tau \right)\right)$ and is (ε, τ) the quasi-solution of the freight transport model with the assigned initial port of delivery loads [8].

4. The Model of Freight Transportation with the Assigned Initial Shipping Ports and the Terminal Port of Cargo Distribution

This model of freight traffic contains the initial departure port for cargo i = 0, the final number of intermediate ports i = 1, 2, …, m, and the terminal port of cargo distribution i = m + 1. Similar to previous models, the organization of traffic flow is carried out using two technologies.

The first technology. It has been described earlier in the situation where there were ports with numbers i = 0, 1, 2, …, m, involved in the model of freight transport with an assigned initial shipping port. The technology of delivering goods to the initial port is described by function ${\psi }_1\left(t\right),t\ge 0$. In the terminal port, the first technology is determined by the rule of interaction with the previous port and described by function ${\psi }_2\left(t\right),t\ge 0$. It is assumed that function ${\psi }_1(·)$ is piecewise infinitely differentiated, and function ${\psi }_2(·)$ is piecewise continuous.

The second technology. The second technology from the two previous models repeats itself exactly for the initial and intermediate ports. The second end-to-end technology functions the same way as in the case of intermediate ports [9].

Taking into account the first and second technologies, the third model of freight transportation is described by the following system of differential equations:

$$\{\begin{array}{c}{\dot{z}}_0\left(t\right)={\psi }_1\left(t\right)-\alpha z_0+\alpha z_1+{\phi }_0\left(z_0\right), t\in \left[0,+\infty \right)\\ {\dot{z}}_i\left(t\right)=\alpha z_{i-1}-2\alpha z_i+\alpha z_{i+1}+\phi \left(z_i\right), i=1,2,\dots ,m, t\in \left[0,+\infty \right)\\ {\dot{z}}_{m+1}\left(t\right)=\alpha z_m-\alpha z_{m+1}-{\phi }_2\left(t\right)+\phi \left(z_{m+1}\right), t\in \left[0,+\infty \right)\\ z_i\left(t\right)=z_{i+1}\left(t+\tau \right), i=1,2,\dots ,m, t\in \left[0,+\infty \right)\end{array}$$

(9)

The class of solutions of system (9) is also extremely narrow; therefore, the quasi-solution (including gaps in the points, multiple characteristics of the control system) of the running wave type is used to describe the cargo being realized.

For the initial data a > 0, $\overline{i}\in \left\{0,1,\dots .,m+1\right\}$, the initial moment $\overline{t}\in \left[0,+\infty \right)$, the characteristics τ satisfying the condition 0 < τ < $\overline{\tau }$, (Figure 2), the functions ${\psi }_1\in C^{\infty }\left(\left[0,\tau \right],R\right)$ and ${\psi }_2\in C\left(\left[0,\tau \right],R\right)$ there exists single piecewise continuous extensions of the functions ψ₁, i, ψ₂, and their corresponding quasi-solution $\{z_i(·){\}}_0^{m+1}$ of the waving wave type with the characteristic τ of system (8) in the phase space $K_{2\mu }^1$, $\mu \in \left({\mu }_1\left(\tau \right),{\mu }_2\left(\tau \right)\right)$, that satisfy the initial condition $z_{\overline{i}}\left(\overline{t}\right)=a$. This quasi-solution is unique and depends continuously on the initial condition a and functions ψ₁ and ψ₂.

The same condition is valid for a model with an assigned initial delivery port, where you can arrange a controlled traffic flow (i.e., obtain an ε-quasi-solution) with the help of a swift change in the number of nodes in the initial port during the initial period of time.

For initial data a > 0, $\overline{i}\in \left\{0,1,\dots ,m+1\right\}$, the initial moments of time $\overline{t}\in \left[0,+\infty \right)$, the characteristics τ satisfying the condition 0 < τ < $\overline{t}$, arbitrary functions ${\psi }_1\in C^{\infty }\left(\left[0,\tau \right],R\right)$ and ${\psi }_2\in C\left(\left[0,\tau \right],R\right)$ and the random ε > 0 there exists function ${\psi }_1\epsilon \in C^{\infty }\left(\left[0,\tau \right],R\right)$ different from ψ₁ in the vicinity of the point 0 such that the extension of the functions ψ₁ε and ψ₂ to (τ, +∞) and the corresponding quasi-solution $\{z_{i\epsilon }(·){\}}_0^{m+1}$ type of a traveling wave with characteristic τ of system (8) satisfies the condition $z_{i\epsilon }\left(\overline{t}\right)=a$, belongs to the phase space $K_{2\mu }^1$ for $\mu \in \left({\mu }_1\left(\tau \right),{\mu }_2\left(\tau \right)\right)$ and is (ε, τ)—quality-solution of the model of freight transport with an assigned initial port of cargo delivery [10].

5. Model of Cargo Transportation in a Circular Chain of Ports

The fourth model is a partial variant of the first model and describes the transport of goods by circular chain from n ports. To study the model, a solution of system (3)–(4) is required, satisfying the following additional condition:

$$z_i\left(t\right)=z_{i+n}\left(t\right), i\in Z, t\in \left[0,+\infty \right).$$

(10)

Thus, this model is described by the following system:

$$\{\begin{array}{c}{\dot{z}}_i\left(t\right)=\alpha z_{i-1}-2\alpha z_i+\alpha z_{i+1}+\phi \left(z_i\right), i\in Z, t\in \left[0,+\infty \right);\\ z_i\left(t\right)=z_{i+n}\left(t\right) i\in Z, t\in \left[0,+\infty \right)\\ z_i\left(t\right)=z_{i+1}\left(t+\tau \right), i\in Z, t\in \left[0,+\infty \right)\end{array}$$

(11)

If ${\left\{{\overline{z}}_i\right\}}_{i\in Z}$ is a solution of system (11), then for i ∈ Z function ${\overline{z}}_i$ is periodic with period τ_n.

The solution of system (11) depends on the solution of the following system:

$$\{\begin{array}{c}{\dot{z}}_1\left(t\right)=\alpha z_n-2\alpha z_1+\alpha z_2+\phi \left(z_1\right), t\in \left[0,+\infty \right);\\ {\dot{z}}_i\left(t\right)=\alpha z_{i-1}-2\alpha z_i+\alpha z_{i+1}+\phi \left(z_i\right) i\in 2,\dots .,n-1, t\in \left[0,+\infty \right)\\ {\dot{z}}_n\left(t\right)=\alpha z_{n-1}-2\alpha z_n+\alpha z_1+\phi \left(z_n\right), t\in \left[0,+\infty \right)\end{array}$$

(12)

$$\{\begin{array}{c}{z}_i\left(t\right)=z_{i+1}\left(t+\tau \right), i\in 1,\dots .,n-1, t\in \left[0,+\infty \right)\\ z_n\left(t\right)=z_1\left(t+\tau \right), t\in \left[0,+\infty \right)\end{array}$$

(13)

If there exists a solution for system (12)–(13), then it will be periodic in nature with period τ_n. One of these solutions is a stationary solution (Δ, Δ, …, Δ). In order to find other solutions (i.e., if they exist), all the solutions of the system of differential equations (1) are required (that is, solutions of the type of a traveling wave satisfying conditions (11)).

For arbitrary α > 0, δ > 0, all the solutions of the system of differential Equations (10) with coordinates whose initial value is greater than 0 are limited. Moreover, each coordinate solution which follows is limited to zero, and is asymptotically limited from the top by the value of Δ.

The stationary solution (Δ, Δ, …, Δ) of the system of differential Equations (10) is locally stable under Lyapunov in the first approximation [11].

To determine the region of stability for this solution, the system of differential Equations (10) is solved in a numerical manner using the Runge-Kutt method of the 4th order.

For α > 0 and δ > 0 the stability domain of the stationary solution (Δ, Δ, …, Δ) of the system of differential Equations (10) with positive coordinates of the initial value is reduced to a stationary solution of the system of equations (Δ, Δ, …, Δ).

From the abovementioned it states to reason that the solution of the system of differential Equations (10) with positive coordinates of the initial value is limited; moreover, it reduces to a stationary solution (Δ, Δ, …, Δ). Consequently, other periodic solutions, in addition to the stationary solution (Δ, Δ, …, Δ), do not contain a system of differential Equations (10) with positive coordinates of the initial value. This, in turn, means that there are no other solutions for system (10)–(11) with positive coordinates of the initial value, in addition to the stationary solution (Δ, Δ, …, Δ). Thus, there exists a single solution of the running wave type, namely, a stationary solution (Δ, Δ, …, Δ), for the original system (9) with positive coordinates of the initial value. The outlined approach to the transport problem solution can also be used in solving other problems which do not concern freight. In this case, the variables that determine the effectiveness are different in content depending on the specific task.

This is to say that the transport task can be employed in any process, such as in production or data process optimization. Application of optimization methods in all models of freight transportation mentioned in machine learning sources helps to exclude the human factor from the optimization calculations which, in turn, results in computer optimization reducing human involvement to a minimum [10].

6. Conclusions

To conclude, we might state that the type of freight is selected by the system based on the task of cargo transportation. Upon the completion of the selection process, the computer performs the choice of the algorithm for the construction of the cargo route and loading in order to achieve optimal cargo transportation. This method eliminates the manual construction of the freight route and minimizes human impact. Algorithms for each type of transportation will allow to apply this technique in many directions of transportation including both land and air transportation.