Far-Field Characteristics of Linear Water Waves Generated by a Submerged Landslide over a Flat Seabed
Abstract
1. Introduction
2. Materials and Methods
2.1. Wave Models
2.2. Landslide Shapes and Motion
2.2.1. Landslide Shapes
2.2.2. Landslide Motion
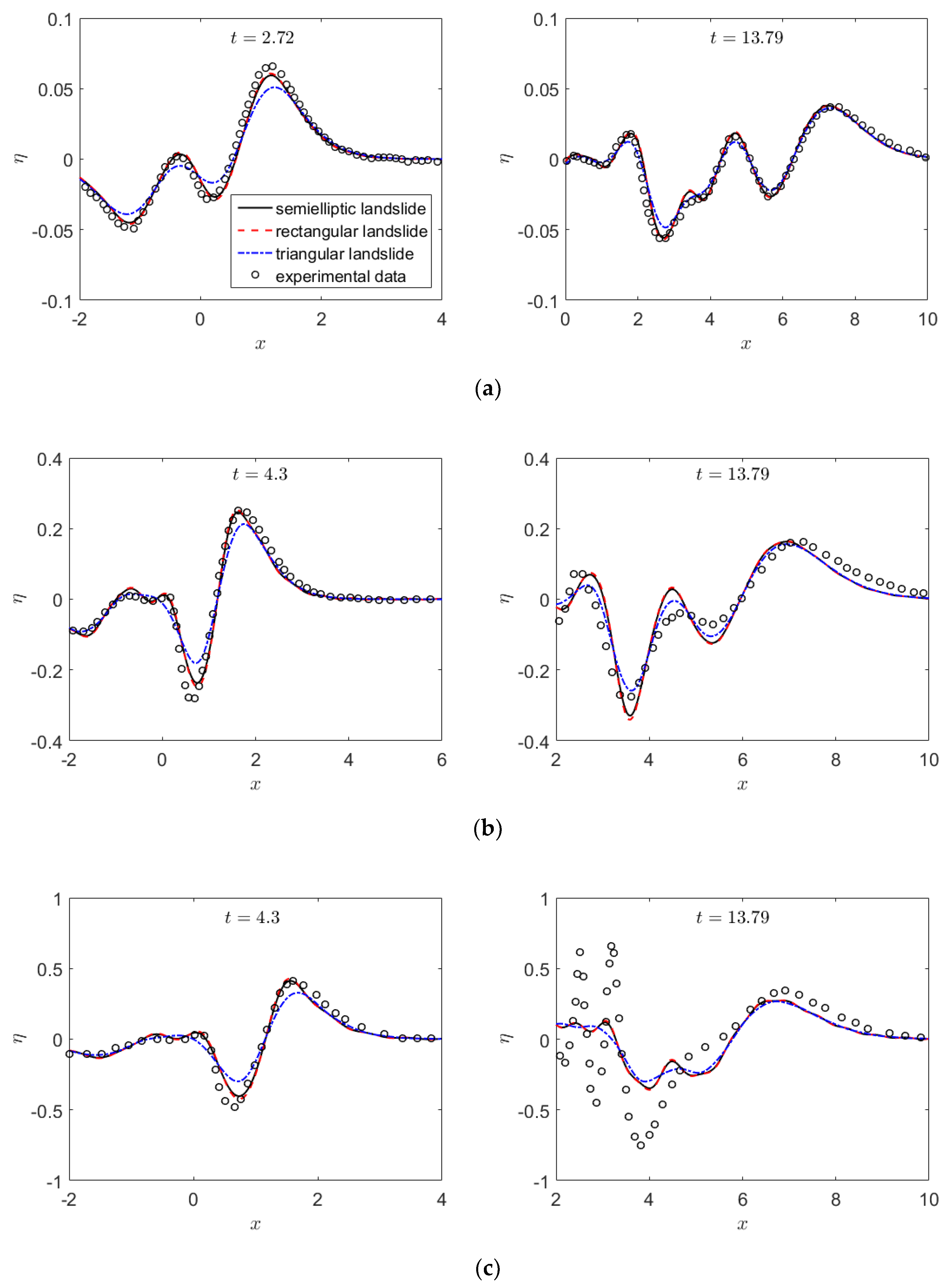
2.3. Numerical Integration and Validation
3. Results and Discussions
3.1. Setup of Cases
3.2. Effect of Water Depth on the Generated Leading Wave
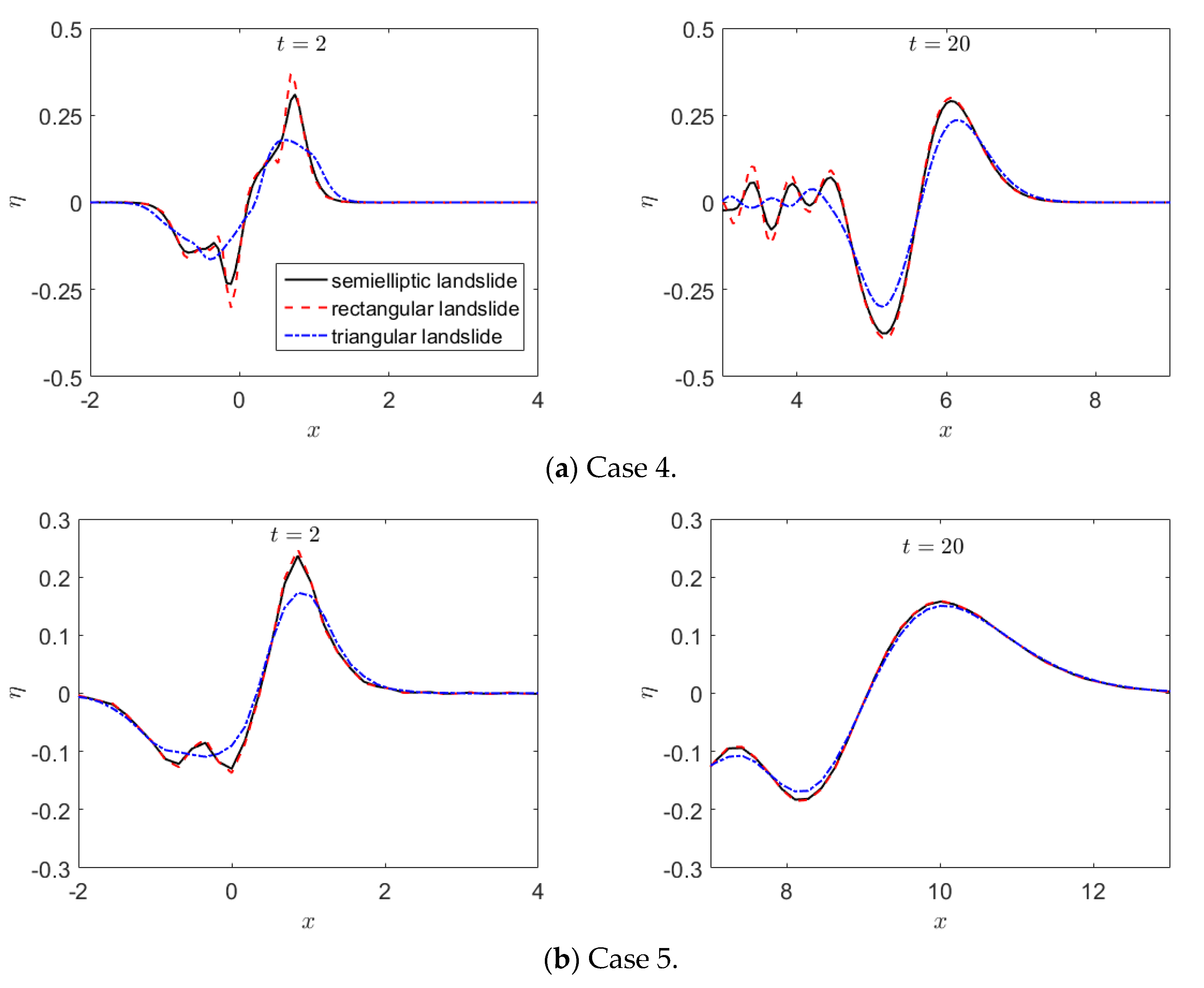
3.3. Effect of the Landslide Fr Number on the Generated Leading Wave
3.4. Availability of LWD and LND models
4. Conclusions
- (1)
- The amplitudes of the generated water waves increase with the increase of the landslide Fr number. Up to Fr = 0.375, the nonlinear effect can be neglected and the LFD model has been demonstrated to be accurate enough;
- (2)
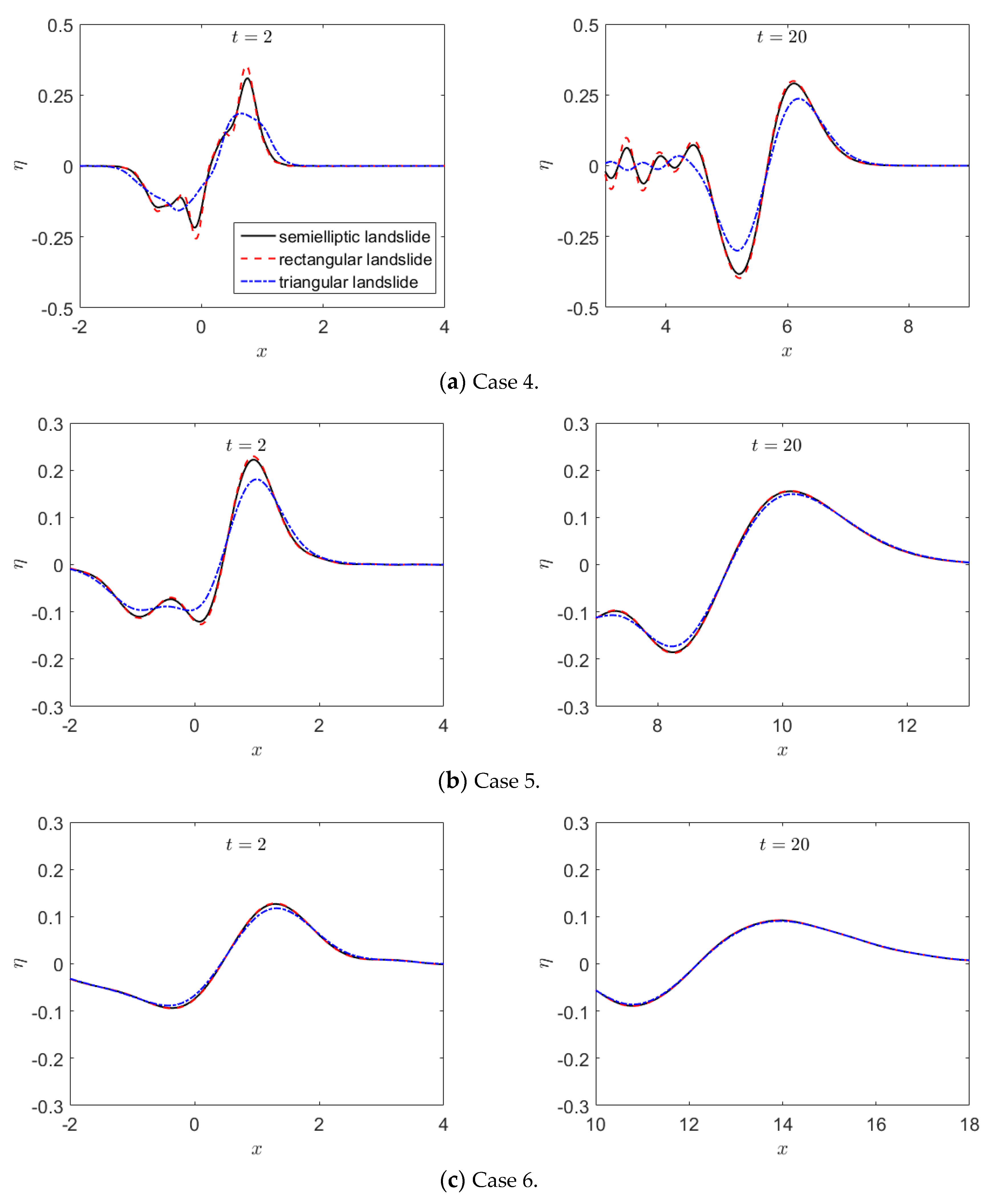
- From the analysis of the results obtained by the LFD model, it can be concluded that the phenomenon above is caused by frequency dispersion and will be invalid for landslide-generated water waves at a shallow water depth. The near-field leading waves in shallower water are sensitive to the shapes of landslides, while the far-field leading waves in deeper water are independent of the exact shapes of landslides. Specifically, the choice of a rectangular or semielliptical shape is not influential for a relative depth of μ ≥ 0.3, and at a deeper water depth (μ = 0.6), the leading waves obtained by all three different landslide shapes (triangular, rectangular, and semielliptical) are almost the same. In addition, the phenomenon mentioned above is insensitive to the landslide Froude number;
- (3)
- The LND model (based on a shallow water assumption), which is one of the most popular models for tsunami wave prediction, cannot be used to reproduce this phenomenon. However, the LWD model can predict the phenomenon properly. For leading wave propagation, the LWD model is demonstrated to be accurate enough up to at least μ = 0.6, although only weakly dispersive effects are included.
Author Contributions
Funding
Conflicts of Interest
Appendix A. Derivation of the LFD Model
References
- Renzi, E.; Sammarco, P. The hydrodynamics of landslide tsunamis: Current analytical models and future research directions. Landslides 2016, 13, 1369–1377. [Google Scholar] [CrossRef]
- Kulikov, E.A.; Rabinovich, A.B.; Thomson, R.E.; Bornhold, B.D. The landslide tsunami of November 3, 1994, Skagway Harbor, Alaska. J. Geophys. Res. Space Phys. 1996, 101, 6609–6615. [Google Scholar] [CrossRef]
- Manenti, S.; Amicarelli, A.; Todeschini, S. WCSPH with Limiting Viscosity for Modeling Landslide Hazard at the Slopes of Artificial Reservoir. Water 2018, 10, 515. [Google Scholar] [CrossRef]
- Manenti, S.; Pierobon, E.; Gallati, M.; Sibilla, S.; D’Alpaos, L.; Macchi, E.; Todeschini, S. Vajont Disaster: Smoothed Particle Hydrodynamics Modeling of the Postevent 2D Experiments. J. Hydraul. Eng. 2016, 142, 5015007. [Google Scholar] [CrossRef]
- Tappin, D.R.; Watts, P.; Grilli, S.T. The Papua New Guinea tsunami of 17 July 1998: Anatomy of a catastrophic event. Nat. Hazards Earth Syst. Sci. 2008, 8, 243–266. [Google Scholar] [CrossRef]
- Løvholt, F.; Pedersen, G.; Harbitz, C.B.; Glimsdal, S.; Kim, J. On the characteristics of landslide tsunamis. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20140376. [Google Scholar] [CrossRef]
- Fine, I.; Rabinovich, A.; Bornhold, B.; Thomson, R.; Kulikov, E. The Grand Banks landslide-generated tsunami of November 18, 1929: Preliminary analysis and numerical modeling. Mar. Geol. 2005, 215, 45–57. [Google Scholar] [CrossRef]
- Fritz, H.M.; Hager, W.H.; Minor, H.-E. Landslide generated impulse waves. Exp. Fluids 2003, 35, 505–519. [Google Scholar] [CrossRef]
- Fritz, H.M.; Hager, W.H.; Minor, H.-E. Landslide generated impulse waves. 2. Hydrodynamic impact craters. Exp. Fluids 2003, 35, 520–532. [Google Scholar] [CrossRef]
- Harbitz, C.B.; Pedersen, G.; Gjevik, B. Numerical Simulations of Large Water Waves due to Landslides. J. Hydraul. Eng. 1993, 119, 1325–1342. [Google Scholar] [CrossRef]
- Heller, V.; Hager, W.H. Impulse Product Parameter in Landslide Generated Impulse Waves. J. Waterw. Port, Coastal Ocean Eng. 2010, 136, 145–155. [Google Scholar] [CrossRef]
- Heller, V.; Hager, W. Wave types of landslide generated impulse waves. Ocean Eng. 2011, 38, 630–640. [Google Scholar] [CrossRef]
- Kim, G.-B.; Cheng, W.; Sunny, R.C.; Horrillo, J.J.; McFall, B.C.; Mohammed, F.; Fritz, H.M.; Beget, J.; Kowalik, Z. Three Dimensional Landslide Generated Tsunamis: Numerical and Physical Model Comparisons. Landslides 2019, 1–17. [Google Scholar] [CrossRef]
- Manenti, S.; Wang, D.; Domínguez, J.M.; Li, S.; Amicarelli, A.; Albano, R. SPH Modeling of Water-Related Natural Hazards. Water 2019, 11, 1875. [Google Scholar] [CrossRef]
- Ataie-Ashtiani, B.; Yavari-Ramshe, S. Numerical simulation of wave generated by landslide incidents in dam reservoirs. Landslides 2011, 8, 417–432. [Google Scholar] [CrossRef]
- Behrens, J.; Dias, F. New computational methods in tsunami science. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20140382. [Google Scholar] [CrossRef]
- Fritz, H.M.; Hager, W.H.; Minor, H.-E. Near Field Characteristics of Landslide Generated Impulse Waves. J. Waterw. Port Coastal, Ocean Eng. 2004, 130, 287–302. [Google Scholar] [CrossRef]
- Løvholt, F.; Harbitz, C.B.; Haugen, K.B. A parametric study of tsunamis generated by submarine slides in the Ormen Lange/Storegga area off western Norway. Mar. Pet. Geol. 2005, 22, 219–231. [Google Scholar] [CrossRef]
- Whittaker, C.; Nokes, R.; Davidson, M. Tsunami forcing by a low Froude number landslide. Environ. Fluid Mech. 2015, 15, 1215–1239. [Google Scholar] [CrossRef]
- Jamin, T.; Gordillo, L.; Ruiz-Chavarría, G.; Berhanu, M.; Falcon, E. Experiments on generation of surface waves by an underwater moving bottom. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20150069. [Google Scholar] [CrossRef]
- Shokina, N.; Aizinger, V. On numerical modelling of impulse water waves generated by submarine landslides. Environ. Earth Sci. 2015, 74, 7387–7405. [Google Scholar] [CrossRef]
- Reymond, D.; Okal, E.A.; Hebert, H.; Bourdet, M. Rapid forecast of tsunami wave heights from a database of pre-computed simulations, and application during the 2011 Tohoku tsunami in French Polynesia. Geophys. Res. Lett. 2012, 39, 11603. [Google Scholar] [CrossRef]
- Dutykh, D.; Poncet, R.; Dias, F. The VOLNA code for the numerical modeling of tsunami waves: Generation, propagation and inundation. Eur. J. Mech. B Fluids 2011, 30, 598–615. [Google Scholar] [CrossRef]
- Lynett, P.; Liu, P. A numerical study of submarine–landslide–generated waves and run–up. Proc. R. Soc. A Math. Phys. Eng. Sci. 2002, 458, 2885–2910. [Google Scholar] [CrossRef]
- Ataie-Ashtiani, B.; Jilani, A.N. A higher-order Boussinesq-type model with moving bottom boundary: Applications to submarine landslide tsunami waves. Int. J. Numer. Methods Fluids 2007, 53, 1019–1048. [Google Scholar] [CrossRef]
- Fuhrman, D.R.; Madsen, P.A. Tsunami generation, propagation, and run-up with a high-order Boussinesq model. Coast. Eng. 2009, 56, 747–758. [Google Scholar] [CrossRef]
- Ruffini, G.; Heller, V.; Briganti, R. Numerical modelling of landslide-tsunami propagation in a wide range of idealised water body geometries. Coast. Eng. 2019, 153, 103518. [Google Scholar] [CrossRef]
- Gisler, G.R.; Weaver, R.; Gittings, M.L. SAGE calculations of the tsunami threat from La Palma. Sci. Tsunami Hazards 2006, 24, 288–301. [Google Scholar]
- Abadie, S.M.; Harris, J.; Grilli, S.T.; Fabre, R. Numerical modeling of tsunami waves generated by the flank collapse of the Cumbre Vieja Volcano (La Palma, Canary Islands): Tsunami source and near field effects. J. Geophys. Res. Space Phys. 2012, 117. [Google Scholar] [CrossRef]
- Ma, G.; Kirby, J.T.; Shi, F. Numerical simulation of tsunami waves generated by deformable submarine landslides. Ocean Model. 2013, 69, 146–165. [Google Scholar] [CrossRef]
- Li, G.; Chen, G.; Li, P.; Jing, H. Efficient and Accurate 3-D Numerical Modelling of Landslide Tsunami. Water 2019, 11, 2033. [Google Scholar] [CrossRef]
- Montagna, F.; Bellotti, G.; Di Risio, M. 3D numerical modeling of landslide-generated tsunamis around a conical island. Nat. Hazards 2011, 58, 591–608. [Google Scholar] [CrossRef]
- Lin, C.; Pastor, M.; Li, T.; Liu, X.; Qi, H.; Lin, C. A SPH two-layer depth-integrated model for landslide-generated waves in reservoirs: Application to Halaowo in Jinsha River (China). Landslides 2019, 16, 2167–2185. [Google Scholar] [CrossRef]
- Fu, L.; Jin, Y.-C. Investigation of non-deformable and deformable landslides using meshfree method. Ocean Eng. 2015, 109, 192–206. [Google Scholar] [CrossRef]
- Lo, H.-Y.; Liu, P. On the analytical solutions for water waves generated by a prescribed landslide. J. Fluid Mech. 2017, 821, 85–116. [Google Scholar] [CrossRef]
- Tinti, S.; Bortolucci, E. Energy of Water Waves Induced by Submarine Landslides. Pure Appl. Geophys. PAGEOPH 2000, 157, 281–318. [Google Scholar] [CrossRef]
- Liu, P.; Lynett, P.; Synolakis, C. Analytical solutions for forced long waves on a sloping beach. J. Fluid Mech. 2003, 478, 101–109. [Google Scholar] [CrossRef]
- Sammarco, P.; Renzi, E. Landslide tsunamis propagating along a plane beach. J. Fluid Mech. 2008, 598, 107–119. [Google Scholar] [CrossRef]
- Renzi, E.; Sammarco, P. The influence of landslide shape and continental shelf on landslide generated tsunamis along a plane beach. Nat. Hazards Earth Syst. Sci. 2012, 12, 1503–1520. [Google Scholar] [CrossRef]
- Madsen, P.A.; Hansen, A.B. Transient waves generated by a moving bottom obstacle: A new near-field solution. J. Fluid Mech. 2012, 697, 237–272. [Google Scholar] [CrossRef][Green Version]
- Antuono, M.; Brocchini, M. The Boundary Value Problem for the Nonlinear Shallow Water Equations. Stud. Appl. Math. 2007, 119, 73–93. [Google Scholar] [CrossRef]
- Matteo, A.; Brocchini, M. Maximum run-up, breaking conditions and dynamical forces in the swash zone: A boundary value approach. Coast. Eng. 2008, 55, 732–740. [Google Scholar] [CrossRef]
- Antuono, M.; Brocchini, M. Swash Zone Dynamics due to Impulsive Waves. J. Waterw. Port Coastal, Ocean Eng. 2011, 137, 192–203. [Google Scholar] [CrossRef]
- Brocchini, M. A reasoned overview on Boussinesq-type models: The interplay between physics, mathematics and numerics. Proc. R. Soc. A Math. Phys. Eng. Sci. 2013, 469, 20130496. [Google Scholar] [CrossRef] [PubMed]
- Jing, H.X.; Chen, G.D.; Liu, C.G.; Wang, W.; Zuo, J.L. Dispersive effects of water waves generated by submerged landslide. Nat. Hazards 2020. Under review. [Google Scholar]
- Zitti, G.; Ancey, C.; Postacchini, M.; Brocchini, M. Impulse waves generated by snow avalanches: Momentum and energy transfer to a water body. J. Geophys. Res. Earth Surf. 2016, 121, 2399–2423. [Google Scholar] [CrossRef]
- Zitti, G.; Ancey, C.; Postacchini, M.; Brocchini, M. Snow avalanches striking water basins: Behaviour of the avalanche’s centre of mass and front. Nat. Hazards 2017, 88, 1297–1323. [Google Scholar] [CrossRef]
- Harbitz, C.B.; Løvholt, F.; Pedersen, G.; Masson, D.G. Mechanisms of tsunami generation by submarine landslides: A short review. Norw. J. Geol. 2006, 86, 255–264. [Google Scholar]
- Mohammed, F.; Fritz, H.M. Physical modeling of tsunamis generated by three-dimensional deformable granular landslides. J. Geophys. Res. Space Phys. 2012, 117, 11. [Google Scholar] [CrossRef]
- Rzadkiewicz, S.A.; Mariotti, C.; Heinrich, P. Numerical Simulation of Submarine Landslides and Their Hydraulic Effects. J. Waterw. Port Coastal, Ocean Eng. 1997, 123, 149–157. [Google Scholar] [CrossRef]
- Whittaker, C. Modelling of Tsunami Generated by the Motion of a Rigid Block along a Horizontal Boundary. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 2013. [Google Scholar]
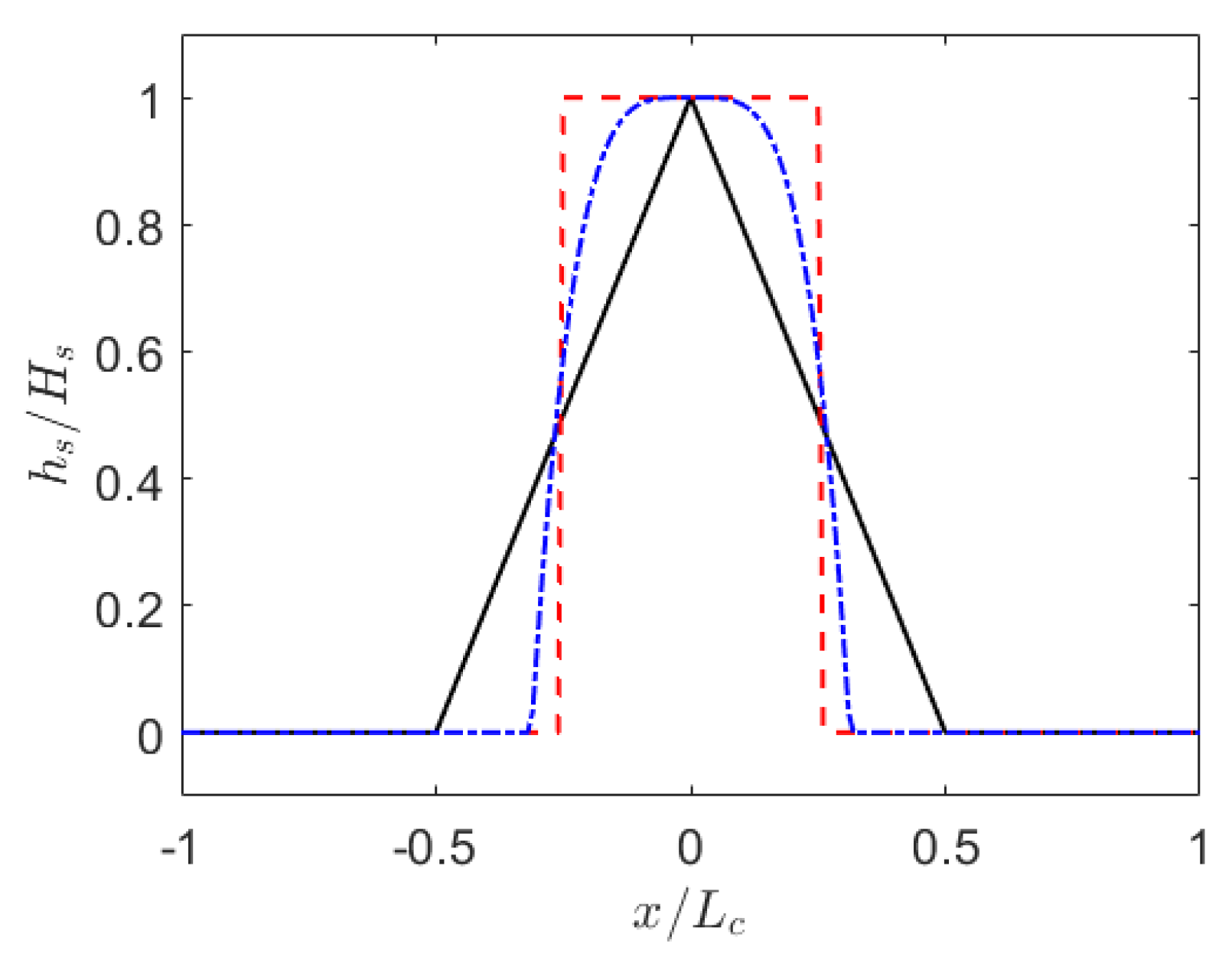
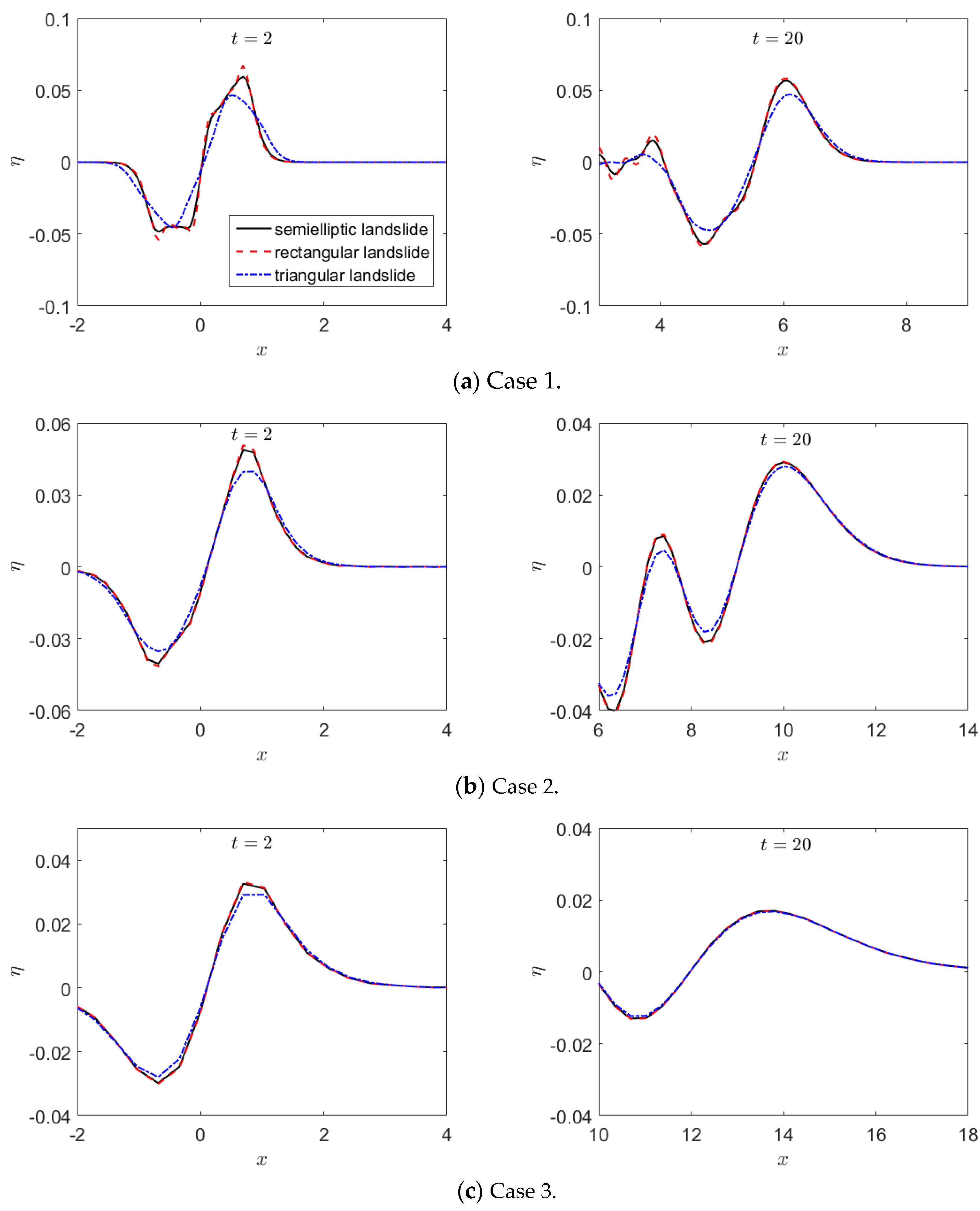


| Case | h0 (m) | Hs (m) | Lc (m) | ut (m/s) | μ | Fr |
|---|---|---|---|---|---|---|
| 1 | 0.175 | 0.026 | 1.75 | 0.131 | 0.1 | 0.1 |
| 2 | 0.175 | 0.026 | 0.58 | 0.131 | 0.3 | 0.1 |
| 3 | 0.175 | 0.026 | 0.29 | 0.131 | 0.6 | 0.1 |
| 4 | 0.175 | 0.026 | 1.75 | 0.491 | 0.1 | 0.375 |
| 5 | 0.175 | 0.026 | 0.58 | 0.491 | 0.3 | 0.375 |
| 6 | 0.175 | 0.026 | 0.29 | 0.491 | 0.6 | 0.375 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, H.; Gao, Y.; Liu, C.; Hou, J. Far-Field Characteristics of Linear Water Waves Generated by a Submerged Landslide over a Flat Seabed. J. Mar. Sci. Eng. 2020, 8, 196. https://doi.org/10.3390/jmse8030196
Jing H, Gao Y, Liu C, Hou J. Far-Field Characteristics of Linear Water Waves Generated by a Submerged Landslide over a Flat Seabed. Journal of Marine Science and Engineering. 2020; 8(3):196. https://doi.org/10.3390/jmse8030196
Chicago/Turabian StyleJing, Haixiao, Yanyan Gao, Changgen Liu, and Jingming Hou. 2020. "Far-Field Characteristics of Linear Water Waves Generated by a Submerged Landslide over a Flat Seabed" Journal of Marine Science and Engineering 8, no. 3: 196. https://doi.org/10.3390/jmse8030196
APA StyleJing, H., Gao, Y., Liu, C., & Hou, J. (2020). Far-Field Characteristics of Linear Water Waves Generated by a Submerged Landslide over a Flat Seabed. Journal of Marine Science and Engineering, 8(3), 196. https://doi.org/10.3390/jmse8030196






