Design of the Blade under Low Flow Velocity for Horizontal Axis Tidal Current Turbine
Abstract
1. Introduction
2. The Design Flow Velocity of the Blade
3. The Shape Design of the Blade
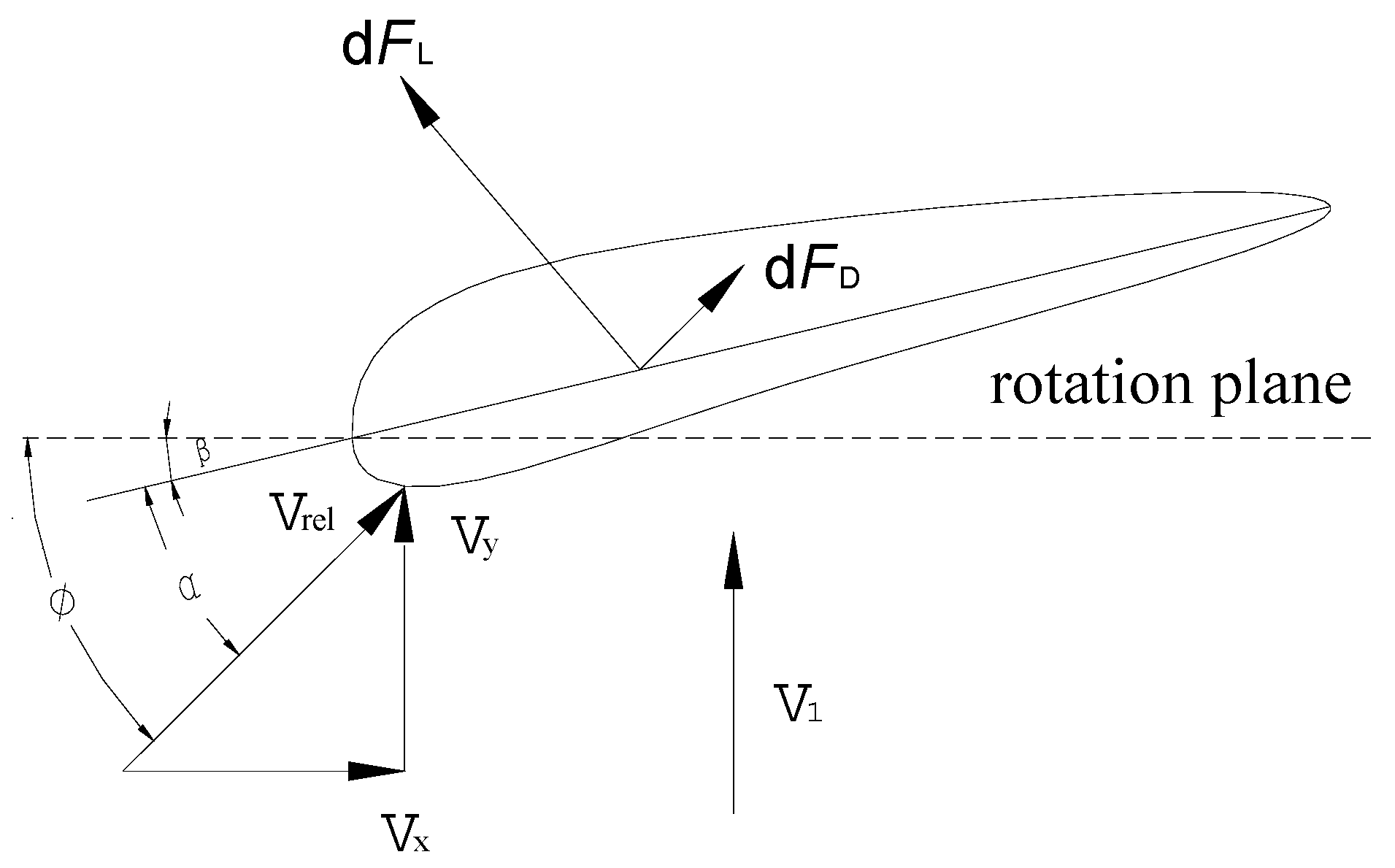
3.1. Blade Element Momentum Theory
3.2. The Geometric Design of the Blade Shape
3.2.1. The Blade Design Flow Velocity
3.2.2. The Solidity of the Blade
3.2.3. Blade Quantities (BQ) and Tip–Speed Ratio (TSR)
3.2.4. Diameter of the Blade
3.2.5. Profile of the Blade
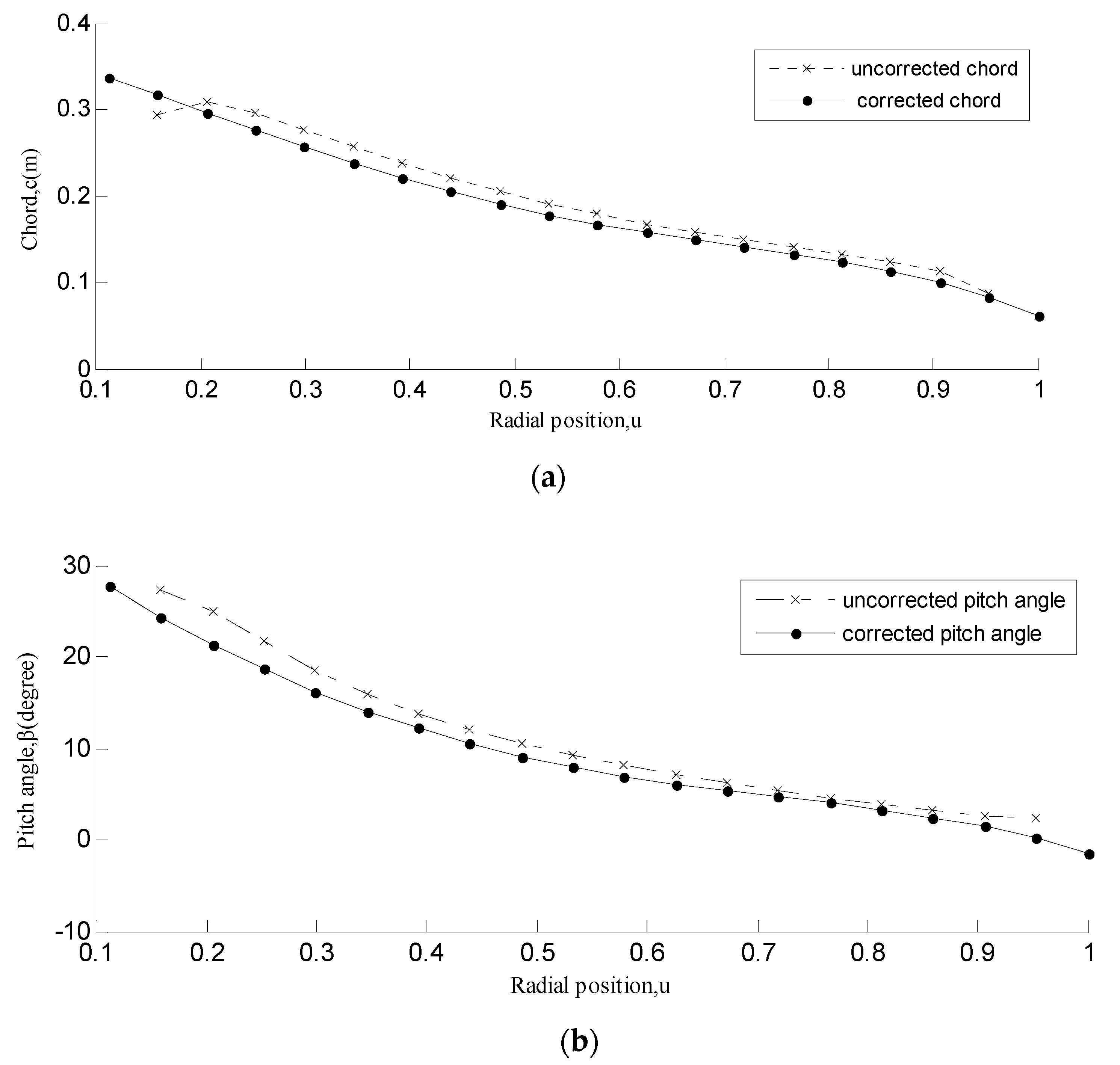
3.3. Blade Geometric Parameter Calculations
3.4. Blade Performance Numerical Forecast
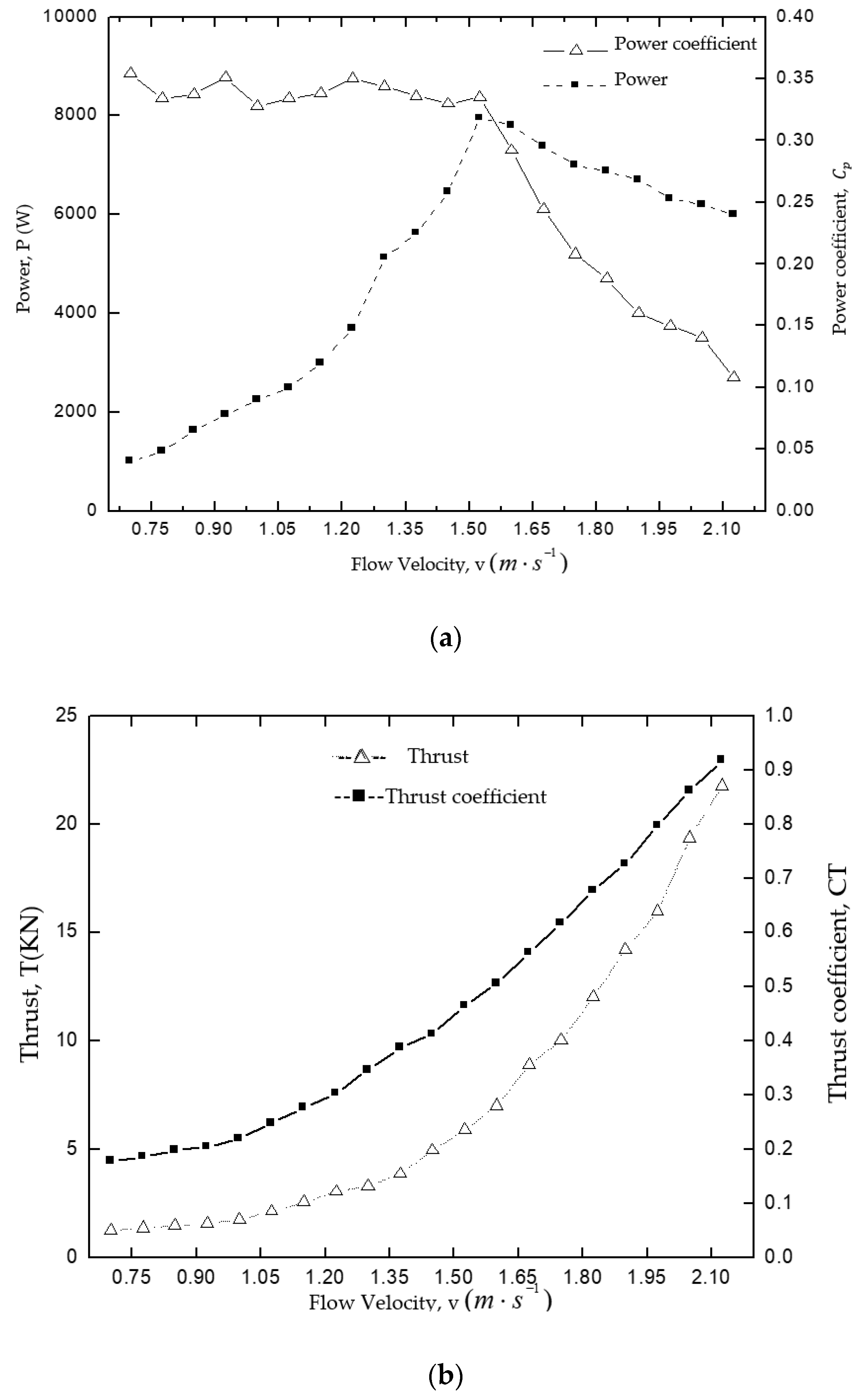
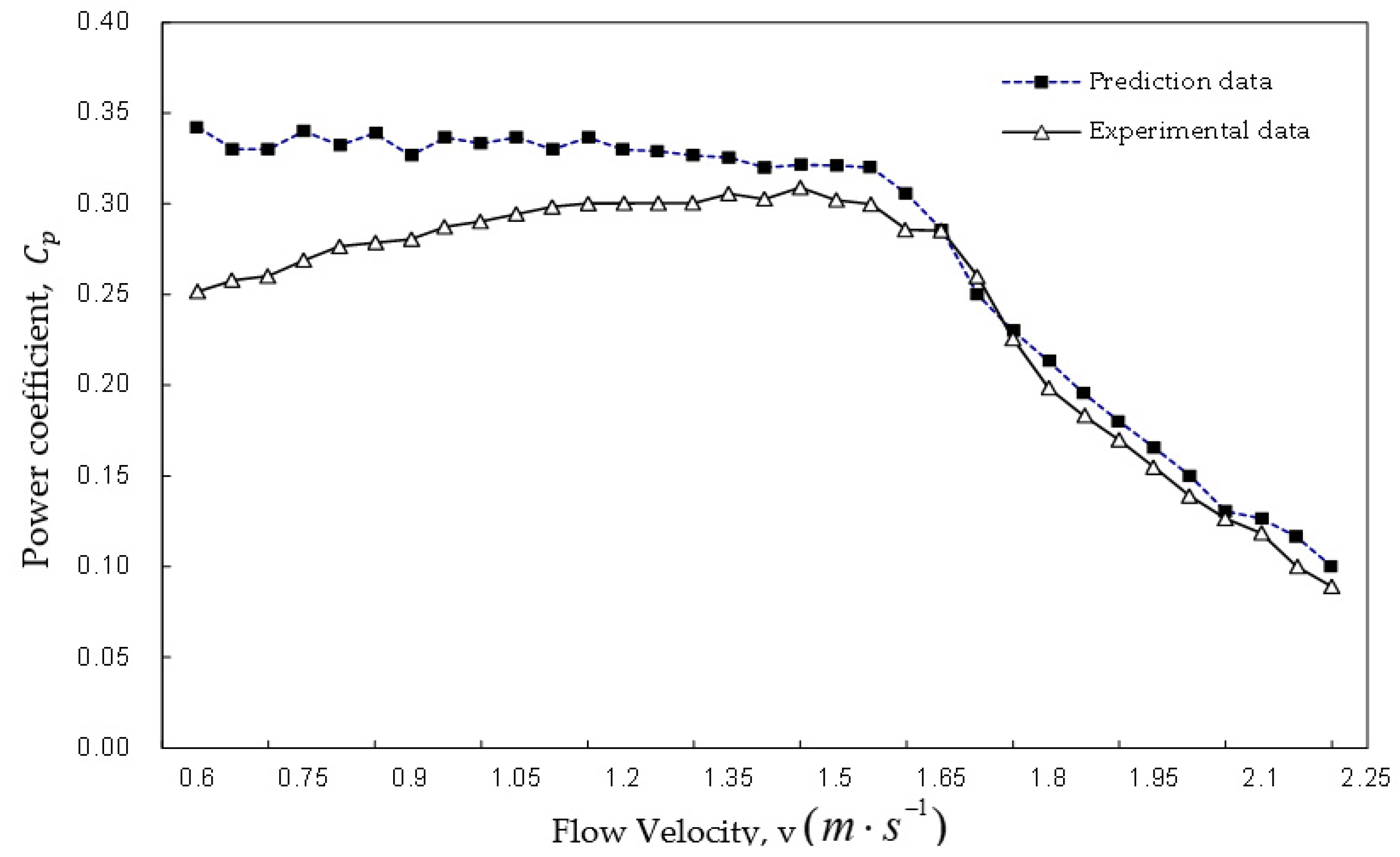
4. Experiment with an Energy Capturing Device in a Sea Trial
- Considering the measurement, the flow velocity tested in the experiment is relatively close to the surface flow velocity, so it is higher than the actual flow velocity at the center of the blade, which will lead to the calculated experiment data are lower.
- The theoretical prediction model cannot fully consider the actual sea conditions at the trial experimental site, which may also cause deviations between experimental data and theoretical data.
5. Conclusions
- (1)
- During the 1.5-month period at the test site, the maximum flow rate of the seawater per day was different and maintained for a short period of time. Flow rates above 2 m/s only appeared on astronomical high-tide days, but were low the majority of the time. Based on this situation, the author proposed a calculation method for designing the flow velocity of the blade to improve the energy capture efficiency of the blade within the range of the changing flow velocity.
- (2)
- The author combined the blade element momentum theory with the Wilson optimization method and used the MATLAB software to compile a general program for the design of an energy capture mechanism for the horizontal-axis tidal current power generation system, to improve the design efficiency and accuracy.
- (3)
- The author deduced the relationship between the solidity of the blade and the TSR. For the design of the blade, when the design flow rate is constant, the appropriate blade solidity can be selected according to the blade speed.
- (4)
- Based on the actual sea experiment, the energy capture device met the basic design requirements, which verifies the effectiveness and correctness of this blade design method.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xu, X.T. The Design and Characteristics Analysis on the Blade of Horizontal Axis Tidal Current Turbine. Master’s Thesis, Zhejiang University, Hangzhou, China, 2012. Available online: http://cdmd.cnki.com.cn/Article/CDMD-10335-1012321157.htm (accessed on 18 November 2020).
- Li, Y.W. The Development on Marine Energy; China Ocean Press: Beijing, China, 2008; pp. 94–101. [Google Scholar]
- Pratumnopharat, P.; Leung, P.S. Validation of various Windmill brake state models used by blade element momentum calculation. Renew. Energy 2011, 36, 3222–3227. [Google Scholar] [CrossRef]
- Xu, Q.-K.; Li, W.; Liu, H.W.; Lin, Y.-G.; Shi, M.-S. Individual blade pitching system for horizontal axis tidal current turbine. J. Zhejiang Univ. Eng. Sci. 2013, 47, 528–534. [Google Scholar]
- Grogan, D.M.; Leen, S.B.; Kennedy, C.R.; Bradaigh, C.O. Design of composite tidal turbine blades. Renew. Energy 2013, 57, 151–162. [Google Scholar] [CrossRef]
- Chen, C.F. Optimization and Hydrodynamic Performance Research on the Blade of Horizontal Axis Tidal Current Turbine. Master’s Thesis, Ocean University of China, Qingdao, China, June 2012. [Google Scholar]
- Wu, H.N.; Chen, L.J.; Yu, M.; Li, W.; Chen, B. On design and performance prediction of the horizontal-axis water turbine. Ocean. Eng. 2012, 50, 23–30. [Google Scholar] [CrossRef]
- Goundar, J.N.; Ahmed, M.R.; Lee, Y.H. Numerical and experimental studies on hydrofoils for marine current turbines. Renew. Energy 2012, 42, 173–179. [Google Scholar] [CrossRef]
- Li, G.N.; Yang, Z.F.; Du, B.S.; Xu, J.J.; Liu, M. The design and modeling on the wind turbine rotor based on MATLAB and Pro/E. Mech. Des. 2009, 26, 3–5. [Google Scholar]
- Ma, S.; Li, W.; Liu, H.W.; Lin, Y.G. The design on energy capture institution of horizontal axis tidal current turbine. Chin. J. Mech. Eng. 2010, 46, 150–157. [Google Scholar]
- Chen, Q.H.; Lai, H. The analysis on different tip loss model of wind turbine aerodynamic performance. Acta Energ. Sol. Sin. 2012, 33, 216–2171. [Google Scholar]
- Balaka, R.; Rachman, A. Pitch angle effect for horizontal axis river current turbine. Procedia Eng. 2012, 50, 343–353. [Google Scholar]






| TSR | BQ | TSR | BQ |
|---|---|---|---|
| 1 2 3 | 8~24 6~12 3~8 | 4 5~8 9~15 | 3~5 2~4 2~3 |
| Parameters | Values |
|---|---|
| Design Velocity v (m∙s−1) Rated Power P (kW) Blade Length D (m) Rotor Diameter Hub Diameter Dhub (m) BQ B TSR Airfoil Profile | 1.60 8 1.665 3.7 0.37 3 3.6 FX 77-W-XXX |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.-H.; Wang, X.-C.; Li, H.; Jiang, C.-H.; Bao, L.-J. Design of the Blade under Low Flow Velocity for Horizontal Axis Tidal Current Turbine. J. Mar. Sci. Eng. 2020, 8, 989. https://doi.org/10.3390/jmse8120989
Chen J-H, Wang X-C, Li H, Jiang C-H, Bao L-J. Design of the Blade under Low Flow Velocity for Horizontal Axis Tidal Current Turbine. Journal of Marine Science and Engineering. 2020; 8(12):989. https://doi.org/10.3390/jmse8120989
Chicago/Turabian StyleChen, Jun-Hua, Xian-Cheng Wang, Hao Li, Chu-Hua Jiang, and Ling-Jie Bao. 2020. "Design of the Blade under Low Flow Velocity for Horizontal Axis Tidal Current Turbine" Journal of Marine Science and Engineering 8, no. 12: 989. https://doi.org/10.3390/jmse8120989
APA StyleChen, J.-H., Wang, X.-C., Li, H., Jiang, C.-H., & Bao, L.-J. (2020). Design of the Blade under Low Flow Velocity for Horizontal Axis Tidal Current Turbine. Journal of Marine Science and Engineering, 8(12), 989. https://doi.org/10.3390/jmse8120989





