Experimental Observation on Beach Evolution Process with Presence of Artificial Submerged Sand Bar and Reef
Abstract
1. Introduction
2. Method
2.1. Experimental Design and Instrumentation
2.2. Data Analysis
2.2.1. Hydrodynamics
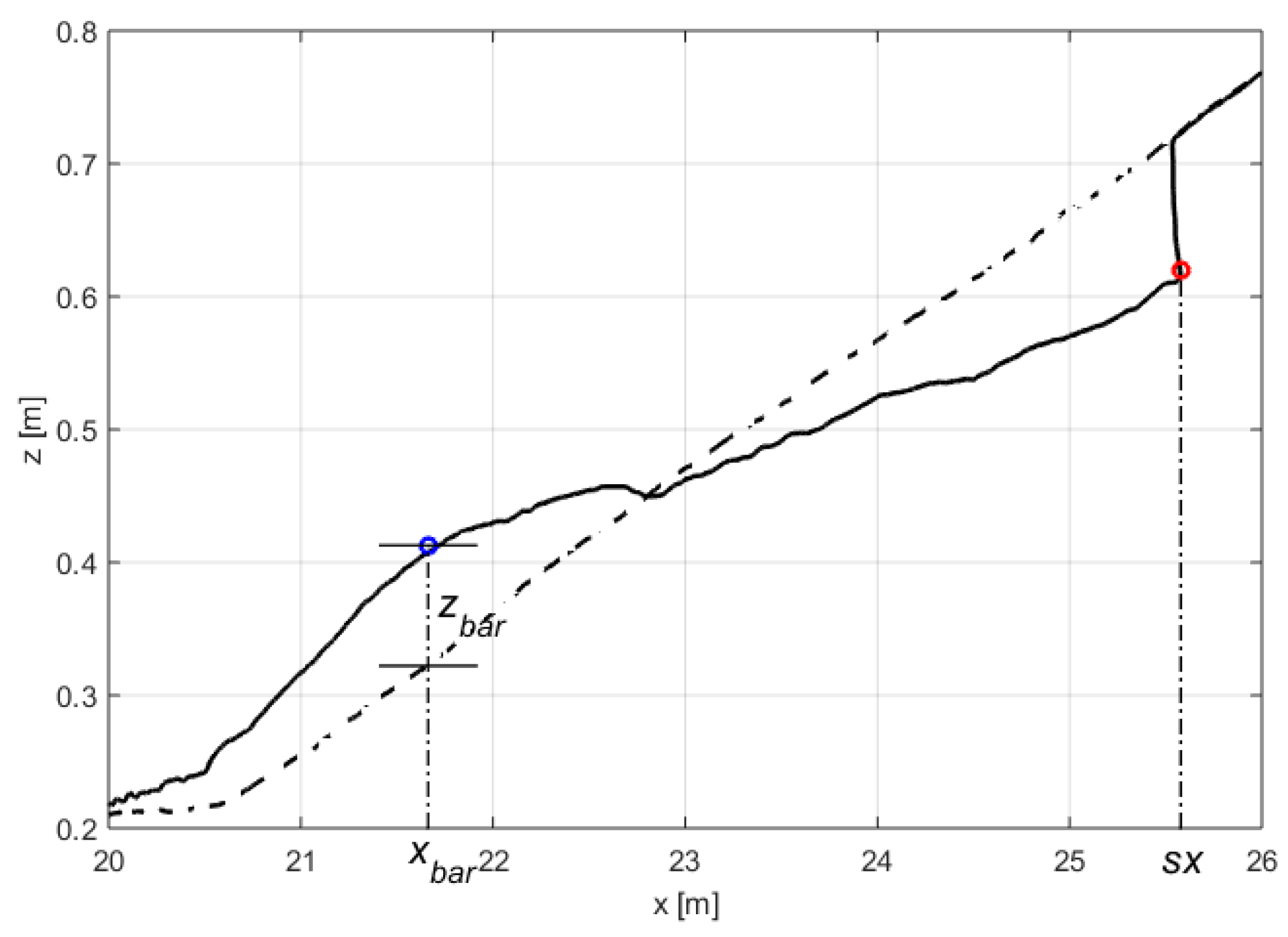
2.2.2. Profile Morphology
2.2.3. Sediment Transport
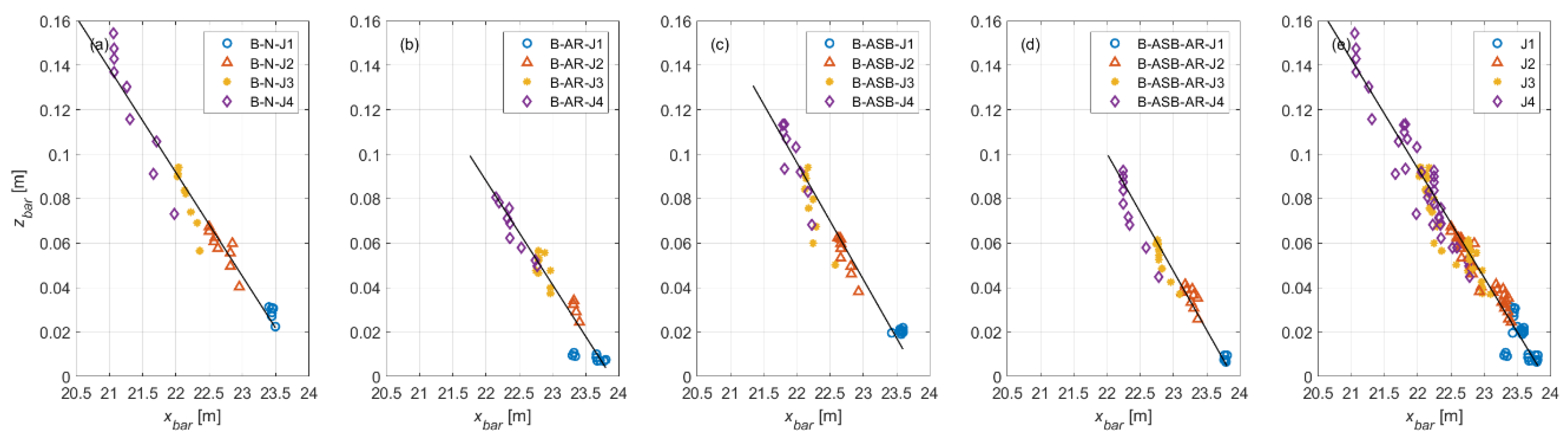
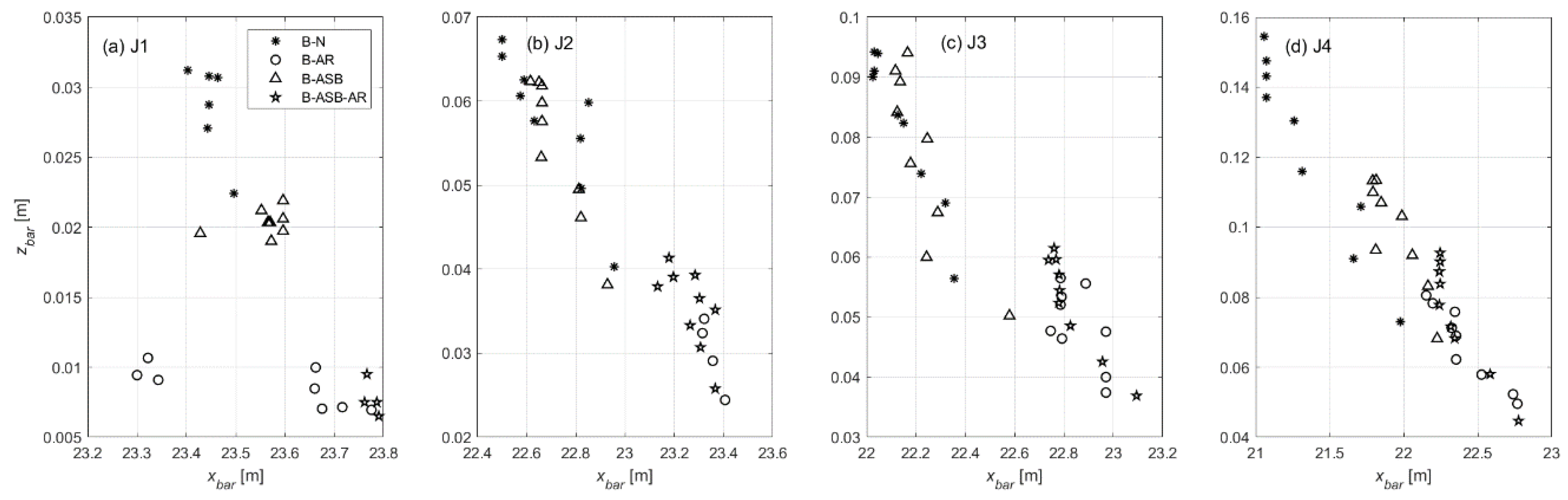
3. Results
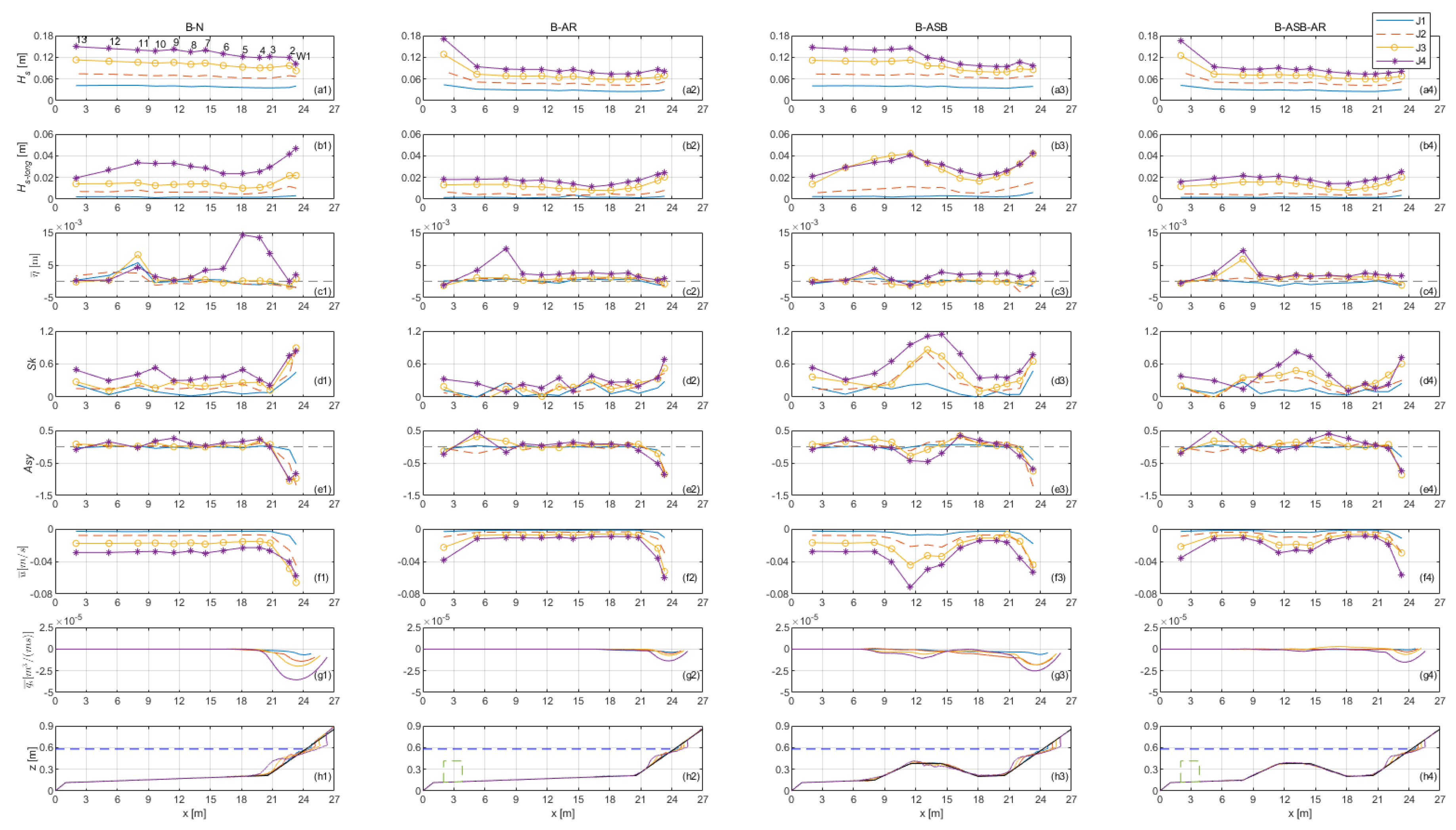
3.1. Hydrodynamics
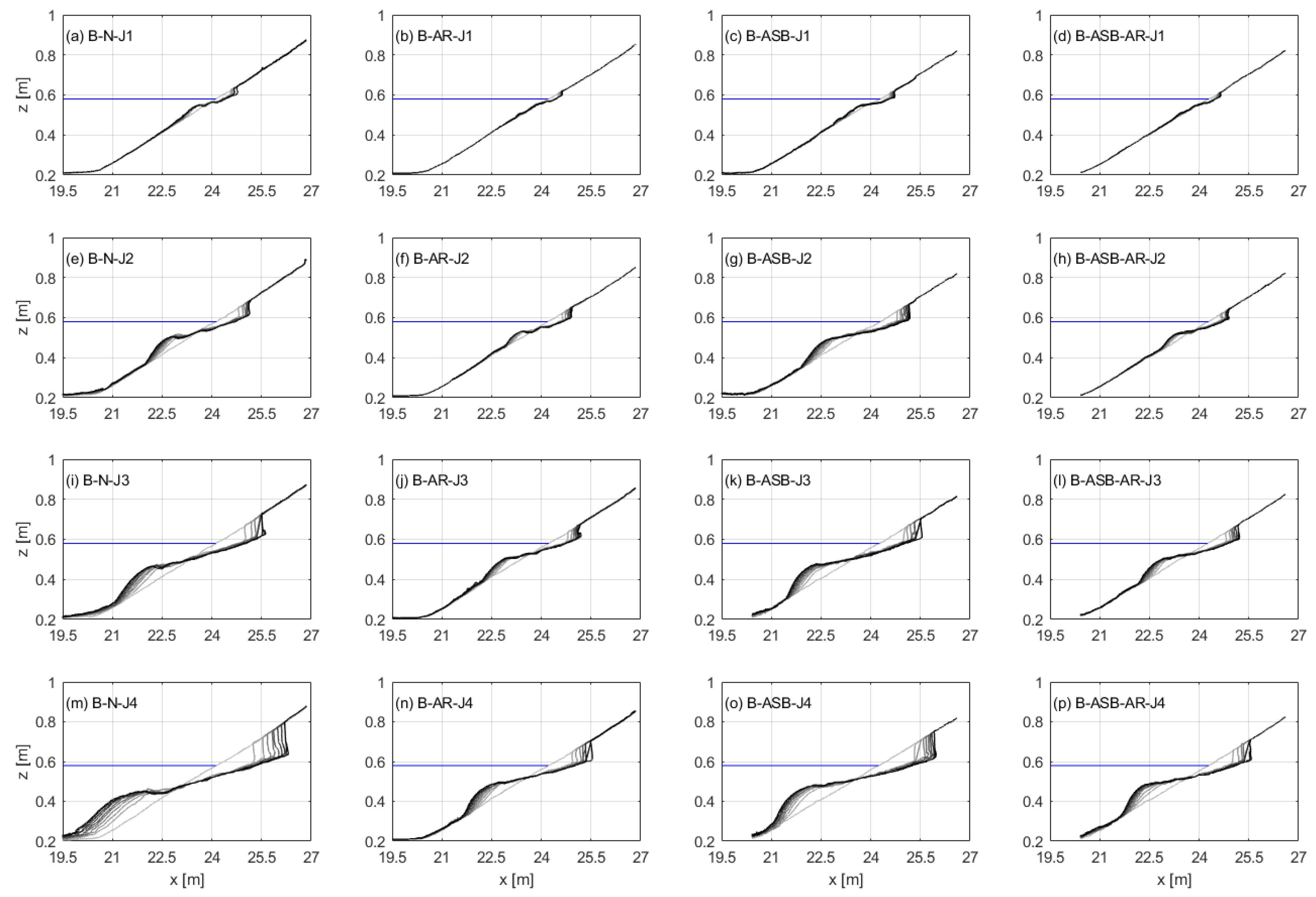
3.2. Beach Profile Behavior
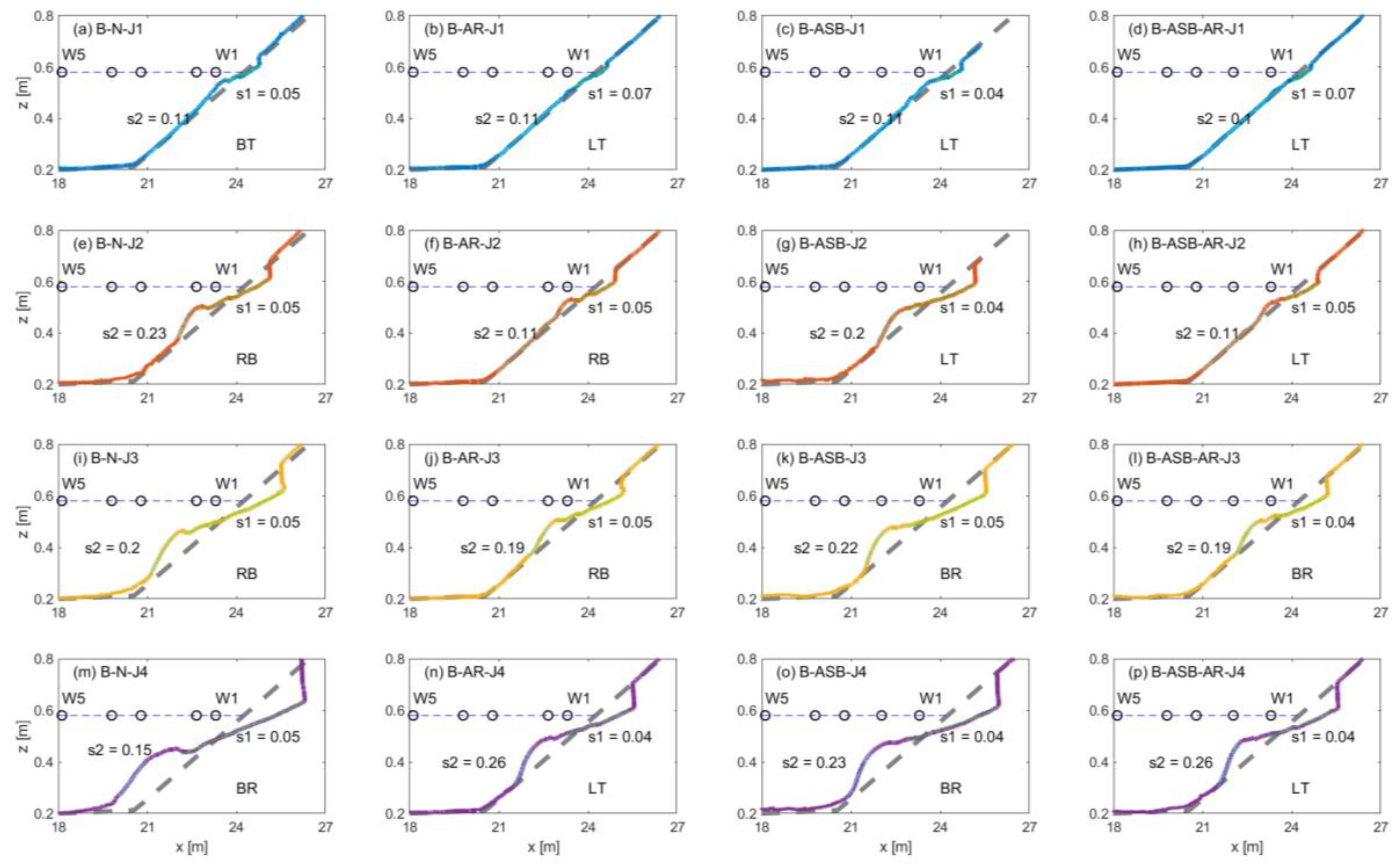
3.2.1. Evolution process
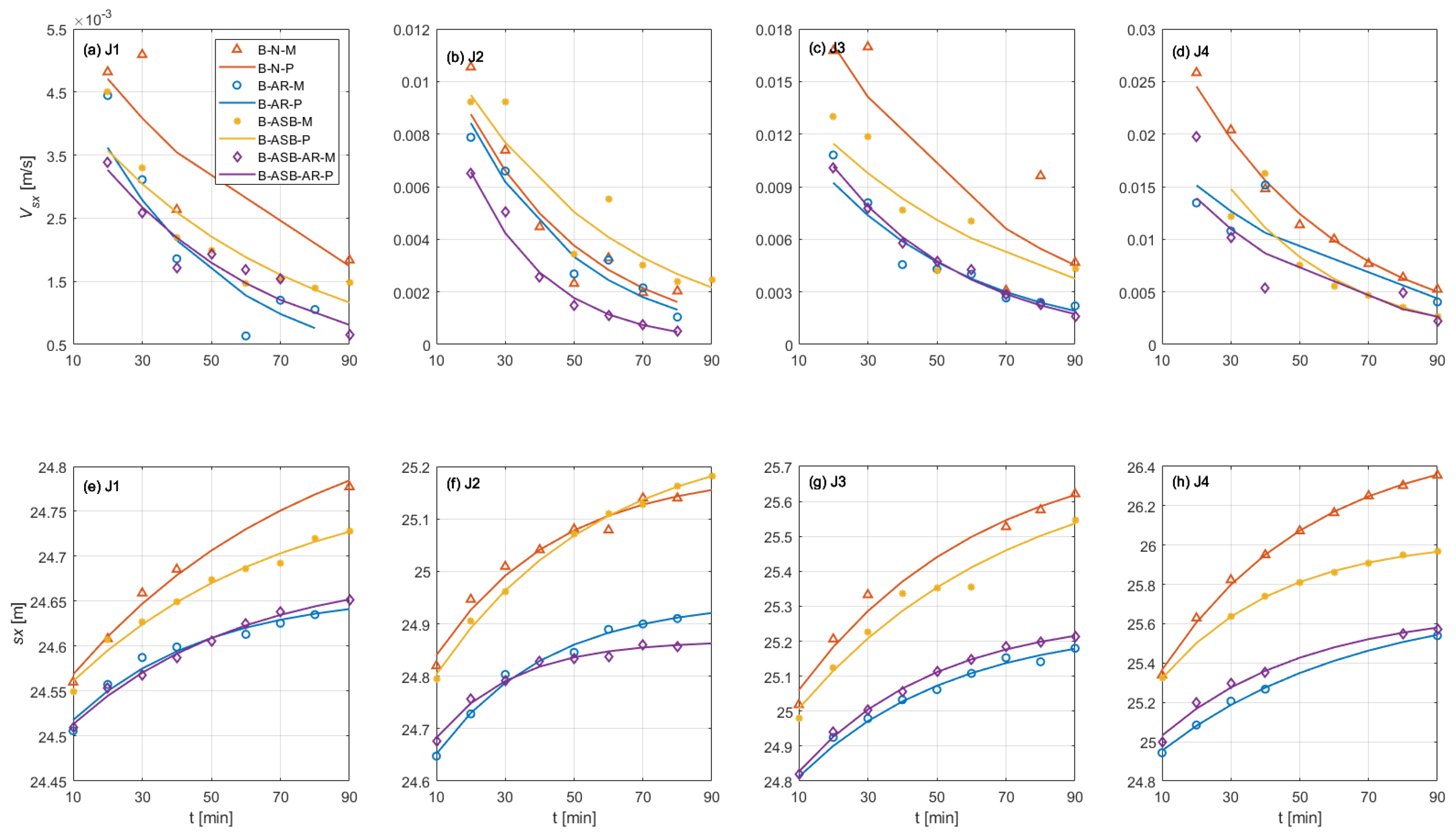
3.2.2. Scarp
3.2.3. Breaker Bar
3.3. Artificial Submerged Sand Bar (ASB)
4. Discussion
4.1. Beach Erosion
4.2. Beach State
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Van Rijn, L.C. Coastal erosion and control. Ocean Coast. Manag. 2011, 54, 867–887. [Google Scholar] [CrossRef]
- Luijendijk, A.; Hagenaars, G.; Ranasinghe, R.; Baart, F.; Donchyts, G.; Aarninkhof, S. The State of the World’s Beaches. Sci. Rep. 2018, 8, 6641. [Google Scholar] [CrossRef] [PubMed]
- Campbell, T.J.; Benedet, L. Beach nourishment magnitudes and trends in the US. J. Coast. Res. 2006, 39, 57–64. [Google Scholar]
- Hanson, H.; Brampton, A.; Capobianco, M.; Dette, H.H.; Hamm, L.; Laustrup, C.; Lechuga, A.; Spanhoff, R. Beach nourishment projects, practices, and objectives—A European overview. Coast. Eng. 2002, 47, 81–111. [Google Scholar] [CrossRef]
- Dean, R.G. Beach Nourishment: Theory and Practice; World Scientific: Singapore, 2003. [Google Scholar]
- Cooke, B.C.; Jones, A.R.; Goodwin, I.D.; Bishop, M.J. Nourishment practices on Australian sandy beaches: A review. J. Environ. Manag. 2012, 113, 319–327. [Google Scholar] [CrossRef] [PubMed]
- Luo, S.; Liu, Y.; Jin, R.; Zhang, J.; Wei, W. A guide to coastal management: Benefits and lessons learned of beach nourishment practices in China over the past two decades. Ocean Coast. Manag. 2016, 134, 207–215. [Google Scholar] [CrossRef]
- Armstrong, S.B.; Lazarus, E.D.; Limber, P.W.; Goldstein, E.B.; Thorpe, C.; Ballinger, R.C. Indications of a positive feedback between coastal development and beach nourishment. Earths Future 2016, 4, 626–635. [Google Scholar] [CrossRef]
- Armstrong, S.B.; Lazarus, E.D. Masked shoreline erosion at large spatial scales as a collective effect of beach nourishment. Earths Future 2019, 7, 74–84. [Google Scholar] [CrossRef]
- Hamm, L.; Capobianco, M.; Dette, H.H.; Lechuga, A.; Spanhoff, R.; Stive, M.J.F. A summary of European experience with shore nourishment. Coast. Eng. 2002, 47, 237–264. [Google Scholar] [CrossRef]
- Van Duin, M.J.P.; Wiersma, N.R.; Walstra, D.J.R.; van Rijn, L.C.; Stive, M.J.F. Nourishing the shoreface: Observations and hindcasting of the Egmond case, The Netherlands. Coast. Eng. 2004, 51, 813–837. [Google Scholar] [CrossRef]
- Bougdanou, M. Analysis of the Shoreface Nourishments, in the Areas of Ter Heijde, Katwijk and Noordwijk; TU Delft: Delft, The Netherlands, 2007. [Google Scholar]
- Peterson, C.H.; Bishop, M.J. Assessing the environmental impacts of beach nourishment. Bioscience 2005, 55, 887–896. [Google Scholar] [CrossRef]
- Fenster, M.S.; Knisley, C.B.; Reed, C.T. Habitat preference and the effects of beach nourishment on the federally threatened northeastern beach tiger beetle, cicindela dorsalis dorsalis: Western Shore, Chesapeake Bay, Virginia. J. Coast. Res. 2006, 22, 1133–1144. [Google Scholar] [CrossRef]
- Baptist, M.J.; Leopold, M.F. The effects of shoreface nourishments on Spisula and scoters in The Netherlands. Mar. Environ. Res. 2009, 68, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Rippy, M.A.; Franks, P.J.S.; Feddersen, F.; Guza, R.T.; Warrick, J.A. Beach nourishment impacts on bacteriological water quality and phytoplankton bloom dynamics. Environ. Sci. Technol. 2013, 47, 6146–6154. [Google Scholar] [CrossRef] [PubMed]
- Hilal, A.H.A.; Rasheed, M.Y.; Hihi, E.A.A.; Rousan, S.A.A. Characteristics and potential environmental impacts of sand material from sand dunes and uplifted marine terraces as potential borrow sites for beach nourishment along the Jordanian coast of the Gulf of Aqaba. J. Coast. Conserv. 2009, 13, 247–261. [Google Scholar] [CrossRef]
- Finkl, C.W.; Benedet, L.; Andrews, J.L.; Suthard, B.; Locker, S.D. Sediment ridges on the west Florida inner continental shelf: Sand resources for beach Nourishment. J. Coast. Res. 2007, 231, 143–159. [Google Scholar] [CrossRef]
- Wildman, J.C. Laboratory Evaluation of Recycled Crushed Glass Cullet for Use as an Aggregate in Beach Nourishment and Marsh Creation Projects in Southeastern Louisiana. Ph.D. Thesis, University of New Orleans, New Orleans, LA, USA, 2018. [Google Scholar]
- Ishikawa, T.; Uda, T.; San-nami, T.; Hosokawa, J.-I.; Tako, T. Possibility of offshore discharge of sand volume and grain size composition. In Proceedings of the 36th Conference on Coastal Engineering, Baltimore, MD, USA, 30 December 2018; p. 47. [Google Scholar]
- Harris, L.E. Submerged reef structures for beach erosion control. In Proceedings of the Coastal Structures 2003, Portland, OR, USA, 26–30 August 2003; pp. 1155–1163. [Google Scholar]
- Coastal, E. Impact of Sand Retention Structures on Southern and Central California Beaches; Department of Earth and Planetary Sciences: Cambridge, MA, USA, 2002. [Google Scholar]
- Lamberti, A.; Archetti, R.; Kramer, M.; Paphitis, D.; Mosso, C.; Risio, M.D. European experience of low crested structures for coastal management. Coast. Eng. 2005, 52, 841–866. [Google Scholar] [CrossRef]
- Sane, M.; Yamagishi, H.; Tateishi, M.; Yamagishi, T. Environmental impacts of shore-parallel breakwaters along Nagahama and Ohgata, District of Joetsu, Japan. J. Environ. Manag. 2007, 82, 399–409. [Google Scholar] [CrossRef]
- Kim, D.; Woo, J.; Yoon, H.-S.; Na, W.-B. Wake lengths and structural responses of Korean general artificial reefs. Ocean Eng. 2014, 92, 83–91. [Google Scholar] [CrossRef]
- Srisuwan, C.; Rattanamanee, P. Modeling of Seadome as artificial reefs for coastal wave attenuation. Ocean Eng. 2015, 103, 198–210. [Google Scholar] [CrossRef]
- Lee, M.O.; Otake, S.; Kim, J.K. Transition of artificial reefs (ARs) research and its prospects. Ocean Coast. Manag. 2018, 154, 55–65. [Google Scholar] [CrossRef]
- Gysens, S.; Rouck, J.D.; Trouw, K.; Bolle, A.; Willems, M. Integrated coastal and maritime plan for Oostende—Design of soft and hard coastal protection measures during the EIA procedures. In Proceedings of the 32nd International Conference on Coastal Engineering, Shanghai, China, 30 June–5 July 2010; p. 37. [Google Scholar]
- Cappucci, S.; Scarcella, D.; Rossi, L.; Taramelli, A. Integrated coastal zone management at Marina di Carrara Harbor: Sediment management and policy making. Ocean Coast. Manag. 2011, 54, 277–289. [Google Scholar] [CrossRef]
- Morang, A.; Waters, J.P.; Stauble, D.K. Performance of submerged prefabricated structures to improve sand retention at beach bourishment projects. J. Coast. Res. 2014, 30, 1140–1156. [Google Scholar] [CrossRef]
- Gu, J.; Ma, Y.; Wang, B.-Y.; Sui, J.; Kuang, C.-P.; Liu, J.-H.; Lei, G. Influence of near-shore marine structures in a beach nourishment project on tidal currents in Haitan Bay, facing the Taiwan Strait. J. Hydrod. 2016, 28, 690–701. [Google Scholar] [CrossRef]
- Pan, Y.; Kuang, C.P.; Chen, Y.P.; Yin, S.; Yang, Y.B.; Yang, Y.X.; Zhang, J.B.; Qiu, R.F.; Zhang, Y. A comparison of the performance of submerged and detached artificial headlands in a beach nourishment project. Ocean Eng. 2018, 159, 295–304. [Google Scholar] [CrossRef]
- Ranasinghe, R.; Turner, I.L. Shoreline response to submerged structures: A review. Coast Eng. 2006, 53, 65–79. [Google Scholar] [CrossRef]
- Marino-Tapia, I.D.J. Cross-Shore sediment Transport Processes on Natural Beaches and their Relation to Sand bar Migration Patterns; University of Plymouth: Plymouth, UK, July 2003. [Google Scholar]
- Archetti, R.; Zanuttigh, B. Integrated monitoring of the hydro-morphodynamics of a beach protected by low crested detached breakwaters. Coast. Eng. 2010, 57, 879–891. [Google Scholar] [CrossRef]
- Kinsman, N.; Griggs, G.B. California coastal sand retention today: Attributes and influence of effective structures. Shore Beach 2010, 78, 64. [Google Scholar]
- Kuang, C.; Pan, Y.; Zhang, Y.; Liu, S.; Yang, Y.; Zhang, J.; Dong, P. Performance Evaluation of a Beach Nourishment Project at West Beach in Beidaihe, China. J. Coast. Res. 2011, 27, 769–783. [Google Scholar] [CrossRef]
- Roberts, T.M.; Wang, P. Four-year performance and associated controlling factors of several beach nourishment projects along three adjacent barrier islands, west-central Florida, USA. Coast. Eng. 2012, 70, 21–39. [Google Scholar] [CrossRef]
- Do, K.; Kobayashi, N.; Suh, K.-D. Erosion of nourished bethany beach in Delaware, USA. Coast. Eng. J. 2014, 56. [Google Scholar] [CrossRef]
- Dally, W.R.; Osiecki, D.A. Evaluating the Impact of beach nourishment on surfing: Surf City, Long Beach Island, New Jersey, U.S.A. J. Coast. Res. 2018, 34, 793–805. [Google Scholar] [CrossRef]
- Grunnet, N.M.; Ruessink, B.G. Morphodynamic response of nearshore bars to a shoreface nourishment. Coast. Eng. 2005, 52, 119–137. [Google Scholar] [CrossRef]
- Ojeda, E.; Ruessink, B.G.; Guillén, J. Morphodynamic response of a two-barred beach to a shoreface nourishment. Coast. Eng. 2008, 55, 1185–1196. [Google Scholar] [CrossRef]
- Barnard, P.L.; Erikson, L.H.; Hansen, J.E. Monitoring and modeling shoreline response due to shoreface nourishment on a high-energy coast. J. Coastal Res. 2009, SI 56, 29–33. [Google Scholar]
- King, P.; McGregor, A. Who’s counting: An analysis of beach attendance estimates and methodologies in southern California. Ocean Coast. Manag. 2012, 58, 17–25. [Google Scholar] [CrossRef]
- Brutsché, K.E.; Wang, P.; Beck, T.M.; Rosati, J.D.; Legault, K.R. Morphological evolution of a submerged artificial nearshore berm along a low-wave microtidal coast, Fort Myers Beach, west-central Florida, USA. Coast. Eng. 2014, 91, 29–44. [Google Scholar] [CrossRef]
- Ludka, B.C.; Guza, R.T.; O’Reilly, W.C. Nourishment evolution and impacts at four southern California beaches: A sand volume analysis. Coast. Eng. 2018, 136, 96–105. [Google Scholar] [CrossRef]
- Leeuwen, S.V.; Dodd, N.; Calvete, D.; Falqués, A. Linear evolution of a shoreface nourishment. Coast. Eng. 2007, 54, 417–431. [Google Scholar] [CrossRef]
- Pan, S. Modelling beach nourishment under macro-tide conditions. J. Coastal Res. 2011, SI 64, 2063–2067. [Google Scholar]
- Spielmann, K.; Certain, R.; Astruc, D.; Barusseau, J.P. Analysis of submerged bar nourishment strategies in a wave-dominated environment using a 2DV process-based model. Coast. Eng. 2011, 58, 767–778. [Google Scholar] [CrossRef]
- Jacobsen, N.G.; Fredsoe, J. Cross-shore redistribution of nourished sand near a breaker bar. J. Waterw. Port. Coast. Ocean. Eng. 2014, 140, 125–134. [Google Scholar] [CrossRef]
- Jayaratne, M.P.R.; Rahman, R.; Shibayama, T. A Cross-shore beach profile evolution model. Coast. Eng. J. 2014, 56. [Google Scholar] [CrossRef]
- Tonnon, P.K.; Huisman, B.J.A.; Stam, G.N.; van Rijn, L.C. Numerical modelling of erosion rates, life span and maintenance volumes of mega nourishments. Coast. Eng. 2018, 131, 51–69. [Google Scholar] [CrossRef]
- Wang, P.; Smith, E.R.; Ebersole, B.A. Large-scale laboratory measurements of longshore sediment transport under spilling and plunging breakers. J. Coastal Res. 2002, 18, 118–135. [Google Scholar]
- Wang, P.; Kraus, N.C. Movable-bed model investigation of groin notching. J. Coastal Res. 2004, SI 33, 342–368. [Google Scholar]
- Gravens, M.B.; Wang, P. Data Report: Laboratory Testing of Longshore Sand Transport by Waves and Currents; Morphology Change Behind Headland Structures; Coastal and Hydraulics Laboratory, U.S. Army Engineer Research and Development Center: Vicksburg, MS, USA, 2007. [Google Scholar]
- Smith, E.R.; Mohr, M.C.; Chader, S.A. Laboratory experiments on beach change due to nearshore mound placement. Coast. Eng. 2017, 121, 119–128. [Google Scholar] [CrossRef]
- Van Thiel de Vries, J.S.M.; van Gent, M.R.A.; Walstra, D.J.R.; Reniers, A.J.H.M. Analysis of dune erosion processes in large-scale flume experiments. Coast. Eng. 2008, 55, 1028–1040. [Google Scholar] [CrossRef]
- Baldock, T.E.; Alsina, J.A.; Caceres, I.; Vicinanza, D.; Contestabile, P.; Power, H.; Sanchez-Arcilla, A. Large-scale experiments on beach profile evolution and surf and swash zone sediment transport induced by long waves, wave groups and random waves. Coast. Eng. 2011, 58, 214–227. [Google Scholar] [CrossRef]
- Masselink, G.; Turner, I.L. Large-scale laboratory investigation into the effect of varying back-barrier lagoon water levels on gravel beach morphology and swash zone sediment transport. Coast. Eng. 2012, 63, 23–38. [Google Scholar] [CrossRef]
- Masselink, G.; Ruju, A.; Conley, D.; Turner, I.; Ruessink, G.; Matias, A.; Thompson, C.; Castelle, B.; Puleo, J.; Citerone, V.; et al. Large-scale Barrier Dynamics Experiment II (BARDEX II): Experimental design, instrumentation, test program, and data set. Coast. Eng. 2016, 113, 3–18. [Google Scholar] [CrossRef]
- Van der A, D.A.; van der Zanden, J.; O’Donoghue, T.; Hurther, D.; Cáceres, I.; McLelland, S.J.; Ribberink, J.S. Large-scale laboratory study of breaking wave hydrodynamics over a fixed bar. J. Geophys. Res. 2017, 122, 3287–3310. [Google Scholar] [CrossRef]
- Nwogu, O.; Demirbilek, Z. Infragravity wave motions and runup over shallow fringing reefs. J. Waterw. Port. Coast. Ocean. Eng. 2010, 136, 295–305. [Google Scholar] [CrossRef]
- Alsina, J.M.; Cáceres, I. Sediment suspension events in the inner surf and swash zone. Measurements in large-scale and high-energy wave conditions. Coast. Eng. 2011, 58, 657–670. [Google Scholar] [CrossRef]
- Pomeroy, A.W.M.; Lowe, R.J.; Van Dongeren, A.R.; Ghisalberti, M.; Bodde, W.; Roelvink, D. Spectral wave-driven sediment transport across a fringing reef. Coast. Eng. 2015, 98, 78–94. [Google Scholar] [CrossRef]
- Baldock, T.E.; Birrien, F.; Atkinson, A.; Shimamoto, T.; Wu, S.; Callaghan, D.P.; Nielsen, P. Morphological hysteresis in the evolution of beach profiles under sequences of wave climates—Part 1; observations. Coast. Eng. 2017, 128, 92–105. [Google Scholar] [CrossRef]
- Rocha, M.V.L.; Michallet, H.; Silva, P.A. Improving the parameterization of wave nonlinearities—The importance of wave steepness, spectral bandwidth and beach slope. Coast. Eng. 2017, 121, 77–89. [Google Scholar] [CrossRef]
- Yao, Y.; He, W.; Deng, Z.; Zhang, Q. Laboratory investigation of the breaking wave characteristics over a barrier reef under the effect of current. Coast. Eng. J. 2019, 61, 210–223. [Google Scholar] [CrossRef]
- Grasso, F.; Michallet, H.; Barthélemy, E. Experimental simulation of shoreface nourishments under storm events: A morphological, hydrodynamic, and sediment grain size analysis. Coast. Eng. 2011, 58, 184–193. [Google Scholar] [CrossRef]
- Grasso, F.; Michallet, H.; Barthélemy, E. Sediment transport associated with morphological beach changes forced by irregular asymmetric, skewed waves. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Capart, H.; Fraccarollo, L. Transport layer structure in intense bed-load. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Berni, C.; Barthélemy, E.; Michallet, H. Surf zone cross-shore boundary layer velocity asymmetry and skewness: An experimental study on a mobile bed. J. Geophys. Res. 2013, 118, 2188–2200. [Google Scholar] [CrossRef]
- Rodríguez-Abudo, S.; Foster, D.; Henriquez, M. Spatial variability of the wave bottom boundary layer over movable rippled beds. J. Geophys. Res.-Oceans 2013, 118, 3490–3506. [Google Scholar] [CrossRef]
- Petruzzelli, V.; Garcia, V.G.; Cobos, F.X.G.i.; Petrillo, A.F. On the use of lightweight mateials in small-scale mobile bed physical models. J. Coastal Res. 2013, 65, 1575–1580. [Google Scholar] [CrossRef]
- Pan, Y.; Yin, S.; Chen, Y.; Yang, Y.; Xu, Z.; Xu, C. A Practical method to scale the sedimentary parameters in a lightweight coastal mobile bed model. J. Coastal Res. 2019, 35, 1351–1357. [Google Scholar] [CrossRef]
- Ma, Y.; Kuang, C.; Han, X.; Niu, H.; Zheng, Y.; Shen, C. Experimental study on the influence of an artificial reef on cross-shore morphodynamic processes of a wave-dominated beach. Water 2020, 12, 2947. [Google Scholar] [CrossRef]
- Roelvink, D.; Reniers, A. A Guide to Modeling Coastal Morphology; World Scientific: Singapore, 2012; p. 292. [Google Scholar]
- Rijnsdorp, D.P.; Smit, P.B.; Zijlema, M. Non-hydrostatic modelling of infragravity waves under laboratory conditions. Coast. Eng. 2014, 85, 30–42. [Google Scholar] [CrossRef]
- Kennedy, A.B.; Chen, Q.; Kirby, J.T.; Dalrymple, R.A. Boussinesq modeling of wave transformation, breaking, and runup. I: 1D. J. Waterw. Port Coast. Ocean. Eng. 2000, 126, 39–47. [Google Scholar] [CrossRef]
- Watanabe, A.; Sato, S. A sheet-flow transport rate formula for asymmetric, forward-leaning waves and currents. In Proceedings of the 29th International Conference on Coastal Engineering, Lisbon, Portugal, 19–24 September 2004; pp. 1703–1714. [Google Scholar]
- Michallet, H.; Cienfuegos, R.; Barthélemy, E.; Grasso, F. Kinematics of waves propagating and breaking on a barred beach. Eur J. Mech B-Fluid 2011, 30, 624–634. [Google Scholar] [CrossRef]
- Elgar, S.; Gallagher, E.L.; Guza, R.T. Nearshore sandbar migration. J. Geophys. Res. 2001, 106, 11623–11627. [Google Scholar] [CrossRef]
- Dally, W.R.; Brown, C.A. A modeling investigation of the breaking wave roller with application to cross-shore currents. J. Geophys. Res. 1995, 100, 24873–24883. [Google Scholar] [CrossRef]
- Goring, D.; Nikora, V.I. Despiking acoustic doppler velocimeter data. J. Hydraul. Eng. 2002, 128, 117–126. [Google Scholar] [CrossRef]
- Soulsby, R. Dynamics of Marine Sands: A Manual for Practical Applications; Thomas Telford Publications: London, UK, 1997. [Google Scholar]
- Alegria-Arzaburu, A.R.d.; Mariño-Tapia, I.; Silva, R.; Pedrozo-Acuña, A. Post-nourishment beach scarp morphodynamics. In Proceedings of the 12th International Coastal Symposium, Plymouth, UK, 8–12 April 2013; pp. 576–581. [Google Scholar]
- Erikson, L.H.; Larson, M.; Hanson, H. Laboratory investigation of beach scarp and dune recession due to notching and subsequent failure. Mar. Geol. 2007, 245, 1–19. [Google Scholar] [CrossRef]
- Eichentopf, S.; Cáceres, I.; Alsina, J.M. Breaker bar morphodynamics under erosive and accretive wave conditions in large-scale experiments. Coast. Eng. 2018, 138, 36–48. [Google Scholar] [CrossRef]
- Stockdon, H.F.; Holman, R.A.; Howd, P.A.; Sallenger, A.H., Jr. Emperical parameterization of setup, swash, and runup. Cost. Eng. 2006, 53, 573–588. [Google Scholar] [CrossRef]
- Wright, L.D.; Short, A.D. Morphodynamic variability of surf zones and beaches: A synthesis. Mar. Geol. 1984, 56, 93–118. [Google Scholar] [CrossRef]
- Guza, R.T.; Inman, D.L. Edge waves and beach cusps. J. Geophys. Res. 1975, 80, 2997–3012. [Google Scholar] [CrossRef]
- LeMehaute, B.J.; Koh, R.C.Y. On the breaking of waves arriving at an abgle to the shore. J. Hydraul. Res. 1967, 5, 67–88. [Google Scholar] [CrossRef]



| Test Name | Wave | Profile Type | Test Name | Wave | Profile Type | ||
|---|---|---|---|---|---|---|---|
| Hs (m) | Tp (s) | Hs (m) | Tp (s) | ||||
| B-N-J1 | 0.04 | 1.20 | Beach (B-N) | B-ASB-J1 | 0.04 | 1.20 | Beach with ASB (B-ASB) |
| B-N-J2 | 0.07 | 1.44 | B-ASB-J2 | 0.07 | 1.44 | ||
| B-N-J3 | 0.10 | 1.57 | B-ASB-J3 | 0.10 | 1.57 | ||
| B-N-J4 | 0.13 | 1.77 | B-ASB-J4 | 0.13 | 1.77 | ||
| B-AR-J1 | 0.04 | 1.20 | Beach with AR (B-AR) | B-ASB-AR-J1 | 0.04 | 1.20 | Beach with ASB and AR (B-ASB-AR) |
| B-AR-J2 | 0.07 | 1.44 | B-ASB-AR-J2 | 0.07 | 1.44 | ||
| B-AR-J3 | 0.10 | 1.57 | B-ASB-AR-J3 | 0.10 | 1.57 | ||
| B-AR-J4 | 0.13 | 1.77 | B-ASB-AR-J4 | 0.13 | 1.77 | ||
| Profile Type | B-N | B-AR | B-ASB | B-ASB-AR | |
|---|---|---|---|---|---|
| Wave Gauges | |||||
| W1 | 23.30 | 23.30 | 23.30 | 23.30 | |
| W2 | 22.65 | 22.65 | 22.03 | 22.03 | |
| W3 | 20.78 | 20.78 | 20.78 | 20.78 | |
| W4 | 19.80 | 19.80 | 19.80 | 19.80 | |
| W5 | 18.12 | 18.12 | 18.12 | 18.12 | |
| W6 | 16.25 | 16.25 | 16.25 | 16.25 | |
| W7 | 14.50 | 14.50 | 14.50 | 14.50 | |
| W8 | 13.12 | 13.12 | 13.12 | 13.12 | |
| W9 | 11.47 | 11.47 | 11.47 | 11.47 | |
| W10 | 9.67 | 9.67 | 9.67 | 9.67 | |
| W11 | 8.00 | 8.00 | 8.00 | 8.00 | |
| W12 | 5.21 | 5.21 | 5.21 | 5.21 | |
| W13 | 2.01 | 2.01 | 2.01 | 2.01 | |
| V1 | 22.03 | 22.03 | 15.72 | 15.72 | |
| V2 | 21.44 | 21.44 | 12.51 | 12.51 | |
| V3 | 20.33 | 20.33 | 10.23 | 10.23 | |
| Parameters | Equation (11) | Equation (12) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Test | V0 (m/s) | Te (s) | Adj R-Square | P1 (m) | P2 (m) | SSE | RMSE | Adj R-Square | |
| B-N-J1 | 0.0052 | 70.35 | 0.71 | 0.37 | 24.89 | 0.0003 | 0.01 | 0.98 | |
| B-AR-J1 | 0.0048 | 38.38 | 0.66 | 0.18 | 24.66 | 0.0004 | 0.01 | 0.96 | |
| B-ASB-J1 | 0.0043 | 62.43 | 0.80 | 0.27 | 24.79 | 0.0004 | 0.01 | 0.99 | |
| B-ASB-AR-J1 | 0.0042 | 50.17 | 0.86 | 0.21 | 24.69 | 0.0002 | 0.01 | 0.99 | |
| B-N-J2 | 0.0132 | 35.47 | 0.83 | 0.47 | 25.19 | 0.0020 | 0.02 | 0.97 | |
| B-AR-J2 | 0.0124 | 32.35 | 0.90 | 0.40 | 24.95 | 0.0005 | 0.01 | 0.99 | |
| B-ASB-J2 | 0.0121 | 47.38 | 0.82 | 0.57 | 25.27 | 0.0004 | 0.01 | 0.98 | |
| B-ASB-AR-J2 | 0.0125 | 22.87 | 0.98 | 0.29 | 24.87 | 0.0004 | 0.01 | 0.98 | |
| B-N-J3 | 0.0164 | 52.60 | 0.47 | 0.86 | 25.77 | 0.0049 | 0.04 | 0.98 | |
| B-AR-J3 | 0.0124 | 44.41 | 0.93 | 0.55 | 25.25 | 0.0019 | 0.02 | 0.98 | |
| B-ASB-J3 | 0.0138 | 62.69 | 0.60 | 0.86 | 25.74 | 0.0070 | 0.04 | 1.00 | |
| B-ASB-AR-J3 | 0.0146 | 39.56 | 0.99 | 0.58 | 25.27 | 0.0004 | 0.01 | 1.00 | |
| B-N-J4 | 0.0338 | 44.01 | 0.99 | 1.49 | 26.55 | 0.0019 | 0.02 | 1.00 | |
| B-AR-J4 | 0.0165 | 56.35 | 0.76 | 0.93 | 25.73 | 0.0006 | 0.01 | 1.00 | |
| B-ASB-J4 | 0.0275 | 34.70 | 0.90 | 0.95 | 26.04 | 0.0001 | 0.00 | 0.99 | |
| B-ASB-AR-J4 | 0.0194 | 42.16 | 0.74 | 0.82 | 25.58 | 0.0026 | 0.03 | 0.99 | |
| Parameters | q1 | q2 | SSE | RMSE | Adj R-Square | |
|---|---|---|---|---|---|---|
| Profile Type | ||||||
| B-N | −0.047 | 1.12 | 0.005 | 0.011 | 0.94 | |
| B-AR | −0.047 | 1.12 | 0.002 | 0.007 | 0.94 | |
| B-ASB | −0.053 | 1.25 | 0.004 | 0.009 | 0.94 | |
| B-ASB-AR | −0.053 | 1.27 | 0.002 | 0.007 | 0.95 | |
| All data | −0.049 | 1.17 | 0.015 | 0.009 | 0.94 | |
| Hydrodynamic Factors | Hs (m) | Hs-long (m) | (m) | Ls (m) | Hs/Ls | (m2) | ||
|---|---|---|---|---|---|---|---|---|
| Profile Types with Parameters | ||||||||
| B-N-P1 (significance level) | 0.9600 (0.04) | 0.9618 (0.04) | 0.9312 (0.07) | 0.9498 (0.05) | 0.7026 (0.30) | −0.7335 (0.27) | 0.9886 (0.01) | |
| B-AR-P1 (significance level) | 0.9774 (0.02) | 0.9811 (0.02) | 0.9951 (0.00) | 0.9678 (0.03) | 0.9495 (0.05) | −0.9413 (0.06) | 0.9923 (0.01) | |
| B-ASB-P1 (significance level) | 0.9897 (0.01) | 0.9916 (0.01) | 0.6559 (0.34) | 0.9486 (0.05) | −0.3857 (0.61) | 0.4090 (0.59) | 0.9357 (0.06) | |
| B-ASB-AR-P1 (significance level) | 0.9724 (0.03) | 0.9734 (0.03) | 0.8933 (0.11) | 0.9588 (0.04) | 0.4411 (0.56) | −0.4703 (0.53) | 0.9786 (0.02) | |
| B-N-P2 (significance level) | 0.9857 (0.01) | 0.9868 (0.01) | 0.8932 (0.10) | 0.9653 (0.03) | 0.7605 (0.24) | −0.7929 (0.21) | 0.9929 (0.01) | |
| B-AR-P2 (significance level) | 0.9872 (0.01) | 0.9894 (0.01) | 0.9837 (0.02) | 0.9749 (0.03) | 0.9703 (0.03) | −0.9625 (0.04) | 0.9984 (0.00) | |
| B-ASB-P2 (significance level) | 0.9946 (0.01) | 0.9952 (0.00) | 0.7313 (0.27) | 0.9774 (0.02) | −0.4727 (0.53) | 0.4973 (0.50) | 0.9686 (0.03) | |
| B-ASB-AR-P2 (significance level) | 0.9823 (0.02) | 0.9841 (0.02) | 0.9114 (0.09) | 0.9730 (0.03) | 0.4378 (0.56) | −0.4709 (0.53) | 0.9870 (0.01) | |
| B-N-Te (significance level) | −0.5172 (0.48) | −0.5269 (0.47) | −0.2953 (0.70) | −0.6217 (0.37) | −0.3079 (0.69) | 0.3753 (0.62) | −0.4849 (0.52) | |
| B-AR-Te (significance level) | 0.8100 (0.19) | 0.8119 (0.19) | 0.8474 (0.15) | 0.7577 (0.24) | 0.8222 (0.18) | −0.7944 (0.21) | 0.8573 (0.14) | |
| B-ASB-Te (significance level) | −0.6430 (0.36) | −0.6321 (0.37) | −0.9133 (0.09) | −0.7086 (0.29) | 0.4635 (0.54) | −0.5137 (0.49) | −0.7156 (0.28) | |
| B-ASB-AR-Te (significance level) | −0.0973 (0.90) | −0.0990 (0.90) | −0.2923 (0.71) | −0.0672 (0.93) | −0.2337 (0.77) | 0.2821 (0.72) | 0.0207 (0.98) | |
| A negative coefficient indicates the correlation between the fitting parameter and the opposite number of the factor. | ||||||||
| Wave | J1 | J2 | J3 | J4 | |
|---|---|---|---|---|---|
| Profile Type with Wave Gauges | |||||
| B-N-W5 | 7.39 | 7.79 | 9.81 | 8.72 | |
| B-N-W1 | 5.56 | 6.47 | 8.39 | 0.07 | |
| B-AR-W5 | 5.90 | 6.06 | 6.50 | 6.63 | |
| B-AR-W1 | 4.37 | 5.00 | 7.45 | 5.98 | |
| B-ASB-W5 | 7.74 | 8.15 | 7.48 | 6.38 | |
| B-ASB-W1 | 5.57 | 6.58 | 0.05 | 0.06 | |
| B-ASB-AR-W5 | 5.93 | 6.24 | 7.07 | 5.90 | |
| B-ASB-AR-W1 | 4.50 | 4.92 | 0.04 | 4.48 | |
| Profile Types | B-N | B-AR | B-ASB | B-ASB-AR | |
|---|---|---|---|---|---|
| Wave | |||||
| J1 | BT P1 = 0.3662 P2 = 24.89 Te = 70.4 | LT P1 = 0.1830 P2 = 24.66 Te = 38.4 | LT P1 = 0.2699 P2 = 24.79 Te = 62.4 | LT P1 = 0.2126 P2 = 24.69 Te = 50.2 | |
| J2 | RB P1 = 0.4666 P2 = 25.19 Te = 35.5 | RB P1 = 0.3999 P2 = 24.95 Te = 32.4 | LT P1 = 0.5724 P2 = 25.27 Te = 47.4 | LT P1 = 0.2869 P2 = 24.87 Te = 22.9 | |
| J3 | RB P1 = 0.8644 P2 = 25.77 Te = 52.6 | RB P1 = 0.5500 P2 = 25.17 Te = 44.4 | BR P1 = 0.8621 P2 = 25.74 Te = 62.7 | BR P1 = 0.5770 P2 = 25.27 Te = 39.6 | |
| J4 | BR P1 = 1.4871 P2 = 26.55 Te = 44.0 | LT P1 = 0.9273 P2 = 25.73 Te = 56.4 | BR P1 = 0.9536 P2 = 26.04 Te = 34.7 | LT P1 = 0.8186 P2 = 25.68 Te = 42.2 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuang, C.; Ma, Y.; Han, X.; Pan, S.; Zhu, L. Experimental Observation on Beach Evolution Process with Presence of Artificial Submerged Sand Bar and Reef. J. Mar. Sci. Eng. 2020, 8, 1019. https://doi.org/10.3390/jmse8121019
Kuang C, Ma Y, Han X, Pan S, Zhu L. Experimental Observation on Beach Evolution Process with Presence of Artificial Submerged Sand Bar and Reef. Journal of Marine Science and Engineering. 2020; 8(12):1019. https://doi.org/10.3390/jmse8121019
Chicago/Turabian StyleKuang, Cuiping, Yue Ma, Xuejian Han, Shunqi Pan, and Lei Zhu. 2020. "Experimental Observation on Beach Evolution Process with Presence of Artificial Submerged Sand Bar and Reef" Journal of Marine Science and Engineering 8, no. 12: 1019. https://doi.org/10.3390/jmse8121019
APA StyleKuang, C., Ma, Y., Han, X., Pan, S., & Zhu, L. (2020). Experimental Observation on Beach Evolution Process with Presence of Artificial Submerged Sand Bar and Reef. Journal of Marine Science and Engineering, 8(12), 1019. https://doi.org/10.3390/jmse8121019





