1. Introduction
Among the different renewable sources, ocean waves represent one of the most powerful and in the last few decades have been widely investigated. Despite this, wave energy remains a relatively untapped resource. The application of Wave Energy Converter (WEC) systems to such irregular sources requires a robust control logic capable of maximizing the extracted energy with acceptable efficiencies. At present, the Optimal Control problem represents an active area of research. The work of [
1] reports a comprehensive review of the advances in Optimal Control, Model Predictive Control (MPC) and MPC-like techniques applied to the wave energy field. Within the context of Optimal Control, accurate knowledge about the future Wave Excitation Force (WEF) is essential to compute the optimal control signal. In literature, several approaches have been proposed to address the problem of the WEF estimation with promising results. An exhaustive classification and comparison of several estimation techniques is presented in the work of [
2]. Some examples are cited hereafter. In [
3,
4] a Kalman Filter (KF) observer is employed on a linear Point-Absorber (PA) WEC. It is assumed that the WEF can be modelled as a linear superposition of fixed and finite harmonic components. Similarly, In [
5] the wave force estimation and prediction problem for arrays of WECs is approached, comparing both global and independent estimators and forecasters. In the work of [
6] two approaches are presented: the first approach is based on a KF coupled with a random-walk model of the WEF; the second performs a receding horizon—unknown input estimation. In [
7] a modified form of the well-known Fast Adaptive actuator Fault Estimation called Fast Adaptive Unknown Input Estimation (FAUIE) is applied to a non-linear PA. In [
8] is studied a direct approach by measuring the pressures at discrete points on the buoy surface, in addition to the buoy heave position, to obtain the estimation of the WEF by an Extended Kalman Filter (EKF). Finally, In [
9] studied the WEF estimation of WaveSub (by Marine Power Systems Ltd. (Swansea, England)), a multiple Degree of Freedom (DoF) non-linear WEC. The estimation problem is tackled with a stochastic and a periodic KF, using only quantities which are measurable in practice. A model-free approach is proposed by [
10] emoploying a Neural Network (NN) framework to estimate the WEF on a PA. Similarly, In [
11] is studied the estimation of the wave elevation using the measurements from a nearby buoy employing a Non-linear AutoRegressive with eXogenous input network (NARX). All the mentioned studies are promising in terms of estimation performances and robustness of the observer. However, most of the work cited refer to single Degree of Freedom (DoF) WECs and few studies on non-linear multiple DoF systems have been conduced so far.
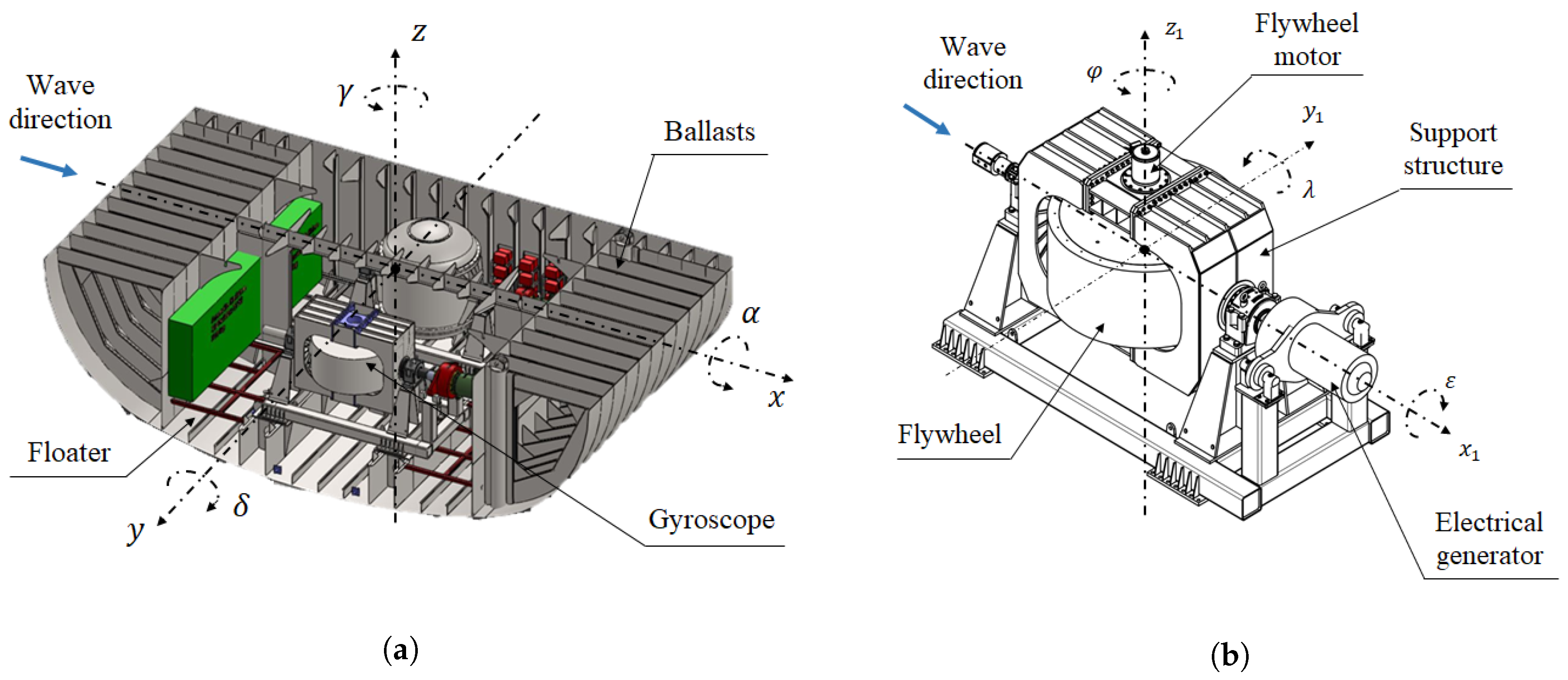
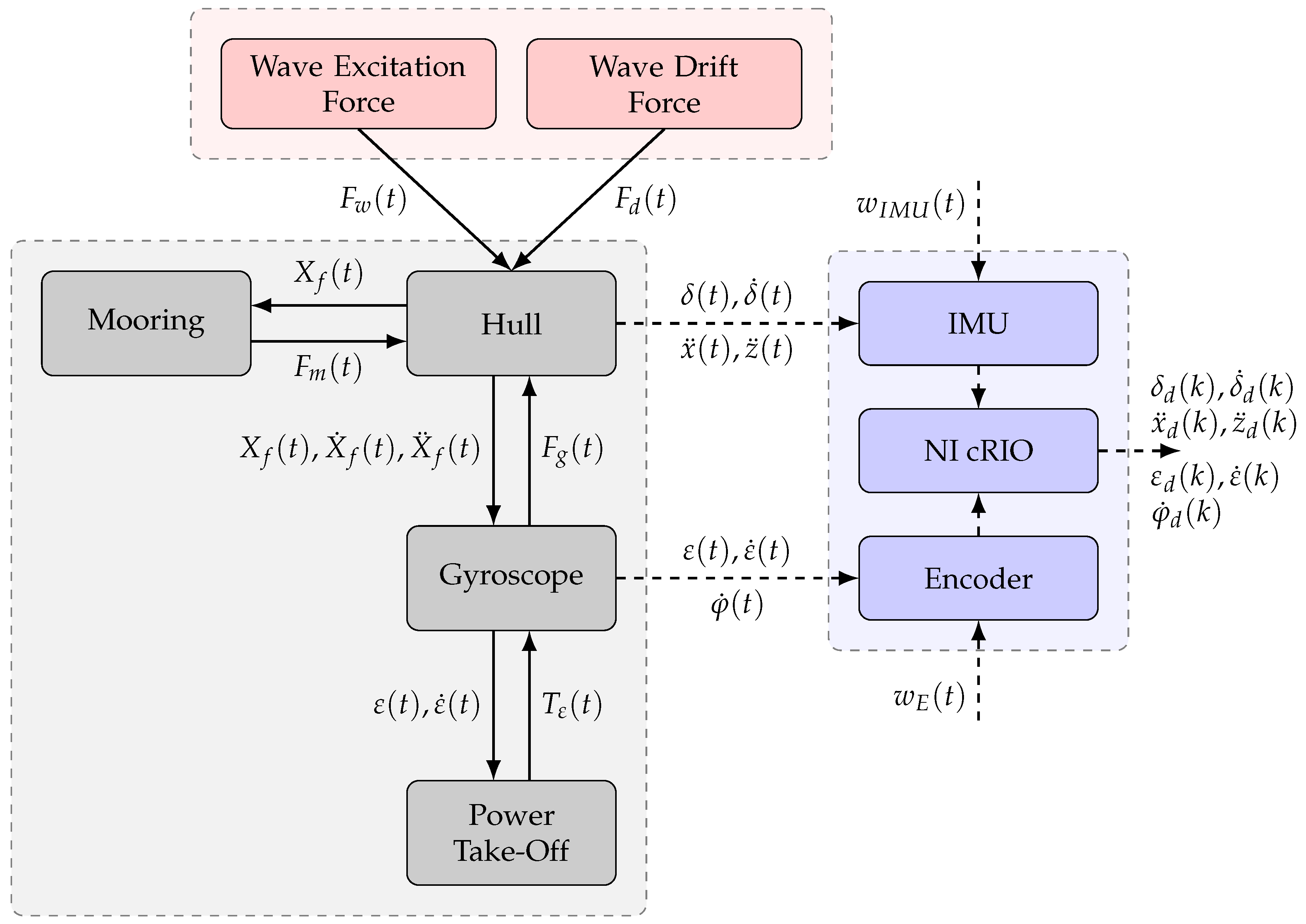
The aim of this work is to estimate the WEFs on a non-linear three Degrees of Freedom (3-DoF) WEC using only readily measureable quantities to perform the estimation. The study is applied to the Inertial Sea Wave Energy Converter (ISWEC) device designed for the Mediterranean Sea. In this context, three different approaches have been applied to the ISWEC device in previous works. In [
12] is built an unknown state observer with a second order augmented state space representation of the ISWEC for the estimation of the pitch excitation torque. The gain of the observer has been found with an LQR optimization. In [
13] is presented a method to estimate the sea state Power Spectral Density (PSD) of the wave climate by using the device motion. The heave motion measurements are used to estimate the PSD of the incoming wave and the results compared with the wave PSD measured by a wave measurement system. Then, in [
14] a feedforward NN is proposed to relate the ISWEC motion to the WEFs acting on surge, heave and pitch DoFs. In the current study two approaches are applied to the non-linear 3-DoF model of the ISWEC to estimate the WEFs acting on surge, heave and pitch DoFs:
Model-Based approach: a KF observer modelling the WEF as an unknown input with a harmonic nature. This estimation framework is studied in [
3,
4] and named Kalman Filter with Harmonic Oscillator (KFHO) in [
2];
Model-Free approach: a feedforward NN to relate the ISWEC motion and gyroscopic reaction to the WEFs. The same approach reported in [
14] is considered.
The main challenges lie in considering a non-linear 3-DoF model of the WEC and estimate the WEFs along three degrees of motion. In the KF context, tuning the system for the best performance in presence of measurement noise is crucial as well as identifying un-modelled phenomena and decoupling them from the signal to be estimated. Moreover, since the ISWEC device is slack-moored to the seabed, an accurate acquisition of the absolute displacements of the WEC is not trivial; in this context, measurement errors of the absolute diplacement could affect the estimation performances. For what concerns the NN, it is key to assess both the ability to estimate data that are not considered in the training process and the accuracy in presence of model uncertanities. The aim is to use the minimum amount of measurements to model the unknown exctitation forces in respect to the ISWEC kinematic. Outcomes of this investigation are the estimators performances in different irregular sea-states and different measurement frameworks in presence of sensors noises and plant uncertainties. The results of the 3-DoF KF estimator and the NN model are compared for different sensors framework in order to analyse the influence of the measurements available. Then, measurements noises and variations of the main plant parameters are introduced. Numerical simulations under different irregular sea conditions aim to compare the estimation results of the two approaches as well as the sensitivity to changes in the plant parameters relative to the case study presented. The novelty of this work is to perform an excitation force estimation for a 3-DoF non-linear WEC decoupling the mooring forces or, more in general, undesired phenomena that will appear in real operating condition. Moreover, the NN represents a novel framework to address the wave extitation force estimation problem, able to handle strong non-linearities. In the NN context, there are very few examples of application to a multi-DOF non-linear WEC system in literature. Finally, investigating the influence of available sensors constitutes a key aspect of this work, which aims to highlight the importance of having reliable measurements in the context of WEF estimation.
This paper is organized as follows. First, in
Section 2 the ISWEC architecture is described together with the non-linear 3-DoF time domain model. Second,
Section 3 presents the linear 3-DoF ISWEC model in conjunction with the KF formulation used to estimate the WEFs.
Section 4 describes the NN approach to estimate the WEFs as well as the network architecture. In
Section 5 the parameters of both KF and NN are tuned considering the operating conditions of the ISWEC. Then, in
Section 6, the numerical results are presented and discussed. Strengths and weaknesses of each method are compared and numerical experiments are used to assess estimation accuracy, robustness to different wave conditions, sensor noises and sensitivity to model errors. Finally,
Section 7 presents conclusions and future works.
3. Wave Excitation Force Estimation with Kalman Filter
One solution to estimate the WEF could be measuring directly the pressure acting on the wetted surface of the hull [
8]. However, this method could be expensive as it requires a large number of sensors. Furthermore, since the pressure measured on the wetted surface is the combination of all the hydrodynamics forces it could be challenging to distinguish the contribution of the WEF. Another method relies on the measurement of the hull dynamics and an estimation is performed. The KF is ubiquitous in many applications to estimate the current state of a linear dynamic system from a set of measurements affected by uncorrelated Gaussian noise with known covariance. Under these assumptions, this estimator is defined as optimal because it estimates the system states minimizing the covariance of the estimation error. In this work, the estimation procedure is carried out by modelling the WEF as an unknown state to be estimated [
4]. In order to obtain the KF formulation the Equation (
2) is taken into account. First, the non-linear model is simplified considering the drift forces included into the
contribution. The viscous damping along the pitch direction is linearized and the surge damping action is neglected in order to obtain a 3-DoF linear state space model. Then, the state space model of the ISWEC is discretized in the time domain to derive the KF formulation. The mooring forces are identified and the filter is designed to decouple them from the WEF. These steps are described in detail in the following sub-sections.
3.1. Linear 3-DoF ISWEC Model
The non-linear model described in the previous chapter is simplified to achieve a compromise between the computational effort required to solve the KF algorithm and the accuracy of the estimation. The non-linear viscous force along the pitch DoF defined by Equation (
5) has to be linearized for inclusion in the estimation process. Four simulations are performed in four different sea-states using the non-linear 3-DoF numerical model and wave data of
Table 1. The pitching rate amplitude time series is extracted and its mean is computed for each simulation. The mean is substituted into Equation (
5) and
is defined as the product between the viscous damping
and the mean pitching amplitude:
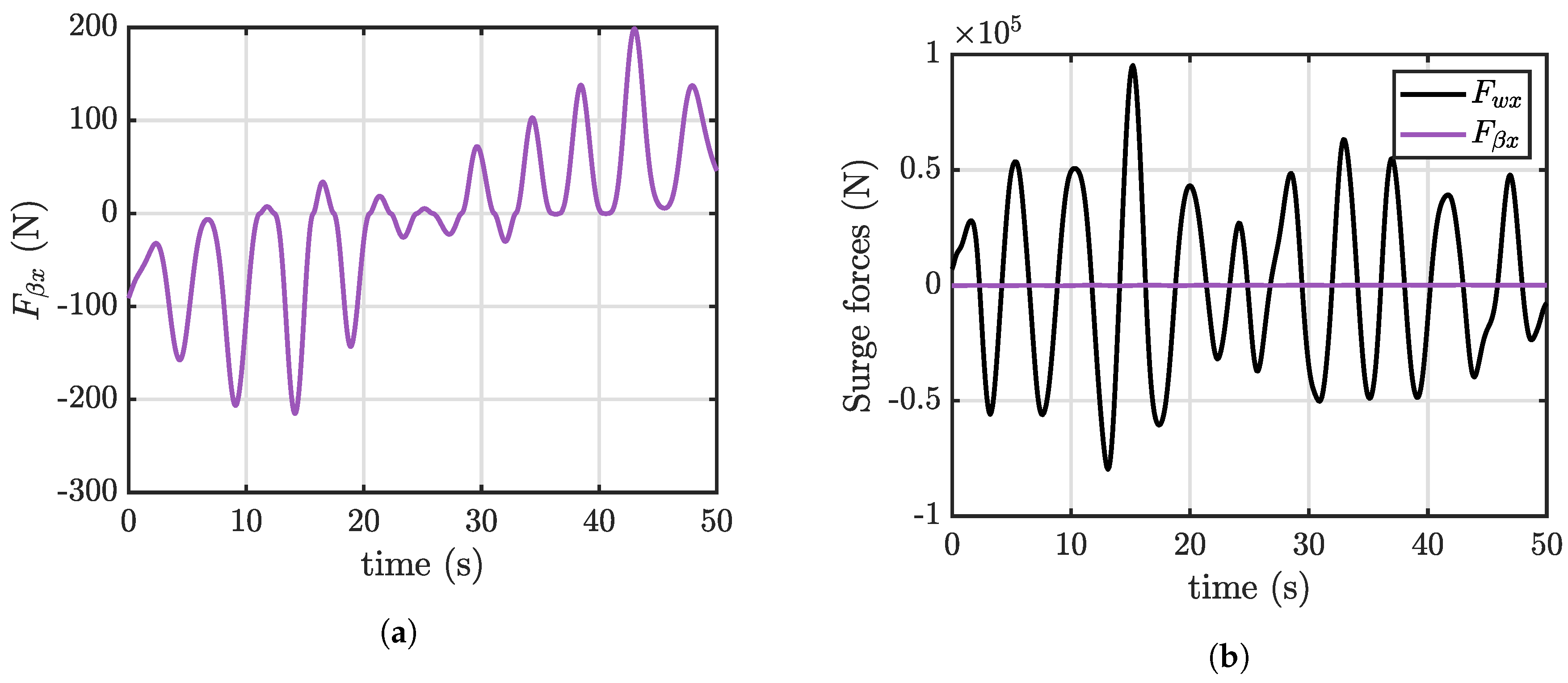
For the surge direction,
Figure 6 demonstrates that the viscous force along the surge DoF can be neglected in respect to the WEF.
The term
can be rewritten as:
Substituting the Equation (
13) in (
2), Equation (
2) can be expressed by the following linear continuous-time state-space model:
where
and
are the states and measurements vectors defined as:
,
,
and
are given by:
Here,
is the number of states,
the number of outputs,
I and 0 stands for identity and zero matrices according to the problem dimensions. The system (
14) represents the most general framework for a linear multi-DoF WEC model. It can be noted that, without loss of generality, gyroscope reaction
is the controlled input (e.g., the PTO action), the WEFs
the exogenous input to be estimated and the mooring forces
could be interpreted as an unknown unmodelled phenomena to be decoupled from the
estimation. The outputs of the linear model (
14) are position, velocity and acceleration of the WEC body resulting in a FM configuration. However, matrices
C and
D can be chosen according to the measurements available on the system as well as the requirements of the observer as defined in
Table 2.
3.2. Kalman Filter Problem Statement
In this work it is assumed that the excitation force
has a harmonic nature and it can be described as a linear combination of different wave components with a finite number of frequencies
[
2,
3,
4]. In this form, the WEF can be included into the state vector as an unknown state. In Equation (
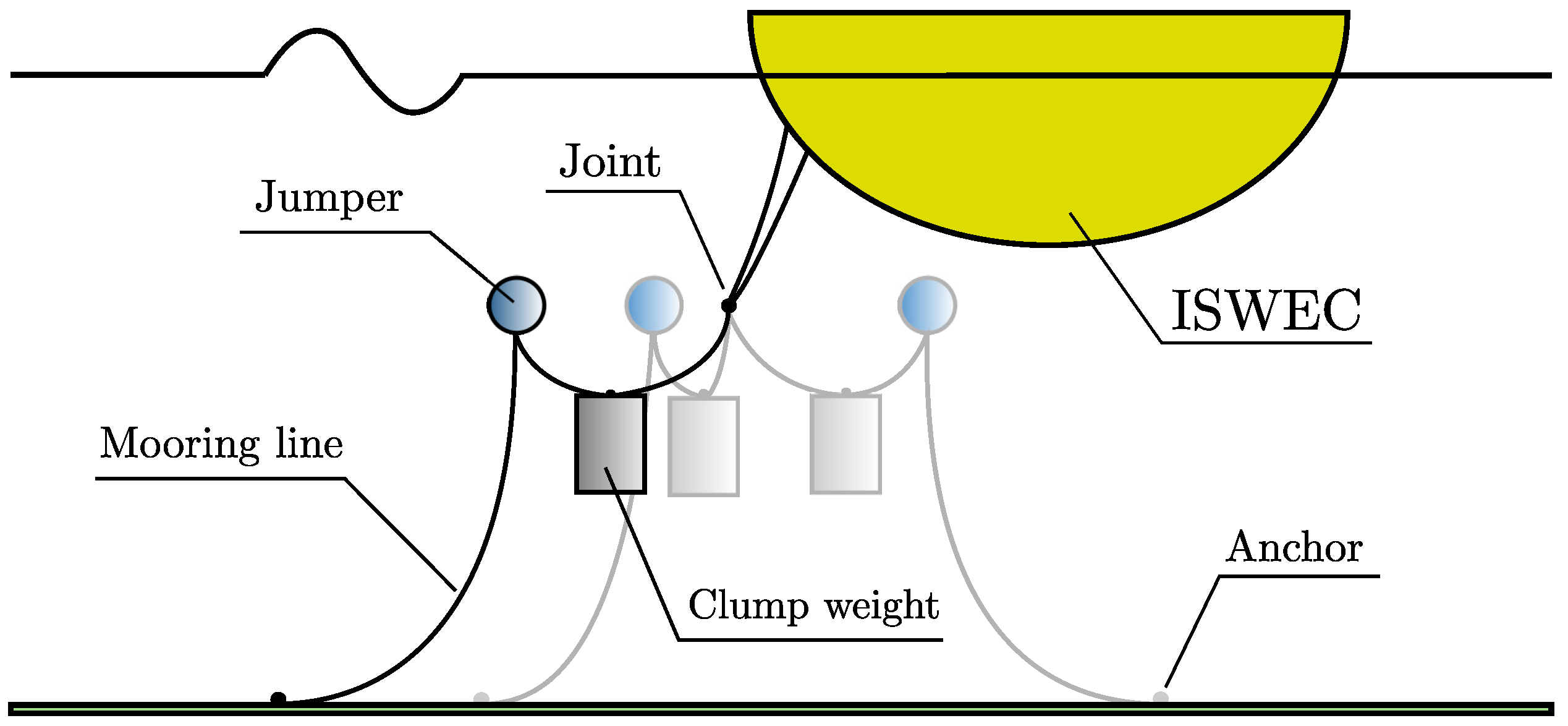
14) the mooring forces are considered as a unmodelled phenomena. In real applications, it would be difficult to directly measure the action of the moorings so they are included into the state vector as unknow states to be estimate. The ISWEC mooring system is designed to minimize the impact on the pitching motion of the device, appointed to the power conversion chain [
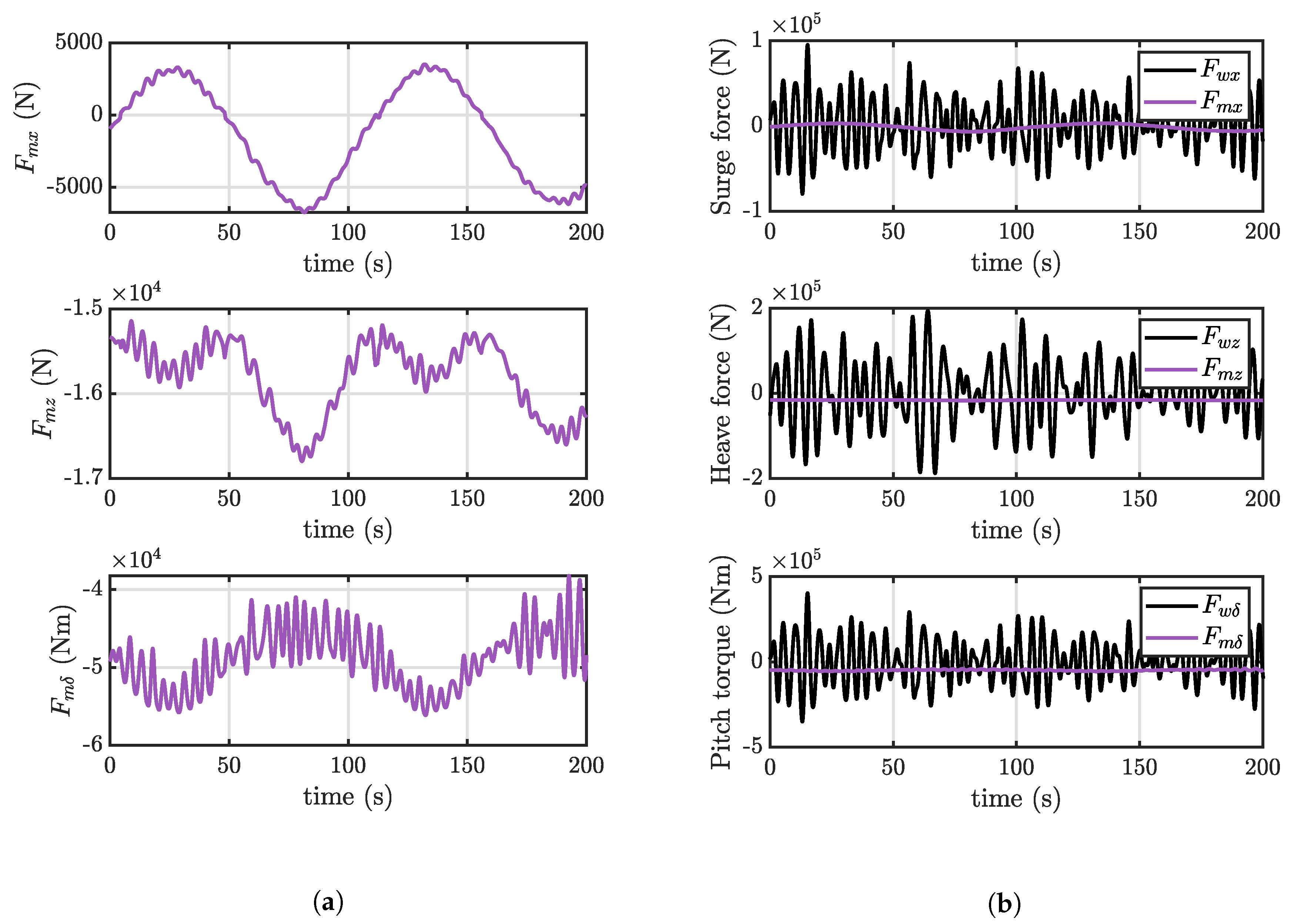
31]. As demonstrated in
Figure 7b, the mooring forces have a very slow dynamics such as the surge component and a constant load in heave and pitch directions compared to the WEF. In normal working conditions, snatch loads do not appear, and the mooring forces have mainly the behaviour as shown in
Figure 7a.
is synthesised using the same method that was detailed for
, using a harmonic model to describe its behaviour. For the sake of simplicity, the mooring forces are modelled with only one frequency for each component representing their main spectral nature.
Under these assumptions the state vector
is augmented including the estimation of
and
and the System (
14) is re-written:
where
is the augmented state vector defined as:
Here
is the augmented state vector dimension.
is the unknown force to be estimated:
The
j-th compoenent of the estimated force is given by the WEF harmonics and the mooring force as follows:
Therefore, the estimated
is obtained by summing up all the harmonic contributions for each of its components:
The augmented matrices
,
,
and
are given by:
Again,
I and 0 are identity and zero matrices according to the context.
is defined as:
where
is a
vector of ones.
is the diagonal matrix with the frequencies identified to approximate the unknown forces along the three DoFs:
In Equation (
24),
,
and
are diagonal matrices containing the frequencies for unknown force components:
where
stores the
harmonics to model the WEF components. The number of frequencies in
, have to be chosen in order to have a compromise between the accuracy of the estimation for each excitation force component and the computational effort. The matrices (
25) include a term at low frequency to represent the contribution of the mooring forces for each DoF.
Let us consider the following linear time-invariant stochastic discrete model representing the discrete-time version of the augmented System (
17):
where
represents the system estimated states,
is the known input and
contains the measurements of the system dynamics.
and
are zero mean white noise sequences with known covariance, uncorrelated with each other and with the initial state of the system.
,
,
and
stand for the discretised versions of the matrices
,
,
and
.
is the weighting matrix for the process disturbances.
Q and
R are the covariance matrices of the process and measurements noise. The KF algorithm performs the estimation in the form of a feedback control: the filter estimates the process state at some time and then obtains feedback in the form of (noisy) measurements. As such, the equations for the KF fall into two groups: time-update equations and measurement-update equations [
43]:
The time update equations can also be thought of as predictor equations, while the measurement update equations can be thought of as corrector equations. In this framework, the KF algorithm can be implemented to estimate the unknown WEF vector by measured system dynamics and known input at any instant k.
4. Wave Excitation Force Estimation with Neural Network
Despite its simplicity and efficacy, the KF filter observer may suffer from several drawbacks: the non-linear effects emerging in sever sea-states conditions as well as the reliabiliy of the WEC model could negatively affect the estimation performances. For example, the slack-mooring of the ISWEC is modelled with a quasi-static approach (developed in-house). The main advantage consists in reducing the computational burden of the simulation at the expense of model accuracy. More accurate mooring models are presented in [
44] considering two dynamic lumped-mass approaches (the open source MoorDyn [
45] and the commercial OrcaFlex 11.0e [
46]) where mooring actions are resolved coupling both the hydrodynamics and gyroscope model of the WEC in the MoorDyn and Orcaflex enviorments. When the system model is not reducible to a series of analytical equations or, even more, is based only on observed data the implementation KF model is not trivial. This argument can be extended to any other complex aspect of WEC modelling that cannot be analytically formulated with acceptable accuracy. In this context, artifical NNs represents powerful tools to map the non-linear relations from sets of input-output data. In NN models the parameters are tuned to fit the input-output data, without reference to the physical background and no information about the model architecture.
In general mathematical terms, WEFs acting on the ISWEC can be expressed as a non-linear function
of the system known inputs and measurements as follows [
14]:
Equation (
29) shows that the estimation of the WEF at instant
k is, at least in principle, addressed combining a series of known system inputs and measurements collected from discrete time
to
k where
represents the delay steps of the available data. More in detail, the WEF could be obtained from the set of WEC motion measurements from the ISWEC on-board sensors and the gyroscopic reaction. In [
14] the same approach is considered including the measures provided by the IMU and encoders mounted on the ISWEC adding the velocity
and position
obtained by numerical integration of the acceleration
. These two inputs were included to improve the estimation accuracy. However, this measurements framework does not consider the effect of the sensor noise: in practice, accelerometer signals are often very noisy, hence velocity and position integration from acceleration are likely to be unreliable, resulting in unreliable estimations in practice. In this work, the NN is evaluated for all the configurations of
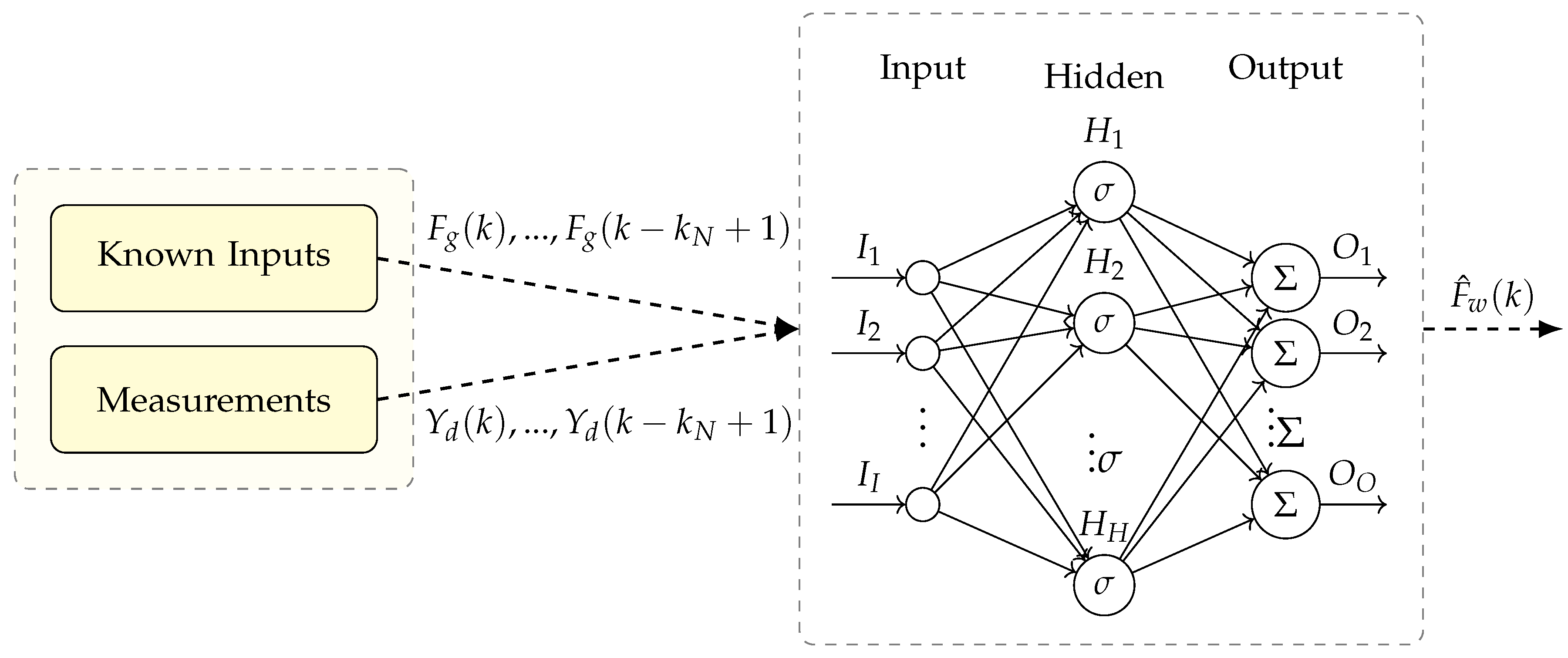
Table 2 and the sensitiveness and roubustness analysis is extended to all the wave domain of the installation site. The input-output architecture of the NN is shown in
Figure 8. The feedforward NN is composed of linked neurons arranged in three layers. The input layer collects a set of inputs
multiplying them by a set of weights, assigned to the data on the basis of their relative importance to other inputs. The hidden neurons apply a non-linear activation function
to the weighted sum of their inputs. Then, the outputs of each hidden neuron are linearly combined by the output functions
to produce the network outputs
. The use of delays in the input variables is considered to increase the reliability of the estimate. For a generic dynamic system, one way to consider its dynamic behaviour using static neurons is to employ past values of the inputs [
47], resulting in good performances in term of estimation accuracy and robustness to different wave conditions as demonstrated in [
14].
5. Kalman Filter and Neural Network Tuning
The matrix
containing the frequencies to model the WEFs as well as
Q and
R are tuned for the system under study. A sensitivity analysis has been performed to tune the number of frequencies. Then, through an iterative process the diagonal coefficients of
Q and
R are identified in order to have the best estimation performances for each measurement framework considered. Numerical experiments are conduced considering the four wave profiles of
Table 1. The estimation performances are valuated considering the Goodness-of-Fit (
) proposed by [
48]:
In Equation (
30),
and
are the true and estimated WEF for the
j-th DoF at discrete time instant
k, respectively.
is the total number of samples.
5.1. Kalman Filter Parameters
For the presented case, 1, 3, 6 and 9 frequencies are tested in order to find a compromise between the accuracy of the estimation process and the KF complexity. The interval is chosen between period 3 s and period 9 s, linearly spaced. Each point refers to the mean of each
obtained from four tuning sea-states. The mooring components are modelled with only one period: 100 s for
and 2000 s for
and
, considered as low frequency contributions (
Figure 7). The FM framework has been considered for this tuning process.
Table 3 sets out the results obtained from each tuning wave gruped in respect to the number of frequencies
.
Increasing the number of harmonics from to leads to a significant improvement of all . On average, an advance of 0.162 is obtained for , 0.138 for and 0.228 for . Passing from to shows a slight increase of and , enchancing the quality of the and estimation of 0.011 and 0.021, respectively. Further enlarge of results in a minimal or null upgrade of any . In this regard, is considered a good trade-off between accuracy and complexity of the observer.
For what concerns the covariance matrices, repeated simulations are conduced to tune the diagonal elements of
Q and
R for each mesurement framework. They are chosen to guarantee an accurate estimation of the unknown states without amplifying the noise level.
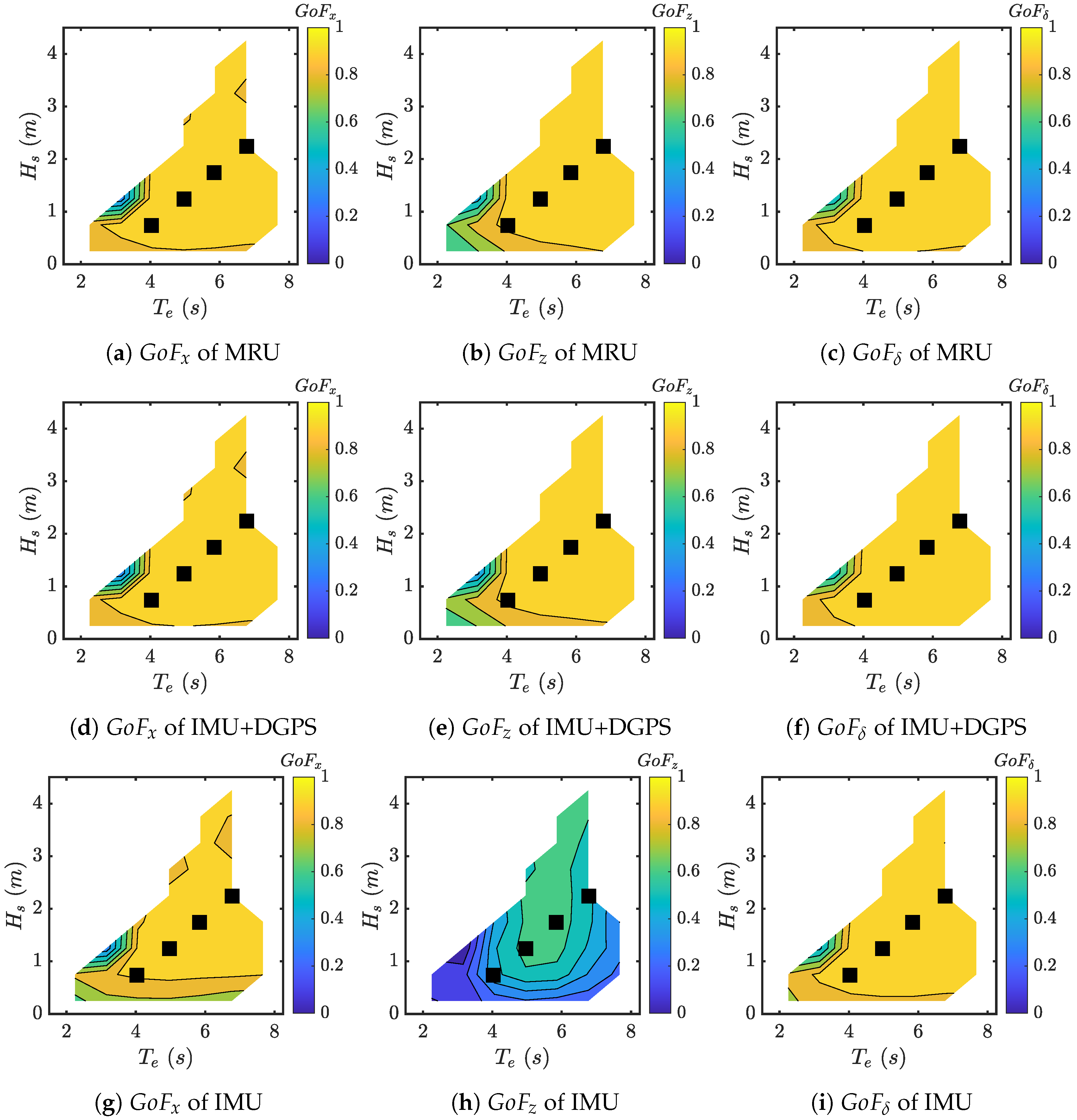
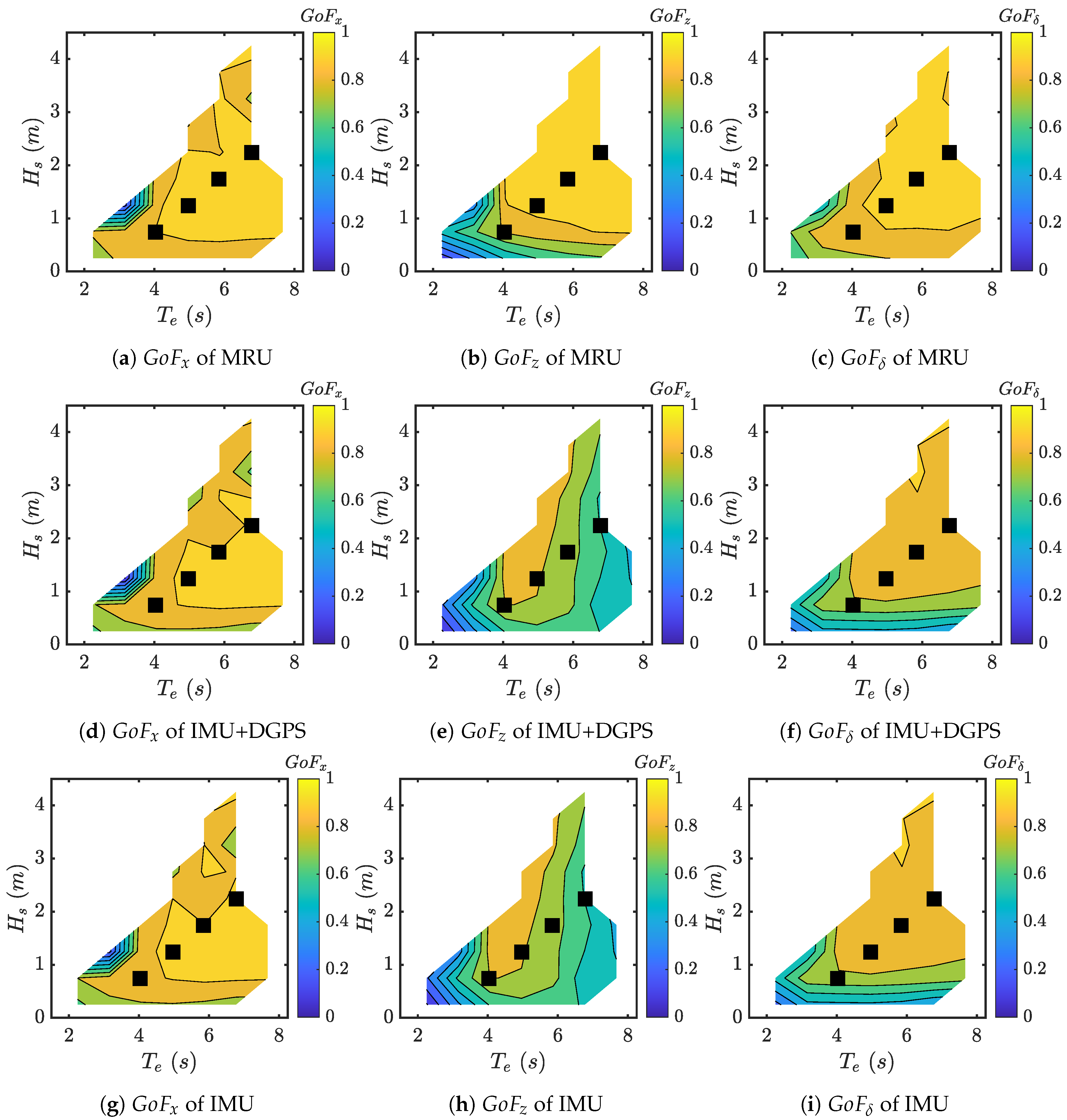
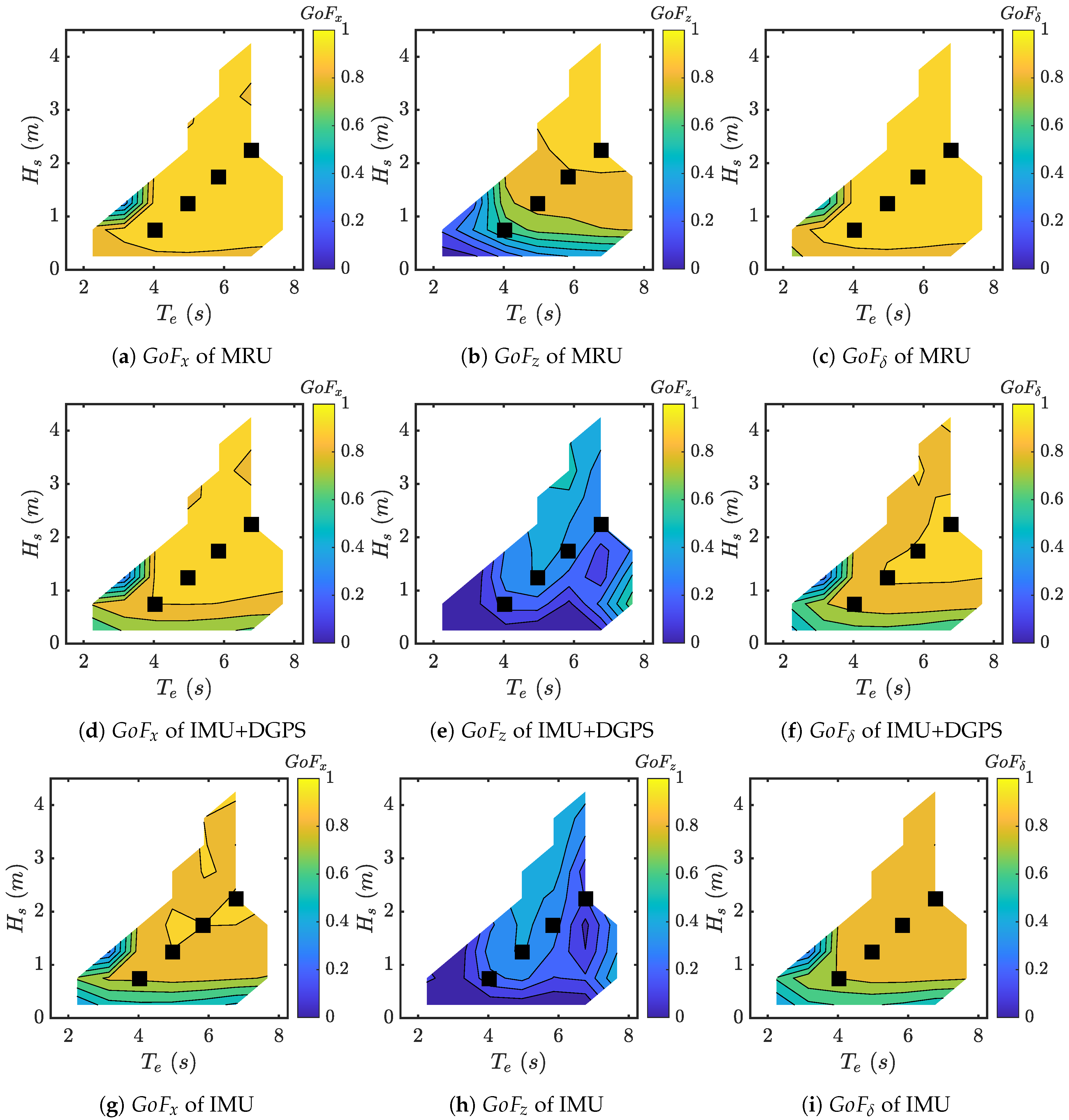
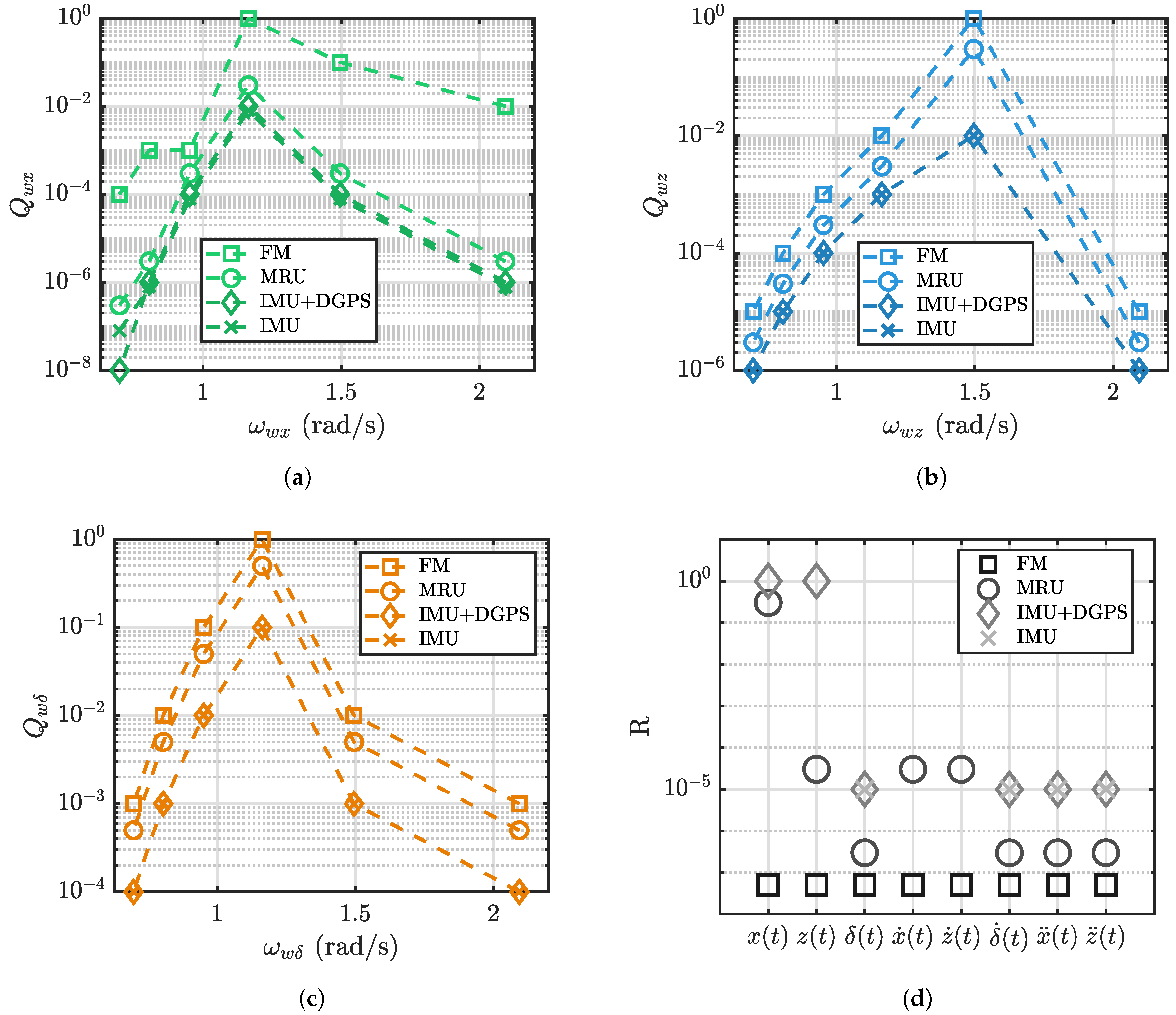
Figure 9a–c compare the
Q coeffcients relative to the WEF components for each measurement framework. From the chart, it can be seen that the
Q coeffcients are reduced as the magnitude of the noise increases and are tuned in respect to the energy content of the WEF. In this way, the most relevant frequency components are amplified more than the others, resulting in a more accurate estimation.
Figure 9d provides the
R coefficients, balanced in order to penalize the most inaccurate measurements (e.g., DGPS positions) giving less importance to the related signals. Data indicate that the
R coefficients grow as the noise magnitudes increase. Missing markers mean that the measurements are not available for that framework.
5.2. Neural Network Parameters
The NN training aims to obtain the weights and bias of the network evaluating the sensitivity of the model to both the delay steps
and neurons
. The four wave profiles of
Table 1 are used to obtain the training data for each measurement framework. The time-series of the WEFs are concatenated to generate a long training set applied to the ISWEC numerical model obtaining the WEC motion measurements. Then, all the time-series are normalized in the
range to avoid problems due to different magnitude between input-output signals. Since the system is non-linear, the data normalization could negatively affect the trainign process if, for example, saturations of the PTO appear. To avoid saturations, the training data are chosen to cover the operating range of the ISWEC. However, in sever sea-states the WEC motion could overcome the normalization range causing estimation errors but, in such extreme conditions, the WEC is shut-down for safety purposes and no control is applied. In order to address over-fitting problem the data are randomly divided into three parts: 50% for training purposes, 30% for validation and 20% for performance evaluation. The performance function is the Mean Squared Error (MSE) normalized between −1 and 1, ensuring that the relative accuracy of output elements of different magnitude are treated as equally important. Then, 1, 3, 5, and 7 delay steps are tested while the number of neurons is fixed to 10; 5, 10, 15 and 20 neurons are evaluated with 3 delay steps. Specific tuning processes are applied for each framework with the same number of delay steps and neurons, considering noisy signals. The FM framework has been considered for tuning the network hyperparameters.
The sensitivity analysis on the delay steps is reported in
Table 4. The mean value of each
reveals that increasing the number of delay steps from
to
results in a revelant increase of estimation accuracy, expecially for the
that passes from 0.880 to 0.977. A similar behaviour is obtained for the
, where the mean estimation performance grows of 0.053 points. On the other hand, no relevant improvements are obtained for the
as well as for the other DoFs employing 5 and 7 delay steps. In this regard, 3 unit delays are chosen for the NN architecture.
Table 5 reports the estimation results obtained for different values of neurons. 10 neurons represents the best choise ensuring the good estimation performances with acceptable network complexity. Surprisingly, increasing the number of neurons over 10 leads to a slight degradation of performances, suggesting that the learning algorithm is not able to converge properly during the learning process over-fitting noisy data.
7. Conclusions
The purpose of this work is to estimate the WEFs of a non-linear WEC employing a KF observer and a NN model. This study proposes a methodology for tuning both estimators and compares them for a wide range of sea-states in presence of noise disturbances and plant variations. Four different measurement frameworks are proposed, one ideal (full measurements available without noise) and three real frameworks composed by three different sensors commercially available. The main aim is to assess the estimation performances in term of GoF for different sensor equipments in all the operating conditions of the ISWEC device. The non-linear 3-DoF model of the ISWEC is considered as the plant of reference. A linear 3-DoF hydrodynamic model is used in the KF assuming linear wave theory and linear viscous damping along the pitch DoF. Moreover, the filter model assumes no viscous damping in both surge and heave directions and the mooring forces are considered as an unknow state to be estimated. The key of the KF is to approximate the expression of the WEFs as a linear superposition of finite harmonic components with variable amplitudes and fixed frequencies. Hence, it is possible to include the excitation forces into the state vector of the system model and perform an unknown state estimation. This method restricts the bandwidth of the estimated disturbance as it can only estimate at the specified discrete frequencies. This makes it more robust to other external disturbances such as unmodelled hydrodynamic forces outside from the frequency range considered. The feedforeward NN is designed according to the hydrodynamic equation of the ISWEC. The WEFs are expressed as a function of the system dynamics at current and past time instants taking into account the dynamic memory of the plant using static neurons with no feedback data.
First, the KF parameters are tuned according to the frequency range, stating the WEF frequencies and the mooring frequencies. The wave energy matrix of the sea-site of interest has been considered to identify the principal wave periods of the incoming sea-states to decouple them from the mooring actions. Moreover, according to the noise magnitudes of the sensors, matrices
Q and
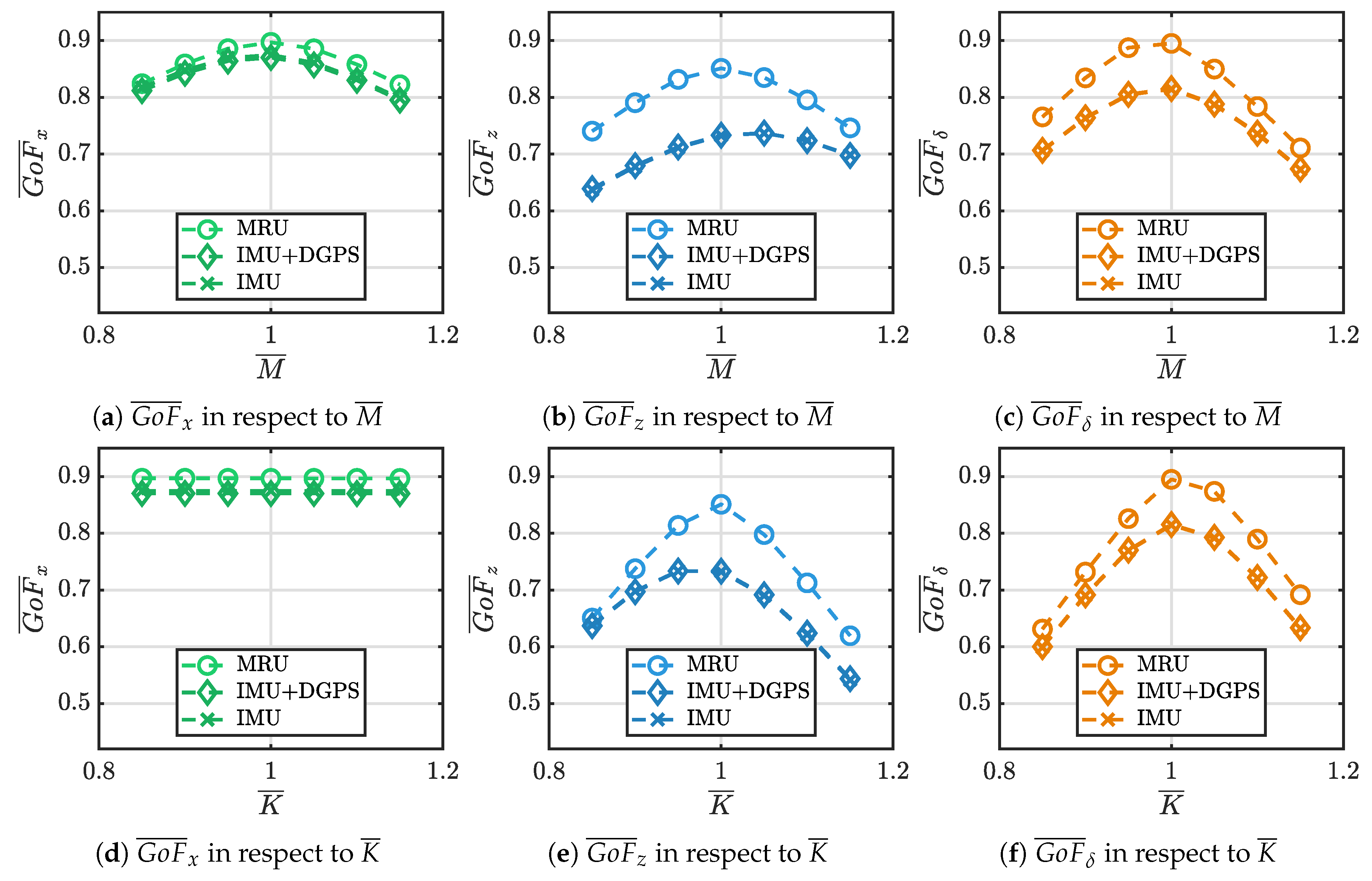
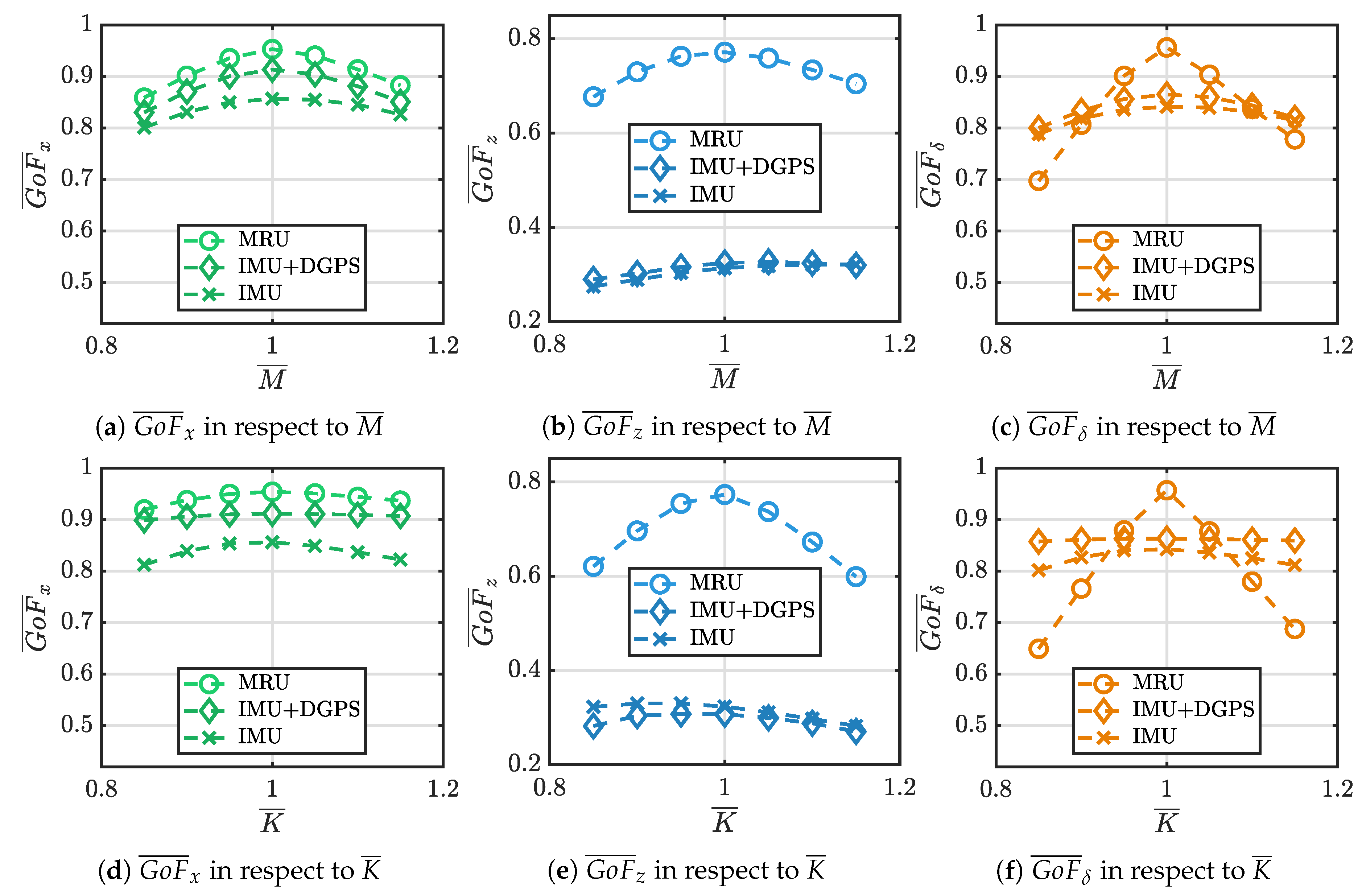
R have been balanced to obtain the best GoF from each measurement framework. The NN has been tuned with the same intent, chosing both delay steps and number of neurons guaranteeing the best compromise between network complexity and estimation accuracy. Second, numerical simulations are performed to investigate the influence of the measurement framework and sensors accuracy. Overrall, it is demonstrated that the 3-DoF KF performs well when applied to a non-linear WEC model. The KF shows best performances with the MRU* and IMU+DGPS* frameworks, expecially in surge and pitch directions where a
and
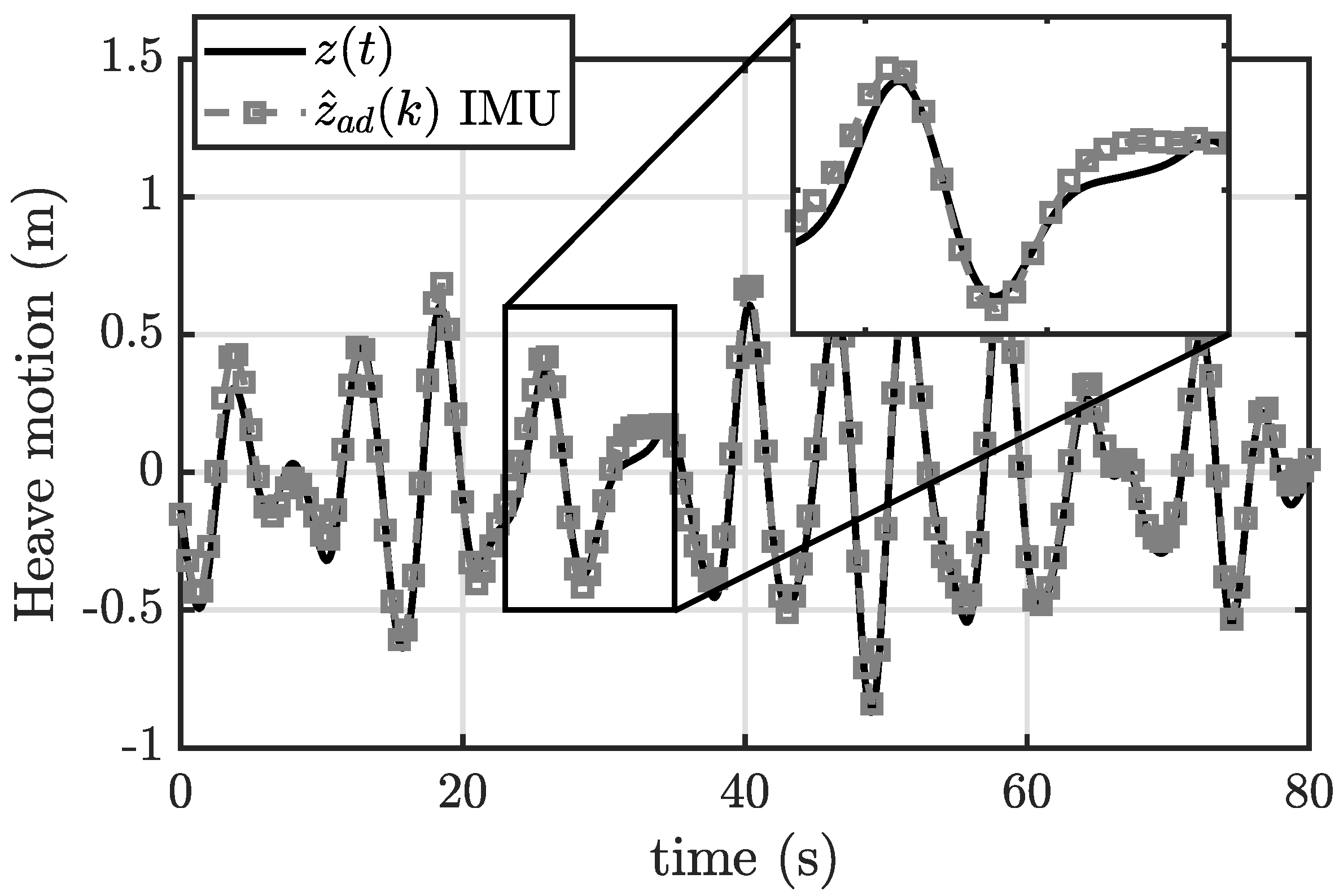
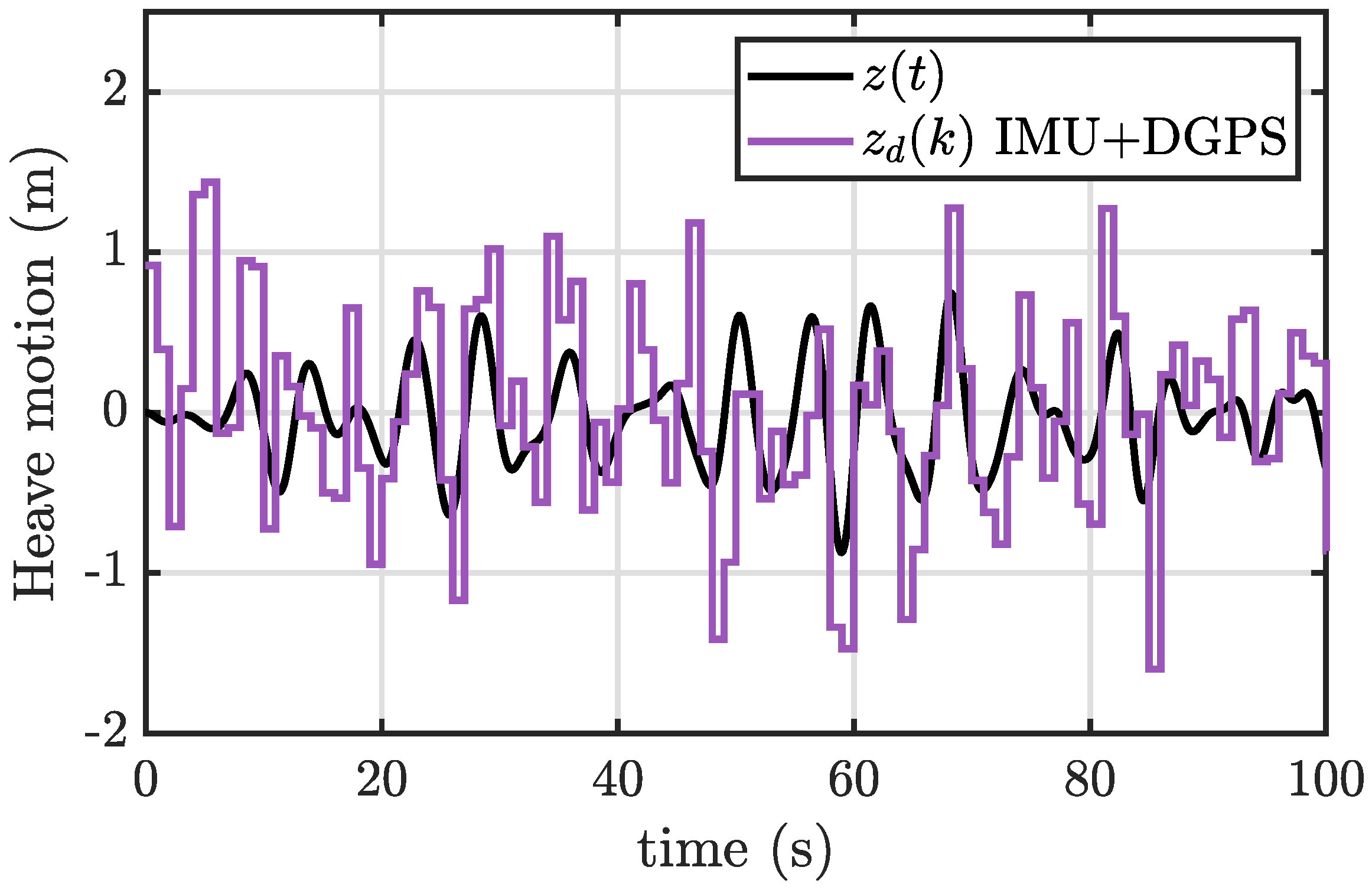
greater than 0.9 are guaranteed. The IMU* framework gives the worst performances along the heave direction performing a
almost equal to 0.75. The same argument applies for the NN, where the estimation performances are maximized in surge and pitch. Adding noisy measurements results in an acceptable decrease of accuracy for
and
. In detail, the comparison shows that the estimation accuracies of NN and KF are approximately the same and a
and
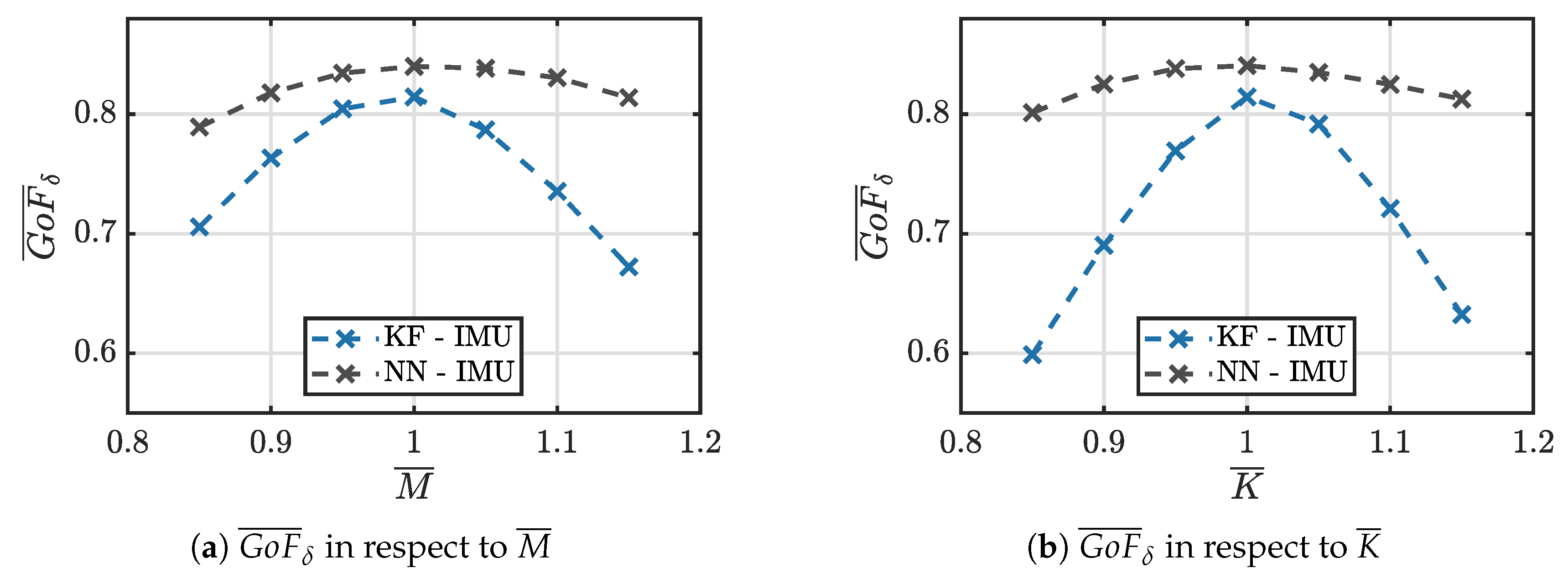
greater than 0.83 is obtained. However, both the KF and NN are considered not reliable for the WEF estimation along the heave DoF if DGPS and IMU are employed. Then, intersting results are obtained comparing the estimation performances under plant variations. Contrary to expectations, the KF is affected by plant variations more than the NN. Despite the KF can handle inaccuracies of the numerical model tuning on the
Q matrix, the NN shows good performances when these inaccuracies become relevant. Further work is required to establish the underlying cause of this outcome, acting on the
Q matrix to improve the mean performances of the KF observer.
Section 6.1,
Section 6.2 and
Section 6.3 demonstrated the good reliability of the IMU framework for the WEF estimation in surge and pitch directions for both KF and NN. However, it is evident how the estimation of the heave component is affected by the absence of the heave motion in the KF and both heave motion and velocity in NN. Despite this outcome, the use of the IMU unit is encourageed since the
is not directly involved in the power extraction of the ISWEC.
In conclusion, the main advantage of the model-based approach is that in presence of a real plant, it is possible to tune the observer on a small number of waves to obtain accurate estimation performances for a large number of sea states. The main strength of the KFHO is to consider only the frequency bandwidth specified; the knowlegde of the spectral properties of the signal to estimate allow to exclude all the undesired components and disturbance from the estimation (e.g., Mooring forces). On the other hand, a model-free non-linear approach should be more suitable to model complex hydrodynamic phenomena when their analytical expression are not available. Future work will approach the problem of the WEF estimation using more non-linear approaches (e.g., Recurrent Neural Networks and Extended Kalman Filter). The non-linear approach is expected to be more accurate in presence of strong non-linearity (e.g., PTO saturations and non-linear mooring models) in respect to a linear model-based observer. The aim will be elaborate on the estimation results between a model-based and model-free approach in term of estimation performances for a broad range of sea states. The best estimation approach will be used for the implementation of the MPC strategy on ISWEC.