A Real-Time Detection System for the Onset of Parametric Resonance in Wave Energy Converters
Abstract
:1. Introduction
1.1. Parametric Resonance in WECs
1.2. Suppression Control Methods for Parametric Resonance in WECs
1.3. Objectives and Outline of the Paper
2. A Real-Time Detection System for Early Warning of Parametric Resonance in WECs
2.1. The Linear Time-Varying Model
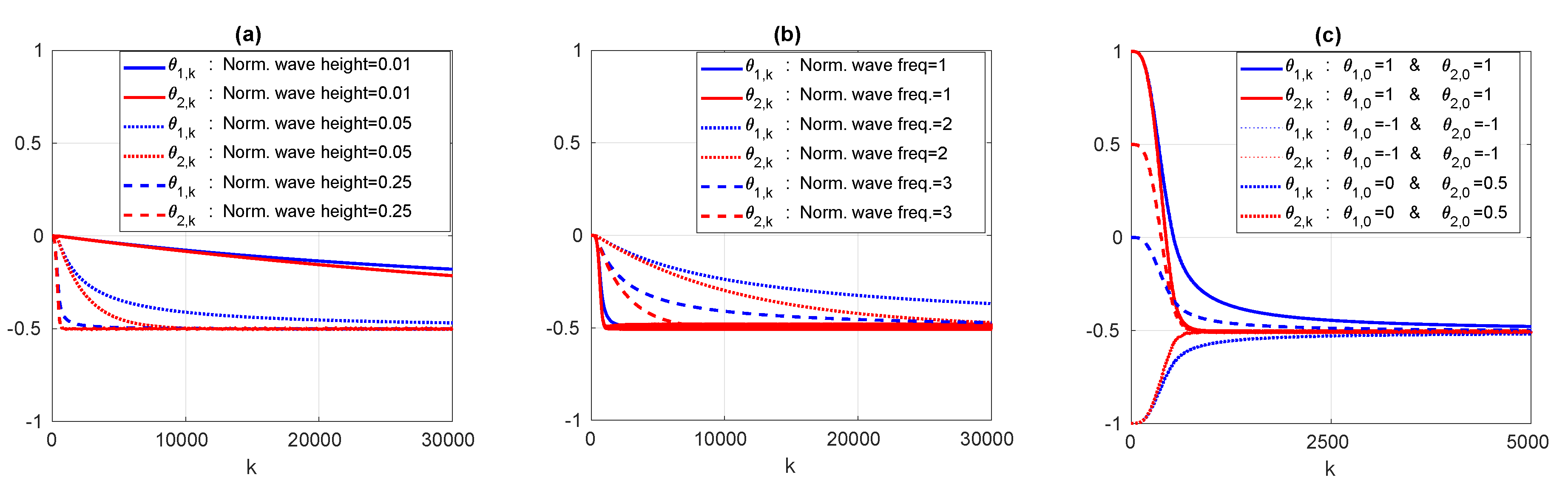
2.2. Real-Time Parameter Identification
2.3. Detecting Instability
3. Test Case
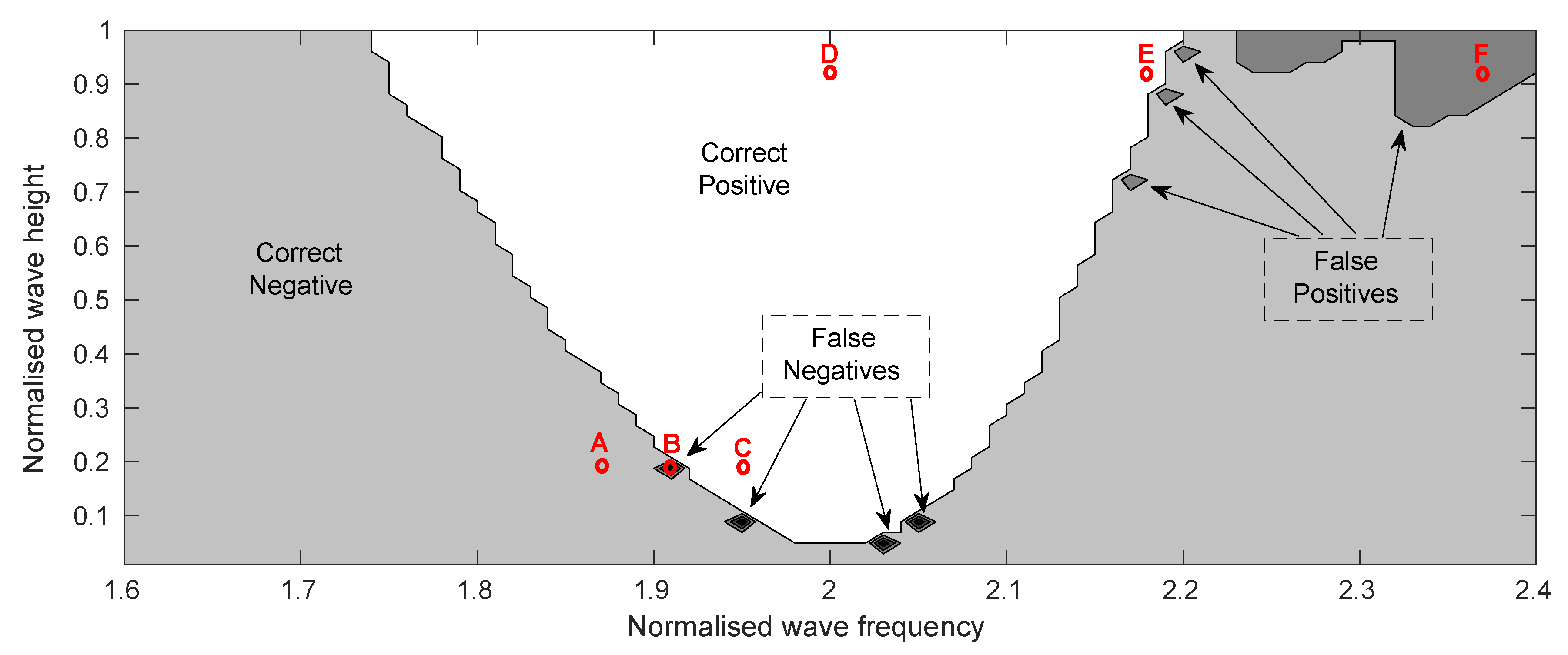
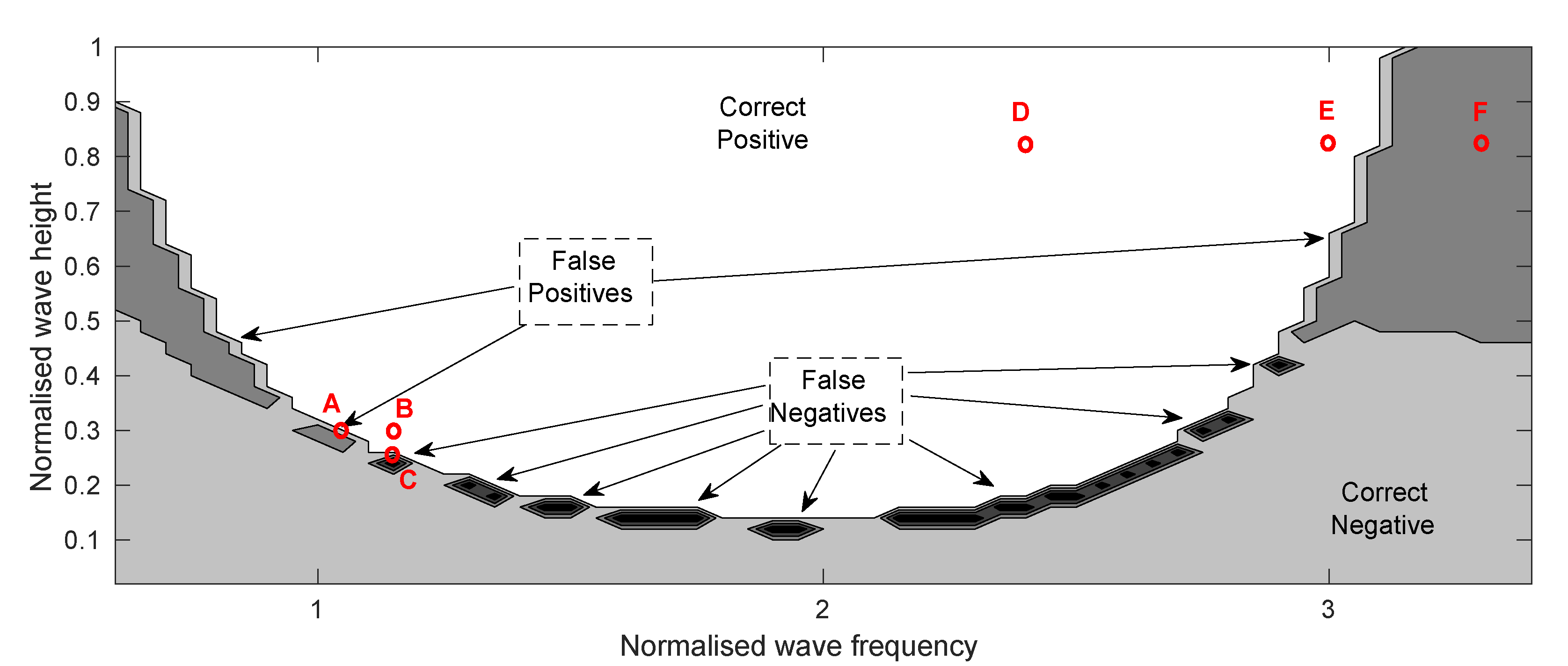
- Correctly warning when parametric resonance occurs (correct positive) and not giving a false warning when parametric resonance does not occur (correct negative).
- How early the system detects the onset of parametric resonance and sends a warning.
3.1. The Device
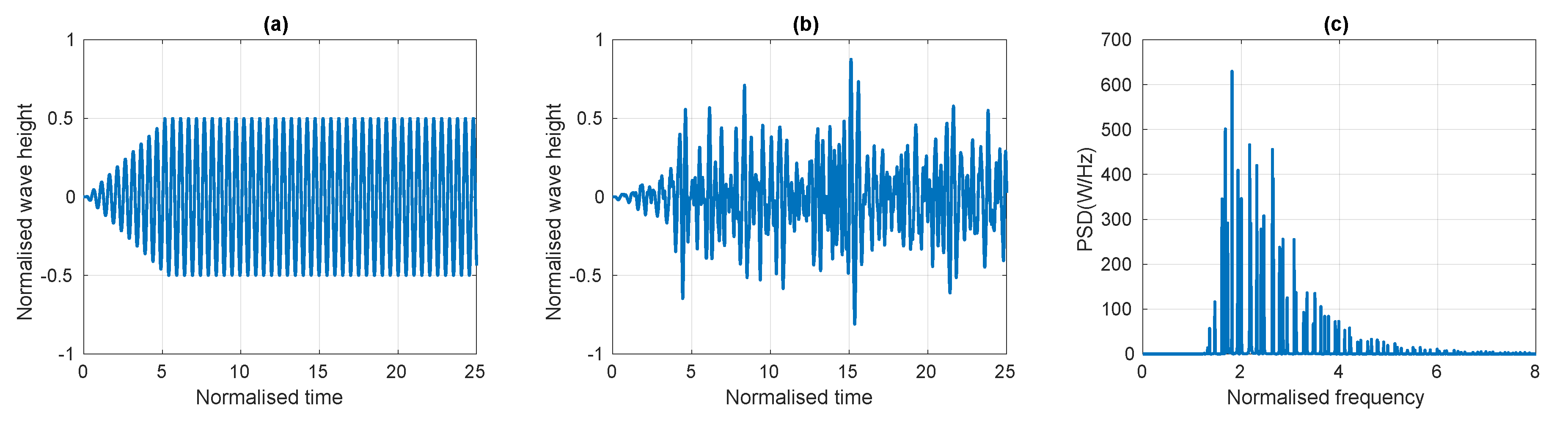
3.2. Input Waves
3.3. Numerical Model
- is the inertia, detailed in Section 3.3.1.
- is the hydrostatic restoring force, detailed in Section 3.3.2.
- is the hydrodynamic damping force, detailed in Section 3.3.3.
- is the wave excitation force, detailed in Section 3.3.4.
3.3.1. Inertia
3.3.2. Hydrostatic Restoring Force/Moment
3.3.3. Hydrodynamic Damping
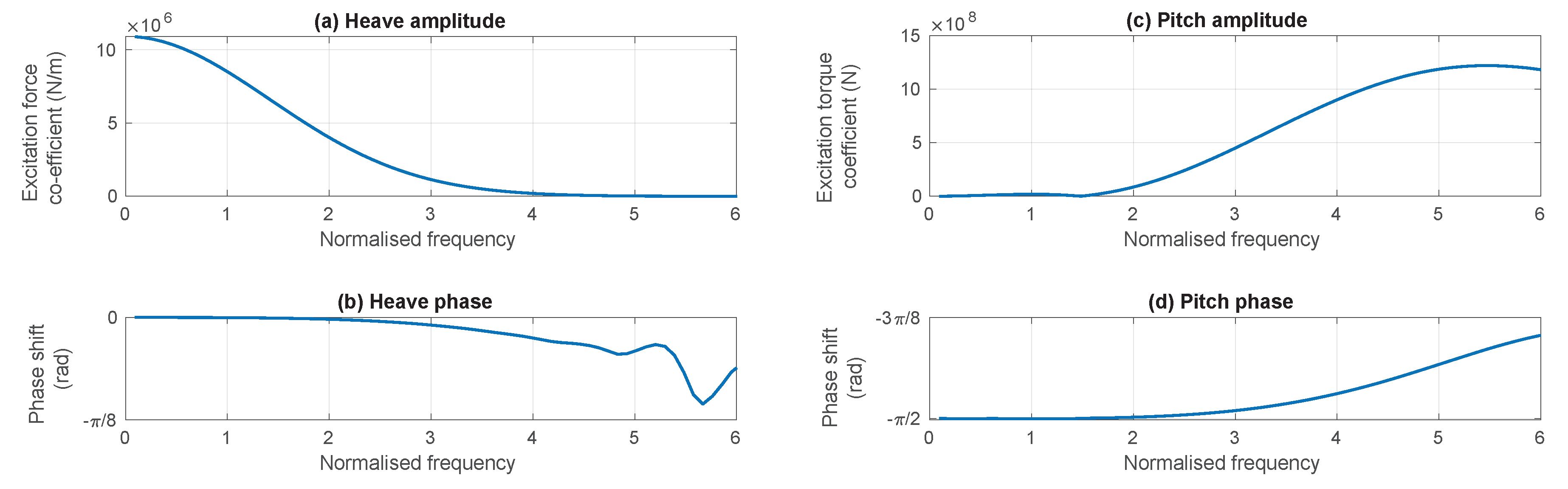
3.3.4. Wave Excitation
3.3.5. Model Parameters
3.4. Simulation Details and the Implementation of an Early Warning Detection System
3.4.1. Simulation Details
3.4.2. Recursive Least Squares Implementation
3.4.3. Detection Syste Implementation
4. Results
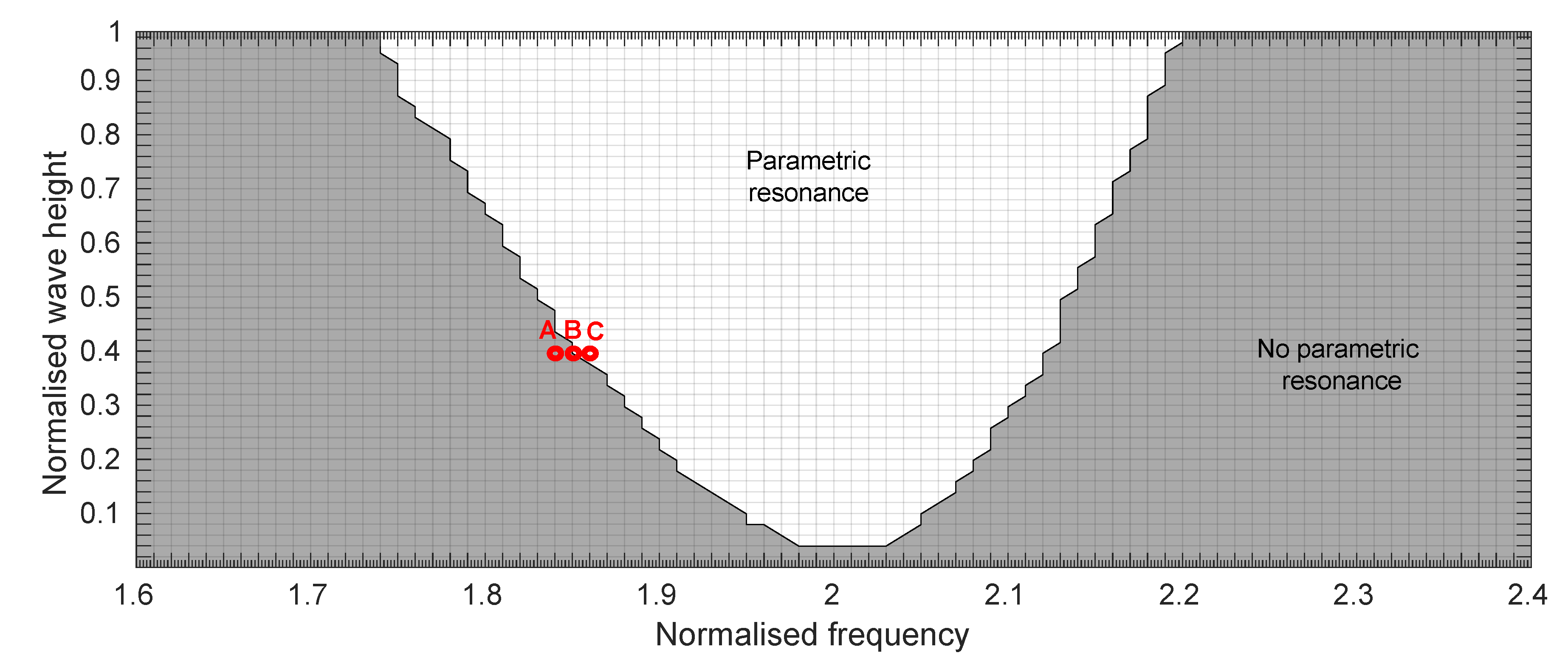
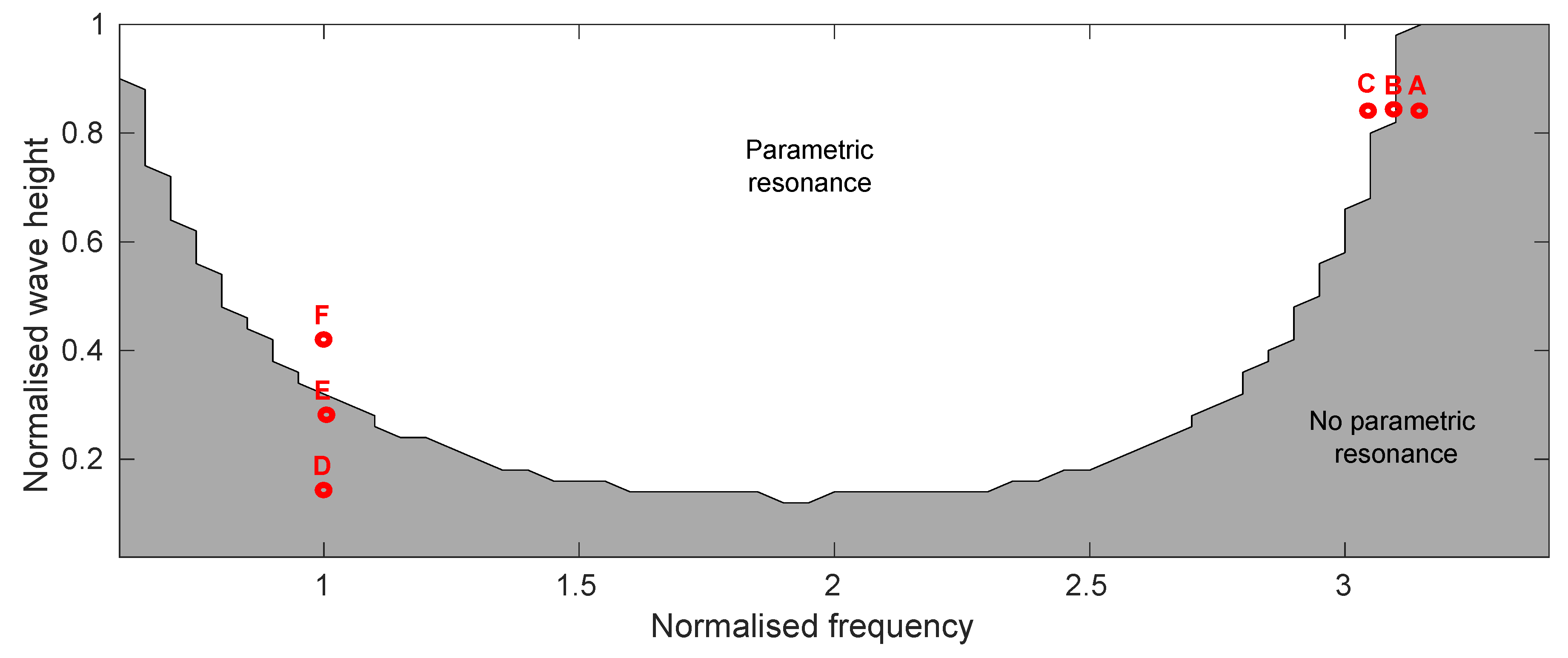
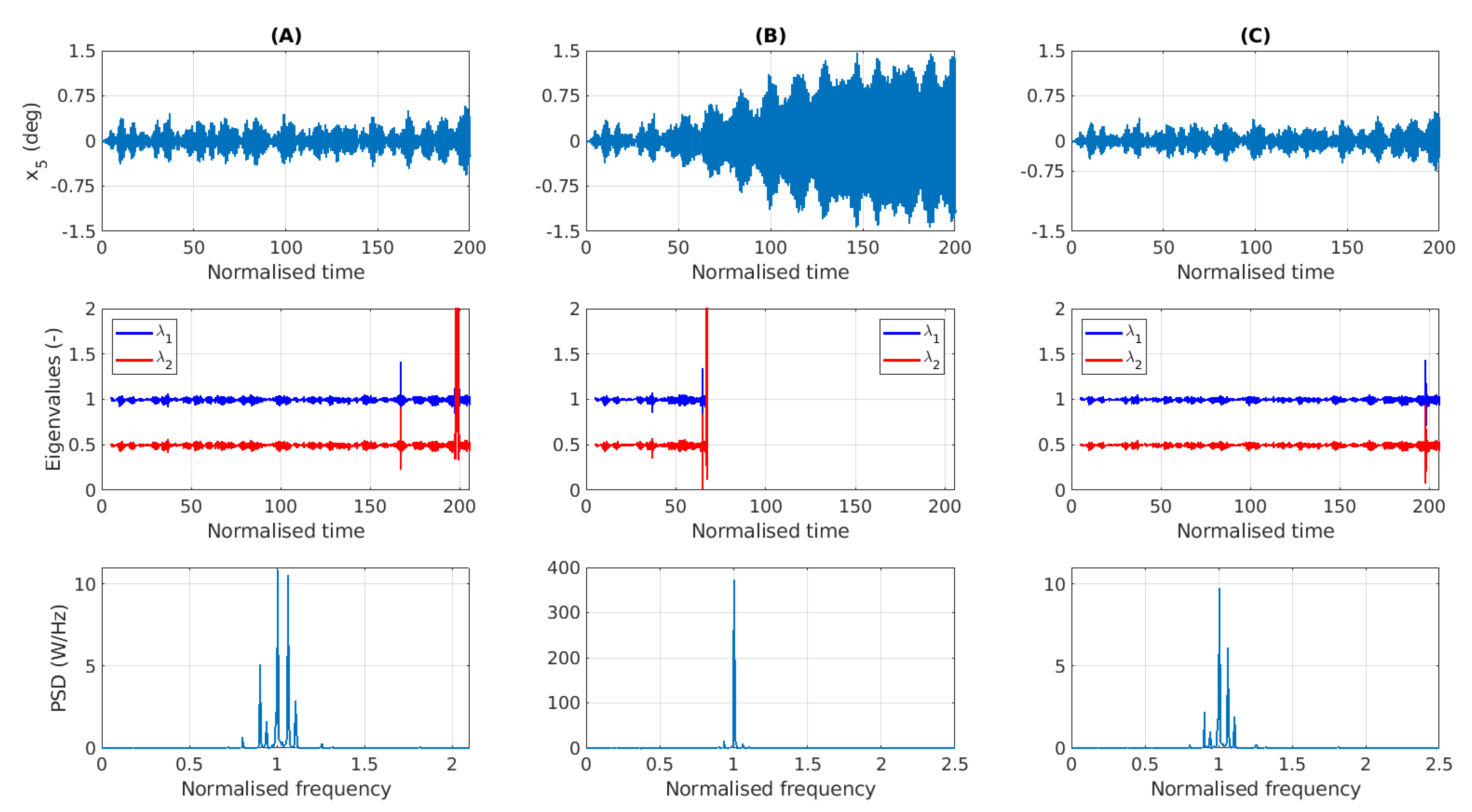
4.1. Monochromatic Waves
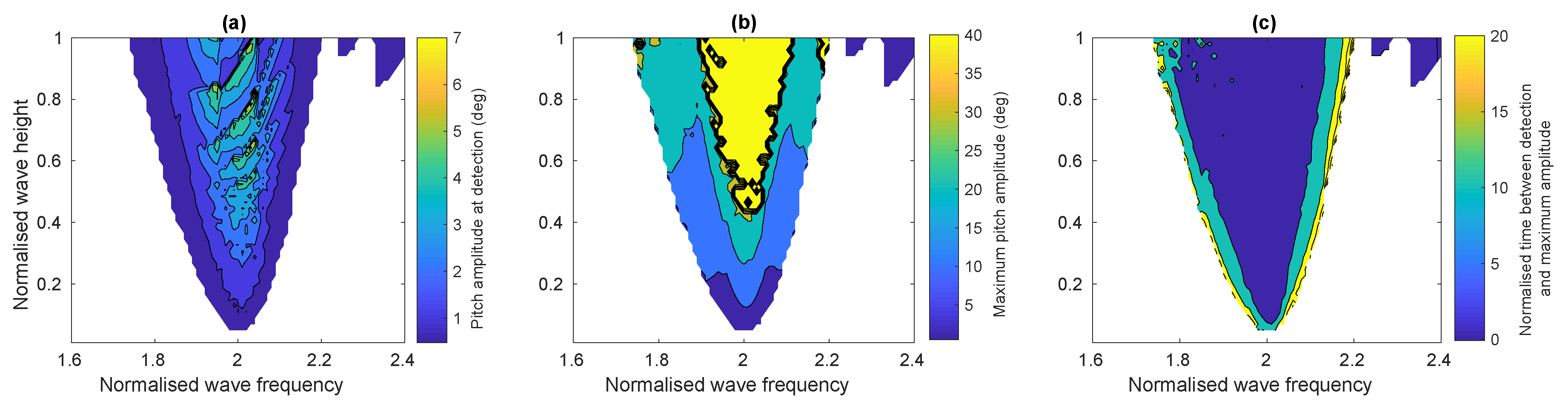
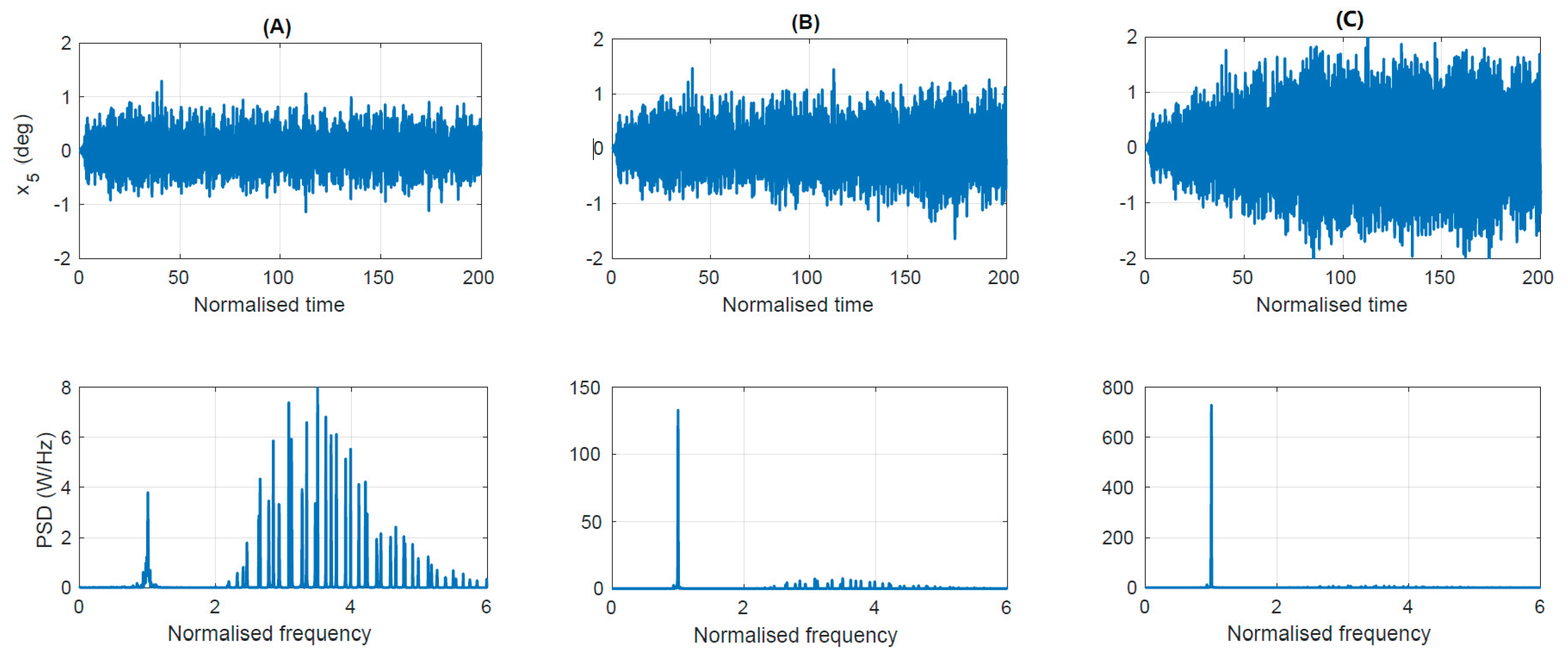
4.1.1. Post Process Identification of Parametric Resonance
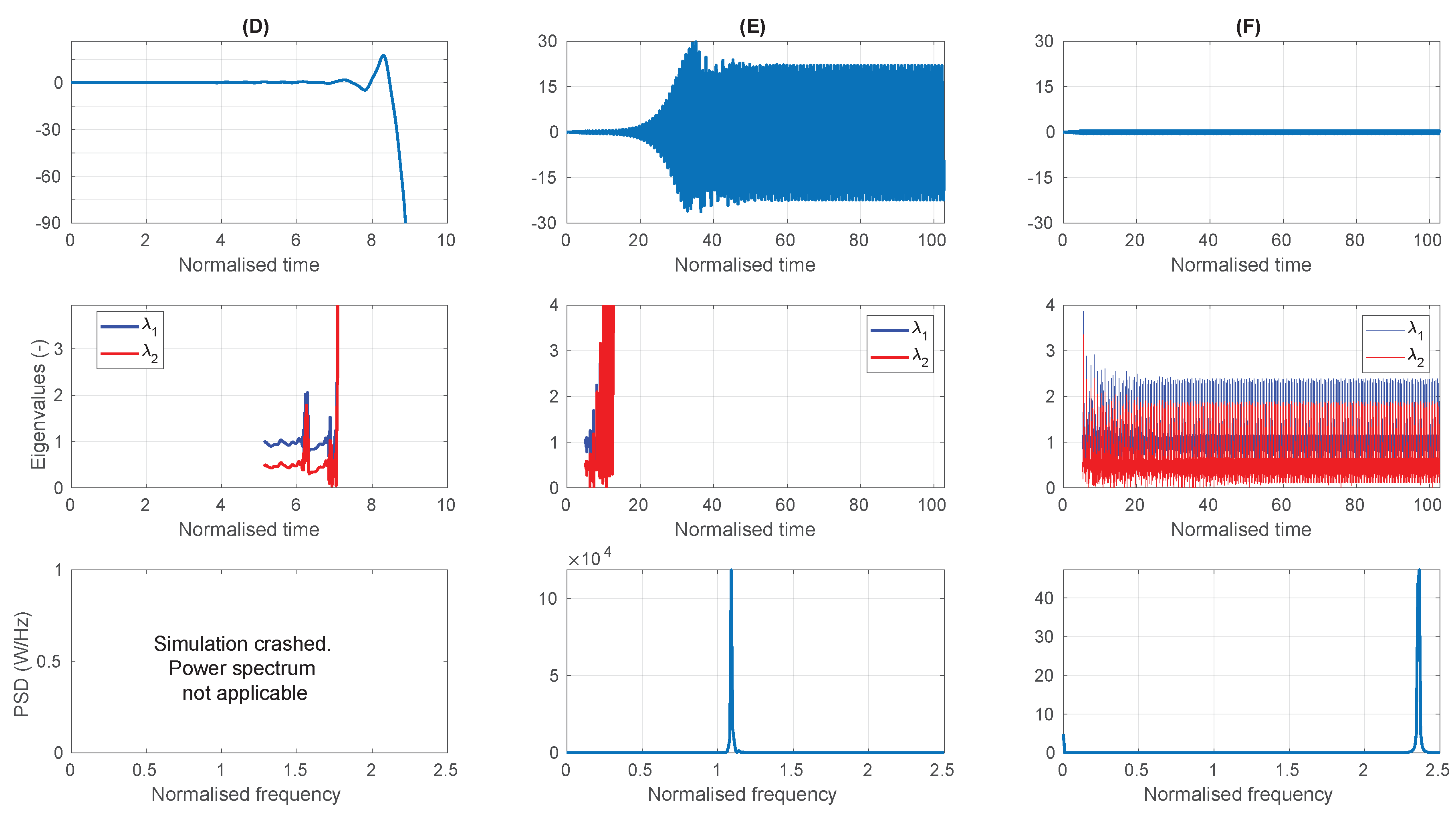
4.1.2. Performance of the Early Warning Detection System
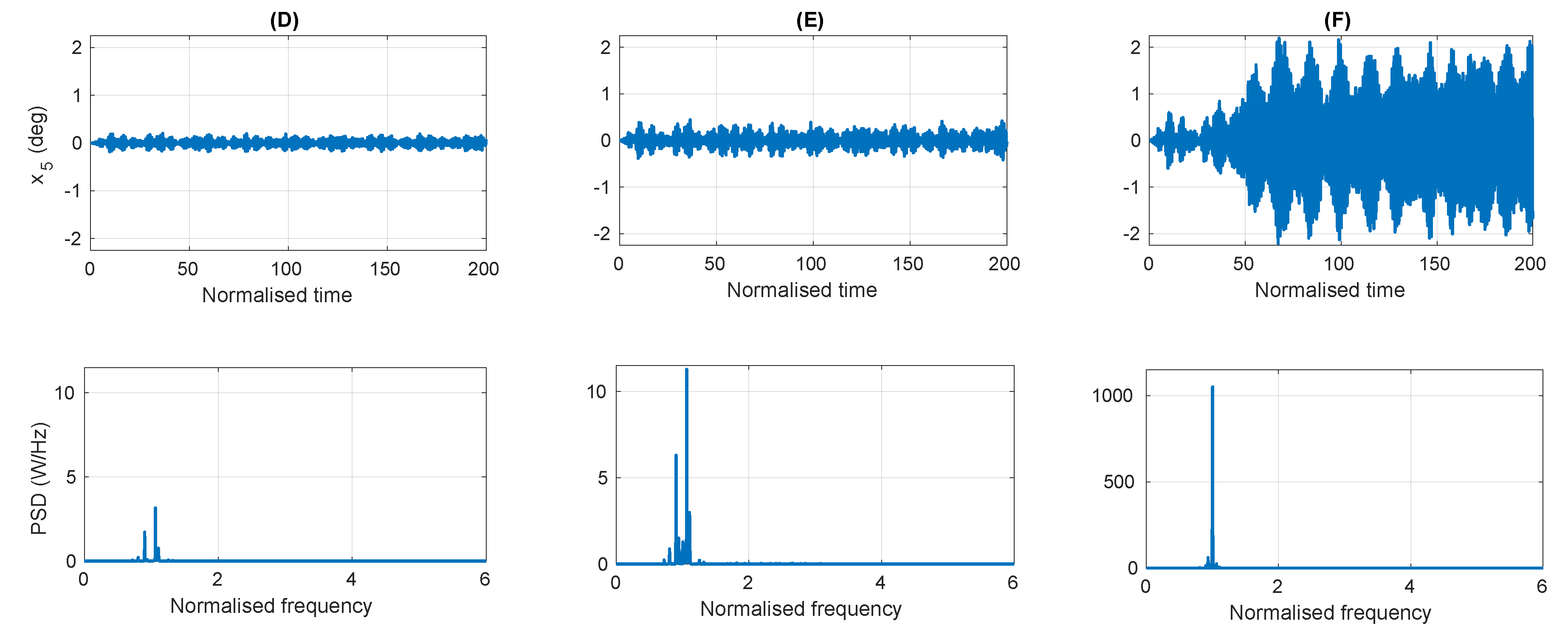
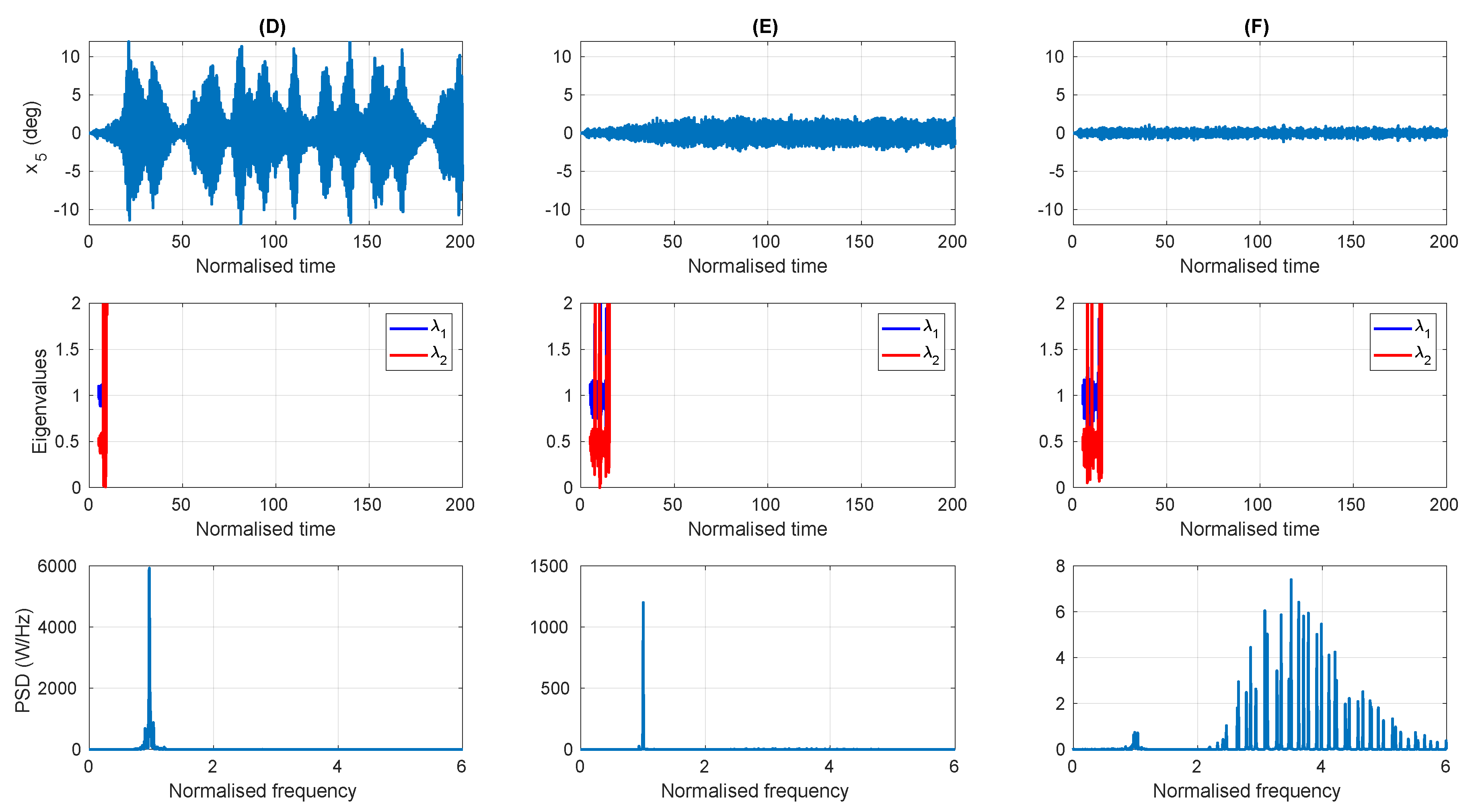
4.2. Polychromatic
4.2.1. Post Process Identification of Parametric Resonance
4.2.2. Performance of the Early Warning Detection System
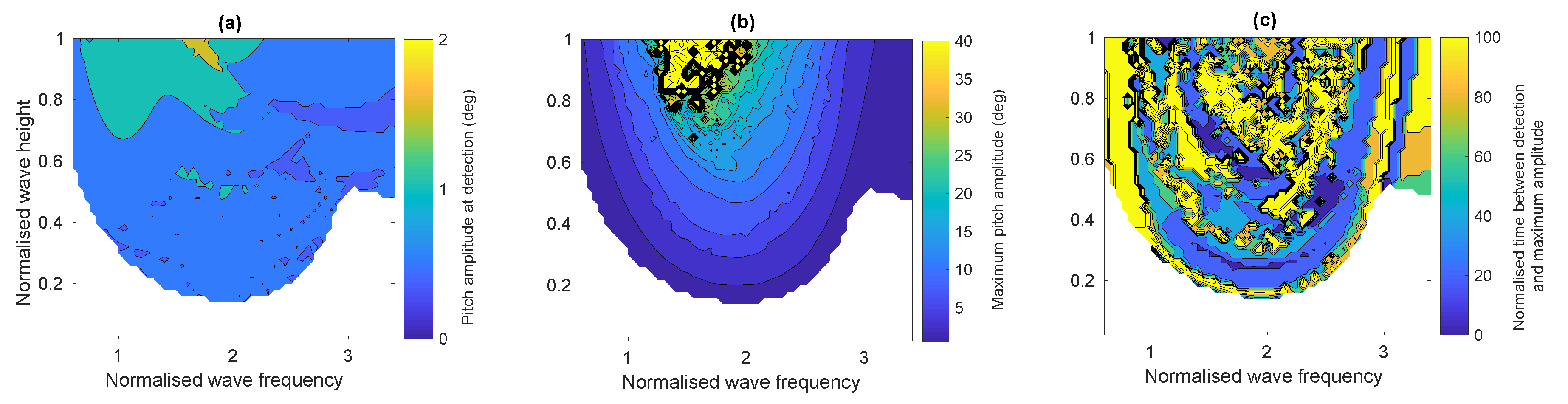
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fossen, T.; Nijmeijer, H. Parametric Resonance in Dynamical Systems; Springer: New York, NY, USA, 2011. [Google Scholar]
- Faraday, M. On a peculiar class of acoustical figures; and on certain forms assumed by groups of particles upon vibrating elastic surfaces. In Philosophical Transactions of the Royal Society of London; The Royal Society: London, UK, 1831; pp. 299–340. [Google Scholar]
- Froude, W. On the Rolling of Ships; Institution of Naval Architects: London, UK, 1861. [Google Scholar]
- Galeazzi, R. Autonomous Supervision and Control of Parametric Roll Resonance. Ph.D. Thesis, Department of Naval Architecture and Offshore Engineering, Technical University of Denmark, Lyngby, Denmark, 2009. [Google Scholar]
- Shigunov, V.; El Moctar, O.; Rathje, H.; Germanischer Lloyd, A. Conditions of parametric rolling. In Proceedings of the 10th International Conference on Stability of Ships and Ocean Vehicles, St Petersberg, Russia, 22–26 June 2009. [Google Scholar]
- Koo, B.; Kim, M.; Randall, R. Mathieu instability of a spar platform with mooring and risers. Ocean Eng. 2004, 31, 2175–2208. [Google Scholar] [CrossRef]
- Neves, M.A.; Sphaier, S.H.; Mattoso, B.M.; Rodri´ guez, C.A.; Santos, A.L.; Vileti, V.L.; Torres, F.G. On the occurrence of Mathieu instabilities of vertical cylinders. In Proceedings of the 27th International Conference on Offshore Mechanics and Arctic Engineering, Estorill, Portugal, 15–20 June 2008. [Google Scholar]
- Li, B.B.; Ou, J.P.; Teng, B. Numerical investigation of damping effects on coupled heave and pitch motion of an innovative deep draft multi-spar. J. Mar. Sci. Technol. 2011, 19, 231–244. [Google Scholar]
- Yang, H.; Xu, P. Effect of hull geometry on parametric resonances of spar in irregular waves. Ocean Eng. 2015, 99, 14–22. [Google Scholar] [CrossRef]
- Jang, H.; Kim, M. Mathieu instability of Arctic Spar by nonlinear time-domain simulations. Ocean Eng. 2019, 176, 31–45. [Google Scholar] [CrossRef]
- Umeda, N.; Hashimoto, H.; Minegaki, S.; Matsuda, A. An investigation of different methods for the prevention of parametric rolling. J. Mar. Sci. Technol. 2008, 13, 16–23. [Google Scholar] [CrossRef]
- Galeazzi, R.; Pettersen, K.Y. Parametric Resonance in Dynamical Systems; Chapter Controlling Parametric Resonance: Induction and Stabilization of Unstable Motions; Fossen, T.I., Nijmeijer, H., Eds.; Springer: New York, NY, USA, 2012; pp. 305–327. [Google Scholar]
- Bracewell, R.H. Frog and PS Frog: A Study of Two Reactionless Ocean Wave Energy Converters. Ph.D. Thesis, University of Lancaster, Lancashire, UK, 1990. [Google Scholar]
- Durand, M.; Babarit, A.; Pettinotti, B.; Quillard, O.; Toularastel, J.; Clément, A. Experimental validation of the performances of the SEAREV wave energy converter with real time latching control. In Proceedings of the 7th European Wave and Tidal Energy Conference, Porto, Portugal, 11–13 September 2007. [Google Scholar]
- Payne, G.S.; Taylor, J.R.; Bruce, T.; Parkin, P. Assessment of boundary-element method for modelling a free-floating sloped wave energy device. Part 2: Experimental validation. Ocean Eng. 2008, 35, 342–357. [Google Scholar] [CrossRef] [Green Version]
- Raftery, M.W. Harnessing Ocean Surface Wave Energy to Generate Electricity. Master’s Thesis, Stevens Institute of Technology, Hoboken, NJ, USA, 2008. [Google Scholar]
- Sheng, W.; Flannery, B.; Lewis, A.; Alcorn, R. Experimental studies of a floating cylindrical OWC WEC. In Proceedings of the 31st International Conference on Ocean, Offshore and Arctic Engineering, Rio de Janeiro, Brazil, 1–6 July 2012. [Google Scholar]
- Gomes, R.; Henriques, J.; Gato, L.; Falcao, A. Testing of a small-scale floating OWC model in a wave flume. In Proceedings of the 4th International Conference on Ocean Energy, Dublin, Ireland, 17–19 October 2012. [Google Scholar]
- Gomes, R.; Henriques, J.; Gato, L.; Falcão, A.d.O. Wave channel tests of a slack-moored floating oscillating water column in regular waves. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015. [Google Scholar]
- Beatty, S.J.; Roy, A.; Bubbar, K.; Ortiz, J.; Buckham, B.J.; Wild, P.; Stienke, D.; Nicoll, R. Experimental and numerical simulations of moored self-reacting point absorber wave energy converters. In Proceedings of the 25th International Ocean and Polar Engineering Conference, Kona, HI, USA, 25–30 June 2015. [Google Scholar]
- Orszaghova, J.; Wolgamot, H.; Taylor, R.E.; Draper, S.; Rafiee, A.; Taylor, P. Simplified dynamics of a moored submerged buoy. In Proceedings of the 32nd International Workshop on Water Waves and Floating Bodies, Dalian, China, 23–26 April 2017. [Google Scholar]
- Sergiienko, N.Y. Three-Tether Wave Energy Converter: Hydrodynamic Modelling, Performance Assessment and Control. Ph.D. Thesis, University Adelaide, Adelaide, Australia, 2018. [Google Scholar]
- Gomes, R.; Henriques, J.; Gato, L.; Falcão, A. Experimental Tests of a 1: 16th-Scale Model of the Spar-Buoy OWC in a Large Scale Wave Flume in Regular Waves. In Proceedings of the 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018. [Google Scholar]
- Kurniawan, A.; Grassow, M.; Ferri, F. Numerical modelling and wave tank testing of a self-reacting two-body wave energy device. Ships Offshore Struct. 2019, 14, 344–356. [Google Scholar] [CrossRef]
- Orszaghova, J.; Wolgamot, H.; Draper, S.; Eatock Taylor, R.; Taylor, P.; Rafiee, A. Transverse motion instability of a submerged moored buoy. Proc. R. Soc. A 2019, 475, 20180459. [Google Scholar] [CrossRef] [Green Version]
- Gomes, R.; Henriques, J.; Gato, L.; Falcão, A. Time-domain simulation of a slack-moored floating oscillating water column and validation with physical model tests. Renew. Energy 2020, 149, 165–180. [Google Scholar] [CrossRef]
- Davidson, J.; Costello, R. Efficient Nonlinear Hydrodynamic Models for Wave Energy Converter Design—A Scoping Study. J. Mar. Sci. Eng. 2020, 8, 35. [Google Scholar] [CrossRef] [Green Version]
- Babarit, A.; Mouslim, H.; Clément, A.; Laporte-Weywada, P. On the numerical modelling of the nonlinear behaviour of a wave energy converter. In Proceedings of the 28th International Conference on Offshore Mechanics & Arctic Engineering, Honolulu, HI, USA, 31 May–5 June 2009. [Google Scholar]
- Tarrant, K.R. Numerical Modelling of Parametric Resonance of a Heaving Point Absorber Wave Energy Converter. Ph.D. Thesis, Trinity College Dublin, Dublin, Ireland, 2015. [Google Scholar]
- Tarrant, K.; Meskell, C. Investigation on parametrically excited motions of point absorbers in regular waves. Ocean Eng. 2016, 111, 67–81. [Google Scholar] [CrossRef]
- Giorgi, G.; Ringwood, J.V. A compact 6-DoF nonlinear wave energy device model for power assessment and control investigations. IEEE Trans. Sustain. Energy 2018, 10, 119–126. [Google Scholar] [CrossRef] [Green Version]
- Giorgi, G.; Ringwood, J.V. Articulating Parametric Nonlinearities in Computationally Efficient Hydrodynamic Models. IFAC-PapersOnLine 2018, 51, 56–61. [Google Scholar] [CrossRef]
- Giorgi, G.; Ringwood, J.V. Parametric motion detection for an oscillating water column spar buoy. In Proceedings of the 3rd International Conference on Renewable Energies Offshore, Lisbon, Portugal, 8–10 October 2018. [Google Scholar]
- Giorgi, G.; Gomes, R.P.; Bracco, G.; Mattiazzo, G. The Effect of Mooring Line Parameters in Inducing Parametric Resonance on the Spar-Buoy Oscillating Water Column Wave Energy Converter. J. Mar. Sci. Eng. 2020, 8, 29. [Google Scholar] [CrossRef] [Green Version]
- Zou, S.; Abdelkhalik, O.; Robinett, R.; Korde, U.; Bacelli, G.; Wilson, D.; Coe, R. Model Predictive Control of parametric excited pitch-surge modes in wave energy converters. Int. J. Mar. Energy 2017, 19, 32–46. [Google Scholar] [CrossRef] [Green Version]
- Yerrapragada, K.; Ansari, M.; Karami, M.A. Enhancing power generation of floating wave power generators by utilization of nonlinear roll-pitch coupling. Smart Mater. Struct. 2017, 26, 094003. [Google Scholar] [CrossRef]
- Abdelkhalik, O.; Zou, S. Time-varying linear quadratic gaussian optimal control for three-degree-of-freedom wave energy converters. In Proceedings of the 12th European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–2 September 2017. [Google Scholar]
- Abdelkhalik, O.; Zou, S.; Robinett, R.; Bacelli, G.; Wilson, D.; Coe, R. Control of three degrees-of-freedom wave energy converters using pseudo-spectral methods. J. Dyn. Syst. Meas. Control 2018, 140, 074501. [Google Scholar] [CrossRef]
- Davidson, J.; Karimov, M.; Szelechman, A.; Windt, C.; Ringwood, J. Dynamic mesh motion in OpenFOAM for wave energy converter simulation. In Proceedings of the 14th OpenFOAM Workshop, Duisburg, Germany, 23–26 July 2019. [Google Scholar]
- Zou, S.; Abdelkhalik, O. Time-varying linear quadratic Gaussian optimal control for three-degree-of-freedom wave energy converters. Renew. Energy 2020, 149, 217–225. [Google Scholar] [CrossRef]
- Palm, J.; Bergdahl, L.; Eskilsson, C. Parametric excitation of moored wave energy converters using viscous and non-viscous CFD simulations. In Advances in Renewable Energies Offshore; Taylor & Francis Group: Abingdon, UK, 2019; pp. 455–462. [Google Scholar]
- Nicoll, R.S.; Wood, C.F.; Roy, A.R. Comparison of physical model tests with a time domain simulation model of a wave energy converter. In Proceedings of the 31st International Conference on Ocean, Offshore and Arctic Engineering, Rio de Janeiro, Brazil, 1–6 July 2012. [Google Scholar]
- Orszaghova, J.; Wolgamot, H.; Draper, S.; Taylor, P.H.; Rafiee, A. Onset and limiting amplitude of yaw instability of a submerged three-tethered buoy. Proc. R. Soc. A 2020, 476, 20190762. [Google Scholar] [CrossRef]
- Rho, J.B.; Choi, H.S.; Shin, H.S.; Park, I.K. A study on Mathieu-type instability of conventional spar platform in regular waves. Int. J. Offshore Polar Eng. 2005, 15, 104–108. [Google Scholar]
- Ortiz, J.P. The Influence of Mooring Dynamics on the Performance of Self Reacting Point Absorbers. Master’s Thesis, University of Victoria, Victoria, BC, Canada, 2016. [Google Scholar]
- Gomes, R.; Malvar Ferreira, J.; Ribeiro e Silva, S.; Henriques, J.; Gato, L. An experimental study on the reduction of the dynamic instability in the oscillating water column spar buoy. In Proceedings of the 12th European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–2 September 2017. [Google Scholar]
- Cordonnier, J.; Gorintin, F.; De Cagny, A.; Clément, A.; Babarit, A. SEAREV: Case study of the development of a wave energy converter. Renew. Energy 2015, 80, 40–52. [Google Scholar] [CrossRef]
- Gomes, R.; Henriques, J.; Gato, L.; Falcao, A. An upgraded model for the design of spar-type floating oscillating water column devices. In Proceedings of the 13th European Wave and Tidal Energy Conference, Naples, Italy, 1–6 September 2019. [Google Scholar]
- Villegas, C.; van der Schaaf, H. Implementation of a pitch stability control for a wave energy converter. In Proceedings of the 10th European Wave and Tidal Energy Conference, Southampton, UK, 5–9 September 2011. [Google Scholar]
- Maloney, P. Performance Assessment of a 3-Body Self-Reacting Point Absorber Type Wave Energy Converter. Master’s Thesis, University of Victoria, Victoria, BC, Canada, 2019. [Google Scholar]
- Holden, C.; Perez, T.; Fossen, T.I. Frequency-motivated observer design for the prediction of parametric roll resonance. IFAC Proc. Vol. 2007, 40, 57–62. [Google Scholar] [CrossRef]
- Shaw McCue, L.; Bulian, G. A numerical feasibility study of a parametric roll advance warning system. J. Offshore Mech. Arct. Eng. 2007, 129. [Google Scholar] [CrossRef]
- Galeazzi, R.; Blanke, M.; Poulsen, N.K. Parametric roll resonance detection on ships from nonlinear energy flow indicator. IFAC Proc. Vol. 2009, 42, 348–353. [Google Scholar] [CrossRef]
- Galeazzi, R.; Blanke, M.; Poulsen, N.K. Early detection of parametric roll resonance on container ships. IEEE Trans. Control Syst. Technol. 2012, 21, 489–503. [Google Scholar] [CrossRef] [Green Version]
- Galeazzi, R.; Blanke, M.; Falkenberg, T.; Poulsen, N.K.; Violaris, N.; Storhaug, G.; Huss, M. Parametric roll resonance monitoring using signal-based detection. Ocean Eng. 2015, 109, 355–371. [Google Scholar] [CrossRef] [Green Version]
- Caamaño, L.S.; González, M.M.; Casás, V.D. On the feasibility of a real time stability assessment for fishing vessels. Ocean Eng. 2018, 159, 76–87. [Google Scholar] [CrossRef]
- Caamaño, L.S.; Galeazzi, R.; Nielsen, U.D.; González, M.M.; Casás, V.D. Real-time detection of transverse stability changes in fishing vessels. Ocean Eng. 2019, 189, 106369. [Google Scholar] [CrossRef]
- Davidson, J.; Genest, R.; Ringwood, J. Adaptive control of a wave energy converter simulated in a numerical wave tank. In Proceedings of the 12th European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–2 September 2017. [Google Scholar]
- Genest, R.; Davidson, J.; Ringwood, J.V. Adaptive control of a wave energy converter. IEEE Trans. Sustain. Energy 2018, 9, 1588–1595. [Google Scholar]
- Peña-Sanchez, Y.; Windt, C.; Davidson, J.; Ringwood, J.V. A Critical Comparison of Excitation Force Estimators for Wave-Energy Devices. IEEE Trans. Control. Syst. Technol. 2019. [Google Scholar] [CrossRef]
- Thompson, J.M.T.; Stewart, H.B. Nonlinear Dynamics and Chaos; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Yong-Pyo, H.; Dong-Yeon, L.; Yong-Ho, C.; Sam-Kwon, H.; Se-Eun, K. An experimental study on the extreme motion responses of a spar platform in the heave resonant waves. In Proceedings of the 15th International Offshore and Polar Engineering Conference, Seol, Korea, 19–24 June 2005. [Google Scholar]
- Zhao, J.; Tang, Y.; Shen, W. A study on the combination resonance response of a classic spar platform. J. Vib. Control 2010, 16, 2083–2107. [Google Scholar] [CrossRef]
- Gavassoni, E.; Gonçalves, P.B.; Roehl, D.M. Nonlinear vibration modes and instability of a conceptual model of a spar platform. Nonlinear Dyn. 2014, 76, 809–826. [Google Scholar] [CrossRef]
- Giorgi, G.; Davidson, J.; Habib, G.; Bracco, G.; Mattiazzo, G.; Kalmar-Nagy, T. Nonlinear Dynamic and Kinematic Model of a Spar-Buoy: Parametric Resonance and Yaw Numerical Instability. Mar. Sci. Eng. 2020, 8, 504. [Google Scholar] [CrossRef]
- Wacher, A.; Nielsen, K. Mathematical and numerical modeling of the AquaBuOY wave energy converter. Math. Case Stud. 2010, 2, 16–33. [Google Scholar]
| 1. | Note: to limit the scale, the maximum amplitude is clipped at 40°, since for any simulation in which the amplitude exceeded this value, the pitch displacement grew to 90° and the simulation was terminated. |


| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| 1087 m2 | 1000 kg/m3 | M | 2.15 × 108 kg | ||
| 198.1 m | g | 9.81 m/s2 | kg | ||
| 10.1 m | kg/s | kgm | |||
| 109.1 m | kgm/s | kg |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Davidson, J.; Kalmár-Nagy, T. A Real-Time Detection System for the Onset of Parametric Resonance in Wave Energy Converters. J. Mar. Sci. Eng. 2020, 8, 819. https://doi.org/10.3390/jmse8100819
Davidson J, Kalmár-Nagy T. A Real-Time Detection System for the Onset of Parametric Resonance in Wave Energy Converters. Journal of Marine Science and Engineering. 2020; 8(10):819. https://doi.org/10.3390/jmse8100819
Chicago/Turabian StyleDavidson, Josh, and Tamás Kalmár-Nagy. 2020. "A Real-Time Detection System for the Onset of Parametric Resonance in Wave Energy Converters" Journal of Marine Science and Engineering 8, no. 10: 819. https://doi.org/10.3390/jmse8100819
APA StyleDavidson, J., & Kalmár-Nagy, T. (2020). A Real-Time Detection System for the Onset of Parametric Resonance in Wave Energy Converters. Journal of Marine Science and Engineering, 8(10), 819. https://doi.org/10.3390/jmse8100819





