An Improved Sub-Array Adaptive Beamforming Technique Based on Multiple Sources of Errors

Abstract

In this paper, a new robust adaptive beamforming method is proposed in order to improve the robustness against steering vector (SV) mismatches that arise from multiple types of array errors. First, the sub-array technique is applied in order to obtain the decoupled sample covariance matrix (DSCM), in which the auxiliary sensors are selected to decouple the array. The decoupled interference-plus-noise covariance matrix (DINCM) is reconstructed with the estimated interference SV and maximum eigenvalue of the DSCM. Furthermore, the desired signal SV is estimated as the corresponding eigenvector determined by the correlation coefficients of the assumed SV and eigenvectors. Finally, the optimal weighting vector is obtained by combining the reconstructed DINCM and the estimated desired signal SV. Our simulation results show significant signal-to-interference-plus-noise ratio (SINR) enhancement of the proposed method over existing methods under multiple types of array errors.

1. Introduction

Adaptive beamforming has gained attention as an effective technique in array signal processing, due to its good target detection performance [1,2]. A Capon beamformer ensures the minimum output power under the premise of distortion-free reception from the desired signal direction, which is essentially equivalent to a minimum variance distortionless response (MVDR) beamformer [3,4], which is an optimal spatial filter, since it maximizes the output signal-to-interference-plus-noise ratio (SINR).

Although standard Capon beamformer is the theoretical optimal beamformer and has been widely applied for its good interference suppression ability, its performance drops sharply when there are mismatches between the assumed and real array model [5] due to various practical factors, such as inaccurate sensor positions [1], inconsistency of channels [6,7], and mutual coupling of antennas [8,9]. The above problems that are faced by the Capon beamformer are mainly divided into two categories: the mismatch of the desired steering vector (SV) and the involvment of the desired signal in the sample covariance matrix (SCM). The existence of the desired signal in the received snapshots significantly degraded the performance of the Capon beamformer, since the desired signal may be regarded as a interfernece and gets self-nulled [2]. The mismatch of the desired SV fails to steering the mainlobe towards the desired signal and, therefore, distorts the desired signal.

Numerous methods have been proposed to improve the robustness of Capon beamforming. Aside from the advantages of the robustness of the beamformer, the drawbacks of these algorithms are also obvious. The diagonal loading algorithm increases the robustness of the beamformer by adding a diagonal matrix on the sample covariance matrix in order to increase the noise power [10,11]. However, it is difficult to choose the appropriate diagonal loading factor. The eigenspace algorithm requires the specific number of interferences and it is able to provide satisfactory performance at some situations, but it is ineffective under low signal-to-noise ratio (SNR) conditions, since the desired signal subpace is swapped with the noise subpace [12,13,14]. The use of uncertainty set (US) algorithm is limited, as the size of the uncertain set is hard to determine and the desired signal is still involved in the SCM [15,16,17,18,19,20,21,22,23,24]. Interference-plus-noise covariance matrix (INCM) reconstruction-based algorithms have been shown to obtain excellent beamforming performance when the array manifold is accurately known [25,26,27], but they are not suitable for situations where an array of manifold mismatches exist [28].

The mutual coupling effect destorys the array structure in the SV and, therefore, affects the traditional methods. Ye et al. proposed a method where the mutual coupling effect could be mitigated by selecting middle array elements [9], but the presence of desired signal degrades its performance at high SNRs. Recently, the researchers combined the middle subarray technique and covariance matrix reconstruction technique in order to obtain the interfernce-noise covariance matrix in [29]. However, it should be noted that the method is based on the accurately known array structure, which is to say, the method is ineffective in the presence of other kinds of array errors, like sensor position errors and the gain-phase errors, since the real array structure is unavailable. In this paper, we improve the previous method in order to overcome the performance degradation tht arises from multiple types of array errors. Specifically, in terms of modification, our contributions are as follows.

• The characteristics of three different array error types and their influence on the recieved data are analyzed, a generalized signal model under the three kinds of errors is given.
• The middle array interference-plus-noise covariance matrix (INCM) is accurately reconstructed with estimated interference SV and power, which not only handles the problem of multiple types of array errors, but also mitigates the effect of the desired signal in the sample snapshots. The interference SVs are correctly estimated using the robust Capon beamforming (RCB) principle, as the SV mismatches that are due to the sensor position and gain-phase errors are relatively small. Furthermore, the estimated interference SVs are combined with the maximum eigenvalue of the decoupled sample covariance matrix (DSCM).
• The desired signal SV is estimated as the corresponding eigenvector of DSCM through the correlated projection process. The correlation coefficient of the SV and eigenvectors reaches the maximum when the eigenvector matches the SV.

The weighting vector is finally derived when combining the reconstructed middle array INCM and estimated desired signal SV. The proposed method is able to deal with multiple types of array errors and obtain superior SINR improvement. Throughout this paper, the superscripts T and H represent transpose and conjugate transpose, respectively. The notation $\mathrm{E}\left[·\right]$ denotes the expectation operator and $\mathit{I}$ stands for the unit matrix. ⊙ is the Hadamard product. ${\left[·\right]}^{-1}$ represents the matrix inversion operator.

2. Problem Formulation

2.1. Array Signal Model

Consider that there are $M+1$ narrowband signals ${\left\{s_m\left(k\right)\right\}}_{m=0}^M$ that impinge on the uniform linear array (ULA) of N array elements and they are uncorrelated with each other. That is to say,

$$\mathrm{E}\left[s_i{s}_j^H\right]=0,i\ne j$$

(1)

Assume that these signals arrive at the array with directions-of-arrivals (DOAs) ${\left\{{\theta }_m\right\}}_{m=0}^M$ and power ${\left\{{\sigma }_m^2\right\}}_{m=0}^M$. Let $s_0\left(k\right)$ represent the desired signal and the ${\left\{s_m\left(k\right)\right\}}_{m=1}^M$ are the interferences that are radiated by the farfield jammer devices. The received data in the k-th snapshot can be expressed as    

$$\mathit{x}\left(k\right)=\mathit{A}\mathit{S}\left(k\right)+\mathit{n}\left(k\right)=s_0\left(k\right)\mathit{a}\left({\theta }_0\right)+\sum _{m=1}^M{s}_m\left(k\right)\mathit{a}\left({\theta }_m\right)+\mathit{n}\left(k\right),$$

(2)

where $\mathit{S}\left(k\right)={[s_0\left(k\right),s_1\left(k\right),\dots ,s_M\left(k\right)]}^T$ denotes the echo signal vector and $\mathit{n}\left(k\right)$ is an $N\times 1$ additive white Gaussian noise vector with power ${\sigma }_n^2$. The noise component is normal white Gaussian in the receiving channels, its model is assumed to be the same with traditional beamforming methods, since we mainly focus on the array errors in this paper. Further, $\mathit{A}=[\mathit{a}\left({\theta }_0\right),\mathit{a}\left({\theta }_1\right),\dots ,\mathit{a}\left({\theta }_M\right)]$ stands for the steering matrix of the array, in which the m-th element is specifically given by $\mathit{a}\left({\theta }_m\right)={[1,b\left({\theta }_m\right),\dots ,b{\left({\theta }_m\right)}^{N-1}]}^T$, where $b\left({\theta }_m\right)=$$exp(j2\pi dsin{\theta }_m/\lambda )$, $\lambda$ is the signal wavelength and d is the inter-element spacing. The $N\times 1$ weighting vector of the well-known Capon beamformer is given as:

$$\mathit{w}=\frac{{\mathit{R}}_{I+n}^{-1}\mathit{a}\left({\theta }_1\right)}{{\mathit{a}}^H\left({\theta }_1\right){\mathit{R}}_{I+n}^{-1}\mathit{a}\left({\theta }_1\right)},$$

(3)

where ${\mathit{R}}_{I+n}={\sum }_{m=1}^M{\sigma }_m^2\mathit{a}\left({\theta }_m\right){\mathit{a}}^H\left({\theta }_m\right)+{\sigma }_n^2{\mathit{I}}_N$ is the INCM. In practice, the exact ${\mathit{R}}_{I+n}$ is usually replaced by the sample covariance matrix (SCM), as ${\widehat{\mathit{R}}}_x\triangleq \left(1/K\right){\sum }_{k=1}^K\mathit{x}\left(k\right){\mathit{x}}^H\left(k\right)$, with K being the number of snapshots.

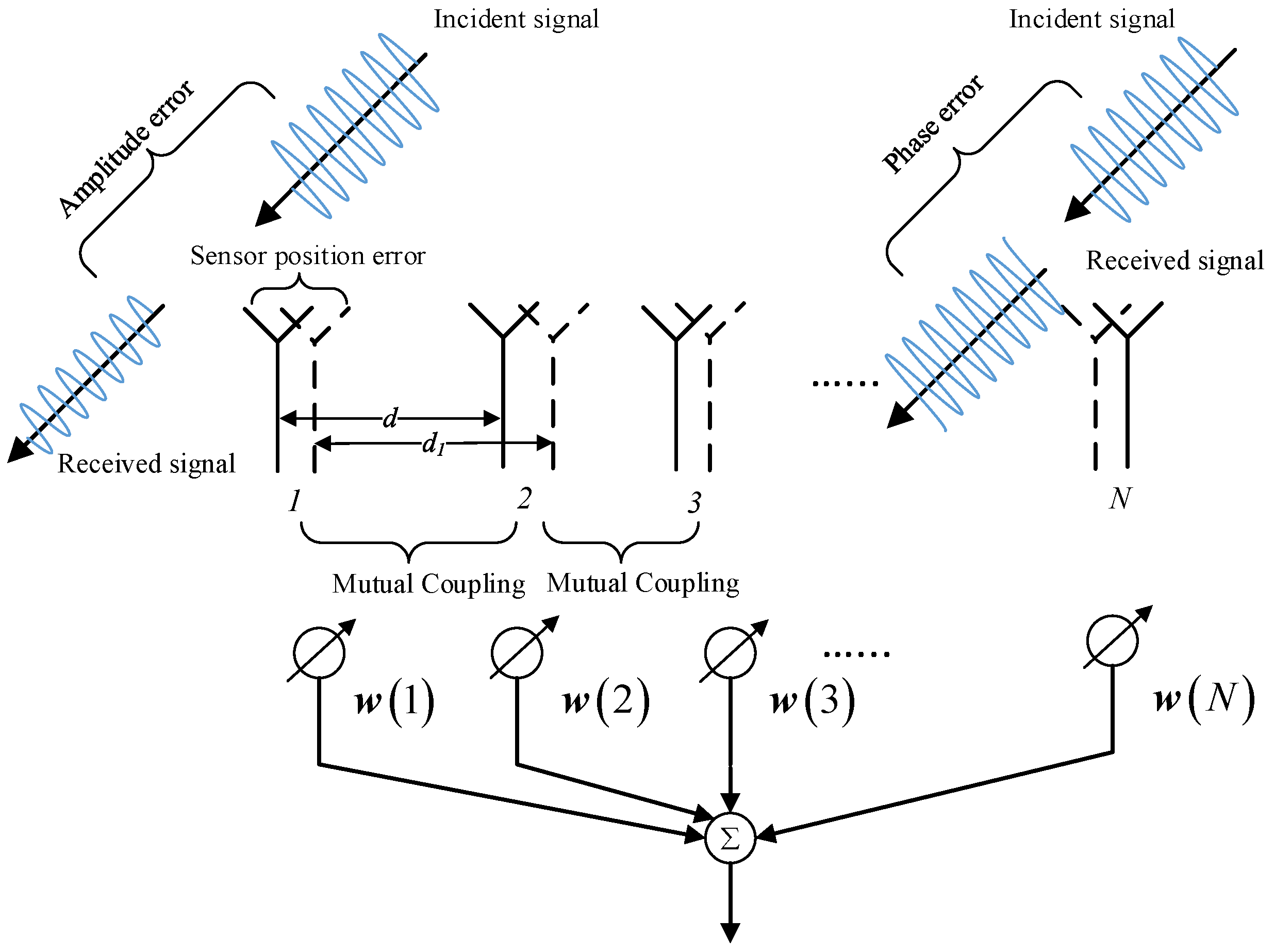
2.2. Array Error Model Analysis

In practice, array model errors essentially result in the mismatch of SV and they degrade the performance of traditional array signal processing algorithms, as shown in Figure 1. Under array errors, the ideal signal model Equation (2) is re-expressed as

$$\begin{array}{cc}\hfill \tilde{\mathit{x}}\left(k\right)=& \tilde{\mathit{A}}\mathit{S}\left(k\right)+\mathit{n}\left(k\right)\hfill \\ \hfill =& s_0\left(k\right)\tilde{\mathit{a}}\left({\theta }_0\right)+\sum _{m=1}^M{s}_m\left(k\right)\tilde{\mathit{a}}\left({\theta }_m\right)+\mathit{n}\left(k\right)\hfill \end{array}$$

(4)

where $\tilde{\mathit{A}}\triangleq f\left(\mathit{A},\mathsf{\Xi }\right)$ is the actual steering matrix and $\mathsf{\Xi }$ is the matrix that identifies the array error. The new array structure is with the steering matrix $\tilde{\mathit{A}}$ containing its array characteristics. In this section, the influences of three array error types are analyzed.

2.2.1. Mutual Coupling

Mutual coupling is an electromagnetic feature, where each sensor interacts with its neighbouring elements [8,9]. Let us define the mutual coupling length as P; that is, when considering the i-th element of the array, it couples with the $(i-P+1)$th, …, $(i-1)$th, $(i+1)$th, …, $(i+P-1)$th elements. The mutual coupling effect of the array can be expressed as a $M\times M$ symmetric Toeplitz matrix, as

$${\mathsf{\Xi }}_{MC}={\left[\begin{array}{cccccc}1& c_1& \cdots & c_{P-1}& \cdots & 0\\ c_1& 1& c_1& \cdots & \ddots & 0\\ ⋮& c_1& 1& \ddots & \cdots & c_{P-1}\\ c_{P-1}& \cdots & \ddots & \ddots & c_1& ⋮\\ 0& \ddots & \cdots & c_1& 1& c_1\\ 0& \cdots & c_{P-1}& \cdots & c_1& 1\end{array}\right]}_{N\times N}$$

(5)

where $c_p$ is the mutual coupling coefficient between the i-th and $(i\pm p)$th sensor. When the mutual coupling effect exists in the receiving array, Equation (4) is actually written as

$$\begin{array}{cc}\hfill \tilde{\mathit{x}}\left(k\right)=& \tilde{\mathit{A}}\mathit{S}\left(k\right)+\mathit{n}\left(k\right)\hfill \\ \hfill =& s_0\left(k\right)\tilde{\mathit{a}}\left({\theta }_0\right)+\sum _{m=1}^M{s}_m\left(k\right)\tilde{\mathit{a}}\left({\theta }_m\right)+\mathit{n}\left(k\right)\hfill \\ \hfill =& s_0\left(k\right)·\left({\mathsf{\Xi }}_{MC}·\mathit{a}\left({\theta }_0\right)\right)+\sum _{m=0}^M{s}_m\left(k\right)·\left({\mathsf{\Xi }}_{MC}·\mathit{a}\left({\theta }_m\right)\right)+\mathit{n}\left(k\right)\hfill \end{array}$$

(6)

2.2.2. Sensor Position Error

Realistic phenomena [1], such as sensor installation errors, measurement errors, and the instability of the antenna platform, inevitably induce sensor position errors. In general, the array element position error can be expressed, in matrix form, as 

$${\mathsf{\Xi }}_{SP}=[\Delta {\mathit{a}}^{\left\{1\right\}},\Delta {\mathit{a}}^{\left\{2\right\}},\dots ,\Delta {\mathit{a}}^{\left\{M\right\}}]=\left[\begin{array}{cccc}\Delta a_1^{\left\{1\right\}}& \Delta a_2^{\left\{1\right\}}& \cdots & \Delta a_M^{\left\{1\right\}}\\ \Delta a_1^{\left\{2\right\}}& \Delta a_2^{\left\{2\right\}}& \cdots & \Delta a_M^{\left\{2\right\}}\\ ⋮& ⋮& ⋮& ⋮\\ \Delta a_1^{\left\{N\right\}}& \Delta a_2^{\left\{N\right\}}& \cdots & \Delta a_M^{\left\{N\right\}}\end{array}\right]$$

(7)

where $\Delta {\mathit{a}}^{\left\{m\right\}}={[\Delta a_m^{\left\{1\right\}},\Delta a_m^{\left\{2\right\}},\dots ,\Delta a_m^{\left\{N\right\}}]}^T$ stands for the array mismatch vector for the signal from direction ${\theta }_m$. Specifically, its n-th element can be expressed as $\Delta a_m^{\left\{n\right\}}=$$exp(j2\pi sin{\theta }_m\Delta d_n/\lambda )$, where $\Delta d_n={\sum }_{i=0}^{n-1}{d}_i-(n-1)d$, with $d_0$ set to 0 and where $d_i$ represents the real spacing between the i-th sensor and the $(i+1)$th sensor. When the sensor position errors exist in the receiving array, Equation (4) is actually written as

$$\begin{array}{cc}\hfill \tilde{\mathit{x}}\left(k\right)=& \tilde{\mathit{A}}\mathit{S}\left(k\right)+\mathit{n}\left(k\right)\hfill \\ \hfill =& s_0\left(k\right)\tilde{\mathit{a}}\left({\theta }_0\right)+\sum _{m=1}^M{s}_m\left(k\right)\tilde{\mathit{a}}\left({\theta }_m\right)+\mathit{n}\left(k\right)\hfill \\ \hfill =& s_0\left(k\right)·\left(\Delta {\mathit{a}}^{\left\{0\right\}}\odot \mathit{a}\left({\theta }_0\right)\right)+\sum _{m=0}^M{s}_m\left(k\right)·\left(\Delta {\mathit{a}}^{\left\{m\right\}}\odot \mathit{a}\left({\theta }_m\right)\right)+\mathit{n}\left(k\right)\hfill \end{array}$$

(8)

2.2.3. Gain-Phase Error in Channel

Because of variations in time and temperature, the gain-phase characteristics of the receiving sensors change accordingly [6,7]. The gain-phase error can be characterized, by a diagonal matrix, as    

$${\mathsf{\Xi }}_{GP}=\left[\begin{array}{cccc}{\gamma }_1& 0& \cdots & 0\\ 0& {\gamma }_2& \cdots & 0\\ 0& 0& \ddots & 0\\ 0& 0& \cdots & {\gamma }_N\end{array}\right]$$

(9)

where ${\gamma }_n={\alpha }_n$$exp\left(j{\beta }_n\right)$, and ${\alpha }_n$ and ${\beta }_n$ are the additional gain-phase errors of the n-th channel. When the gain-phase error exists in the receiving array, Equation (4) is actually written as

$$\begin{array}{cc}\hfill \tilde{\mathit{x}}\left(k\right)=& \tilde{\mathit{A}}\mathit{S}\left(k\right)+\mathit{n}\left(k\right)\hfill \\ \hfill =& s_0\left(k\right)\tilde{\mathit{a}}\left({\theta }_0\right)+\sum _{m=1}^M{s}_m\left(k\right)\tilde{\mathit{a}}\left({\theta }_m\right)+\mathit{n}\left(k\right)\hfill \\ \hfill =& s_0\left(k\right)·\left({\mathsf{\Xi }}_{GP}·\mathit{a}\left({\theta }_0\right)\right)+\sum _{m=0}^M{s}_m\left(k\right)·\left({\mathsf{\Xi }}_{GP}·\mathit{a}\left({\theta }_m\right)\right)+\mathit{n}\left(k\right)\hfill \end{array}$$

(10)

When all three kinds of errors detailed above exist in the array, the actual steering matrix $\tilde{\mathit{A}}$ can be calculated, as

$$f\left(\mathit{A},\mathsf{\Xi }\right)={\mathsf{\Xi }}_{MC}·{\mathsf{\Xi }}_{GP}·\left({\mathsf{\Xi }}_{SP}\odot \mathit{A}\right).$$

(11)

From the above analysis, it can be seen that SV mismatches are due to the array errors, which severely degrade the performance of beamforming methods. Furthermore, the SV mismatches that arise from mutual coupling are far larger than those of sensor position and gain-phase errors.

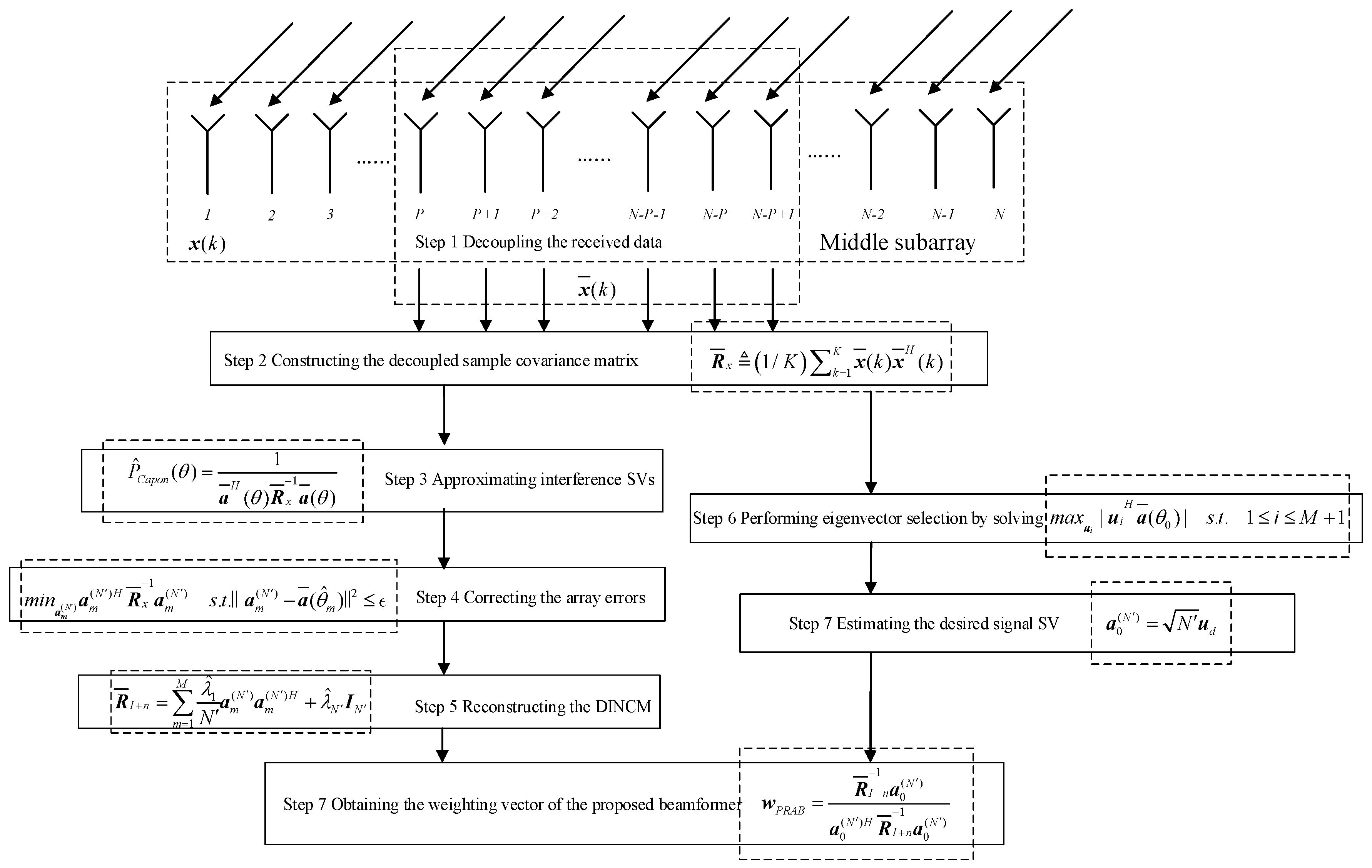
3. Proposed Robust Adaptive Beamforming Method

In this section, we propose a new beamforming method to effectively suppress the interferences and noise in the presence of multiple types of array errors. The DINCM is accurately reconstructed based on the constructed DSCM, together with the estimated desired signal SV, in order to form the proposed beamformer. The detailed procedures are as follows:

3.1. DSCM Construction Based on Sub-Array

When the three types of array errors that are introduced above coexist in the array, then the actual steering matrix $\tilde{\mathit{A}}$ can be calculated as $f\left(\mathit{A},\mathsf{\Xi }\right)={\mathsf{\Xi }}_{MC}·{\mathsf{\Xi }}_{GP}·\left({\mathsf{\Xi }}_{SP}\odot \mathit{A}\right)$. To begin with, the actual received data Equation (4) can be further modified as

$$\begin{array}{cc}\hfill \tilde{\mathit{x}}\left(k\right)=& \tilde{\mathit{A}}\mathit{S}\left(k\right)+\mathit{n}\left(k\right)\hfill \\ \hfill =& {\mathsf{\Xi }}_{MC}\widetilde{{\mathit{A}}^{\prime }}\mathit{S}\left(k\right)+\mathit{n}\left(k\right)\hfill \end{array}$$

(12)

where $\widetilde{{\mathit{A}}^{\prime }}={\mathsf{\Xi }}_{GP}·\left({\mathsf{\Xi }}_{SP}\odot \mathit{A}\right)$. The signal expression in Equation (12) can be viewed as an array with mutual coupling, with ideal steering matrix $\widetilde{{\mathit{A}}^{\prime }}=[\widetilde{{\mathit{a}}^{\prime }}\left({\theta }_0\right),\widetilde{{\mathit{a}}^{\prime }}\left({\theta }_1\right),\dots ,\widetilde{{\mathit{a}}^{\prime }}\left({\theta }_M\right)]$. Its elements have the form $\widetilde{{\mathit{a}}^{\prime }}\left({\theta }_m\right)={[\Delta b^{\left\{1\right\}}\left({\theta }_m\right),\Delta b^{\left\{2\right\}}\left({\theta }_m\right)·b\left({\theta }_m\right),\dots ,\Delta b^{\left\{N\right\}}\left({\theta }_m\right)·b{\left({\theta }_m\right)}^{N-1}]}^T$, where $\Delta b^{\left\{n\right\}}\left({\theta }_m\right)={\alpha }_n·\Delta a_m^{\left\{n\right\}}·\exp \left(j{\beta }_n\right)$. In order to mitigate the mutual coupling effect in the array $\widetilde{{\mathrm{Y}}^{\prime }}$, the $N-2P+2$ sensors in the middle are chosen as the sub-array. In this sense, the $P-1$ sensors in the front and end are used as auxiliary sensors [9]. For convenience, we use $N^{\prime }$ to represent $N-2P+2$ in the rest of this paper. Therefore, the data of the sub-array is selected as

$$\overline{\mathit{x}}\left(k\right)=\mathsf{\Gamma }\tilde{\mathit{x}}\left(k\right)=\mathsf{\Gamma }{\mathsf{\Xi }}_{MC}\widetilde{{\mathit{A}}^{\prime }}\mathit{S}\left(k\right)+\mathsf{\Gamma }\mathit{n}\left(k\right),$$

(13)

where $\mathsf{\Gamma }=\left[\mathit{O}{\mathit{I}}_{N^{\prime }}\mathit{O}\right]$ is the selective matrix, $\mathit{O}$ is an $N^{\prime }\times (P-1)$ matrix with all elements being zero. If we use $\widetilde{{\mathit{A}}^{″}}$ to denote $\mathsf{\Gamma }{\mathsf{\Xi }}_{MC}\widetilde{{\mathit{A}}^{\prime }}$, then $\widetilde{{\mathit{A}}^{″}}=[\widetilde{{\mathit{a}}^{″}}\left({\theta }_0\right),\widetilde{{\mathit{a}}^{″}}\left({\theta }_1\right),\dots ,\widetilde{{\mathit{a}}^{″}}\left({\theta }_M\right)]$, in which $\widetilde{{\mathit{a}}^{″}}\left({\theta }_m\right)$ is expressed as $\widetilde{{\mathit{a}}^{″}}\left({\theta }_m\right)=g\left({\theta }_m\right)·[\Delta b^{\left\{1\right\}}\left({\theta }_m\right),\Delta b^{\left\{2\right\}}\left({\theta }_m\right)·b\left({\theta }_m\right),\dots ,\Delta b^{\left\{N^{\prime }\right\}}\left({\theta }_m\right)·b{\left({\theta }_m\right)}^{N^{\prime }-1}]T$, where $g\left({\theta }_m\right)=1+{\sum }_{i=1}^{P-1}{c}_{i+1}\left({b^{\prime }\left({\theta }_m\right)}^{-i}+{b^{\prime }\left({\theta }_m\right)}^i\right)$ and $b^{\prime }\left({\theta }_m\right)=\Delta b^{\left\{2\right\}}\left({\theta }_m\right)·b\left({\theta }_m\right)$. It can be shown that the mutual coupling effect in the data is eliminated by multiplying the original data with the selection matrix. Therefore, the DSCM is constructed, as ${\widehat{\overline{\mathit{R}}}}_x\triangleq \left(1/K\right){\sum }_{k=1}^K\overline{\mathit{x}}\left(k\right){\overline{\mathit{x}}}^H\left(k\right)$.

3.2. Accurate DINCM Reconstruction

In [29], the researchers simply utilize the Capon spectrum to integrate in the interference region to reconstruct the INCM. However, this method is ineffective and it suffers severe performance degradation when multiple types of array errors exist, as shown in the simualtion part. To effectively form deep nulls in the interferences and noise, in this paper, we shall show how the DINCM is reconstructed in a improved way in order to achieve robustness to multiple type of errors. To begin with, the Capon spatial spectrum [30] is utilized to obtain an approximate estimate of the interference DOAs. The expression is given as

$${\widehat{P}}_{Capon}\left(\theta \right)=\frac{1}{{\overline{\mathit{a}}}^H\left(\theta \right){\widehat{\overline{\mathit{R}}}}_x^{-1}\overline{\mathit{a}}\left(\theta \right)},$$

(14)

where $\overline{\mathit{a}}\left({\theta }_m\right)={[1,b\left({\theta }_m\right),\dots ,b{\left({\theta }_m\right)}^{N^{\prime }-1}]}^T$. By searching in the complement sector of the desired signal region, the DOAs of the searched peaks ${\widehat{\theta }}_1,{\widehat{\theta }}_2,\dots ,{\widehat{\theta }}_M$ are utilized in order to obtain an approximate estimate of interference SV as $\overline{\mathit{a}}({\widehat{\theta }}_1),\overline{\mathit{a}}({\widehat{\theta }}_2),\dots ,\overline{\mathit{a}}({\widehat{\theta }}_M)$. As the SV mismatches due to gain-phase and sensor position errors are relatively small, the accuracy can be enhanced by correcting the SVs with the RCB principle. The correction processing for the m-th SV can be performed by solving

$$\underset{{\mathit{a}}_m^{\left(N^{\prime }\right)}}{min}{\mathit{a}}_m^{\left(N^{\prime }\right)H}{\widehat{\overline{\mathit{R}}}}_x^{-1}{\mathit{a}}_m^{\left(N^{\prime }\right)}s.t.{\parallel {\mathit{a}}_m^{\left(N^{\prime }\right)}-\overline{\mathit{a}}({\widehat{\theta }}_m)\parallel }^2\le ϵ,$$

(15)

where $ϵ$ is the uncertainty level, which indicates the extent of SV mismatches. Therefore, after solving M problems, the corrected SVs ${\left\{{\mathit{a}}_m^{\left(N^{\prime }\right)}\right\}}_{m=1}^M$ can be obtained. The solution of the m-th problem is given by ${\mathit{a}}_m^{\left(N^{\prime }\right)}=\overline{\mathit{a}}({\widehat{\theta }}_m)-{\left({\mathit{I}}_{N^{\prime }}+\delta {\widehat{\overline{\mathit{R}}}}_x\right)}^{-1}\overline{\mathit{a}}({\widehat{\theta }}_m)$, where $\delta$ is the Lagrange multiplier and it can be calculated by solving $\parallel {\left({\mathit{I}}_{N^{\prime }}+\delta {\widehat{\overline{\mathit{R}}}}_x\right)}^{-1}\overline{\mathit{a}}({\widehat{\theta }}_m){\parallel }^2=ϵ$. On the other hand, the power of the interferences can be approximated by the corresponding eigenvalue divided by the array size [28]. If we denote the eigendecomposition of DSCM as ${\widehat{\overline{\mathit{R}}}}_x={\sum }_{n=1}^{N^{\prime }}{\widehat{\lambda }}_n{\widehat{\mathit{u}}}_n{\widehat{\mathit{u}}}_n^H$, where ${\widehat{\lambda }}_1\ge {\widehat{\lambda }}_2\ge \cdots \ge {\widehat{\lambda }}_{N^{\prime }}$ are eigenvalues that are arranged in a descending order and ${\widehat{\mathit{u}}}_n$ corresponds to ${\widehat{\lambda }}_n$. Subsequently, in terms of the interference powers, they can be specifically estimated as

$${\sigma }_m^2\approx \frac{{\widehat{\lambda }}_m}{N},m=1,\dots ,$$

(16)

In practice, in order to make sure that the interference powers are not underestimated, the maximum power is used for all of the interference powers. The following estimate is derived

$${\sigma }_m^2\approx \frac{{\widehat{\lambda }}_1}{N},m=1,\dots ,$$

(17)

With the estimated power and SV of the interferences, the interference covariance matrix is reconstructed as

$${\widehat{\overline{\mathit{R}}}}_{I+n}=\sum _{m=1}^M\frac{{\widehat{\lambda }}_1}{N^{\prime }}{\mathit{a}}_m^{\left(N^{\prime }\right)}{\mathit{a}}_m^{\left(N^{\prime }\right)H}$$

(18)

On the other hand, using the minimum eigenvalue ${\widehat{\lambda }}_{N^{\prime }}$ as the estimate of noise power [31], the noise covariance matrix is reconstructed as

$${\widehat{\overline{\mathit{R}}}}_n={\widehat{\lambda }}_{N^{\prime }}{\mathit{I}}_{N^{\prime }}$$

(19)

Combining the above processes, the following DINCM reconstruction expression can be derived

$${\widehat{\overline{\mathit{R}}}}_{I+n}=\sum _{m=1}^M\frac{{\widehat{\lambda }}_1}{N^{\prime }}{\mathit{a}}_m^{\left(N^{\prime }\right)}{\mathit{a}}_m^{\left(N^{\prime }\right)H}+{\widehat{\lambda }}_{N^{\prime }}{\mathit{I}}_{N^{\prime }}.$$

(20)

3.3. Desired Signal SV Estimation

The SV of the desired signal can be replaced by the corresponding eigenvector, as the desired signal covariance matrix is rank one. The eigenvector that corresponds to the desired signal SV can be chosen by projecting the eigenvectors into the assumed SV (i.e., the correlation coefficient of the SV and the eigenvectors reaches the maximum when the eigenvector matches the SV) [32]. The correlation coefficient between the i-th eigenvector and assumed SV is defined as

$$cor({\widehat{\mathit{u}}}_i,\overline{\mathit{a}}\left({\theta }_0\right))=\frac{|{{\widehat{\mathit{u}}}_i}^H\overline{\mathit{a}}\left({\theta }_0\right)|}{\parallel {\widehat{\mathit{u}}}_i\parallel \parallel \overline{\mathit{a}}\left({\theta }_0\right)\parallel }$$

(21)

The correlation coefficient between ${\widehat{\mathit{u}}}_i$ and $\overline{\mathit{a}}\left({\theta }_0\right)$ reaches maximum when ${\widehat{\mathit{u}}}_i$ is the eigenvector that corresponds to the desired signal. Therefore, the desired signal SV is obtained as

$${\mathit{a}}_0^{\left(N^{\prime }\right)}=\sqrt{N^{\prime }}{\mathit{u}}_d,$$

(22)

where ${\mathit{u}}_d$ is the solution to the problem

$$\underset{{\widehat{\mathit{u}}}_i}{max}|{{\widehat{\mathit{u}}}_i}^H\overline{\mathit{a}}\left({\theta }_0\right)|s.t.1\le i\le M+1.$$

(23)

By replacing the theoretical DINCM and SV of desired signal with ${\widehat{\overline{\mathit{R}}}}_{I+n}$ and ${\mathit{a}}_0^{\left(N^{\prime }\right)}$, the proposed beamformer is given as

$${\mathit{w}}_{PRAB}=\frac{{\widehat{\overline{\mathit{R}}}}_{I+n}^{-1}{\mathit{a}}_0^{\left(N^{\prime }\right)}}{{\mathit{a}}_0^{\left(N^{\prime }\right)H}{\widehat{\overline{\mathit{R}}}}_{I+n}^{-1}{\mathit{a}}_0^{\left(N^{\prime }\right)}}.$$

(24)

By applying the weighting vector ${\mathit{w}}_{PRAB}$ to the beamformer, the received data can be processed in order to effectively suppress the interference and noise. Specifically, the output of the beamformer at instant k is given as

$${\mathbf{y}}_{out}\left(k\right)={\mathit{w}}_{PRAB}^H\overline{\mathit{x}}\left(k\right).$$

(25)

The main complexity of our proposed method lies in the interference SV estimation and DSCM eigendecomposition. Let us define J as the number of search points in the Capon spectrum, and then the computational complexity of the interference SV estimation and DSCM eigendecomposition are about $\mathcal{O}\left(N^{\prime 3}+N^{\prime 2}J+N^{\prime 2}K\right)$ and $\mathcal{O}\left(N^{\prime 3}\right)$, in terms of the number of flops, respectively. When considering the fact that $J>K>N^{\prime }$, the above complexity actually becomes $\mathcal{O}\left(N^{\prime 2}J\right)$. Therefore, the overall complexity of the proposed approach is about $\mathcal{O}\left(N^{\prime 2}J\right)$. Algorithm 1 summarizes the proposed method. An additional flow chart figure of the proposed method is provided in Figure 2, where the application of sub-array technique is presented in a clearer way.

Algorithm 1 Steps of the proposed robust adaptive beamforming method

Part 1. DSCM construction based on sub-array

1. Decoupling the received data as $\overline{\mathit{x}}\left(k\right)=\mathsf{\Gamma }\tilde{\mathit{x}}\left(k\right)=\mathsf{\Gamma }{\mathsf{\Xi }}_{MC}\widetilde{{\mathit{A}}^{\prime }}\mathit{S}\left(k\right)+\mathsf{\Gamma }\mathit{n}\left(k\right)$.

2. Constructing the DSCM as ${\widehat{\overline{\mathit{R}}}}_x\triangleq \left(1/K\right){\sum }_{k=1}^K\overline{\mathit{x}}\left(k\right){\overline{\mathit{x}}}^H\left(k\right)$.

Part 2. Accurate DINCM reconstruction

3. Obtaining approximate estimates of the interference SVs utilizing the Capon spectrum as $\overline{\mathit{a}}({\widehat{\theta }}_1),\overline{\mathit{a}}({\widehat{\theta }}_2),\dots ,\overline{\mathit{a}}({\widehat{\theta }}_M)$.

4. Correcting the interference SVs with RCB principle and obtaining the corrected SVs ${\left\{{\mathit{a}}_m^{\left(N^{\prime }\right)}\right\}}_{m=1}^M$.

5. Eigendecomposing the DSCM as ${\widehat{\overline{\mathit{R}}}}_x={\sum }_{n=1}^{N^{\prime }}{\widehat{\lambda }}_n{\widehat{\mathit{u}}}_n{\widehat{\mathit{u}}}_n^H$ and reconstructing the DINCM as ${\widehat{\overline{\mathit{R}}}}_{I+n}={\sum }_{m=1}^M\frac{{\widehat{\lambda }}_1}{N^{\prime }}{\mathit{a}}_m^{\left(N^{\prime }\right)}{\mathit{a}}_m^{\left(N^{\prime }\right)H}+{\widehat{\lambda }}_{N^{\prime }}{\mathit{I}}_{N^{\prime }}$.

Part 3. Desired signal SV estimation

6. Choosing out the eigenvector of ${\widehat{\overline{\mathit{R}}}}_x$ maximizes the projection into the assumed SV by solving ${max}_{{\widehat{\mathit{u}}}_i}|{{\widehat{\mathit{u}}}_i}^H\overline{\mathit{a}}\left({\theta }_0\right)|s.t.1\le i\le M+1$.

7. Obtaining the desired signal SV as ${\mathit{a}}_0^{\left(N^{\prime }\right)}=\sqrt{N^{\prime }}{\mathit{u}}_d$.

Final Calculating the weighting vector ${\mathit{w}}_{PRAB}=\frac{{\widehat{\overline{\mathit{R}}}}_{I+n}^{-1}{\mathit{a}}_0^{\left(N^{\prime }\right)}}{{\mathit{a}}_0^{\left(N^{\prime }\right)H}{\widehat{\overline{\mathit{R}}}}_{I+n}^{-1}{\mathit{a}}_0^{\left(N^{\prime }\right)}}.$

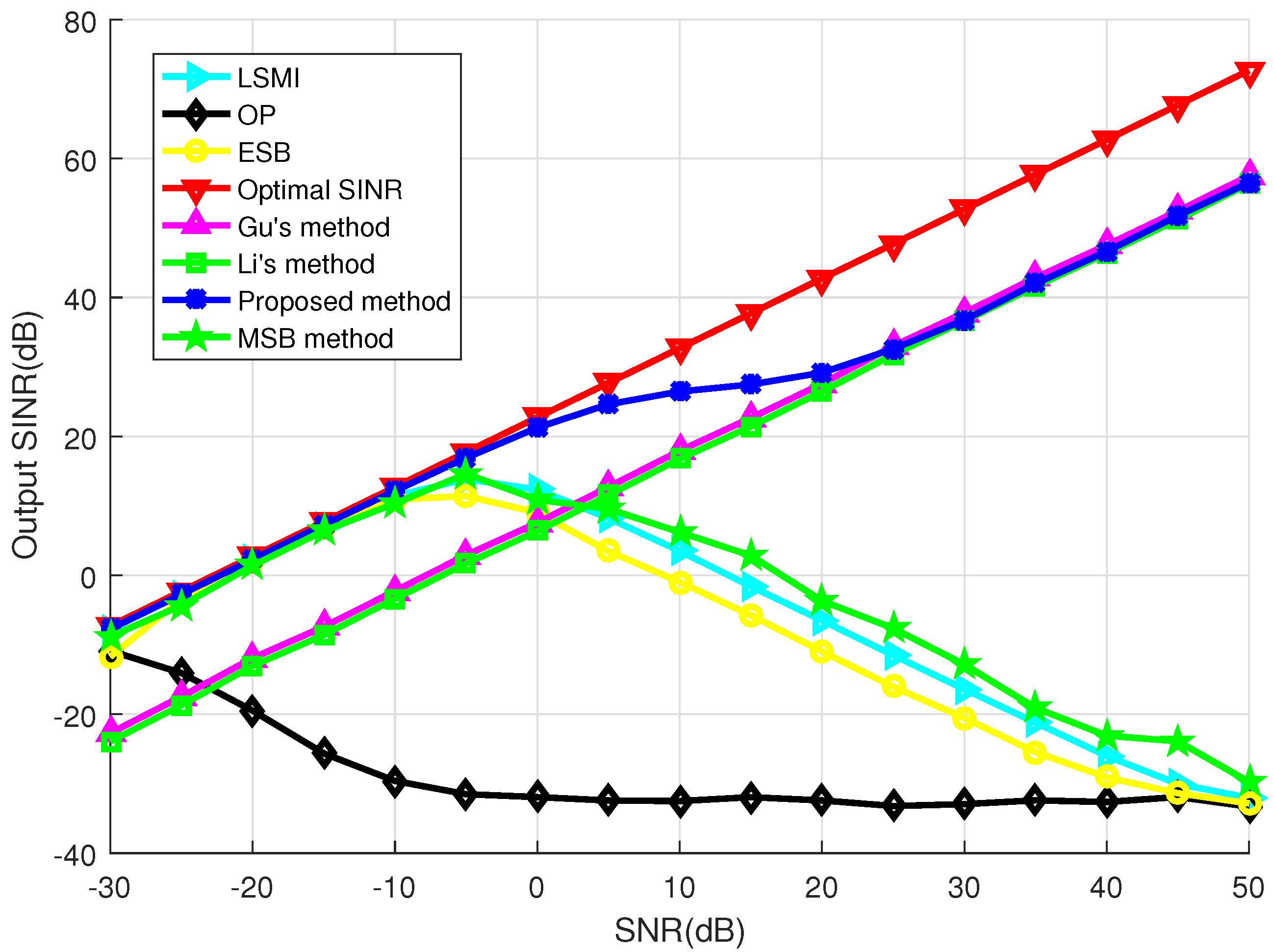
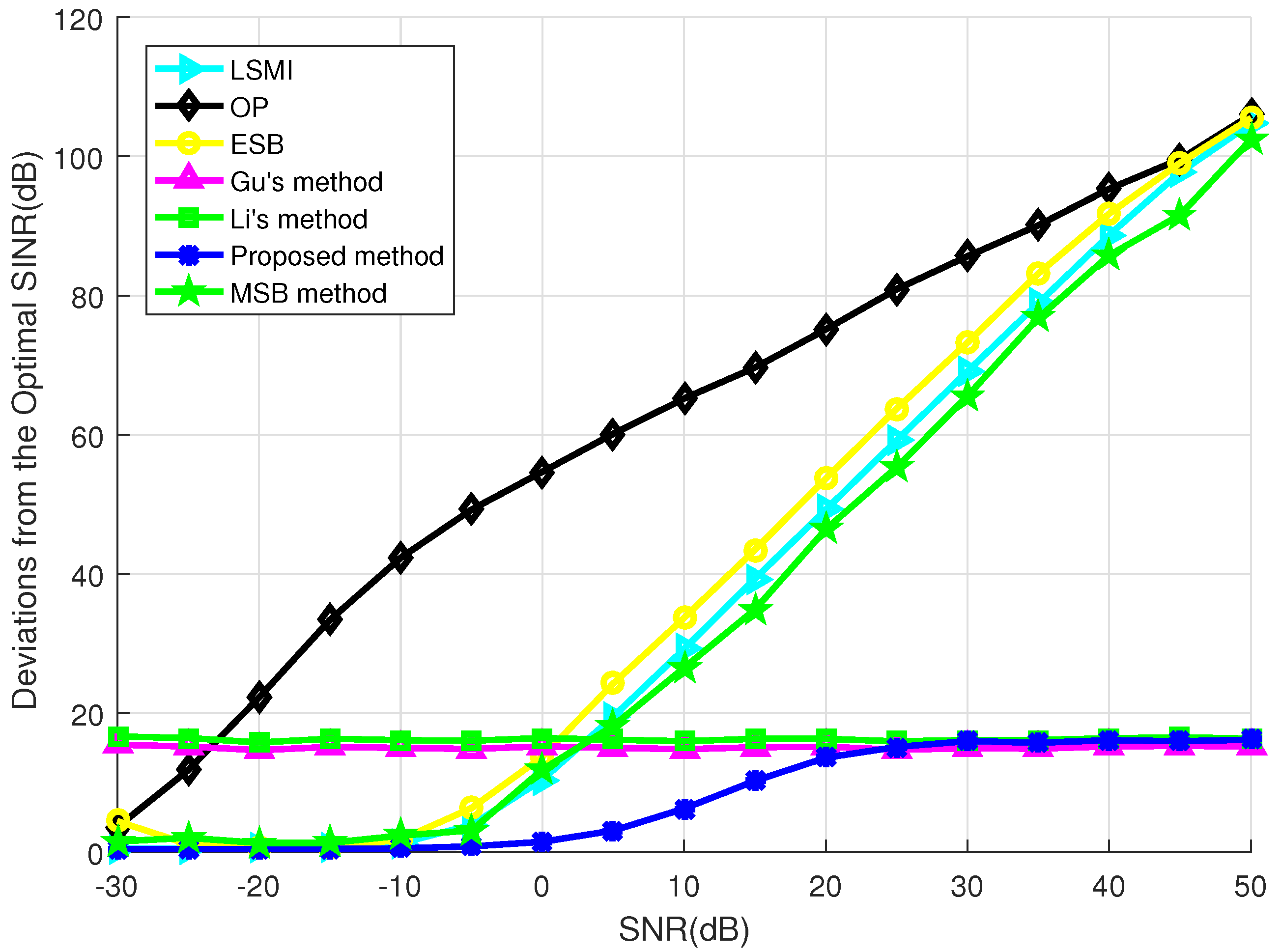
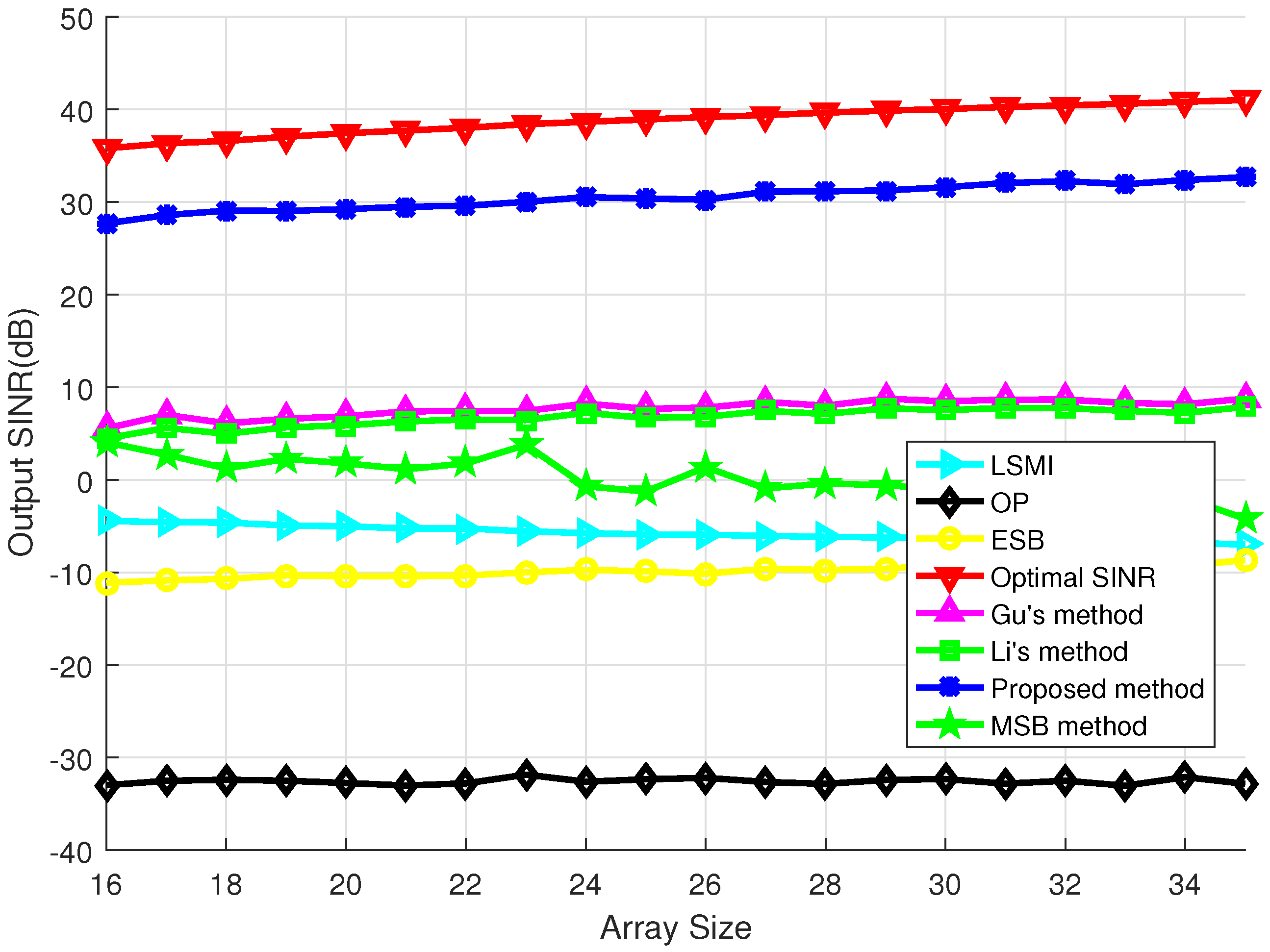
4. Simulation Results

A ULA with 28 receiving sensors with half-wavelength inter-element spacing was deployed in the considered scenario. Two interferences were assumed from DOAs of $-{50}^{\circ }$ and ${32}^{\circ }$ with INR 20 dB, while the desired signal was pointed with a DOA of $0^{\circ }$. The additive noise was set to be white Gaussian noise with unit variance.

The simulation considered all three types of array model errors. The sensor position error satisfied the normal distribution $N(d,{\left(0.025\right)}^2)$. The gain-phase error followed the normal distributions $N(1,0.1^2)$ and $N(0,{\left(5^{\circ }\right)}^2)$, respectively. $P=4$ mutual coupling was considered in the scene and $c_1=1.65{\mathrm{e}}^{-j\pi /3}$, $c_2=2.35{\mathrm{e}}^{j\pi /2}$, and $c_3=0.25{\mathrm{e}}^{-j2\pi /5}$.

We compared the proposed method with the diagonal loading sample matrix inversion (LSMI) method, middle sub-array based (MSB) beamformer [9] method, orthogonal projection (OP) approach, eigenspace-based (ESB) beamformer method, optimal beamformer method, Li’s method [29], and the reconstruction method by Gu [25]. For the proposed beamformer, the RCB uncertainty extent was set as $ϵ=2$. For Gu’s beamformer (introduced in [25]), Li’s method [29], and our proposed beamformer, the desired signal sector was set as $\Theta =\left[-5^{\circ },5^{\circ }\right]$, while the complement sector for the interferences was $\overline{\Theta }=[-{90}^{\circ },-5^{\circ })\cup (5^{\circ },{90}^{\circ }]$.

The output SINR curves versus the SNR were investigated (with the number of snapshots $K=500$), as shown in Figure 3. The results clearly show the superiority of the proposed method, which outperformed the others at all SNRs. It is worth noting that the Gu’s method is parallel to Optimal SINR method at all SNRs. This is because the deviation between the assumed and real SV structure is determined by the DOA and, therefore, once the DOA distribution of the interferences is set, the deviation between the Gu’s method and the optimal is stable at all SNRs. Specifically, when there is no array error, the output SINR of Gu’s method can be very close to the optimal. Similarly, Li’s method is also parallel to the optimal, since the same INCM reconstruction process is involved. While Gu’s method is superior to Li’s method, this is due to the array aperture loss in Li’s method degrading its performance.

The output SINR of our method is close to the optimal result at low SNRs and outperformed all of the other methods at high SNRs. At low SNRs, the mismatches of the steering vector bring significant influence to the output SINR. The proposed method is able to attain the optimal due to the SV correcting process. It should be noted that, at high SNRs, the performance improvement of the proposed method over other methods decreases, but it still enjoyed the best performance. The proposed method gradually converges to Gu’s method at high SNRs. Because, at high input SNRs, the performance increase that arises from the SV correction process gradually decreases, as the higher input SNR is the more important factor for improving the output SINR, rather than the correcting process.

In Figure 4, the gap between the optimal SINR and beamformers are depicted in curves. The deviations from the optimal SINR versus the input SNR can be clearly observed. It can be observed that the proposed method showed similar performance at high SNRs to Gu’s method, and it achieved about 18 dB higher at low input SNRs. In terms of Gu’s method, its performance was stable, retaining a deviation of about 17 dB from optimal performance. The proposed method achieved fast convergence, while the other beamformers showed slow convergence.

With the SNR set at 0 dB, the output SINR versus the number of snapshots is plotted in Figure 5. The depicted curves illustrate the superiority of the proposed method; it was very close to optimal. It can be observed that the proposed method was not sensitive to the number of snapshots and it showed almost the same convergence rate as the optimal beamformer, with the performance improving slightly with an increase of the number of snapshots.

In the last example, we further investigated the influence of the array aperture on the performance of beamformers. We explored the output SINR curves of different methods with the array length varying from 16 to 35 and the input SNR fixed at 0 dB. Figure 6 clearly shows that, as the array aperture gets larger, the output SINR of the proposed method gets better accordingly. It is also noted that the output SINR of Gu’s method as well as the Li’s method gets slightly higher with the larger array aperture. The array length reflects the array sampling ability of the signals in the spatial domain. When the array aperture gets larger, the spatial solution of the array gets better and it can more effectively form nulls at the directions that correspond to the interferences. On the other hand, in terms of some other methods, as the solution of the array gets more precise, the mismatches of steering vector become increasingly obvious and degrade the performance more. Therefore, the performance of some methods are slightly getting worse.

5. Conclusions

This paper introduced a new robust adaptive beamforming method, which is robust to the sensor position, gain-phase, and mutual coupling errors. In the proposed method, the mutual coupling effect is mitigated while using the sub-array technique, where the DINCM is reconstructed by combining the corrected SVs and maximum eigenvalue of the DSCM. Moreover, the desired signal SV is obtained using the matched eigenvector. The proposed method is capable of simultaneously dealing with multiple types of array errors. Our simulation results validated the superiority of the proposed method over existing methods in the presence of multiple types of array errors.