Resonant Forcing of the Climate System in Subharmonic Modes
Abstract
1. Introduction
2. Method
2.1. GRWs and Surface Temperature
2.2. Subharmonic Modes
2.3. Positive Feedback Loop
3. Data
4. Wavelet Analysis
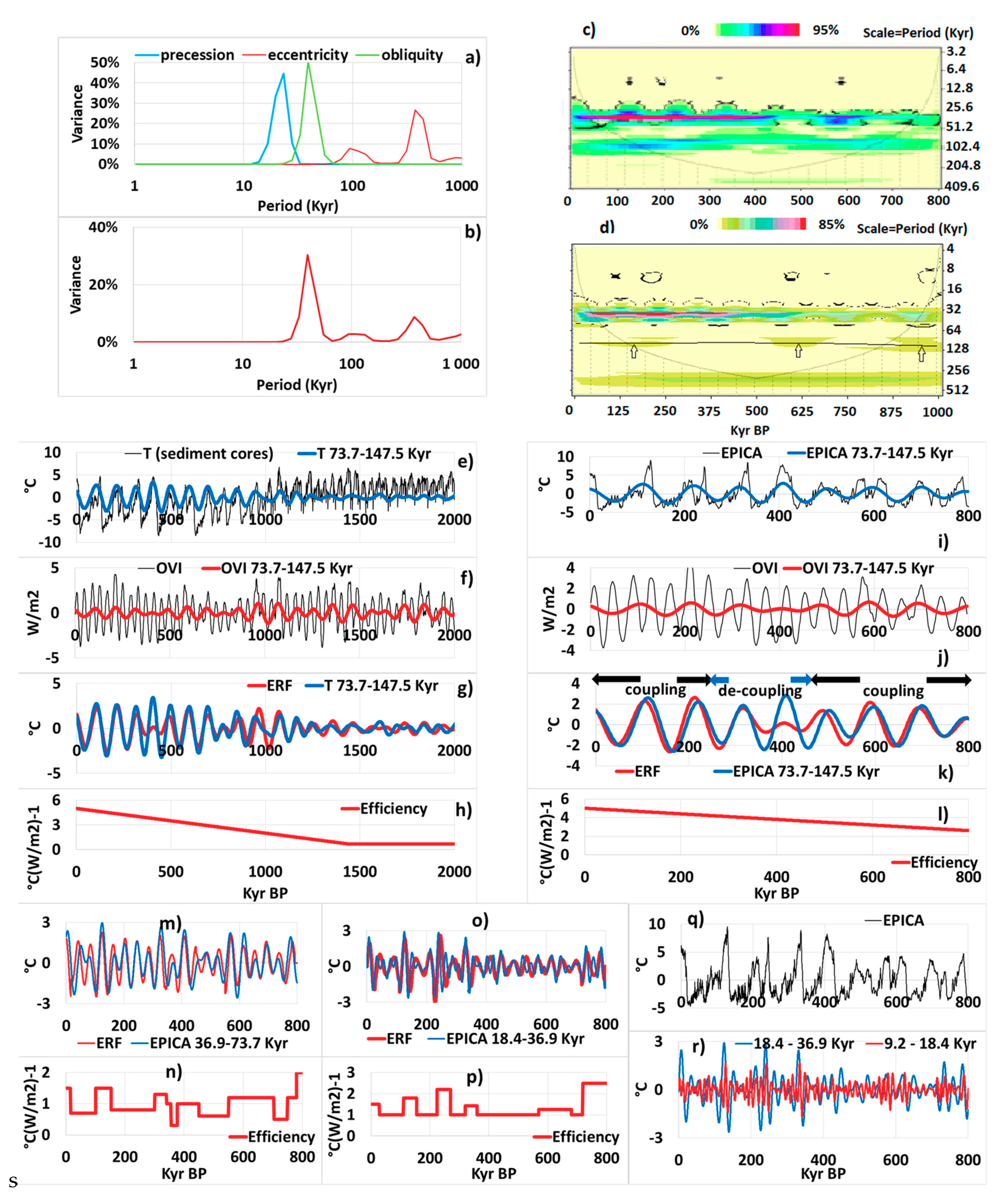
5. Results
5.1. The Glacial-Interglacial Period
5.1.1. The 73.7–147.5 Kyr Band
5.1.2. The 36.9–73.7 Kyr Band
5.1.3. The 18.4–36.9 Kyr Band
5.1.4. The 2.3–4.6, 4.6–9.2 and 9.2–18.4 Kyr Bands
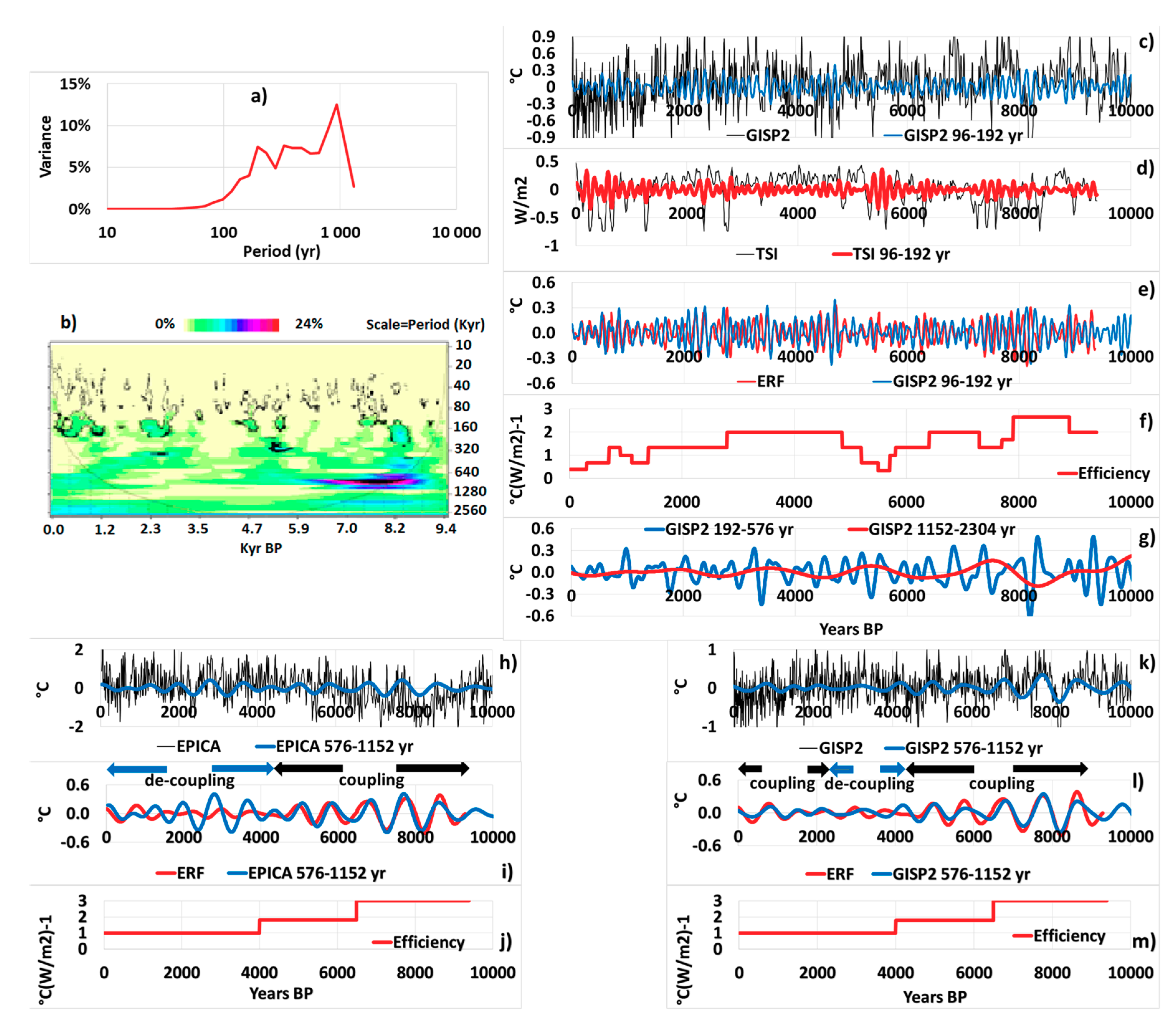
5.2. The Holocene
5.2.1. The 576–1152 yr Band
5.2.2. The 1152–2304 and 192–576 yr Bands
5.2.3. The 96–192 yr Band
6. Discussion
- (1)
- Concerning the transition problem [35,36,37,38,39,40], the abrupt change in the dominant subharmonic mode during the Pleistocene, namely , when the forcing period was ruled by the obliquity results from the variation in the forcing period ruled by the eccentricity [8] (Figure 1d) while getting very close to the natural period according to the subharmonic mode. The transition that occurred 0.8 million years ago supposes a 2°30′ equatorward drift of the latitude of the centroid of the gyres to adjust to the new dominant subharmonic mode.
- (2)
- With regard to the first half of the Holocene sudden cooling always arise during the cooling phase of the 768-yr period GRW according to the subharmonic mode both in the GISP2 and the EPICA data. Nevertheless, cooling arises very rapidly in the North Atlantic but more slowly in the southern hemisphere. The most striking sudden cooling event occurs 8200 yrs BP [41] as benefiting both from the advance of the polar front during the early Holocene, and a large magnitude solar irradiance into the 576–1152 yr band. Although having the most acuity in the North Atlantic, sudden cooling turns out to be ubiquitous, implying all subtropical gyres. The rapidity of both the cooling and the warming that follows involves the SST at high latitudes of the gyres where the climate is most impacted. This suggests a phenomenon of inversion of the stratification of the mixed layer, which supposes a sudden rise to the surface of cold waters with low salinity. This assumption is all the more plausible as the cooling occurs while the modulated polar current is cyclonic. So, cold waters at high latitudes of the gyres are mainly fed by the melting of the polar caps. The current resurfaces while being renewed with sea water warmer although more salty, which occurs after a few decades.
Funding
Acknowledgments
Conflicts of Interest
Data Availability
References
- Hays, J.D.; Imbrie, J.; Shackleton, N. Variations in the Earth’s Orbit: Pacemaker of the Ice Ages. Science 1976, 194, 1121–1132. [Google Scholar] [CrossRef]
- Bond, G.; Kromer, B.; Beer, J.; Muscheler, R.; Evans, M.N.; Showers, W.; Hoffmann, S.; Lotti-Bond, R.; Hajdas, I.; Bonani, G. Persistent Solar Influence on North Atlantic Climate During the Holocene. Science 2001, 294, 2130–2136. [Google Scholar] [CrossRef]
- Chambers, F.M.; Ogel, M.I.; Blavkford, J.J. Palaeoenvironmental evidence for solar forcing of Holocene climate: Linkages to solar science. Prog. Phys. Geogr. 1999, 23, 181–204. [Google Scholar] [CrossRef]
- Gavin, D.G.; Henderson, A.C.G.; Westover, K.S.; Fritz, S.C.; Walker, I.R.; Leng, M.J.; Hu, F.S. Abrupt Holocene climate change and potential response to solar forcing in western Canada. Quat. Sci. Rev. 2011, 30, 1243–1255. [Google Scholar] [CrossRef]
- Karlén, W.; Kuylenstierna, J. On solar forcing of Holocene climate: Evidence from Scandinavia. Holocene 1996, 6, 359–365. [Google Scholar] [CrossRef]
- Magny, M. Solar Influences on Holocene Climatic Changes Illustrated by Correlations between Past Lake-Level Fluctuations and the Atmospheric 14C Record. Quat. Res. 1993, 40, 1–9. [Google Scholar] [CrossRef]
- Nicolis, C. Self-oscillations and predictability in climate dynamics-periodic forcing and phase locking. Tellus 1984, 36, 217–227. [Google Scholar]
- Pinault, J.-L. Modulated Response of Subtropical Gyres: Positive Feedback Loop, Subharmonic Modes, Resonant Solar and Orbital Forcing. J. Mar. Sci. Eng. 2018, 6, 107. [Google Scholar] [CrossRef]
- Jacobs, G.A.; Hurlburt, H.E.; Kindle, J.C.; Metzger, E.J.; Mitchell, J.L.; Teague, W.J.; Wallcraft, A.J.; Jacobs, H.E.H.G.A. Decade-scale trans-Pacific propagation and warming effects of an El Niño anomaly. Nature 1994, 370, 360–363. [Google Scholar] [CrossRef]
- Xie, S.-P.; Hu, K.; Hafner, J.; Tokinaga, H.; Du, Y.; Huang, G.; Sampe, T. Indian Ocean Capacitor Effect on Indo–Western Pacific Climate during the Summer following El Niño. J. Clim. 2009, 22, 730–747. [Google Scholar] [CrossRef]
- Jury, M.R.; Huang, B. The Rossby wave as a key mechanism of Indian Ocean climate variability. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2004, 51, 2123–2136. [Google Scholar] [CrossRef]
- Huang, B.; Kinter, J.L., III. Inter-annual variability in the tropical Indian Ocean. J. Geophys. Res. 2002, 107, 3199–3229. [Google Scholar] [CrossRef]
- Schneider, N.; Miller, A.J. Predicting Western North Pacific Ocean Climate. J. Clim. 2001, 14, 3997–4002. [Google Scholar] [CrossRef]
- Pinault, J.-L. Regions Subject to Rainfall Oscillation in the 5–10 Year Band. Climate 2018, 6, 2. [Google Scholar] [CrossRef]
- Choi, M.Y.; Thouless, D.J. Topological interpretation of subharmonic mode locking in coupled oscillators with inertia. Phys. Rev. B 2001, 64. [Google Scholar] [CrossRef]
- Suarez, M.J.; Schopf, P.S. A Delayed Action Oscillator for ENSO. J. Atmospheric Sci. 1988, 45, 3283–3287. [Google Scholar] [CrossRef]
- Minobe, S.; Jin, F. Generation of interannual and interdecadal climate oscillations through nonlinear subharmonic resonance in delayed oscillators. Geophys. Res. Lett. 2004, 31, L16206. [Google Scholar] [CrossRef]
- Pinault, J.-L. Anthropogenic and Natural Radiative Forcing: Positive Feedbacks. J. Mar. Sci. Eng. 2018, 6, 146. [Google Scholar] [CrossRef]
- Pinault, J.-L. Resonantly Forced Baroclinic Waves in the Oceans: Subharmonic Modes. J. Mar. Sci. Eng. 2018, 6, 78. [Google Scholar] [CrossRef]
- Pinault, J.-L. Long Wave Resonance in Tropical Oceans and Implications on Climate: The Atlantic Ocean. Pure Appl. Geophys. 2013, 170, 1913–1930. [Google Scholar] [CrossRef]
- Pinault, J.-L. Long Wave Resonance in Tropical Oceans and Implications on Climate: The Pacific Ocean. Pure Appl. Geophys. 2015. [Google Scholar] [CrossRef]
- Pinault, J.-L. The Anticipation of the ENSO: What Resonantly Forced Baroclinic Waves Can Teach Us (Part II). J. Mar. Sci. Eng. 2018, 6, 63. [Google Scholar] [CrossRef]
- Explain with Realism Climate Variability. Available online: http://climatorealist.neowordpress.fr/longperiod-gyral-waves/ (accessed on 2 August 2019).
- Lisiecki, L.E.; Raymo, M.E. LR04 Global Pliocene-Pleistocene Benthic d18O Stack; IGBP PAGES/World Data Center for Paleoclimatology Data Contribution Series #2005-008; NOAA/NGDC Paleoclimatology Program: Boulder, CO, USA, 2005. [Google Scholar]
- Jouzel, J.; Masson-Delmotte, V.; Cattani, O.; Dreyfus, G.; Falourd, S.; Hoffmann, G.; Minster, B.; Nouet, J.; Barnola, J.M.; Chappellaz, J.; et al. Orbital and Millennial Antarctic Climate Variability over the Past 800,000 Years. Science 2007, 317, 793–796. [Google Scholar] [CrossRef] [PubMed]
- Grootes, P.M.; Stuiver, M. Oxygen 18/16 variability in Greenland snow and ice with 10−3- to 105-year time resolution. J. Geophys. Res. Space Phys. 1997, 102, 26455–26470. [Google Scholar] [CrossRef]
- Jouzel, J.; Merlivat, L. Deuterium and oxygen 18 in precipitation: Modeling of the isotopic effects during snow formation. J. Geophys. Res. Space Phys. 1984, 89, 11749–11757. [Google Scholar] [CrossRef]
- Steinhilber, F.; Abreu, J.A.; Beer, J.; Brunner, I.; Christl, M.; Fischer, H.; Heikkilä, U.; Kubik, P.W.; Mann, M.; McCracken, K.G.; et al. 9400 Year Cosmogenic Isotope Data and Solar Activity Reconstruction; IGBP PAGES/World Data Center for Paleoclimatology Data Contribution Series # 2012-040; NOAA/NCDC Paleoclimatology Program: Boulder, CO, USA, 2012. Available online: ftp://ftp.ncdc.noaa.gov/pub/data/paleo/climate_forcing/solar_variability/steinhilber2012.txt (accessed on 19 September 2018).
- Berger, A. Orbital Variations and Insolation Database; IGBP PAGES/World Data Center for Paleoclimatology Data Contribution Series # 92-007; NOAA/NGDC Paleoclimatology Program: Boulder, CO, USA, 1992. [Google Scholar]
- Torrence, C.; Compo, G.P. A practical guide for wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Davis, B.A.S.; Mauri, A.; Brewer, S.; Gajewski, K.J.; Kühl, N.; Viau, A.E.; Wu, H.; Kaplan, J.O. The Equable Climate Problem During Interglacial Warming. 2011. Available online: http://adsabs.harvard.edu/abs/2011AGUFMPP13B1830D (accessed on 20 January 2020).
- Davis, B.A.S.; Brewer, S. Orbital forcing and role of the latitudinal nsolation/temperature gradient. Clim. Dyn. 2009, 32, 143–165. [Google Scholar] [CrossRef]
- Münch, T.; Laepple, T. What climate signal is contained in decadal- to centennial-scale isotope variations from Antarctic ice cores? Clim. Past 2018, 14, 2053–2070. [Google Scholar] [CrossRef]
- Rehfeld, K.; Münch, T.; Ho, S.L.; Laepple, T. Global patterns of declining temperature variability from the Last Glacial Maximum to the Holocene. Nature 2018, 554, 356–359. [Google Scholar] [CrossRef]
- Raymo, M.E.; Nisancioglu, K.H. The 41 kyr world: Milankovitch’s other unsolved mystery. Paleoceanography 2003, 18. [Google Scholar] [CrossRef]
- Maslin, M.A.; Ridgwell, A.J. Mid-Pleistocene revolution and the ‘eccentricity myth’. Geol. Soc. Lond. Spéc. Publ. 2005, 247, 19–34. [Google Scholar] [CrossRef]
- Clark, P.U.; Archer, D.; Pollard, D.; Blum, J.D.; Rial, J.A.; Brovkin, V.; Mix, A.C.; Pisias, N.G.; Roy, M. The middle Pleistocene transition: characteristics, mechanisms, and implications for long-term changes in atmospheric pCO2. Quat. Sci. Rev. 2006, 25, 3150–3184. [Google Scholar] [CrossRef]
- Chalk, T.B.; Hain, M.P.; Foster, G.L.; Rohling, E.J.; Sexton, P.F.; Badger, M.P.S.; Cherry, S.G.; Hasenfratz, A.P.; Haug, G.H.; Jaccard, S.L.; et al. Causes of ice age intensification across the Mid-Pleistocene Transition. Proc. Natl. Acad. Sci. USA 2017, 114, 13114–13119. [Google Scholar] [CrossRef] [PubMed]
- Denton, G.H.; Anderson, R.F.; Toggweiler, J.R.; Edwards, R.L.; Schaefer, J.M.; Putnam, A.E. The Last Glacial Termination. Science 2010, 328, 1652–1656. [Google Scholar] [CrossRef] [PubMed]
- Bol’Shakov, V.A. On the mechanism of the Middle Pleistocene Transition. Strat. Geol. Correl. 2015, 23, 536–550. [Google Scholar] [CrossRef]
- Björck, S.; Kromer, B.; Johnsen, S.; Bennike, O.; Hammarlund, D.; Lemdahl, G.; Possnert, G.; Rasmussen, T.L.; Wohlfarth, B.; Hammer, C.U.; et al. Synchronized TerrestrialAtmospheric Deglacial Records Around the North Atlantic. Science 1996, 274, 1155–1160. [Google Scholar] [CrossRef]
| Band Width (yr) | Period of Resonance (yr) | Subharmonic Mode in the Atlantic | Forcing Mode |
|---|---|---|---|
| 48–96 | 64 | No external forcing [18] | |
| 96–192 | 128 | Solar forcing (Gleissberg cycle) | |
| 192–576 | 256 | No external forcing | |
| 576–1152 | 768 | Solar forcing | |
| 1152–2304 | 1536 | No external forcing | |
| 2304–4608 | 3072 | No external forcing | |
| 4608–9216 | 6144 | No external forcing | |
| 9216–18,432 | 12,288 | No external forcing | |
| 18,432–36,864 | 24,576 | Orbital forcing (Precession) | |
| 36,864–73,728 | 49,152 | Orbital forcing (Obliquity) | |
| 73,728–14,7456 | 98,304 | Orbital forcing (Eccentricity) |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinault, J.-L. Resonant Forcing of the Climate System in Subharmonic Modes. J. Mar. Sci. Eng. 2020, 8, 60. https://doi.org/10.3390/jmse8010060
Pinault J-L. Resonant Forcing of the Climate System in Subharmonic Modes. Journal of Marine Science and Engineering. 2020; 8(1):60. https://doi.org/10.3390/jmse8010060
Chicago/Turabian StylePinault, Jean-Louis. 2020. "Resonant Forcing of the Climate System in Subharmonic Modes" Journal of Marine Science and Engineering 8, no. 1: 60. https://doi.org/10.3390/jmse8010060
APA StylePinault, J.-L. (2020). Resonant Forcing of the Climate System in Subharmonic Modes. Journal of Marine Science and Engineering, 8(1), 60. https://doi.org/10.3390/jmse8010060





